Structural Optimization and Simulation of Dual-Frequency Piezoelectric Micromachined Ultrasonic Transducers
Abstract
1. Introduction
2. Structural Design and Simulation
2.1. Structural Design of Sensors
2.2. Equivalent Circuit Model and Finite Element Modeling
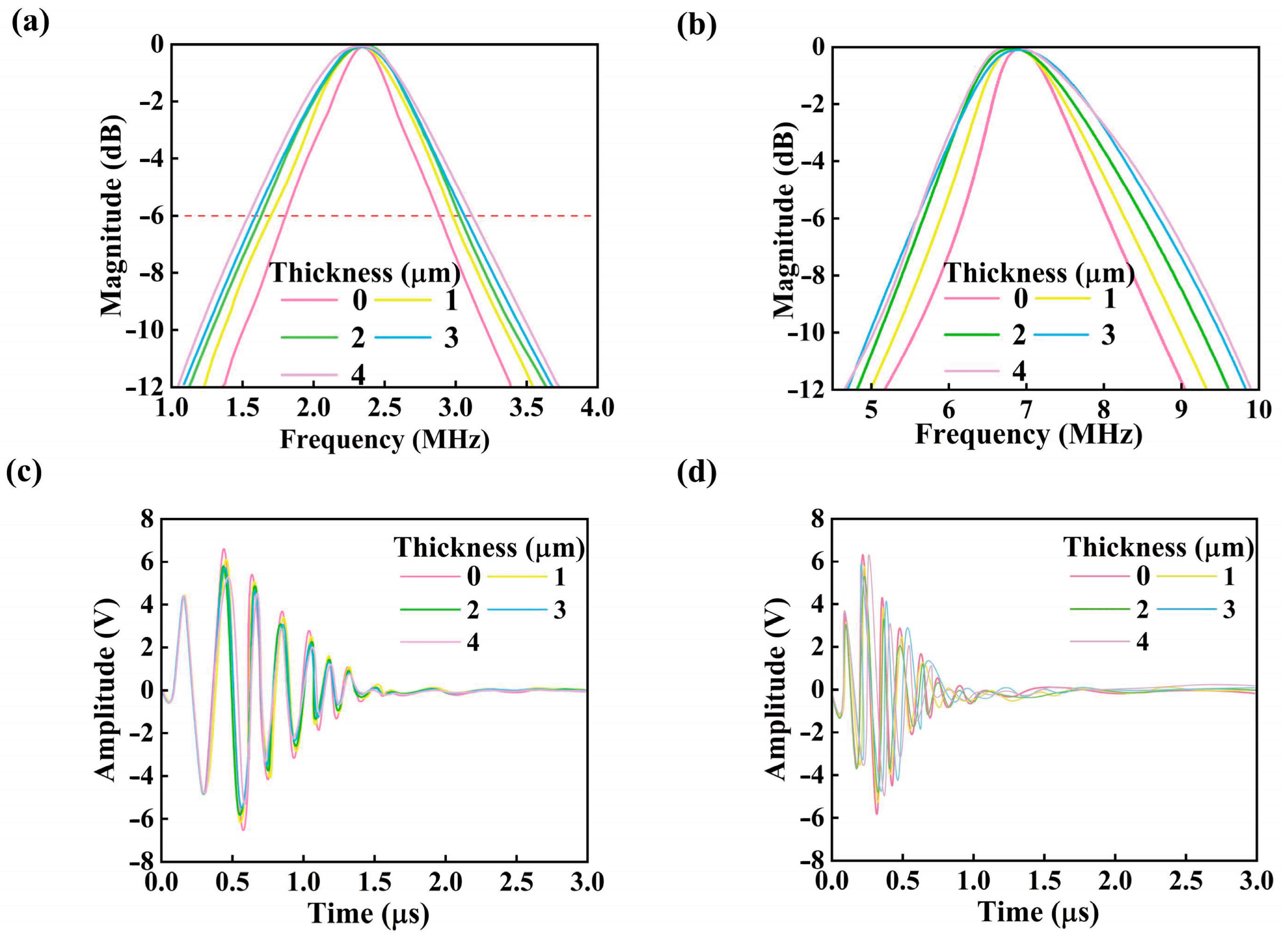
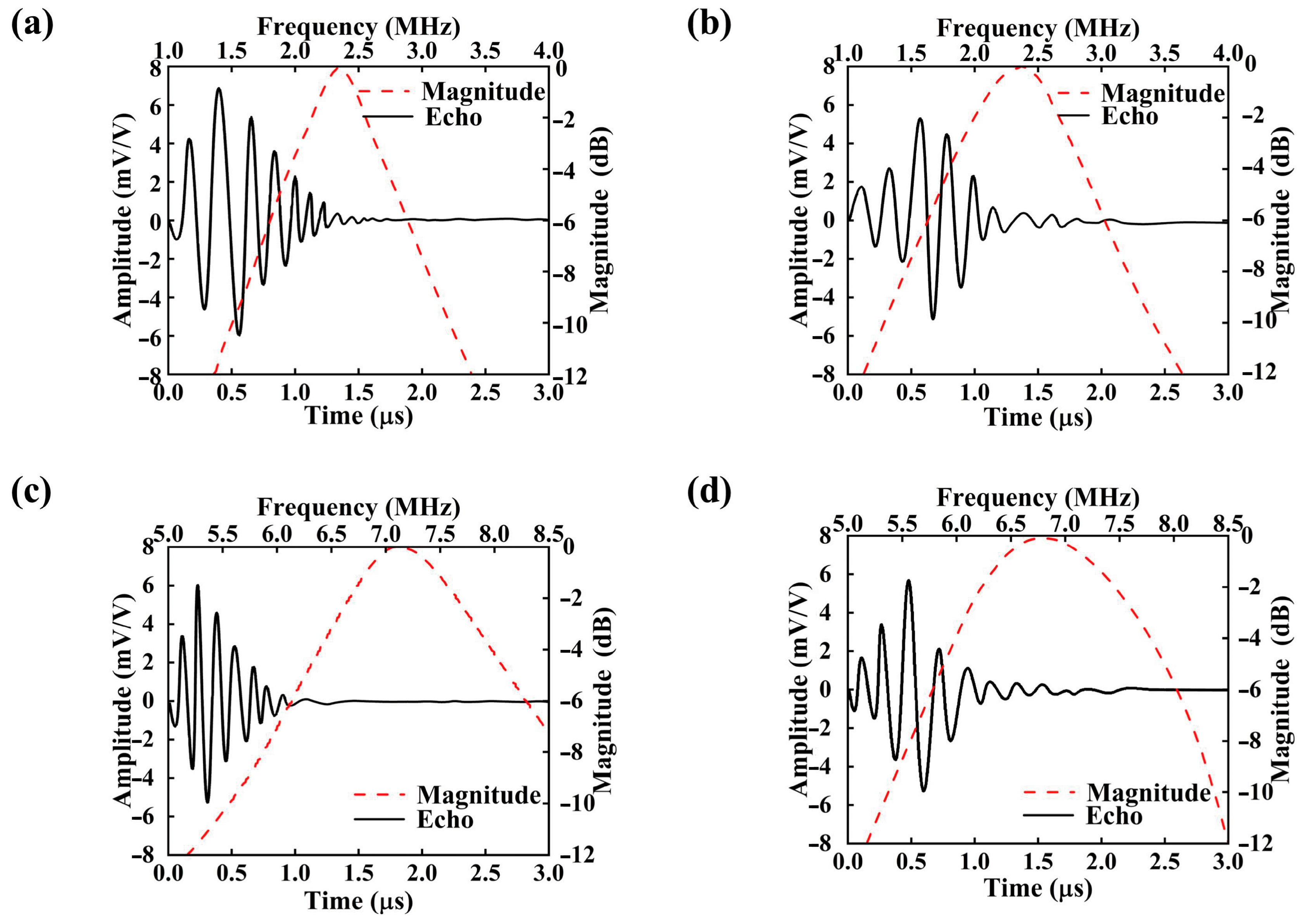
3. Simulation Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Swets, J.A. Measuring the accuracy of diagnostic systems. Science 1988, 240, 1285–1293. [Google Scholar] [CrossRef]
- Morris, P.; Perkins, A. Diagnostic imaging. Lancet 2012, 379, 1525–1533. [Google Scholar] [CrossRef]
- Su, M.; Dai, Q.; Chen, C.; Zeng, Y.; Chu, C. Nano-medicine for thrombosis: A precise diagnosis and treatment strategy. Nano-Micro Lett. 2020, 12, 96. [Google Scholar] [CrossRef] [PubMed]
- Mongodi, S.; De Luca, D.; Colombo, A.; Stella, A.; Santangelo, E. Quantitative lung ultrasound: Technical aspects and clinical applications. Anesthesiology 2021, 134, 949–965. [Google Scholar] [CrossRef]
- Errico, C.; Pierre, J.; Pezet, S.; Desailly, Y.; Lenkei, Z.; Couture, O.; Tanter, M. Ultrafast ultrasound localization microscopy for deep super-resolution vascular imaging. Nature 2015, 527, 499–502. [Google Scholar] [CrossRef] [PubMed]
- Lanza, G.M. Ultrasound imaging: Something old or something new? Investig. Radiol. 2020, 55, 573–577. [Google Scholar] [CrossRef]
- Wang, J.; Zheng, Z.; Chan, J.; Yeow, J.T.W. Capacitive micromachined ultrasound transducers for intravascular ultrasound imaging. Microsyst. Nanoeng. 2020, 6, 73. [Google Scholar] [CrossRef]
- Qian, X.; Pei, J.; Zheng, H.; Xie, X.; Yan, L.; Zhang, H.; Han, C.; Gao, X.; Zhang, H.; Zheng, W. Prospective assessment of breast cancer risk from multimodal multiview ultrasound images via clinically applicable deep learning. Nat. Biomed. Eng. 2021, 5, 522–532. [Google Scholar] [CrossRef] [PubMed]
- Chatelain, P.; Krupa, A.; Navab, N. Confidence-driven control of an ultrasound probe. IEEE Trans. Robot. 2017, 33, 1410–1424. [Google Scholar] [CrossRef]
- Makvandi, P.; Shabani, M.; Rabiee, N.; Anjani, Q.K.; Maleki, A. Engineering and development of a tissue model for the evaluation of microneedle penetration ability, drug diffusion, photothermal activity, and ultrasound imaging: A promising surrogate to ex vivo and in vivo tissues. Adv. Mater. 2023, 35, 2210034. [Google Scholar] [CrossRef]
- Ma, J.; Zhao, J.; Chen, H.; Sun, L.-P. Transparent microfiber Fabry-Perot ultrasound sensor with needle-shaped focus for multiscale photoacoustic imaging. Photoacoustics 2023, 30, 100482. [Google Scholar] [CrossRef]
- Peralta, L.; Ramalli, A.; Reinwald, M.; Eckersley, R.J.; Hajnal, J.V. Impact of aperture, depth, and acoustic clutter on the performance of coherent multi-transducer ultrasound imaging. SN Appl. Sci. 2020, 10, 7655. [Google Scholar] [CrossRef]
- Basiri-Esfahani, S.; Armin, A.; Forstner, S.; Bowen, W.P. Precision ultrasound sensing on a chip. Nat. Commun. 2019, 10, 132. [Google Scholar] [CrossRef]
- Dizeux, A.; Gesnik, M.; Ahnine, H.; Blaize, K.; Arcizet, F. Functional ultrasound imaging of the brain reveals propagation of task-related brain activity in behaving primates. Nat. Commun. 2019, 10, 1400. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Bao, X.; Wong, C.-M.; Cheng, J.; Wu, H. PZT ceramics fabricated based on stereolithography for an ultrasound transducer array application. Ceram. Int. 2018, 44, 22725–22730. [Google Scholar] [CrossRef]
- Peng, C.; Chen, M.; Wang, H.; Shen, J.; Jiang, X. Broadband piezoelectric transducers for under-display ultrasonic fingerprint sensing applications. IEEE Trans. Ind. Electron. 2020, 68, 4426–4434. [Google Scholar] [CrossRef]
- Liu, X.; Liu, M.; Xin, F. Sound absorption of a perforated panel backed with perforated porous material: Energy dissipation of Helmholtz resonator cavity. Mech. Syst. Signal Process. 2023, 185, 109762. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhang, Z.; Zhang, Y.; Pan, Q.; Yan, X.; Li, X.; Yang, Z. Enhancing ultrasound power transfer: Efficiency, acoustics, and future directions. Adv. Mater. 2025, 37, 2407395. [Google Scholar] [CrossRef]
- Cho, S.; Kim, M.; Ahn, J.; Kim, Y.; Lim, J.; Park, J. An ultrasensitive and broadband transparent ultrasound transducer for ultrasound and photoacoustic imaging in-vivo. Nat. Commun. 2024, 15, 1444. [Google Scholar] [CrossRef]
- Chen, R.; Jiang, L.; Zhang, T.; Matsuoka, T.; Yamazaki, M. Eco-friendly highly sensitive transducers based on a new KNN–NTK–FM lead-free piezoelectric ceramic for high-frequency biomedical ultrasonic imaging applications. IEEE Trans. Biomed. Eng. 2018, 66, 1580–1587. [Google Scholar] [CrossRef]
- Zhang, Y.; Demosthenous, A. Integrated circuits for medical ultrasound applications: Imaging and beyond. IEEE Trans. Biomed. Circuits Syst. 2021, 15, 838–858. [Google Scholar] [CrossRef]
- Zuo, P.; Ma, D.; Li, X.; Chen, Y. Improving the accuracy and resolution of filter-and frequency-to-time mapping-based time and frequency acquisition methods by broadening the filter bandwidth. IEEE Trans. Microw. Theory Tech. 2023, 71, 3668–3677. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, Y.; Zheng, B.; Huo, Y.; Fan, Y.; Ma, D.; Gu, Y.; Wang, P. Ultrawide-bandwidth high-resolution all-optical intravascular ultrasound using miniaturized photoacoustic transducer. Sci. Adv. 2023, 9, eadg8600. [Google Scholar] [CrossRef]
- Cloutier, G.; Destrempes, F.; Yu, F.; Tang, A. Quantitative ultrasound imaging of soft biological tissues: A primer for radiologists and medical physicists. Insights Imaging 2021, 12, 127. [Google Scholar] [CrossRef]
- Hou, C.; Fei, C.; Li, Z.; Zhang, S.; Man, J. Optimized backing layers design for high frequency broad bandwidth ultrasonic transducer. IEEE Trans. Biomed. Eng. 2021, 69, 475–481. [Google Scholar] [CrossRef]
- Cai, Y.; Xu, L.; Zhang, T.; Suo, D. Ultrasound transducers with both imaging and power output capabilities by anti-matching at backing layers. Appl. Phys. Lett. 2024, 124. [Google Scholar] [CrossRef]
- Zhang, D.; Wang, X.; Lin, J.; Xiong, Y.; Lu, H.; Huang, J.; Lou, X. Multi-frequency therapeutic ultrasound: A review. Ultrason. Sonochem. 2023, 100, 106608. [Google Scholar] [CrossRef]
- Suo, D.; Govind, B.; Zhang, S.; Jing, Y. Numerical investigation of the inertial cavitation threshold under multi-frequency ultrasound. Ultrason. Sonochem. 2018, 41, 419–426. [Google Scholar] [CrossRef]
- Zheng, Q.; Wang, H.; Yang, H.; Jiang, H.; Chen, Z. Thin ceramic PZT dual-and multi-frequency pMUT arrays for photoacoustic imaging. Microsyst. Nanoeng. 2022, 8, 122. [Google Scholar] [CrossRef]
- Park, J.S.; Jung, S.Y.; Kim, D.H.; Park, J.H.; Jang, H.W.; Kim, T.G.; Baek, S.-H.; Lee, B.C. Dual-frequency piezoelectric micromachined ultrasound transducer based on polarization switching in ferroelectric thin films. Microsyst. Nanoeng. 2023, 9, 122. [Google Scholar] [CrossRef]
- Birjis, Y.; Swaminathan, S.; Nazemi, H.; Raj, G.C.A. Piezoelectric micromachined ultrasonic transducers (PMUTs): Performance metrics, advancements, and applications. Sensors 2022, 22, 9151. [Google Scholar] [CrossRef]
- Wei, H.; Wang, H.; Xia, Y.; Cui, D.; Shi, Y. An overview of lead-free piezoelectric materials and devices. J. Mater. Chem.C 2018, 6, 12446–12467. [Google Scholar] [CrossRef]
- Wang, K.; He, Y. Recent advances in metal titanate-based piezocatalysts: Enhancing catalytic performance through improved piezoelectric properties and regulated carrier transport. Chin. J. Catal. 2024, 61, 24. [Google Scholar] [CrossRef]
- Chen, L.; Liu, H.; Qi, H.; Chen, J. High-electromechanical performance for high-power piezoelectric applications: Fundamental, progress, and perspective. Prog. Mater. Sci. 2022, 127, 100944. [Google Scholar] [CrossRef]
- Zhou, Q.; Lau, S.; Wu, D.; Shung, K.K. Piezoelectric films for high frequency ultrasonic transducers in biomedical applications. Prog. Mater. Sci. 2011, 56, 139–174. [Google Scholar] [CrossRef]
- Zameer, A.; Majeed, M.; Mirza, S.M.; Raja, M.A.Z.; Khan, A. Bio-inspired heuristics for layer thickness optimization in multilayer piezoelectric transducer for broadband structures. Soft Comput. 2019, 23, 3449–3463. [Google Scholar] [CrossRef]
- Wang, K.; Liu, W.; Wu, J.; Li, H.; Peng, H.; Zhang, J.; Ding, K.; Wang, X.; Hou, C.; Zhang, H. Smart Wearable Sensor Fuels Noninvasive Body Fluid Analysis. ACS Appl. Mater. Interfaces 2025, 17, 13279–13301. [Google Scholar] [CrossRef]
- Wang, X.-B.; He, L.-M.; Ma, Y.-C.; Liu, W.-J.; Xu, W.-J. Development of broadband high-frequency piezoelectric micromachined ultrasonic transducer array. Sensors 2021, 21, 1823. [Google Scholar] [CrossRef]
- Guillermic, R.-M.; Lanoy, M.; Strybulevych, A. A PDMS-based broadband acoustic impedance matched material for underwater applications. Ultrasonics 2019, 94, 152–157. [Google Scholar] [CrossRef]
- Lin, L.L.; Alvarez-Puebla, R.; Liz-Marzán, L.M.; Trau, M.; Wang, J. Surface-enhanced Raman spectroscopy for biomedical applications: Recent advances and future challenges. ACS Appl. Mater. Interfaces 2025, 17, 16287–16379. [Google Scholar] [CrossRef]
- Liu, W.; He, L.; Wang, X.; Zhou, J.; Xu, W.; Smagin, N.; Toubal, M.; Yu, H.; Gu, Y.; Xu, J. 3D FEM analysis of high-frequency AlN-based PMUT arrays on cavity SOI. Sensors 2019, 19, 4450. [Google Scholar] [CrossRef]
- Su, Y.; Li, S.; Li, R.; Dagdeviren, C. Splitting of neutral mechanical plane of conformal, multilayer piezoelectric mechanical energy harvester. Appl. Phys. Lett. 2015, 107. [Google Scholar] [CrossRef]
- Ren, D.; Li, C.; Shi, J.; Chen, R. A review of high-frequency ultrasonic transducers for photoacoustic imaging applications. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2021, 69, 1848–1858. [Google Scholar] [CrossRef]
- Bertolotti, J.; Katz, O. Imaging in complex media. Nat. Phys. 2022, 18, 1008–1017. [Google Scholar] [CrossRef]
- Moisello, E.; Novaresi, L.; Sarkar, E.; Malcovati, P.; Costa, T.L.; Bonizzoni, E. PMUT and CMUT devices for biomedical applications: A review. IEEE Access 2024, 12, 18640–18657. [Google Scholar] [CrossRef]
- Joshi, S.V.; Sadeghpour, S.; Kraft, M. Polyimide-on-silicon 2d piezoelectric micromachined ultrasound transducer (PMUT) array. Sensors 2023, 23, 4826. [Google Scholar] [CrossRef]
- Liu, J.; Chen, D.S.-H.; Wai, D.C.S.; Jian, G.D. Dual-electrode pMUT with Switch Mode Operation to Enhance Receive Sensitivity. In Proceedings of the 2024 IEEE Ultrasonics, Ferroelectrics, and Frequency Control Joint Symposium (UFFC-JS), Taipei, Taiwan, 22–26 September 2024; IEEE: New York, NY, USA; pp. 1–4. [Google Scholar]
- Sun, S.; Wang, J.; Zhang, M.; Ning, Y.; Ma, D. MEMS ultrasonic transducers for safe, low-power and portable eye-blinking monitoring. Microsyst. Nanoeng. 2022, 8, 63. [Google Scholar] [CrossRef]
- Khan, B.; Amara, U.; Khan, B.; Khan, W.U.; Ahmad, R.u.S.; Khan, M.S.; Hilal, M.E.; Khoo, B.L. Next-Generation Piezoelectric Materials in Wearable and Implantable Devices for Continuous Physiological Monitoring. Adv. Sci. 2025, 12, e07853. [Google Scholar] [CrossRef]
- Sakthivel, T.; Rajendran, A.; Chang, J.W. Advancements in piezoelectric membrane technology: Fundamentals and future outlook. Sep. Purif. Technol. 2024, 342, 127021. [Google Scholar] [CrossRef]
- Sharma, S.K.; Gaur, H.; Kulkarni, M.; Patil, G.; Bhattacharya, B. PZT–PDMS composite for active damping of vibrations. Compos. Sci. Technol. 2013, 77, 42–51. [Google Scholar] [CrossRef]
- Tonazzi, D.; Meziane, A.; Culla, A.; Biateau, C.; Pepe, G.; Massi, F. Material Damping Estimation within Low-, Medium-and High-Frequency Ranges. Int. J. Appl. Mech. 2024, 16, 2450056. [Google Scholar] [CrossRef]
- Ji, S.M.; Sung, J.H.; Park, C.Y.; Jeong, J.S. Phase-canceled backing structure for lightweight ultrasonic transducer. Sens. Actuators A Phys. 2017, 260, 161–168. [Google Scholar] [CrossRef]
- Açıkgöz, H.N.; Karaman, A.; Şahin, M.A.; Çaylan, Ö.R.; Büke, G.C. Assessment of silicon, glass, FR4, PDMS and PMMA as a chip material for acoustic particle/cell manipulation in microfluidics. Ultrasonics 2023, 129, 106911. [Google Scholar] [CrossRef]
- Bajrami, D.; Spano, F.; Wei, K.; Bonmarin, M.; Rossi, R.M. Human Skin Models in Biophotonics: Materials, Methods, and Applications. Adv. Healthc. Mater. 2025, 14, 2501894. [Google Scholar] [CrossRef]
- Lin, Z.; Duan, S.; Liu, M.; Dang, C. Insights into materials, physics, and applications in flexible and wearable acoustic sensing technology. Adv. Mater. 2024, 36, 2306880. [Google Scholar] [CrossRef] [PubMed]
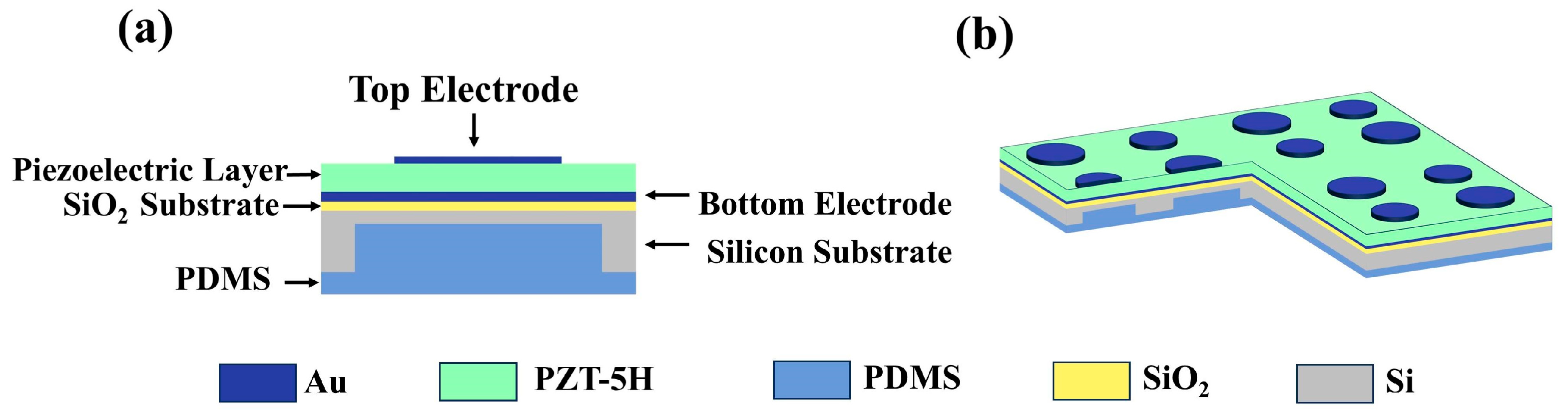
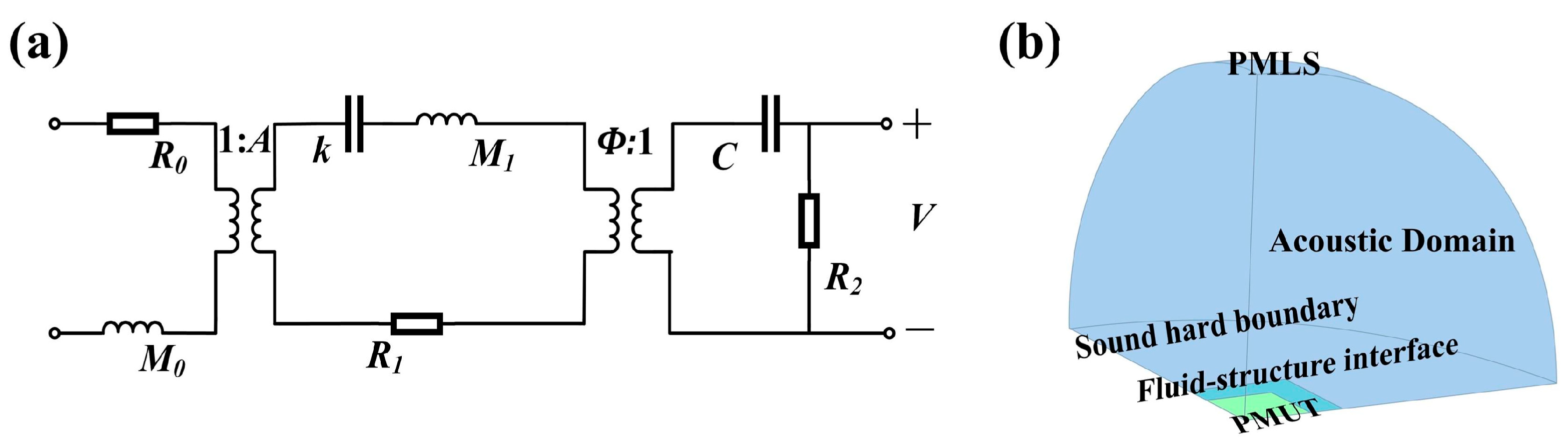
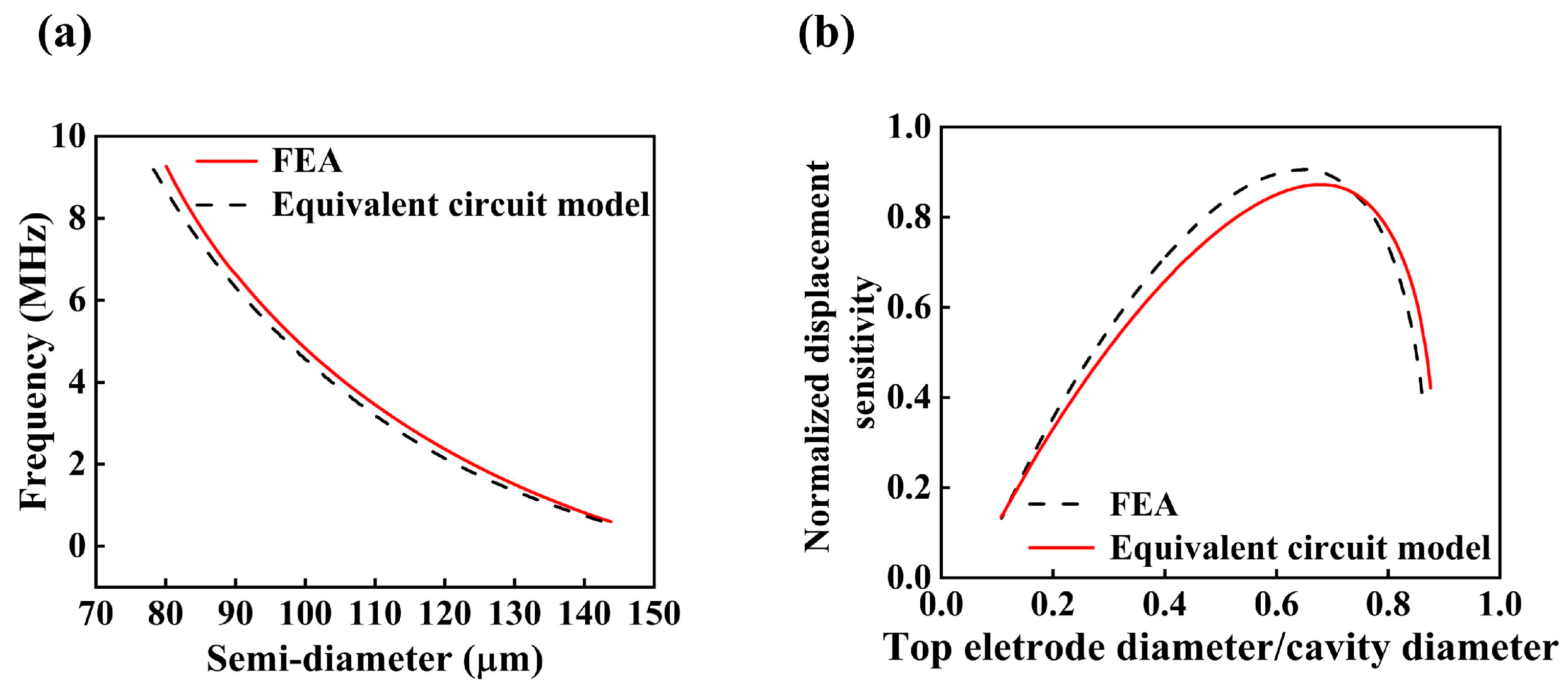
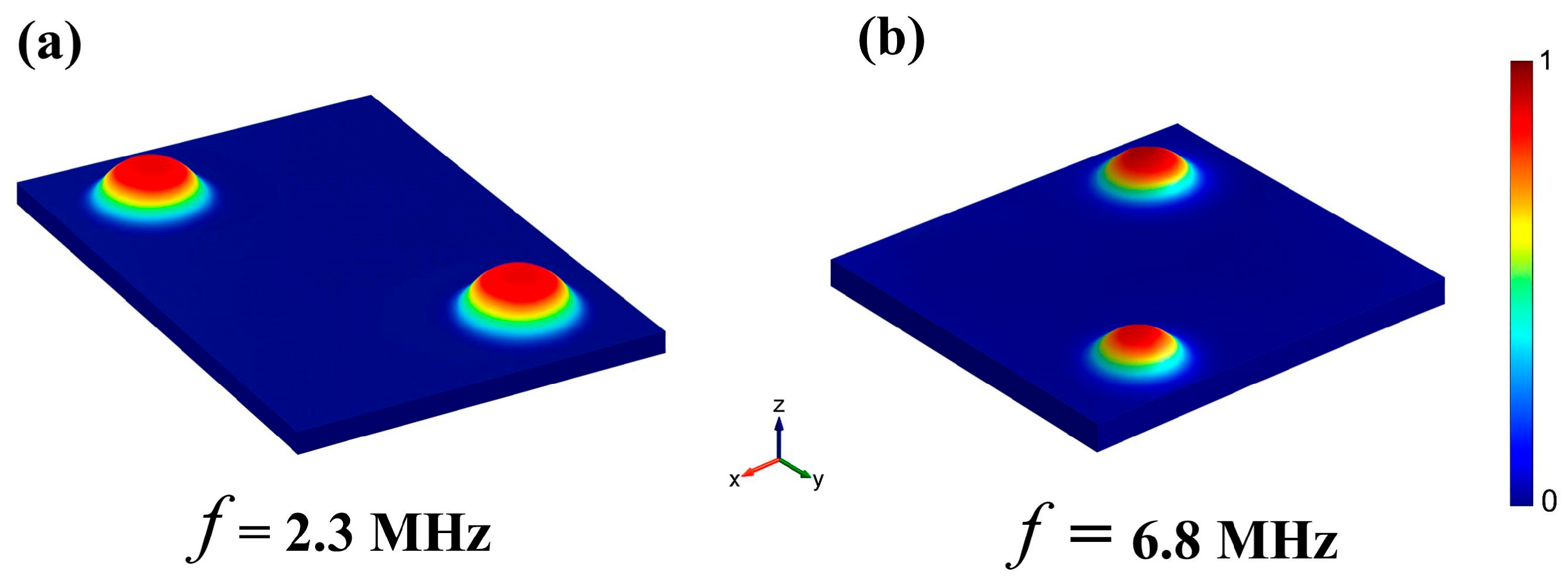

| Name | Value (μm) | Name | Value (μm) |
|---|---|---|---|
| PDMS thickness | 2 | Diaphragm thickness | 2 |
| PZT diameter | 280 | Cavity depth | 3 |
| PZT thickness | 4 | / | / |
| Material | d33 (pC/N) | ε33 | E/GPa | ν | ρ (kg/m3) | t (μm) |
|---|---|---|---|---|---|---|
| PZT-5H | 650 | 3400 | 68 | 0.32 | 7750 | 4 |
| PDMS | / | 2.75 | 0.75 | 1000 | 970 | 2 |
| SiO2 | / | / | 170 | 0.28 | 2329 | 1 |
| Si | / | / | 70 | 0.17 | 2200 | 4 |
| PDMS (μm) | fr (MHz) | fa (MHz) | BW (%) | φ | |
|---|---|---|---|---|---|
| 2.3 MHz | 0 | 2.3 | 2.61 | 47.4 ± 1.3 | 0.21 |
| 2 | 2.18 | 2.52 | 72.7 ± 2.1 | 0.23 | |
| 6.8 MHz | 0 | 6.8 | 7.77 | 28.0 ± 1 | 0.22 |
| 2 | 6.5 | 6.95 | 49.0 ± 1.8 | 0.17 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.; Cao, L.; Jin, M. Structural Optimization and Simulation of Dual-Frequency Piezoelectric Micromachined Ultrasonic Transducers. Micromachines 2025, 16, 1296. https://doi.org/10.3390/mi16111296
Wang F, Cao L, Jin M. Structural Optimization and Simulation of Dual-Frequency Piezoelectric Micromachined Ultrasonic Transducers. Micromachines. 2025; 16(11):1296. https://doi.org/10.3390/mi16111296
Chicago/Turabian StyleWang, Fengwen, Longlong Cao, and Mingliang Jin. 2025. "Structural Optimization and Simulation of Dual-Frequency Piezoelectric Micromachined Ultrasonic Transducers" Micromachines 16, no. 11: 1296. https://doi.org/10.3390/mi16111296
APA StyleWang, F., Cao, L., & Jin, M. (2025). Structural Optimization and Simulation of Dual-Frequency Piezoelectric Micromachined Ultrasonic Transducers. Micromachines, 16(11), 1296. https://doi.org/10.3390/mi16111296







