Secure Angle-Based Geometric Elimination (SAGE) for Microrobot Path Planning
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
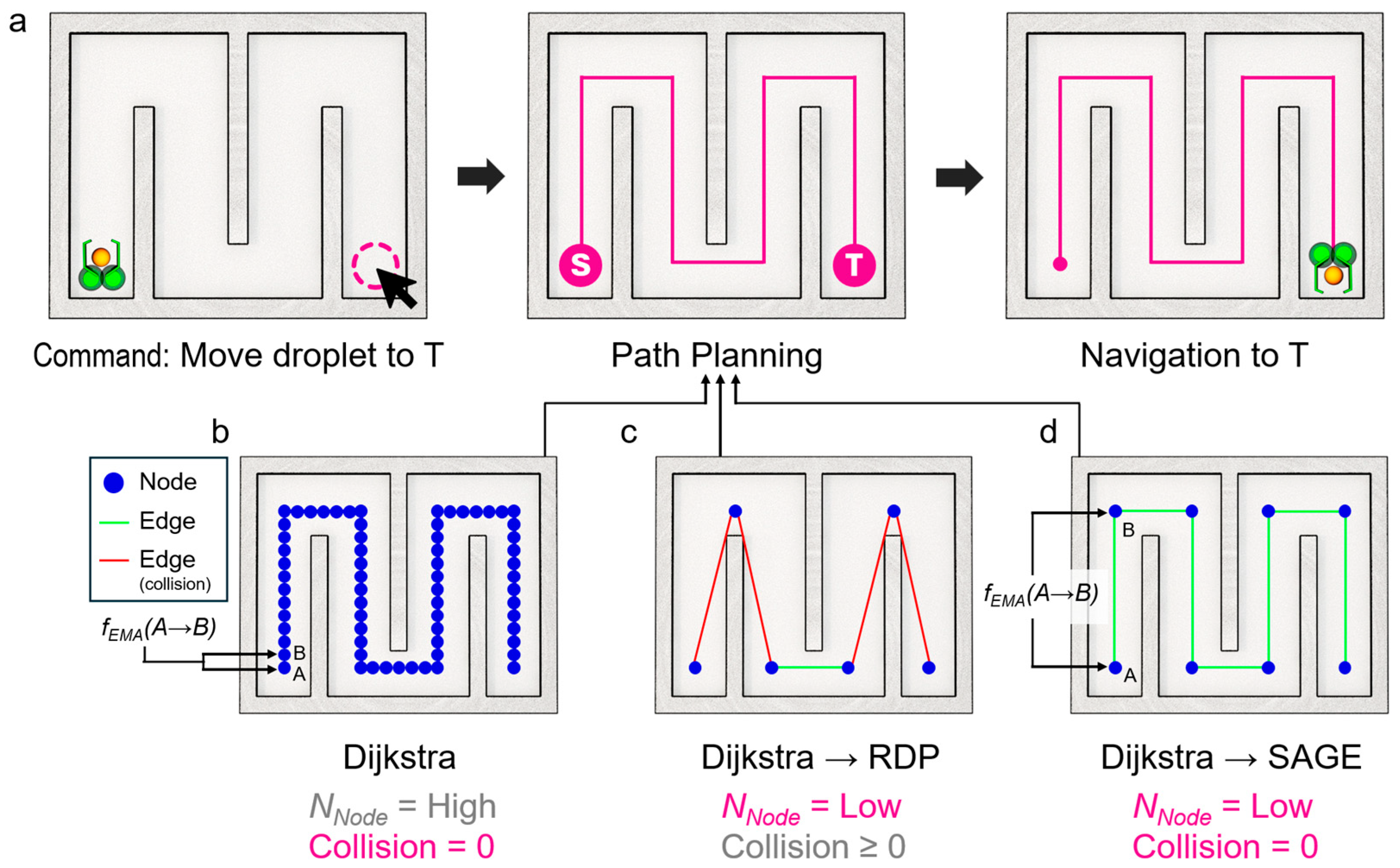
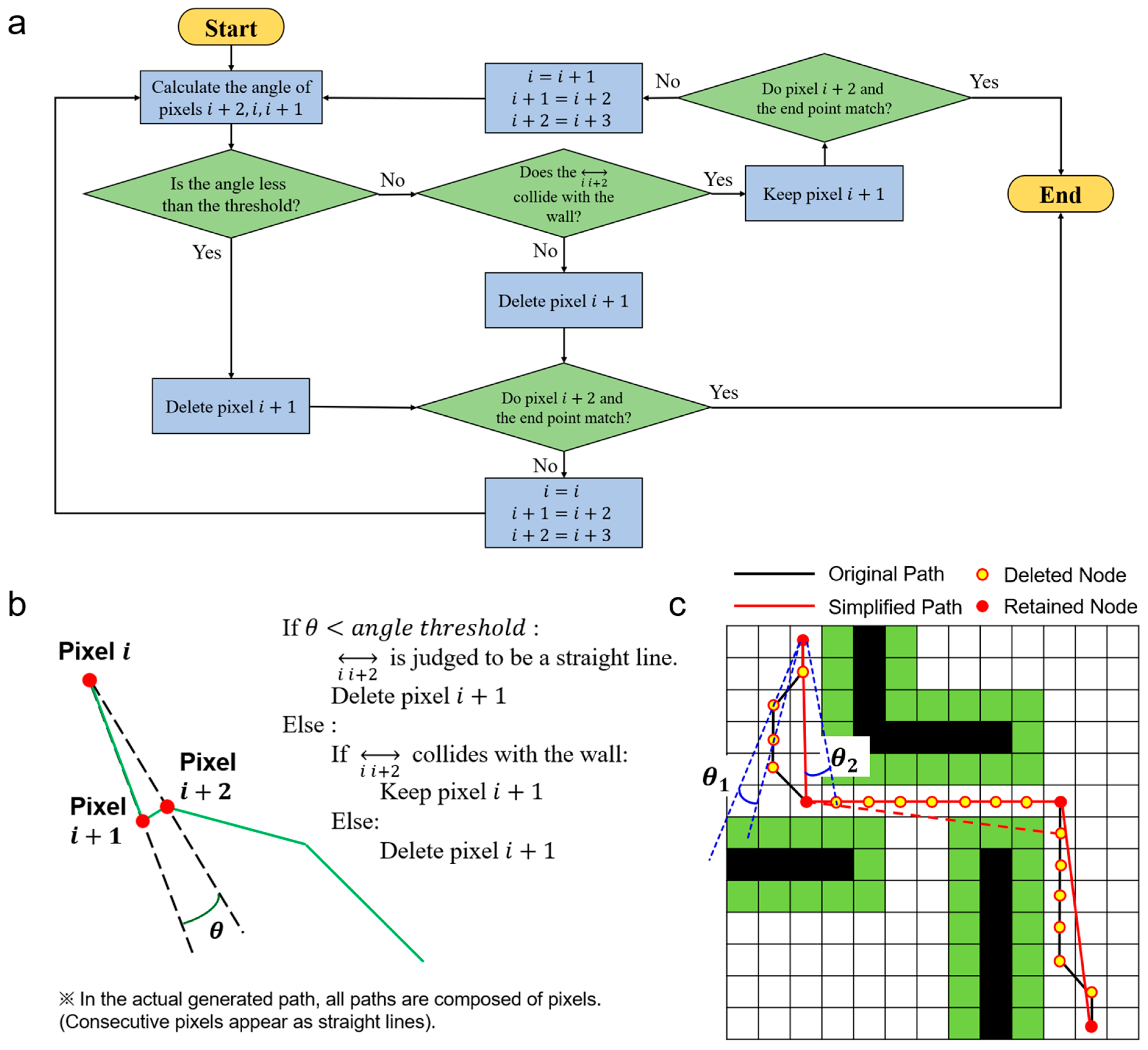
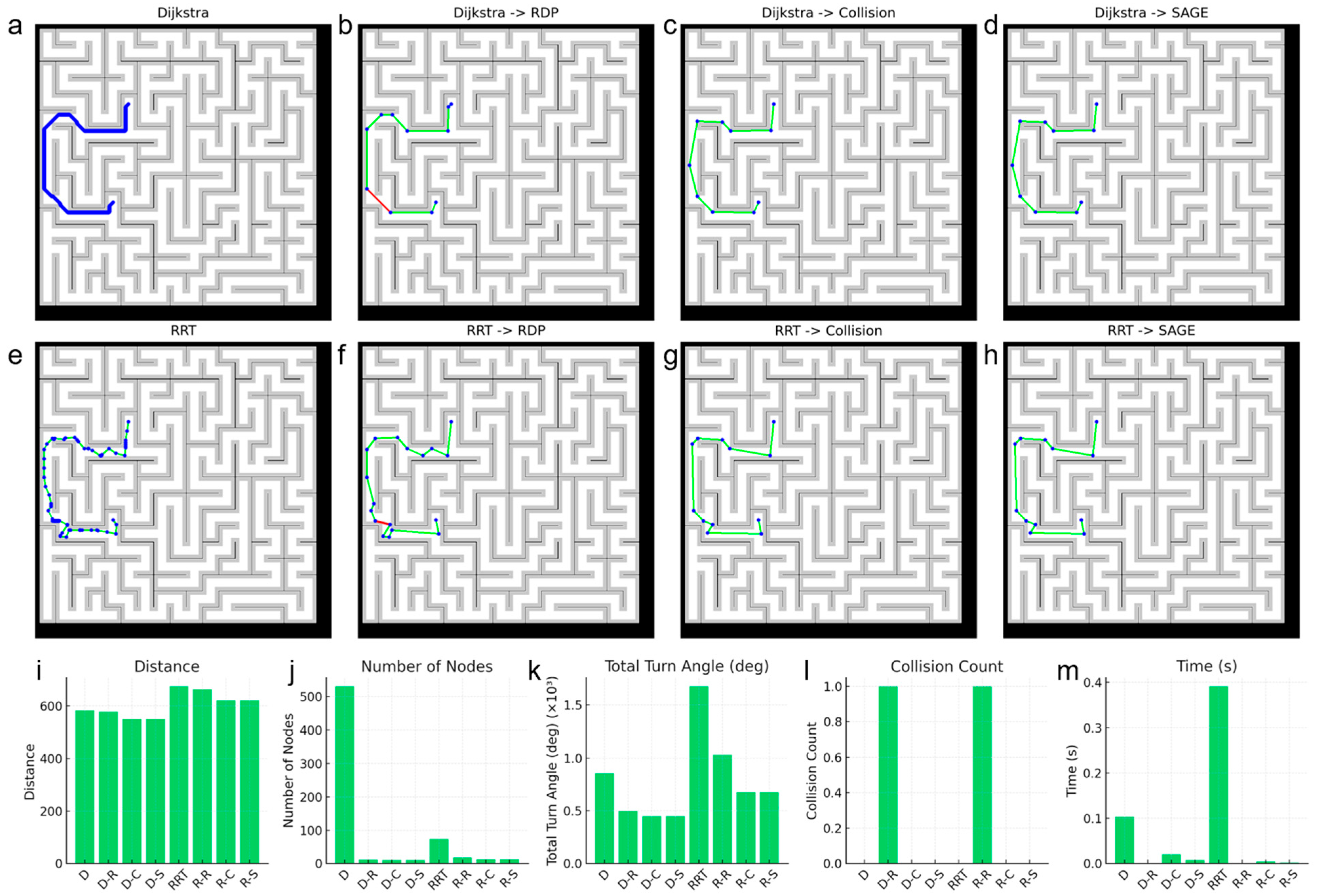
2.2.1. Secure Angle-Based Geometric Elimination (SAGE) Algorithm
- If the calculated angle is less than or equal to a small angle threshold, SAGE identifies this as a straight-line segment of the already-safe path. The intermediate pixel (i + 1) is rapidly removed without a collision check. This action is inherently safe, as simplifying a straight line that already exists in a free-space region cannot create a collision. This step ensures SAGE’s high computational speed.
- Conversely, if the calculated angle is greater than the threshold, SAGE treats this route as a potential shortcut, which needs collision verification. If this new shortcut is found to be unsafe at any point, the simplification is rejected, and the original, safe intermediate point (i + 1) is kept.
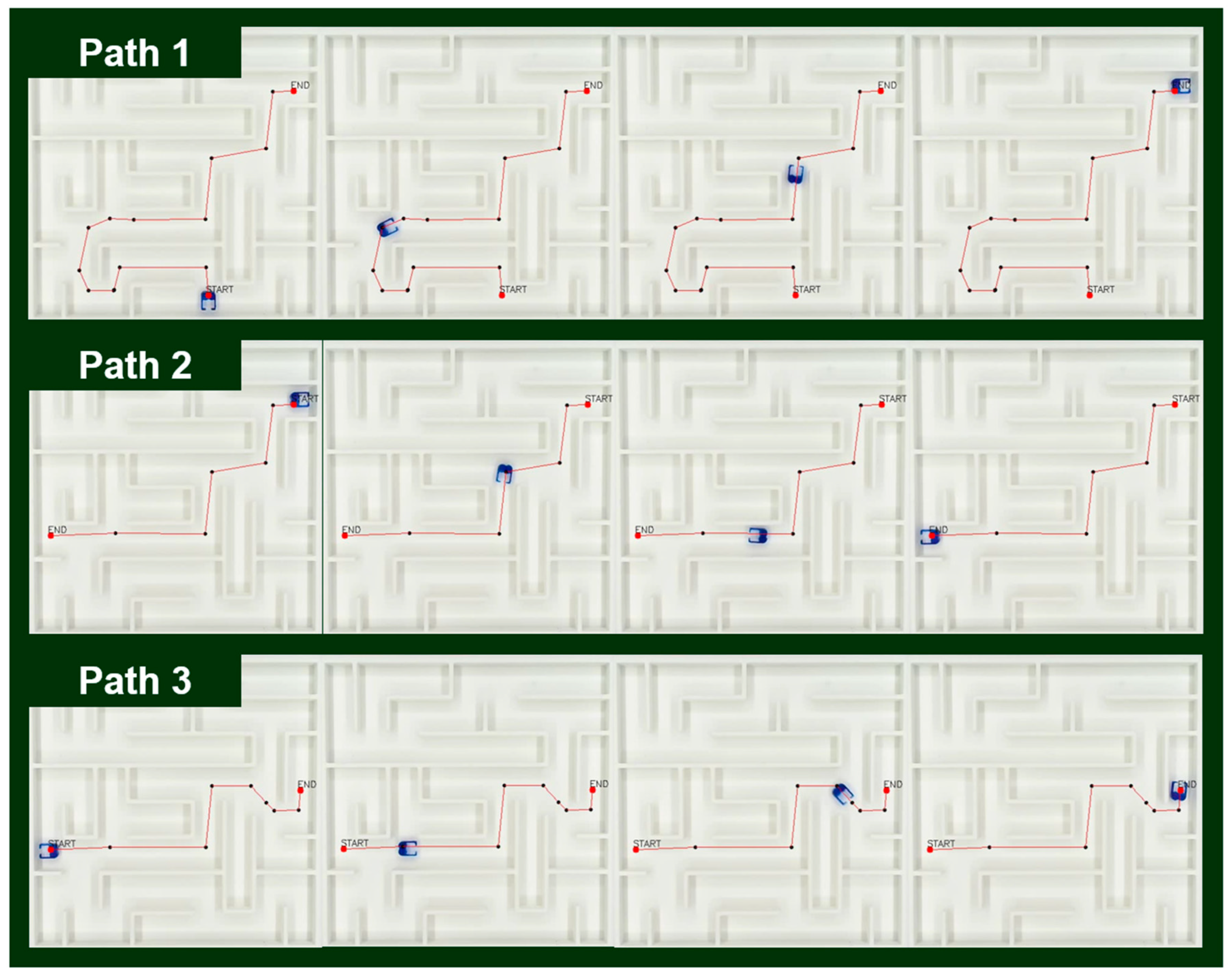
2.2.2. Experiments
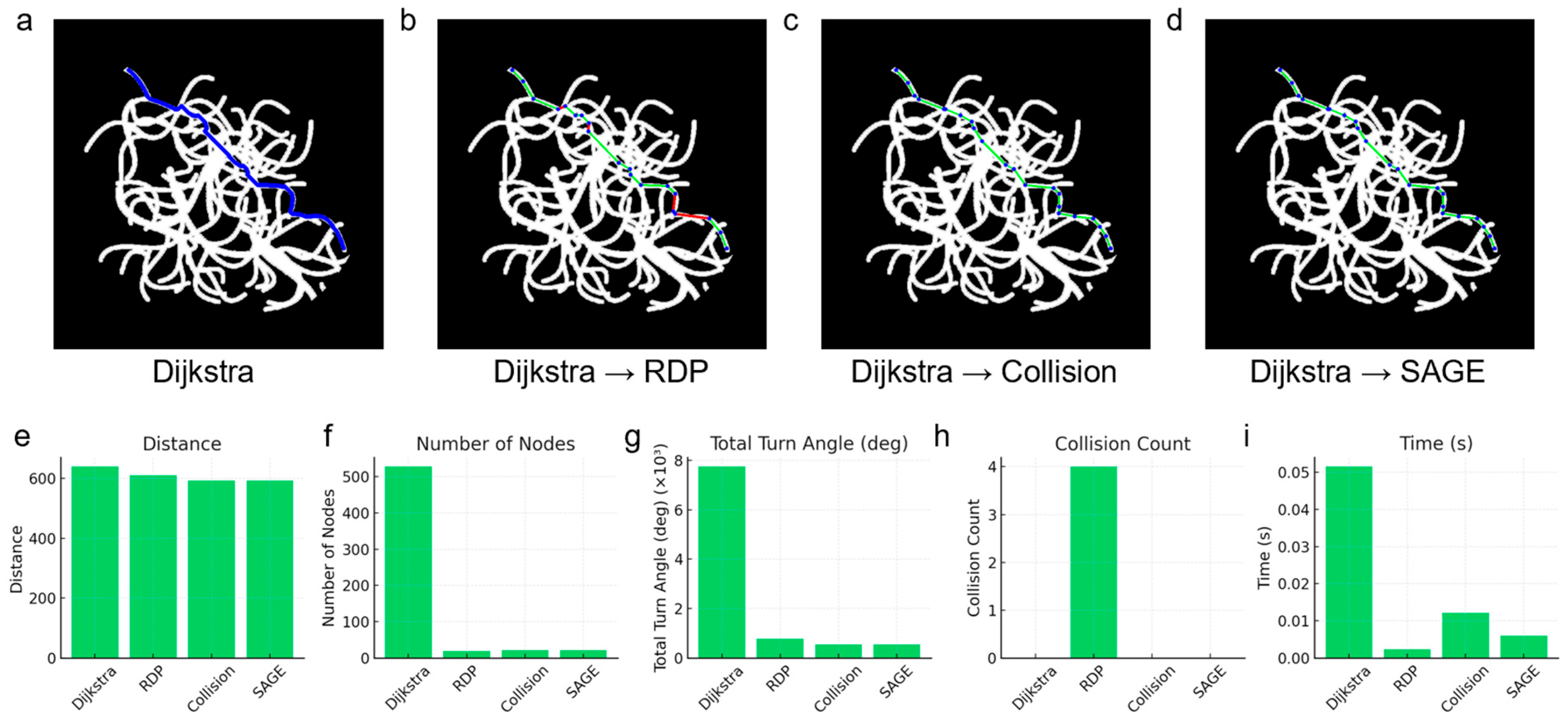
2.2.3. Performance Evaluation Metrics
3. Results & Discussion
4. Limitations & Future Development
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, D.; Wang, T.; Lu, Y. Untethered Microrobots for Active Drug Delivery: From Rational Design to Clinical Settings. Adv. Healthc. Mater. 2022, 11, 2102253. [Google Scholar] [CrossRef]
- Tian, M.; Keshavarz, M.; Demircali, A.A.; Han, B.; Yang, G.Z. Localized Microrobotic Delivery of Enzyme-Responsive Hydrogel-Immobilized Therapeutics to Suppress Triple-Negative Breast Cancer. Small 2025, 21, e2408813. [Google Scholar] [CrossRef]
- Nguyen, K.T.; Go, G.; Jin, Z.; Darmawan, B.A.; Yoo, A.; Kim, S.; Nan, M.; Lee, S.B.; Kang, B.; Kim, C.S.; et al. A Magnetically Guided Self-Rolled Microrobot for Targeted Drug Delivery, Real-Time X-Ray Imaging, and Microrobot Retrieval. Adv. Healthc. Mater. 2021, 10, 2001681. [Google Scholar] [CrossRef] [PubMed]
- Li, A.; Li, H.; Li, Z.; Zhao, Z.; Li, K.; Li, M.; Song, Y. Programmable Droplet Manipulation by a Magnetic-Actuated Robot. Sci. Adv. 2020, 6, eaay5808. [Google Scholar] [CrossRef]
- Zhou, A.; Zhang, Y. Intelligent 3D-Printed Magnetic Micro Soft Robotic Hand with Visual Feedback for Droplet Manipulation. In Proceedings of the 2023 WRC Symposium on Advanced Robotics and Automation (WRC SARA), Beijing, China, 19 August 2023; pp. 200–205. [Google Scholar] [CrossRef]
- Medany, M.; Piglia, L.; Achenbach, L.; Mukkavilli, S.K.; Ahmed, D. Model-Based Reinforcement Learning for Ultrasound-Driven Autonomous Microrobots. Nat. Mach. Intell. 2025, 7, 1076–1090. [Google Scholar] [CrossRef] [PubMed]
- Tang, Y.; Duan, F.; Zhou, A.; Kanitthamniyom, P.; Luo, S.; Hu, X.; Jiang, X.; Vasoo, S.; Zhang, X.; Zhang, Y. Image-based Real-time Feedback Control of Magnetic Digital Microfluidics by Artificial Intelligence-empowered Rapid Object Detector for Automated in Vitro Diagnostics. Bioeng. Transl. Med. 2023, 8, e10428. [Google Scholar] [CrossRef]
- Qian, J.; Xia, J.; Chiang, S.; Liu, J.F.; Li, K.; Li, F.; Wei, F.; Aziz, M.; Kim, Y.; Go, V.; et al. Rapid and Comprehensive Detection of Viral Antibodies and Nucleic Acids via an Acoustofluidic Integrated Molecular Diagnostics Chip: AIMDx. Sci. Adv. 2025, 11, eadt5464. [Google Scholar] [CrossRef]
- Zhong, R.; Sullivan, M.; Upreti, N.; Chen, R.; De Ganzó, A.; Yang, K.; Yang, S.; Jin, K.; He, Y.; Li, K.; et al. Cellular Immunity Analysis by a Modular Acoustofluidic Platform: CIAMAP. Sci. Adv. 2023, 9, eadj9964. [Google Scholar] [CrossRef]
- Naquin, T.D.; Canning, A.J.; Gu, Y.; Chen, J.; Naquin, C.M.; Xia, J.; Lu, B.; Yang, S.; Koroza, A.; Lin, K.; et al. Acoustic Separation and Concentration of Exosomes for Nucleotide Detection: ASCENDx. Sci. Adv. 2024, 10, eadm8597. [Google Scholar] [CrossRef]
- Rufo, J.; Zhang, P.; Zhong, R.; Lee, L.P.; Huang, T.J. A Sound Approach to Advancing Healthcare Systems: The Future of Biomedical Acoustics. Nat. Commun. 2022, 13, 3459. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Tian, Z.; Jin, K.; Yang, K.; Collyer, W.; Rufo, J.; Upreti, N.; Dong, X.; Lee, L.P.; Huang, T.J. Automating Life Science Labs at the Single-Cell Level through Precise Ultrasonic Liquid Sample Ejection: PULSE. Microsyst. Nanoeng. 2024, 10, 172. [Google Scholar] [CrossRef]
- Asadi, F.; Hurmuzlu, Y. Motion Planning for Multiple Heterogeneous Magnetic Robots under Global Input. IEEE Trans. Robot. 2024, 40, 697–713. [Google Scholar] [CrossRef]
- Xiang, D.; Lin, H.; Ouyang, J.; Huang, D. Combined Improved A* and Greedy Algorithm for Path Planning of Multi-Objective Mobile Robot. Sci. Rep. 2022, 12, 13273. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Liu, H.; Su, W. Topology Optimization Techniques for Mobile Robot Path Planning. Appl. Soft Comput. J. 2019, 78, 528–544. [Google Scholar] [CrossRef]
- Abbasi, S.A.; Ahmed, A.; Noh, S.; Gharamaleki, N.L.; Kim, S.; Chowdhury, A.M.M.B.; Kim, J.; Pané, S.; Nelson, B.J.; Choi, H. Autonomous 3D Positional Control of a Magnetic Microrobot Using Reinforcement Learning. Nat. Mach. Intell. 2024, 6, 92–105. [Google Scholar] [CrossRef]
- Kumar, R.H.; Vanjare, A.M.; Omkar, S.N. Autonomous Drone Navigation Using Monocular Camera and Light Weight Embedded System. In Proceedings of the 2023 International Conference for Advancement in Technology (ICONAT), Goa, India, 24–26 January 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Wang, H.; Qiu, Y.; Hou, Y.; Shi, Q.; Huang, H.W.; Huang, Q.; Fukuda, T. Deep Reinforcement Learning-Based Collision-Free Navigation for Magnetic Helical Microrobots in Dynamic Environments. IEEE Trans. Autom. Sci. Eng. 2024, 22, 7810–7820. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, L.; Liu, X.; Fan, Q. Safety-Enhanced Navigation Planning for Magnetic Microrobots. IEEE Trans. Autom. Sci. Eng. 2025, 22, 10586–10595. [Google Scholar] [CrossRef]
- Liu, Y.; Hou, Z.; Qu, J.; Liu, X.; Fan, Q. Optimized RRT Planning With CMA-ES for Autonomous Navigation of Magnetic Microrobots in Complex Environments. IEEE/ASME Trans. Mechatronics 2024, 29, 4826–4835. [Google Scholar] [CrossRef]
- Chehelgami, S.; Ashtari, E.; Basiri, M.A.; Tale Masouleh, M.; Kalhor, A. Safe Deep Learning-Based Global Path Planning Using a Fast Collision-Free Path Generator. Rob. Auton. Syst. 2023, 163, 104384. [Google Scholar] [CrossRef]
- Frazzoli, E. Incremental Random Sampling Algorithms for Optimal Motion Planning. Proc. Robot. Sci. 2010, 1–8. [Google Scholar]
- Dijkstra, E.W. A Note on Two Problems in Connexion with Graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Poiker, T.; Douglas, D.H. Reflection Essay: Algorithms for the Reduction of the Number of Points Required to Represent a Digitized Line or Its Caricature. Class. Cartogr. Reflect. Influ. Artic. Cartogr. 2011, 10, 29–36. [Google Scholar] [CrossRef]
- Bresenham, J.E. Algorithm for Computer Control of a Digital Plotter. In Seminal Graphics; ACM: New York, NY, USA, 1998; pp. 1–6. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ko, Y.; Im, S.-h.; Choi, H.; Kang, B.; Kim, J.; Lee, T.; Park, J.-O.; Bang, D. Secure Angle-Based Geometric Elimination (SAGE) for Microrobot Path Planning. Micromachines 2025, 16, 1273. https://doi.org/10.3390/mi16111273
Ko Y, Im S-h, Choi H, Kang B, Kim J, Lee T, Park J-O, Bang D. Secure Angle-Based Geometric Elimination (SAGE) for Microrobot Path Planning. Micromachines. 2025; 16(11):1273. https://doi.org/10.3390/mi16111273
Chicago/Turabian StyleKo, Youngji, Seung-hyun Im, Hana Choi, Byungjeon Kang, Jayoung Kim, Taeksu Lee, Jong-Oh Park, and Doyeon Bang. 2025. "Secure Angle-Based Geometric Elimination (SAGE) for Microrobot Path Planning" Micromachines 16, no. 11: 1273. https://doi.org/10.3390/mi16111273
APA StyleKo, Y., Im, S.-h., Choi, H., Kang, B., Kim, J., Lee, T., Park, J.-O., & Bang, D. (2025). Secure Angle-Based Geometric Elimination (SAGE) for Microrobot Path Planning. Micromachines, 16(11), 1273. https://doi.org/10.3390/mi16111273







