Student’s t-Distributed Extended Kalman Filter with Switch Factor for UWB Localization Under Colored Measurement Noise
Abstract
1. Introduction
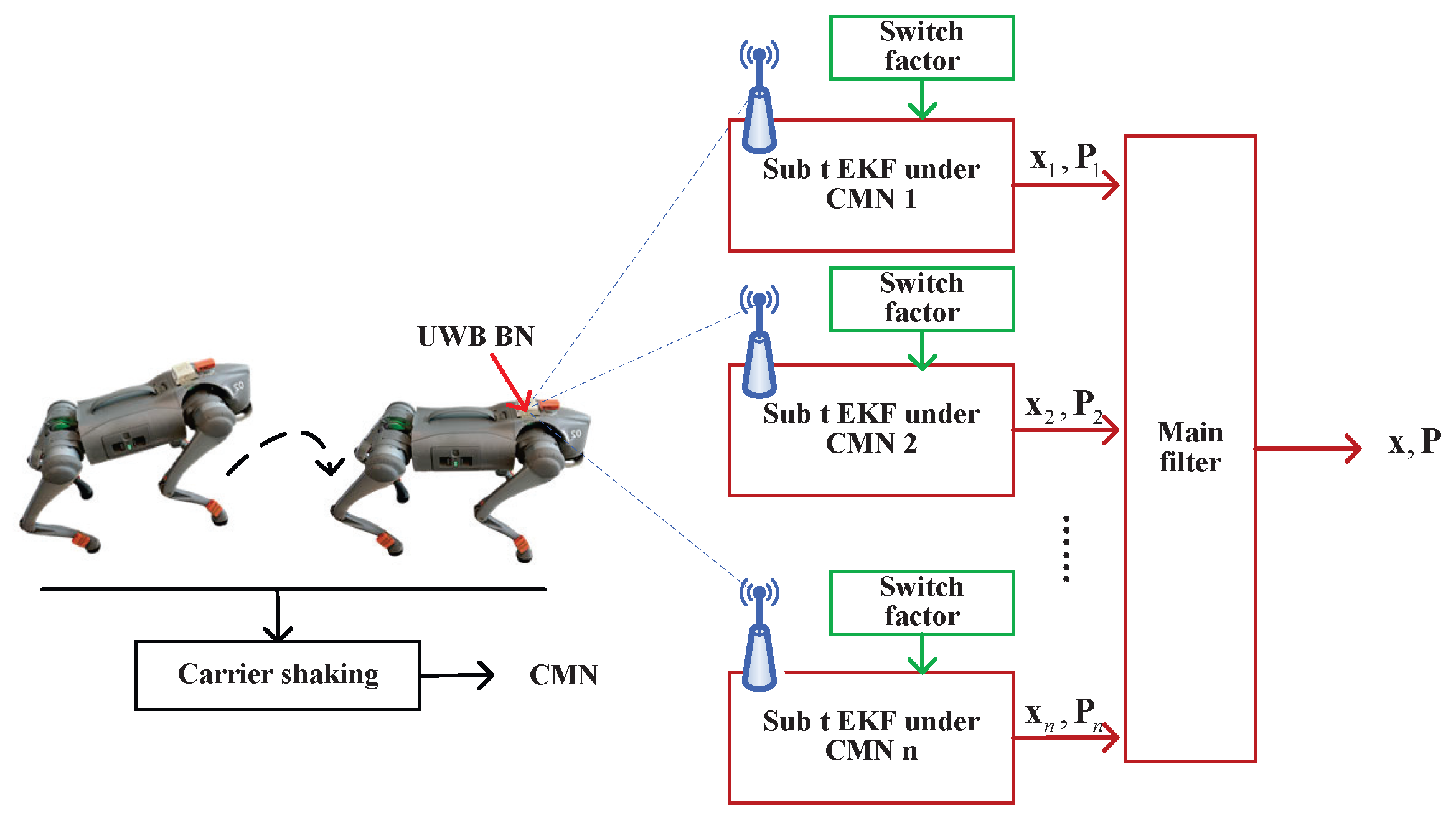
- A distributed UWB localization framework is introduced. It employs the position and velocity of a robotic dog as the state vector and the range measurement from a UWB reference node (RN) to the target blind node (BN) as the measurement vector. Filter submodules independently determine the position information of the target robotic dog, while the main filter performs hierarchical data fusion of the distributed estimates.
- The Student’s t-distributed cEKF using a switch CMN factor is derived. Specifically, we derive the EKF under CMN considering the Student’s t-distribution. Then, we employ CMN factor settings and design a switch scheme for the Student’s t-distributed cEKF.
- We employ three kind of paths, with one path being repeatedly tested across four trials, to evaluate the developed localization method.
2. UWB Localization for Robotic Dog
2.1. Indoor Integrated Localization
2.2. State and Measurement Equations
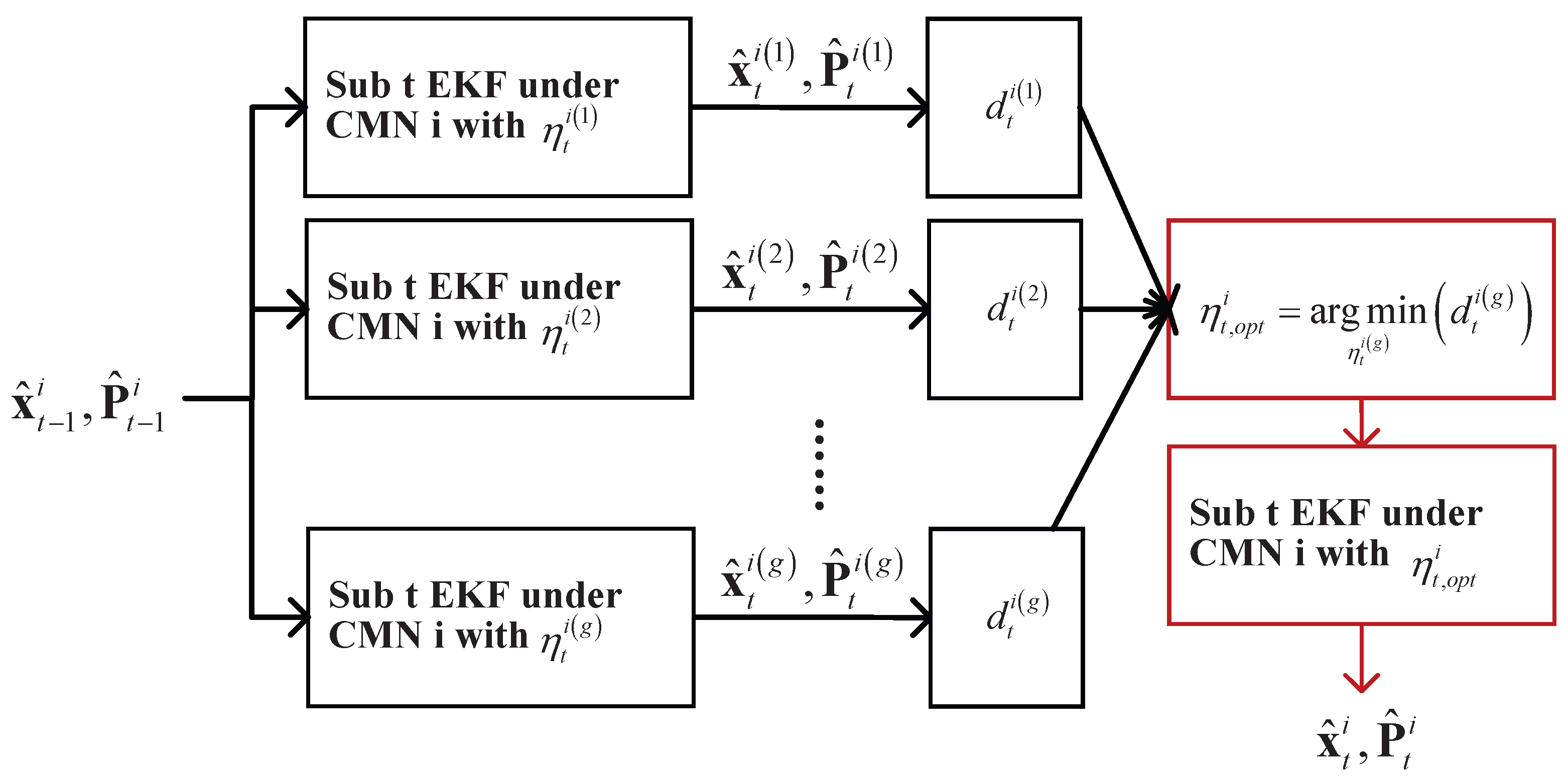
3. Student’s -Distributed EKF with Switch CMN Factor
3.1. EKF Under CMN
| Algorithm 1: EKF submodule under CMN for model given by Equations (1) and (4) |
Data: , , , , , Result: , 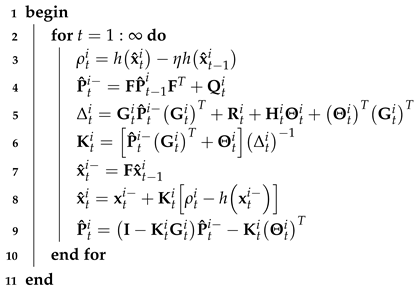 |
3.2. Student’s t-Distributed EKF
3.3. Switch CMN Factor
4. Experimental Evaluations
4.1. Indoor Performance Evaluation
4.2. Outdoor Performance Evaluation
4.3. The Performance with Different
4.4. Running Time
4.5. Observability
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| BDS | BeiDou navigation satellite system |
| BN | Blind node |
| CDF | Cumulative distribution function |
| CMN | Colored measurement noise |
| EKF | Extended Kalman filter |
| KF | Kalman filter |
| RFID | Radiofrequency identification |
| RMSE | Root mean square error |
| RN | Reference node |
| SLAM | Simultaneous localization and mapping |
| UWB | Ultrawide band |
References
- Tang, K.; Tokuda, F.; Seino, A.; Kobayashi, A.; Tien, N.C.; Kosuge, K. Time-Scaling Modeling and Control of Robotic Sewing System. IEEE-ASME Trans. Mechatron. 2024, 29, 3166–3174. [Google Scholar] [CrossRef]
- Kosmyna, N.; Hauptmann, E.; Hmaidan, Y. A Brain-Controlled Quadruped Robot: A Proof-of-Concept Demonstration. Sensors 2024, 24, 80. [Google Scholar] [CrossRef]
- Wan, Q.; Luo, A.; Meng, Y.; Zhang, C.; Chi, W.; Zhang, S.; Liu, Y.; Zhu, Q.; Kong, S.; Yu, J. Learning and Reusing Quadruped Robot Movement Skills from Biological Dogs for Higher-Level Tasks. Sensors 2024, 24, 28. [Google Scholar] [CrossRef]
- Li, J.; Shang, Z.; Li, R.; Cui, B. Adaptive Sliding Mode Path Tracking Control of Unmanned Rice Transplanter. Agriculture 2022, 12, 1225. [Google Scholar] [CrossRef]
- Cui, B.; Cui, X.; Wei, X.; Zhu, Y.; Ma, Z.; Zhao, Y.; Liu, Y. Design and Testing of a Tractor Automatic Navigation System Based on Dynamic Path Search and a Fuzzy Stanley Model. Agriculture 2024, 14, 2136. [Google Scholar] [CrossRef]
- Xu, X.; Chen, Z.; Cheng, H.; Yang, J.; Wang, T.; Ran, Y.; Tan, Z. Research on Mobile Robot Localization Method Based on Adaptive Motion Model and Double-Threshold Relocation Strategy. IEEE Trans. Instrum. Meas. 2025, 74, 8508412. [Google Scholar] [CrossRef]
- Ahmed, S.; Qiu, B.; Kong, C.W.; Xin, H.; Ahmad, F.; Lin, J. A Data-Driven Dynamic Obstacle Avoidance Method for Liquid-Carrying Plant Protection UAVs. Agronomy 2022, 12, 873. [Google Scholar] [CrossRef]
- Shen, C.; Wu, Y.; Qian, G.; Wu, X. Intelligent Bionic Polarization Orientation Method Using Biological Neuron Model for Harsh Conditions. IEEE Trans. Pattern Anal. Mach. Intell. 2025, 47, 789–806. [Google Scholar] [CrossRef]
- Hu, G.; Xu, L.; Gao, B.; Chang, L.; Zhong, Y. Robust Unscented Kalman Filter-Based Decentralized Multisensor Information Fusion for INS/GNSS/CNS Integration in Hypersonic Vehicle Navigation. IEEE Trans. Instrum. Meas. 2023, 72, 8504011. [Google Scholar] [CrossRef]
- He, P.; Li, Z.; Wu, Q.; Sun, M.; Shao, K. Wi-Fi fingerprint localization model via synergistic manifold and feature optimization. Meas. Sci. Technol. 2025, 36, 086306. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, G. Robust cubature Kalman filter based on generalized hyperbolic distribution for SLAM under colored heavy-tailed measurement noise. Digit. Signal Process. 2025, 166, 105390. [Google Scholar] [CrossRef]
- Mao, J.; Song, W.; Liang, H.; Xia, F.; Zhang, C. Graph-Optimized Encoder-IMU Fusion for Robust Pipeline Robot Localization in Confined Spaces. IEEE Trans. Instrum. Meas. 2025, 74, 7507112. [Google Scholar] [CrossRef]
- Xu, Y.; Zang, X.; Shmaliy, Y.S.; Yu, J.; Zhuang, Y.; Sun, M. UWB-based robot localization using distributed adaptive EFIR filtering. IEEE Internet Things J. 2024, 11, 30704–30713. [Google Scholar] [CrossRef]
- Jiang, X.; Kuroiwa, T.; Cao, Y.; Sun, L.; Zhang, H.; Kawaguchi, T.; Hashimoto, S. Enhanced Pure Pursuit Path Tracking Algorithm for Mobile Robots Optimized by NSGA-II with High-Precision GNSS Navigation. Sensors 2025, 25, 745. [Google Scholar] [CrossRef]
- Gao, W.; Zhou, W.; Tang, C.; Li, X.; Yuan, Y.; Hu, X. High-precision services of BeiDou navigation satellite system (BDS): Current state, achievements, and future directions. Satell. Navig. 2024, 5, 20. [Google Scholar] [CrossRef]
- Meng, D.; Ren, Y.; Yu, X.; Yin, X.; Wang, W.; Men, J. High-Precision Positioning and Rotation Angle Estimation for a Target Pallet Based on BeiDou Navigation Satellite System and Vision. Sensors 2024, 24, 5330. [Google Scholar] [CrossRef]
- Xie, X.; Dong, L.; Wang, H.; Di, Y.; Guo, W.; Wang, P.; Zhang, J. High-Sensitivity RFID Tag Sensor with Coupled Ring Resonators for Multiposition Crack Monitoring. IEEE Sens. J. 2024, 24, 37869–37878. [Google Scholar] [CrossRef]
- Abdelgawad, A. Auto-Localization System for Indoor Mobile Robot Using RFID Fusion. Robotica 2014, 33, 1899–1908. [Google Scholar] [CrossRef]
- Benjamin, B.; Erinc, G.; Carpin, S. Real-time WiFi localization of heterogeneous robot teams using an online random forest. Auton. Robot. 2015, 39, 155–167. [Google Scholar] [CrossRef]
- Alonso, J.M.; Ocana, M.; Hernandez, N.; Herranz, F.; Llamazares, A.; Sotelo, M.A.; Bergasa, L.M.; Magdalena, L. Enhanced WiFi localization system based on Soft Computing techniques to deal with small-scale variations in wireless sensors. Appl. Soft Comput. 2011, 11, 4677–4691. [Google Scholar] [CrossRef]
- He, S.; Yang, B.; Liu, T.; Zhang, H. Multi-Tag UWB Localization With Spatial-Temporal Attention Graph Neural Network. IEEE Trans. Instrum. Meas. 2024, 73, 2531112. [Google Scholar] [CrossRef]
- Salimpour, S.; Mor’On, P.T.; Yu, X.; Queralta, J.P.; Westerlund, T. Exploiting Redundancy for UWB Anomaly Detection in Infrastructure-Free Multi-Robot Relative Localization. Front. Robot. AI 2023, 10, 1190296. [Google Scholar] [CrossRef]
- Lin, H.Y.; Yeh, M.C. Drift-Free Visual SLAM for Mobile Robot Localization by Integrating UWB Technology. IEEE Access 2022, 10, 93636–93645. [Google Scholar] [CrossRef]
- Sun, M.; Gao, Y.; Jiao, Z.; Xu, Y.; Zhuang, Y.; Qian, P. R-T-S Assisted Kalman Filtering for Robot Localization Using UWB Measurement. Mob. Netw. Appl. 2022, 29, 1089–1098. [Google Scholar] [CrossRef]
- Shen, T.; Yuan, Z.; Wang, X. Stability analysis for digital filters with multiple saturation nonlinearities. Automatica 2012, 48, 2717–2720. [Google Scholar] [CrossRef]
- Shen, T.; Yuan, Z. Stability of fixed-point state-space digital filters using two’s complement arithmetic: Further insight. Automatica 2010, 46, 2109–2111. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, T.; Shmaliy, Y.S.; Luan, X.; Liu, F. Bayesian Transfer Filtering Using Pseudo Marginal Measurement Likelihood. IEEE Trans. Cybern. 2025, 55, 562–573. [Google Scholar] [CrossRef]
- Zhao, S.; Huang, B. Trial-and-error or avoiding a guess? Initialization of the Kalman filter. Automatica 2020, 121, 109184. [Google Scholar] [CrossRef]
- Zhao, S.; Li, K.; Ahn, C.K.; Huang, B.; Liu, F. Tuning-Free Bayesian Estimation Algorithms for Faulty Sensor Signals in State-Space. IEEE Trans. Ind. Electron. 2022, 70, 921–929. [Google Scholar] [CrossRef]
- Juston, M.; Gupta, S.; Mathur, S.; Norris, W.R.; Nottage, D.; Soylemezoglu, A. Robust Error State Sage-Husa Adaptive Kalman Filter for UWB Localization. IEEE Sens. J. 2025, 25, 16034–16049. [Google Scholar] [CrossRef]
- Juston, M.; Gupta, S.; Mathur, S.; Norris, W.R.; Nottage, D.; Soylemezoglu, A. Kalman Filter-Based One-Shot Sim-to-Real Transfer Learning. IEEE Robot. Autom. Lett. 2024, 9, 311–318. [Google Scholar]
- Zhao, W.; Chen, Z.; Yin, F. Distributed extended Kalman filtering for acoustic simultaneous localization and environment mapping. Appl. Acoust. 2024, 224, 110139. [Google Scholar] [CrossRef]
- Kim, J.H.; Lee, S.H.; Kim, J.G.; Jang, W.J.; Kim, D.H. Localization of solar panel cleaning robot combining vision processing and extended Kalman filter. Sci. Prog. 2024, 107, 00368504241250176. [Google Scholar] [CrossRef]
- Zhang, T.; Zhao, S.; Luan, X.; Liu, F. Bayesian Inference for State-Space Models with Student-t Mixture Distributions. IEEE Trans. Cybern. 2022, 53, 4435–4445. [Google Scholar] [CrossRef]
- Li, K.; Zhao, S.; Huang, B.; Liu, F. Bayesian Filtering for High-Dimensional State-Space Models With State Partition and Error Compensation. IEEE-CAA J. Autom. Sin. 2024, 11, 1239–1249. [Google Scholar] [CrossRef]
- Gao, Y.; Yang, M.; Zang, X.; Deng, L.; Li, M.; Xu, Y.; Sun, M. Adaptive Distributed Student’s T Extended Kalman Filter Employing Allan Variance for UWB Localization. Sensors 2025, 25, 1883. [Google Scholar] [CrossRef]
- Shmaliy, Y.S.; Zhao, S.; Ahn, C.K. Kalman and UFIR State Estimation with Colored Measurement Noise using Backward Euler Method. IET Signal Process. 2019, 14, 1–8. [Google Scholar]
- Roth, M.; Ozkan, E.; Gustafsson, F. A Student’s t filter for heavy tailed process and measurement noise. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Vancouver, BC, Canada, 26–31 May 2013. [Google Scholar]
- Chen, W.; Jiang, S.; Cao, J.; Sun, R. An adaptive EKF-SLAM algorithm for cooperative navigation of multi-aircrafts. IET Control Theory Appl. 2024, 18, 2823–2829. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, W.; Feng, J.; Tang, R. Distributed Acoustic Source Tracking in Noisy and Reverberant Environments With Distributed Microphone Networks. IEEE Access 2020, 8, 9913–9927. [Google Scholar] [CrossRef]
- Xu, Y.; Chen, X.; Shen, C.; Zhou, M.; Wang, X. Maximum-correntropy-criterion-based extended Kalman filter for ultrawideband distance data fusion under colored measurement noise. IEEE Sens. J. 2025. [Google Scholar] [CrossRef]


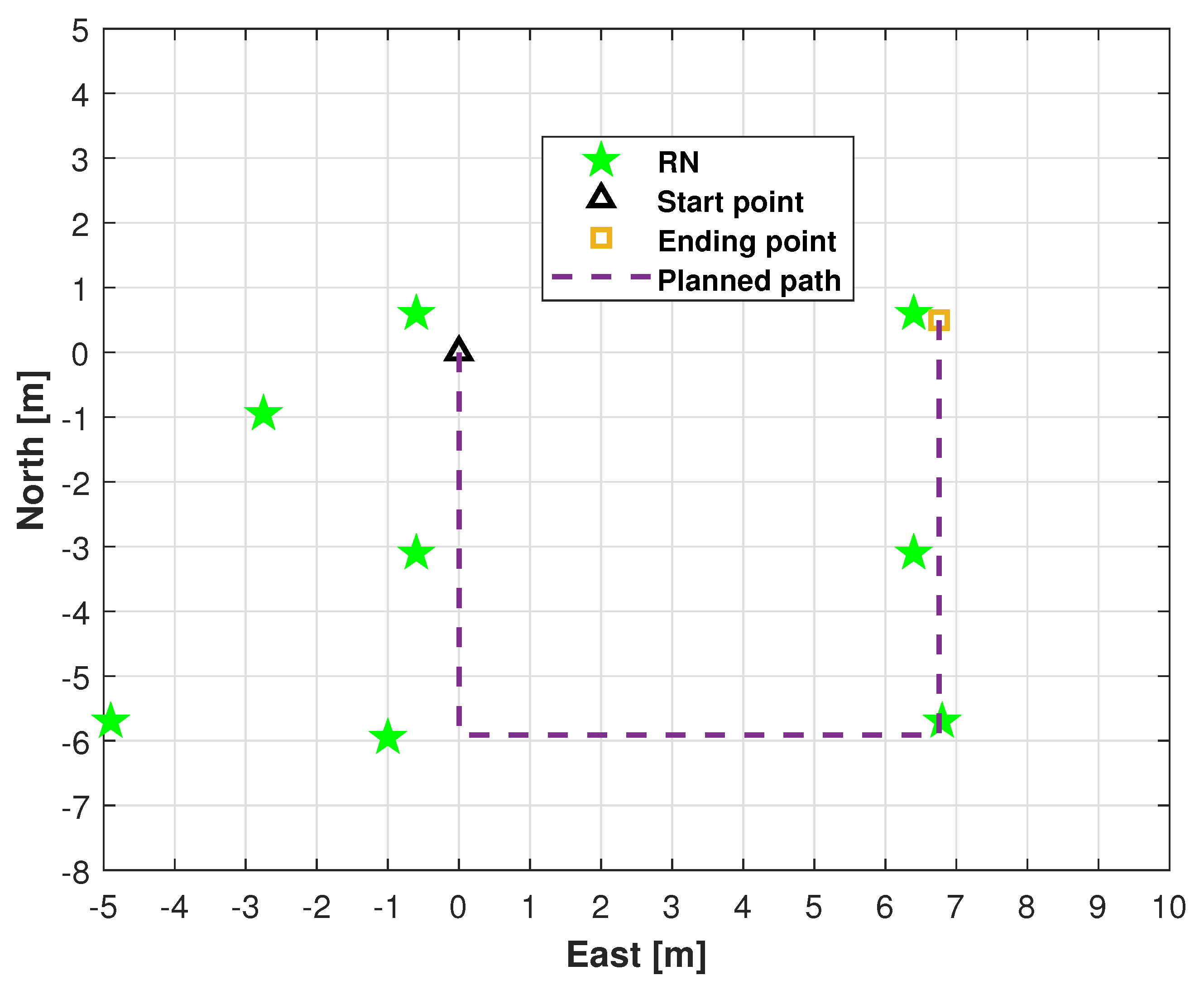
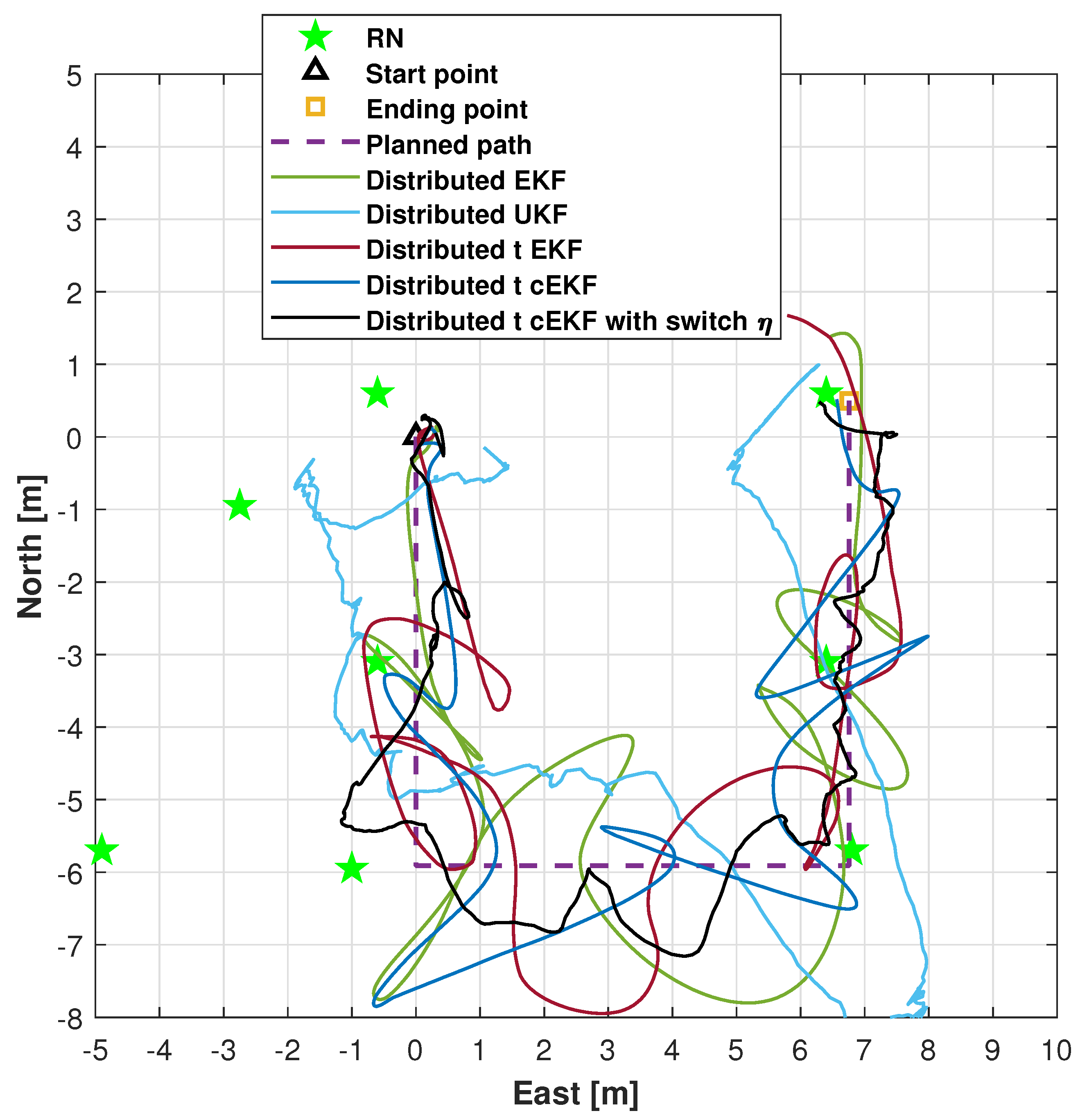
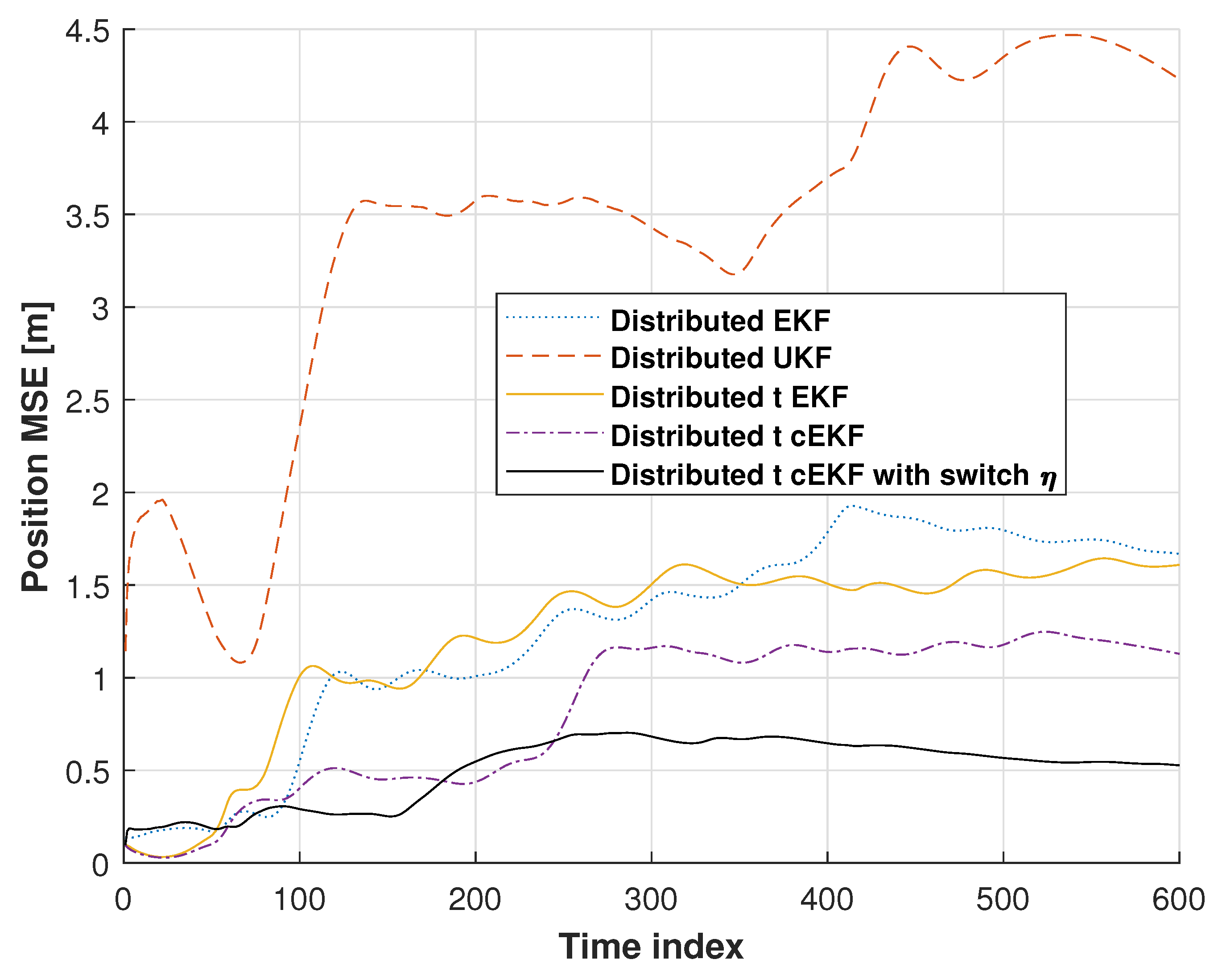
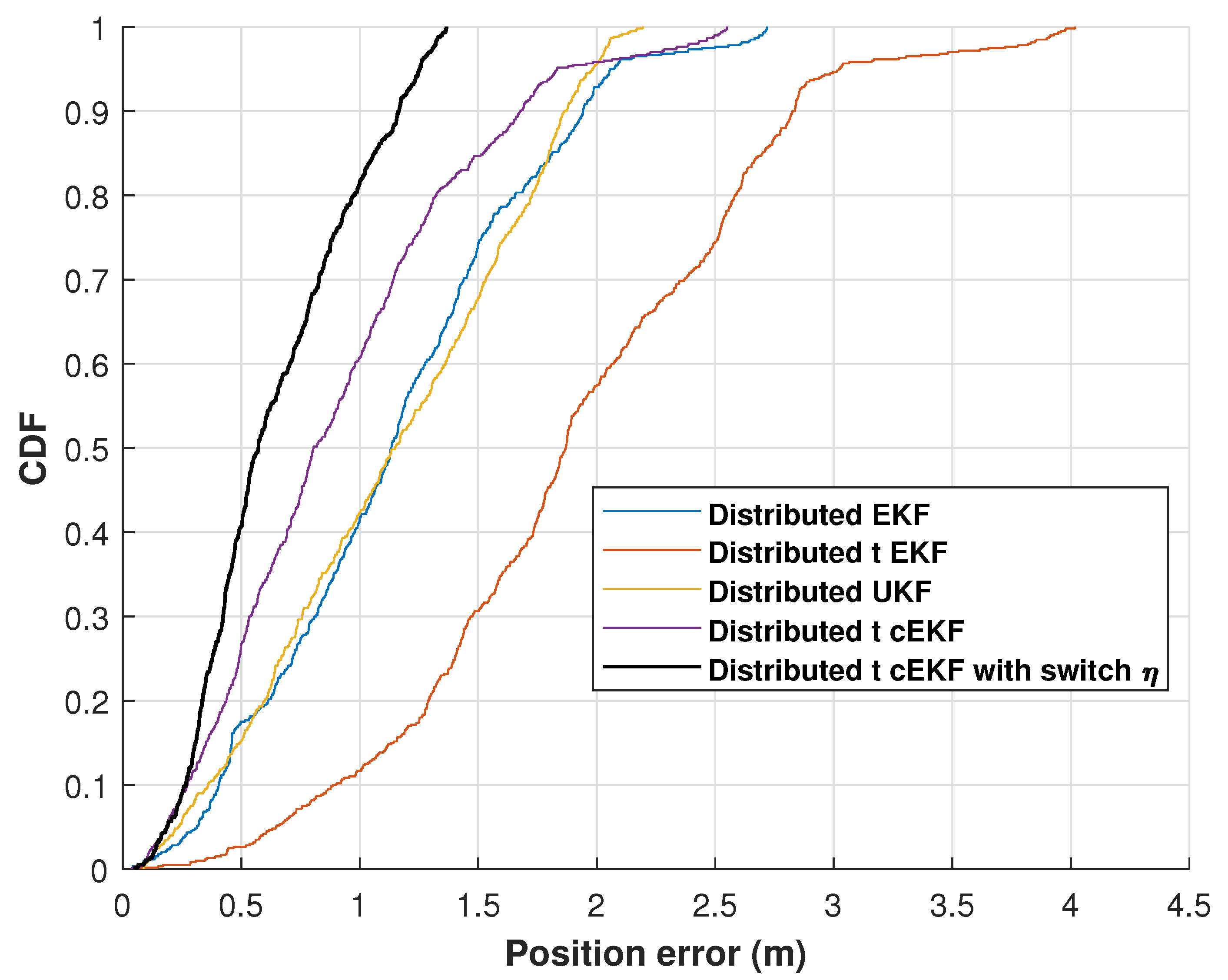


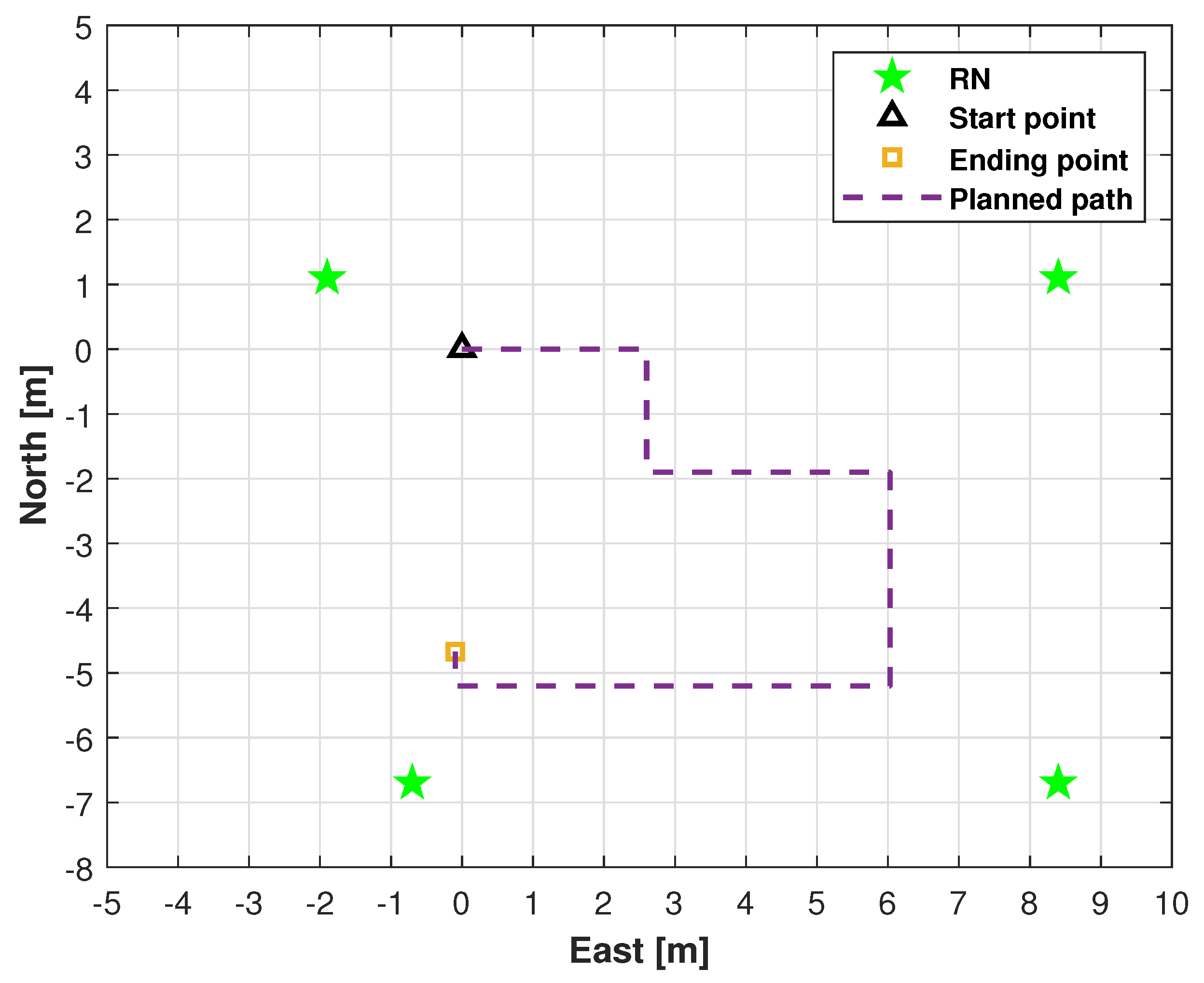

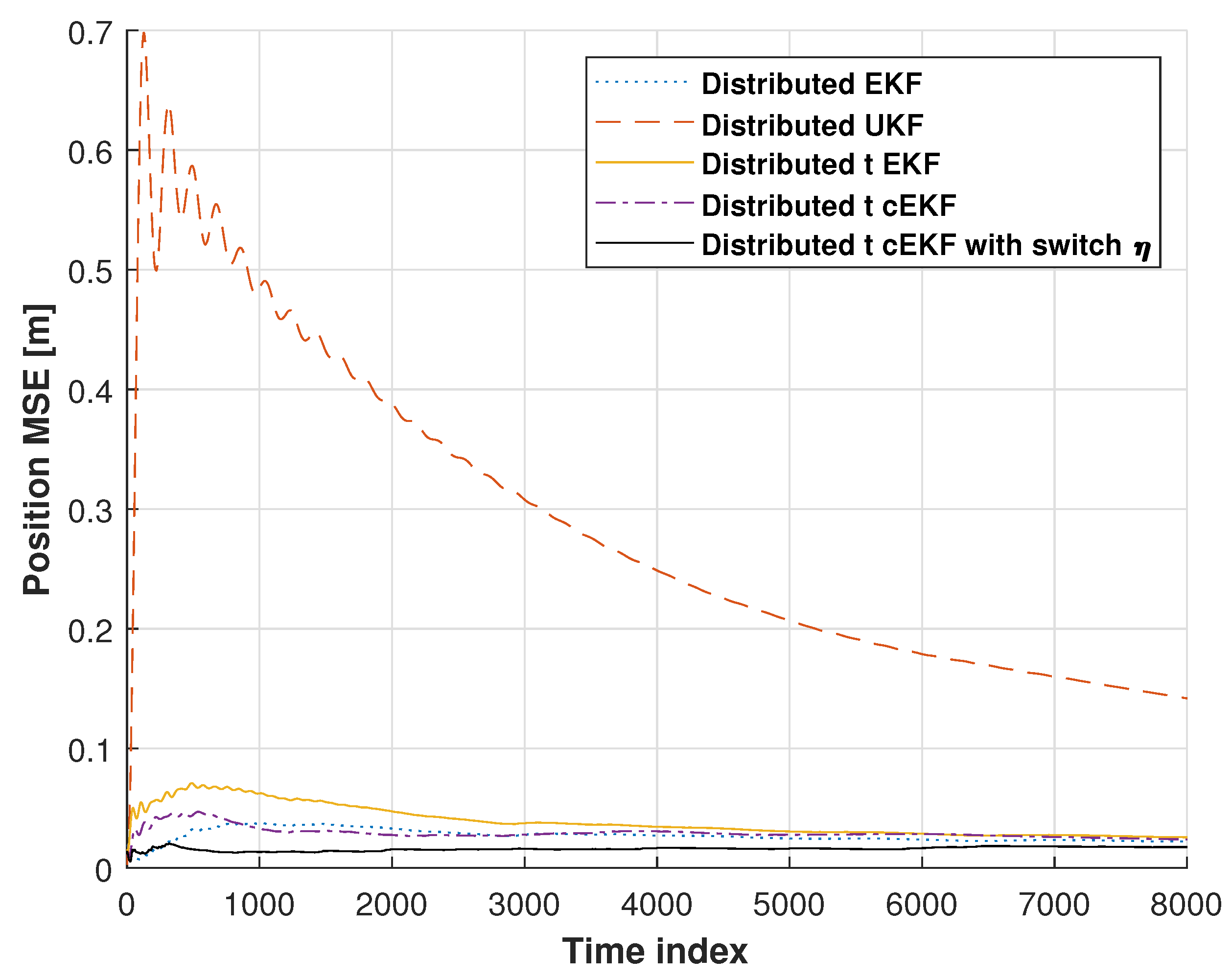
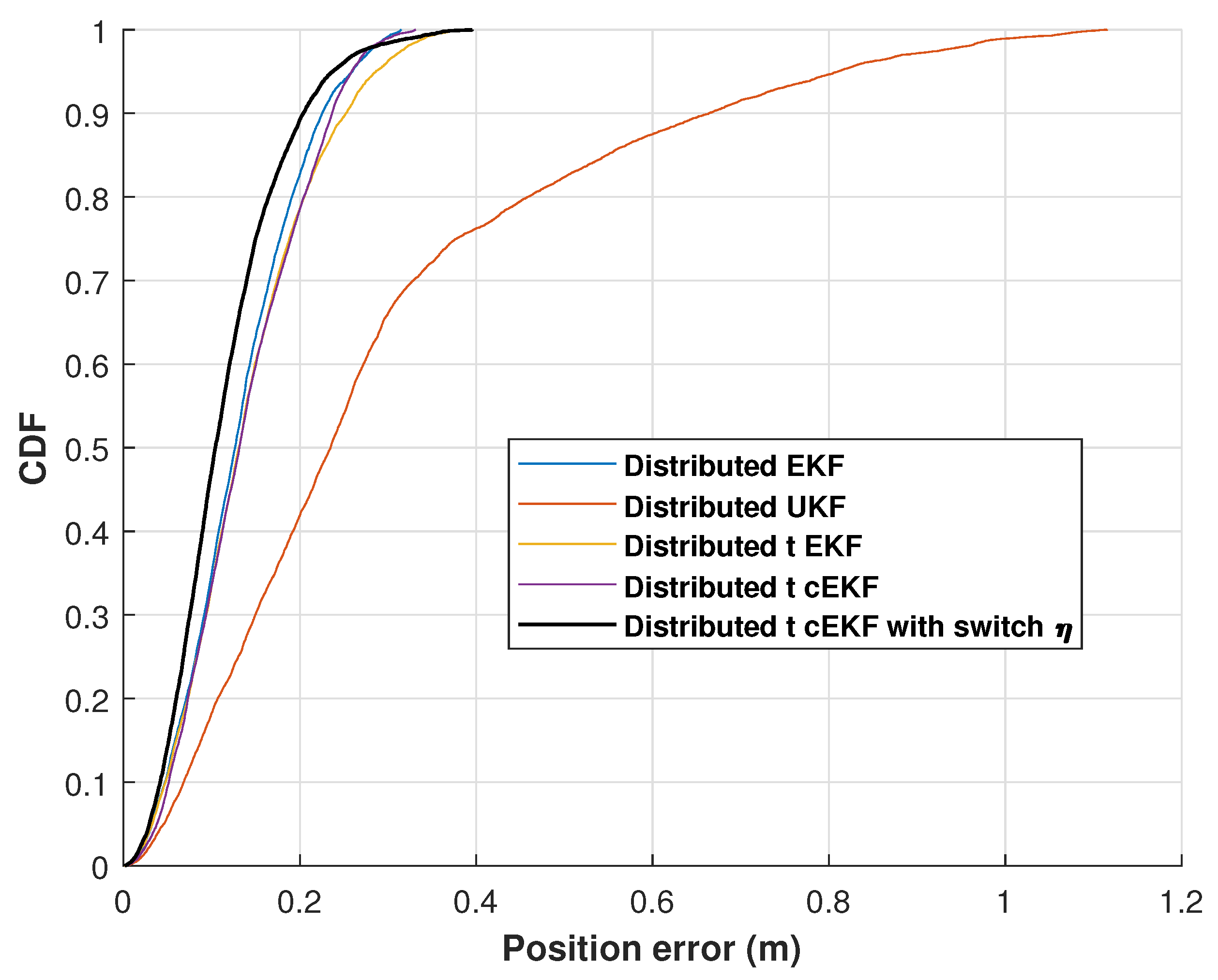
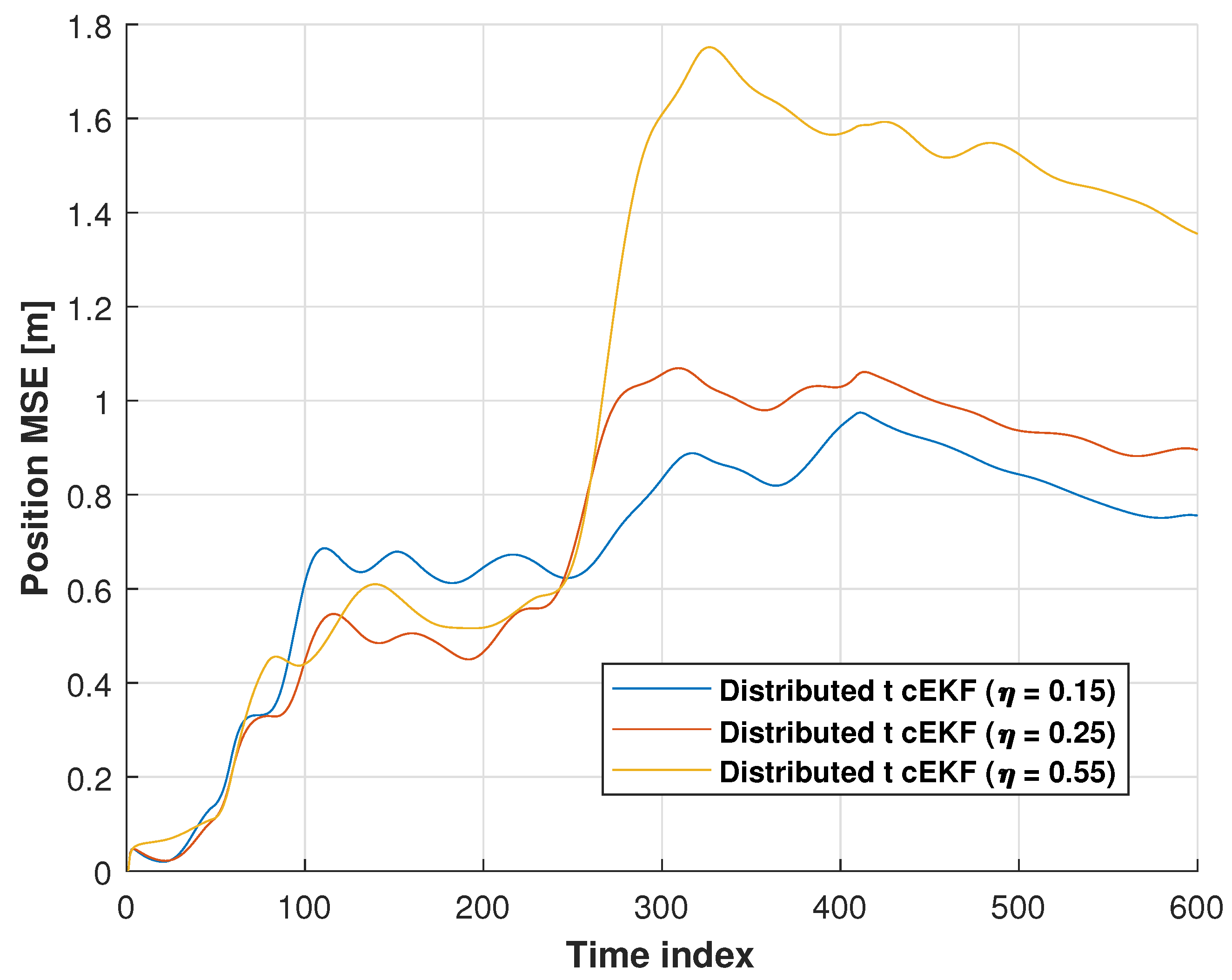
| Method | RMSE (m) | ||
|---|---|---|---|
| East Direction | North Direction | Mean | |
| Distributed EKF | 0.66 | 1.10 | 0.88 |
| Distributed UKF | 1.21 | 1.66 | 1.43 |
| Distributed EKF with Student’s t-distribution | 0.55 | 1.14 | 0.85 |
| t-distributed cEKF | 0.78 | 0.72 | 0.75 |
| t-distributed cEKF with switch | 0.54 | 0.49 | 0.52 |
| Method | RMSE (m) | ||
|---|---|---|---|
| East Direction | North Direction | Mean | |
| Distributed EKF | 0.08 | 0.11 | 0.10 |
| Distributed UKF | 0.19 | 0.32 | 0.26 |
| Distributed EKF with Student’s t-distribution | 0.09 | 0.12 | 0.11 |
| t-distributed cEKF | 0.09 | 0.12 | 0.11 |
| t-distributed cEKF with switch | 0.08 | 0.09 | 0.09 |
| RMSE (m) | |||
|---|---|---|---|
| East Direction | North Direction | Mean | |
| 0.15 | 0.61 | 0.62 | 0.62 |
| 0.25 | 0.67 | 0.66 | 0.67 |
| 0.55 | 0.80 | 0.85 | 0.83 |
| Method | Indoor Test (μs) | Outdoor Test (μs) |
|---|---|---|
| Distributed EKF | ||
| Distributed UKF | ||
| Distributed EKF with Student’s t-distribution | ||
| t-distributed cEKF | ||
| t-distributed cEKF with switch |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Yin, H.; Yang, M.; Deng, L.; Sun, M. Student’s t-Distributed Extended Kalman Filter with Switch Factor for UWB Localization Under Colored Measurement Noise. Micromachines 2025, 16, 1231. https://doi.org/10.3390/mi16111231
Xu Y, Yin H, Yang M, Deng L, Sun M. Student’s t-Distributed Extended Kalman Filter with Switch Factor for UWB Localization Under Colored Measurement Noise. Micromachines. 2025; 16(11):1231. https://doi.org/10.3390/mi16111231
Chicago/Turabian StyleXu, Yuan, Haoran Yin, Maosheng Yang, Lei Deng, and Mingxu Sun. 2025. "Student’s t-Distributed Extended Kalman Filter with Switch Factor for UWB Localization Under Colored Measurement Noise" Micromachines 16, no. 11: 1231. https://doi.org/10.3390/mi16111231
APA StyleXu, Y., Yin, H., Yang, M., Deng, L., & Sun, M. (2025). Student’s t-Distributed Extended Kalman Filter with Switch Factor for UWB Localization Under Colored Measurement Noise. Micromachines, 16(11), 1231. https://doi.org/10.3390/mi16111231









