A Review of Optical Metrology Techniques for Advanced Manufacturing Applications
Abstract
1. Introduction
2. Positioning Technology in Precision Manufacturing
2.1. Linear Displacement Measurement
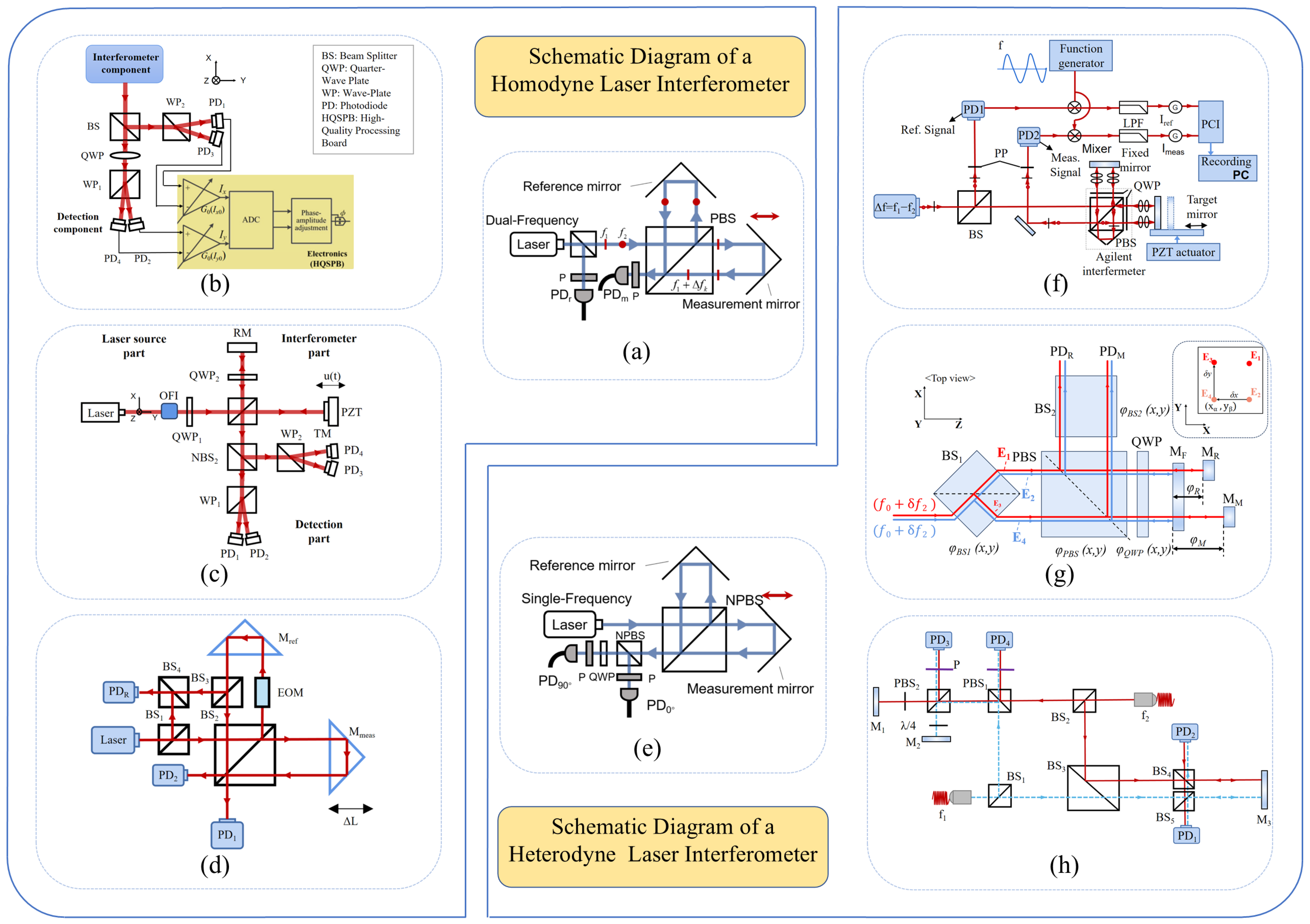
2.1.1. Laser Interferometer
2.1.2. Optical Linear Encoder
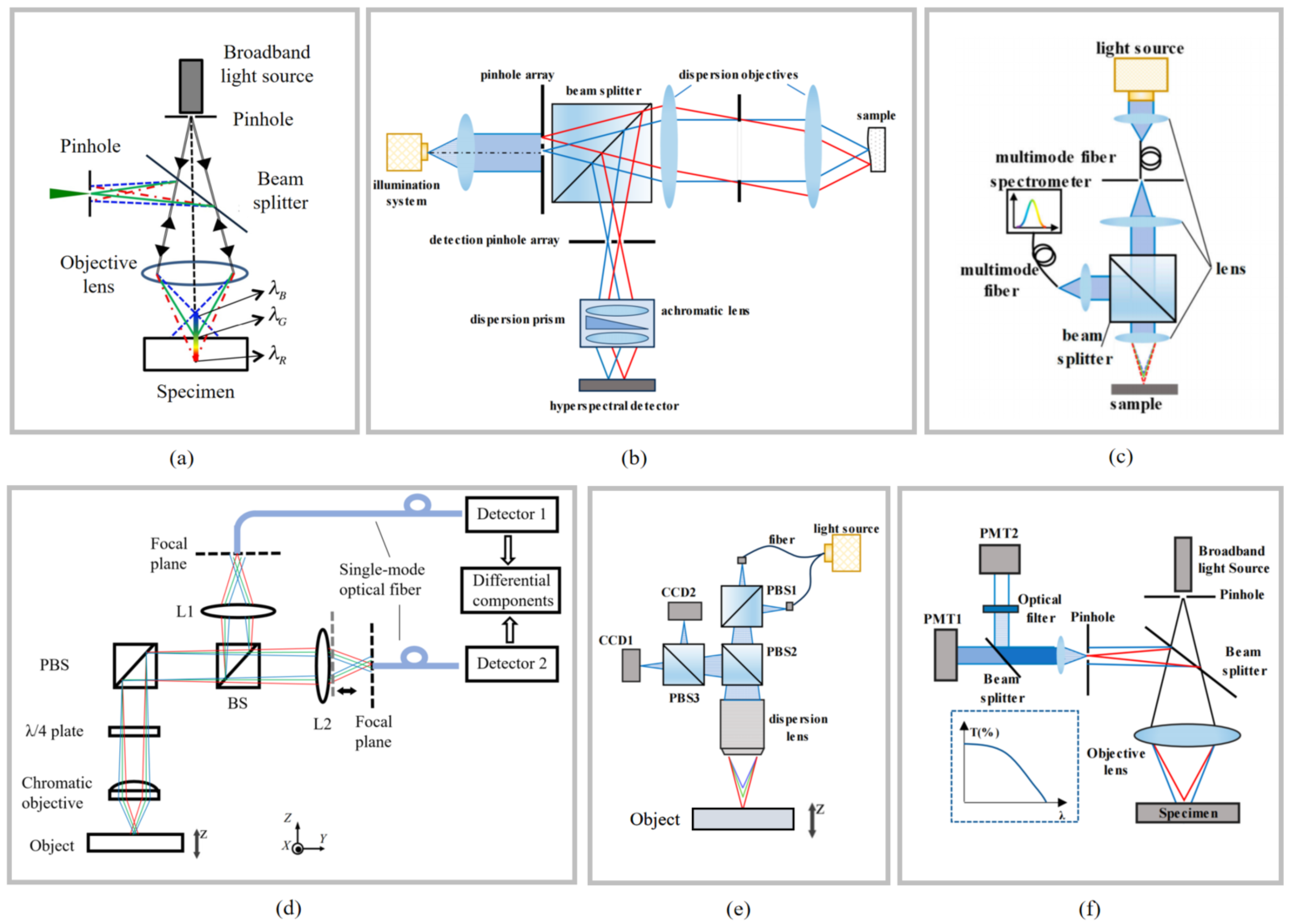
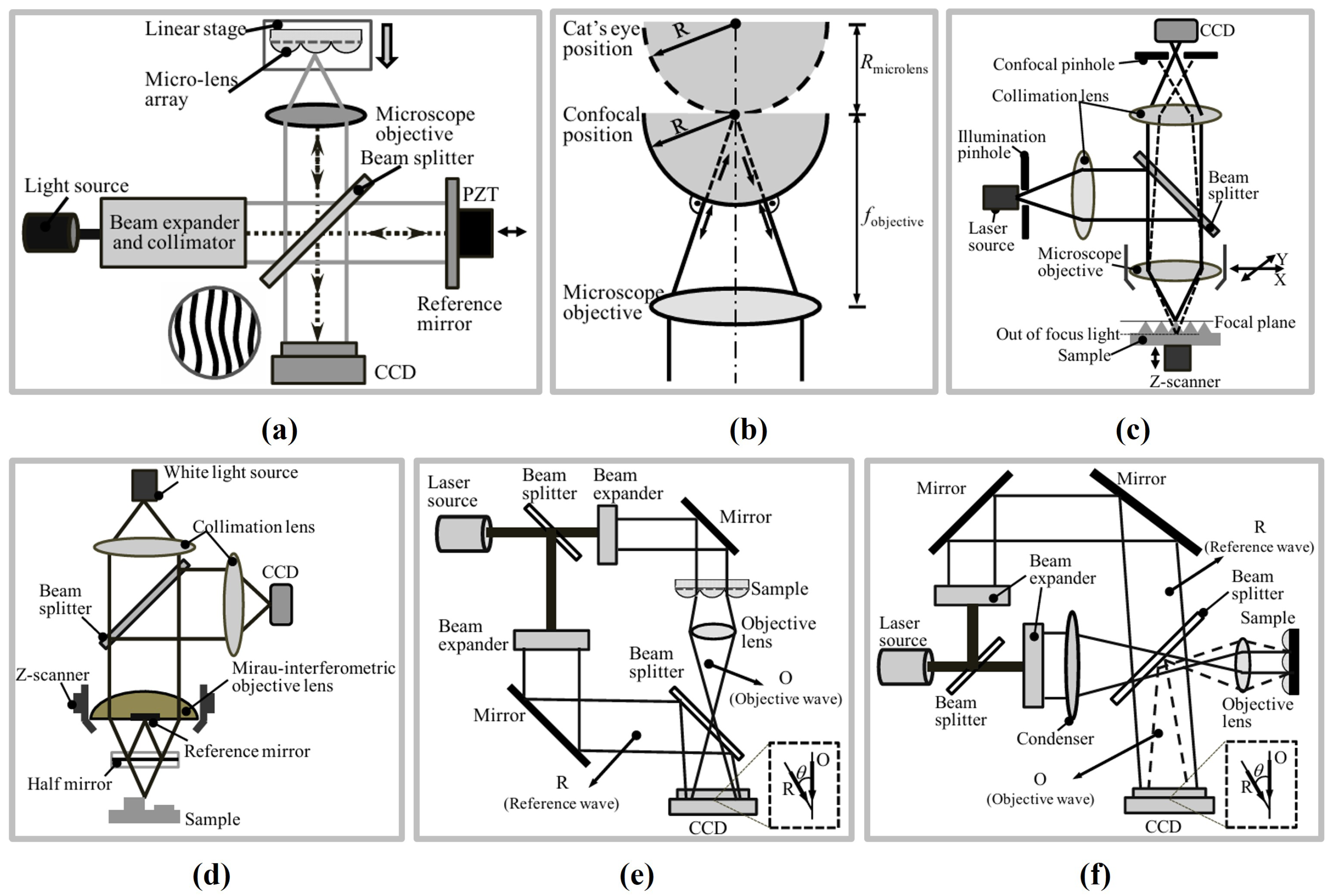
2.1.3. Confocal Measurement Method
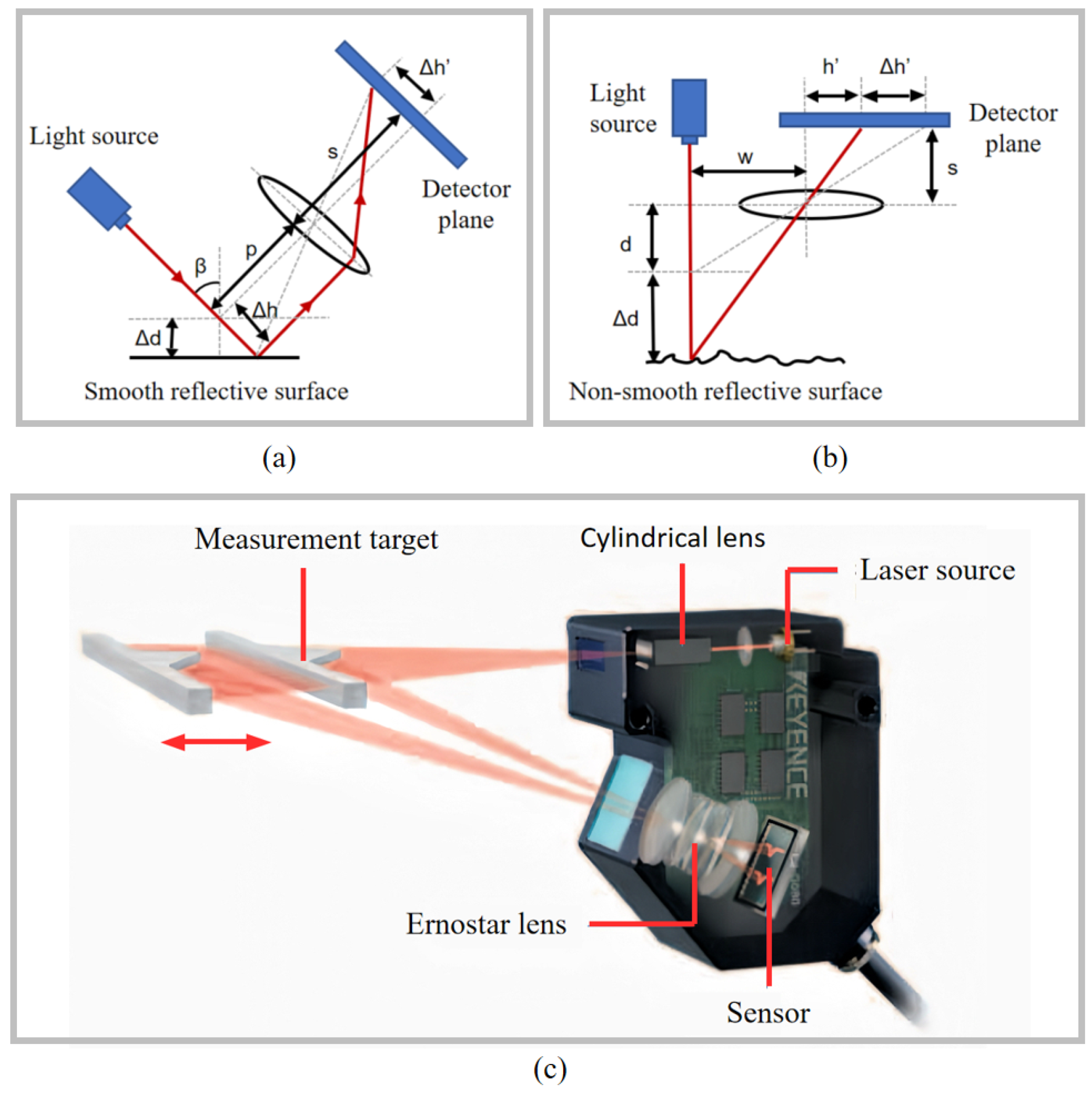
2.1.4. Laser Triangulation
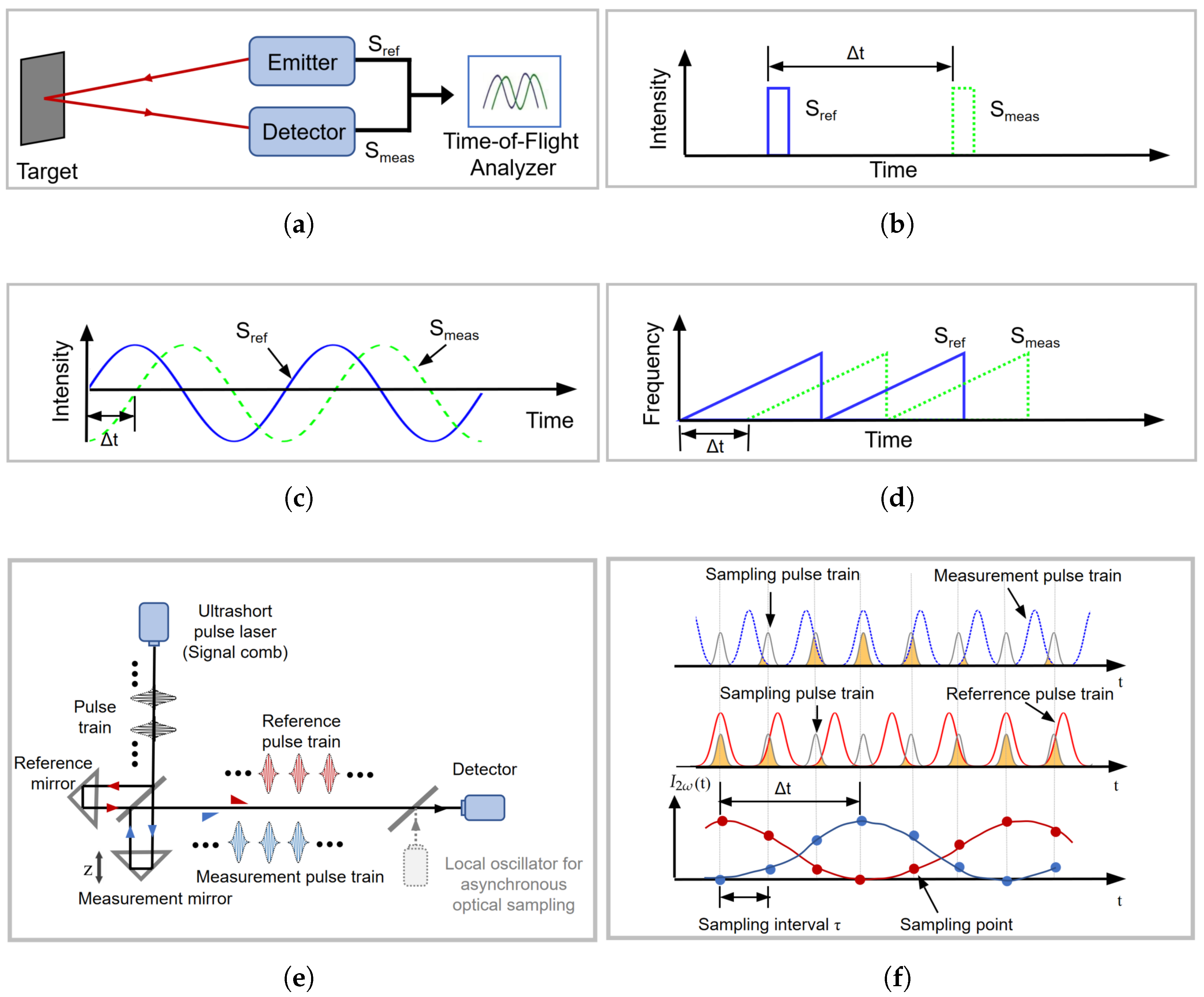
2.1.5. Time-of-Flight Measurement Method
2.2. Angular Displacement Measurement
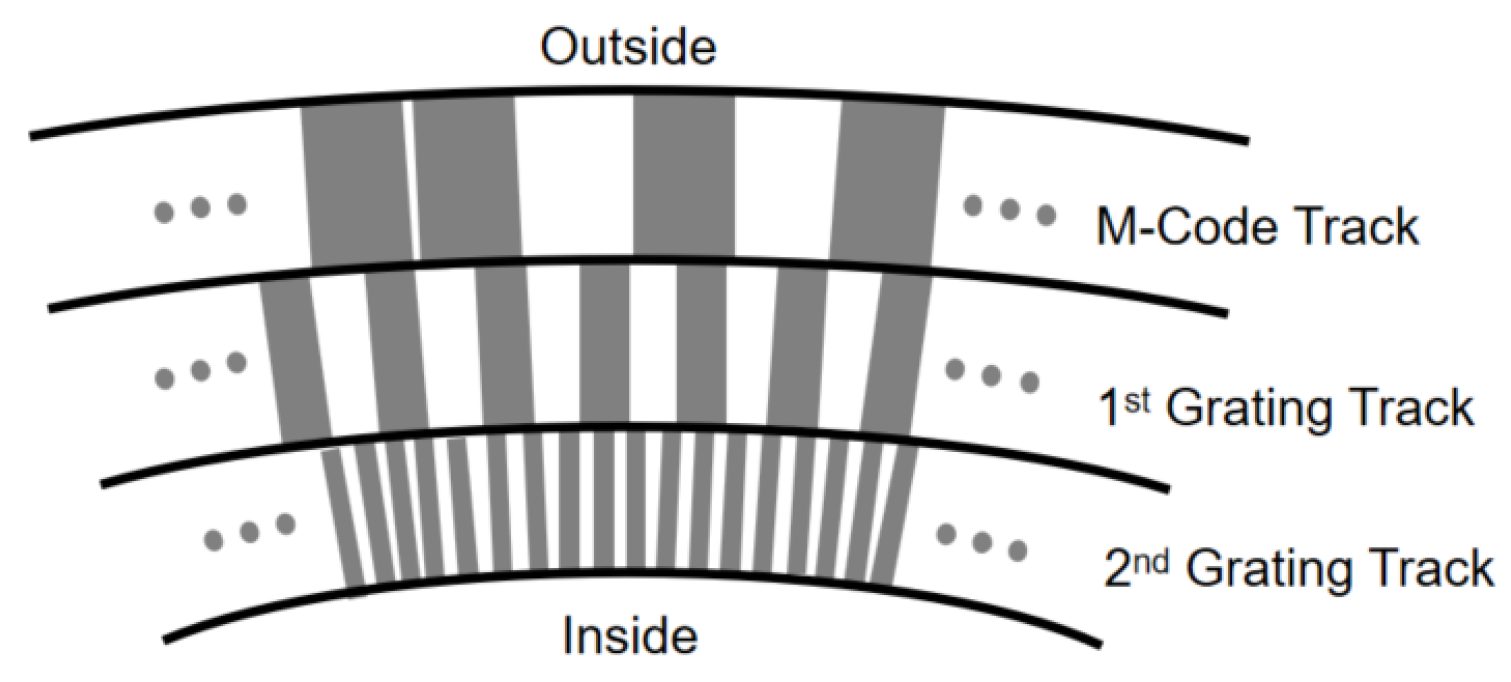
2.2.1. Rotary Encoder
2.2.2. Autocollimator
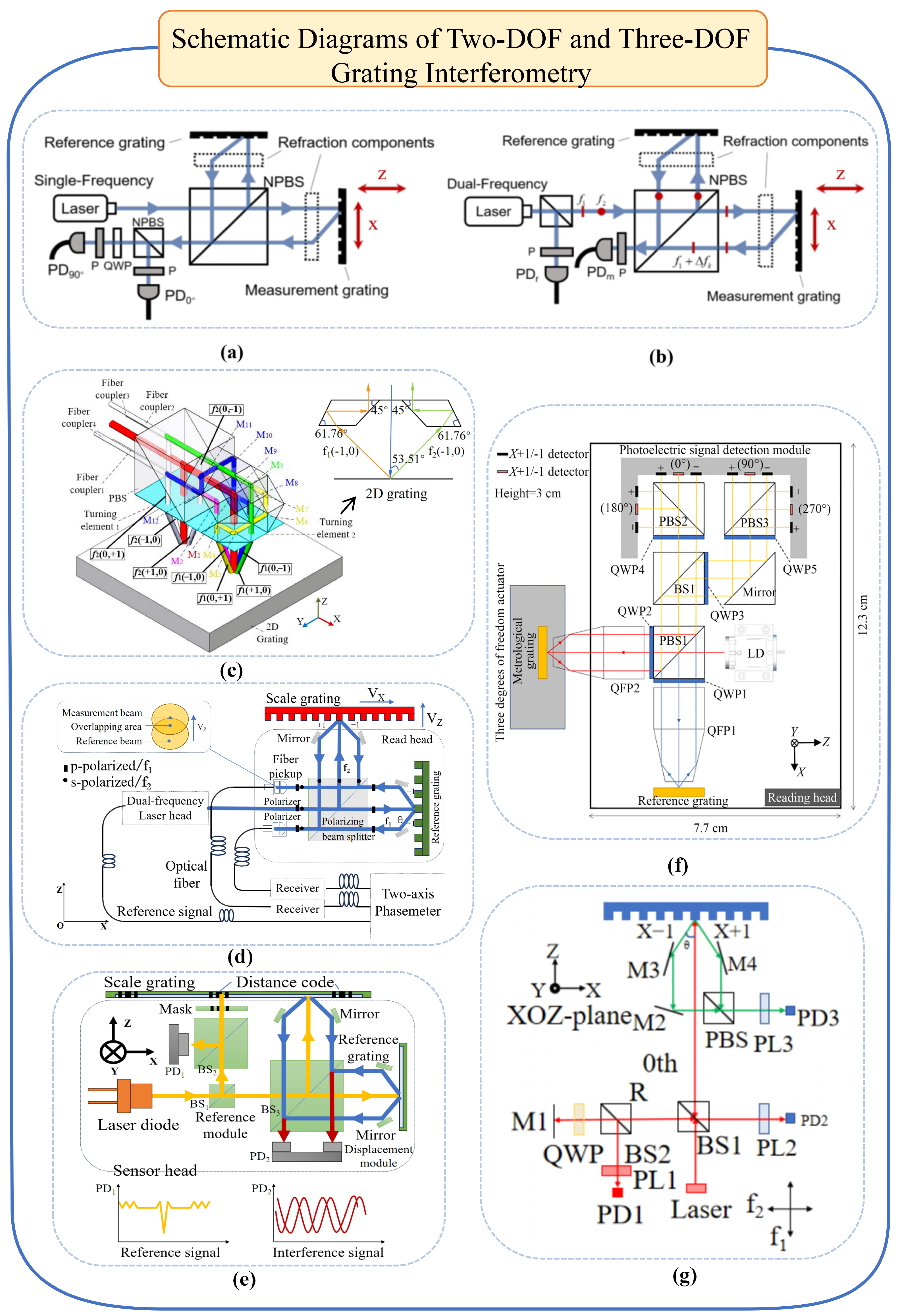
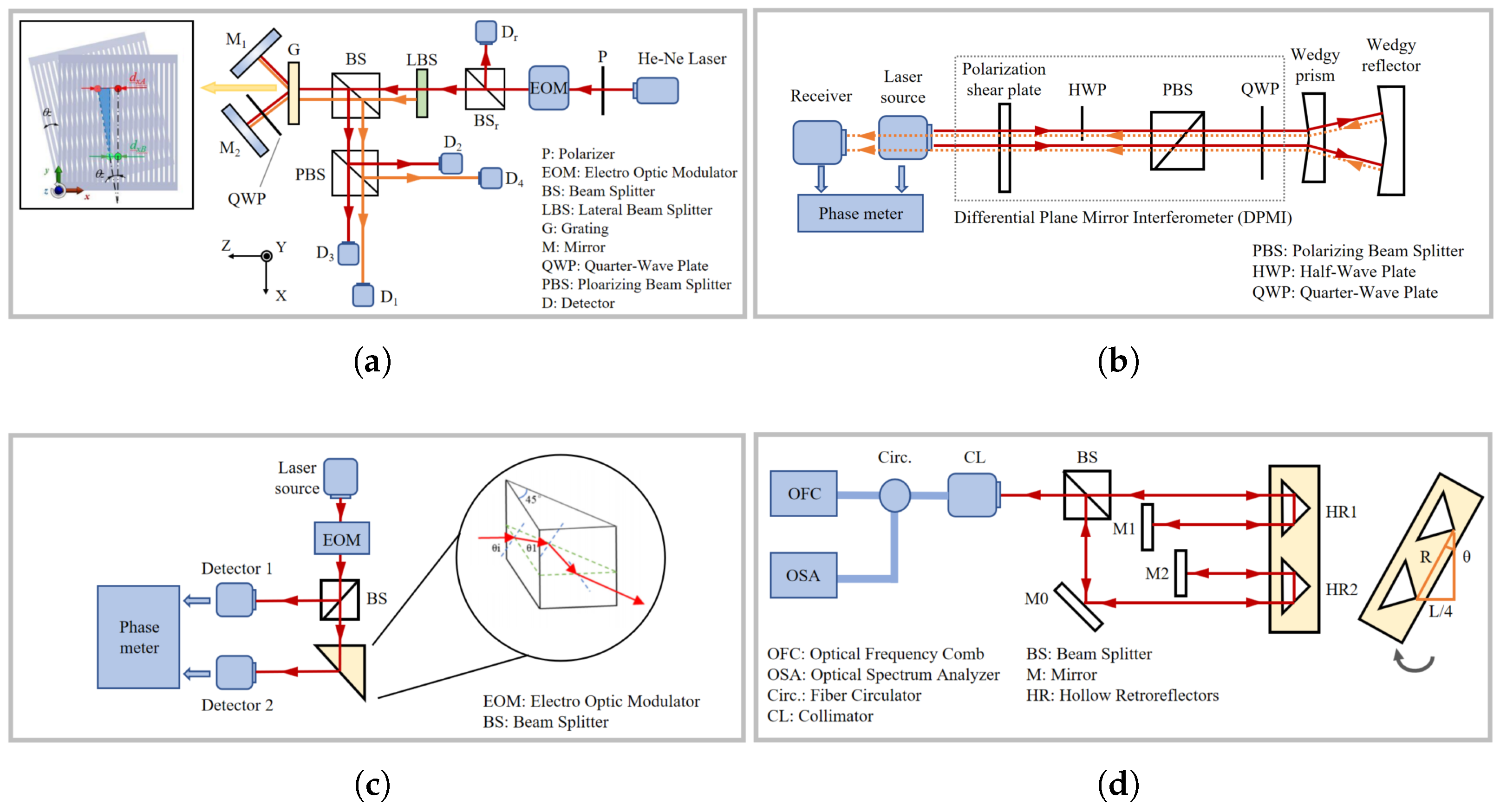
2.2.3. Interferometric Methods
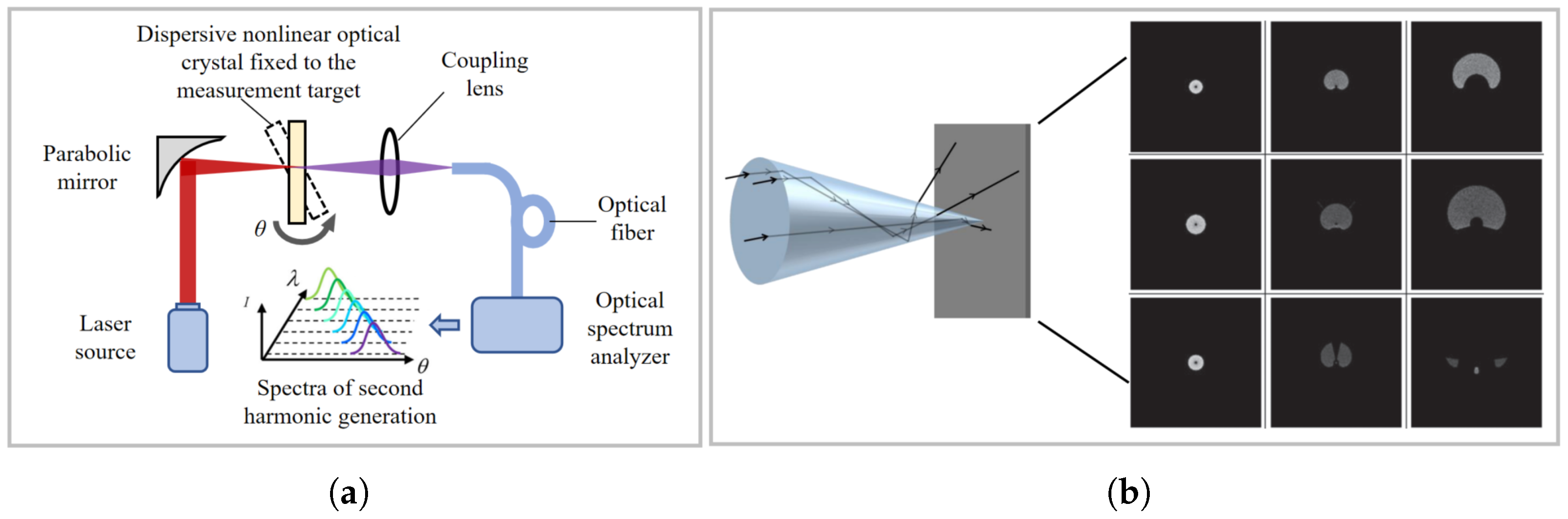
2.2.4. Emerging Angle Measurement Methods
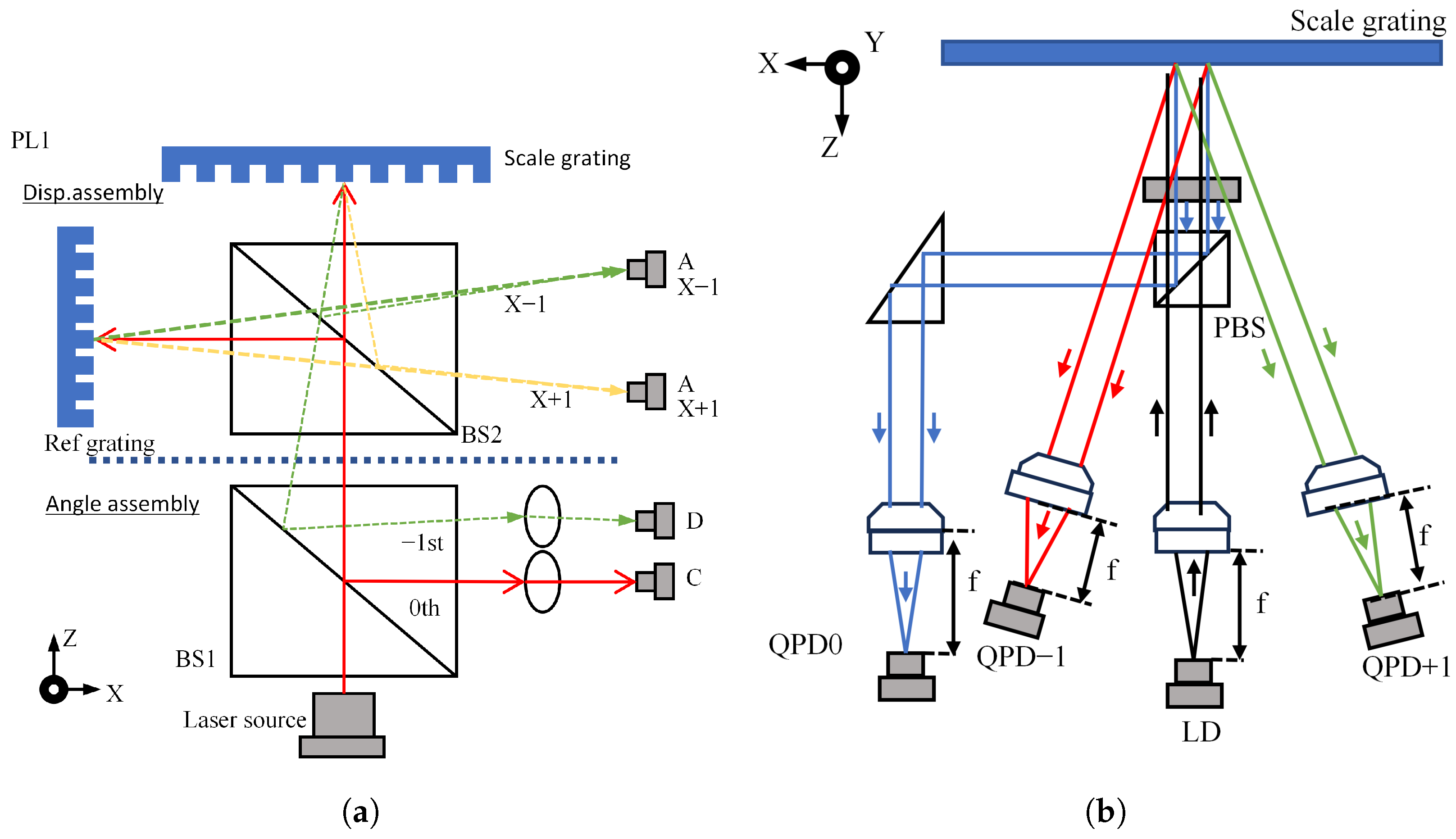
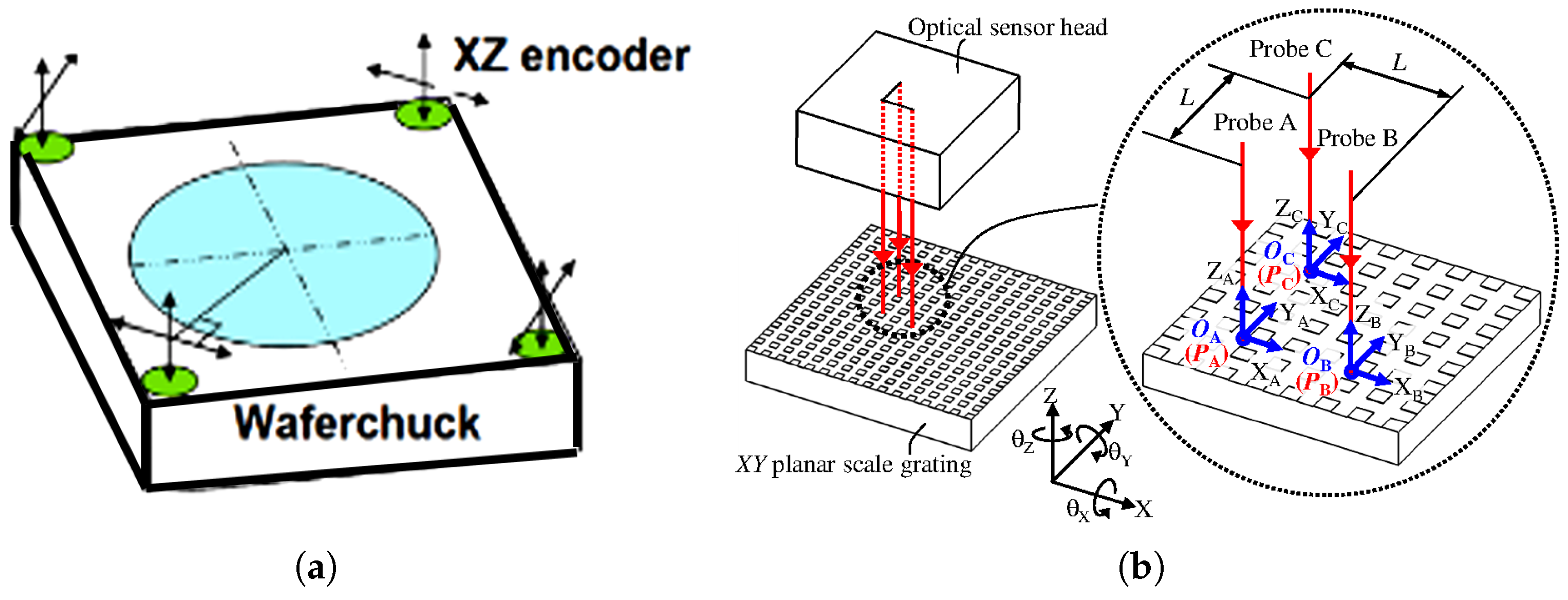
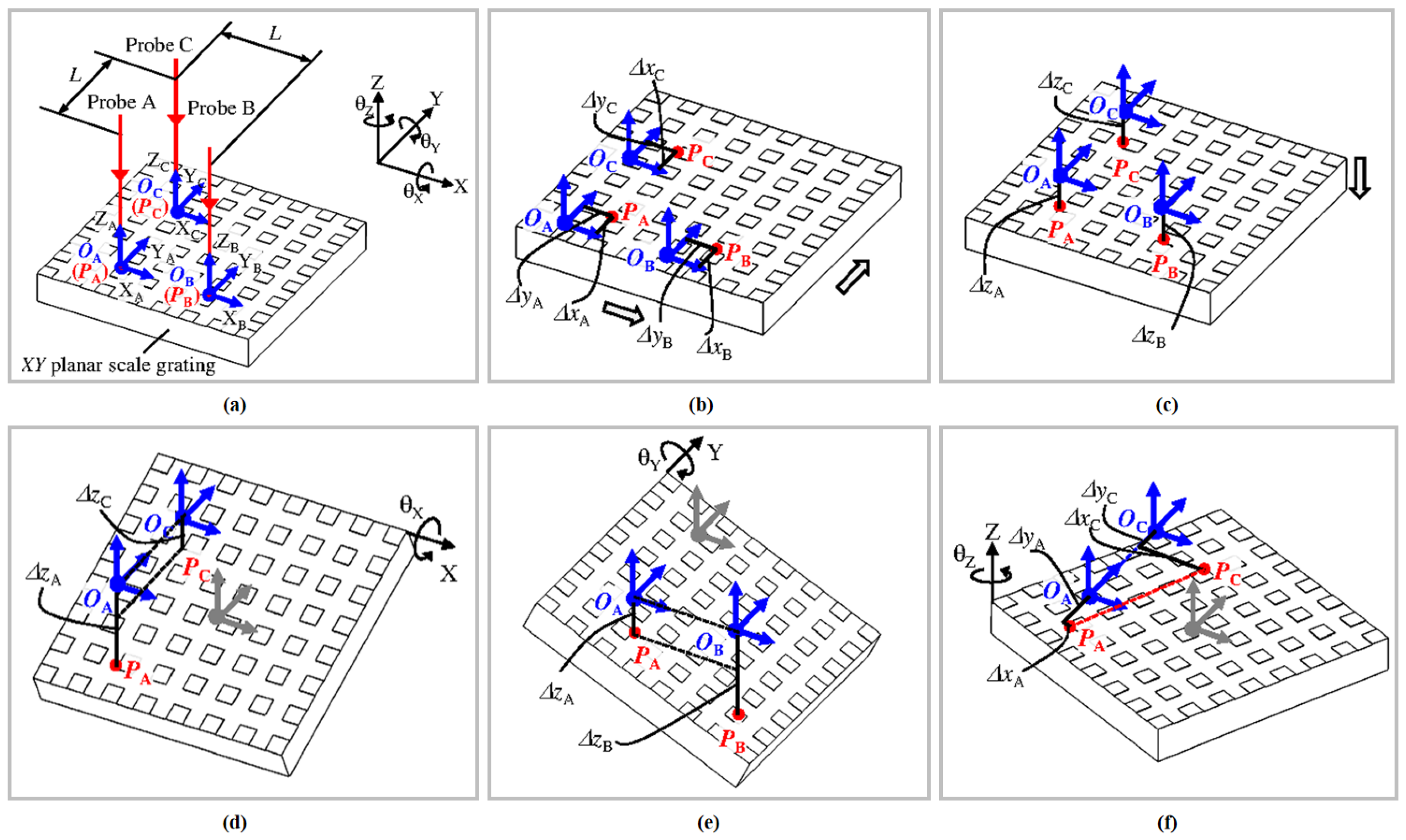
2.3. Integrated Linear and Angular Displacement Measurement
3. High-Precision Surface Characterization in Advanced Manufacturing
3.1. Large-Scale Freeform Surface Metrology
3.1.1. Synthetic Aperture Interferometry
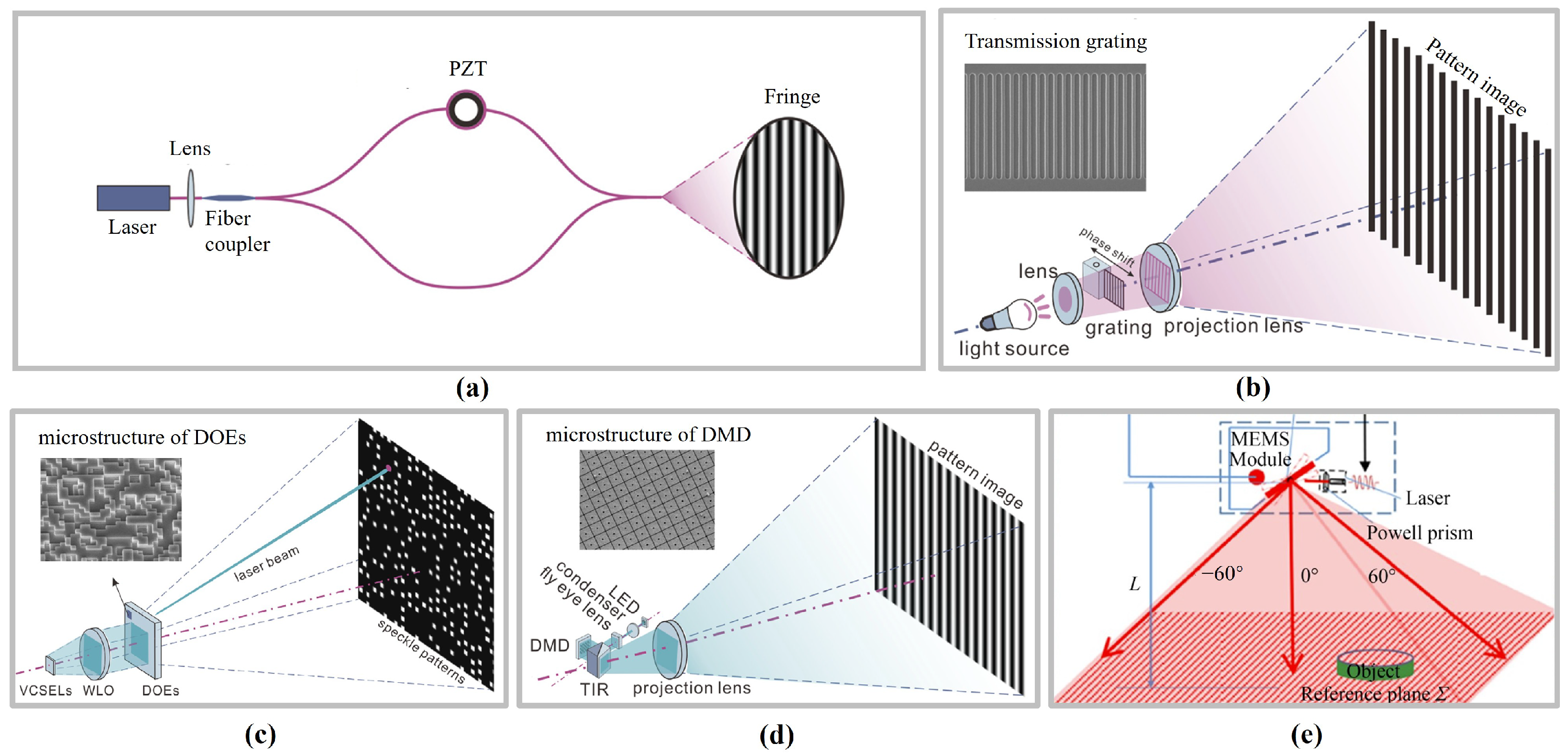
3.1.2. Structured Light Techniques
3.2. Micro- and Nano-Scale Surface Metrology
4. Conclusions and Outlook
4.1. Conclusions
4.2. Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- President’s Council of Advisors on Science and Technology (PCAST). Report to the President on Capturing Domestic Competitive Advantage in Advanced Manufacturing; Technical Report; Executive Office of the President: Washington, DC, USA, 2012. [Google Scholar]
- European Factories of the Future Research Association (EFFRA). Factories of the Future 2020: Strategic Multi-Annual Roadmap; Technical Report; European Commission and EFFRA: Brussels, Belgium, 2020. [Google Scholar]
- Gao, W.; Kim, S.W.; Bosse, H.; Haitjema, H.; Chen, Y.; Lu, X.; Knapp, W.; Weckenmann, A.; Estler, W.; Kunzmann, H. Measurement technologies for precision positioning. CIRP Ann. 2015, 64, 773–796. [Google Scholar] [CrossRef]
- Riemer, O. Advances in ultra precision manufacturing. Proc. Jpn. Soc. Precis. Eng 2011, 1–6. [Google Scholar]
- Yuan, J.; Lyu, B.; Hang, W.; Deng, Q. Review on the progress of ultra-precision machining technologies. Front. Mech. Eng. 2017, 12, 158–180. [Google Scholar] [CrossRef]
- Kwak, H.; Kim, J. Semiconductor multilayer nanometrology with machine learning. Nanomanuf. Metrol. 2023, 6, 15. [Google Scholar] [CrossRef]
- Cheng, C.; Wang, X.; Dong, J.; Wang, Z. Effect of Probe Lifting Height in Jumping Mode AFM for Living Cell Imaging. Nanomanuf. Metrol. 2023, 6, 24. [Google Scholar] [CrossRef]
- Fang, F. On the three paradigms of manufacturing advancement. Nanomanuf. Metrol. 2023, 6, 35. [Google Scholar] [CrossRef]
- Schwenke, H.; Neuschaefer-Rube, U.; Pfeifer, T.; Kunzmann, H. Optical methods for dimensional metrology in production engineering. CIrP Ann. 2002, 51, 685–699. [Google Scholar] [CrossRef]
- Kubina, P.; Adel, P.; Adler, F.; Grosche, G.; Hänsch, T.W.; Holzwarth, R.; Leitenstorfer, A.; Lipphardt, B.; Schnatz, H. Long term comparison of two fiber based frequency comb systems. Opt. Express 2005, 13, 904–909. [Google Scholar] [CrossRef]
- Jin, J. Dimensional metrology using the optical comb of a mode-locked laser. Meas. Sci. Technol. 2015, 27, 022001. [Google Scholar] [CrossRef]
- Zhang, C.; Duan, F.-J. Phase stepping methods based on PTDC for fiber-optic projected-fringe digital interferometry. Opt. Laser Technol. 2012, 44, 1089–1094. [Google Scholar]
- Osten, W.; Faridian, A.; Gao, P.; Körner, K.; Naik, D.; Pedrini, G.; Singh, A.K.; Takeda, M.; Wilke, M. Recent advances in digital holography. Appl. Opt. 2014, 53, G44–G63. [Google Scholar] [CrossRef]
- Huang, G.; Cui, C.; Lei, X.; Li, Q.; Yan, S.; Li, X.; Wang, G. A Review of Optical Interferometry for High-Precision Length Measurement. Micromachines 2024, 16, 6. [Google Scholar] [CrossRef]
- Zhao, P.; Gao, L.; Cui, C.; Ma, Y.; Yang, M.; Liu, L.; Li, X. A grating interferometer for improving optical subdivision in Z-axis measurement. In Proceedings of the Optical Metrology and Inspection for Industrial Applications XI, Nantong, China, 12–14 October 2024; Volume 13241, pp. 238–246. [Google Scholar]
- Wang, Y.; Shi, N.; Li, L.; Ni, K.; Li, X. Instantaneous grating signal subdivision system with non-linear Kalman filters. In Proceedings of the Optical Design and Testing XII, Virtual, 5–11 December 2022; Volume 12315, pp. 90–96. [Google Scholar]
- Wang, Y.; Zhao, F.; Luo, L.; Li, X. A Review on Recent Advances in Signal Processing in Interferometry. Sensors 2025, 25, 5013. [Google Scholar] [CrossRef]
- Luo, L.; Zhao, M.; Li, X. A Review: Grating Encoder Technologies for Multi-Degree-of-Freedom Spatial Measurement. Sensors 2025, 25, 6071. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Ma, R.; Bai, J. High-precision chromatic confocal technologies: A review. Micromachines 2024, 15, 1224. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.; Li, J.; Zhong, Z.; Li, X. Global alignment reference strategy for laser interference lithography pattern arrays. Microsystems Nanoeng. 2025, 11, 41. [Google Scholar] [CrossRef]
- Shao, C.; Li, X. Technologies for Fabricating Large-Size Diffraction Gratings. Sensors 2025, 25, 1990. [Google Scholar] [CrossRef] [PubMed]
- Yoshimoto, S. Handbook of Precision Positioning; Industrial Technologies Service Center Co., Ltd.: Tokyo, Japan, 2010. [Google Scholar]
- Oiwa, T.; Katsuki, M.; Karita, M.; Gao, W.; Makinouchi, S.; Sato, K.; Oohashi, Y. Questionnaire Survey on Ultra-Precision Positioning. Int. J. Autom. Technol. 2011, 5, 766–772. [Google Scholar] [CrossRef]
- Damm, C.; Peschel, T.; Risse, S.; Kirschstein, U.C. Wafer stage assembly for ion projection lithography. Microelectron. Eng. 2001, 57, 181–185. [Google Scholar] [CrossRef]
- Lan, H.; Ding, Y.; Liu, H.; Lu, B. Review of the wafer stage for nanoimprint lithography. Microelectron. Eng. 2007, 84, 684–688. [Google Scholar] [CrossRef]
- Kunzmann, H.; Pfeifer, T.; Flügge, J. Scales vs. laser interferometers performance and comparison of two measuring systems. CIRP Ann. 1993, 42, 753–767. [Google Scholar] [CrossRef]
- Estler, W.T.; Edmundson, K.; Peggs, G.; Parker, D. Large-scale metrology—An update. CIRP Ann. 2002, 51, 587–609. [Google Scholar] [CrossRef]
- Jywe, W.; Hsu, T.H.; Liu, C.H. Non-bar, an optical calibration system for five-axis CNC machine tools. Int. J. Mach. Tools Manuf. 2012, 59, 16–23. [Google Scholar] [CrossRef]
- Ruijl, T.A.M. Ultra Precision Coordinate Measuring Machine: Design, Calibration and Error Compensation. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2001. [Google Scholar]
- Manske, E.; Jäger, G.; Hausotte, T.; Füßl, R. Recent developments and challenges of nanopositioning and nanomeasuring technology. Meas. Sci. Technol. 2012, 23, 074001. [Google Scholar] [CrossRef]
- Gao, W.; Saito, Y.; Muto, H.; Arai, Y.; Shimizu, Y. A three-axis autocollimator for detection of angular error motions of a precision stage. CIRP Ann. 2011, 60, 515–518. [Google Scholar] [CrossRef]
- Hsieh, H.; Lee, J.; Wu, W.; Chen, J.; Deturche, R.; Lerondel, G. Quasi-common-optical-path heterodyne grating interferometer for displacement measurement. Meas. Sci. Technol. 2010, 21, 115304. [Google Scholar] [CrossRef]
- Shimizu, Y.; Chen, L.C.; Kim, D.W.; Chen, X.; Li, X.; Matsukuma, H. An insight into optical metrology in manufacturing. Meas. Sci. Technol. 2021, 32, 042003. [Google Scholar] [CrossRef]
- Gao, W.; Haitjema, H.; Fang, F.; Leach, R.; Cheung, C.; Savio, E.; Linares, J.M. On-machine and in-process surface metrology for precision manufacturing. Cirp Ann. 2019, 68, 843–866. [Google Scholar] [CrossRef]
- Yang, T.; Gu, F. Overview of modulation techniques for spatially structured-light 3D imaging. Opt. Laser Technol. 2024, 169, 110037. [Google Scholar] [CrossRef]
- Körner, K.; Windecker, R.; Fleischer, M.; Tiziani, H.J. One-grating projection for absolute three-dimensional profiling. Opt. Eng. 2001, 40, 1653–1660. [Google Scholar] [CrossRef]
- Harding, K.; Demuth, R.; Tait, R. 3D measurements using a programmable projector and a grating. In Proceedings of the Two- and Three-Dimensional Methods for Inspection and Metrology III, Boston, MA, USA, 24–26 October 2005; Volume 6000, pp. 118–124. [Google Scholar]
- Xu, B.; Jia, Z.; Li, X.; Chen, Y.L.; Shimizu, Y.; Ito, S.; Gao, W. Surface form metrology of micro-optics. In Proceedings of the International Conference on Optics in Precision Engineering and Nanotechnology (icOPEN2013), Singapore, 9–11 April 2013; Volume 8769, p. 876902. [Google Scholar]
- De Groot, P.J. A review of selected topics in interferometric optical metrology. Rep. Prog. Phys. 2019, 82, 056101. [Google Scholar] [CrossRef] [PubMed]
- Yacoot, A.; Kuetgens, U. Sub-atomic dimensional metrology: Developments in the control of x-ray interferometers. Meas. Sci. Technol. 2012, 23, 074003. [Google Scholar] [CrossRef]
- Meiners-Hagen, K.; Meyer, T.; Mildner, J.; Pollinger, F. SI-traceable absolute distance measurement over more than 800 meters with sub-nanometer interferometry by two-color inline refractivity compensation. Appl. Phys. Lett. 2017, 111, 191104. [Google Scholar] [CrossRef]
- Renishaw. XL-80 Laser Interferometer System. 2024. Available online: https://www.renishaw.com/en/xl-80-laser-system--8268 (accessed on 20 October 2025).
- Collaboration, L.S. LIGO—Laser Interferometer Gravitational-Wave Observatory. 2024. Available online: https://www.ligo.caltech.edu (accessed on 20 October 2025).
- Pisani, M. A homodyne Michelson interferometer with sub-picometer resolution. Meas. Sci. Technol. 2009, 20, 084008. [Google Scholar] [CrossRef]
- Lawall, J.; Kessler, E. Michelson interferometry with 10 pm accuracy. Rev. Sci. Instrum. 2000, 71, 2669–2676. [Google Scholar] [CrossRef]
- Hu, P.; Zhu, J.; Zhai, X.; Tan, J. DC-offset-free homodyne interferometer and its nonlinearity compensation. Opt. Express 2015, 23, 8399–8408. [Google Scholar] [CrossRef]
- Cui, J.; He, Z.; Jiu, Y.; Tan, J.; Sun, T. Homodyne laser interferometer involving minimal quadrature phase error to obtain subnanometer nonlinearity. Appl. Opt. 2016, 55, 7086–7092. [Google Scholar] [CrossRef]
- Yan, L.; Chen, B.; Chen, Z.; Xie, J.; Zhang, E.; Zhang, S. Phase-modulated dual-homodyne interferometer without periodic nonlinearity. Meas. Sci. Technol. 2017, 28, 115006. [Google Scholar] [CrossRef]
- Shi, N.; Zhu, J.; Wang, S.; Han, Y.; Yu, K.; Li, X.; Wang, X. FPGA displacement calculation platform and test of two-phase grating interference encoder. In Proceedings of the 2021 International Conference on Optical Instruments and Technology: Optoelectronic Measurement Technology and Systems, Online, 8–10 April 2022; Volume 12282, pp. 372–383. [Google Scholar]
- Lu, S.; Wang, Y.; Li, X. Robust phase measurement of high-speed signals using frequency tracking lock-in method. In Proceedings of the Holography, Diffractive Optics, and Applications XIV, Nantong, China, 12–15 October 2024; Volume 13240, pp. 188–197. [Google Scholar]
- He, Y.; Orr, B.J. Optical heterodyne signal generation and detection in cavity ringdown spectroscopy based on a rapidly swept cavity. Chem. Phys. Lett. 2001, 335, 215–220. [Google Scholar] [CrossRef]
- Takenaka, T.; Tanaka, K.; Fukumitsu, O. Signal-to-noise ratio in optical heterodyne detection for Gaussian fields. Appl. Opt. 1978, 17, 3466–3471. [Google Scholar] [CrossRef] [PubMed]
- Hu, P.; Wang, J.; Lin, X.; Xing, X.; Fu, H.; Tan, J. Phase measurement method based on digital dual frequency comb for high-precision high-speed heterodyne interferometry. IEEE Sens. J. 2023, 23, 9707–9715. [Google Scholar] [CrossRef]
- Ma, Y.; Wang, Y.; Lu, S.; Wang, S.; Li, X. High-accuracy and real-time phase solution algorithm based on extended Kalman filter for multi-degree-of-freedom grating interferometer. In Proceedings of the Optoelectronic Devices and Integration XIII, SPIE, Nantong, China, 2–14 October 2024; Volume 13236, pp. 99–108. [Google Scholar]
- Demarest, F.C. High-resolution, high-speed, low data age uncertainty, heterodyne displacement measuring interferometer electronics. Meas. Sci. Technol. 1998, 9, 1024. [Google Scholar] [CrossRef]
- Joo, K.N.; Ellis, J.D.; Spronck, J.W.; van Kan, P.J.; Schmidt, R.H.M. Simple heterodyne laser interferometer with subnanometer periodic errors. Opt. Lett. 2009, 34, 386–388. [Google Scholar] [CrossRef] [PubMed]
- Joo, K.N.; Ellis, J.D.; Buice, E.S.; Spronck, J.W.; Schmidt, R.H.M. High resolution heterodyne interferometer without detectable periodic nonlinearity. Opt. Express 2010, 18, 1159–1165. [Google Scholar] [CrossRef]
- Yan, H.; Duan, H.Z.; Li, L.T.; Liang, Y.R.; Luo, J.; Yeh, H.C. A dual-heterodyne laser interferometer for simultaneous measurement of linear and angular displacements. Rev. Sci. Instruments 2015, 86, 123102. [Google Scholar] [CrossRef] [PubMed]
- Joo, K.N.; Clark, E.; Zhang, Y.; Ellis, J.D.; Guzmán, F. A compact high-precision periodic-error-free heterodyne interferometer. J. Opt. Soc. Am. A 2020, 37, B11–B18. [Google Scholar] [CrossRef]
- Dong, N.T.; Tai, N.T.; Hoang, D.V.; Mai, N.T.P.; Tung, V.T.; Thang, V.T. Sub-nanometer displacement measurement using heterodyne interferometer and down-beat frequency technique. In Proceedings of the Regional Conference in Mechanical Manufacturing Engineering; Springer: Berlin/Heidelberg, Germany, 2021; pp. 1170–1176. [Google Scholar]
- Lay, O.P.; Dubovitsky, S.; Peters, R.D.; Burger, J.; Steier, W.H.; Ahn, S.W.; Fetterman, H.R. MSTAR: An absolute metrology system with submicrometer accuracy. In Proceedings of the New Frontiers in Stellar Interferometry, SPIE, Glasgow, UK, 21–25 June 2004; Volume 5491, pp. 1068–1078. [Google Scholar]
- Mildner, J.; Meiners-Hagen, K.; Pollinger, F. Dual-frequency comb generation with differing GHz repetition rates by parallel Fabry–Perot cavity filtering of a single broadband frequency comb source. Meas. Sci. Technol. 2016, 27, 074011. [Google Scholar] [CrossRef]
- Yang, R.; Pollinger, F.; Meiners-Hagen, K.; Krystek, M.; Tan, J.; Bosse, H. Absolute distance measurement by dual-comb interferometry with multi-channel digital lock-in phase detection. Meas. Sci. Technol. 2015, 26, 084001. [Google Scholar] [CrossRef]
- Kim, S.W. Combs rule. Nat. Photonics 2009, 3, 313–314. [Google Scholar] [CrossRef]
- Xiaoli, D.; Katuo, S. High-accuracy absolute distance measurement by means of wavelength scanning heterodyne interferometry. Meas. Sci. Technol. 1998, 9, 1031. [Google Scholar] [CrossRef]
- Swinkels, B.; Bhattacharya, N.; Braat, J. Correcting movement errors in frequency-sweeping interferometry. Opt. Lett. 2005, 30, 2242–2244. [Google Scholar] [CrossRef]
- Coveney, T. A review of state-of-the-art 1D length scale calibration instruments. Meas. Sci. Technol. 2020, 31, 042002. [Google Scholar] [CrossRef]
- Jang, Y.S.; Kim, S.W. Compensation of the refractive index of air in laser interferometer for distance measurement: A review. Int. J. Precis. Eng. Manuf. 2017, 18, 1881–1890. [Google Scholar] [CrossRef]
- de Groot, P.J.; Badami, V.G.; Liesener, J. Concepts and geometries for the next generation of precision heterodyne optical encoders. In Proceedings of the Annual Meeting of the American Society for Precision Engineering (ASPE 2016), Portland, OR, USA, 23–28 October 2016; pp. 23–28. [Google Scholar]
- Teimel, A. Technology and applications of grating interferometers in high-precision measurement. Precis. Eng. 1992, 14, 147–154. [Google Scholar] [CrossRef]
- Wang, H.; Wang, J.; Chen, B.; Xiao, P.; Chen, X.; Cai, N.; Ling, B.W.K. Absolute optical imaging position encoder. Measurement 2015, 67, 42–50. [Google Scholar] [CrossRef]
- Magnescale, C. Feedback Scale General Catalog. 2018. Available online: https://www.magnescale.com/product/catalog/FeedbackScale_en.pdf (accessed on 20 October 2025).
- Elektronik, R. MS 15 Product Page. Available online: https://www.rsf.at/en/produkte/ms-15/ (accessed on 20 October 2025).
- DR. JOHANNES HEIDENHAIN GmbH. LC 200 Series—Sealed Linear Encoders. 2024. Available online: https://www.heidenhain.com/products/linear-encoders/sealed/lc-200 (accessed on 20 October 2025).
- Renishaw plc. TONiC™ Optical Incremental Encoder Series. 2024. Available online: https://www.renishaw.com/en/tonic-optical-incremental-encoder-series--37824 (accessed on 20 October 2025).
- Magnescale Co., Ltd. BL50H—Ultra-Precision Laserscale Position Sensor. 2024. Available online: https://www.magnescale.com/en/news/BL50H.html (accessed on 20 October 2025).
- Zygo Corporation. Precision Metrology Solutions for Photolithography Stages. 2024. Available online: https://www.zygo.com/applications/what-we-measure/photolithography-stages (accessed on 20 October 2025).
- Lee, C.; Lee, S.K. Multi-degree-of-freedom motion error measurement in an ultraprecision machine using laser encoder. J. Mech. Sci. Technol. 2013, 27, 141–152. [Google Scholar] [CrossRef]
- Bai, Y.; Hu, P.; Lu, Y.; Li, Z.; Zhang, Z.; Tan, J. A six-axis heterodyne interferometer system for the joule balance. IEEE Trans. Instrum. Meas. 2016, 66, 1579–1585. [Google Scholar] [CrossRef]
- Gao, Z.; Hu, J.; Zhu, Y.; Duan, G. A new 6-degree-of-freedom measurement method of XY stages based on additional information. Precis. Eng. 2013, 37, 606–620. [Google Scholar] [CrossRef]
- Lazar, J.; Číp, O.; Čížek, M.; Hrabina, J.; Šerỳ, M.; Rapublic, C.; Klapetek, P. Multiaxis interferometric system for positioning in nanometrology. In Proceedings of the 9th WSEAS International Conference on Microelectronics, Nanoelectronics, Optoelectronics, Catania, Italy, 29–31 May 2010; Volume 9, pp. 92–95. [Google Scholar]
- Deng, J.; Yan, X.; Wei, C.; Lu, Y.; Li, M.; Xiang, X.; Jia, W.; Zhou, C. Eightfold optical encoder with high-density grating. Appl. Opt. 2018, 57, 2366–2375. [Google Scholar] [CrossRef]
- Hori, Y.; Gonda, S.; Bitou, Y.; Watanabe, A.; Nakamura, K. Periodic error evaluation system for linear encoders using a homodyne laser interferometer with 10 picometer uncertainty. Precis. Eng. 2018, 51, 388–392. [Google Scholar] [CrossRef]
- Wang, S.; Liao, B.; Shi, N.; Li, X. A compact and high-precision three-degree-of-freedom grating encoder based on a quadrangular frustum pyramid prism. Sensors 2023, 23, 4022. [Google Scholar] [CrossRef]
- Han, Y.; Ni, K.; Li, X.; Wu, G.; Yu, K.; Zhou, Q.; Wang, X. An fpga platform for next-generation grating encoders. Sensors 2020, 20, 2266. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Shi, Y.; Xiao, X.; Zhou, Q.; Wu, G.; Lu, H.; Ni, K. Design and testing of a compact optical prism module for multi-degree-of-freedom grating interferometry application. Appl. Sci. 2018, 8, 2495. [Google Scholar] [CrossRef]
- Lin, C.; Yan, S.; Du, Z.; Wei, C.; Wang, G. High-efficiency gold-coated cross-grating for heterodyne grating interferometer with improved signal contrast and optical subdivision. Opt. Commun. 2015, 339, 86–93. [Google Scholar] [CrossRef]
- Cui, C. Grating interferometric precision nanometric measurement technology. Opt. Precis. Eng. 2024, 32, 2591–2611. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, S.; Li, X. Ultraprecision grating positioning technology for wafer stage of lithography machine. Laser Optoelectron. Prog 2022, 59, 0922019. [Google Scholar]
- Cui, C.; Li, X.; Wang, X. Grating interferometer: The dominant positioning strategy in atomic and close-to-atomic scale manufacturing. J. Manuf. Syst. 2025, 82, 1227–1251. [Google Scholar] [CrossRef]
- Lin, C.; Yan, S.; Ding, D.; Wang, G. Two-dimensional diagonal-based heterodyne grating interferometer with enhanced signal-to-noise ratio and optical subdivision. Opt. Eng. 2018, 57, 064102. [Google Scholar] [CrossRef]
- Yang, F.; Zhang, M.; Zhu, Y.; Ye, W.; Wang, L.; Xia, Y. Two degree-of-freedom fiber-coupled heterodyne grating interferometer with milli-radian operating range of rotation. Sensors 2019, 19, 3219. [Google Scholar] [CrossRef]
- Chang, D.; Xing, X.; Hu, P.; Wang, J.; Tan, J. Double-diffracted spatially separated heterodyne grating interferometer and analysis on its alignment tolerance. Appl. Sci. 2019, 9, 263. [Google Scholar] [CrossRef]
- Yin, Y.; Liu, Z.; Jiang, S.; Wang, W.; Yu, H.; Jiri, G.; Hao, Q.; Li, W. High-precision 2D grating displacement measurement system based on double-spatial heterodyne optical path interleaving. Opt. Lasers Eng. 2022, 158, 107167. [Google Scholar] [CrossRef]
- Molnar, G.; Strube, S.; Köchert, P.; Danzebrink, H.; Flügge, J. Simultaneous multiple degrees of freedom (DoF) measurement system. Meas. Sci. Technol. 2016, 27, 084011. [Google Scholar] [CrossRef]
- Feng, X.; Lin, X.; Yu, L. 3-DOF angle measurement method based on two interference images. In Proceedings of the International Academic Conference on Optics and Photonics (IACOP 2023), Online, 29–30 October 2024; Volume 12972, pp. 14–25. [Google Scholar]
- Wu, Q.; Yang, M.; Liu, Z.; Cai, C.; Wang, Y.; Wang, D. Monocular vision-based decoupling measurement method for multi-degree-of-freedom motion. IEEE Sens. J. 2024, 24, 35092–35100. [Google Scholar] [CrossRef]
- Kimura, A.; Gao, W.; Arai, Y.; Lijiang, Z. Design and construction of a two-degree-of-freedom linear encoder for nanometric measurement of stage position and straightness. Precis. Eng. 2010, 34, 145–155. [Google Scholar] [CrossRef]
- Kimura, A.; Gao, W.; Lijiang, Z. Position and out-of-straightness measurement of a precision linear air-bearing stage by using a two-degree-of-freedom linear encoder. Meas. Sci. Technol. 2010, 21, 054005. [Google Scholar] [CrossRef]
- Kimura, A.; Hosono, K.; Kim, W.; Shimizu, Y.; Gao, W.; Zeng, L. A two-degree-of-freedom linear encoder with a mosaic scale grating. Int. J. Nanomanuf. 2011, 7, 73–91. [Google Scholar] [CrossRef]
- Zhu, K.; Guo, B.; Lu, Y.; Zhang, S.; Tan, Y. Single-spot two-dimensional displacement measurement based on self-mixing interferometry. Optica 2017, 4, 729–735. [Google Scholar] [CrossRef]
- Shi, Y.; Ni, K.; Li, X.; Zhou, Q.; Wang, X. Highly accurate, absolute optical encoder using a hybrid-positioning method. Opt. Lett. 2019, 44, 5258–5261. [Google Scholar] [CrossRef] [PubMed]
- Ren, W.; Cui, J.; Tan, J. A three-dimensional small angle measurement system based on autocollimation method. Rev. Sci. Instrum. 2022, 93, 055102. [Google Scholar] [CrossRef]
- Shimizu, Y.; Ito, T.; Li, X.; Kim, W.; Gao, W. Design and testing of a four-probe optical sensor head for three-axis surface encoder with a mosaic scale grating. Meas. Sci. Technol. 2014, 25, 094002. [Google Scholar] [CrossRef]
- Lin, J.; Guan, J.; Wen, F.; Tan, J. High-resolution and wide range displacement measurement based on planar grating. Opt. Commun. 2017, 404, 132–138. [Google Scholar] [CrossRef]
- Wang, S.; Zhu, J.; Shi, N.; Luo, L.; Wen, Y.; Li, X. Modeling and test of an absolute four-degree-of-freedom (DOF) grating encoder. In Proceedings of the Optical Metrology and Inspection for Industrial Applications IX, Online, 5–11 December 2022; Volume 12319, pp. 72–78. [Google Scholar]
- Luo, L.; Gao, L.; Wang, S.; Deng, F.; Wu, Y.; Li, X. An ultra-precision error estimation for a multi-axes grating encoder using quadrant photodetectors. In Proceedings of the Optical Metrology and Inspection for Industrial Applications IX, Online, 5–11 December 2022; Volume 12319, pp. 57–65. [Google Scholar]
- Saito, Y.; Arai, Y.; Gao, W. Detection of three-axis angles by an optical sensor. Sens. Actuators A Phys. 2009, 150, 175–183. [Google Scholar] [CrossRef]
- Lee, C.; Kim, G.H.; Lee, S.K. Design and construction of a single unit multi-function optical encoder for a six-degree-of-freedom motion error measurement in an ultraprecision linear stage. Meas. Sci. Technol. 2011, 22, 105901. [Google Scholar]
- Zhu, J.; Wang, G.; Wang, S.; Li, X. A reflective-type heterodyne grating interferometer for three-degree-of-freedom subnanometer measurement. IEEE Trans. Instrum. Meas. 2022, 71, 7007509. [Google Scholar]
- Zhou, S.; Le, V.; Xiong, S.; Yang, Y.; Ni, K.; Zhou, Q.; Wu, G. Dual-comb spectroscopy resolved three-degree-of-freedom sensing. Photonics Res. 2021, 9, 243–251. [Google Scholar] [CrossRef]
- Weichert, C.; Köchert, P.; Köning, R.; Flügge, J.; Andreas, B.; Kuetgens, U.; Yacoot, A. A heterodyne interferometer with periodic nonlinearities smaller than ±10 pm. Meas. Sci. Technol. 2012, 23, 094005. [Google Scholar] [CrossRef]
- Chen, L.C.; Le, M.T.; Lin, Y.S. 3-D micro surface profilometry employing novel Mirau-based lateral scanning interferometry. Meas. Sci. Technol. 2014, 25, 094004. [Google Scholar] [CrossRef]
- Matsuzoe, Y.; Tsuji, N.; Nakayama, T.; Fujita, K.; Yoshizawa, T. High-performance absolute rotary encoder using multitrack and M-code. Opt. Eng. 2003, 42, 124–131. [Google Scholar] [CrossRef]
- Ishimura, S.; Kikuchi, K. Eight-state trellis-coded optical modulation with signal constellations of four-dimensional M-ary quadrature-amplitude modulation. Opt. Express 2015, 23, 6692–6704. [Google Scholar] [CrossRef]
- Wang, S.; Luo, L.; Li, X. Design and parameter optimization of zero position code considering diffraction based on deep learning generative adversarial networks. Nanomanuf. Metrol. 2024, 7, 2. [Google Scholar] [CrossRef]
- Zhao, M.; Yuan, Y.; Luo, L.; Li, X. A Review: Absolute Linear Encoder Measurement Technology. Sensors 2025, 25, 5997. [Google Scholar] [CrossRef]
- DR. JOHANNES HEIDENHAIN GmbH. LC 115 Series—Absolute Sealed Linear Encoders. 2024. Available online: https://www.machinetoolproducts.com/heidenhain-lc-115-series-absolute-encoders-140mm-4240mm/ (accessed on 20 October 2025).
- HEIDENHAIN GmbH. Linear Encoders for Numerically Controlled Machine Tools; Product Brochure; HEIDENHAIN: Traunreut, Germany, 2023. [Google Scholar]
- Renishaw. RESOLUTE™ Absolute Encoder System. 2023. Available online: https://www.renishaw.com.cn/zh/resolute-optical-absolute-encoder-series--37823 (accessed on 20 October 2025).
- Wilson, T.; Sheppard, C. Theory and practice of scanning optical microscopy. J. Opt. Soc. Am. A 1987, 4, 551–560. [Google Scholar] [CrossRef]
- Minsky, M. Microscopy apparatus US patent 3013467. USP Off. Ed. US 1961, 658. [Google Scholar]
- Bai, J.; Li, J.; Wang, X.; Li, X. Research progress of high precision chromatic confocal displacement measurement technology. Laser Optoelectron. Prog. 2023, 60, 0312014. [Google Scholar]
- Davidovits, P.; Egger, M.D. Scanning laser microscope. Nature 1969, 223, 831. [Google Scholar] [CrossRef]
- Hwang, J.; Kim, S.; Heo, J.; Lee, D.; Ryu, S.; Joo, C. Frequency-and spectrally-encoded confocal microscopy. Opt. Express 2015, 23, 5809–5821. [Google Scholar] [CrossRef]
- Hillenbrand, M.; Weiss, R.; Endrödy, C.; Grewe, A.; Hoffmann, M.; Sinzinger, S. Chromatic confocal matrix sensor with actuated pinhole arrays. Appl. Opt. 2015, 54, 4927–4936. [Google Scholar] [CrossRef]
- Ye, Y.; Yi, D.; Liu, Z.; Jiang, W.; Liu, Y. Novel Chromatic Differential Confocal Matrix Sensor Using Multiband Spectral Images. IEEE Photonics Technol. Lett. 2022, 35, 31–34. [Google Scholar] [CrossRef]
- Luo, D.; Kuang, C.; Liu, X. Fiber-based chromatic confocal microscope with Gaussian fitting method. Opt. Laser Technol. 2012, 44, 788–793. [Google Scholar] [CrossRef]
- Bai, J.; Li, X.; Zhou, Q.; Ni, K.; Wang, X. Improved chromatic confocal displacement-sensor based on a spatial-bandpass-filter and an X-shaped fiber-coupler. Opt. Express 2019, 27, 10961–10973. [Google Scholar] [PubMed]
- Wang, A.S.; Xie, B.; Liu, Z.W. Design of measurement system of 3D surface profile based on chromatic confocal technology. In Proceedings of the 2017 International Conference on Optical Instruments and Technology: Optical Systems and Modern Optoelectronic Instruments, Beijing, China, 28–30 October 2017; Volume 10616, pp. 342–347. [Google Scholar]
- Jones, D.J.; Diddams, S.A.; Ranka, J.K.; Stentz, A.; Windeler, R.S.; Hall, J.L.; Cundiff, S.T. Carrier-envelope phase control of femtosecond mode-locked lasers and direct optical frequency synthesis. Science 2000, 288, 635–639. [Google Scholar] [PubMed]
- Gao, W.; Kim, S.; Bosse, H.; Minoshima, K. Dimensional metrology based on ultrashort pulse laser and optical frequency comb. CIRP Ann. 2025, 74, 993–1018. [Google Scholar] [CrossRef]
- Yariv, A. Optical Electronics in Modern Communications, 5th ed.; Oxford University Press: New York, NY, USA, 1997. [Google Scholar]
- Shi, K.; Nam, S.H.; Li, P.; Yin, S.; Liu, Z. Wavelength division multiplexed confocal microscopy using supercontinuum. Opt. Commun. 2006, 263, 156–162. [Google Scholar] [CrossRef]
- Shi, K.; Li, P.; Yin, S.; Liu, Z. Chromatic confocal microscopy using supercontinuum light. Opt. Express 2004, 12, 2096–2101. [Google Scholar] [CrossRef]
- Minoni, U.; Manili, G.; Bettoni, S.; Varrenti, E.; Modotto, D.; De Angelis, C. Chromatic confocal setup for displacement measurement using a supercontinuum light source. Opt. Laser Technol. 2013, 49, 91–94. [Google Scholar] [CrossRef]
- Sato, R.; Chen, C.; Matsukuma, H.; Shimizu, Y.; Gao, W. A new signal processing method for a differential chromatic confocal probe with a mode-locked femtosecond laser. Meas. Sci. Technol. 2020, 31, 094004. [Google Scholar] [CrossRef]
- Chen, X.; Nakamura, T.; Shimizu, Y.; Chen, C.; Chen, Y.L.; Matsukuma, H.; Gao, W. A chromatic confocal probe with a mode-locked femtosecond laser source. Opt. Laser Technol. 2018, 103, 359–366. [Google Scholar] [CrossRef]
- Chen, L.C.; Nguyen, D.T.; Chang, Y.W. Precise optical surface profilometry using innovative chromatic differential confocal microscopy. Opt. Lett. 2016, 41, 5660–5663. [Google Scholar] [CrossRef]
- Kim, T.; Kim, S.H.; Do, D.; Yoo, H.; Gweon, D. Chromatic confocal microscopy with a novel wavelength detection method using transmittance. Opt. Express 2013, 21, 6286–6294. [Google Scholar] [CrossRef]
- Micro-Epsilon. Confocal Sensors for Displacement and Thickness; Micro-Epsilon: Ortenburg, Germany, 2024. [Google Scholar]
- KEYENCE Corporation. CL-3000 Series: Confocal Displacement Sensor; KEYENCE Corporation: Osaka, Japan, 2024. [Google Scholar]
- Omron Corporation. ZW-7000 Series: Confocal Fiber Displacement Sensor; Omron Corporation: Kyoto, Japan, 2024. [Google Scholar]
- Precitec Optronik GmbH. CHRocodile Sensors—Confocal and Interferometric Sensors; Precitec Optronik GmbH: Neu-Isenburg, Germany, 2024. [Google Scholar]
- Furukawa, M.; Gao, W.; Shimizu, H.; Kiyono, S.; Yasutake, M.; Takahashi, K. Slit width measurement of a long precision slot die. J. Jpn. Soc. Precis. Eng. 2003, 69, 1013–1017. [Google Scholar] [CrossRef]
- Ito, S.; Matsuura, D.; Meguro, T.; Goto, S.; Shimizu, Y.; Gao, W.; Adachi, S.; Omiya, K. On-machine form measurement of high precision ceramics parts by using a laser displacement sensor. J. Adv. Mech. Des. Syst. Manuf. 2014, 8, JAMDSM0048. [Google Scholar] [CrossRef]
- Wen, B.; Shimizu, Y.; Watanabe, Y.; Matsukuma, H.; Gao, W. On-machine profile measurement of a micro cutting edge by using a contact-type compact probe unit. Precis. Eng. 2020, 65, 230–239. [Google Scholar] [CrossRef]
- Osawa, S.; Ito, S.; Shimizu, Y.; Jang, S.; Gao, W.; Fukuda, T.; Kato, A.; Kubota, K. Cutting edge height measurement of a rotary cutting tool by a laser displacement sensor. J. Adv. Mech. Des. Syst. Manuf. 2012, 6, 815–828. [Google Scholar] [CrossRef]
- Metrology, Z.I. Triangulation Technology: Measurement of 3D Surfaces. 2023. Available online: https://www.zeiss.com/metrology/us/explore/topics/triangulation.html (accessed on 20 October 2025).
- KEYENCE Corporation. LJ-G Series 2D Laser Displacement Sensor. 2025. Available online: https://www.keyence.com.cn/products/measure/laser-2d/lj-g/ (accessed on 20 October 2025).
- Dorsch, R.G.; Häusler, G.; Herrmann, J.M. Laser triangulation: Fundamental uncertainty in distance measurement. Appl. Opt. 1994, 33, 1306–1314. [Google Scholar] [CrossRef] [PubMed]
- Csencsics, E.; Schlarp, J.; Glaser, T.; Wolf, T.; Schitter, G. Simulation and reduction of speckle-induced uncertainty in laser triangulation sensors. In Proceedings of the 2022 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Ottawa, ON, Canada, 16–19 May 2022; pp. 1–6. [Google Scholar]
- Roos-Hoefgeest, S.; Roos-Hoefgeest, M.; Álvarez, I.; González, R.C. Simulation of laser profilometer measurements in the presence of speckle using perlin noise. Sensors 2023, 23, 7624. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Ren, Y.; Liu, C.; Zhu, J. Flying spot laser triangulation scanner using lateral synchronization for surface profile precision measurement. Appl. Opt. 2014, 53, 4405–4412. [Google Scholar] [CrossRef]
- Giacomo, P. News from the BIPM. Metrologia 1984, 20, 25. [Google Scholar] [CrossRef]
- Amann, M.C.; Bosch, T.M.; Lescure, M.; Myllylae, R.A.; Rioux, M. Laser ranging: A critical review of unusual techniques for distance measurement. Opt. Eng. 2001, 40, 10–19. [Google Scholar]
- Strzelecki, E.; Cohen, D.; Coldren, L. Investigation of tunable single frequency diode lasers for sensor applications. J. Light. Technol. 2002, 6, 1610–1618. [Google Scholar] [CrossRef]
- Lescure, M.; Bosch, T.; Dziadowiec, A. An electro-optical frequency doubling method to remove electrical noise in laser rangefinders. IEEE Trans. Instrum. Meas. 1991, 40, 1046–1047. [Google Scholar] [CrossRef]
- Fujima, I.; Iwasaki, S.; Seta, K. High-resolution distance meter using optical intensity modulation at 28 GHz. Meas. Sci. Technol. 1998, 9, 1049. [Google Scholar] [CrossRef]
- Pellegrini, S.; Buller, G.S.; Smith, J.M.; Wallace, A.M.; Cova, S. Laser-based distance measurement using picosecond resolutiontime-correlated single-photon counting. Meas. Sci. Technol. 2000, 11, 712. [Google Scholar] [CrossRef]
- Ye, J. Absolute measurement of a long, arbitrary distance to less than an optical fringe. Opt. Lett. 2004, 29, 1153–1155. [Google Scholar] [CrossRef]
- Balling, P.; Křen, P.; Mašika, P.; van den Berg, S. Femtosecond frequency comb based distance measurement in air. Opt. Express 2009, 17, 9300–9313. [Google Scholar] [CrossRef]
- Cui, M.; Zeitouny, M.; Bhattacharya, N.; Van den Berg, S.; Urbach, H.; Braat, J. High-accuracy long-distance measurements in air with a frequency comb laser. Opt. Lett. 2009, 34, 1982–1984. [Google Scholar] [CrossRef]
- Wei, D.; Takahashi, S.; Takamasu, K.; Matsumoto, H. Experimental observation of pulse trains’ destructive interference with a femtosecond optical frequency-comb-based interferometer. Opt. Lett. 2009, 34, 2775–2777. [Google Scholar] [CrossRef]
- Jiang, L.A.; Wong, S.T.; Grein, M.E.; Ippen, E.P.; Haus, H.A. Measuring timing jitter with optical cross correlations. IEEE J. Quantum Electron. 2002, 38, 1047–1052. [Google Scholar] [CrossRef]
- Shelton, R.K.; Foreman, S.M.; Ma, L.S.; Hall, J.L.; Kapteyn, H.C.; Murnane, M.M.; Notcutt, M.; Ye, J. Subfemtosecond timing jitter between two independent, actively synchronized, mode-locked lasers. Opt. Lett. 2002, 27, 312–314. [Google Scholar] [CrossRef] [PubMed]
- Duguay, M.; Hansen, J. Optical sampling of subnanosecond light pulses. Appl. Phys. Lett. 1968, 13, 178–180. [Google Scholar] [CrossRef]
- Schibli, T.; Kim, J.; Kuzucu, O.; Gopinath, J.; Tandon, S.; Petrich, G.; Kolodziejski, L.; Fujimoto, J.; Ippen, E.; Kaertner, F. Attosecond active synchronization of passively mode-locked lasers by balanced cross correlation. Opt. Lett. 2003, 28, 947–949. [Google Scholar] [CrossRef]
- Kim, J.; Chen, J.; Zhang, Z.; Wong, F.; Kärtner, F.; Loehl, F.; Schlarb, H. Long-term femtosecond timing link stabilization using a single-crystal balanced cross correlator. Opt. Lett. 2007, 32, 1044–1046. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Kim, Y.J.; Lee, K.; Lee, S.; Kim, S.W. Time-of-flight measurement with femtosecond light pulses. Nat. Photonics 2010, 4, 716–720. [Google Scholar] [CrossRef]
- Lee, J.; Lee, K.; Lee, S.; Kim, S.W.; Kim, Y.J. High precision laser ranging by time-of-flight measurement of femtosecond pulses. Meas. Sci. Technol. 2012, 23, 065203. [Google Scholar] [CrossRef]
- Elzinga, P.A.; Kneisler, R.J.; Lytle, F.E.; Jiang, Y.; King, G.B.; Laurendeau, N.M. Pump/probe method for fast analysis of visible spectral signatures utilizing asynchronous optical sampling. Appl. Opt. 1987, 26, 4303–4309. [Google Scholar] [CrossRef]
- Zhang, H.; Wei, H.; Wu, X.; Yang, H.; Li, Y. Absolute distance measurement by dual-comb nonlinear asynchronous optical sampling. Opt. Express 2014, 22, 6597–6604. [Google Scholar] [CrossRef]
- Shi, H.; Song, Y.; Liang, F.; Xu, L.; Hu, M.; Wang, C. Effect of timing jitter on time-of-flight distance measurements using dual femtosecond lasers. Opt. Express 2015, 23, 14057–14069. [Google Scholar] [CrossRef] [PubMed]
- Coddington, I.; Swann, W.C.; Nenadovic, L.; Newbury, N.R. Rapid and precise absolute distance measurements at long range. Nat. Photonics 2009, 3, 351–356. [Google Scholar] [CrossRef]
- Lauri, J.; Czajkowski, J.; Myllylä, R.; Fabritius, T. Measuring flow dynamics in a microfluidic chip using optical coherence tomography with 1 μm axial resolution. Flow Meas. Instrum. 2015, 43, 1–5. [Google Scholar] [CrossRef]
- Hu, D.; Wu, Z.; Cao, H.; Shi, Y.; Li, R.; Tian, H.; Song, Y.; Hu, M. Dual-comb absolute distance measurement of non-cooperative targets with a single free-running mode-locked fiber laser. Opt. Commun. 2021, 482, 126566. [Google Scholar] [CrossRef]
- Liu, T.A.; Newbury, N.R.; Coddington, I. Sub-micron absolute distance measurements in sub-millisecond times with dual free-running femtosecond Er fiber-lasers. Opt. Express 2011, 19, 18501–18509. [Google Scholar] [CrossRef]
- Wang, S.; Ma, R.; Cao, F.; Luo, L.; Li, X. A review: High-precision angle measurement technologies. Sensors 2024, 24, 1755. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.D.; Graetz, R.; Amin-Shahidi, D.; Smeds, K. On-axis self-calibration of angle encoders. CIRP Ann. 2010, 59, 529–534. [Google Scholar] [CrossRef]
- Kokuyama, W.; Watanabe, T.; Nozato, H.; Ota, A. Measurement of angle error of gyroscopes using a rotary table enhanced by self-calibratable rotary encoder. In Proceedings of the 2015 IEEE International Symposium on Inertial Sensors and Systems (INERTIAL) Proceedings, Hapuna Beach, HI, USA, 23–26 March 2015; pp. 1–4. [Google Scholar]
- Eggenstein, F.; Schwarz, L.; Zeschke, T.; Viefhaus, J. New UHV angle encoder for high resolution monochromators, a modern spare part for the Heidenhain UHV RON 905. Nucl. Instru. Methods Phys. Res. Sect. A Accel. Spec. Detect. Assoc. Equip. 2021, 1014, 165645. [Google Scholar] [CrossRef]
- Sun, S.; Han, Y.; Zhang, H.; He, Z.; Tang, Q. A novel inductive angular displacement sensor with multi-probe symmetrical structure. IEEE Sens. J. 2022, 22, 3087–3096. [Google Scholar] [CrossRef]
- Guo, Q.; Wang, X.; Xu, C. Design of high precision angle measuring instrument based on Kalman filter. J. Physics Conf. Ser. 2022, 2183, 012004. [Google Scholar] [CrossRef]
- Xia, Y.; Wu, Z.; Huang, M.; Liu, X.; Mi, L.; Tang, Q. An improved angle calibration method of a high-precision angle comparator. Metrol. Meas. Syst. 2021, 28, 181–190. [Google Scholar] [CrossRef]
- Li, Z.; Li, J.; Han, B.; Tang, Y.; Yanf, Y.; Ma, Y. Compensation Method of Circular Grating Angle Measurement Error. Instrum. Technol. Sens 2021, 89, 56–59. [Google Scholar]
- Janson, N.; Abt, M.; Kuester, B.; Overmeyer, L. Optimization of optical rotation angle measurement by improved encodings. TM-TECHNISCHES MESSEN 2023, 90, 355–364. [Google Scholar] [CrossRef]
- Renishaw. REXM20 Ultra-High Accuracy Ring with TONiC Encoder System. 2023. Available online: https://www.renishaw.com/en/tonic-encoder-system-with-rexm20-rotary-angle-ring--39026 (accessed on 20 October 2025).
- Möller-Wedel Optical GmbH. ELCOMAT® HR—Electronic Autocollimators (Catalogue 2014). 2014. Available online: https://moeller-wedel-optical.com/en/product/elcomat-hr/ (accessed on 20 October 2025).
- Nikon. Autocollimators 6B-LED and 6D-LED. 2019. Available online: https://industry.nikon.com/en-us/products/optical-manual-measuring/others/autocollimators-6b-led-6d-led/ (accessed on 20 October 2025).
- Gao, W.; Ohnuma, T.; Satoh, H.; Shimizu, H.; Kiyono, S. A precision angle sensor using a multi-cell photodiode array. CIRP Ann. 2004, 53, 425–428. [Google Scholar] [CrossRef]
- Chen, S.H.; Hsieh, H.L.; Chen, H.Y.; Lai, Y.X. Development of a double-diffraction grating interferometer for measurements of displacement and angle. In Proceedings of the Optics and Photonics for Advanced Dimensional Metrology, Online, 6–10 April 2020; Volume 11352, pp. 330–338. [Google Scholar]
- Hsu, Y.T.; Hsieh, H.L. Development of a coplanar grating interferometer for displacement and angle measurements. In Proceedings of the Optics and Photonics for Advanced Dimensional Metrology II, Strasbourg, France, 5–7 April 2022; Volume 12137, pp. 22–29. [Google Scholar]
- Shi, K.; Su, J.; Hou, W. Roll angle measurement system based on differential plane mirror interferometer. Opt. Express 2018, 26, 19826–19834. [Google Scholar] [CrossRef]
- Chiu, M.H.; Su, D.C. Angle measurement using total-internal-reflection heterodyne interferometry. Opt. Eng. 1997, 36, 1750–1753. [Google Scholar] [CrossRef]
- Liang, X.; Lin, J.; Wu, T.; Yang, L.; Wang, Y.; Liu, Y.; Zhu, J. Absolute angular measurement with optical frequency comb using a dispersive interferometry. Opt. Express 2020, 28, 36095–36108. [Google Scholar] [CrossRef]
- Dwi Astuti, W.; Matsukuma, H.; Nakao, M.; Li, K.; Shimizu, Y.; Gao, W. An optical frequency domain angle measurement method based on second harmonic generation. Sensors 2021, 21, 670. [Google Scholar] [CrossRef]
- Liu, X.; Wang, Y.; Zhu, L.; Wang, B.; Yan, P. High-precision dynamic measurement of roll angle based on digital holography. Opt. Lasers Eng. 2023, 169, 107711. [Google Scholar] [CrossRef]
- Chen, H.; Chen, Q.; Chen, H.; Yang, X.; Wang, X. Measurement of displacement and top beam attitude angle of advanced hydraulic support based on visual detection. Measurement 2023, 219, 113264. [Google Scholar] [CrossRef]
- Kim, H.; Yamakawa, Y.; Senoo, T.; Ishikawa, M. Visual encoder: Robust and precise measurement method of rotation angle via high-speed RGB vision. Opt. Express 2016, 24, 13375–13386. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Pei, Y.; Qu, C.; Yang, F. A position and attitude measurement method based on laser displacement sensor and infrared vision camera. IEEE Trans. Instrum. Meas. 2022, 71, 1004209. [Google Scholar] [CrossRef]
- Liu, H.; Zhao, S.; Liu, J.; Chen, P.; Zhang, L.; Wang, K. Non-imaging method for angle measurement based on an axicon. Appl. Opt. 2023, 62, 5077–5084. [Google Scholar] [CrossRef] [PubMed]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Xue, N.; Bai, S.; Wang, F.; Xia, G.S.; Wu, T.; Zhang, L. Learning attraction field representation for robust line segment detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 1595–1603. [Google Scholar]
- Grompone von Gioi, R.; Jakubowicz, J.; Morel, J.M.; Randall, G. LSD: A fast line segment detector with a false detection control. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 722–732. [Google Scholar] [CrossRef]
- Wei, Z.; Feng, G.; Zhou, D.; Ma, Y.; Liu, M.; Luo, Q.; Huang, T. A review of position and orientation visual measurement methods and applications. Laser Optoelectron. Prog 2023, 60, 0312010. [Google Scholar]
- Yan, S.; Tao, X.; Xu, D. High-precision robotic assembly system using three-dimensional vision. Int. J. Adv. Robot. Syst. 2021, 18, 17298814211027029. [Google Scholar] [CrossRef]
- Wen, T.; Hu, J.; Zhu, Y.; Hua, G. Multi-axis laser interferometer not affected by installation errors based on nonlinear computation. Appl. Sci. 2023, 13, 10887. [Google Scholar] [CrossRef]
- Yin, Y.; Liu, L.; Bai, Y.; Jirigalantu; Yu, H.; Bayanheshig; Liu, Z.; Li, W. Littrow 3D measurement based on 2D grating dual-channel equal-optical path interference. Opt. Express 2022, 30, 41671–41684. [Google Scholar] [CrossRef]
- Li, S.; Wang, J.; Zhang, W.; Du, H.; Xiong, X. Real-time direction judgment system of sub-nanometer scale grating ruler. IEEE Access 2021, 9, 74939–74948. [Google Scholar] [CrossRef]
- Jiao, B.; Chen, F.; Liu, Y.; Fan, X.; Zeng, S.; Dong, Q.; Deng, L.; Gao, H.; Xiong, W. Acousto-optic scanning spatial-switching multiphoton lithography. Int. J. Extrem. Manuf. 2023, 5, 035008. [Google Scholar] [CrossRef]
- Cai, Z.; Li, B.; Bai, Z.; Liu, D.; Yang, K.; Liu, B.; Zhao, C.; Zou, M.; Zhou, J.; Jiang, S.; et al. Encrypted optical fiber tag based on encoded fiber Bragg grating array. Int. J. Extrem. Manuf. 2023, 5, 035502. [Google Scholar] [CrossRef]
- Chang, D.; Hu, P.; Tan, J. Fused-like angles: Replacement for roll-pitch-yaw angles for a six-degree-of-freedom grating interferometer. Front. Inf. Technol. Electron. Eng. 2021, 22, 1677–1684. [Google Scholar] [CrossRef]
- Hsieh, H.L.; Pan, S.W. Development of a grating-based interferometer for six-degree-of-freedom displacement and angle measurements. Opt. Express 2015, 23, 2451–2465. [Google Scholar] [CrossRef]
- Wang, S.; Luo, L.; Zhu, J.; Shi, N.; Li, X. An ultra-precision absolute-type multi-degree-of-freedom grating encoder. Sensors 2022, 22, 9047. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Shimizu, Y.; Ito, T.; Cai, Y.; Ito, S.; Gao, W. Measurement of six-degree-of-freedom planar motions by using a multiprobe surface encoder. Opt. Eng. 2014, 53, 122405. [Google Scholar] [CrossRef]
- Ye, W.; Zhang, M.; Zhu, Y.; Wang, L.; Hu, J.; Li, X.; Hu, C. Real-time displacement calculation and offline geometric calibration of the grating interferometer system for ultra-precision wafer stage measurement. Precis. Eng. 2019, 60, 413–420. [Google Scholar] [CrossRef]
- Matsukuma, H.; Ishizuka, R.; Furuta, M.; Li, X.; Shimizu, Y.; Gao, W. Reduction in cross-talk errors in a six-degree-of-freedom surface encoder. Nanomanuf. Metrol. 2019, 2, 111–123. [Google Scholar] [CrossRef]
- Martin, H.M.; Angel, J.R.P.; Angeli, G.Z.; Burge, J.H.; Gressler, W.; Kim, D.; Kingsley, J.S.; Law, K.; Liang, M.; Neill, D.; et al. Manufacture and final tests of the LSST monolithic primary/tertiary mirror. In Proceedings of the Advances in Optical and Mechanical Technologies for Telescopes and Instrumentation II, Edinburgh, UK, 26 June–1 July 2016; Volume 9912, pp. 278–294. [Google Scholar]
- Chen, S.; Xue, S.; Dai, Y.; Li, S. Subaperture stitching test of large steep convex spheres. Opt. Express 2015, 23, 29047–29058. [Google Scholar] [CrossRef]
- Chen, S.; Li, S.; Wang, G. Subaperture test of wavefront error of large telescopes: Error sources and stitching performance simulations. In Proceedings of the International Symposium on Optoelectronic Technology and Application 2014: Imaging Spectroscopy; and Telescopes and Large Optics, Beijing, China, 13–15 May 2014; Volume 9298, pp. 287–293. [Google Scholar]
- Kulawiec, A.; Murphy, P.; DeMarco, M. Measurement of high-departure aspheres using subaperture stitching with the Variable Optical Null (VON). In Proceedings of the 5th International Symposium on Advanced Optical Manufacturing and Testing Technologies: Advanced Optical Manufacturing Technologies, Dalian, China, 26–29 April 2010; Volume 7655, pp. 265–268. [Google Scholar]
- Chen, S.; Xue, S.; Dai, Y.; Li, S. Subaperture stitching test of convex aspheres by using the reconfigurable optical null. Opt. Laser Technol. 2017, 91, 175–184. [Google Scholar] [CrossRef]
- Martin, H.; Allen, R.; Burge, J.; Kim, D.; Kingsley, J.; Tuell, M.; West, S.; Zhao, C.; Zobrist, T. Fabrication and testing of the first 8.4-m off-axis segment for the Giant Magellan Telescope. In Proceedings of the Modern Technologies in Space-and Ground-based Telescopes and Instrumentation, San Diego, CA, USA, 27 June–2 July 2010; Volume 7739, pp. 84–96. [Google Scholar]
- Martin, H.; Allen, R.; Burge, J.; Davis, J.; Davison, W.; Johns, M.; Kim, D.; Kingsley, J.; Law, K.; Lutz, R.; et al. Production of primary mirror segments for the Giant Magellan Telescope. In Proceedings of the Advances in optical and mechanical technologies for telescopes and instrumentation, Montréal, QC, Canada, 22–27 June 2014; Volume 9151, pp. 186–199. [Google Scholar]
- Scheiding, S.; Beier, M.; Zeitner, U.D.; Risse, S.; Gebhardt, A. Freeform Mirror Fabrication and Metrology Using a High Performance Test CGH and Advanced Alignment Features. In Proceedings of the Advanced fabrication technologies for micro/nano optics and photonics VI, San Francisco, CA, USA, 2–7 February 2013; Volume 8613, pp. 76–90. [Google Scholar]
- Saif, B.; Chaney, D.; Scott Smith, W.; Greenfield, P.; Hack, W.; Bluth, J.; Otten, A.V.; Bluth, M.; Sanders, J.; Keski-Kuha, R.; et al. Nanometer level characterization of the James Webb Space Telescope optomechanical systems using high-speed interferometry. Appl. Opt. 2015, 54, 4285–4298. [Google Scholar] [CrossRef]
- Pant, L.; Singh, M.; Pant, K.; Ghosh, A. In process metrology of aspheric optical surfaces during sub-aperture polishing process. In Proceedings of the International Conference on Optics and Photonics 2015, Kolkata, India, 20–22 February 2015; Volume 9654, pp. 172–177. [Google Scholar]
- Zhao, Z.; Zhao, H.; Gu, F.; Du, H.; Li, K. Non-null testing for aspheric surfaces using elliptical sub-aperture stitching technique. Opt. Express 2014, 22, 5512–5521. [Google Scholar] [CrossRef] [PubMed]
- Oh, C.J.; Lowman, A.E.; Dubin, M.; Smith, G.; Frater, E.; Zhao, C.; Burge, J.H. Modern technologies of fabrication and testing of large convex secondary mirrors. In Proceedings of the Advances in Optical and Mechanical Technologies for Telescopes and Instrumentation II, Edinburgh, UK, 26 June–1 July 2016; Volume 9912, pp. 238–249. [Google Scholar]
- Rowe, S.; Welford, W. Surface topography of non-optical surfaces by projected interference fringes. Nature 1967, 216, 786–787. [Google Scholar] [CrossRef]
- Anna, T.; Dubey, S.K.; Shakher, C.; Roy, A.; Mehta, D.S. Sinusoidal fringe projection system based on compact and non-mechanical scanning low-coherence Michelson interferometer for three-dimensional shape measurement. Opt. Commun. 2009, 282, 1237–1242. [Google Scholar] [CrossRef]
- Li, E.; Peng, X.; Xi, J.; Chicharo, J.F.; Yao, J.; Zhang, D. Multi-frequency and multiple phase-shift sinusoidal fringe projection for 3D profilometry. Opt. Express 2005, 13, 1561–1569. [Google Scholar] [CrossRef]
- Harizanova, J.; Stoykova, E.; Sainov, V. Phase retrieval techniques in coordinates measurement. Aip Conf. Proc. 2007, 899, 321–322. [Google Scholar]
- Duan, X.; Duan, F.; Lv, C. Phase stabilizing method based on PTAC for fiber-optic interference fringe projection profilometry. Opt. Laser Technol. 2013, 47, 137–143. [Google Scholar]
- Pennington, T.L.; Xiao, H.; May, R.; Wang, A. Miniaturized 3-D surface profilometer using a fiber optic coupler. Opt. Laser Technol. 2001, 33, 313–320. [Google Scholar] [CrossRef]
- Huang, T.; Li, X.; Fu, X.; Zhang, C.; Duan, F.; Jiang, J. Arbitrary phase shifting method for fiber-optic fringe projection profilometry based on temporal sinusoidal phase modulation. Opt. Lasers Eng. 2019, 121, 300–306. [Google Scholar] [CrossRef]
- Inanç, A.; Kösoğlu, G.; Yüksel, H.; Inci, M.N. 3-d optical profilometry at micron scale with multi-frequency fringe projection using modified fibre optic lloyd’s mirror technique. Opt. Lasers Eng. 2018, 105, 14–26. [Google Scholar] [CrossRef]
- Cheng, Y.Y.; Wyant, J.C. Multiple-wavelength phase-shifting interferometry. Appl. Opt. 1985, 24, 804–807. [Google Scholar] [CrossRef] [PubMed]
- Motyka, Z.; Passia, H. Dual integrated laser interferometer for fringe projection techniques. Aip Conf. Proc. 2012, 1457, 451–458. [Google Scholar]
- Creath, K. Step height measurement using two-wavelength phase-shifting interferometry. Appl. Opt. 1987, 26, 2810–2816. [Google Scholar] [CrossRef] [PubMed]
- Dupont, S.H.; Kastelik, J.C.; Pommeray, M. Structured light fringe projection setup using optimized acousto-optic deflectors. IEEE/ASME Trans. Mechatronics 2010, 15, 557–560. [Google Scholar] [CrossRef]
- Schaffer, M.; Große, M.; Harendt, B.; Kowarschik, R. Coherent two-beam interference fringe projection for highspeed three-dimensional shape measurements. Appl. Opt. 2013, 52, 2306–2311. [Google Scholar] [CrossRef]
- Windecker, R.; Fleischer, M.; Tiziani, H.J. Three-dimensional topometry with stereo microscopes. Opt. Eng. 1997, 36, 3372–3377. [Google Scholar] [CrossRef]
- Han, M.; Shi, W.; Lu, S.; Lei, F.; Li, Y.; Wang, X.; Li, X. Internal–External Layered Phase Shifting for Phase Retrieval. IEEE Trans. Instrum. Meas. 2023, 73, 4501013. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, H.; Jiang, H.; Li, X. Defocusing parameter selection strategies based on PSF measurement for square-binary defocusing fringe projection profilometry. Opt. Express 2018, 26, 20351–20367. [Google Scholar] [CrossRef]
- Li, J.; Su, X.Y.; Guo, L.R. Improved Fourier transform profilometry for the automatic measurement of three-dimensional object shapes. Opt. Eng 1990, 29, 1439–1444. [Google Scholar]
- Su, X.Y.; Zhou, W.S.; Von Bally, G.; Vukicevic, D. Automated phase-measuring profilometry using defocused projection of a Ronchi grating. Opt. Commun. 1992, 94, 561–573. [Google Scholar] [CrossRef]
- Miklyaev, Y.V.; Imgrunt, W.; Pavelyev, V.S.; Kachalov, D.G.; Bizjak, T.; Aschke, L.; Lissotschenko, V.N. Novel continuously shaped diffractive optical elements enable high efficiency beam shaping. In Proceedings of the Optical Microlithography XXIII, San Jose, CA, USA, 21–25 February 2010; Volume 7640, pp. 786–792. [Google Scholar]
- Wang, H.; He, X.; Zhang, C.; Liang, X.; Zhu, P.; Wang, X.; Gui, W.; Li, X.; Qian, X. Accelerating surface defect detection using normal data with an attention-guided feature distillation reconstruction network. Measurement 2025, 246, 116702. [Google Scholar] [CrossRef]
- Tyagi, A.; Chatterjee, D.S. Liquid crystal display: Environment & technology. Int. J. Environ. Eng. Sci. Technol. Res. 2013, 1, 110–123. [Google Scholar]
- Li, Y.; Li, Z.; Liang, X.; Huang, H.; Qian, X.; Feng, F.; Zhang, C.; Wang, X.; Gui, W.; Li, X. Global phase accuracy enhancement of structured light system calibration and 3D reconstruction by overcoming inevitable unsatisfactory intensity modulation. Measurement 2024, 236, 114952. [Google Scholar] [CrossRef]
- Yu, J.; Gao, N.; Meng, Z.; Zhang, Z. High-accuracy projector calibration method for fringe projection profilometry considering perspective transformation. Opt. Express 2021, 29, 15053–15066. [Google Scholar] [CrossRef]
- Geng, J. DLP-based structured light 3D imaging technologies and applications. In Proceedings of the Emerging Digital Micromirror Device Based Systems and Applications III, San Francisco, CA, USA, 22–27 January 2011; Volume 7932, pp. 95–109. [Google Scholar]
- Frankowski, G.; Hainich, R. DLP-based 3D metrology by structured light or projected fringe technology for life sciences and industrial metrology. In Proceedings of the Emerging digital micromirror device based systems and applications, San Jose, CA, USA, 24–29 January 2009; Volume 7210, pp. 102–113. [Google Scholar]
- Huntley, J.M.; Coggrave, C. Progress in phase unwrapping. In Proceedings of the International Conference on Applied Optical Metrology, Balatonfured, Hungary, 8–11 June 1998; Volume 3407, pp. 86–93. [Google Scholar]
- Huang, P.S.; Hu, Q.; Jin, F.; Chiang, F.P. Color-encoded fringe projection and phase shifting for 3D surface contouring. In Proceedings of the International Conference on Applied Optical Metrology, Balatonfured, Hungary, 8–11 June 1998; Volume 3407, pp. 477–482. [Google Scholar]
- Zhang, K.; Huang, Y.; Yan, J.; Sun, L. Dynamic infrared scene simulation using grayscale modulation of digital micro-mirror device. Chin. J. Aeronaut. 2013, 26, 394–400. [Google Scholar] [CrossRef]
- Li, Y.; Li, Z.; Chen, W.; Zhang, C.; Wang, H.; Wang, X.; Gui, W.; Gao, W.; Liang, X.; Li, X. Reliable 3D Reconstruction with Single-Shot Digital Grating and Physical Model-Supervised Machine Learning. IEEE Trans. Instrum. Meas. 2025, 74, 5505413. [Google Scholar]
- Kovacovsky, T.; Zizka, J.; Maly, M. Methods and Apparatus for Superpixel Modulation with Ambient Light Suppression. US Patent 10,158,844, 18 December 2018. [Google Scholar]
- Li, Y.; Li, Z.; Zhang, C.; Han, M.; Lei, F.; Liang, X.; Wang, X.; Gui, W.; Li, X. Deep learning-driven one-shot dual-view 3-D reconstruction for dual-projector system. IEEE Trans. Instrum. Meas. 2023, 73, 5021314. [Google Scholar] [CrossRef]
- Yoshizawa, T.; Wakayama, T.; Takano, H. Applications of a MEMS scanner to profile measurement. In Proceedings of the Two-and Three-Dimensional Methods for Inspection and Metrology V, Boston, MA, USA, 9–12 September 2007; Volume 6762, pp. 89–93. [Google Scholar]
- Zabatani, A.; Surazhsky, V.; Sperling, E.; Moshe, S.B.; Menashe, O.; Silver, D.H.; Karni, Z.; Bronstein, A.M.; Bronstein, M.M.; Kimmel, R. Intel® realsense™ sr300 coded light depth camera. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 42, 2333–2345. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, H.; Li, Y.; Li, Z.; Gui, W.; Wang, X.; Zhang, C.; Liang, X.; Li, X. Fringe-Based Structured-Light 3D Reconstruction: Principles, Projection Technologies, and Deep Learning Integration. Sensors 2025, 25, 6296. [Google Scholar] [CrossRef]
- Revopoint 3D Technologies Inc. Revopoint 3D Official Website; Revopoint 3D Technologies Inc.: Los Angeles, CA, USA, 2025. [Google Scholar]
- Han, M.; Jiang, H.; Lei, F.; Xing, Y.; Wang, X.; Li, X. Modeling window smoothing effect hidden in fringe projection profilometry. Measurement 2025, 242, 115852. [Google Scholar] [CrossRef]
- Li, Y.; Chen, W.; Li, Z.; Zhang, C.; Wang, X.; Gui, W.; Gao, W.; Liang, X.; Li, X. SL3D-BF: A Real-World Structured Light 3D Dataset with Background-to-Foreground Enhancement. IEEE Trans. Circuits Syst. Video Technol. 2025, 35, 9850–9864. [Google Scholar] [CrossRef]
- Han, M.; Xing, Y.; Wang, X.; Li, X. Projection superimposition for the generation of high-resolution digital grating. Opt. Lett. 2024, 49, 4473–4476. [Google Scholar] [CrossRef]
- Wang, H.; Lu, Z.; Huang, Z.; Li, Y.; Zhang, C.; Qian, X.; Wang, X.; Gui, W.; Liang, X.; Li, X. A High-Accuracy and Reliable End-to-End Phase Calculation Network and Its Demonstration in High Dynamic Range 3D Reconstruction. Nanomanuf. Metrol. 2025, 8, 5. [Google Scholar] [CrossRef]
- Han, M.; Lei, F.; Shi, W.; Lu, S.; Li, X. Uniaxial MEMS-based 3D reconstruction using pixel refinement. Opt. Express 2022, 31, 536–554. [Google Scholar] [CrossRef] [PubMed]
- Han, M.; Lei, F.; Tao, Y.; Shi, W.; Lu, S.; Tian, H.; Liao, C.; Zhu, P.; Zhu, S.; Wang, X.; et al. A novel calibration method for a uniaxial MEMS-based 3D reconstruction system. In Proceedings of the Optoelectronic Imaging and Multimedia Technology IX, Online, 5–12 December 2022; Volume 12317, pp. 40–46. [Google Scholar]
- Lei, F.; Han, M.; Jiang, H.; Wang, X.; Li, X. A phase-angle inspired calibration strategy based on MEMS projector for 3D reconstruction with markedly reduced calibration images and parameters. Opt. Lasers Eng. 2024, 176, 108078. [Google Scholar] [CrossRef]
- Davis, W.O.; Sprague, R.; Miller, J. MEMS-based pico projector display. In Proceedings of the 2008 IEEE/LEOS International Conference on Optical MEMs and Nanophotonics, Freiburg, Germany, 11–14 August 2008; pp. 31–32. [Google Scholar]
- Hocken, R.; Chakraborty, N.; Brown, C. Optical metrology of surfaces. CIRP Ann. 2005, 54, 169–183. [Google Scholar] [CrossRef]
- Nussbaum, P.; Voelkel, R.; Herzig, H.P.; Eisner, M.; Haselbeck, S. Design, fabrication and testing of microlens arrays for sensors and microsystems. Pure Appl. Opt. J. Eur. Opt. Soc. Part A 1997, 6, 617. [Google Scholar] [CrossRef]
- Schwider, J.; Falkenstoerfer, O.R. Twyman-Green interferometer for testing microspheres. Opt. Eng. 1995, 34, 2972–2975. [Google Scholar] [CrossRef]
- Reichelt, S.; Zappe, H. Combined Twyman–Green and Mach–Zehnder interferometer for microlens testing. Appl. Opt. 2005, 44, 5786–5792. [Google Scholar] [CrossRef]
- Charrière, F.; Kühn, J.; Colomb, T.; Montfort, F.; Cuche, E.; Emery, Y.; Weible, K.; Marquet, P.; Depeursinge, C. Characterization of microlenses by digital holographic microscopy. Appl. Opt. 2006, 45, 829–835. [Google Scholar] [CrossRef]
- Jiang, M.; Zhang, D.; Wang, X.; Gong, Y.; Zou, W. Characterization of the Binary Micro-Grating Surface by Scanning White Light Interferometry. In Proceedings of the 2012 Symposium on Photonics and Optoelectronics, Shanghai, China, 21–23 May 2012; pp. 1–4. [Google Scholar]
- Li, C.; Pan, X.; Zhu, P.; Zhu, S.; Liao, C.; Tian, H.; Qian, X.; Li, X.; Wang, X.; Li, X. Style Adaptation module: Enhancing detector robustness to inter-manufacturer variability in surface defect detection. Comput. Ind. 2024, 157, 104084. [Google Scholar] [CrossRef]
- Raymond, C.J.; Murnane, M.R.; Prins, S.L.; Sohail, S.; Naqvi, H.; McNeil, J.R.; Hosch, J.W. Multiparameter grating metrology using optical scatterometry. J. Vac. Sci. Technol. B Microelectron. Nanometer Struct. Process. Meas. Phenom. 1997, 15, 361–368. [Google Scholar] [CrossRef]
- Minhas, B.K.; Coulombe, S.A.; Naqvi, S.S.H.; McNeil, J.R. Ellipsometric scatterometry for the metrology of sub-0.1-μm-linewidth structures. Appl. Opt. 1998, 37, 5112–5115. [Google Scholar] [CrossRef]
- Marciante, J.R.; Farmiga, N.O.; Hirsh, J.I.; Evans, M.S.; Ta, H.T. Optical measurement of depth and duty cycle for binary diffraction gratings with subwavelength features. Appl. Opt. 2003, 42, 3234–3240. [Google Scholar] [CrossRef]
- Li, L.; Zeng, L. Measurement of duty cycles of photoresist grating masks made on top of multilayer dielectric stacks. Appl. Opt. 2005, 44, 4494–4500. [Google Scholar] [CrossRef]
- Jordan, H.J.; Wegner, M.; Tiziani, H. Highly accurate non-contact characterization of engineering surfaces using confocal microscopy. Meas. Sci. Technol. 1998, 9, 1142. [Google Scholar] [CrossRef]
- Savio, E.; De Chiffre, L.; Schmitt, R. Metrology of freeform shaped parts. CIRP Ann. 2007, 56, 810–835. [Google Scholar] [CrossRef]
- Tiftikci, K. Development and Verification of a Micromirror Based High Accuracy Confocal Microscope. Ph.D. Thesis, Eindhoven University of Technology, Eindhoven, The Netherlands, 2005. [Google Scholar]
- Flournoy, P.; McClure, R.; Wyntjes, G. White-light interferometric thickness gauge. Appl. Opt. 1972, 11, 1907–1915. [Google Scholar] [CrossRef]
- Deck, L.; De Groot, P. High-speed noncontact profiler based on scanning white-light interferometry. Appl. Opt. 1994, 33, 7334–7338. [Google Scholar] [CrossRef]
- Wilson, T. Confocal Microscopy; Academic Press: London, UK, 1990; Volume 426. [Google Scholar]
- Müller, J.; Kebbel, V.; Jüptner, W. Digital holography as a tool for testing high-aperture micro-optics. Opt. Lasers Eng. 2005, 43, 739–751. [Google Scholar] [CrossRef]
- Kebbel, V.; Mueller, J.; Jueptner, W.P. Characterization of aspherical micro-optics using digital holography: Improvement of accuracy. In Proceedings of the Interferometry XI: Applications, Seattle, WA, USA, 7–11 July 2002; Volume 4778, pp. 188–197. [Google Scholar]
- Cuche, E.; Marquet, P.; Depeursinge, C. Simultaneous amplitude-contrast and quantitative phase-contrast microscopy by numerical reconstruction of Fresnel off-axis holograms. Appl. Opt. 1999, 38, 6994–7001. [Google Scholar] [CrossRef]
- Gao, W.; Kimura, A. A fast evaluation method for pitch deviation and out-of-flatness of a planar scale grating. CIRP Ann. 2010, 59, 505–508. [Google Scholar] [CrossRef]
- Shimizu, Y.; Kim, W.J.; Ito, S.; Gao, W. Form error characterization of reflective-type gratings. Key Eng. Mater. 2012, 523, 859–864. [Google Scholar] [CrossRef]
- Paesler, M.A.; Moyer, P.J.; Lewis, A. Near-Field Optics: Theory, Instrumentation, and Applications; Wiley: Hoboken, NJ, USA, 1997. [Google Scholar]
- Courjon, D. Near-Field Microscopy and Near-Field Optics; World Scientific Publishing Company: Singapore, 2003. [Google Scholar]
- Mayes, T.; Riley, M.; Edward, K.; Fesperman, R.; Suraktar, A.; Shahid, U.; Williams, S.; Hocken, R. Phase imaging in the near field. CIRP Ann. 2004, 53, 483–486. [Google Scholar] [CrossRef]
- Lin, Y.H.; Tsai, D.P. Near-field scanning optical microscopy using a super-resolution cover glass slip. Opt. Express 2012, 20, 16205–16211. [Google Scholar] [CrossRef]
- Price, J.H.; Gough, D.A. Autofocus System for Scanning Microscopy. US Patent 5,790,710, 4 August 1998. [Google Scholar]
- Fan, K.C.; Chu, C.L.; Mou, J.I. Development of a low-cost autofocusing probe for profilemeasurement. Meas. Sci. Technol. 2001, 12, 2137. [Google Scholar] [CrossRef]
- Firestone, L.; Cook, K.; Culp, K.; Talsania, N.; Preston, K., Jr. Comparison of autofocus methods for automated microscopy. Cytom. J. Int. Soc. Anal. Cytol. 1991, 12, 195–206. [Google Scholar] [CrossRef] [PubMed]



| Method | Typical Accuracy | Typical Application Scenarios | Advantages and Disadvantages |
|---|---|---|---|
| Laser Interferometer | Nanometre to picometre level; measurement range from tens of meters to several kilometre | Large-scale ultra-high-precision linear positioning (lithography stage, synchrotron beamline, calibration of precision machine tool axes) |
|
| Optical Linear Encoder | Incremental interferometric type: picometre level (e.g., 6.1 pm); absolute type: ∼1 nm; measurement length typically ≤20 m (up to 40 m in special designs) | Position feedback for machine tools, semiconductor lithography stages, coordinate measuring machines (CMMs), automated production line positioning |
|
| Confocal Measurement | Nanometer-level resolution in commercial systems (e.g., 12 nm); measuring range typically ≤ tens of millimeters | Thickness measurement of transparent multilayer structures, deep-hole inspection, microstructure surface measurement, MEMS inspection, height measurement in precision assembly |
|
| Laser Triangulation | Micrometre to sub-micrometre level (depending on sensor resolution and optical design) | Industrial profile scanning, surface topography inspection, position feedback, large-stroke in-line displacement measurement |
|
| Time-of-Flight (TOF) Measurement | Conventional TOF: ∼100 m; femtosecond pulse interferometry/BOC: nanometre to sub-nanometre level | Large-scale distance measurement (conventional TOF), medium- to long-range high-precision positioning (femtosecond-laser dual-comb), satellite formation navigation |
|
| Method | Typical Accuracy | Typical Application Scenarios | Advantages and Disadvantages |
|---|---|---|---|
| Rotary Encoder | ∼ rad | Rotary axis positioning of machine tools, angular feedback for rotary tables, joint angle detection in robots |
|
| Autocollimator | ∼ rad | Flatness adjustment, angular deviation inspection, optical platform attitude adjustment, rotary accuracy check, multi-degree-of-freedom tilt measurement |
|
| Interferometric Methods | ∼ rad | Multi-DOF measurement of precision stages, roll angle detection in nanometer positioning systems, high-accuracy tilt measurement |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, F.; Tang, H.; Zou, X.; Li, X. A Review of Optical Metrology Techniques for Advanced Manufacturing Applications. Micromachines 2025, 16, 1224. https://doi.org/10.3390/mi16111224
Zhao F, Tang H, Zou X, Li X. A Review of Optical Metrology Techniques for Advanced Manufacturing Applications. Micromachines. 2025; 16(11):1224. https://doi.org/10.3390/mi16111224
Chicago/Turabian StyleZhao, Fangyuan, Hanyao Tang, Xuerong Zou, and Xinghui Li. 2025. "A Review of Optical Metrology Techniques for Advanced Manufacturing Applications" Micromachines 16, no. 11: 1224. https://doi.org/10.3390/mi16111224
APA StyleZhao, F., Tang, H., Zou, X., & Li, X. (2025). A Review of Optical Metrology Techniques for Advanced Manufacturing Applications. Micromachines, 16(11), 1224. https://doi.org/10.3390/mi16111224






