Simulation Analysis of Temperature Change in FDM Process Based on ANSYS APDL and Birth–Death Element Technology
Abstract
1. Introduction
2. Methodology
2.1. Programmable Control of the FDM Process
2.1.1. Ansys Parametric Design Language
2.1.2. Birth and Death Unit Technology
2.1.3. Integrated Simulation Framework for FDM Temperature Field
- (1)
- Dynamic process replication: It allows for the precise, time-accurate activation of material elements (EALIVE command) in direct sequence with a user-defined, nonlinear printing path (linear reciprocating in this case), mirroring the actual manufacturing process rather than simulating a static, pre-deposited geometry.
- (2)
- Automated multi-physics coupling: It automates the sequential thermo-mechanical analysis, ensuring perfect consistency in the history of deposition between the thermal and structural models. The critical data transfer of the temperature field is handled programmatically via the LDREAD command.
- (3)
- Complex boundary condition management: It facilitates the application of complex, time-varying thermal boundary conditions (convection, radiation) on a dynamically changing model geometry, a task that is highly cumbersome and often approximated in standard graphical interface-based simulations.
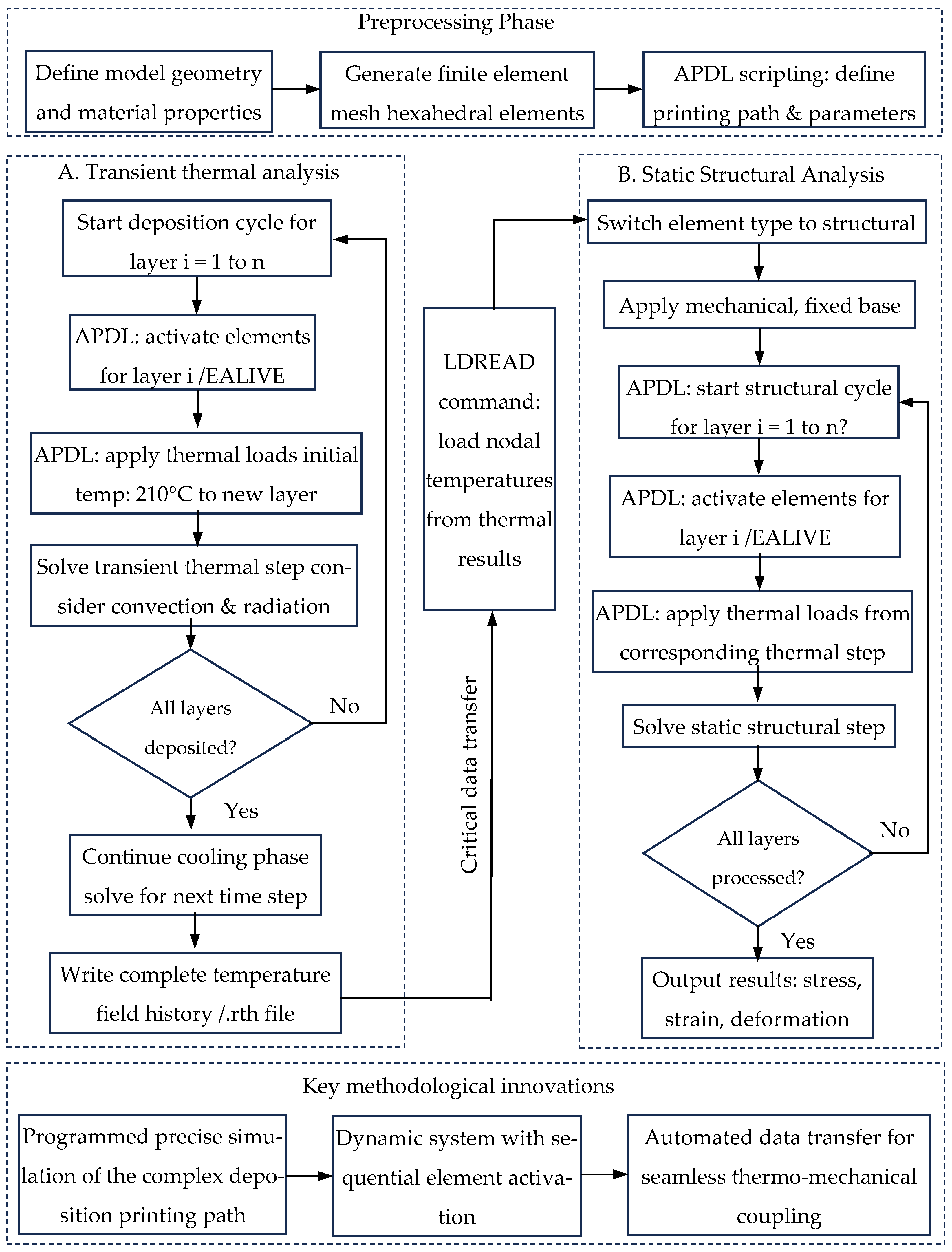
2.2. A Sequentially Coupled Thermo-Mechanical Model for FDM Printing
2.2.1. Modeling of Latent Heat of Fusion
2.2.2. Sequentially Coupled Thermo-Mechanical Formulation
2.2.3. Implementation of the Moving Heat Source
2.3. Material Model and Process Parameterization
- (1)
- The PLA material is assumed to obey the von Mises yield criterion and the associated flow rule.
- (2)
- The extruded filament is idealized as a perfectly flat strip, neglecting potential defects such as necking or fracture.
- (3)
- Perfect contact is assumed between the newly deposited filament and the underlying layer, with heat transfer mechanisms including conduction, convection, and radiation.
- (4)
- Heat dissipation during the forming process occurs solely through natural convection; the ambient temperature remains constant, and no additional external heat sources are considered.
- (5)
- The effects of high-temperature material degradation and crystallization behavior are not accounted for in the model.
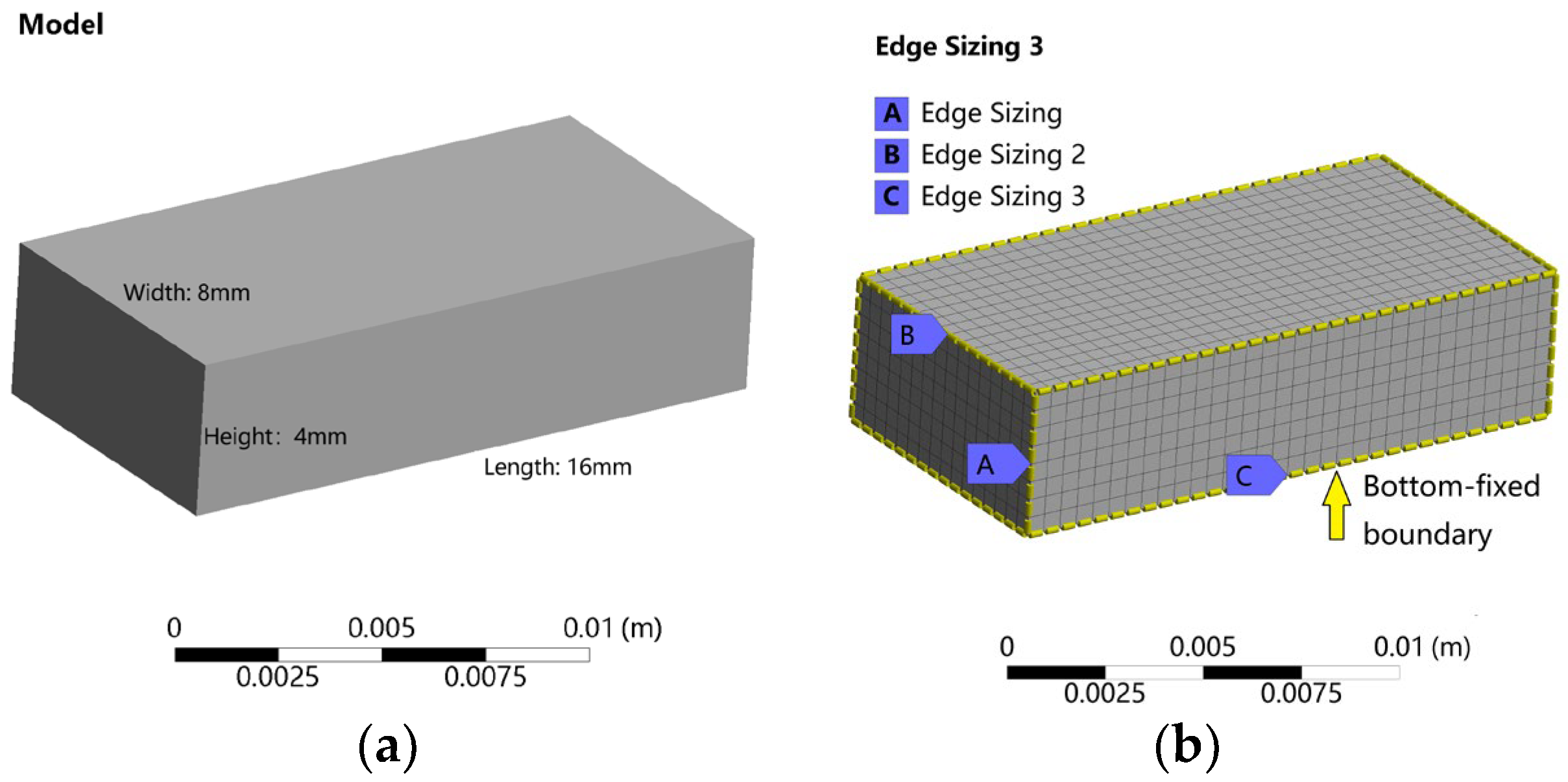
2.4. Finite Element Modeling and Boundary Setting
2.5. Numerical Implementation with APDL
2.5.1. Element Birth–Death Activation and Path Control
2.5.2. Thermal Boundary Condition and Heat Exchange
2.5.3. Thermo-Mechanical Coupling Procedure
3. Results Analysis and Discussion
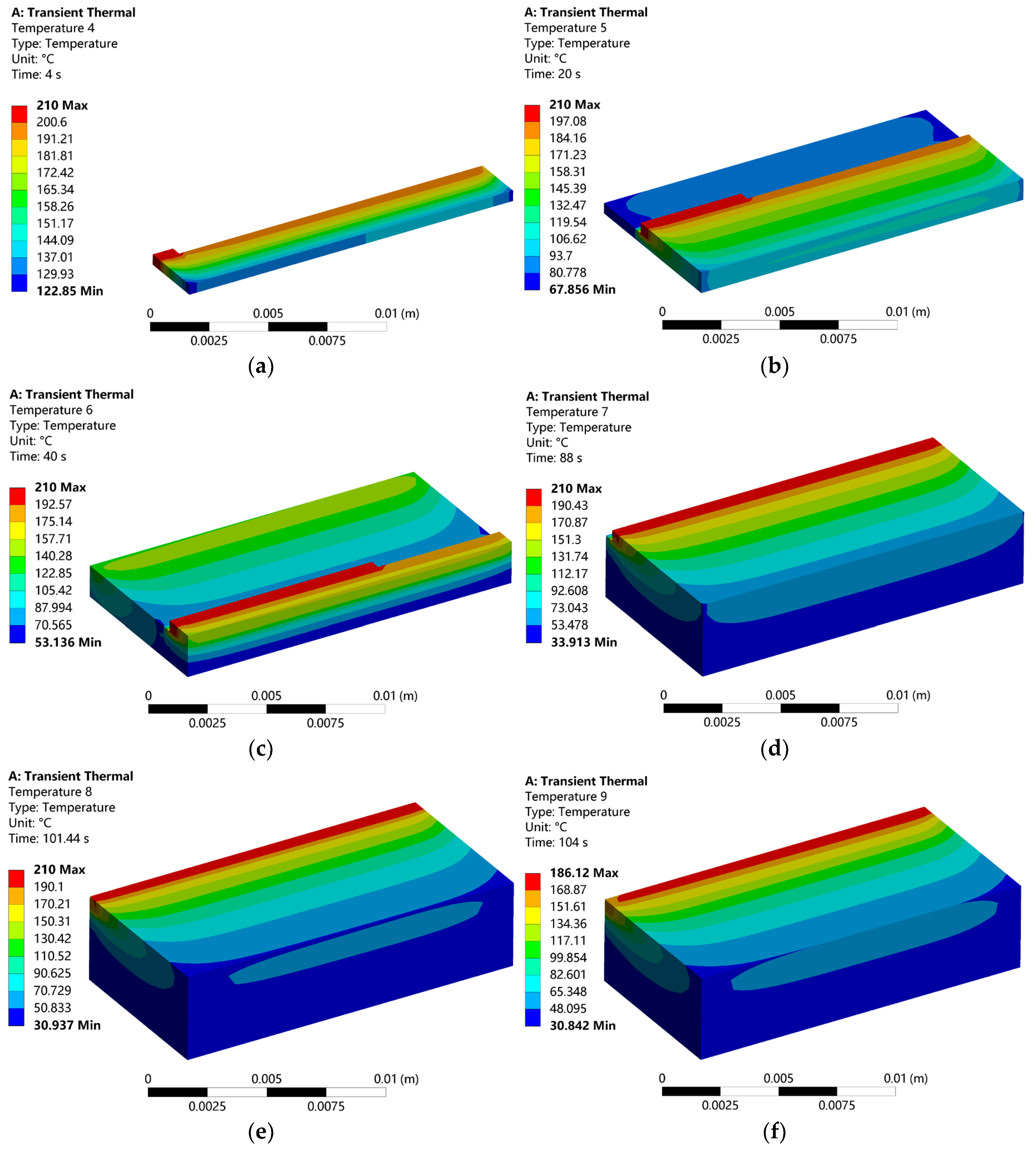
3.1. Temperature Distribution at Different Times During the Printing Process
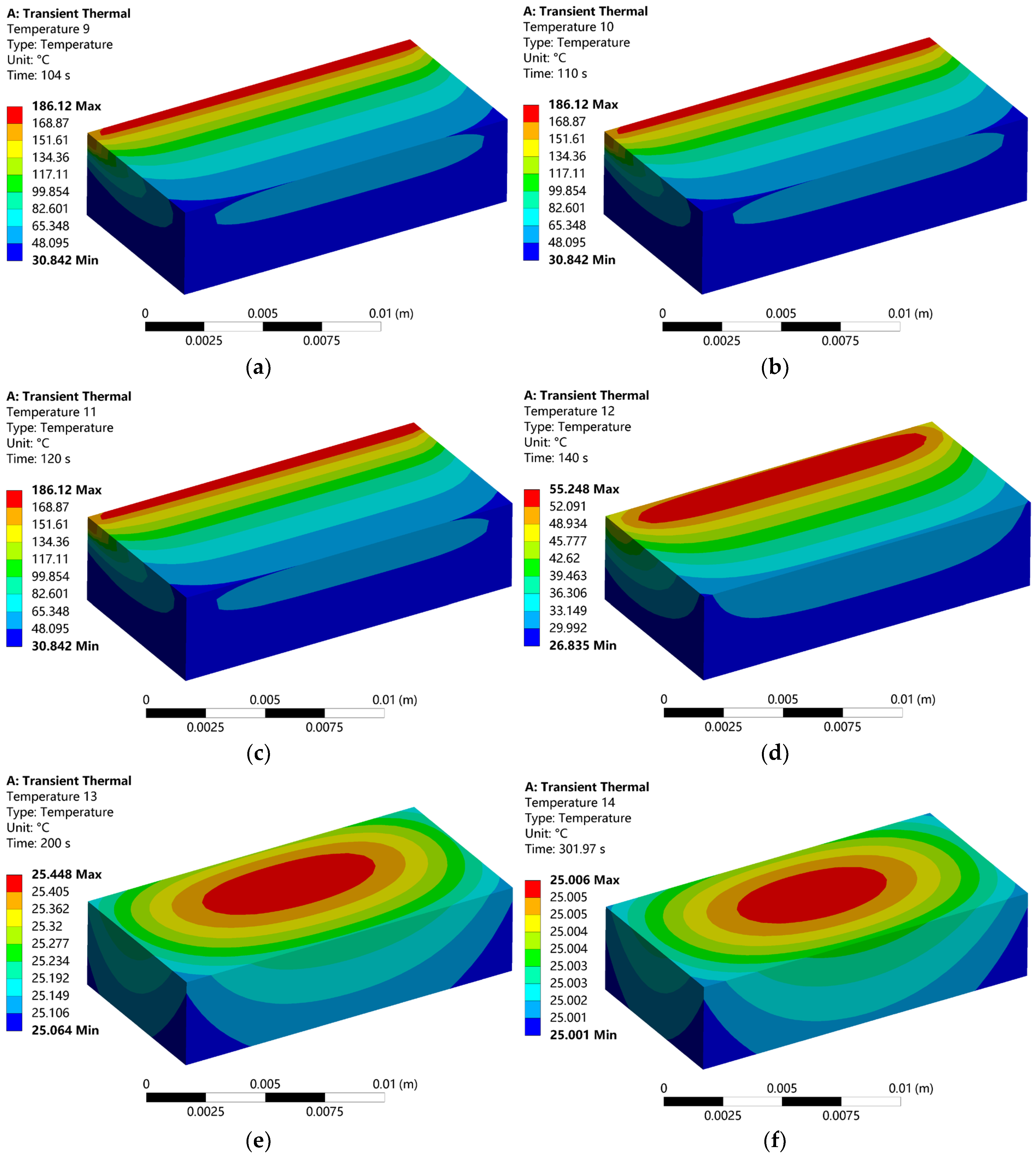
3.2. Temperature Distribution at Different Times During the Cooling Process
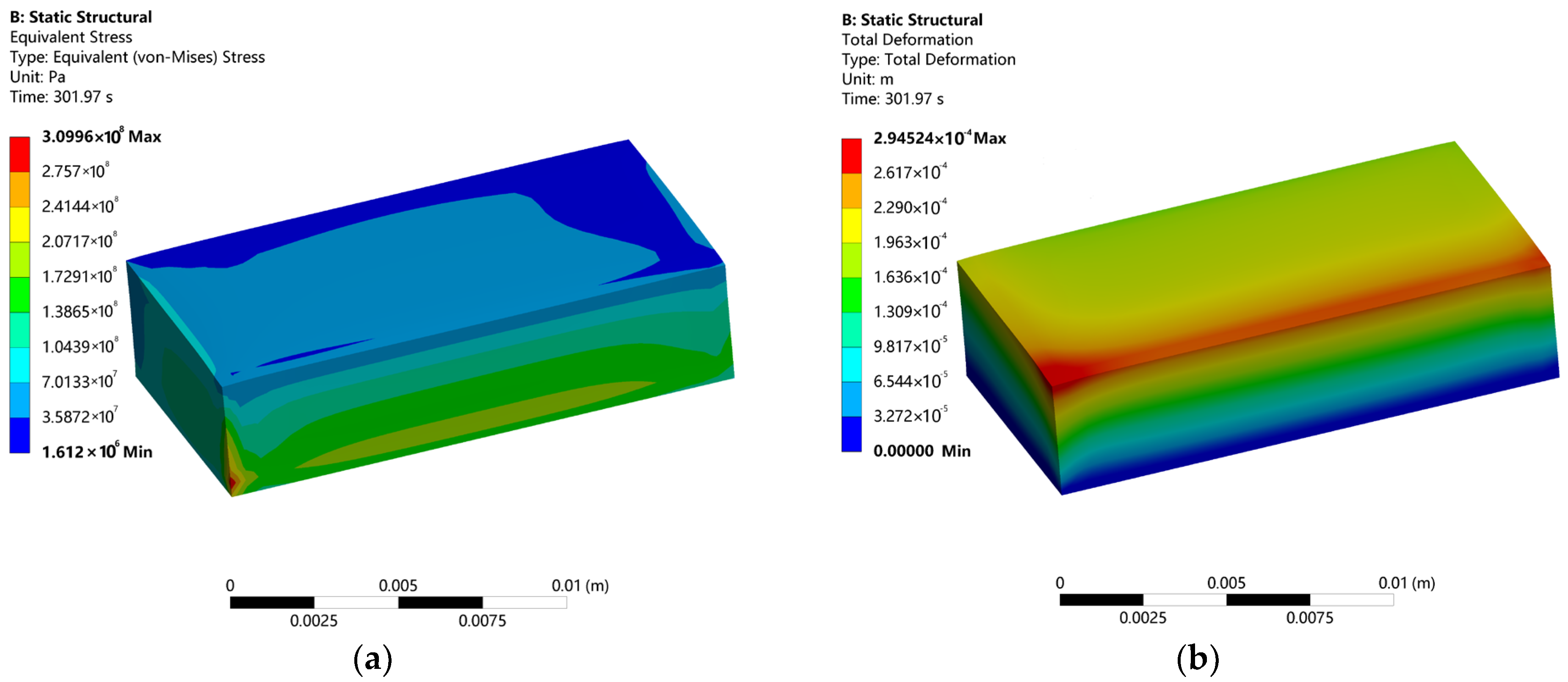
3.3. Stress–Strain Analysis of FDM Process
4. Experimental Verification
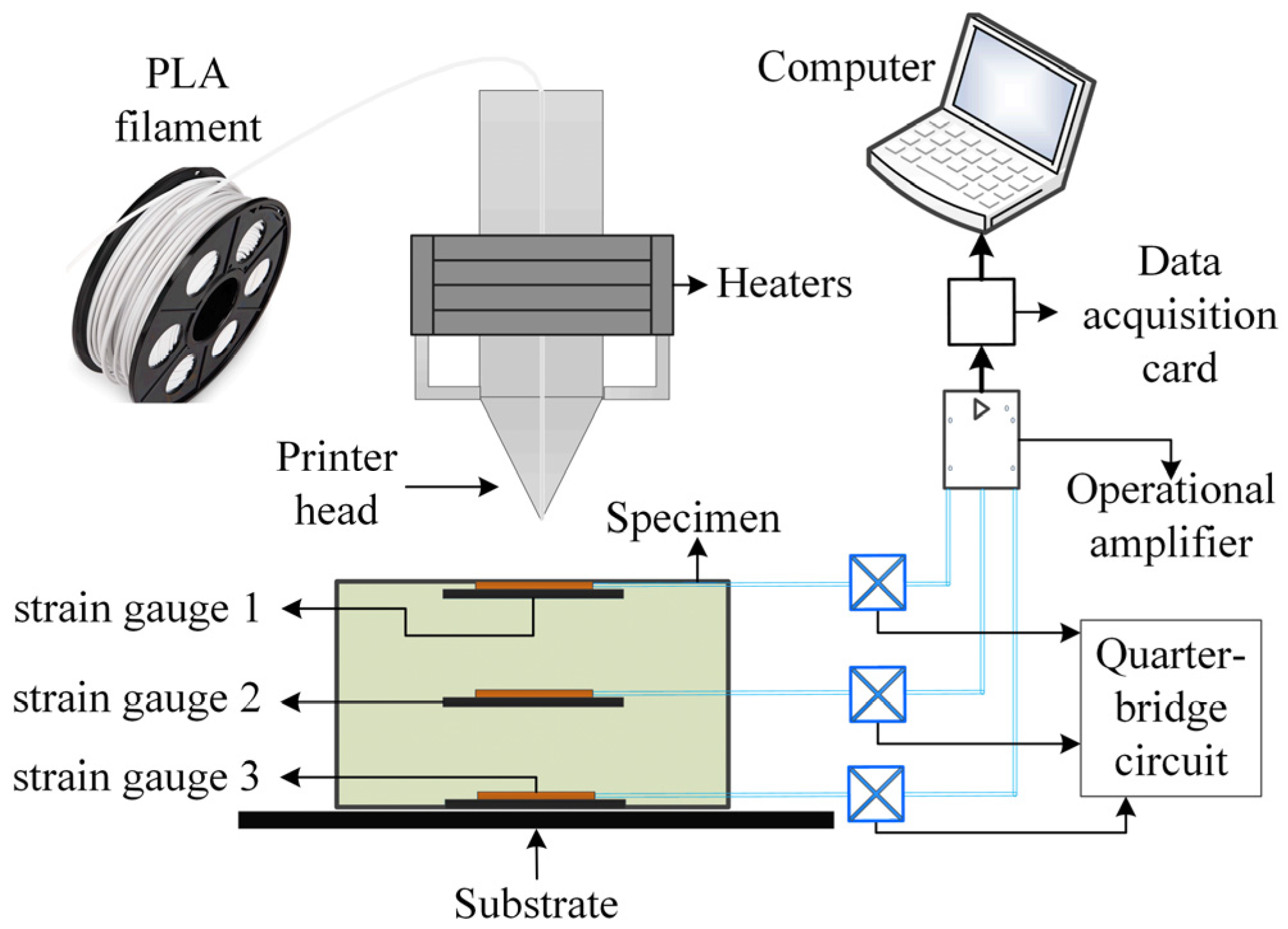
4.1. Experimental Setup and Procedure
4.2. Comparison of Temperature Field
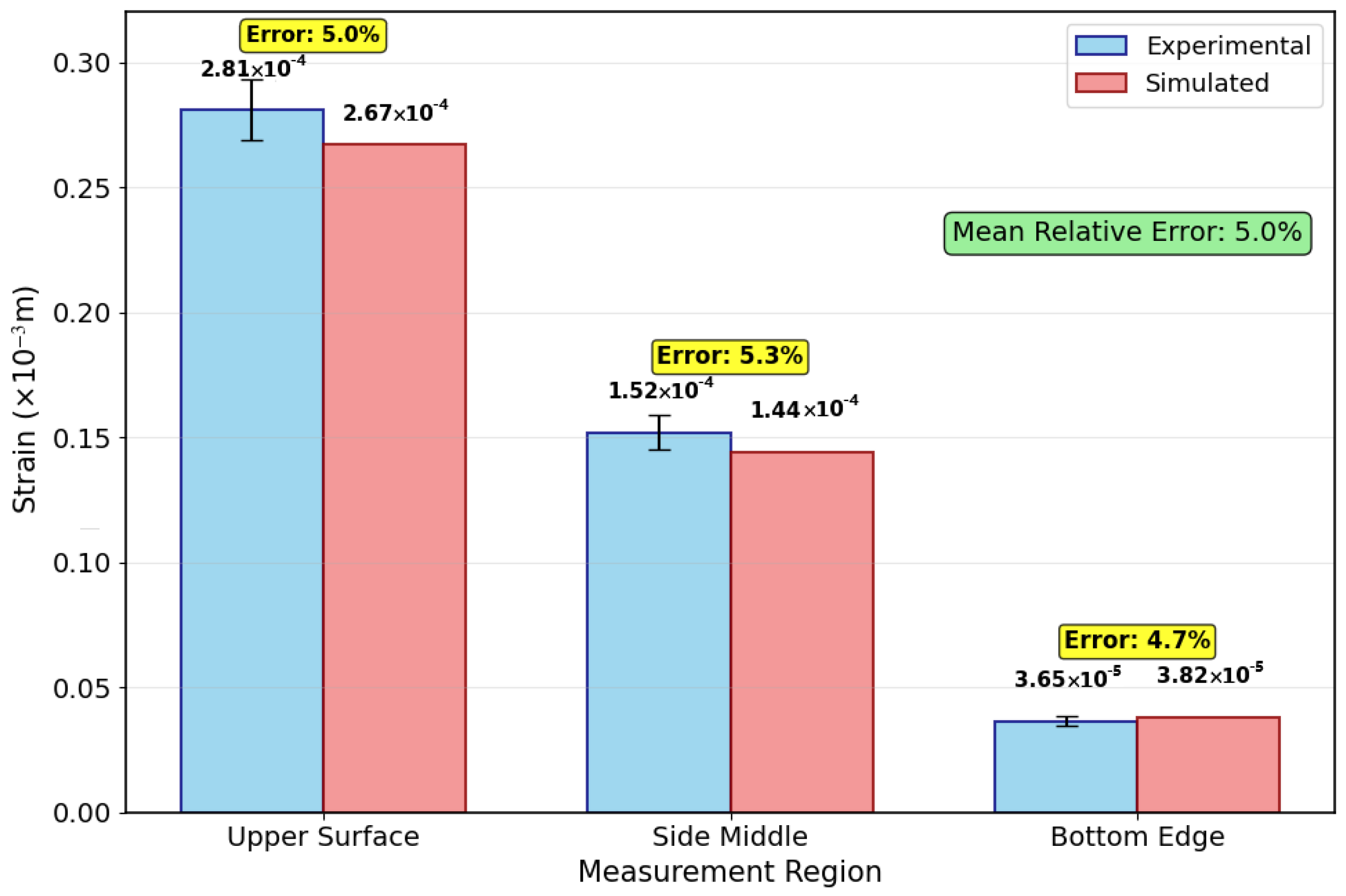
4.3. Validation of Stress and Strain Distribution
4.4. Model Validation and Limitations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tanwar, R.; Kumar, D.; Shivani; Bahmani, K.; Gulati, P. Fundamental Principles of Fused Deposition Modelling (FDM) Technology; Springer Nature: Singapore, 2025; pp. 31–41. [Google Scholar] [CrossRef]
- Bedi, S.S.; Vasu, M.; Vinyas, M. Impact of Chloroform Treatment on the Tensile Property of PETG and PLA Materials Fabricated via the Fused Deposition Modeling (FDM) Technique; Springer Nature: Singapore, 2024; pp. 59–70. [Google Scholar] [CrossRef]
- Johar, M.; Rosli, A.A.; Shuib, R.K.; Abdul Hamid, Z.A.; Abdullah, M.K.; Ku Ishak, K.M.; Rusli, A. Dimensional stability of poly (lactic acid) (PLA) parts fabricated using fused deposition modelling (FDM). Prog. Rubber Plast. Recycl. Technol. 2025, 41, 218–232. [Google Scholar] [CrossRef]
- Elsonbaty, A.A.; MRashad, A.; Abass, O.Y.; Abdelghany, T.Y.; MAlfauiomy, A. A Survey of Fused Deposition Modeling (FDM) Technology in 3D Printing. J. Eng. Res. Rep. 2024, 26, 304–312. [Google Scholar] [CrossRef]
- Halevi, S.; Tulpan, I.; Shirizly, A.; Levy, G.K. A design framework for multi-thermal optimization of ULTEM 1010 using open-source FDM: Unlocking its additive manufacturing potential. Mater. Des. 2025, 257, 114407. [Google Scholar] [CrossRef]
- Haque, M.M.M.; Dhrubo, S.R.; Pranto, A.F.Z.; Ahmed, A.; Arefin, M.M.; Arifuzzaman, M.; Islam, M.S. Impact of process parameters and material selection on the mechanical performance of FDM 3D-Printed components. Hybrid Adv. 2025, 10, 100502. [Google Scholar] [CrossRef]
- Nishida, G.; Ueda, T.; Yamada, T.; Matsuzaki, R.; Hirano, Y. Numerical modeling of the fiber–polymer interaction in additive manufacturing of composite materials. Compos. Part A Appl. Sci. Manuf. 2021, 151, 106658. [Google Scholar] [CrossRef]
- Zhao, L.; Zhao, Z.; Ma, L.; Li, S.; Men, Z.; Wu, L. Developing the optimized control scheme for digital light processing 3D printing by combining numerical simulation and machine learning-guided temperature prediction. J. Manuf. Process. 2024, 132, 363–374. [Google Scholar] [CrossRef]
- Yang, R.; Xiao, J.; Liu, Y.; Xu, S. The die swell eliminating mechanism of hot air assisted 3D printing of GF/PP and its influence on the product performance. e-Polymers 2024, 24, 20240008. [Google Scholar] [CrossRef]
- Willy, H.J.; Li, X.; Tan, Y.H.; Chen, Z.; Cagirici, M.; Borayek, R.; Herng, T.S.; Ong, C.Y.A.; Li, C.; Ding, J. Overview of Finite Elements simulation of temperature profile to estimate properties of materials 3D-printed by Laser Powder-Bed Fusion. Chin. Phys. B 2020, 29, 048101. [Google Scholar] [CrossRef]
- Mosleh, N.; Esfandeh, M.; Dariushi, S. Simulation of temperature profile in fused filament fabrication 3D printing method. Rapid Prototyp. J. 2024, 30, 134–144. [Google Scholar] [CrossRef]
- Baeza-Campuzano, A.; Castao, V.M. The effect of printing velocity on the temperature and viscosity of the polymer thread at the nozzle exit in 3D printers. Polimery 2021, 2, 127–138. [Google Scholar] [CrossRef]
- Lei, M.; Wei, Q.; Li, M.; Zhang, J.; Yang, R.; Wang, Y. Numerical Simulation and Experimental Study the Effects of Process Parameters on Filament Morphology and Mechanical Properties of FDM 3D Printed PLA/GNPs Nanocomposite. Polymers 2022, 14, 3081. [Google Scholar] [CrossRef]
- Apaçoğlu-Turan, B.; Kırkköprü, K.; Çakan, M. Numerical Modeling and Analysis of Transient and Three-Dimensional Heat Transfer in 3D Printing via Fused-Deposition Modeling (FDM). Computation 2024, 12, 27. [Google Scholar] [CrossRef]
- Prasad, M.J.H.; Sudhakar, I.; Adinarayana, S.; Rao, D.V.N.J.J. Simulation and validation of experimental residual stresses of dissimilar AA2124 and AA7075 TIG weld joint using ANSYS APDL. IJIDeM Int. J. Interact. Des. Manuf. 2024, 18, 71–82. [Google Scholar] [CrossRef]
- Schmidtke, V.; Rüger, M.; Stursberg, O. Model Predictive Control of PDEs for Temperature Control in 3D-Printing Processes. In Proceedings of the 2023 European Control Conference (ECC), Bucharest, Romania, 13–16 June 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Equbal, A.; Murmu, R.; Kumar, V.; Equbal, M.A. A recent review on advancements in dimensional accuracy in fused deposition modeling (fdm) 3d printing. AIMS Mater. Sci. 2024, 11, 950–990. [Google Scholar] [CrossRef]
- Zniker, H.; El Magri, A.; Feddal, I.; Marbouh, M.; El Hasnaoui, M. Effect of printing temperature on the mechanical properties of 3D printed polyphenylene sulfide (PPS) during simple and repeated impact tests. Int. Rev. Appl. Sci. Eng. 2025, 16, 210. [Google Scholar] [CrossRef]
- Morvayová, A.; Contuzzi, N.; Casalino, G. Defects and residual stresses finite element prediction of FDM 3D printed wood/PLA biocomposite. Int. J. Adv. Manuf. Technol. 2023, 129, 2281–2293. [Google Scholar] [CrossRef]
- Rizky, M.A.; Setiawan, A.; Sukamto, U. Analysis Nozzle Temperature Effect In 3D Printer Fused Deposition Modelling (FDM) On Mechanical Properties and Characteristics of Polylactic Acid (PLA). Mek. Maj. Ilm. Mek. 2022, 21, 1–12. [Google Scholar] [CrossRef]
- Bijari, F.; Bagheri, N.B. A Comprehensive Review of Fused Deposition Modeling: State of the Art and Current Challenges. J. Mater. Eng. Perform. 2025, 34, 2007–2032. [Google Scholar] [CrossRef]
- Cano-Vicent, A.; Tambuwala, M.M.; Hassan, S.S.; Barh, D.; Aljabali, A.A.; Birkett, M.; Arjunan, A.; Serrano-Aroca, Á. Fused deposition modelling: Current status, methodology, applications and future prospects. Addit. Manuf. 2021, 47, 102378. [Google Scholar] [CrossRef]
- Arslan, Y. Effects of ultra-cold temperature on thermoplastic (ASA, PLA) parts produced by 3D FDM printing technology. Sādhanā 2025, 50, 250. [Google Scholar] [CrossRef]
- Mastrisiswadi, H.; Atsani, S.I.; Sari, W.P.; Herianto, H. Design and parameters optimisation of fused deposition modelling (FDM) technology in the fabrication of sensorised soft pneumatic actuator. Prog. Addit. Manuf. 2025, 10, 287–314. [Google Scholar] [CrossRef]
- Li, Z.; Chang, L. Development of Wear-Resistant Polymeric Materials Using Fused Deposition Modelling (FDM) Technologies: A Review. Lubricants 2025, 13, 98. [Google Scholar] [CrossRef]
- Bui, T.H.; Khoa, T.L.; Huynh, H.N. Analysis, Numerical Simulation of Convective Heat Flow in the Fabrication Chamber of an Open Source FDM Device; Springer Nature: Cham, Switzerland, 2024; pp. 121–137. [Google Scholar] [CrossRef]
- Fernández, V.; García, A.; Camacho, A.M.; Claver, J.; Rodríguez, A.; Sebastián, A.M. Methodology to estimate the modulus of elasticity of parts manufactured by FFF/FDM combining finite element simulations and experimental tests. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1193, 012001. [Google Scholar] [CrossRef]
- Panico, M.; Genna, S.; Langella, A.; Papa, I. Laser joining of FDM-printed PLA components: Feasibility and thermo-mechanical analysis. Int. J. Adv. Manuf. Technol. 2025, 139, 2657–2669. [Google Scholar] [CrossRef]
- Song, W.; Wu, Z.; He, S.; Liu, J.; Yang, G.; Liu, Y.; Jin, H.; He, Y.; Heng, Z. Effects of Friction Stir Processing on the Microstructure and Mechanical Properties of an Ultralight Mg-Li Alloy. Crystals 2024, 14, 64. [Google Scholar] [CrossRef]
- Mirasadi, K.; Yousefi, M.A.; Jin, L.; Rahmatabadi, D.; Baniassadi, M.; Liao, W.; Bodaghi, M.; Baghani, M. 4D Printing of Magnetically Responsive Shape Memory Polymers: Toward Sustainable Solutions in Soft Robotics, Wearables, and Biomedical Devices. Adv. Sci. 2025, 12, e13091. [Google Scholar] [CrossRef]
- Kumar, S.; Chandramohan, S.; Sujatha, S. Optimal Design of Magnetorheological Valve Using the Coupling of FE Magnetic Analysis and MOGA Optimization for Prosthetic Ankle. J. Vib. Eng. Technol. 2024, 12, 2205–2217. [Google Scholar] [CrossRef]
- Ma, H.; Jiao, Z.; Wang, C.; Luo, B.; Yang, W. The forming process of polymer melt droplet deposition three dimensional printing. Polym. Eng. Sci. 2020, 60, 2890–2901. [Google Scholar] [CrossRef]
- Struzziero, G.; Teuwen, J.J.E.; Skordos, A.A. Numerical optimisation of thermoset composites manufacturing processes: A review. Compos. Part A Appl. Sci. Manuf. 2019, 127, 105499. [Google Scholar] [CrossRef]
- Ghorbel, R.; Ktari, A.; Oudhini, M.; Dhib, Z.; Haddar, N. Numerical Simulation of Clad Steel Plates Joined by a Multi-Pass Welding Process Based on Element Birth and Death Technique: A Case Study; Springer Nature: Cham, Switzerland, 2024; pp. 74–84. [Google Scholar] [CrossRef]
- Hou, H.; Yue, Y.; Liu, J.; Xi, D.; Liu, S. Numerical Simulation and Experimental Study of the Stress Formation Mechanism of FDM with Different Printing Paths. J. Renew. Mater. 2023, 11, 273–289. [Google Scholar] [CrossRef]


| Density (kg/m3) | Thermal Conductivity (W/m·°C) | Elastic Modulus (MPa) | Poisson’s Ratio | Specific Heat Capacity (J/kg·°C) | Temperature (°C) |
|---|---|---|---|---|---|
| 1250 | 0.25 | 3.5 × 103 | 0.35 | 1560 | 47.5 |
| 1700 | 54.9 | ||||
| 1820 | 60.3 | ||||
| 1900 | 109.3 | ||||
| 2320 | 134.9 | ||||
| 4360 | 145.6 | ||||
| 2100 | 152.0 | ||||
| 1980 | 172.3 |
| ConsumaBles | Fill Rate | Layer Height | Print Temperature | Print Speed | Print Spacing | Print Trajectory |
|---|---|---|---|---|---|---|
| PLA | 30% | 0.2 mm | 210 °C | 80 mm/s | 0.4 mm | Linear reciprocating scanning |
| Strain Gauge | Strain Grid | Resistance | Temperature Range | Resolution | Error |
|---|---|---|---|---|---|
| TSK-89561H | 0.7 mm | 120 Ω | −30–250 °C | 1 με | <1% |
| Platinum Resistance Thermometer | Structural Type | Temperature Measurement Range | Accuracy | Error |
|---|---|---|---|---|
| PRT-PT100 | Thin-Film Type | −200–+600 °C | High | <±0.15 °C |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mi, Y.; Hashemi Sohi, S.H. Simulation Analysis of Temperature Change in FDM Process Based on ANSYS APDL and Birth–Death Element Technology. Micromachines 2025, 16, 1181. https://doi.org/10.3390/mi16101181
Mi Y, Hashemi Sohi SH. Simulation Analysis of Temperature Change in FDM Process Based on ANSYS APDL and Birth–Death Element Technology. Micromachines. 2025; 16(10):1181. https://doi.org/10.3390/mi16101181
Chicago/Turabian StyleMi, Yuehua, and Seyed Hamed Hashemi Sohi. 2025. "Simulation Analysis of Temperature Change in FDM Process Based on ANSYS APDL and Birth–Death Element Technology" Micromachines 16, no. 10: 1181. https://doi.org/10.3390/mi16101181
APA StyleMi, Y., & Hashemi Sohi, S. H. (2025). Simulation Analysis of Temperature Change in FDM Process Based on ANSYS APDL and Birth–Death Element Technology. Micromachines, 16(10), 1181. https://doi.org/10.3390/mi16101181






