Research on Piezoelectric Guided Wave Frequency Diverse Array-Based Damage Location Method for Thin-Walled Structures
Abstract
1. Introduction
2. Frequency Diverse Piezoelectric Sensor Array-Based Damage Location Method
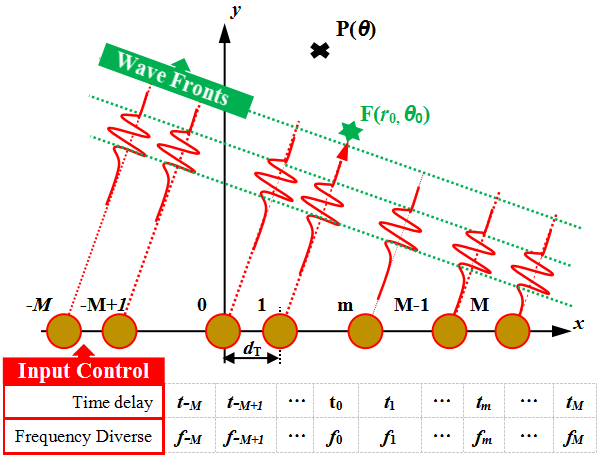
2.1. Frequency Diverse Array Signal Transmitter Model
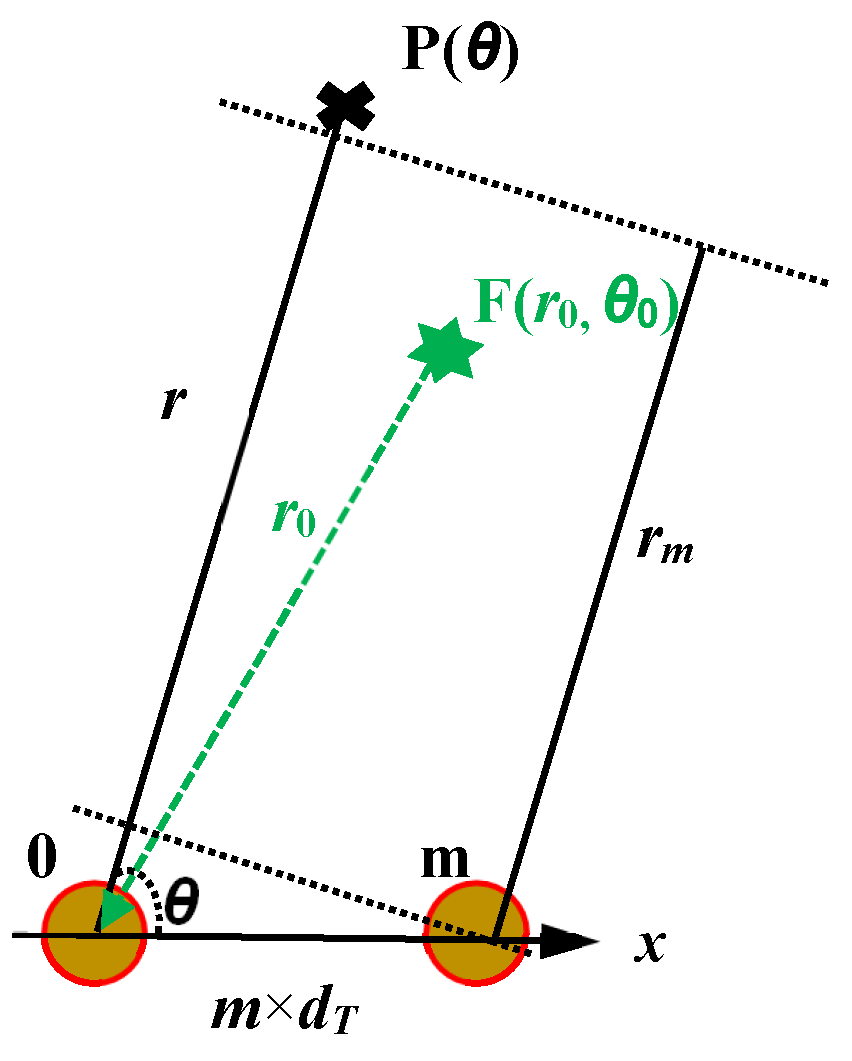
2.2. Two-Dimensional MUSIC-Based Damage Location
3. Simulation Results and Discussion
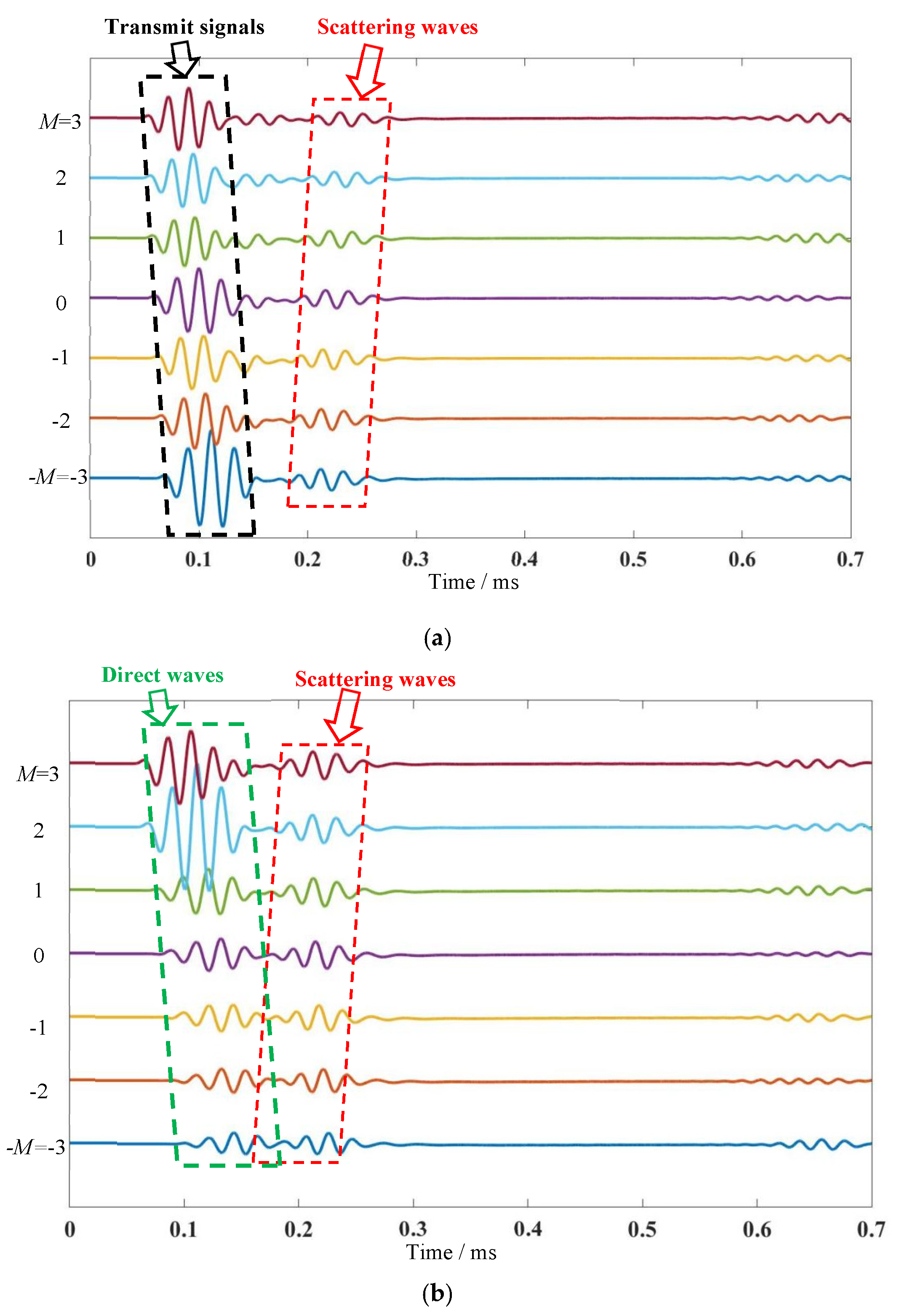
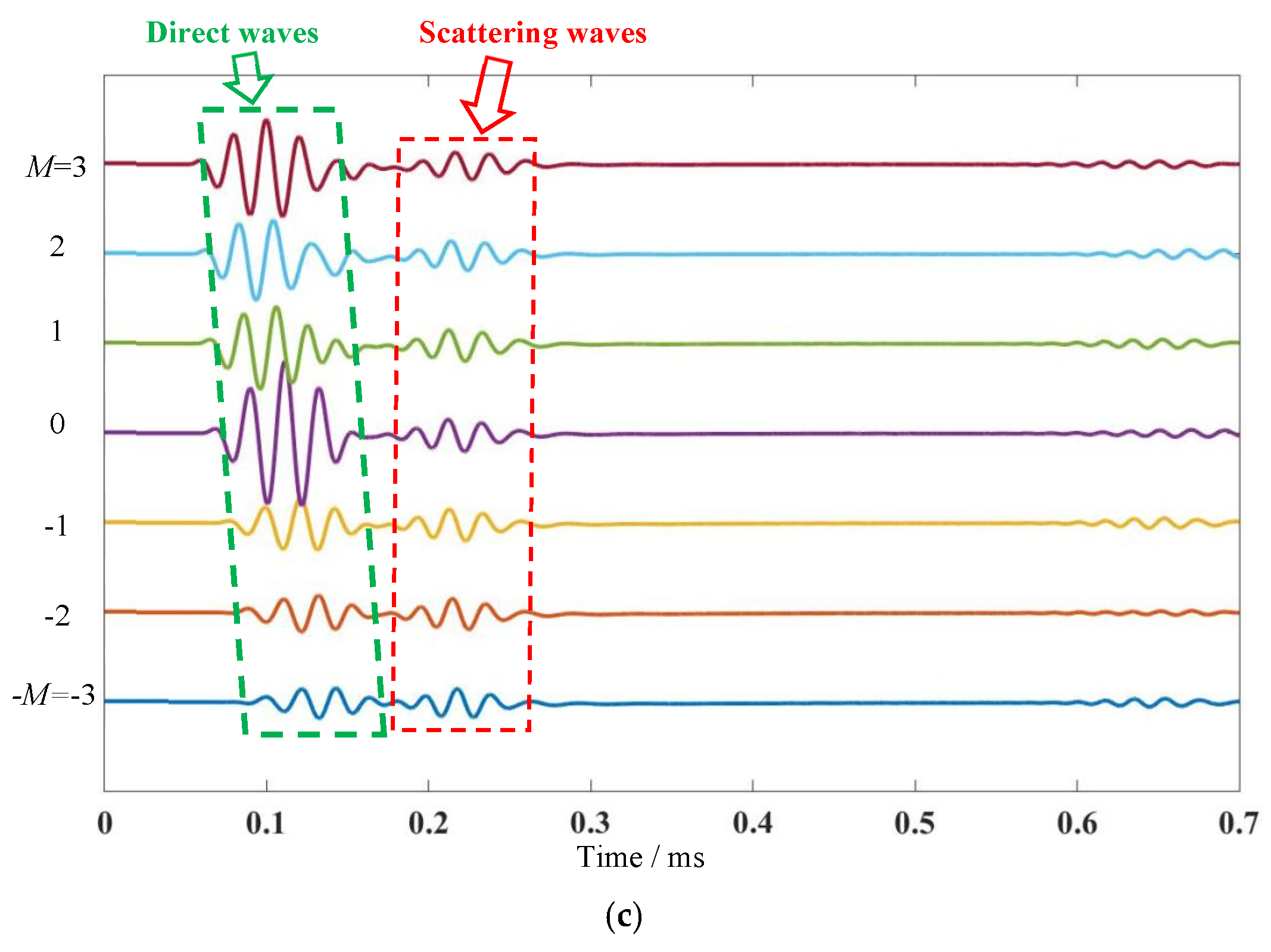
3.1. Transmitting–Receiving Array Signals
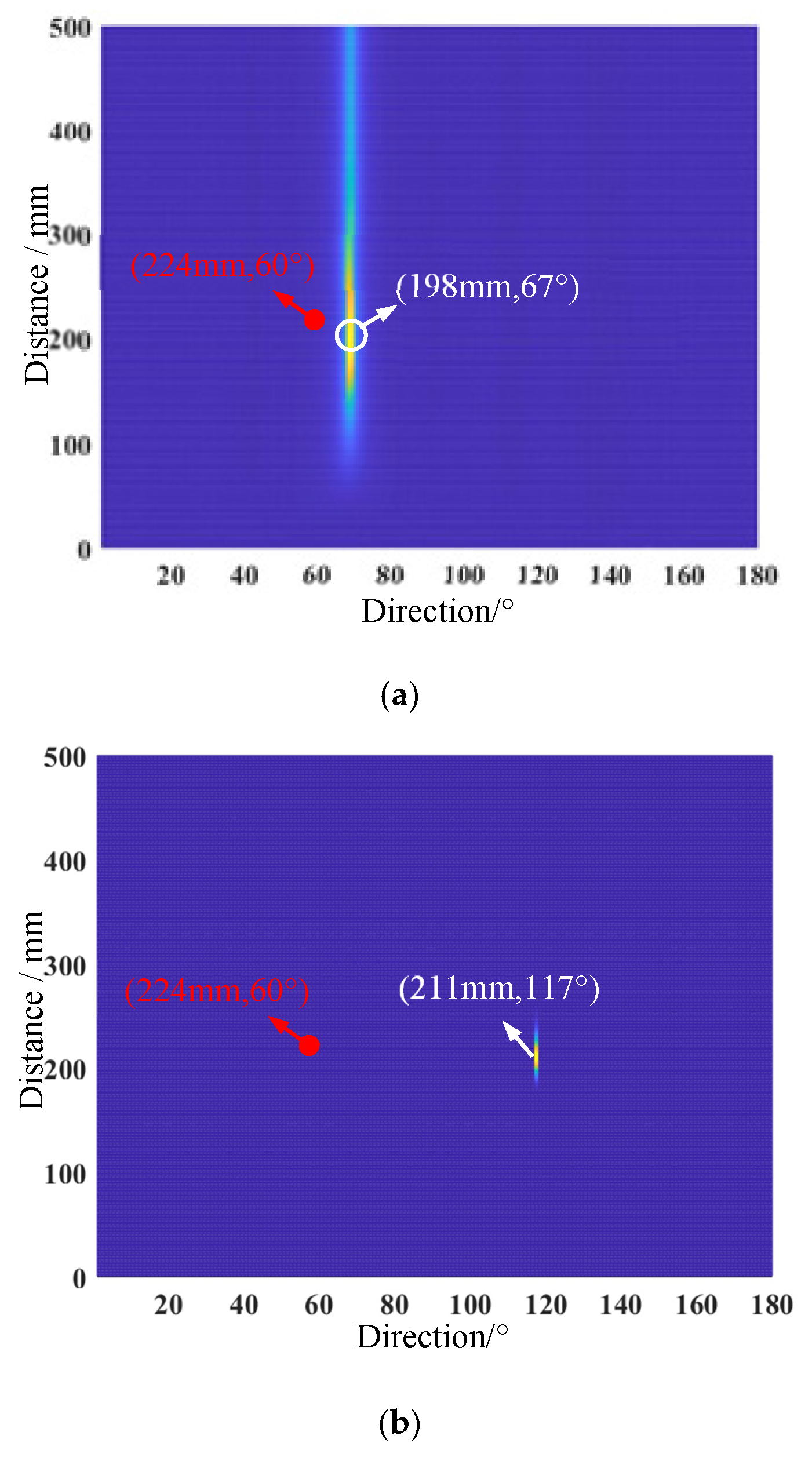
3.2. Damage Imaging Results
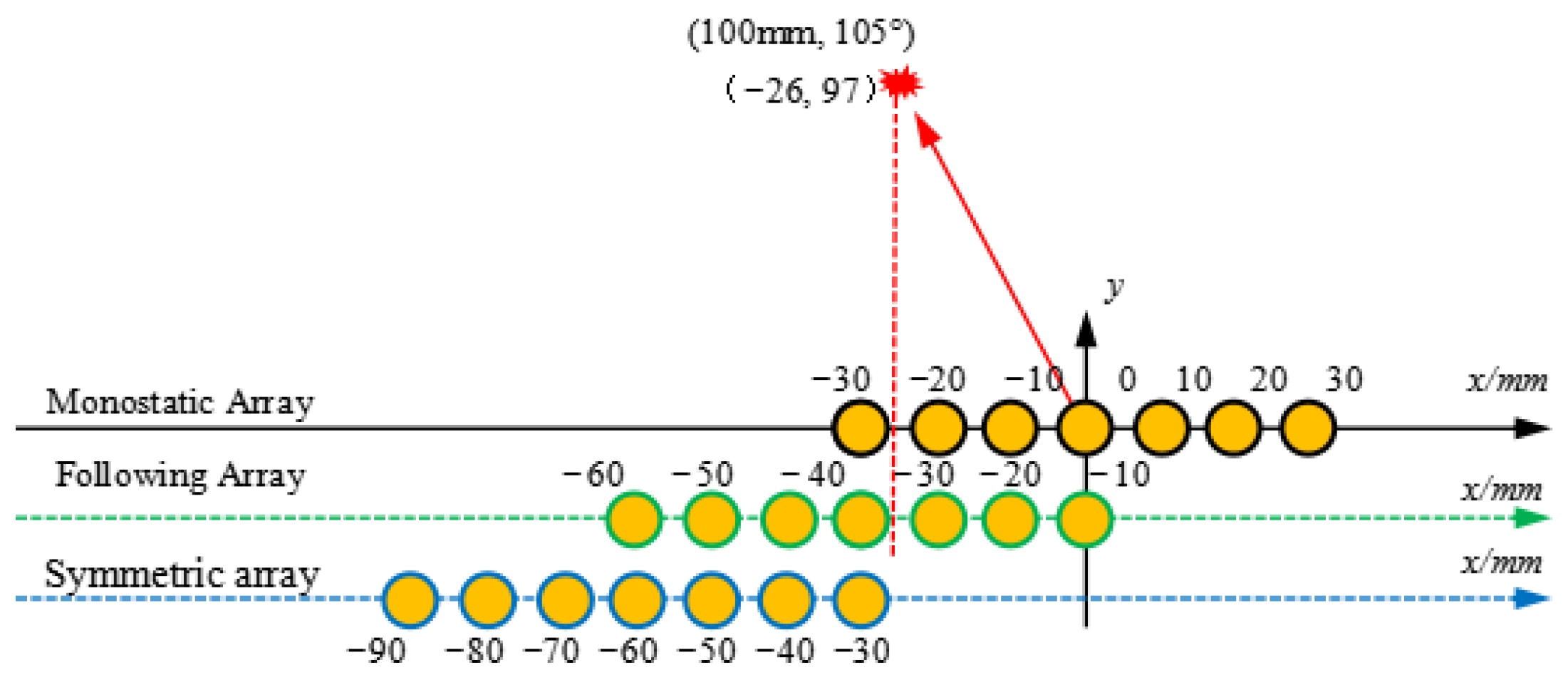
4. Experimental Verification on an Epoxy Laminate Plate
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yuan, S.F.; Jing, H.T.; Wang, Y.; Zhang, J.J. A whole service time SHM damage quantification model hierarchical evolution mechanism. Mech. Syst. Signal Process. 2024, 209, 111064. [Google Scholar] [CrossRef]
- Yu, Z.X.; Yue, Y.Q.; Liang, Z.Z.; Zhao, X.L.; Li, F.P.; Peng, W.B.; Zhu, Q.Z.; He, Y.N. Physical sensors based on lamb wave resonators. Micromachines 2024, 15, 1243. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Qin, T.C.; Bao, Y.P.; Liu, R.G.; He, J.P. Experimental study on damage monitoring of FRP plate using FBG sensors. Micromachines 2025, 16, 649. [Google Scholar] [CrossRef]
- Yu, S.Q.; Fan, C.G.; Zhao, Y. A rapid 2D-FDTD method for damage detection in stiffened plate using time-reversed Lamb wave. Struct. Health Monit. 2023, 22, 3827–3839. [Google Scholar] [CrossRef]
- Nokhbatolfoghahai, A.; Navazi, H.M.; Groves, R.M. Evaluation of the sparse reconstruction and the delay-and-sum damage imaging methods for structural health monitoring under different environmental and operational conditions. Measurement 2021, 169, 108495. [Google Scholar]
- Ling, F.Y.; Chen, H.L.; Lang, Y.F.; Yang, Z.B.; Xu, K.L.; Ta, D. Lamb wave tomography for defect localization using wideband dispersion reversal method. Measurement 2023, 216, 112965. [Google Scholar] [CrossRef]
- Yuan, Q.; Kato, B.; Fan, K.Q.; Wang, Y. Phased array guided wave propagation in curved plates. Mech. Syst. Signal Process. 2023, 185, 109821. [Google Scholar]
- Xu, C.B.; Peng, L.H.; Deng, M.X. Phased array imaging for damage localization using multi-narrowband Lamb waves. Mech. Syst. Signal Process. 2023, 190, 110134. [Google Scholar] [CrossRef]
- Gao, X.L.; Yang, T.X.; Li, D.; Fang, Y.Y.; Zhang, J.Q.; Ta, D. Lamb wave imaging via dual-frequency fusion for grating lobe effect compensation. Ultrasonics 2025, 146, 107512. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.Y.; Xu, R.; Yang, H.J.; Ma, J.T.; Yang, L.; Guo, H.F.; Zhang, H.P.; Wu, Z.J. Modeling and designing of a phased array comprising piezoelectric stack transducer for ultrasonic Lamb wave based damage detection. Struct. Health Monit. 2024, 24, 1241–1259. [Google Scholar] [CrossRef]
- Li, W.T.; Hei, Y.Q.; Shi, X.W.; Cheung, S.H. Range-angle-dependent beamforming with FDA using four-dimensional arrays. Signal Process. 2018, 147, 68–79. [Google Scholar] [CrossRef]
- Lang, Y.F.; Yang, Z.B.; Yang, L.H.; Chen, X.F. Lamb Wave Frequency Diverse Array. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2022, 69, 2526–2539. [Google Scholar] [PubMed]
- Agarwal, K.; Machán, R. Multiple signal classification algorithm for super-resolution fluorescence microscopy. Nature. Commun. 2016, 7, 13752. [Google Scholar] [CrossRef] [PubMed]
- Zheng, F.; Chen, J.; Yuan, S.F.; Xu, Q.H.; Qiu, L. Guided wave-MUSIC based damage monitoring method for complex composite structures. Int. J. Mech. Sci. 2024, 277, 109450. [Google Scholar] [CrossRef]
- Zhong, Y.T.; Yuan, S.F.; Qiu, L. Multiple damage detection on aircraft composite structures using near-field MUSIC algorithm. Sens. Actuators A Phys. 2014, 214, 234–244. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, C.Q.; Pu, W.; Qiu, L. A Large-Scale Sensing-Monitoring Integrated Aircraft Smart Skin with Ultralow Weight and Ultralow Power Consumption for Structural Health Monitoring. IEEE Trans. Ind. Electron. 2025, 72, 2130–2139. [Google Scholar] [CrossRef]


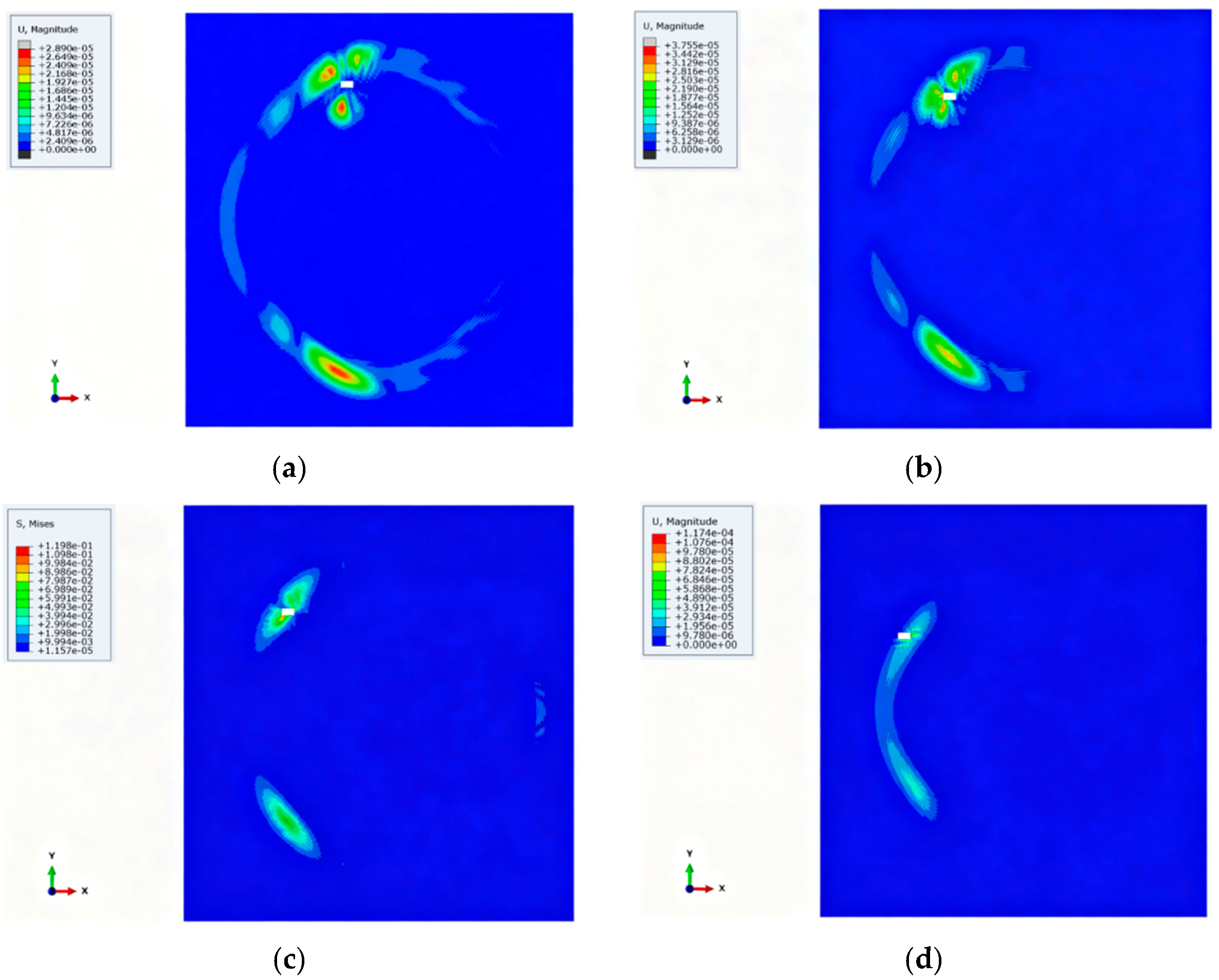

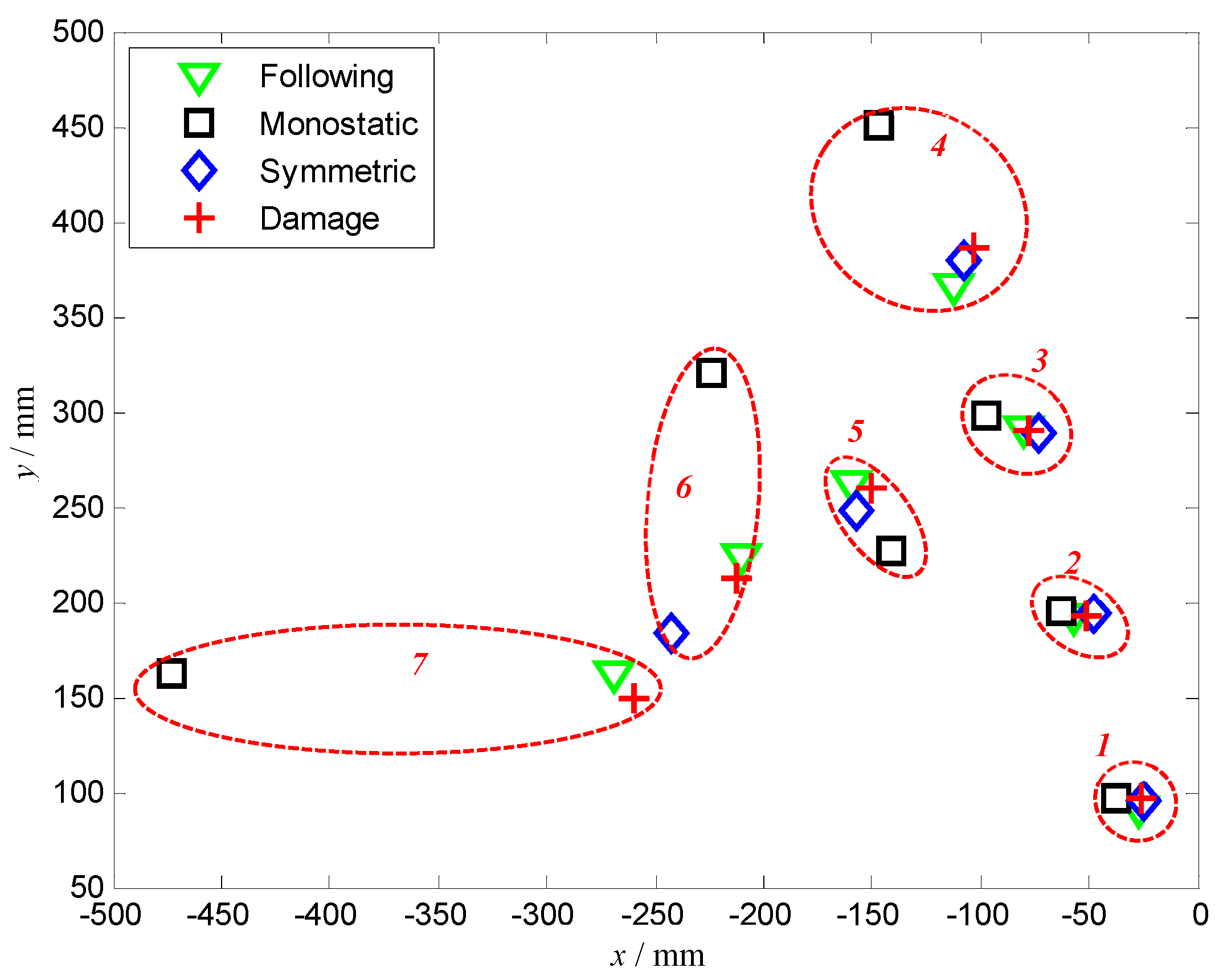

| Damage | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| r/mm | 100 | 200 | 300 | 400 | 300 | 300 | 300 |
| θ/° | 105 | 105 | 105 | 105 | 120 | 135 | 150 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Hu, Q.; Zhong, Y. Research on Piezoelectric Guided Wave Frequency Diverse Array-Based Damage Location Method for Thin-Walled Structures. Micromachines 2025, 16, 1172. https://doi.org/10.3390/mi16101172
Wang C, Hu Q, Zhong Y. Research on Piezoelectric Guided Wave Frequency Diverse Array-Based Damage Location Method for Thin-Walled Structures. Micromachines. 2025; 16(10):1172. https://doi.org/10.3390/mi16101172
Chicago/Turabian StyleWang, Changlin, Quanyao Hu, and Yongteng Zhong. 2025. "Research on Piezoelectric Guided Wave Frequency Diverse Array-Based Damage Location Method for Thin-Walled Structures" Micromachines 16, no. 10: 1172. https://doi.org/10.3390/mi16101172
APA StyleWang, C., Hu, Q., & Zhong, Y. (2025). Research on Piezoelectric Guided Wave Frequency Diverse Array-Based Damage Location Method for Thin-Walled Structures. Micromachines, 16(10), 1172. https://doi.org/10.3390/mi16101172






