Enhancing the Machinability of Sapphire via Ion Implantation and Laser-Assisted Diamond Machining
Abstract
1. Introduction
2. Materials and Methods
2.1. Basic Principles and Simulation of Ion Implantation
2.2. Subsurface Structural Characterization
2.3. Groove Cutting Tests
2.4. Characterization Method
3. Results and Discussions
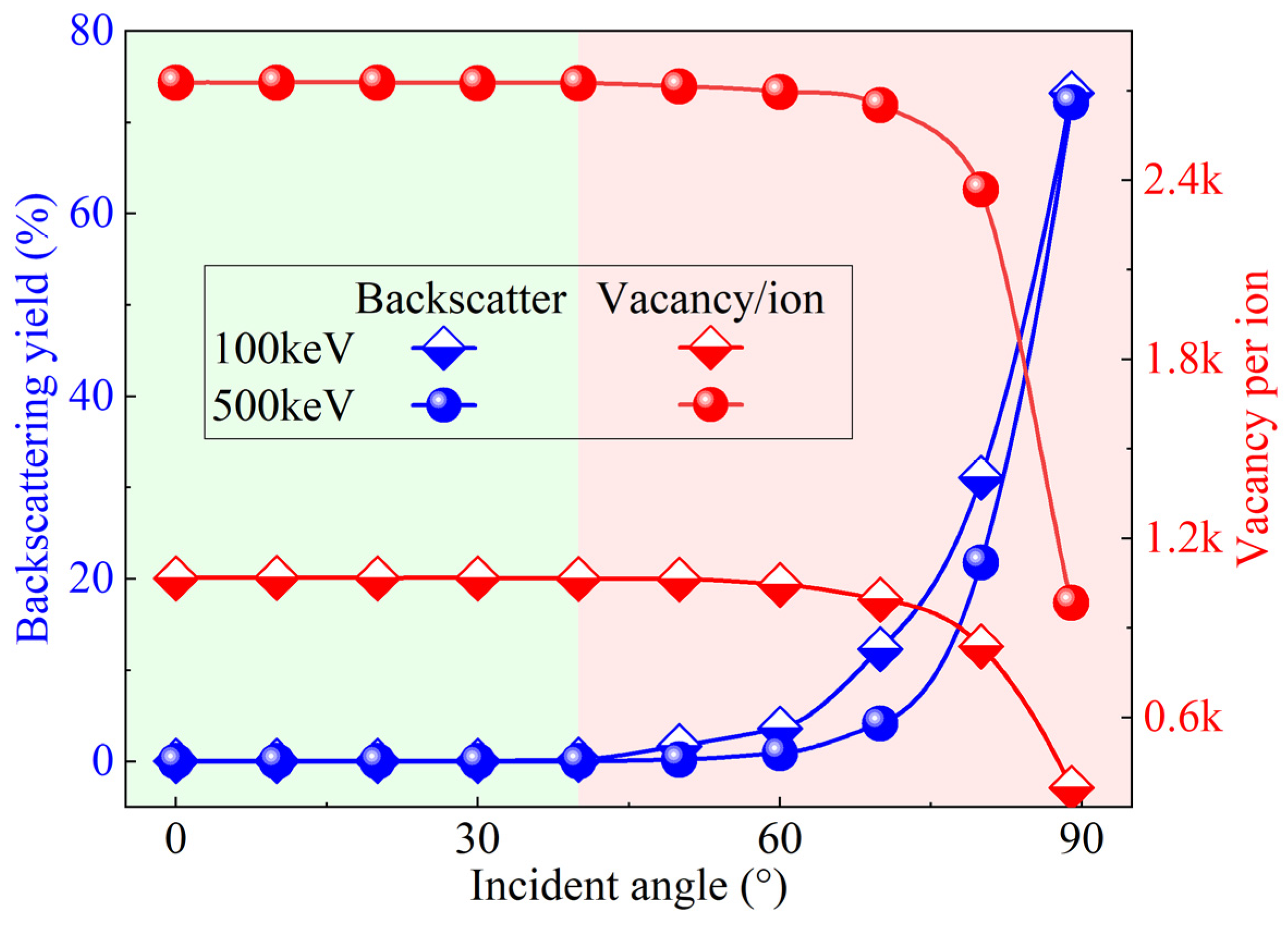
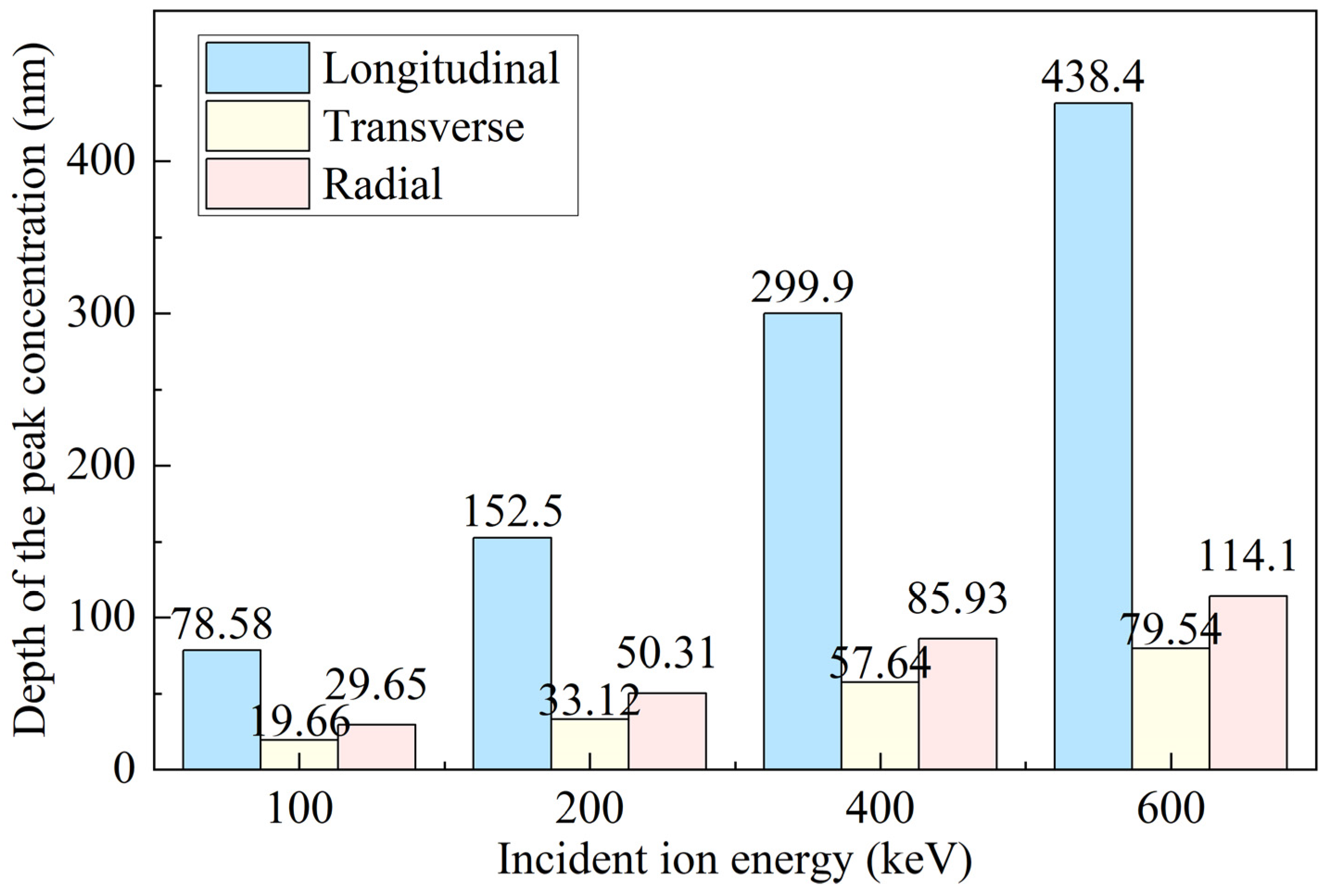
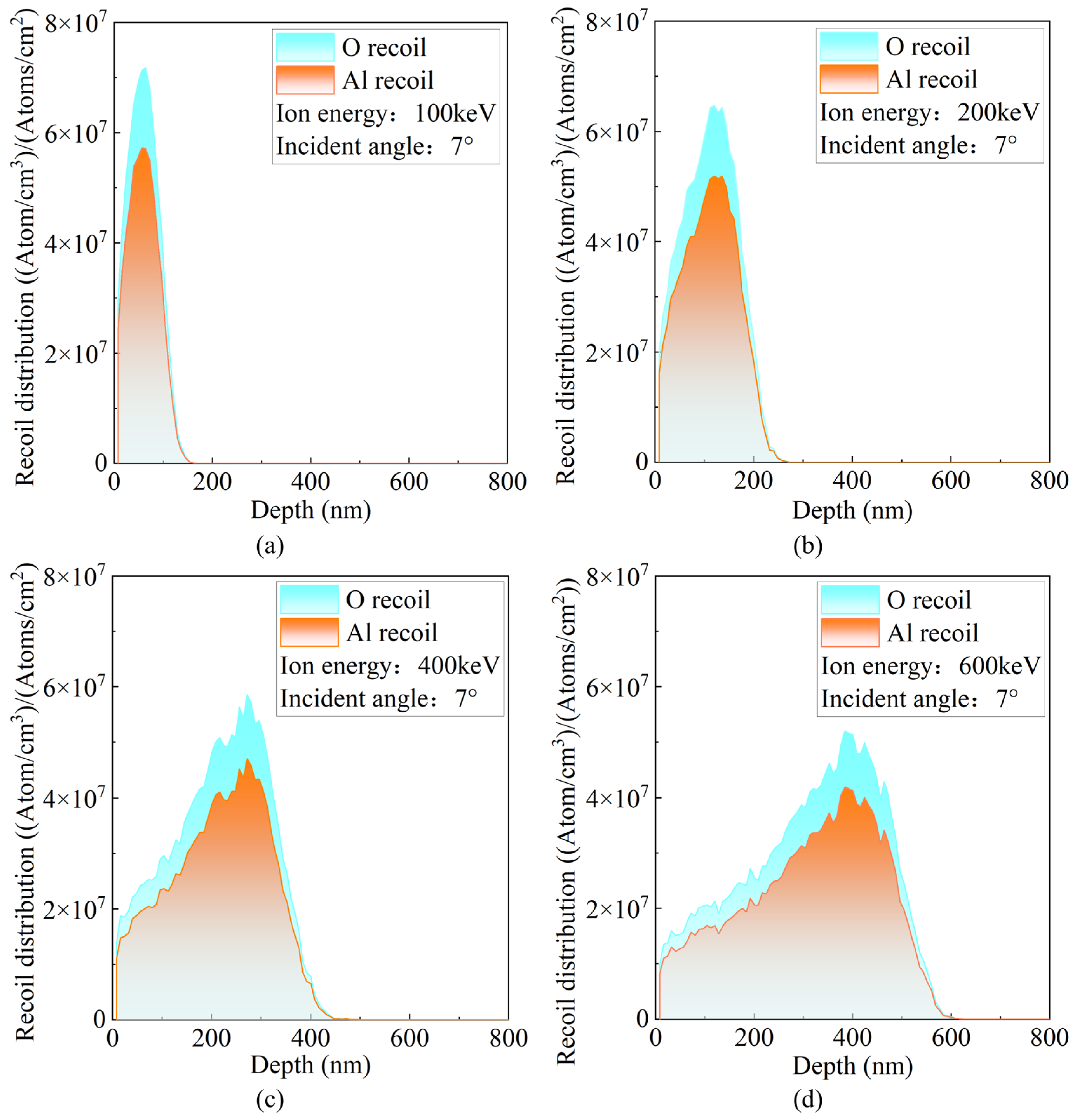
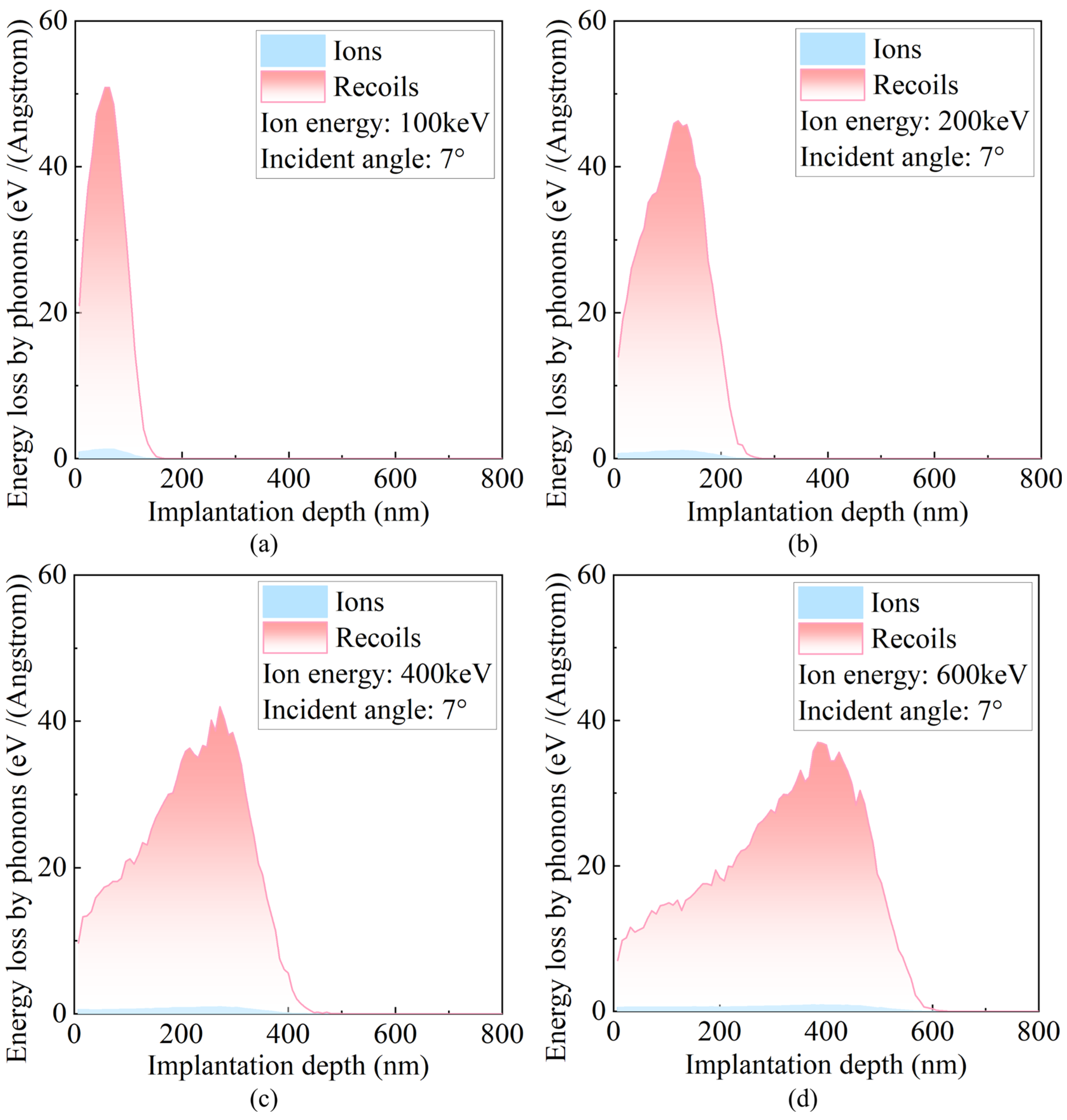
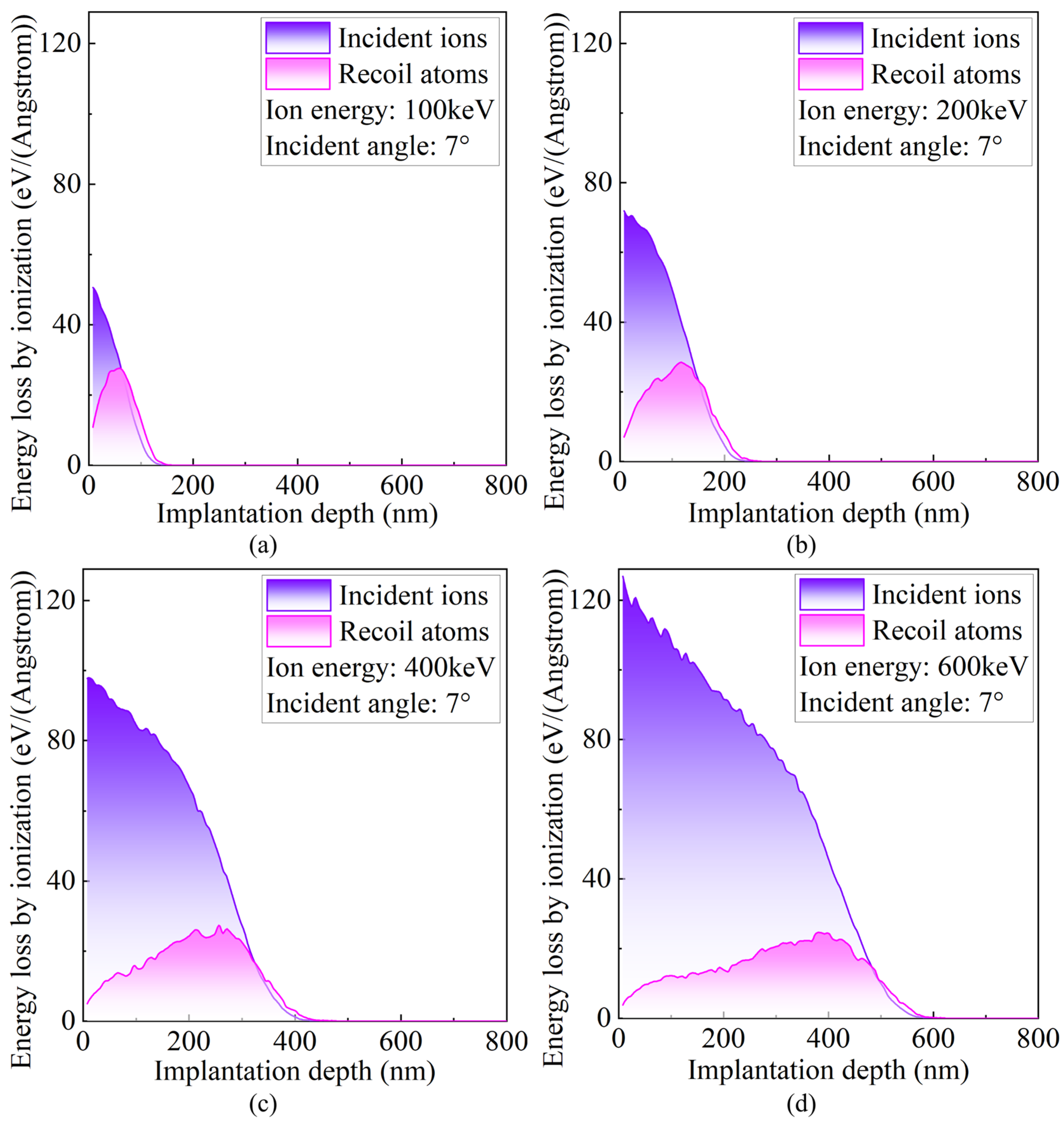
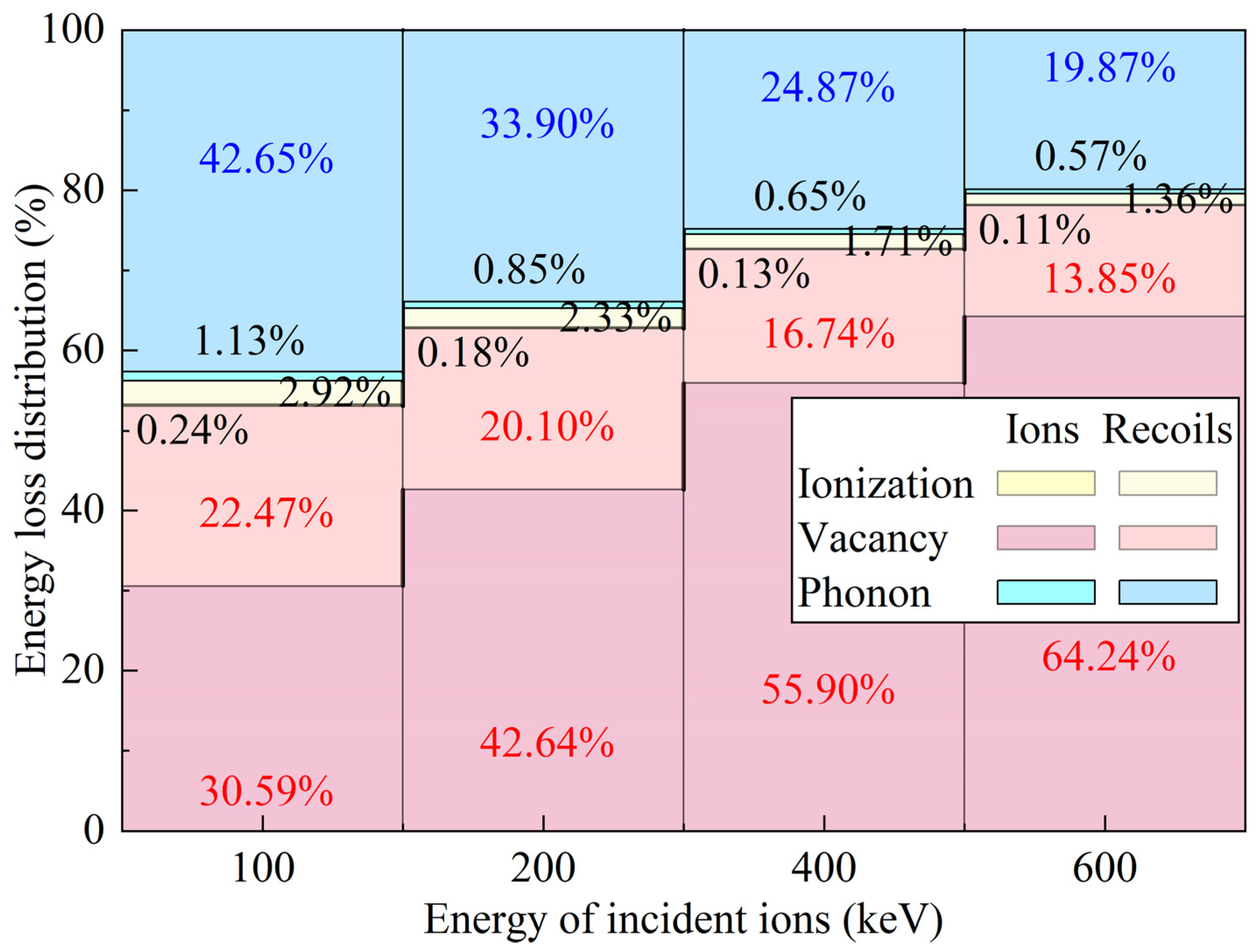
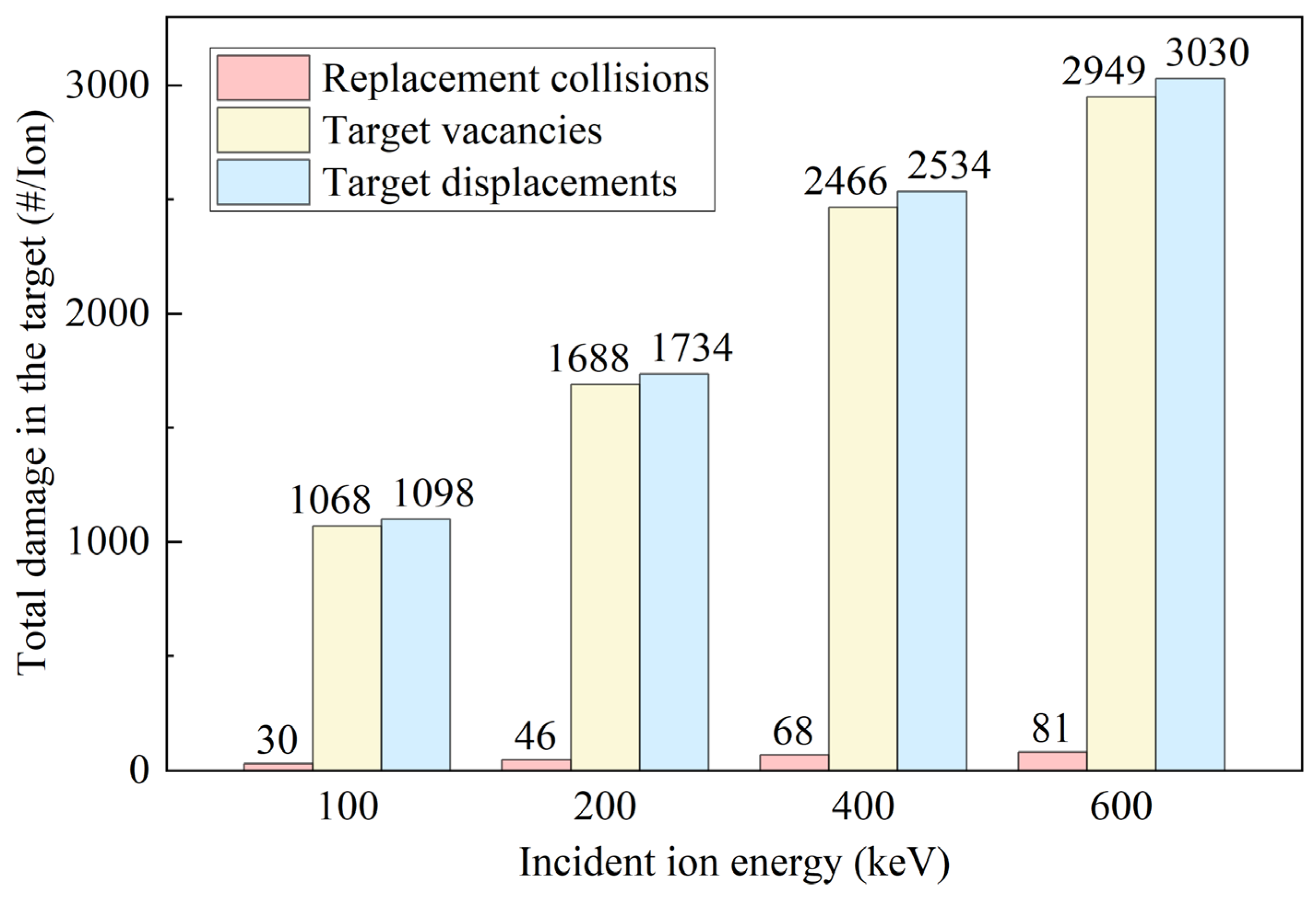
3.1. Effect of Energy on Ion–Target Interactions
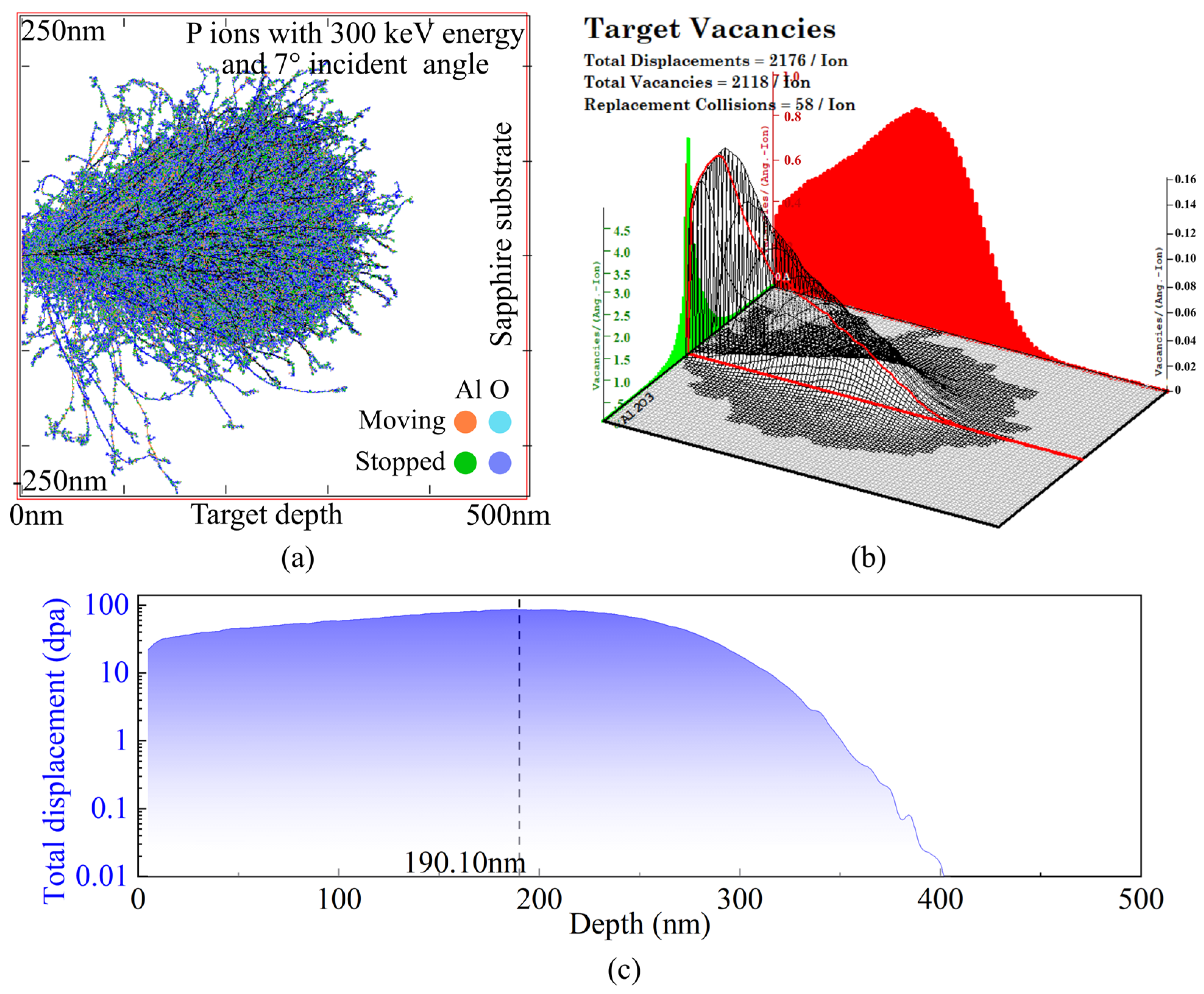
3.2. Microstructural Evolution of the Modification Layer
3.3. Ductile–Brittle Transition Behavior
4. Conclusions
- (1)
- The incidence angle and energy selection in the ion implantation process significantly affect the interaction mechanisms between ions and the target atoms. With increasing energy, the projected range of incident ions increases, the distributions of recoil atoms and energy deposition shift deeper into the material, and the damage evolves from a near-surface concentration to a more dispersed deep-layer profile.
- (2)
- Under all energy conditions, at least 53% of the total energy of the incident ions is dissipated through vacancy formation, inducing internal defects within the crystal. Phonon-mediated energy dissipation serves as the primary pathway for converting kinetic energy into internal energy. Additionally, the total number of displacements equals the sum of vacancies and replacement collisions.
- (3)
- Implantation of 300 keV phosphorus ions at a 7° incidence angle produced a uniform amorphous modified layer with a thickness of 461.18 nm. The resulting microstructural changes within the crystal increased the material’s absorption at 1070 nm from 0.39% to 4.74%, enabling the application of LADM techniques.
- (4)
- LADM significantly enhances the ductile cutting performance of modified sapphire. With increasing laser power, the extent of the ductile region expands, while the size and density of brittle fracture defects on the groove surface decrease. At 16 W, the ductile–brittle transition depth increased to 450.67 nm, representing a 51.57% improvement over conventional cutting.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Merberg, G.N.; Harrington, J.A. Optical and Mechanical Properties of Single-Crystal Sapphire Optical Fibers. Appl. Opt. 1993, 32, 3201–3209. [Google Scholar] [CrossRef] [PubMed]
- Yang, D.; Thomas, M.E.; Kaplan, S.G. Measurement of the Infrared Refractive Index of Sapphire as a Function of Temperature. In Proceedings of the Window and Dome Technologies and Materials VII, Orlando, FL, USA, 7 September 2001; SPIE: Bellingham, WA, USA, 2001; Volume 4375, pp. 53–63. [Google Scholar]
- Voloshin, A.V.; Litvinov, L.A.; Slyunin, E.V. The Influence of Sapphire Crystallographic Orientation on Surface Roughness Achievable by Diamond Abrasive Machining. J. Superhard Mater. 2013, 35, 56–59. [Google Scholar] [CrossRef]
- Locher, J.; Jones, C.; Bates, H.; Rioux, J. Characteristics of Thick (>12 mm) Class225 EFG Sapphire Sheet for IR Window Applications. In Proceedings of the Window and Dome Technologies and Materials XI, Orlando, FL, USA, 11 May 2009; SPIE: Bellingham, WA, USA, 2009; Volume 7302, pp. 21–25. [Google Scholar]
- Wun, J.-M.; Lin, C.-W.; Chen, W.; Sheu, J.-K.; Lin, C.-L.; Li, Y.-L.; Bowers, J.E.; Shi, J.-W.; Vinogradov, J.; Kruglov, R.; et al. GaN-Based Miniaturized Cyan Light-Emitting Diodes on a Patterned Sapphire Substrate With Improved Fiber Coupling for Very High-Speed Plastic Optical Fiber Communication. IEEE Photonics J. 2012, 4, 1520–1529. [Google Scholar] [CrossRef]
- Savage, J.A. Preparation and Properties of Hard Crystalline Materials for Optical Applications—A Review. J. Cryst. Growth 1991, 113, 698–715. [Google Scholar] [CrossRef]
- Wang, Y.; Liang, Z.; Zhao, W.; Wang, X.; Wang, H. Anisotropic Cutting Mechanisms on the Surface Quality in Ultra-Precision Machining of R-Plane Sapphire. Appl. Surf. Sci. 2023, 622, 156868. [Google Scholar] [CrossRef]
- Ma, Y.; Cao, L.; Hang, W.; Zhang, T.; Yuan, J. Crystallographic Orientation Effect on the Incipient Plasticity and Its Stochastic Behavior of a Sapphire Single Crystal by Spherical Nanoindentation. Ceram. Int. 2020, 46, 15554–15564. [Google Scholar] [CrossRef]
- Bum Kwon, S.; Min, S. Characteristics of Force Generation on C-, R-, A- and M- Planes of Single-Crystal Sapphire during Ultra-Precision Machining. Manuf. Lett. 2022, 33, 349–354. [Google Scholar] [CrossRef]
- Wang, J.; Guo, B.; Zhao, Q.; Zeng, Z.; Zhai, W.; Chen, H.; Sun, J. Investigation into the Anisotropy of Cross-Grinding Surface Quality in C- and M-Planes of Sapphire. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2019, 233, 44–54. [Google Scholar] [CrossRef]
- Maas, P.; Mizumoto, Y.; Kakinuma, Y.; Min, S. Anisotropic Brittle-Ductile Transition of Monocrystalline Sapphire during Orthogonal Cutting and Nanoindentation Experiments. Nanotechnol. Precis. Eng. 2018, 1, 157–171. [Google Scholar] [CrossRef]
- Zhang, S.J.; To, S.; Wang, S.J.; Zhu, Z.W. A Review of Surface Roughness Generation in Ultra-Precision Machining. Int. J. Mach. Tools Manuf. 2015, 91, 76–95. [Google Scholar] [CrossRef]
- Bifano, T.G.; Dow, T.A.; Scattergood, R.O. Ductile-Regime Grinding: A New Technology for Machining Brittle Materials. J. Eng. Ind. 1991, 113, 184–189. [Google Scholar] [CrossRef]
- Wang, X.; Zheng, W.; Bao, X.; Wang, S.; Zhao, Q. Investigation of Anisotropic Characteristics in Ultra-Precision Grinding of Sapphire Crystal Planes and Strategies for Suppression. J. Manuf. Process. 2025, 133, 55–85. [Google Scholar] [CrossRef]
- Wang, X.; Ning, Y.; Zheng, W.; Bao, X.; Zhao, Q.; Wang, S. Anisotropic Mechanism of Material Removal and Ductile-Brittle Transition in Sapphire Scratching Based on Acoustic Emission Signal. J. Mater. Res. Technol. 2024, 31, 2876–2899. [Google Scholar] [CrossRef]
- Maslen, E.N.; Streltsov, V.A.; Streltsova, N.R.; Ishizawa, N.; Satow, Y. Synchrotron X-Ray Study of the Electron Density in α-Al2O3. Acta Cryst. B 1993, 49, 973–980. [Google Scholar] [CrossRef]
- Cao, L.; Zhang, X.; Yuan, J.; Guo, L.; Hong, T.; Hang, W.; Ma, Y. Study on the Influence of Sapphire Crystal Orientation on Its Chemical Mechanical Polishing. Appl. Sci. 2020, 10, 8065. [Google Scholar] [CrossRef]
- Kwon, S.B.; Min, S. Studying Mechanism of Anisotropic Crack Generation on C-, R-, A-, and M-Planes of Sapphire during Ultra-Precision Orthogonal Cutting Using a Visualized Slip/Fracture Activation Model. Nanotechnol. Precis. Eng. 2024, 7, 043006. [Google Scholar] [CrossRef]
- Fang, F.Z.; Chen, Y.H.; Zhang, X.D.; Hu, X.T.; Zhang, G.X. Nanometric Cutting of Single Crystal Silicon Surfaces Modified by Ion Implantation. CIRP Ann. 2011, 60, 527–530. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, X.; Fang, F.; Chen, R. Diamond Cutting of Micro-Structure Array on Brittle Material Assisted by Multi-Ion Implantation. Int. J. Mach. Tools Manuf. 2019, 137, 58–66. [Google Scholar] [CrossRef]
- Skuratov, V.A.; Zagorski, D.L.; Efimov, A.E.; Kluev, V.A.; Toporov, Y.P.; Mchedlishvili, B.V. Swift Heavy Ion Irradiation Effect on the Surface of Sapphire Single Crystals. Radiat. Meas. 2001, 34, 571–576. [Google Scholar] [CrossRef]
- Kabir, A.; Meftah, A.; Stoquert, J.P.; Toulemonde, M.; Monnet, I. Amorphization of Sapphire Induced by Swift Heavy Ions: A Two Step Process. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2008, 266, 2976–2980. [Google Scholar] [CrossRef]
- Pelaz, L.; Marqués, L.A.; Barbolla, J. Ion-Beam-Induced Amorphization and Recrystallization in Silicon. J. Appl. Phys. 2004, 96, 5947–5976. [Google Scholar] [CrossRef]
- Xu, Z.W.; Fang, F.Z.; Fu, Y.Q.; Zhang, S.J.; Han, T.; Li, J.M. Fabrication of Micro/Nano-Structures Using Focused Ion Beam Implantation and XeF2 Gas-Assisted Etching. J. Micromech. Microeng. 2009, 19, 054003. [Google Scholar] [CrossRef]
- Wang, J.; Chen, R.; Zhang, X.; Fang, F. Study on Machinability of Silicon Irradiated by Swift Ions. Precis. Eng. 2018, 51, 577–581. [Google Scholar] [CrossRef]
- To, S.; Wang, H.; Jelenković, E.V. Enhancement of the Machinability of Silicon by Hydrogen Ion Implantation for Ultra-Precision Micro-Cutting. Int. J. Mach. Tools Manuf. 2013, 74, 50–55. [Google Scholar] [CrossRef]
- He, Y.; Xiao, G.; Liu, Z.; Ni, Y.; Liu, S. Subsurface Damage in Laser-Assisted Machining Titanium Alloys. Int. J. Mech. Sci. 2023, 258, 108576. [Google Scholar] [CrossRef]
- Zhao, B.; Xu, J.; Chen, G.; Zhai, C.; Zhou, F.; Li, J. Study on Chip Formation and Surface Integrity of Nickel-Based Superalloy Inconel 718 by Laser Assisted Micro-Cutting. J. Manuf. Process. 2024, 113, 34–46. [Google Scholar] [CrossRef]
- Du, H.; Yip, W.S.; Sun, W.; Kang, C.; To, S. In-Situ Laser-Assisted Ultraprecision Cutting of WC-Co Cemented Carbide for Creating Microstructure Arrays. Ceram. Int. 2023, 49, 38698–38707. [Google Scholar] [CrossRef]
- Mohammadi, H.; Ravindra, D.; Kode, S.K.; Patten, J.A. Experimental Work on Micro Laser-Assisted Diamond Turning of Silicon (111). J. Manuf. Process. 2015, 19, 125–128. [Google Scholar] [CrossRef]
- Ke, J.; Chen, X.; Liu, C.; Zhang, J.; Yang, H.; Xu, J. Enhancing the Ductile Machinability of Single-Crystal Silicon by Laser-Assisted Diamond Cutting. Int. J. Adv. Manuf. Technol. 2022, 118, 3265–3282. [Google Scholar] [CrossRef]
- Liu, C.; Ke, J.; Yin, T.; Yip, W.S.; Zhang, J.; To, S.; Xu, J. Cutting Mechanism of Reaction-Bonded Silicon Carbide in Laser-Assisted Ultra-Precision Machining. Int. J. Mach. Tools Manuf. 2024, 203, 104219. [Google Scholar] [CrossRef]
- Ke, J.; Chen, X.; Liu, C.; Xu, G.; She, Z.; Zhang, J.; Xu, J. Ultra-Precision Cutting Characteristics of Binderless Tungsten Carbide by in-Heat-Process Laser-Assisted Diamond Machining. Int. J. Refract. Met. Hard Mater. 2023, 115, 106311. [Google Scholar] [CrossRef]
- You, K.; Fang, F.; Yan, G. Surface Generation of Tungsten Carbide in Laser-Assisted Diamond Turning. Int. J. Mach. Tools Manuf. 2021, 168, 103770. [Google Scholar] [CrossRef]
- Zhang, J.; Zheng, Z.; Huang, K.; Lin, C.; Huang, W.; Chen, X.; Xiao, J.; Xu, J. Field-Assisted Machining of Difficult-to-Machine Materials. Int. J. Extrem. Manuf. 2024, 6, 032002. [Google Scholar] [CrossRef]
- Li, Y.; Xing, Y.; Sun, L.; Li, D.; Yin, T.; Wang, J.; Yip, W.S.; To, S. Analytical Thermal Modeling for Conventional and In-Situ Laser Assisted Turning. Int. J. Mech. Sci. 2025, 287, 109919. [Google Scholar] [CrossRef]
- Bauer, P.; Golser, R.; Semrad, D.; Maier-Komor, P.; Aumayr, F.; Arnau, A. Influence of the Chemical State on the Stopping of Protons and He-Ions in Some Oxides. Nucl. Instrum. Methods Phys. Res. B Beam Interact. Mater. At. 1998, 136–138, 103–108. [Google Scholar] [CrossRef]
- Porter, L.E. Analyses of Stopping Power Measurements for 0.90–2.50 MeV Protons and Deuterons Traversing Al2O3 Targets. Nucl. Instrum. Methods Phys. Res. B Beam Interact. Mater. At. 2000, 170, 35–38. [Google Scholar] [CrossRef]
- Shulga, V.I. Note on the Artefacts in SRIM Simulation of Sputtering. Appl. Surf. Sci. 2018, 439, 456–461. [Google Scholar] [CrossRef]
- Hofsäss, H.; Zhang, K.; Mutzke, A. Simulation of Ion Beam Sputtering with SDTrimSP, TRIDYN and SRIM. Appl. Surf. Sci. 2014, 310, 134–141. [Google Scholar] [CrossRef]
- Yoshimura, S.; Hine, K.; Kiuchi, M.; Hashimoto, J.; Terauchi, M.; Honda, Y.; Nishitani, M.; Hamaguchi, S. Experimental Evaluation of CaO, SrO and BaO Sputtering Yields by Ne+ or Xe+ Ions. J. Phys. D Appl. Phys. 2011, 44, 255203. [Google Scholar] [CrossRef]
- Ke, J.; Zhang, J.; Chen, X.; Liu, C.; Long, G.; Sun, H.; Xu, J. Investigation on the Material Removal Mechanism in Ion Implantation-Assisted Elliptical Vibration Cutting of Hard and Brittle Material. Int. J. Mach. Tools Manuf. 2024, 203, 104220. [Google Scholar] [CrossRef]
- Egeland, G.W.; Valdez, J.A.; Maloy, S.A.; McClellan, K.J.; Sickafus, K.E.; Bond, G.M. Heavy-Ion Irradiation Defect Accumulation in ZrN Characterized by TEM, GIXRD, Nanoindentation, and Helium Desorption. J. Nucl. Mater. 2013, 435, 77–87. [Google Scholar] [CrossRef]
- Yoon, H.-S.; Kwon, S.B.; Nagaraj, A.; Lee, S.; Min, S. Study of Stress Intensity Factor on the Anisotropic Machining Behavior of Single Crystal Sapphire. CIRP Ann. 2018, 67, 125–128. [Google Scholar] [CrossRef]
- Yoon, H.-S.; Kwon, S.B.; Kim, J.-H.; Ahn, S.-H.; Min, S. Effects of Surface Coating Materials on Cutting Forces and Ductile-to-Brittle Transition in Orthogonal Cutting of Monocrystalline Sapphire. J. Manuf. Process. 2022, 84, 375–382. [Google Scholar] [CrossRef]
- Yoon, H.-S.; Kwon, S.B.; Nagaraj, A.; Min, S. Effect of the Initial-Flaw on Crack-Propagation in Two-Step Cutting of Monocrystalline Sapphire. J. Manuf. Process. 2020, 56, 1211–1218. [Google Scholar] [CrossRef]






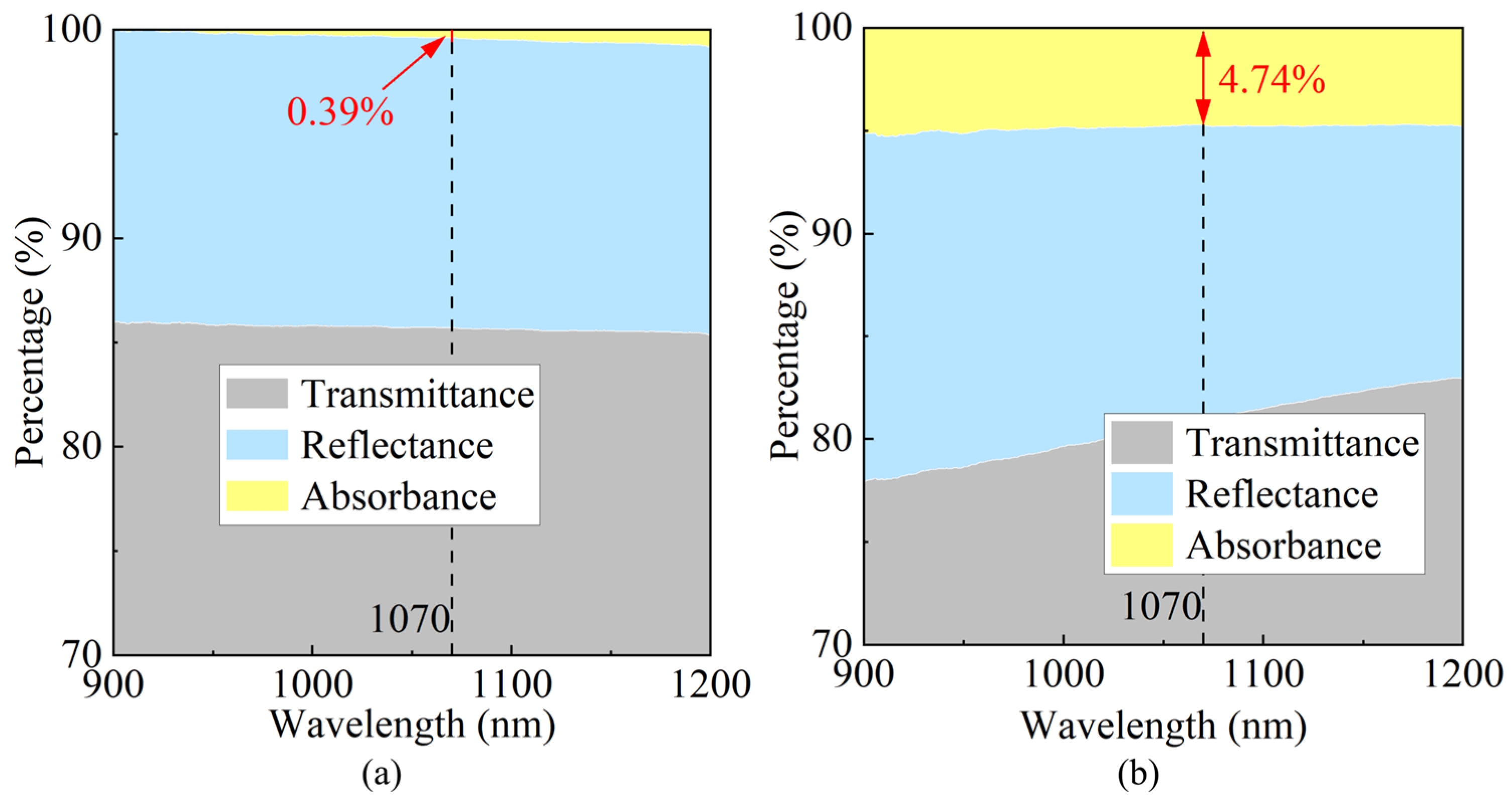
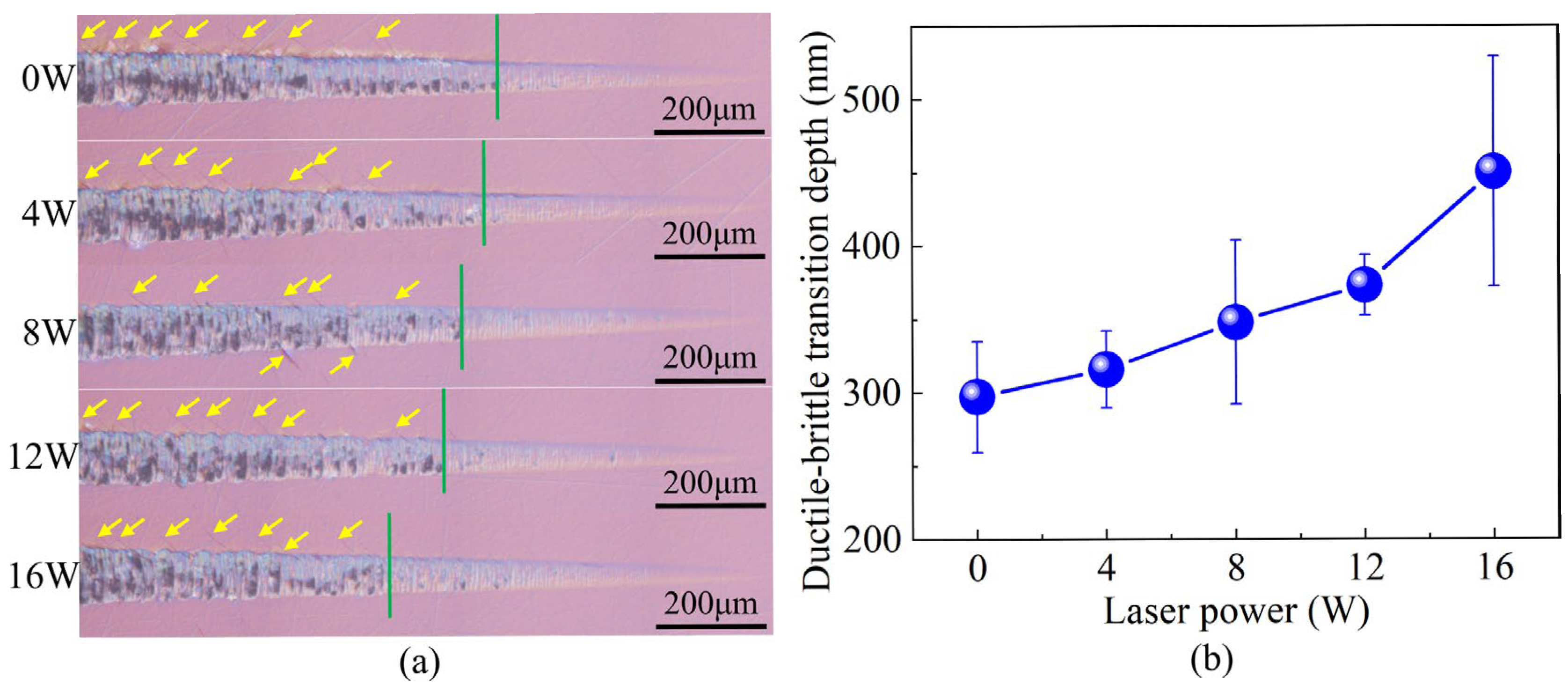

| Description | Value |
|---|---|
| Workpiece | C plane sapphire |
| Laser source | 1070 nm continuous-wave laser |
| Tool nose radius | 0.506 mm |
| Rake angle | −35° |
| Flank angle | 10° |
| Cutting speed | 200 mm/min |
| Groove slope | D/L = 1:1000 |
| Laser power | 0 W, 4 W, 8 W, 12 W, 16 W |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ke, J.; Mo, H.; Ling, K.; Chu, J.; Chen, X.; Xu, J. Enhancing the Machinability of Sapphire via Ion Implantation and Laser-Assisted Diamond Machining. Micromachines 2025, 16, 1165. https://doi.org/10.3390/mi16101165
Ke J, Mo H, Ling K, Chu J, Chen X, Xu J. Enhancing the Machinability of Sapphire via Ion Implantation and Laser-Assisted Diamond Machining. Micromachines. 2025; 16(10):1165. https://doi.org/10.3390/mi16101165
Chicago/Turabian StyleKe, Jinyang, Honglei Mo, Ke Ling, Jianning Chu, Xiao Chen, and Jianfeng Xu. 2025. "Enhancing the Machinability of Sapphire via Ion Implantation and Laser-Assisted Diamond Machining" Micromachines 16, no. 10: 1165. https://doi.org/10.3390/mi16101165
APA StyleKe, J., Mo, H., Ling, K., Chu, J., Chen, X., & Xu, J. (2025). Enhancing the Machinability of Sapphire via Ion Implantation and Laser-Assisted Diamond Machining. Micromachines, 16(10), 1165. https://doi.org/10.3390/mi16101165





