Machining Micro-Error Compensation Methods for External Turning Tool Wear of CNC Machines
Abstract
1. Introduction
2. Design of CNC External Turning Tool Wear Detection
2.1. Shape Visual Modeling of the Tool Nose Rake Face
2.2. Tool Nose Straight Line Detection and Radius Measurement Algorithm Based on Edge Images and Input Features
3. Tool Path Optimization and Machining Code Design for Corner Radius Error Compensation
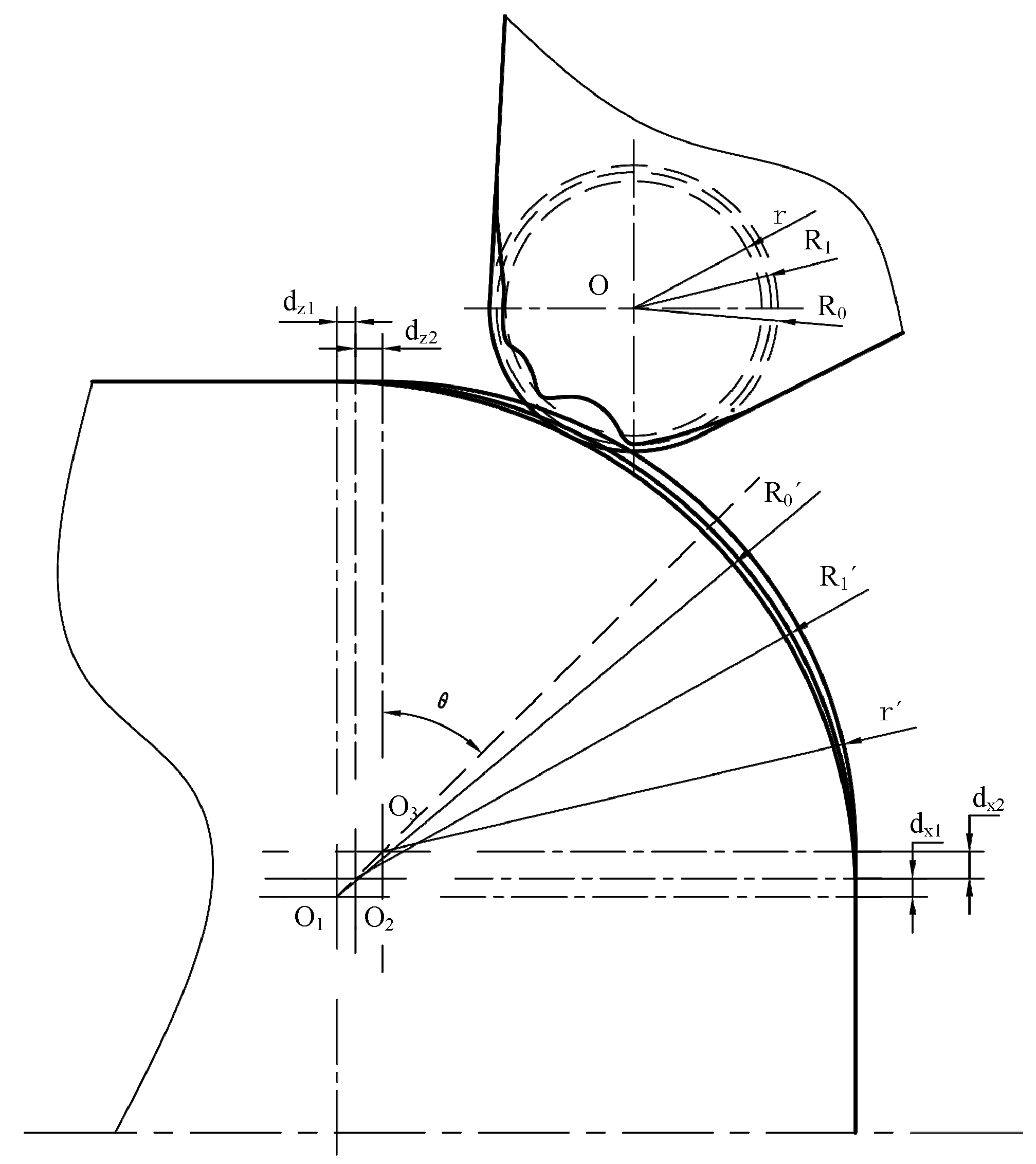
3.1. Tool Path Optimization for the Error Compensation of Corner Radius
3.2. CNC Machining Code Design
4. Error Compensation Experiments and Result Analysis
5. Web Display Platform of Wear Error Compensation System
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cheng, M.; Jiao, L.; Yan, P.; Li, S.; Dai, Z.; Qiu, T.; Wang, X. Prediction and evaluation of surface roughness with hybrid kernel extreme learning machine and monitored tool wear. J. Manuf. Process. 2022, 84, 1541–1556. [Google Scholar] [CrossRef]
- Xu, R.; Li, X.; Zheng, G.; Cheng, X.; Tian, Y. A radius compensation method of barrel tool based on macro variables in five-axis flank machining of sculptured surfaces. Int. J. Prod. Res. 2020, 58, 2335–2351. [Google Scholar] [CrossRef]
- Ruan, D.; Mao, J.; Liu, G.; Ma, L. Synchronous motion error identification method of dual-five-axis CNC machine tool based on R-test. Int. J. Adv. Manuf. Technol. 2021, 2, 1–9. [Google Scholar] [CrossRef]
- Lin, F.J.; Zhang, H.; Zhou, Y.F.; Zhang, Z.S.; Zhang, L. Tool Reliability Modeling Based on Gamma Process in Multiple Working Conditions. In Proceedings of the Global Reliability and Prognostics and Health Management, Nanjing, China, 15–17 October 2021; pp. 1–6. [Google Scholar] [CrossRef]
- He, Y.; Xiang, H.; Zhou, H.; Chen, J.H. In-situ fault detection for the spindle motor of CNC machines via multi-stage residual fusion convolution neural networks. Comput. Ind. 2023, 145, 103810. [Google Scholar] [CrossRef]
- Wright, L.G.; Onodera, T.; Stein, M.M.; Wang, T.Y.; Schachter, D.T.; Hu, Z.; McMahon, P.L. Deep physical neural networks trained with backpropagation. Nature 2022, 601, 549–560. [Google Scholar] [CrossRef]
- Li, Z.; Dai, Y.; Guan, C.; Yong, J.; Sun, Z.; Du, C. High-Precision Machining Method of Weak-Stiffness Mirror Based on Fast Tool Servo Error Compensation Strategy. Micromachines 2021, 12, 607. [Google Scholar] [CrossRef]
- Zhang, X.; Gao, Y.; Guo, Z.; Zhang, W.; Yin, J.; Zhao, W. Physical model-based tool wear and breakage monitoring in milling process. Mech. Syst. Signal Process. 2023, 184, 109641. [Google Scholar] [CrossRef]
- Gomes, M.C.; Brito, L.C.; da Silva, M.B.; Duarte, M.A.V. Tool wear monitoring in micromilling using support vector machine with vibration and sound sensors. Precis. Eng. 2021, 67, 137–151. [Google Scholar] [CrossRef]
- Li, T.; Shi, T.; Tang, Z.; Liao, G.; Duan, J.; Han, J.; He, Z. Real-time tool wear monitoring using thin-film thermocouple. J. Mater. Process. Technol. 2021, 88, 116901. [Google Scholar] [CrossRef]
- Lei, T.; Zou, B.; Chen, W.; Zheng, Q.B.; Yang, J.Z.; Li, L.; Liu, J.K. Research on reconstruction and high-precision detection of tool wear edges under complex lighting environmental influences. Int. J. Adv. Manuf. Technol. 2023, 129, 4529–4540l. [Google Scholar] [CrossRef]
- Zhang, X.; Yu, H.; Li, C.; Yu, Z.; Xu, J.; Li, Y.; Yu, H. Study on In-Situ Tool Wear Detection during Micro End Milling Based on Machine Vision. Micromachines 2023, 14, 100. [Google Scholar] [CrossRef]
- Hu, S.; Wen, H.Y.; Zhang, Z.S.; Sun, M.Z.; Zhang, H.; Xia, Z.J.; Dai, M. Attention Mechanism Based CNC Milling Cutter Wear Detection Using Machine Vision. In Proceedings of the 29th International Conference on Mechatronics and Machine Vision in Practice (M2VIP), Queenstown, New Zealand, 21–24 November 2023. [Google Scholar] [CrossRef]
- Zhu, K.; Guo, H.; Li, S.; Lin, X. Online tool wear monitoring by super-resolution based machine vision. Comput. Ind. 2023, 144, 103782. [Google Scholar] [CrossRef]
- Eslami, S.M.A.; Rezende, D.J.; Besse, F.; Viola, F.; Morcos, A.S.; Garnelo, M.; Ruderman, A.; Rusu, A.A.; Danihelka, I.; Gregor, K.; et al. Neural scene representation and rendering. Science 2018, 360, 1204–1210. [Google Scholar] [CrossRef] [PubMed]
- Malhotra, J.; Jha, S. Fuzzy c-means clustering based colour image segmentation for tool wear monitoring in micro-milling. Precis. Precis. Eng. 2021, 72, 690–705. [Google Scholar] [CrossRef]
- Li, S.P.; Zhang, H.; Zhang, Z.S.; Xia, Z.J. A New Method for Polygon Detection Based on Hough Transform Space and USAN Region. In Proceedings of the 5th International Conference on Image, Vision and Computing (ICIVC), Beijing, China, 10–12 July 2020; pp. 44–49. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, H.; Zhang, Z.S.; Xia, Z.J. A New Method for Polygon Detection Based on Clustering. In Proceedings of the 6th International Conference on Image, Vision and Computing, Qingdao, China, 23–25 July 2021; pp. 31–35. [Google Scholar] [CrossRef]
- Laouamer, L.; Alswaili, M. Hough transform-based robust informed watermarking approach for medical images. Trait. Signal 2024, 41, 1557–1564. [Google Scholar] [CrossRef]
- Dong, L.; Ma, D.; Ma, D.; Xu, W. Fast infrared horizon detection algorithm based on gradient directional filtration. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2020, 37, 1795–1805. [Google Scholar] [CrossRef] [PubMed]
- Rasiq, S.M.; Krishnakumar, S. Fast Color Straight Line Pattern Recognition in an Object using High Speed Self Learning Devices. Int. J. Eng. Trans. B Appl. 2021, 34, 1225–1232. [Google Scholar] [CrossRef]
- Li, J.; Wang, Q.; Zhong, G. Planar tool radius compensation for CNC systems based on NURBS interpolation. Mech. Ind. 2020, 21, 107. [Google Scholar] [CrossRef]
- Maeng, S.; Min, S. Simultaneous geometric error identification of rotary axis and tool setting in an ultra-precision 5-axis machine tool using on-machine measurement. Precis. Eng. 2020, 63, 94–104. [Google Scholar] [CrossRef]
- Li, J.F.; Gu, M.H.; Li, Y.L.; Wen, S.T.; Zhang, G.B. Predictive analysis of the precision remaining useful life of CNC machine tools based on meta-action unit. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2024, 239, 185–197. [Google Scholar] [CrossRef]
- Pu, Y.; Wang, L.; Yin, M.; Yin, G.; Xie, L. Modeling, identification, and measurement of geometric errors for a rotary axis of a machine tool using a new R-test. Int. J. Adv. Manuf. Technol. 2021, 117, 1491–1503. [Google Scholar] [CrossRef]
- Li, Q.Z.; Wang, W.; Zhang, J.; Shen, R.; Li, H.; Jiang, Z. Measurement method for volumetric error of five-axis machine tool considering measurement point distribution and adaptive identification process. Int. J. Mach. Tools Manuf. 2019, 147, 103465. [Google Scholar] [CrossRef]
- Laoui, L.A.; Khlifi, H.; Sai, W.B.; Hamdi, H. Tool nose radius effects in turning process. Mach. Sci. Technol. 2020, 25, 1–30. [Google Scholar] [CrossRef]
- Zhang, X.Q.; Chen, G.H.; Zhang, L.; Hu, Y.W.; Mao, J.; Zhang, Z.Y. Modeling of CNC machine tool’s spatial geometric error based on two-dimensional angle error. SN Appl. Sci. 2023, 5, 20. [Google Scholar] [CrossRef]
- Lin, Z.X.; Tian, W.J.; Zhang, D.W.; Gao, W.; Wang, L. A method of geometric error identification and compensation of CNC machine tools based on volumetric diagonal error measurements. Int. J. Adv. Manuf. Technol. 2023, 124, 51–68. [Google Scholar] [CrossRef]
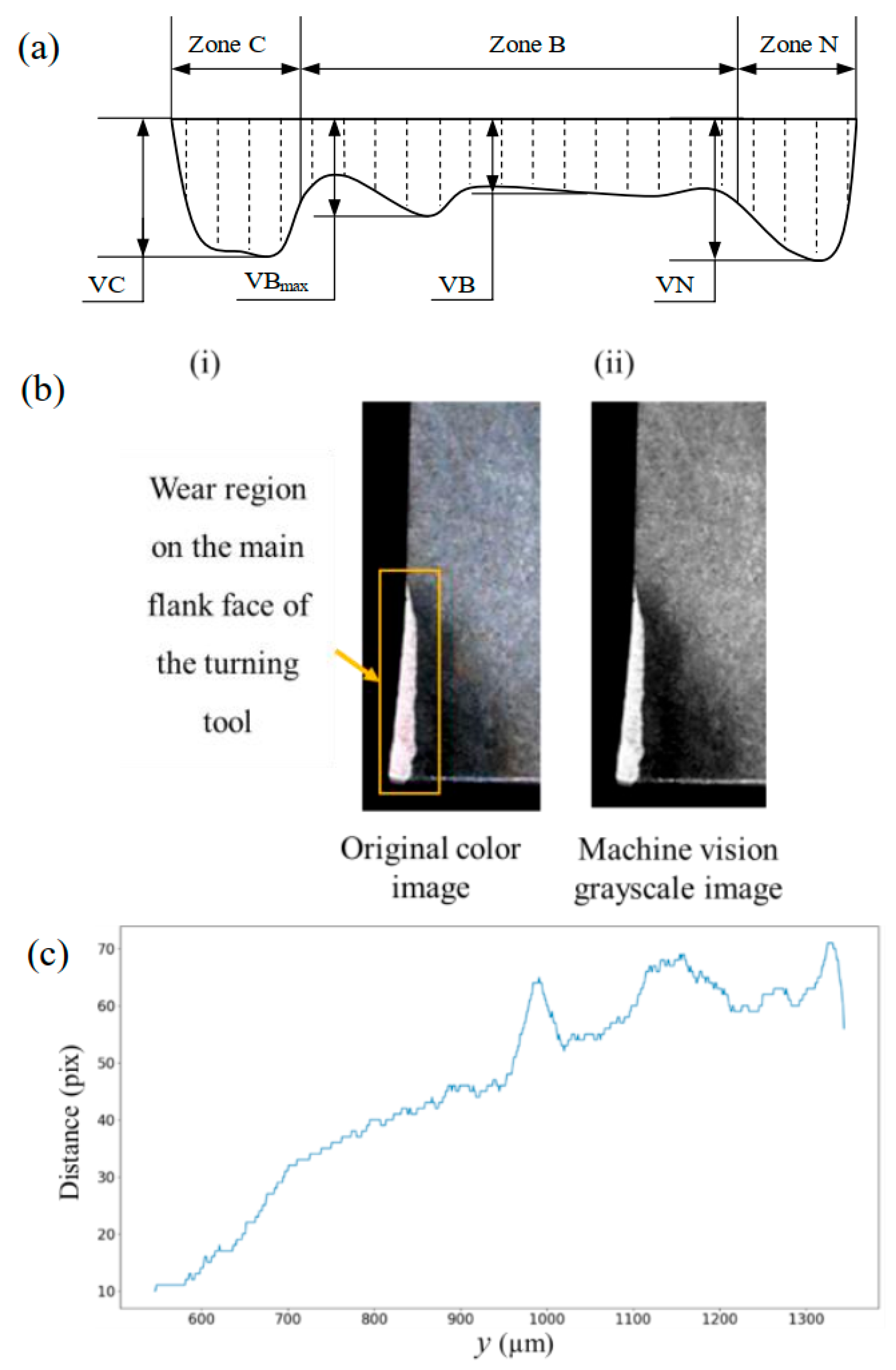


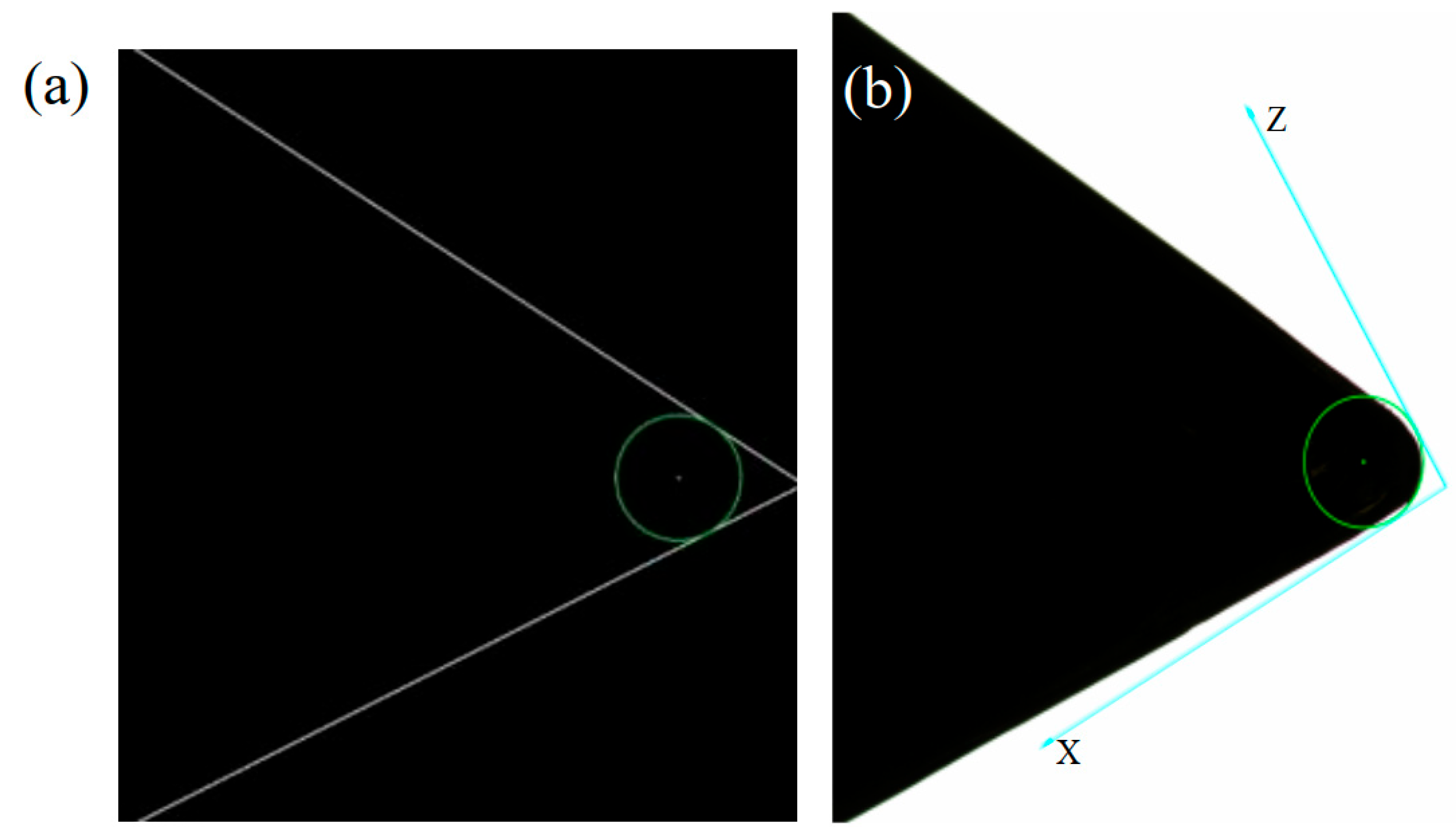
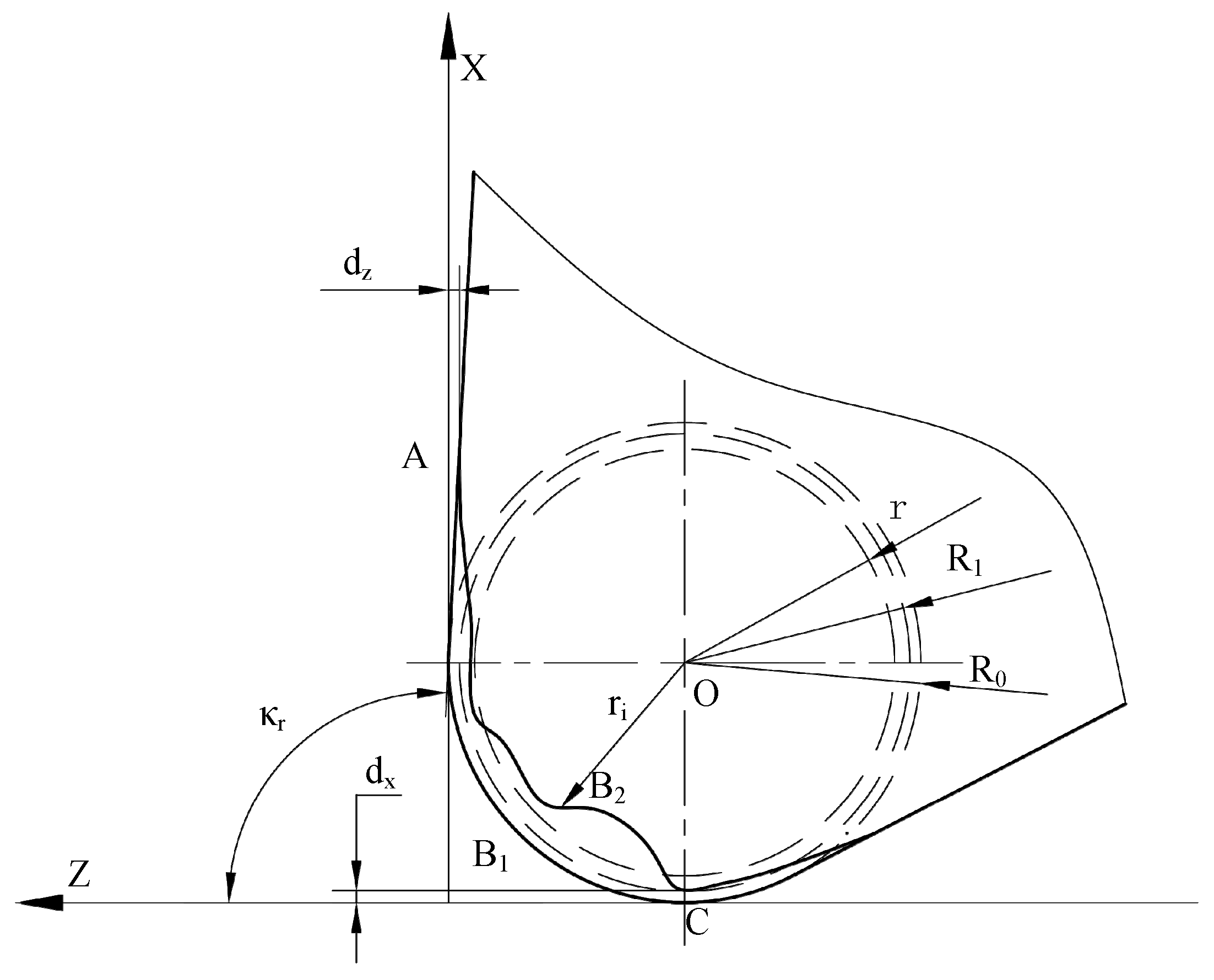

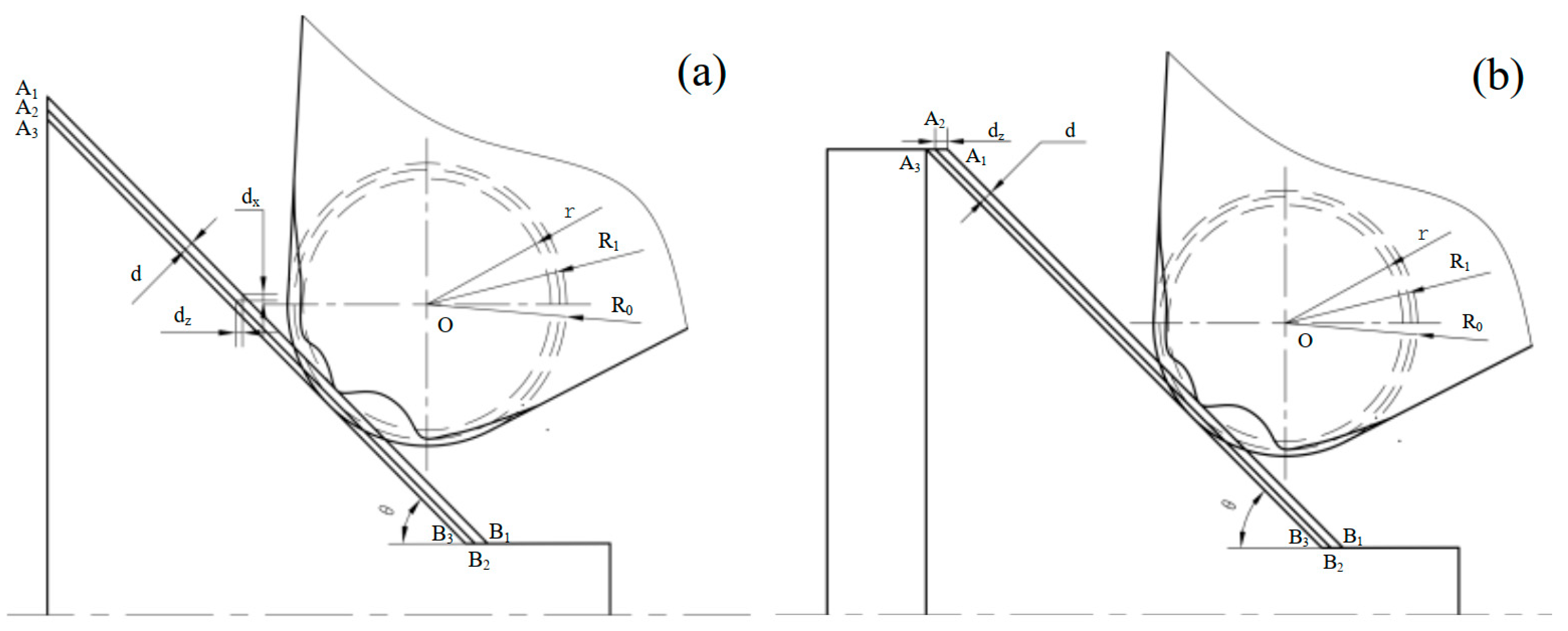




| Wear Type | Slight Wear (mm) | Uniform Wear (mm) | Non-Uniform Wear (mm) | |
|---|---|---|---|---|
| Wear Index | ||||
| VB | 0.048 | 0.156 | 0.190 | |
| VBmax | 0.079 | 0.241 | 0.429 | |
| Items | Specification |
|---|---|
| Maximum rotary diameter | 560 mm |
| Maximum cutting length | 500 mm |
| Maximum cutting diameter | 360 mm |
| Main shaft hole diameter | 65 mm |
| Maximum machining bar diameter | 50 mm |
| X-axis stroke | 200 mm |
| Z-axis stroke | 560 mm |
| Tailstock stroke | 450 mm |
| External turning tool size | 25 × 25 mm |
| Mainshaft speed range | 50~4500 r/min |
| Parameters | Specification (mm) |
|---|---|
| Positioning accuracy (X-axis) | 0.008 |
| Positioning accuracy (Z-axis) | 0.008 |
| Repeated positioning accuracy (X-axis) | 0.004 |
| Repeated positioning accuracy (Z-axis) | 0.005 |
| Workpiece Type | Error Type | Error Value (mm) | Average Error Reduction Rate | ||||
|---|---|---|---|---|---|---|---|
| 1 | Length error compensation of cone | Original | 0.034 | 0.036 | 0.020 | 0.026 | 75.8% |
| Compensated | 0.005 | 0.009 | 0.008 | 0.007 | |||
| 2 | Diameter error compensation of large conical surface | Original | 0.022 | 0.026 | 0.028 | 0.019 | 79.2% |
| Compensated | 0.005 | 0.004 | 0.007 | 0.002 | |||
| 3 | Radius error compensation of the arc surface | Original | 0.02 | 0.01 | 0.02 | 0.03 | 37.5% |
| Compensated | 0.01 | 0.01 | 0.01 | 0.02 | |||
| 4 | Diameter error compensation of cylindrical surface | Original | 0.014 | 0.020 | 0.016 | 0.019 | 69.6% |
| Compensated | 0.006 | 0.008 | 0.005 | 0.002 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Lu, T.; Xia, Z.; Zhang, Z.; Zhu, J. Machining Micro-Error Compensation Methods for External Turning Tool Wear of CNC Machines. Micromachines 2025, 16, 1143. https://doi.org/10.3390/mi16101143
Zhang H, Lu T, Xia Z, Zhang Z, Zhu J. Machining Micro-Error Compensation Methods for External Turning Tool Wear of CNC Machines. Micromachines. 2025; 16(10):1143. https://doi.org/10.3390/mi16101143
Chicago/Turabian StyleZhang, Hui, Tongwei Lu, Zhijie Xia, Zhisheng Zhang, and Jianxiong Zhu. 2025. "Machining Micro-Error Compensation Methods for External Turning Tool Wear of CNC Machines" Micromachines 16, no. 10: 1143. https://doi.org/10.3390/mi16101143
APA StyleZhang, H., Lu, T., Xia, Z., Zhang, Z., & Zhu, J. (2025). Machining Micro-Error Compensation Methods for External Turning Tool Wear of CNC Machines. Micromachines, 16(10), 1143. https://doi.org/10.3390/mi16101143








