Forked-Crossing Metasurface for Multi-Band Polarization Conversion with Distinct Bandwidths
Abstract
1. Introduction
2. Modeling and Numerical Results
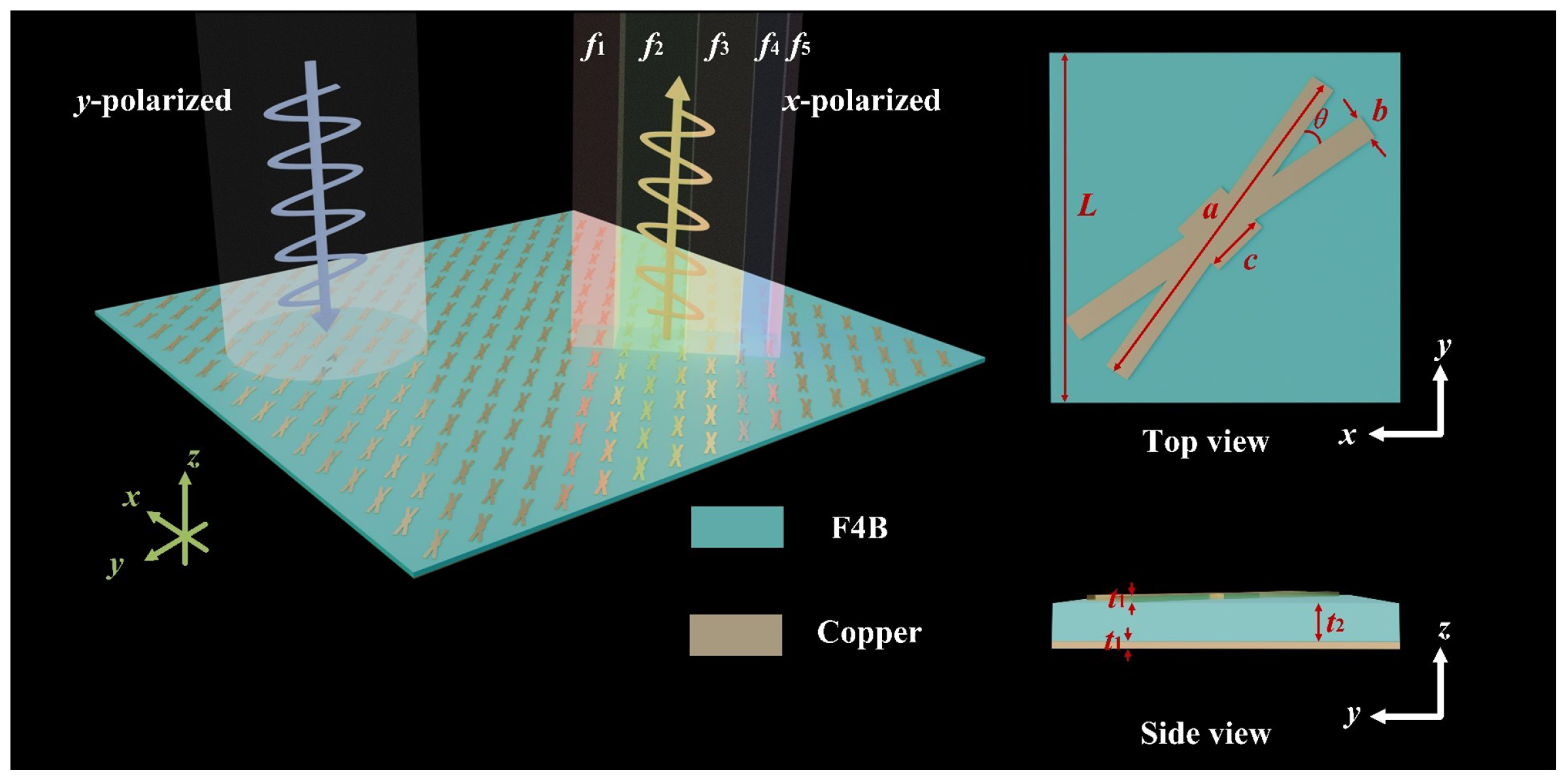
2.1. Simulation Setup
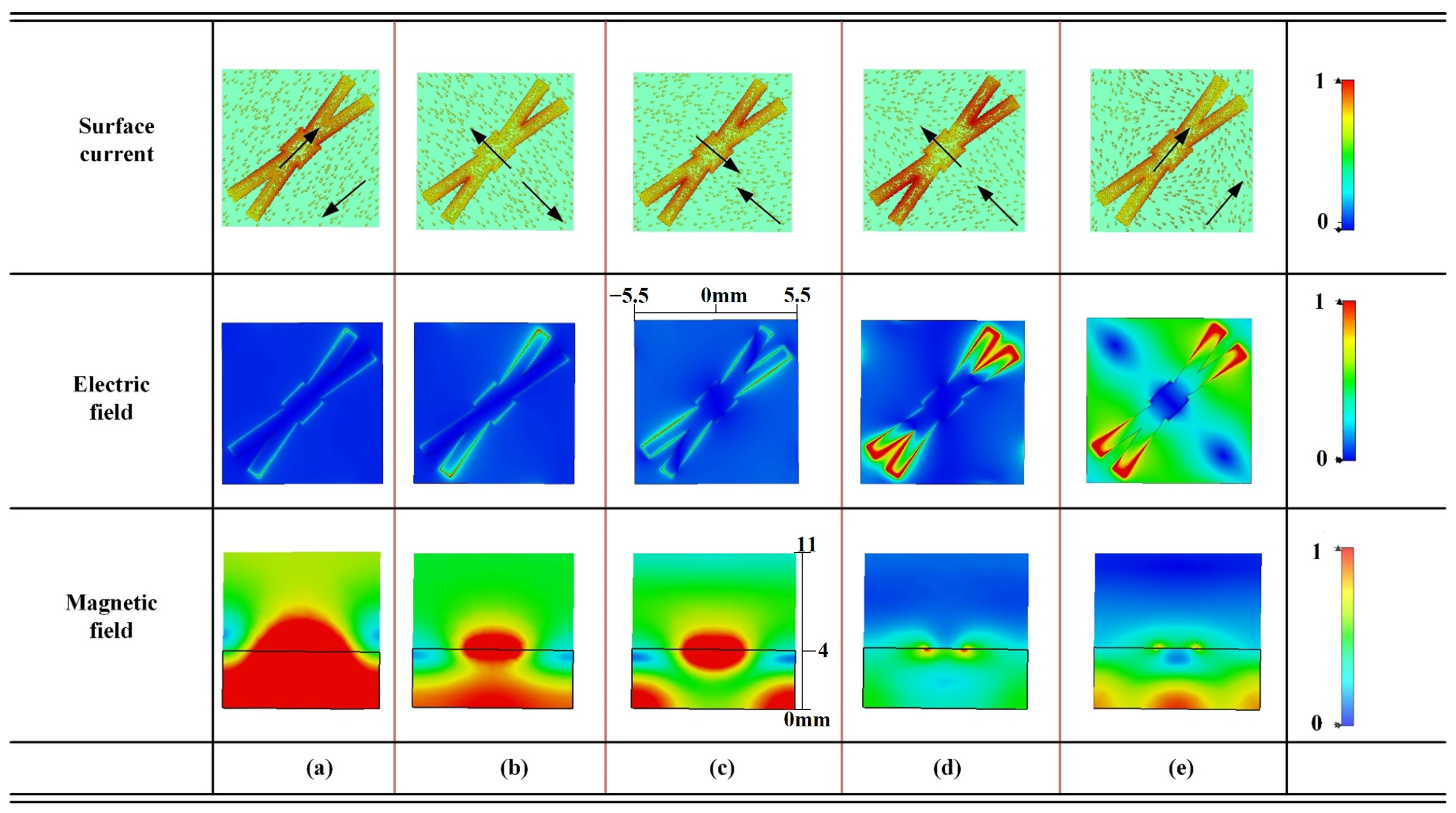
2.2. Analysis of Resonance Mechanism
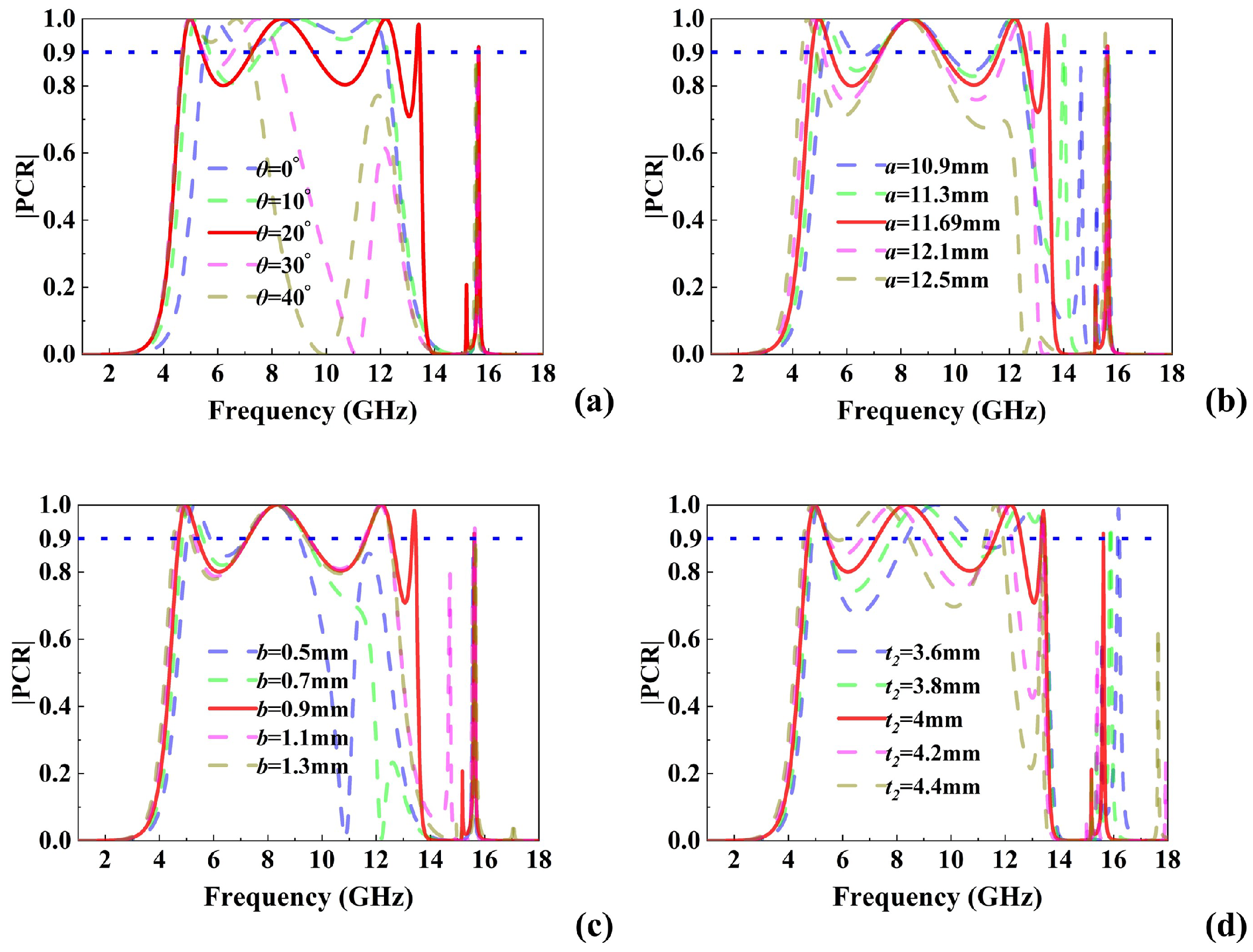
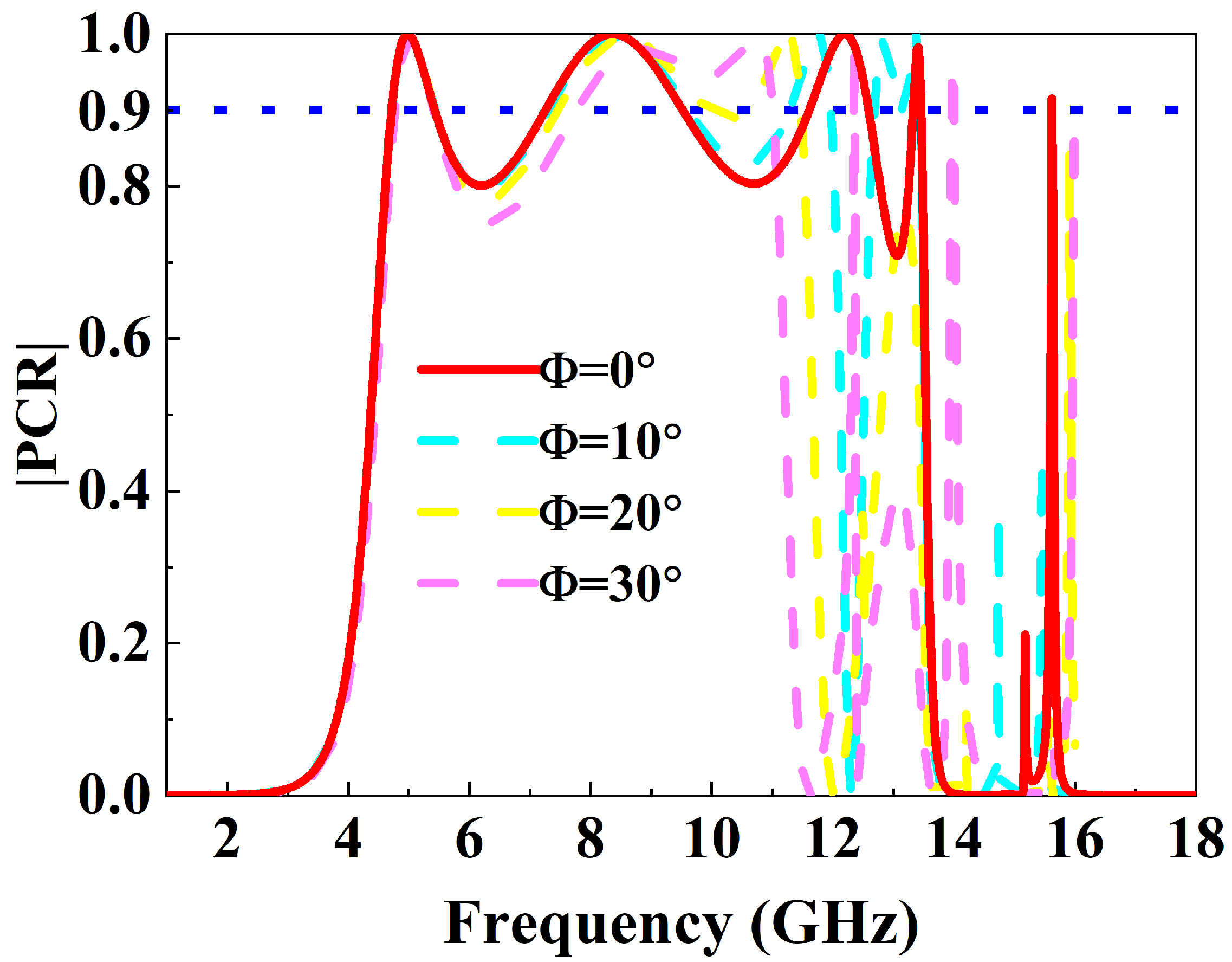
2.3. Parameter Optimization and Angular Stability
3. Experimental Verification and Comparisons
3.1. Fabrication and Calibration
3.2. Experimental Setup and Results
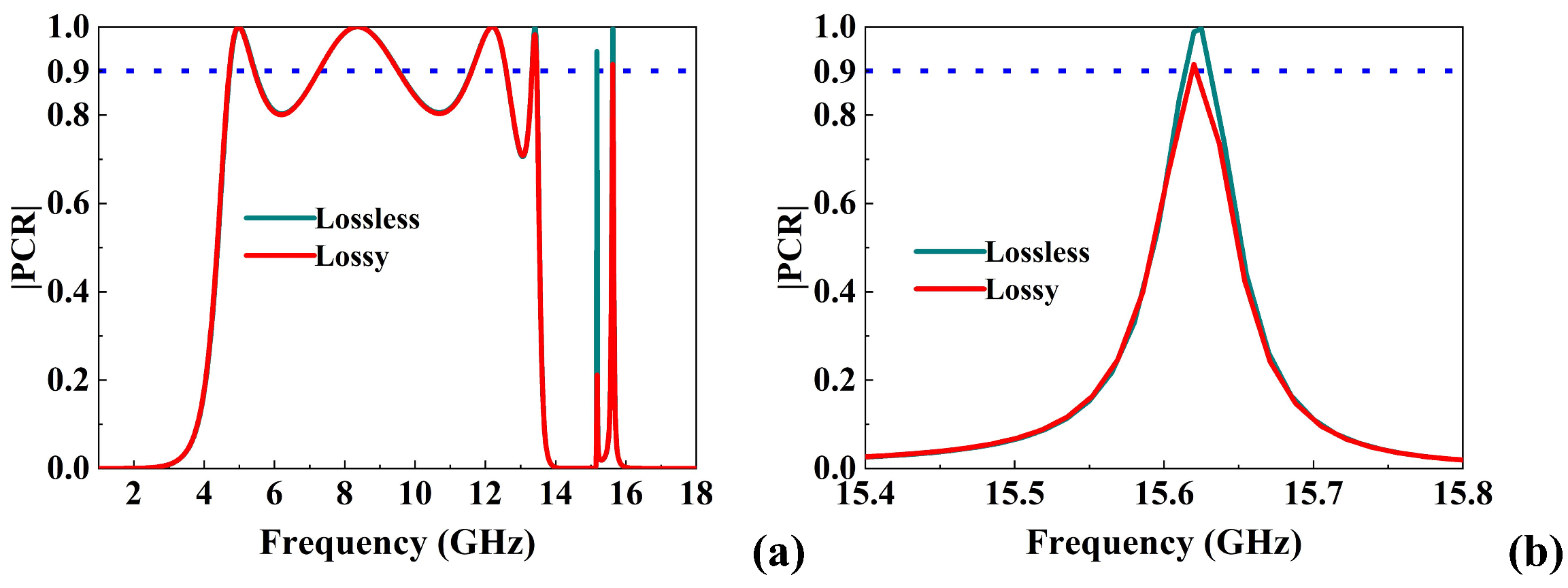
3.3. Impact of Material Losses
3.4. Comparison with Previous Works
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, R.; Ji, C.; Zhao, Z.; Zhou, T. Metamaterials: Reshape and Rethink. Engineering 2015, 1, 179–184. [Google Scholar] [CrossRef]
- Hao, J.; Yuan, Y.; Ran, L.; Jiang, T.; Kong, J.A.; Chan, C.T.; Zhou, L. Manipulating Electromagnetic Wave Polarizations by Anisotropic Metamaterials. Phys. Rev. Lett. 2007, 99, 063908. [Google Scholar] [CrossRef]
- Lin, J.; Mueller, J.P.B.; Wang, Q.; Yuan, G.; Antoniou, N.; Yuan, X.-C.; Capasso, F. Polarization-Controlled Tunable Directional Coupling of Surface Plasmon Polaritons. Science 2013, 340, 331–334. [Google Scholar] [CrossRef]
- Sun, S.; He, Q.; Xiao, S.; Xu, Q.; Li, X.; Zhou, L. Gradient-Index Meta-Surfaces as a Bridge Linking Propagating Waves and Surface Waves. Nat. Mater. 2012, 11, 426–431. [Google Scholar] [CrossRef]
- Ren, X.; Liu, Y.; Ji, Z.; Zhang, Q.; Cao, W. Ultra-Wideband Passive Polarization Conversion Metasurface for Radar Cross-Section Reduction Across C-, X-, Ku-, and K-Bands. Micromachines 2025, 16, 292. [Google Scholar] [CrossRef] [PubMed]
- Zafar, J.; Khan, H.Z.; Jabbar, A.; Kazim, J.U.R.; Ur Rehman, M.; Siddiqui, A.M.; Abbasi, Q.H.; Imran, M.A. Multi-Band Reflective Metasurface for Efficient Linear and Circular Polarization Conversion. Opt. Quant. Electron. 2025, 57, 149. [Google Scholar] [CrossRef]
- Kamal, B.; Chen, J.; Yingzeng, Y.; Ren, J.; Ullah, S.; Khan, W.U.R. High Efficiency and Ultra-Wideband Polarization Converter Based on an L-Shaped Metasurface. Opt. Mater. Express 2021, 11, 1343. [Google Scholar]
- Sheheryar, T.; Waqar, F.; Lv, B.; Gao, L. An Ultra-Wideband Terahertz Linear Cross-Polarization Converter with Integrated Biosensing for Multi-Disease Diagnosis. J. Mater. Chem. C 2025, 13, 12460–12471. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, J.; Fu, X.; Jia, Y.; Chen, H.; Feng, M.; Zhu, R.; Qu, S. Single-Layer Metasurface for Ultra-Wideband Polarization Conversion: Bandwidth Extension via Fano Resonance. Sci. Rep. 2021, 11, 585. [Google Scholar]
- Rashid, A.; Murtaza, M.; Zaidi, S.A.A.; Zaki, H.; Tahir, F.A. A Single-Layer, Wideband and Angularly Stable Metasurface Based Polarization Converter for Linear-to-Linear Cross-Polarization Conversion. PLoS ONE 2023, 18, e0280469. [Google Scholar] [CrossRef]
- Lv, B.; Sheheryar, T.; Wekalao, J.; Gao, L. Ultra-Wideband and Angular-Stable Terahertz Reflective Cross-Polarization Converter Integrated with Highly Sensitive Biosensing. Mater. Res. Bull. 2026, 193, 113641. [Google Scholar] [CrossRef]
- Nochian, P.; Atlasbaf, Z. An Ultra-Wideband Thin Metamaterial Linear Cross-Polarization Conversion. Sci. Rep. 2025, 15, 3062. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Q.; Qi, J.; PourMohammadi, P. Flexible Polarization Manipulation Using Multi-Band and Wide-Angle Multi-Function Reflective Polarization Metasurface for Terahertz Regime. Plasmonics 2023, 18, 2263–2272. [Google Scholar] [CrossRef]
- Zubair Khan, H.; Jabbar, A.; Ur Rehman Kazim, J.; Zafar, J.; Ur-Rehman, M.; Ali Imran, M.; Abbasi, Q.H. Reflective Metasurface for Multi-Band Polarization Conversion for Satellite Applications in 6G Networks. IEEE Open J. Antennas Propag. 2025, 6, 332–343. [Google Scholar] [CrossRef]
- Kosar Fahad, A.; Ruan, C.; Nazir, R.; Taskeen Raza, M. Multifunctional Multi-Band Metasurface for Linear to Circular Polarization Conversion in Transmission and Reflection Modes. Results Phys. 2023, 50, 106595. [Google Scholar] [CrossRef]
- Maurya, V.; Singhal, S. Dual Band Terahertz Reflective Linear Cross Polarization Converter-Based Biosensor. IEEE Sensors J. 2024, 24, 6103–6110. [Google Scholar] [CrossRef]
- Chaudhuri, A.; Rai, B.; Pal, P. Design of a Dual-Band Metasurface Cross-Polarization Converter for Cancer Detection in the Terahertz Band. IEEE Sensors J. 2024, 24, 7292–7298. [Google Scholar] [CrossRef]
- Hossain, I.; Islam, M.T.; Alsaif, H.; Alharbi, A.G.; Sahar, N.B.M.; Samsuzzaman, M. An Angular Stable Triple-Band Anisotropic Cross-Polarization Conversion Metasurface. Results Phys. 2022, 37, 105564. [Google Scholar] [CrossRef]
- Yang, Z.; Yu, S.; Kou, N.; Long, F.; Ding, Z.; Zhang, Z. Ultrathin Tri-Band Reflective Cross-Polarization Artificial Electromagnetic Metasurface. J. Electromagn. Waves Appl. 2020, 34, 1491–1501. [Google Scholar] [CrossRef]
- Abbas, M.B.; Raza, F.; Baqir, M.A.; Altintas, O.; Abbas, M.; KaraaSlan, M.; Naqvi, Q.A. Ultra-Wideband Cross-Polarization Converter Using Metasurface Operating in the X- and K-Band. Photonics 2024, 11, 863. [Google Scholar] [CrossRef]
- Mustafa, M.-E.-; Tahir, F.A.; Amin, M. Broadband Waveplate Operation by Orthotropic Metasurface Reflector. J. Appl. Phys. 2019, 126, 185108. [Google Scholar] [CrossRef]
- Han, J.; Chen, R. Dual-Band Metasurface for Broadband Asymmetric Transmission with High Efficiency. J. Appl. Phys. 2021, 130, 034503. [Google Scholar] [CrossRef]


| Resonance (GHz) | Mode Type | FCF | Q Factor | Bandwidth Type |
|---|---|---|---|---|
| 5.0 | Magnetic | 0.022 | 6.95 | Wide |
| 8.36 | Magnetic | 0.007 | 3.67 | Wide |
| 12.2 | Magnetic | 0.037 | 12.35 | Wide |
| 13.41 | Electric | 0.070 | 103.04 | Narrow |
| 15.618 | Electric | 0.081 | 1561.5 | Ultra-narrow |
| Reference | Operating Bandwidth (GHz) | Bandwidth Type | Max/Min Relative Bandwidth (%) | Q Factor | Structural Complexity | Reported Applications |
|---|---|---|---|---|---|---|
| [5] | 7.1–22.3 | Ultra-wideband | 103.4 | 0.97 | single layer | 6G communications, radar imaging, anti-interference measures, and electromagnetic stealth |
| [18] | 5.35–5.69; 7.60–8.76; 12.41–13.96 | Wideband and narrowband coexistence | 14.2/6.2 | 16.24, 7.05, 8.51 | single layer | Radar, satellite communications, and wireless communications |
| [19] | 9.1–12.4; 15.55–23.8; 24.71–30.00 | Wideband | 41.9/3.3 | 3.3, 2.4, 5.2 | two metallic rectangular ring resonators, single layer | Radar, satellite communication |
| [20] | 12.94–16.54; 17.54–26 | Ultra-wideband | 38.9/24.4 | 4.09, 2.57 | three anisotropic stair-shaped resonators, single layer | navigation systems, satellite communication, and imaging systems |
| [21] | 7.48–10.55; 18.47–19.52 | Wideband | 34.1/5.5 | 2.94, 18.09 | Orthotropic reflector metasurface, single layer | satellite systems, navigation systems, and stealth surfaces |
| This Method | 4.71–5.44; 7.26–9.55; 11.62–12.6; 13.33–13.46; 15.61–15.62 | Wideband and ultra-narrowband coexistence | 27.2/0.06 | 6.95, 3.67, 12.35, 103.04, 1561.5 | Forked-crossing patch, single layer | Multi-band devices, radars, target locking |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, P.; Zhang, Y.; Li, Z.; Yang, R. Forked-Crossing Metasurface for Multi-Band Polarization Conversion with Distinct Bandwidths. Micromachines 2025, 16, 1100. https://doi.org/10.3390/mi16101100
Zhang P, Zhang Y, Li Z, Yang R. Forked-Crossing Metasurface for Multi-Band Polarization Conversion with Distinct Bandwidths. Micromachines. 2025; 16(10):1100. https://doi.org/10.3390/mi16101100
Chicago/Turabian StyleZhang, Pengpeng, Yifei Zhang, Ziang Li, and Rui Yang. 2025. "Forked-Crossing Metasurface for Multi-Band Polarization Conversion with Distinct Bandwidths" Micromachines 16, no. 10: 1100. https://doi.org/10.3390/mi16101100
APA StyleZhang, P., Zhang, Y., Li, Z., & Yang, R. (2025). Forked-Crossing Metasurface for Multi-Band Polarization Conversion with Distinct Bandwidths. Micromachines, 16(10), 1100. https://doi.org/10.3390/mi16101100







