Sensitivity Improvement via Differential Detection for Frequency-Locking Diamond Magnetometers
Abstract
1. Introduction
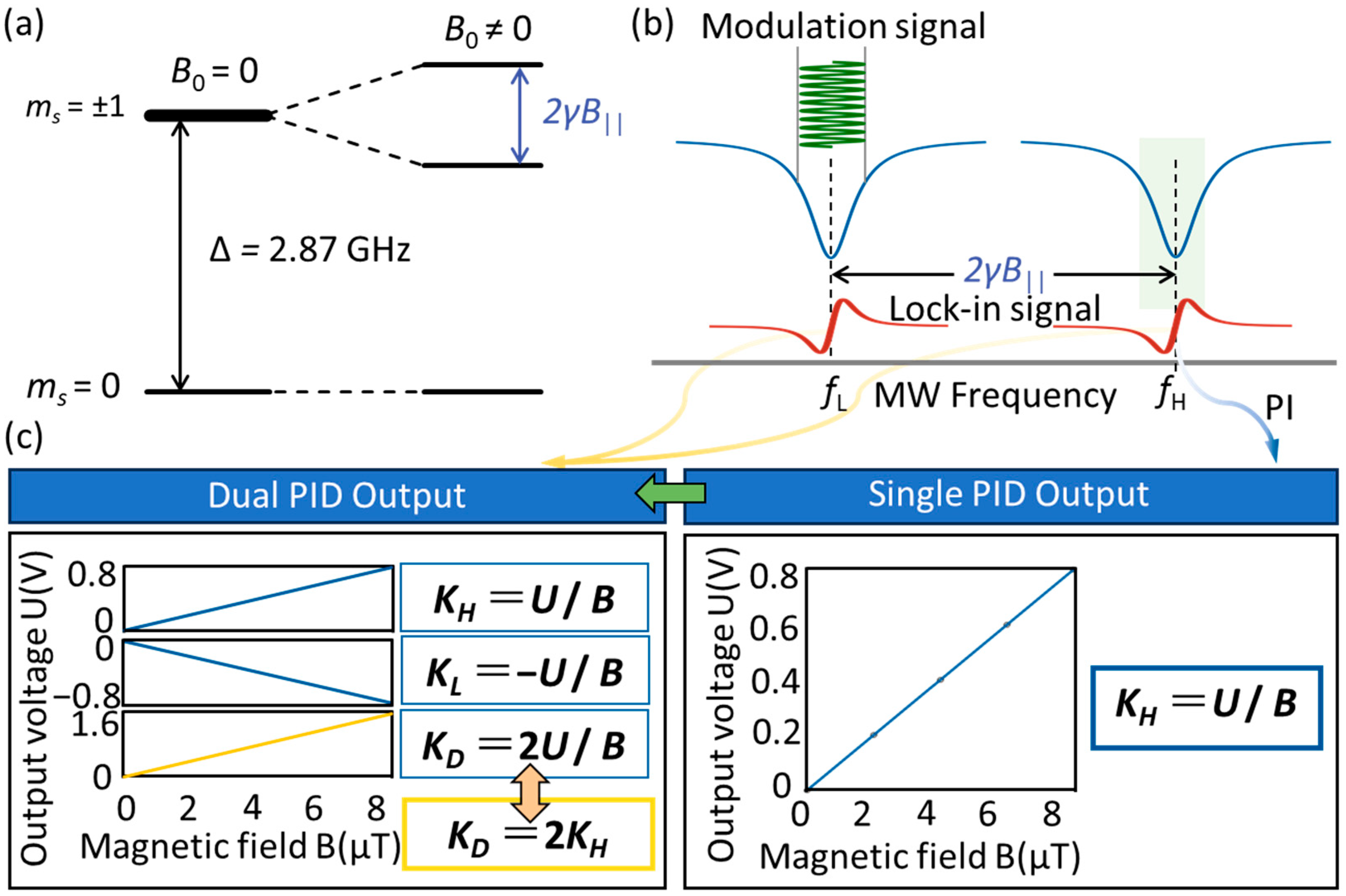
2. Principle
3. Experimental Setup
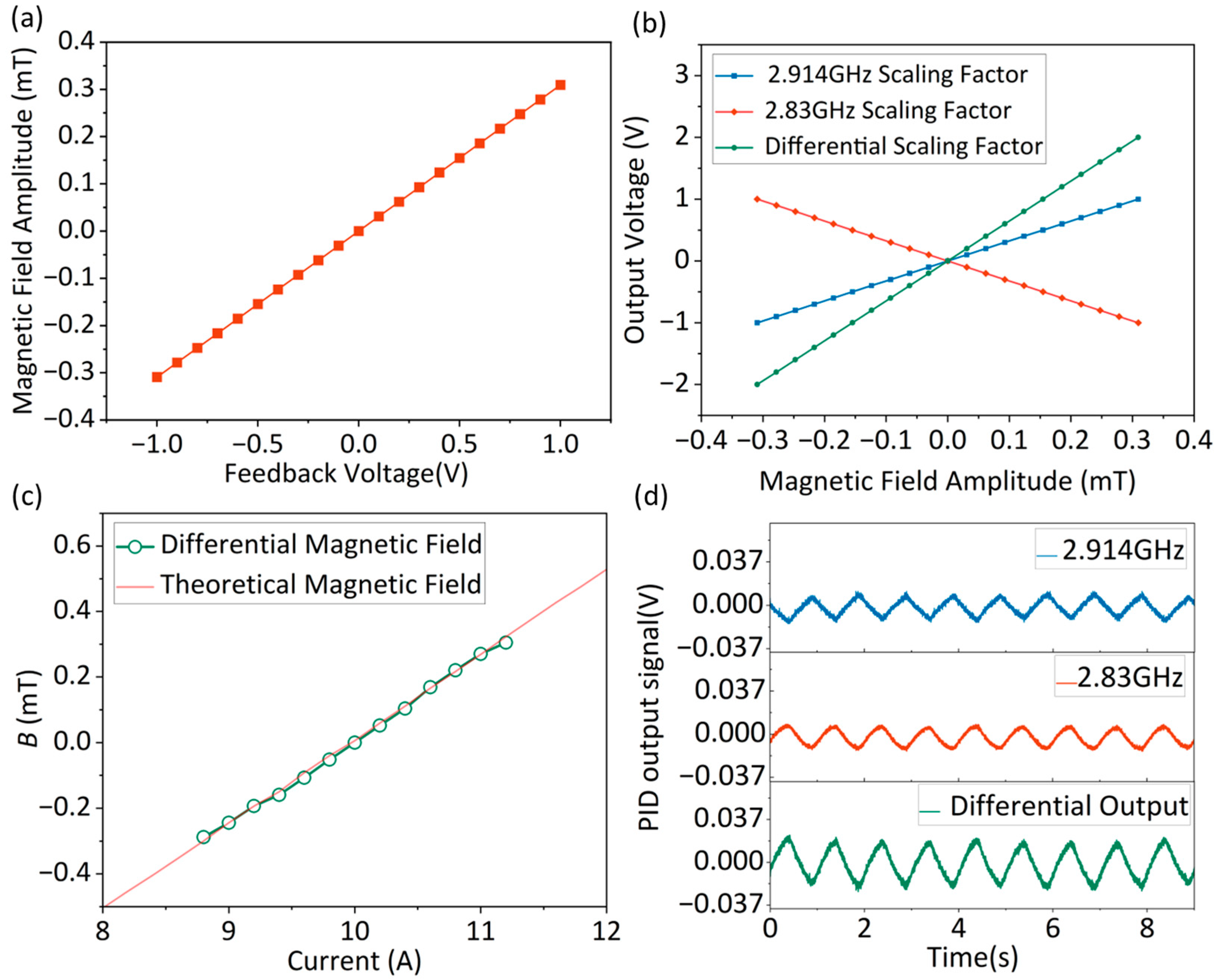
4. Results and Discussion
4.1. Scaling Factor
4.2. Sensitivity
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Silani, Y.; Smits, J.; Fescenko, I.; Malone, M.W.; Mcdowell, A.F.; Jarmola, A.; Kehayias, P.; Richards, B.A.; Mosavian, N.; Ristoff, N.; et al. Nuclear quadrupole resonance spectroscopy with a femtotesla diamond magnetometer. Sci. Adv. 2023, 9, eadh3189. [Google Scholar] [CrossRef]
- Graham, S.M.; Rahman, A.; Munn, L.; Patel, R.L.; Newman, A.J.; Stephen, C.J.; Colston, G.; Nikitin, A.; Edmonds, A.M.; Twitchen, D.J.; et al. Fiber-coupled diamond magnetometry with an unshielded sensitivity of 30 pT/Hz. Phys. Rev. 2023, 19, 044042. [Google Scholar]
- Herb, K.; Völker, L.A.; Abendroth, J.M.; Meinhardt, N.; van Schie, L.; Gambardella, P.; Degen, C.L. Quantum magnetometry of transient signals with a time resolution of 1.1 nanoseconds. Nat. Commun. 2025, 16, 822. [Google Scholar] [CrossRef]
- Findler, C.; Blinder, R.; Schüle, K.; Balasubramanian, P.; Osterkamp, C.; Jelezko, F. Detecting nitrogen-vacancy-hydrogen centers on the nanoscale using nitrogen-vacancy centers in diamond. Phys. Rev. Mater. 2024, 8, 026203. [Google Scholar] [CrossRef]
- Trofimov, S.; Naydenov, B. Combined Confocal-Atomic-Force Microscope Setup for Quantum Sensing Applications with Sub-diffractional Spatial Resolution. Phys. Status Solidi (A) 2025, 222, 2400541. [Google Scholar] [CrossRef]
- Stürner, F.M.; Brenneis, A.; Buck, T.; Kassel, J.; Rolver, R.; Fuchs, T.; Savitsky, A.; Suter, D.; Grimmel, J.; Hengesbach, S.; et al. Integrated and portable magnetometer based on nitrogen-vacancy ensembles in diamond. Adv. Quantum Technol. 2021, 4, 2000111. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, W.; Chai, H.; Zhang, Z.; Lin, S.; Qin, X.; Du, J. Fully integrated quantum magnetometer based on nitrogen-vacancy centers. Phys. Rev. Appl. 2025, 23, 034008. [Google Scholar] [CrossRef]
- Kim, D.; Ibrahim, M.I.; Foy, C.; Trusheim, M.E.; Han, R.; Englund, D.R. A CMOS-integrated quantum sensor based on nitrogen–vacancy centres. Nat. Electron. 2019, 2, 284–289. [Google Scholar] [CrossRef]
- Frontera, P.; Alessandrini, S.; Stetson, J. Shipboard calibration of a diamond nitrogen vacancy magnetic field sensor. In Proceedings of the 2018 IEEE/ION Position, Location and Navigation Symposium (PLANS), Monterey, CA, USA, 23–26 April 2018; IEEE: New York, NY, USA, 2018; pp. 497–504. [Google Scholar]
- Kocak, D.M.; Thayer, B.; Stumvoll, H.; Drakes, J. Quantum Magnetometry for Enhanced Sensing in Autonomous Underwater Vehicles. In Proceedings of the OCEANS 2024, Halifax, NS, Canada, 23–26 September 2024. [Google Scholar] [CrossRef]
- Graham, S.M.; Newman, A.J.; Stephen, C.J.; Edmonds, A.M.; Twitchen, D.J.; Markham, M.L.; Morley, G.W. On the road with a diamond magnetometer. Diam. Relat. Mater. 2025, 152, 111945. [Google Scholar] [CrossRef]
- Newman, A.J.; Graham, S.M.; Edmonds, A.M.; Twitchen, D.J.; Markham, M.L.; Morley, G.W. Tensor gradiometry with a diamond magnetometer. Phys. Rev. Appl. 2024, 21, 014003. [Google Scholar] [CrossRef]
- Basso, L.; Kehayias, P.; Henshaw, J.; Ziabari, M.S.; Byeon, H.; Lilly, M.P.; Bussmann, E.; Campbell, D.M.; Misra, S.; Mounce, A.M. Current Paths in an Atomic Precision Advanced Manufactured Device Imaged by Nitrogen Vacancy Diamond Magnetic Microscopy. arXiv 2022, arXiv:2207.14254. [Google Scholar]
- Hansen, N.W.; Webb, J.L.; Troise, L.; Olsson, C.; Tomasevic, L.; Brinza, O.; Achard, J.; Staacke, R.; Kieschnick, M.; Meijer, J.; et al. Microscopic-scale magnetic recording of brain neuronal electrical activity using a diamond quantum sensor. Sci. Rep. 2023, 13, 12407. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; Xie, F.; Peng, X.; Zhang, Y.; Wang, N. Closed-loop diamond quantum sensor for large range and high precision current measurement. IEEE Sens. J. 2024, 24, 4356–4364. [Google Scholar] [CrossRef]
- Hatano, Y.; Shin, J.; Tanigawa, J.; Shigenobu, Y.; Nakazono, A.; Sekiguchi, T.; Onoda, S.; Ohshima, T.; Arai, K.; Iwasaki, T.; et al. High-precision robust monitoring of charge/discharge current over a wide dynamic range for electric vehicle batteries using diamond quantum sensors. Sci. Rep. 2022, 12, 13991. [Google Scholar] [CrossRef]
- Clevenson, H.; Pham, L.M.; Teale, C.; Johnson, K.; Englund, D.; Braje, D. Robust high-dynamic-range vector magnetometry with nitrogen-vacancy centers in diamond. Appl. Phys. Lett. 2018, 112, 252406. [Google Scholar] [CrossRef]
- Kumar, H.; Dasika, S.; Mangat, M.; Tallur, S.; Saha, K. High dynamic-range and portable magnetometer using ensemble nitrogen-vacancy centers in diamond. Rev. Sci. Instrum. 2024, 95, 075002. [Google Scholar] [CrossRef]
- Wang, C.; Liu, Q.; Hu, Y.; Xie, F.; Krishna, K.; Wang, N.; Wang, L.; Wang, Y.; Toussaint, K.C., Jr.; Cheng, J.; et al. Realization of high-dynamic-range broadband magnetic-field sensing with ensemble nitrogen-vacancy centers in diamond. Rev. Sci. Instrum. 2023, 94, 015109. [Google Scholar] [CrossRef]
- Zhang, J.; Yuan, H.; Liu, T.; Xu, L.; Bian, G.; Fan, P.; Li, M. A pulsed lock-in method for DC ensemble nitrogen-vacancy center magnetometry. Diam. Relat. Mater. 2022, 125, 109035. [Google Scholar] [CrossRef]
- Ambal, K.; McMichael, R.D. A differential rate meter for real-time peak tracking in optically detected magnetic resonance at low photon count rates. Rev. Sci. Instrum. 2019, 90, 023907. [Google Scholar] [CrossRef]
- Hatano, Y.; Shin, J.; Nishitani, D.; Watsuka, H.; Masuyama, Y.; Sugiyama, H.; Ishii, M.; Onoda, S.; Ohshima, T.; Arai, K.; et al. Simultaneous thermometry and magnetometry using a fiber-coupled quantum diamond sensor. Appl. Phys. Lett. 2021, 118, 034001. [Google Scholar] [CrossRef]
- Maze, J.R.; Stanwix, P.L.; Hodges, J.S.; Hong, S.; Taylor, J.M.; Cappellaro, P.; Jiang, L.; Dutt, G.; Togan, E.; Zibrov, A.S.; et al. Nanoscale magnetic sensing with an individual electronic spin in diamond. Nature 2008, 455, 644–647. [Google Scholar] [CrossRef] [PubMed]
- Ma, Z.; Zhang, S.; Fu, Y.; Yuan, H.; Shi, Y.; Gao, J.; Qin, L.; Tang, J.; Liu, J.; Li, Y.; et al. Magnetometry for precision measurement using frequency-modulation microwave combined efficient photon-collection technique on an ensemble of nitrogen-vacancy centers in diamond. Opt. Express 2018, 26, 382–390. [Google Scholar] [CrossRef] [PubMed]
- Zheng, D.; Ma, Z.; Guo, W.; Niu, L.; Wang, J.; Chai, X.; Li, Y.; Sugawara, Y.; Yu, C.; Shi, Y.; et al. A hand-held magnetometer based on an ensemble of nitrogen-vacancy centers in diamond. J. Phys. D Appl. Phys. 2020, 53, 155004. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, D.; Gao, J.; Li, Y.; Wang, H.; Yang, Y.; Guo, H.; Wen, H.; Li, Z.; Tang, J.; Ma, Z.; et al. Sensitivity Improvement via Differential Detection for Frequency-Locking Diamond Magnetometers. Micromachines 2025, 16, 1095. https://doi.org/10.3390/mi16101095
Zheng D, Gao J, Li Y, Wang H, Yang Y, Guo H, Wen H, Li Z, Tang J, Ma Z, et al. Sensitivity Improvement via Differential Detection for Frequency-Locking Diamond Magnetometers. Micromachines. 2025; 16(10):1095. https://doi.org/10.3390/mi16101095
Chicago/Turabian StyleZheng, Doudou, Jian Gao, Yang Li, Hui Wang, Yingjie Yang, Hao Guo, Huanfei Wen, Zhonghao Li, Jun Tang, Zongmin Ma, and et al. 2025. "Sensitivity Improvement via Differential Detection for Frequency-Locking Diamond Magnetometers" Micromachines 16, no. 10: 1095. https://doi.org/10.3390/mi16101095
APA StyleZheng, D., Gao, J., Li, Y., Wang, H., Yang, Y., Guo, H., Wen, H., Li, Z., Tang, J., Ma, Z., & Liu, J. (2025). Sensitivity Improvement via Differential Detection for Frequency-Locking Diamond Magnetometers. Micromachines, 16(10), 1095. https://doi.org/10.3390/mi16101095






