Design and Simulation of a Simple-Structure and High-Performance Plasmonic Polarization Filter Based on Gold Layers Deposited on Photonic Crystal Fiber
Abstract
1. Introduction
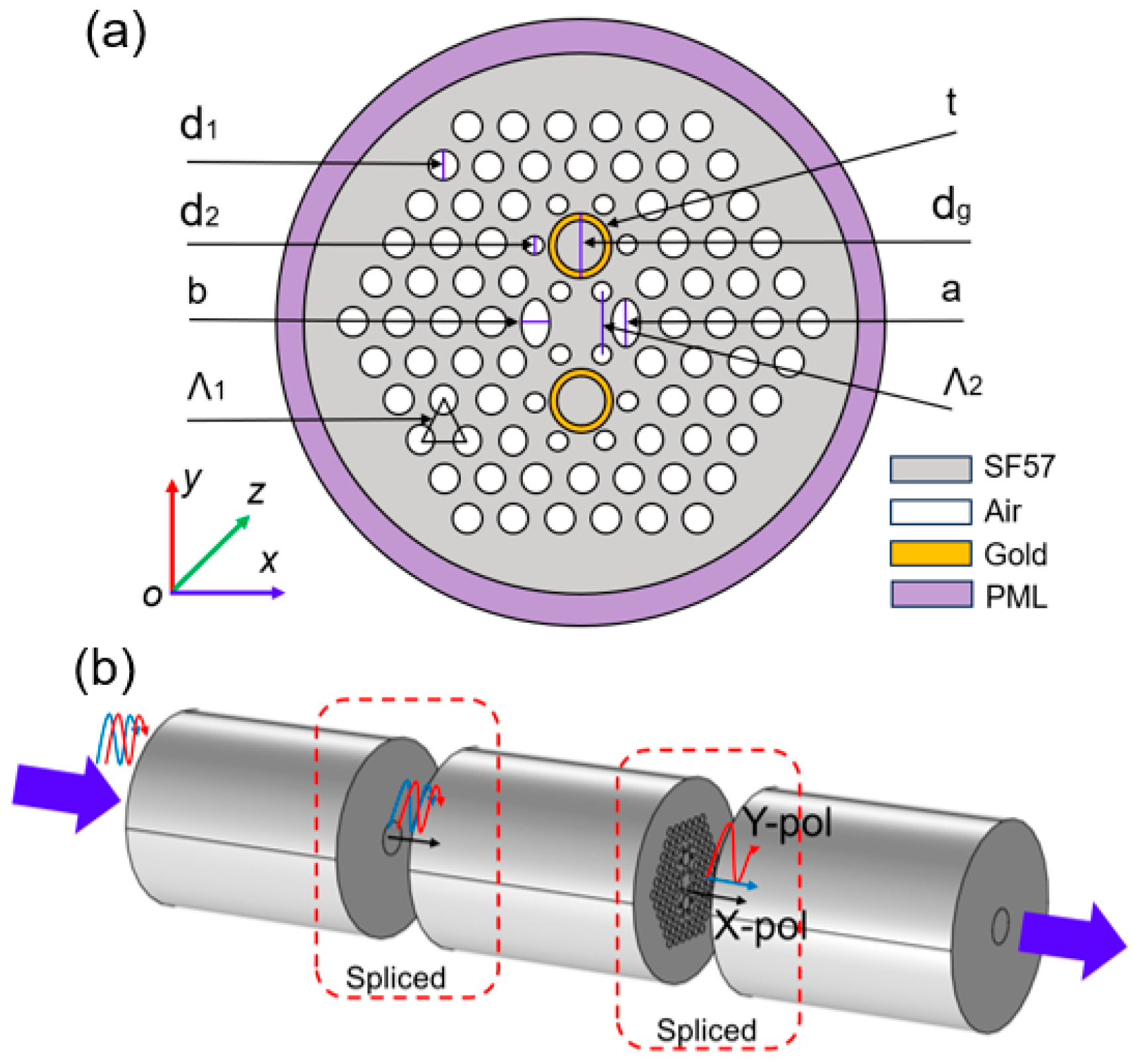
2. Modeling and Theory
3. Results and Discussion
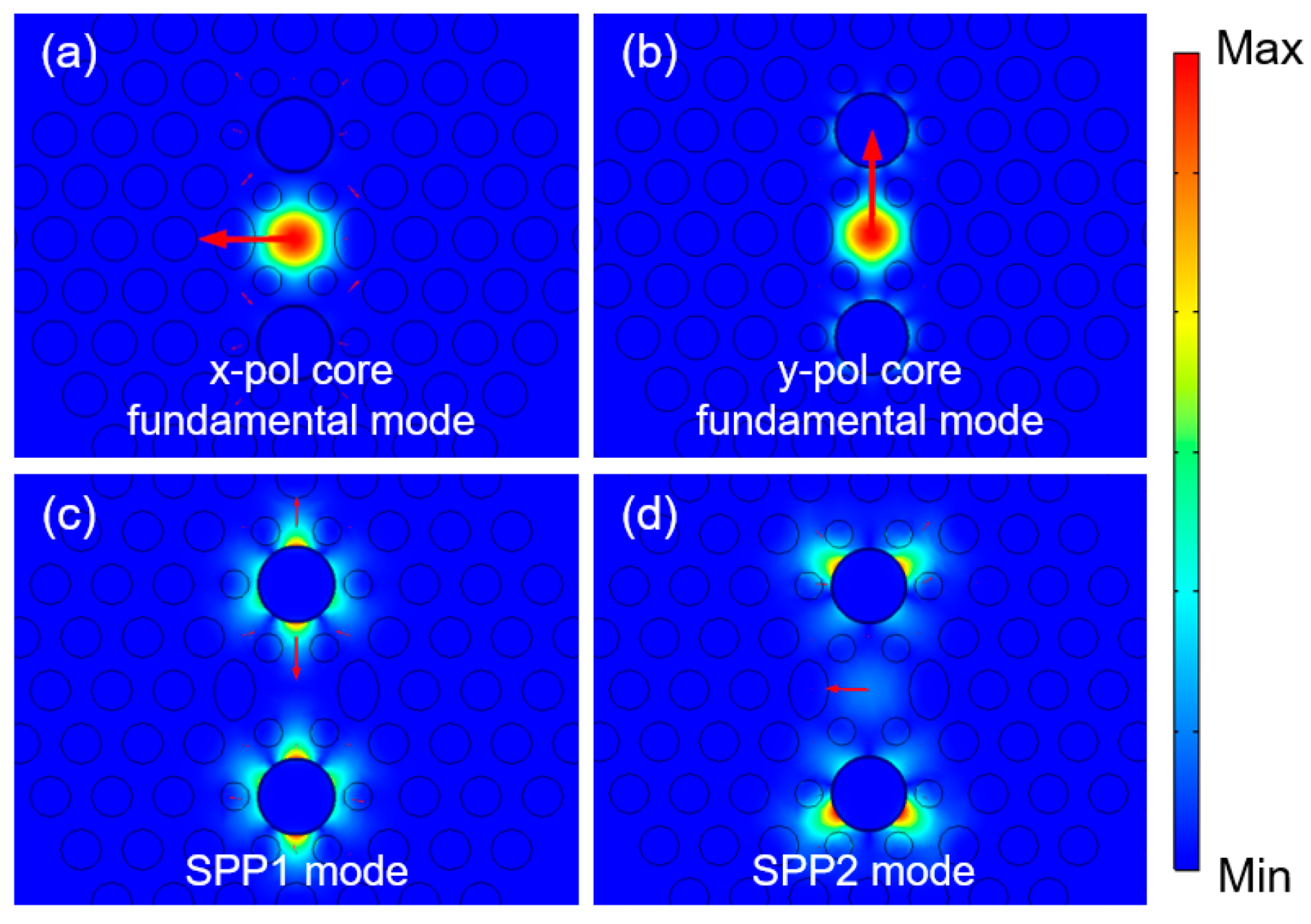
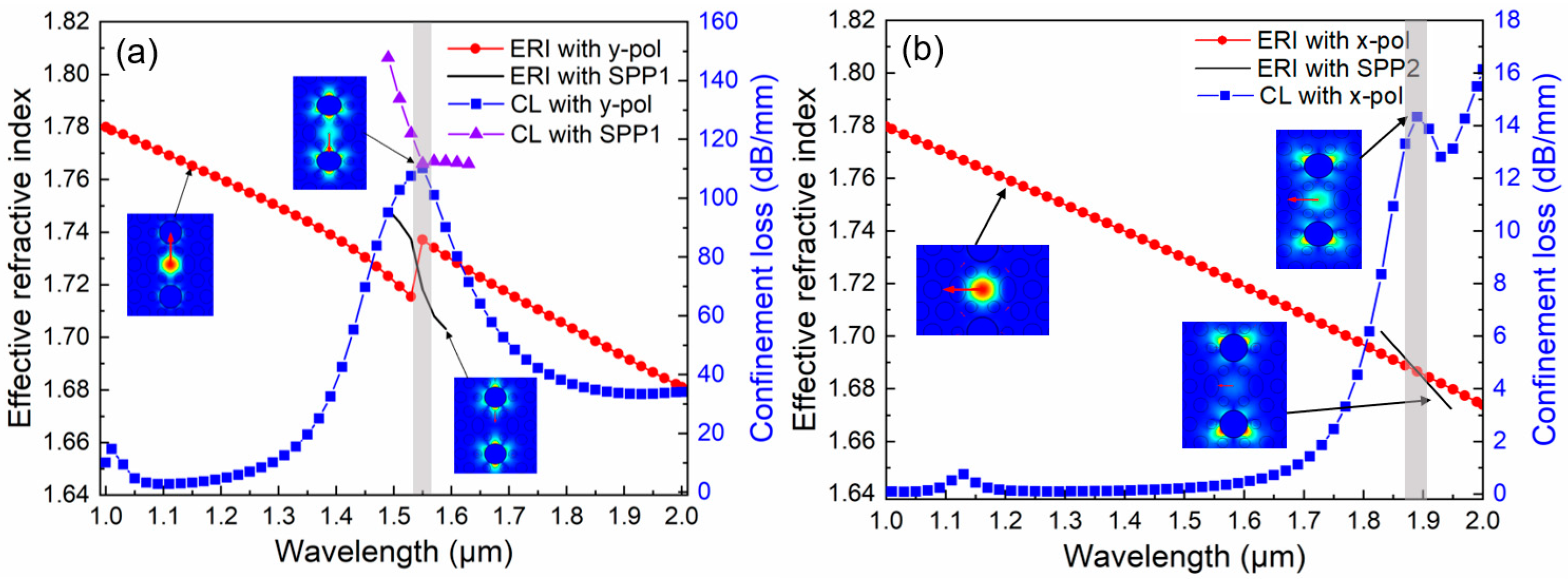
3.1. Dispersion Relationship
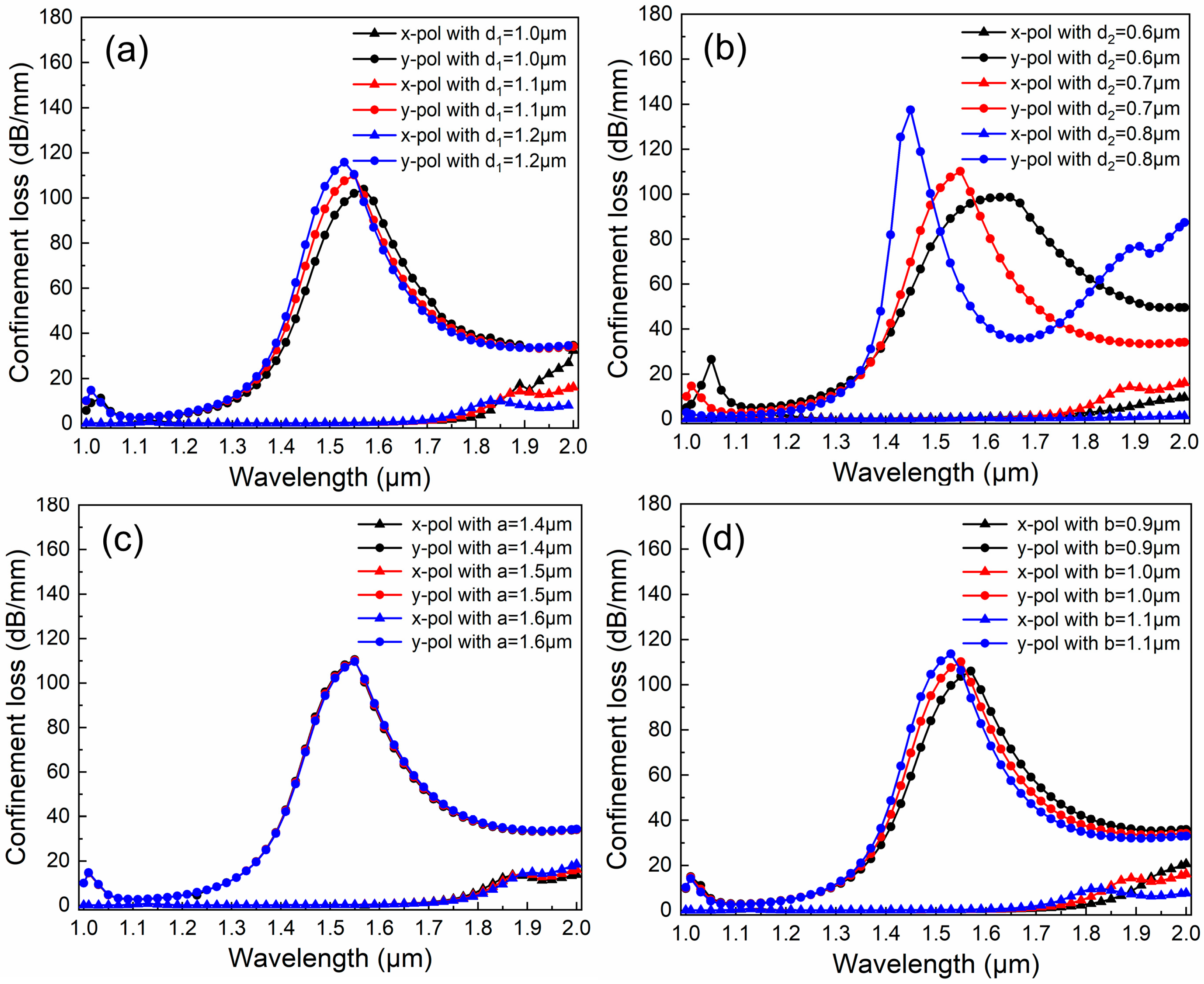
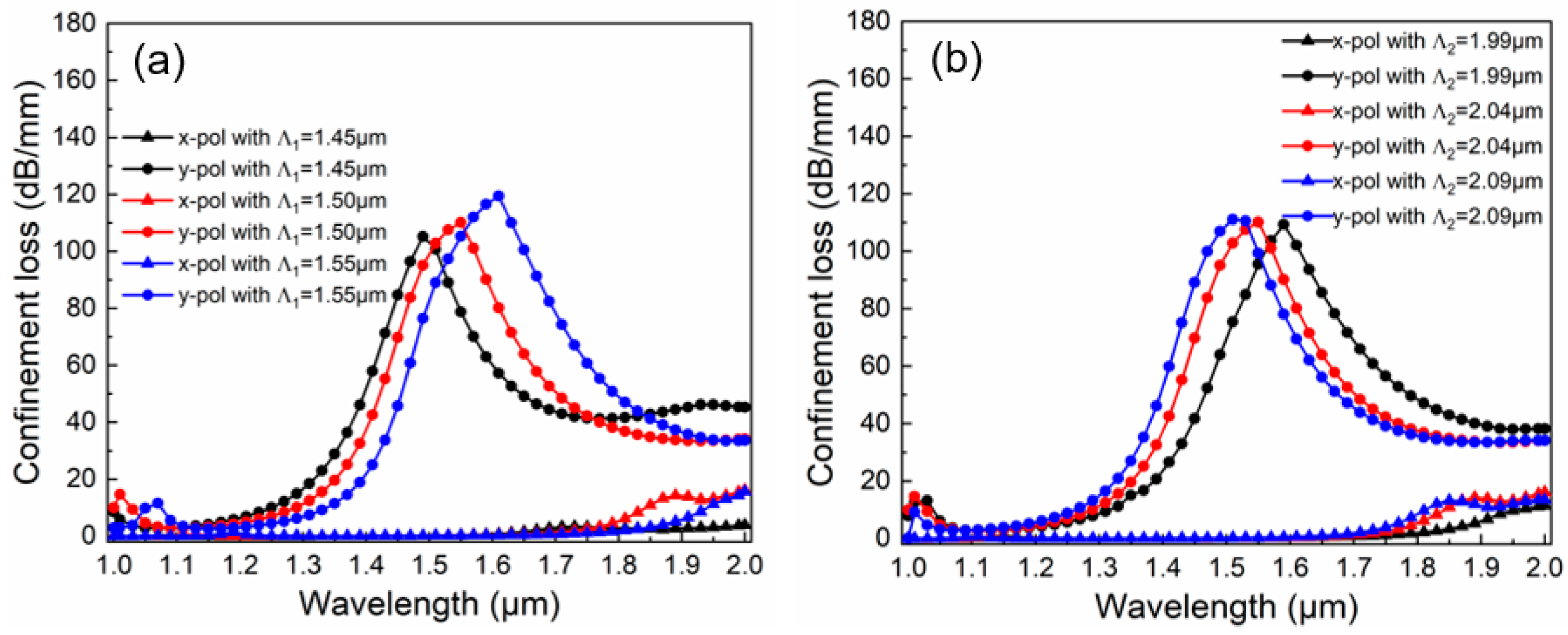
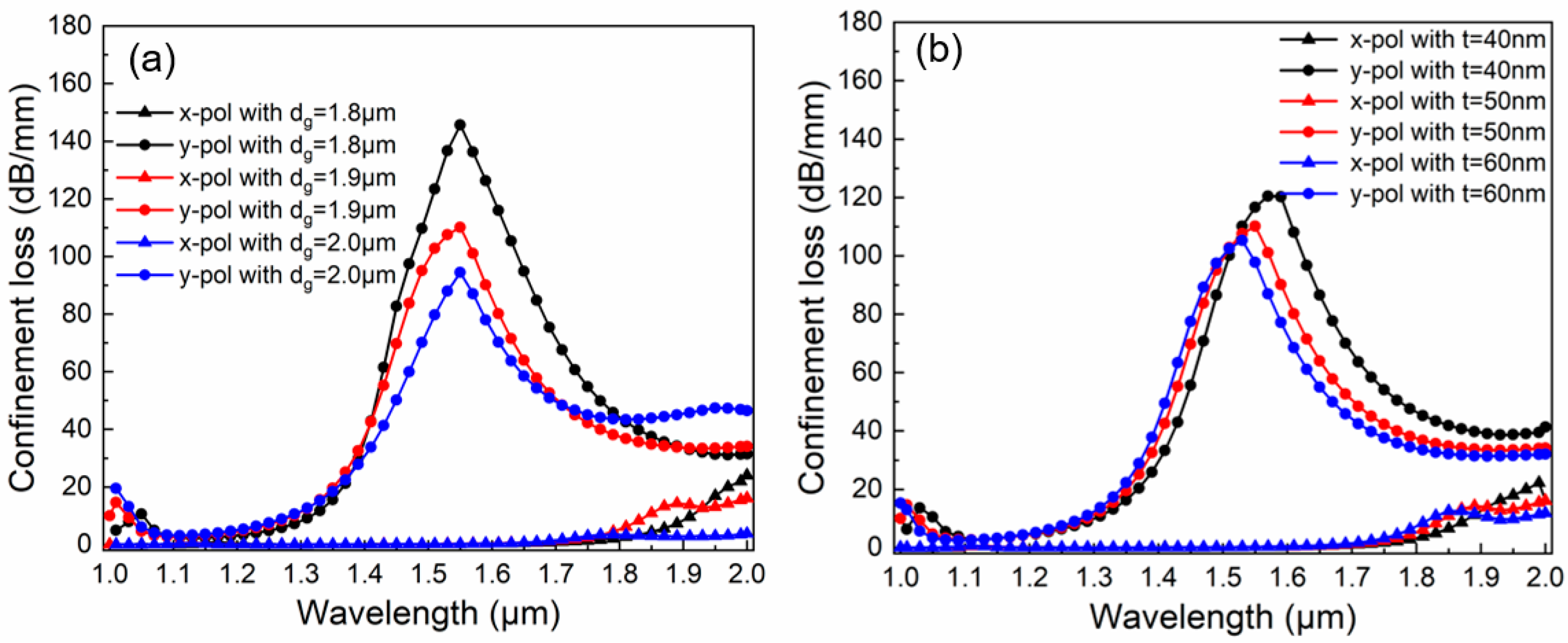
3.2. The Effect of Structural Parameters on Cl
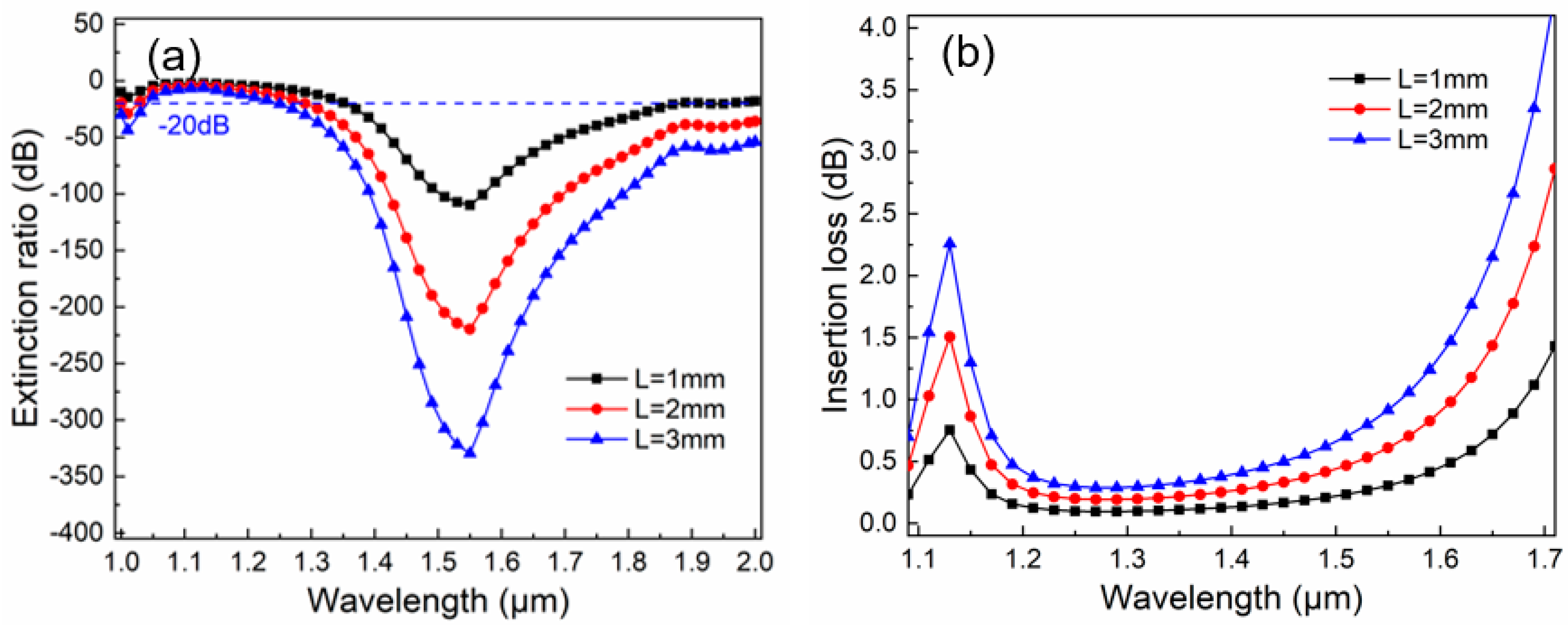
3.3. Filtering Performance Analysis
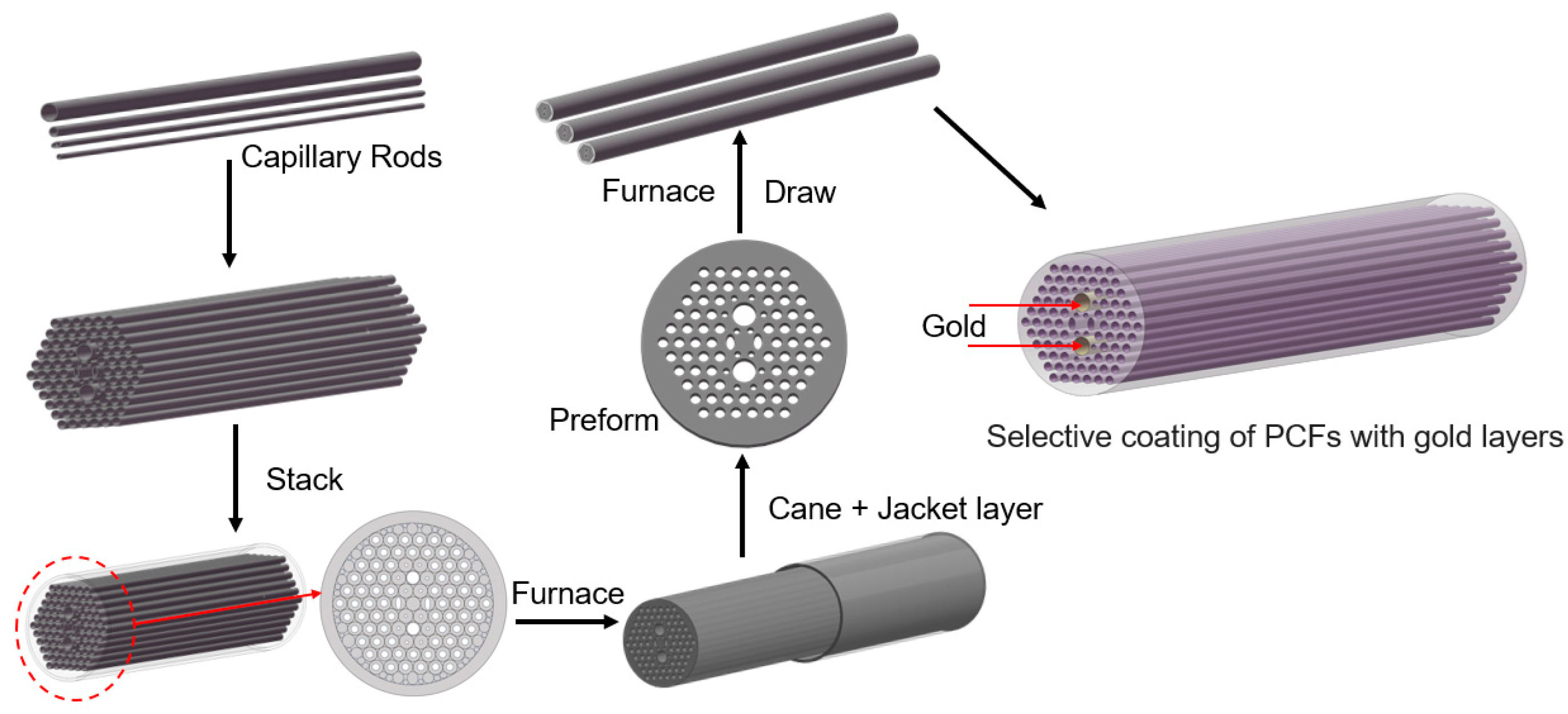
4. Fabrication Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Marom, D.M.; Miyamoto, Y.; Neilson, D.T.; Tomkos, I. Optical switching in future fiber-optic networks utilizing spectral and spatial degrees of freedom. Proc. IEEE 2022, 110, 1835–1852. [Google Scholar] [CrossRef]
- Wan, Z.; Shen, Y.; Wang, Z.; Shi, Z.; Liu, Q.; Fu, X. Divergence-degenerate spatial multiplexing towards future ultrahigh capacity, low error-rate optical communications. Light Sci. Appl. 2022, 11, 144. [Google Scholar] [CrossRef]
- Renaudier, J.; Napoli, A.; Ionescu, M.; Calo, C.; Fiol, G.; Mikhailov, V.; Forysiak, W.; Fontaine, N.; Polettiet, F.; Poggiolini, F. Devices and fibers for ultrawideband optical communications. Proc. IEEE 2022, 110, 1742–1759. [Google Scholar] [CrossRef]
- Wei, C.; Menyuk, C.R.; Hu, J. Polarization-filtering and polarization-maintaining low-loss negative curvature fibers. Opt. Express 2018, 26, 9528–9540. [Google Scholar] [CrossRef] [PubMed]
- Khonina, S.N.; Kazanskiy, N.L.; Butt, M.A.; Karpeev, S.V. Optical multiplexing techniques and their marriage for on-chip and optical fiber communication: A review. Opto-Electron. Adv. 2022, 5, 210127-1–210127-25. [Google Scholar] [CrossRef]
- Yu, F.; Di, K.; Chen, W.; Yan, S.; Yao, Y.; Chen, S.; Zhang, X.; Zhang, Y.; Zou, N.; Jiang, W. Time-wavelength multiplexed photonic neural network accelerator for distributed acoustic sensing systems. Adv. Photonics 2025, 7, 026008. [Google Scholar] [CrossRef]
- Maigyte, L.; Staliunas, K. Spatial filtering with photonic crystals. Appl. Phys. Rev. 2015, 2, 011102. [Google Scholar] [CrossRef]
- Klitis, C.; Cantarella, G.; Strain, M.J.; Sorel, M. High-extinction-ratio TE/TM selective Bragg grating filters on silicon-on-insulator. Opt. Lett. 2017, 42, 3040–3043. [Google Scholar] [CrossRef] [PubMed]
- Yang, W.; Chen, S.; Xue, Q.; Che, W.; Shen, G.; Feng, W. Novel filtering method based on metasurface antenna and its application for wideband high-gain filtering antenna with low profile. IEEE Trans. Antennas Propag. 2018, 67, 1535–1544. [Google Scholar] [CrossRef]
- Wang, W.; Zhu, G.; Liu, Q.; Li, X.; Sa, T.; Fang, X.; Zhu, H.; Wang, Y. Angle-and polarization-dependent spectral characteristics of circular grating filters. Opt. Express 2016, 24, 11033–11042. [Google Scholar] [CrossRef]
- Chen, N.; Xiao, Y.; Xu, Y.; Ding, X.; Chen, H.; Guo, W.; Wu, T.; Xu, Y.; Zhu, Y.; Liu, C. Numerical simulation of an in-fiber broadband plasmonic polarization filter using photonic crystal fiber with dual elliptical gold layers. Phys. Lett. A 2024, 520, 129733. [Google Scholar] [CrossRef]
- Bertoncini, A.; Liberale, C. 3D printed waveguides based on photonic crystal fiber designs for complex fiber-end photonic devices. Optica 2020, 7, 1487–1494. [Google Scholar] [CrossRef]
- Garcia-Vidal, F.J.; Fernández-Domínguez, A.I.; Martin-Moreno, L.; Zhang, H.C.; Tang, W.; Peng, R.; Cui, T.J. Spoof surface plasmon photonics. Rev. Mod. Phys. 2022, 94, 025004. [Google Scholar] [CrossRef]
- Chen, T.; Xin, J.; Chang, S.J.; Chen, C.J.; Liu, J.T. Surface plasmon resonance (SPR) combined technology: A powerful tool for investigating interface phenomena. Adv. Mater. Interfaces 2023, 10, 2202202. [Google Scholar] [CrossRef]
- Hu, L.; Li, J.; Yin, Z.; Zhang, Z.; Li, H.; Li, S.; Wang, P.; Du, H.; Wang, R. A cascade SPR sensor based on Ag/Au coated coreless optical fiber for RI and pH measurement. Opt. Laser Technol. 2025, 180, 111452. [Google Scholar] [CrossRef]
- Guo, P.; Du, H.; Li, J.; Yin, Z.; Li, Y.; Li, H.; Zhang, L.; Li, S. Study on SPR sensors modulated by ZnO films of different thicknesses for dual-parameter measurement of ocean salinity and temperature. Measurement 2025, 251, 117331. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, H.; Li, S.; Ma, M. Surface plasmon resonance induced tunable ultra-wideband polarization filters based on gold film coated photonic crystal fibers. Opt. Laser Technol. 2018, 107, 174–179. [Google Scholar] [CrossRef]
- Hossen, M.N.; Ferdous, M.; Ahmed, K.; Khalek, M.A.; Chakma, S.; Paul, B.K. Single polarization photonic crystal fiber filter based on surface plasmon resonance. Front. Optoelectron. 2019, 12, 157–164. [Google Scholar] [CrossRef]
- Yan, X.; Guo, Z.; Cheng, T.; Li, S. A novel gold-coated PCF polarization filter based on surface plasmon resonance. Opt. Laser Technol. 2020, 126, 106125. [Google Scholar] [CrossRef]
- Jiang, L.; Wang, C.; Zou, J.; Zhang, Y.; Qi, Y.; Wang, W.; Hou, L. Design of two miniaturized and broadband polarization filters based on two types of square-lattice gold-filled photonic crystal fibers. Opt. Fiber Technol. 2021, 61, 102454. [Google Scholar] [CrossRef]
- Wang, Y.; Li, S.; Li, J.; Chen, H. High-sensitivity refractive index sensing and broadband tunable polarization filtering characteristics of D-shaped micro-structured fiber with single-layer air-holes and gold film based on SPR. J. Light. Technol. 2022, 40, 863–871. [Google Scholar] [CrossRef]
- Zhang, S.; Zhou, H.; Bai, Y.; Xue, L.; Guo, B.; Yan, W.; Li, B. Design of a broadband dual-cladding PCF polarization filter via triple surface plasmon resonance effects. Opt. Commun. 2023, 546, 129770. [Google Scholar] [CrossRef]
- Ullah, S.; Chen, H.; Gao, Z.; Li, Z.; Guo, P.; Wang, C.; Li, S. Dual-side polished surface plasmon resonance-based photonic crystal fiber for refractive index sensing and polarization filtering. Plasmonics 2024, 19, 2615–2625. [Google Scholar] [CrossRef]
- Zhang, Z.; Guo, H.; Li, J.; Zhao, Y.; Li, S.; Xu, Y.; Chang, Y.; Zhang, H. Chalcogenide dual-core all-solid anti-resonant fiber polarization beam splitter operating at 3 μm band. Phys. Scr. 2025, 100, 025511. [Google Scholar] [CrossRef]
- Wu, X.; Wu, T.; Chen, N.; Xu, Y.; Yang, F.; Chen, H.; Tao, C. Numerical simulation of in-fiber plasmonic polarization filter using silicon hollow-core anti-resonant fiber with dual aluminum wires. Appl. Phys. B. 2025, 131, 27. [Google Scholar] [CrossRef]
- Bykov, D.S.; Xie, S.; Zeltner, R.; Machnev, A.; Wong, G.K.; Euser, T.G.; Russell, P.S.J. Long-range optical trapping and binding of microparticles in hollow-core photonic crystal fibre. Light Sci. Appl. 2018, 7, 22. [Google Scholar] [CrossRef]
- Chen, N.; Feng, Y.; Ren, Z.; Ding, X.; Cao, S.; Xu, Y.; Song, M. Mid-infrared broadband in-fiber polarization beam splitter based on dual core photonic crystal fiber with dual aluminum wires. Opt. Commun. 2025, 586, 131920. [Google Scholar] [CrossRef]
- Hameed, M.F.O.; Obayya, S.S.A.; Wiltshire, R.J. Beam propagation analysis of polarization rotation in soft glass nematic liquid crystal photonic crystal fibers. IEEE Photonics Technol. Lett. 2010, 22, 188–190. [Google Scholar] [CrossRef]
- Liu, Q.; Ma, Z.; Wu, Q.; Wang, W. The biochemical sensor based on liquid-core photonic crystal fiber filled with gold, silver and aluminum. Opt. Laser Technol. 2020, 130, 106363. [Google Scholar] [CrossRef]
- Rakić, A.D.; Djurišić, A.B.; Elazar, J.M.; Majewski, M.L. Optical properties of metallic films for vertical-cavity optoelectronic devices. Appl. Opt. 1998, 37, 5271–5283. [Google Scholar] [CrossRef] [PubMed]
- Olmon, R.L.; Slovick, B.; Johnson, T.W.; Shelton, D.; Oh, S.H.; Boreman, G.D.; Raschke, M.B. Optical dielectric function of gold. Phys. Rev. B—Condens. Matter Mater. Phys. 2012, 86, 235147. [Google Scholar] [CrossRef]
- Xue, J.; Li, S.; Xiao, Y.; Qin, W.; Xin, X.; Zhu, X. Polarization filter characters of the gold-coated and the liquid filled photonic crystal fiber based on surface plasmon resonance. Opt. Express 2013, 21, 13733–13740. [Google Scholar] [CrossRef]
- Wu, X.; Wu, T.; Chen, N.; Ding, X.; Chen, H.; Cao, S.; Xu, Y. Numerical simulation of surface plasmon resonance polarization filter using hollow core anti-resonance fiber with dual graphene-coated aluminum wires. Plasmonics 2025, 20, 4053–4065. [Google Scholar] [CrossRef]
- Li, L.; Xiao, L. Plasmonic nodeless hollow-core photonic crystal fibers for in-fiber polarizers. J. Light. Technol. 2019, 37, 5199–5211. [Google Scholar] [CrossRef]
- Hui, Z.; Qiu, Z.; Zhao, Y.; Han, D.; Li, T.; Miao, K.; Soliman, A.H. Broadband dual channel mode filter based on triple-core photonic crystal fiber. Opt. Fiber Technol. 2025, 93, 104232. [Google Scholar] [CrossRef]
- Tuniz, A.; Song, A.Y.; Della Valle, G.; de Sterke, C.M. Coupled mode theory for plasmonic couplers. Appl. Phys. Rev. 2024, 11, 021309. [Google Scholar] [CrossRef]
- Huang, W.P.; Mu, J. Complex coupled-mode theory for optical waveguides. Opt. Express 2009, 17, 19134–19152. [Google Scholar] [CrossRef]
- Fan, Z.; Li, S.; Liu, Q.; An, G.; Chen, H.; Li, G.; Chao, D.; Li, H.; Zi, J.; Tian, W. High sensitivity of refractive index sensor based on analyte-filled photonic crystal fiber with surface plasmon resonance. IEEE Photonics J. 2015, 7, 4800809. [Google Scholar] [CrossRef]
- Yu, Y.L.; Kishikawa, H.; Liaw, S.K.; Adiya, M.; Goto, N. Broadband silicon core photonics crystal fiber polarization filter based on surface plasmon resonance effect. Opt. Commun. 2021, 482, 126587. [Google Scholar] [CrossRef]
- Wu, J.; Wang, Y.; Liu, M.; Ma, Y.; Wang, C. Six high-performance photonic crystal fiber polarization filters based on surface plasmon resonance. Opt. Quantum Electron. 2023, 55, 886. [Google Scholar] [CrossRef]
- Chen, N.; Guo, L.; Xu, Y.; Huang, Y.; Ding, X.; Xu, Y.; Wang, L.; Liu, C.; Wu, T.; Zhu, Y.; et al. Design and simulation of a compact plasmonic photonic crystal fiber filter with wide band and high extinction ratio. Opt. Commun. 2024, 565, 130690. [Google Scholar] [CrossRef]
- Wang, J.; Pei, L.; Li, Z.; Hu, K.; Xu, L. Wavelength-switchable polarization filter based on graphene-coated d-shaped photonic crystal fiber. Plasmonics 2024, 19, 2363–2370. [Google Scholar] [CrossRef]
- Ying, Y.; Ge, H.; Si, G.; Gao, Z. Characteristics study of a dual-wavelength polarization filter based on gold-filled square lattice photonic crystal fiber. Appl. Opt. 2024, 63, 7598–7607. [Google Scholar] [CrossRef]
- Chen, N.; Zhu, Y.; Ding, X.; Chen, H.; Cao, S.; Xu, Y.; Wu, T. Broadband and high-extinction plasmonic polarization filter using photonic crystal fiber with dual elliptical graphene-coated silver layers. Phys. Lett. A. 2025, 533, 130706. [Google Scholar] [CrossRef]
- Jing, Y.; Du, J.; Hua, J.; Li, X.; Li, J.; Li, S. Polarization filter of hollow-core anti-resonant fiber in the 1550 nm band based on SPR effect. Opt. Laser Technol. 2025, 180, 111407. [Google Scholar] [CrossRef]
- Chen, N.; Zhang, X.; Chang, M.; Lu, X.; Zhou, J. Broadband plasmonic polarization filter based on photonic crystal fiber with dual-ring gold layer. Micromachines 2020, 11, 470. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, G.; Wu, Z.; Zhang, Y.; Zhang, Y.; Jiang, L.; Bi, W. A broadband gold-coated photonic crystal fiber polarization filter with a high loss ratio of both polarizations at 1550 and 1310 nm. Photonics 2021, 8, 488. [Google Scholar] [CrossRef]
- Pysz, D.; Kujawa, I.; Stępień, R.; Klimczak, M.; Filipkowski, A.; Franczyk, M.; Kociszewski, L.; Buźniak, J.; Haraśny, K.; Buczyński, R. Stack and draw fabrication of soft glass microstructured fiber optics. Bull. Pol. Acad. Sci. Tech. Sci. 2014, 62, 667–682. [Google Scholar] [CrossRef]
- Xu, B.; Shen, H.; Wu, D.; Wang, N.; Liu, Y.; Lin, X.; Yu, F. Study of microbubble defects in high-NA silicate-glass multi-core imaging fibers fabricated by the stack-and-draw method. Opt. Express 2025, 33, 18225–18234. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Wang, R.; Cox, F.M.; Kuhlmey, B.T.; Large, M.C.J. Selective coating of holes in microstructured optical fiber and its application to in-fiber absorptive polarizers. Opt. Express 2007, 15, 16270–16278. [Google Scholar] [CrossRef]
- Chen, N.; Guo, W.; Chen, H.; Ding, X.; Yang, F.; Zhu, Y.; Song, M.; Xu, Y. Multifunctional in-fiber polarization beam splitter using liquid crystal infiltrated dual-core photonic crystal fiber with gold layers and its temperature sensing characteristic. Opt. Laser Technol. 2025, 191, 113350. [Google Scholar] [CrossRef]
- Bala, A.; Chowdhury, K.R.; Mia, M.B.; Faisal, M. Highly birefringent, highly negative dispersion compensating photonic crystal fiber. Appl. Opt. 2017, 56, 7256–7261. [Google Scholar] [CrossRef]
- Xiao, L.; Demokan, M.S.; Jin, W.; Wang, Y.; Zhao, C.L. Fusion splicing photonic crystal fibers and conventional single-mode fibers: Microhole collapse effect. J. Light. Technol. 2007, 25, 3563–3574. [Google Scholar] [CrossRef]
- Azman, M.F.; Mahdiraji, G.A.; Wong, W.R.; Aoni, R.A.; Mahamd Adikan, F.R. Design and fabrication of copper-filled photonic crystal fiber based polarization filters. Appl. Opt. 2019, 58, 2068–2075. [Google Scholar] [CrossRef] [PubMed]
- Wu, M.; Li, B.; Li, J.; Zhou, G. Research on fabrication and performance of hollow-core anti-resonant fiber coated with copper film. IEEE Photonics J. 2019, 12, 7101708. [Google Scholar] [CrossRef]
| Parameter | ωp | m | f0 | Γ0 | ƒ1 | Γ1 | ω1 | ƒ2 | Γ2 | ω2 |
| Value | 12.84 | 5 | 0.760 | 0.053 | 0.024 | 0.241 | 0.415 | 0.010 | 0.345 | 0.830 |
| Parameter | ƒ3 | Γ3 | ω3 | ƒ4 | Γ4 | ω4 | ƒ5 | Γ5 | ω5 | |
| Value | 0.071 | 0.870 | 2.969 | 0.601 | 2.494 | 4.304 | 4.384 | 2.214 | 13.32 |
| Strut. Para. | Δλres (μm) | ΔER (dB) | ΔBW (nm) | ΔIL (dB) |
|---|---|---|---|---|
| d1 + 0.1 μm | +0.02 | −6.4 | +10 | −0.02 |
| d1 − 0.1 μm | −0.02 | +5.7 | −140 | +0.09 |
| d2 + 0.1 μm | +0.08 | −12.3 | +10 | −0.06 |
| d2 − 0.1 μm | −0.10 | +27.4 | +10 | +0.03 |
| dg + 0.1 μm | 0 | +35.5 | 0 | +0.18 |
| dg − 0.1 μm | 0 | −15.7 | −100 | −0.2 |
| a + 0.1 μm | 0 | +0.3 | 0 | 0 |
| a − 0.1 μm | 0 | −0.6 | 0 | 0 |
| b + 0.1 μm | +0.02 | −4.2 | −70 | −0.18 |
| b − 0.1 μm | −0.02 | +3.4 | +10 | +0.16 |
| Λ1 + 0.05 μm | −0.06 | −4.9 | −50 | +0.16 |
| Λ1 − 0.05 μm | +0.06 | +9.1 | +40 | −0.1 |
| Λ2 + 0.05 μm | +0.04 | −1.0 | +30 | +0.14 |
| Λ2 − 0.05 μm | −0.04 | +0.9 | −30 | −0.17 |
| t + 10 nm | +0.02 | +10.2 | −130 | +0.14 |
| t − 10 nm | −0.02 | −4.9 | −40 | −0.19 |
| Ref. | Res. Wave. (µm) | Length (mm) | Max. ER (dB) | BW (nm) | IL (dB) |
|---|---|---|---|---|---|
| [39] | 1.887 | 1 | / | 1552 | / |
| [40] | 1.55 | 2 | 4520 | / | / |
| [41] | 1.56 | 1 | 133 | >800 | 0.59 |
| [42] | 1.06 | 0.1 | >25 | 400 | / |
| [43] | 1.31/1.55 | 0.5 | 588.2/370.6 | 640 | / |
| [44] | 1.31 | 0.4 | 249.1 | >880 | / |
| [45] | 1.55 | 6 | 734 | 390 | / |
| [46] | 1.25 | 2 | 478 | 750 | ~0.48 |
| This work | 1.55 | 1 | 109.9 | 620 | 0.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, N.; Zhao, M.; Zhu, Y.; Gao, L.; Lu, C.; Sun, X.; Ding, X.; Wang, X. Design and Simulation of a Simple-Structure and High-Performance Plasmonic Polarization Filter Based on Gold Layers Deposited on Photonic Crystal Fiber. Micromachines 2025, 16, 1088. https://doi.org/10.3390/mi16101088
Chen N, Zhao M, Zhu Y, Gao L, Lu C, Sun X, Ding X, Wang X. Design and Simulation of a Simple-Structure and High-Performance Plasmonic Polarization Filter Based on Gold Layers Deposited on Photonic Crystal Fiber. Micromachines. 2025; 16(10):1088. https://doi.org/10.3390/mi16101088
Chicago/Turabian StyleChen, Nan, Ming Zhao, Yuxin Zhu, Leilei Gao, Cheng Lu, Xingjian Sun, Xin Ding, and Xianping Wang. 2025. "Design and Simulation of a Simple-Structure and High-Performance Plasmonic Polarization Filter Based on Gold Layers Deposited on Photonic Crystal Fiber" Micromachines 16, no. 10: 1088. https://doi.org/10.3390/mi16101088
APA StyleChen, N., Zhao, M., Zhu, Y., Gao, L., Lu, C., Sun, X., Ding, X., & Wang, X. (2025). Design and Simulation of a Simple-Structure and High-Performance Plasmonic Polarization Filter Based on Gold Layers Deposited on Photonic Crystal Fiber. Micromachines, 16(10), 1088. https://doi.org/10.3390/mi16101088






