Impact of Vein Wall Hyperelasticity and Blood Flow Turbulence on Hemodynamic Parameters in the Inferior Vena Cava with a Filter
Abstract
1. Introduction
2. Methods
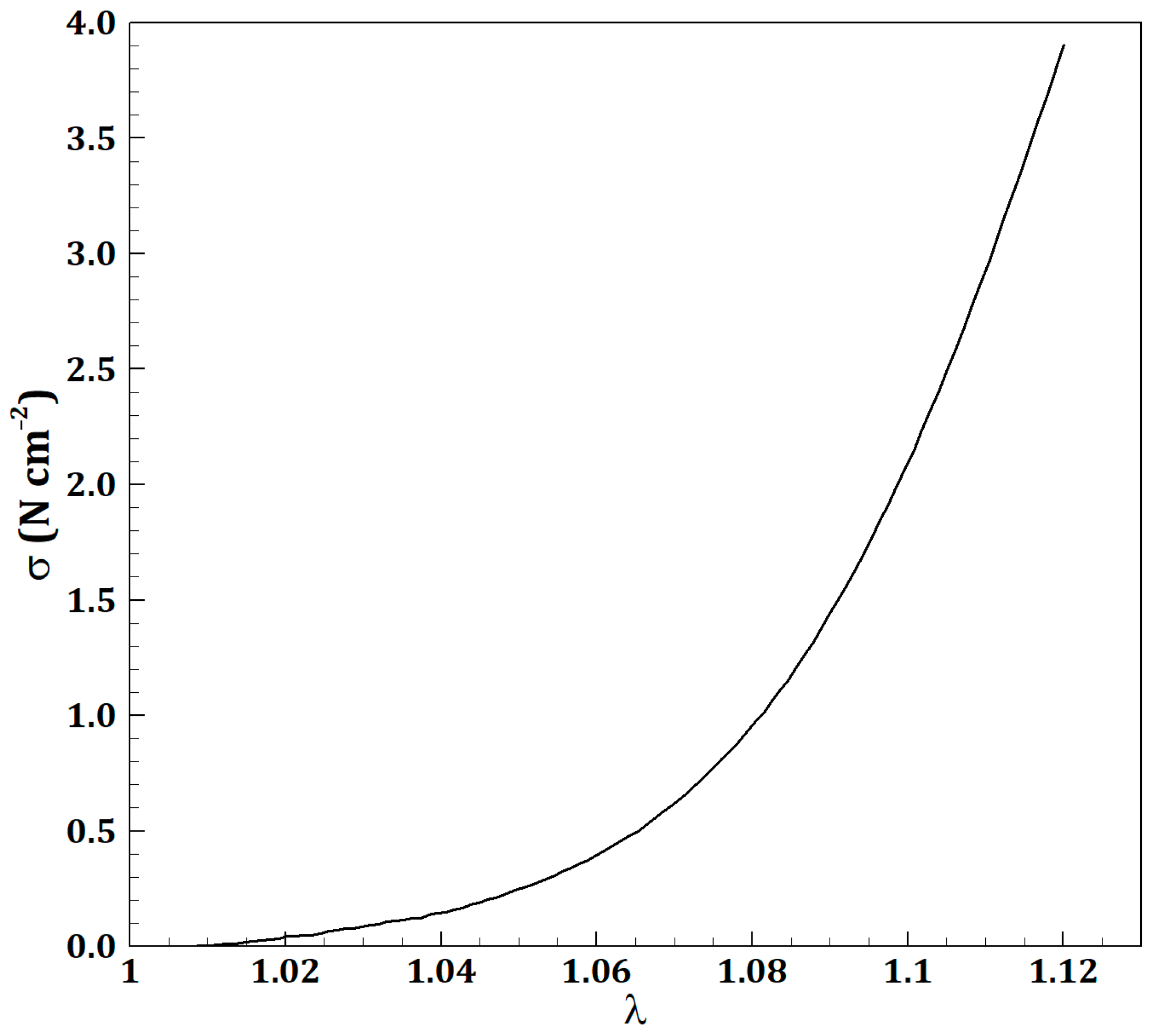
2.1. Governing Equations
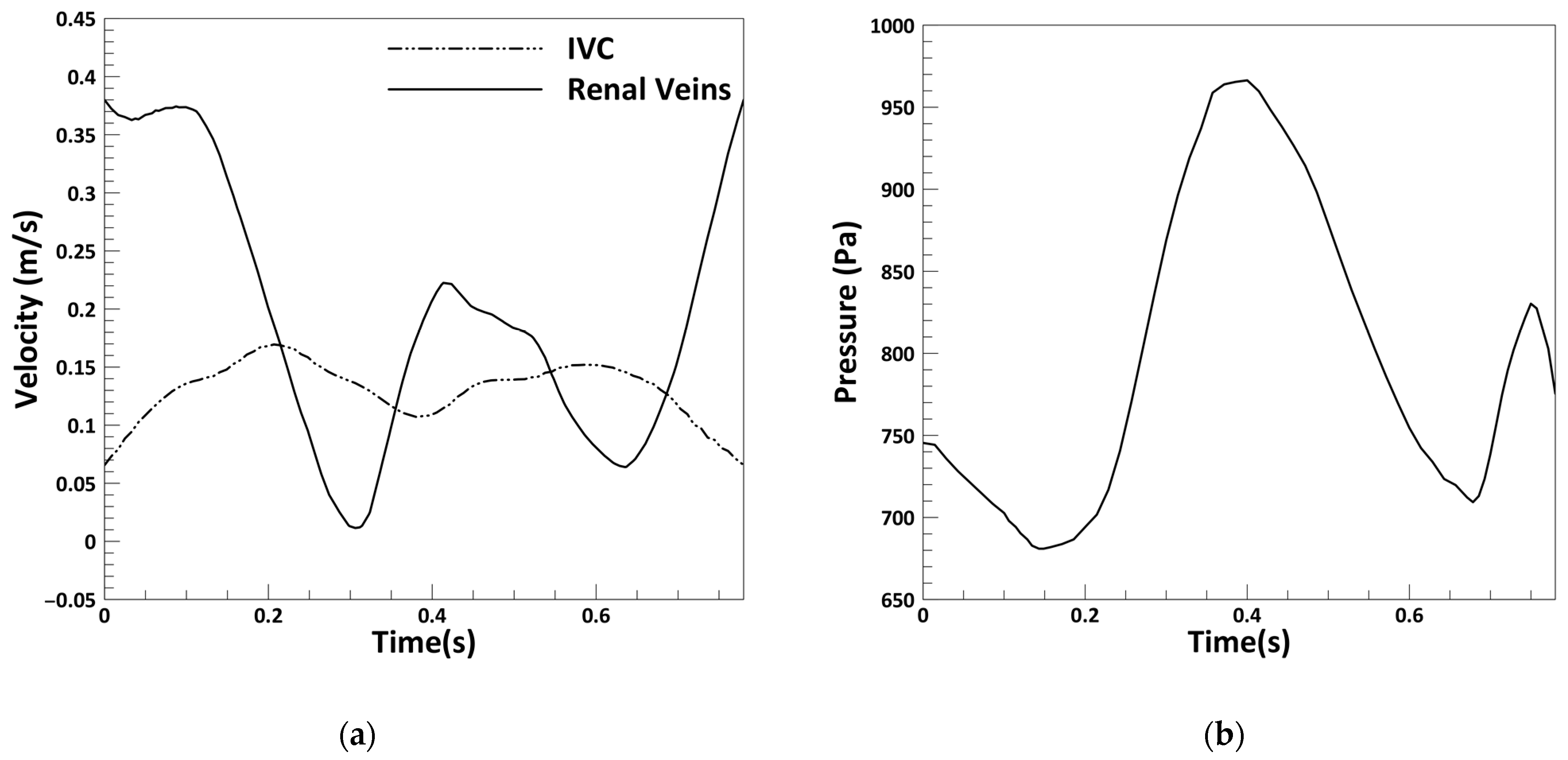
2.2. Problem Statement
2.3. Hemodynamic Parameters
3. Results
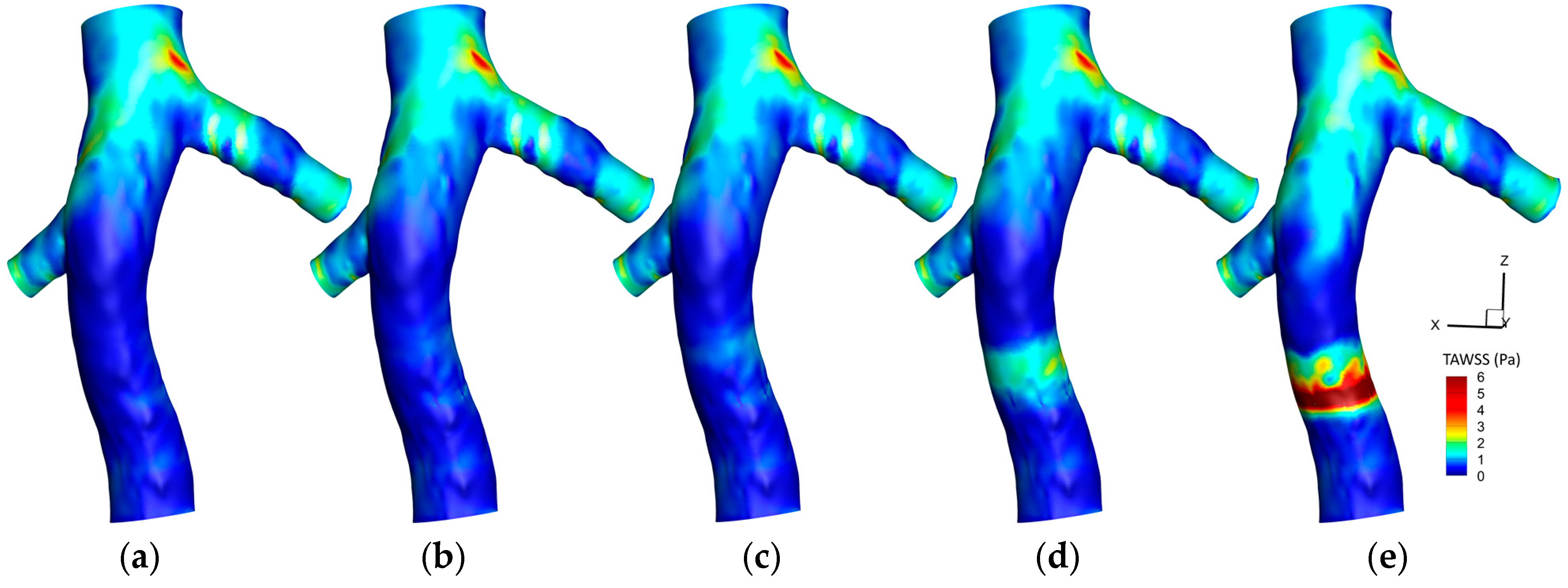
3.1. The Effect of Hyperelasticity
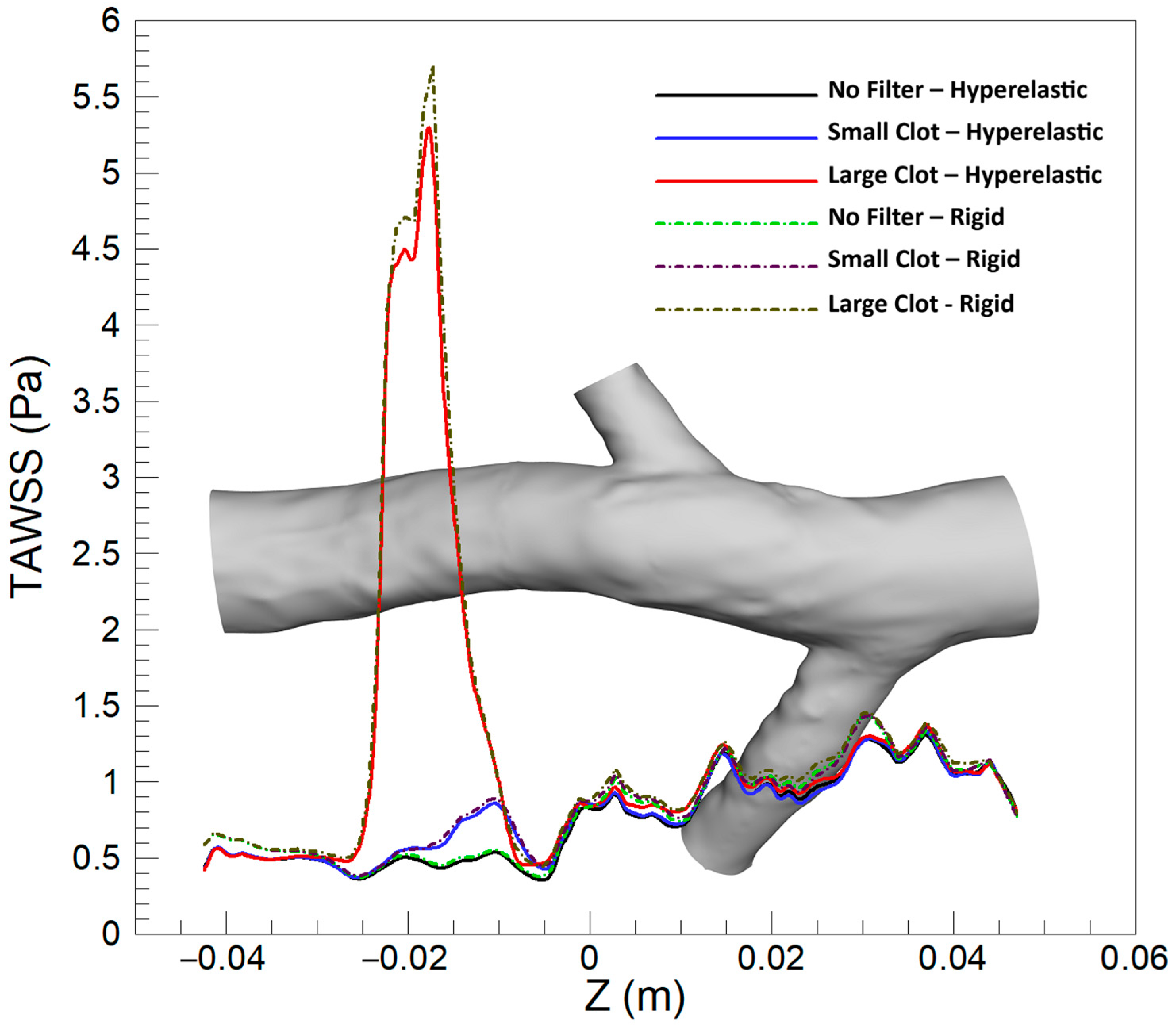
3.1.1. Time-Averaged Wall Shear Stress (TAWSS)
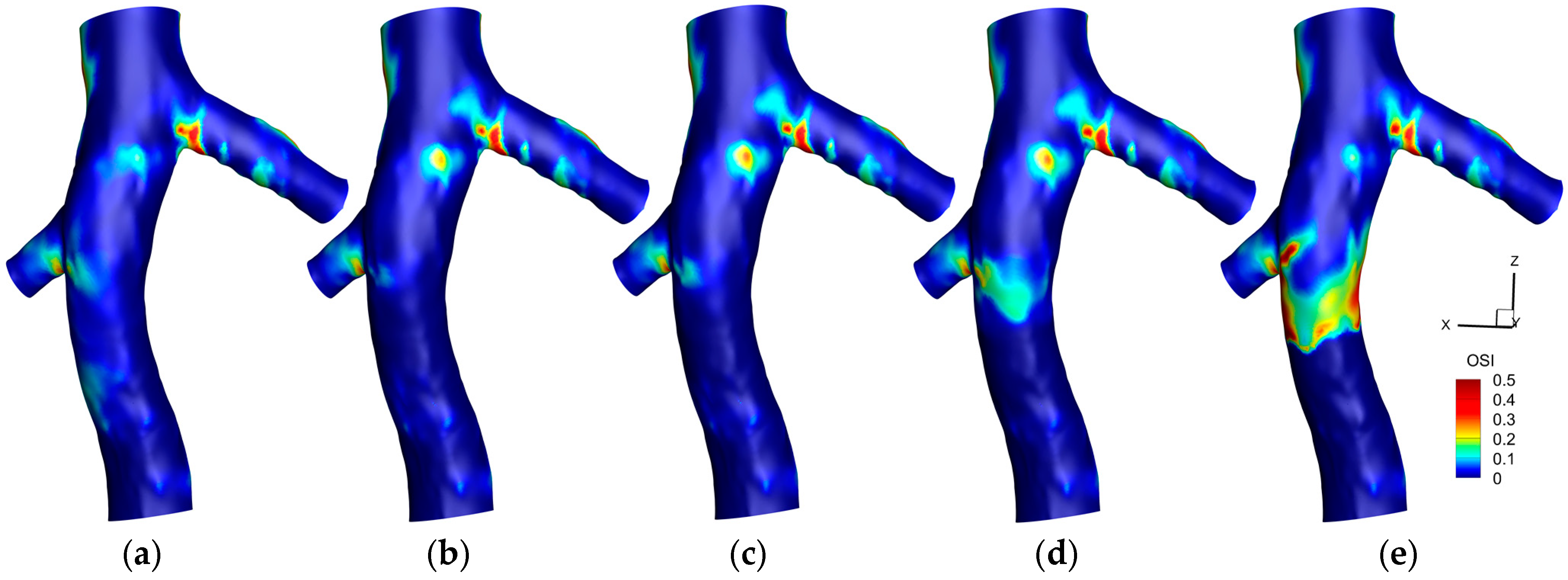
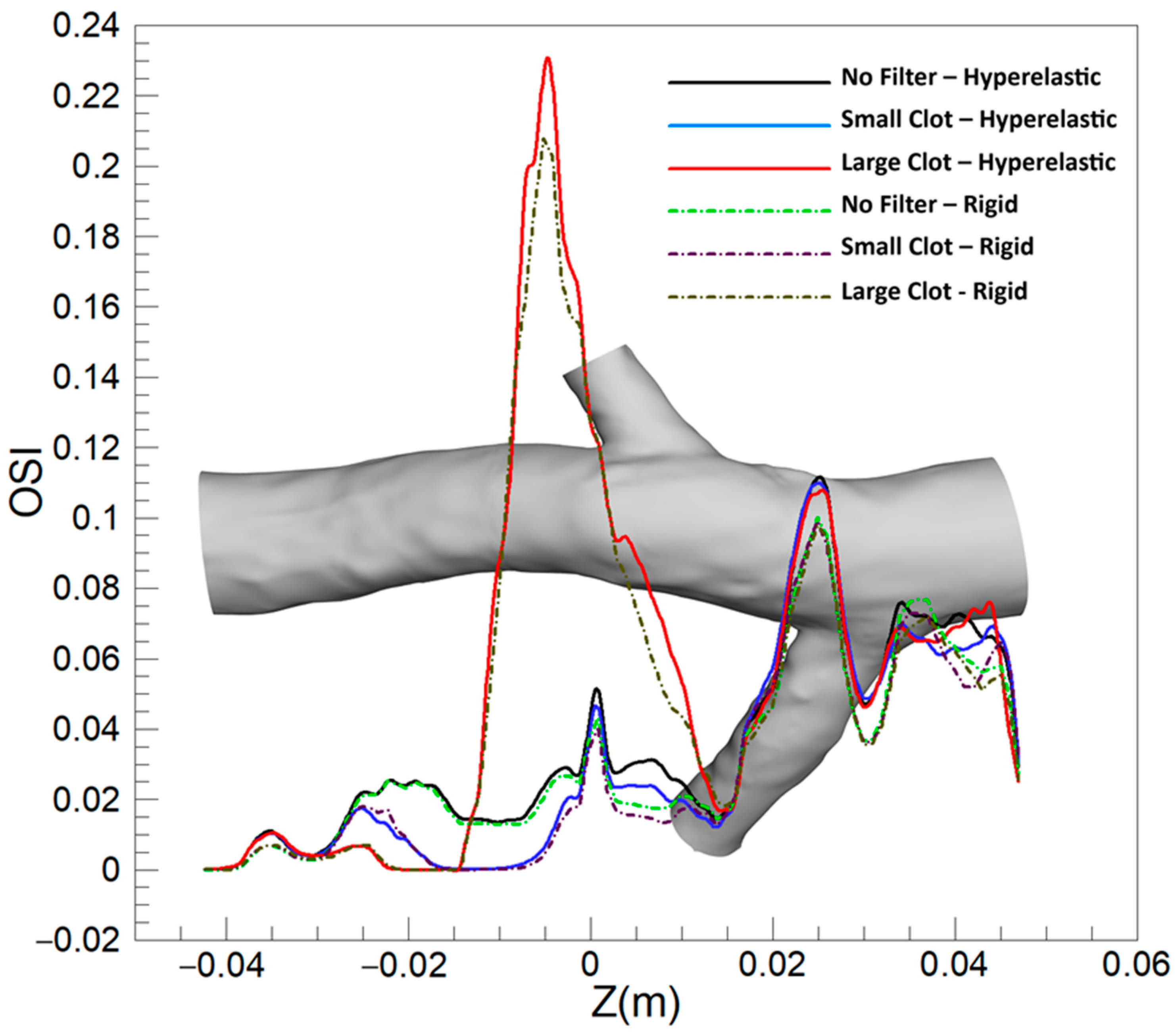
3.1.2. Oscillating Shear Index (OSI)
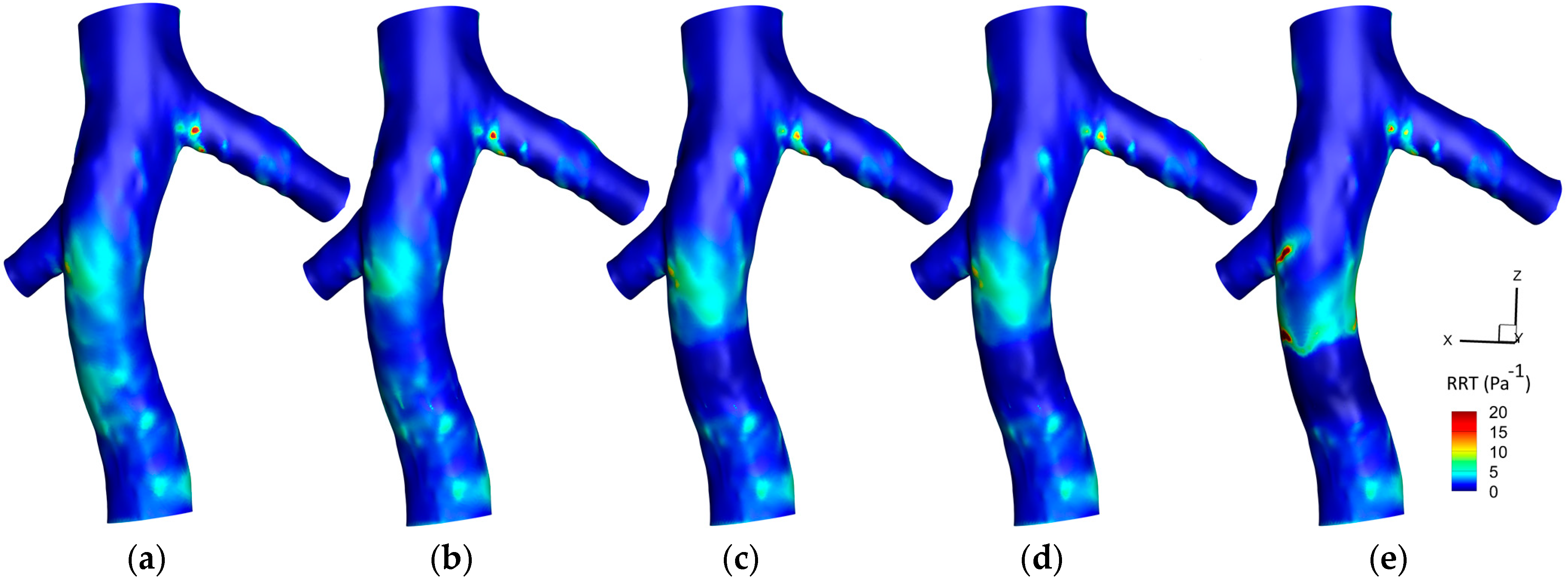
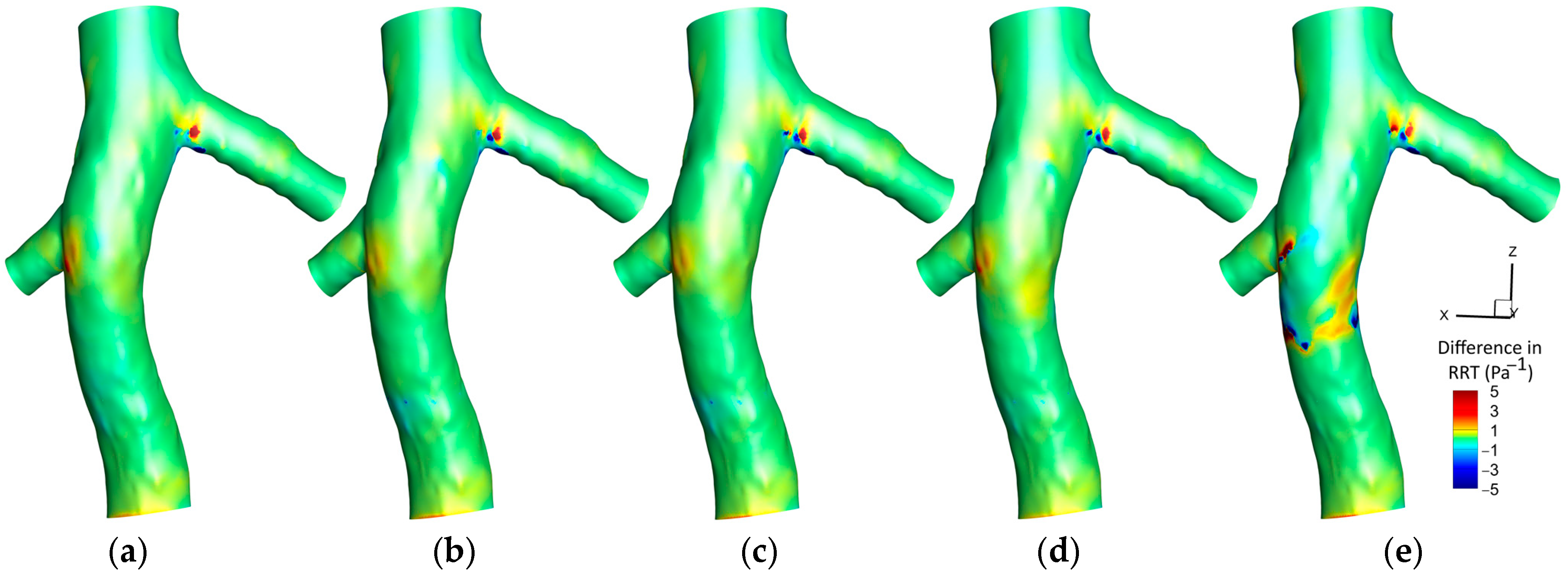
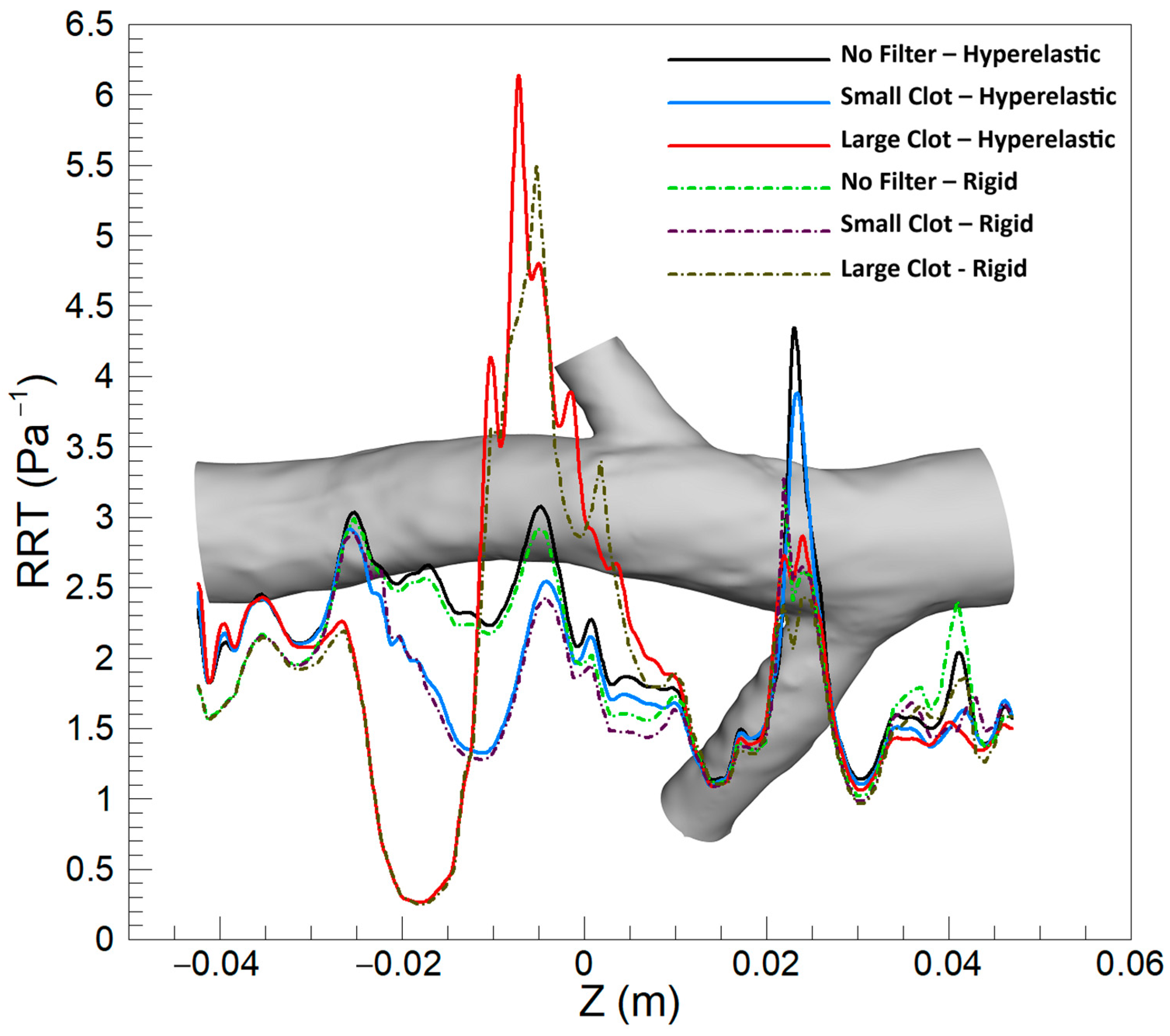
3.1.3. Relative Residence Time (RRT)
3.2. The Effect of Turbulence
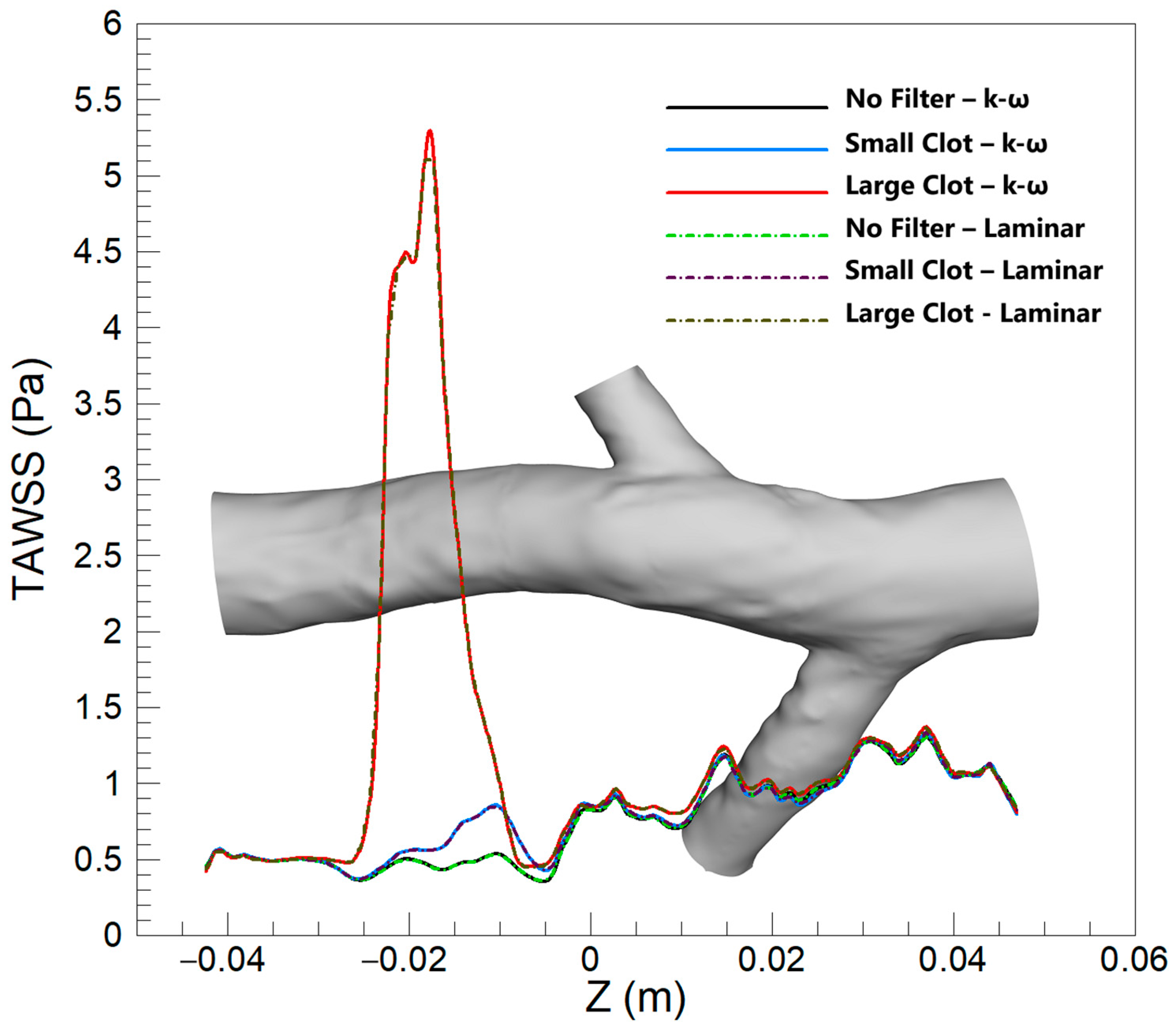
3.2.1. TAWSS
3.2.2. OSI
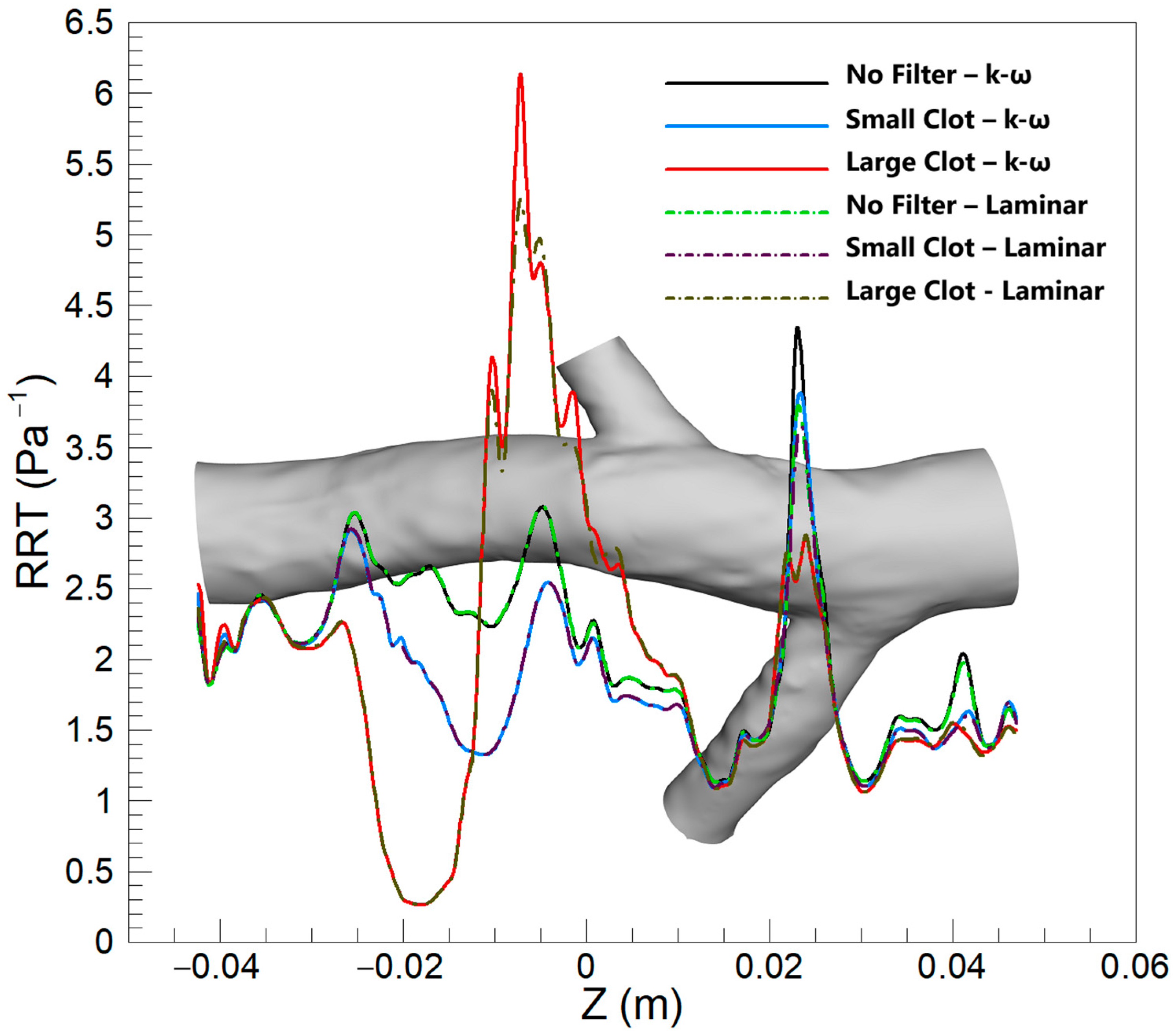
3.2.3. RRT
3.3. Mean Values in Critical Areas
4. Discussion
4.1. TAWSS
4.2. OSI
4.3. RRT
5. Conclusions
- The inclusion of hyperelasticity in the vein wall model significantly impacts the distribution and magnitude of hemodynamic parameters, such as TAWSS, OSI, and RRT.
- The presence of a filter and the size of the captured clot notably influence these parameters, with larger clots causing pronounced changes in flow dynamics.
- The rigid wall model, while generally effective, fails to capture the nuanced hemodynamic environment in scenarios with a substantial vessel deformation, particularly in the presence of large clots.
- The laminar flow assumption is valid for cases with empty filters and for small to moderate-sized clots. However, its accuracy diminishes in scenarios involving large clots.
- The turbulence model introduces subtle differences in hemodynamic parameters, which become increasingly evident and clinically significant in cases with larger clots.
6. Limitations
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Goldhaber, S.Z. Pulmonary embolism. Lancet 2004, 363, 1295–1305. [Google Scholar] [CrossRef] [PubMed]
- Konstantinides, S.V.; Meyer, G.; Becattini, C.; Bueno, H.; Geersing, G.J.; Harjola, V.P.; Huisman, M.V.; Humbert, M.; Jennings, C.S.; Jiménez, D.; et al. 2019 ESC Guidelines for the diagnosis and management of acute pulmonary embolism developed in collaboration with the European Respiratory Society (ERS). Eur. Heart J. 2020, 41, 543–603. [Google Scholar] [CrossRef] [PubMed]
- Heit, J.A. Epidemiology of venous thromboembolism. Nat. Rev. Cardiol. 2015, 12, 464–474. [Google Scholar] [CrossRef]
- Cushman, M. Epidemiology and risk factors for venous thrombosis. Semin. Hematol. 2007, 44, 62–69. [Google Scholar] [CrossRef] [PubMed]
- Jaff, M.R.; McMurtry, M.S.; Archer, S.L.; Cushman, M.; Goldenberg, N.; Goldhaber, S.Z.; Jenkins, J.S.; Kline, J.A.; Michaels, A.D.; Thistlethwaite, P.; et al. Management of massive and submassive pulmonary embolism, iliofemoral deep vein thrombosis, and chronic thromboembolic pulmonary hypertension: A scientific statement from the American Heart Association. Circulation 2011, 123, 1788–1830. [Google Scholar] [CrossRef]
- Angel, L.F.; Tapson, V.; Galgon, R.E.; Restrepo, M.I.; Kaufman, J. Systematic review of the use of retrievable inferior vena cava filters. J. Vasc. Interv. Radiol. 2011, 22, 1522–1530.e3. [Google Scholar] [CrossRef] [PubMed]
- Harlal, A.; Ojha, M.; Johnston, K.W. Vena cava filter performance based on hemodynamics and reported thrombosis and pulmonary embolism patterns. J. Vasc. Interv. Radiol. 2007, 18, 103–115. [Google Scholar] [CrossRef]
- Zhang, F.; Li, D.; Liu, J.; Zhang, H. The vena tech LP permanent caval filter: Effectiveness and safety in the clinical setting in three chinese medical centers. Thromb. Res. 2015, 136, 40–44. [Google Scholar] [CrossRef]
- Decousus, H.; Leizorovicz, A.; Parent, F.; Page, Y.; Tardy, B.; Girard, P.; Laporte, S.; Faivre, R.; Charbonnier, B.; Barral, F.-G. A clinical trial of vena caval filters in the prevention of pulmonary embolism in patients with proximal deep-vein thrombosis. N. Engl. J. Med. 1998, 338, 409–416. [Google Scholar] [CrossRef] [PubMed]
- Moradicheghamahi, J.; Qasim, M.; Jafarpour, S.; Farokhi, H. Investigation of the Effects of an Inferior Vena Cava Filter and Captured Clot Size on the Hemodynamic Parameters in Non-Newtonian Turbulent Pulsatile Blood Flow. Appl. Bionics Biomech. 2023, 2023, 2439775. [Google Scholar] [CrossRef]
- Moradicheghamahi, J.; Jahangiri, M.; Mousaviraad, M.; Sadeghi, M.R. Computational studies of comparative and cumulative effects of turbulence, fluid–structure interactions, and uniform magnetic fields on pulsatile non-Newtonian flow in a patient-specific carotid artery. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 518. [Google Scholar] [CrossRef]
- Ku, D.N. Blood flow in arteries. Annu. Rev. Fluid. Mech. 1997, 29, 399–434. [Google Scholar] [CrossRef]
- López, J.M.; Fortuny, G.; Puigjaner, D.; Herrero, J.; Marimon, F. Hemodynamic effects of blood clots trapped by an inferior vena cava filter. Int. J. Numer. Methods Biomed. Eng. 2020, 36, e3343. [Google Scholar] [CrossRef]
- López, J.M.; Fortuny, G.; Puigjaner, D.; Herrero, J.; Marimon, F. A comparative CFD study of four inferior vena cava filters. Int. J. Numer. Methods Biomed. Eng. 2018, 34, e2990. [Google Scholar] [CrossRef] [PubMed]
- Bluestein, D. Research approaches for studying flow-induced thromboembolic complications in blood recirculating devices. Expert. Rev. Med. Devices 2004, 1, 65–80. [Google Scholar] [CrossRef] [PubMed]
- Leask, R.L.; Johnston, K.W.; Ojha, M. Hemodynamic effects of clot entrapment in the TrapEase inferior vena cava filter. J. Vasc. Interv. Radiol. 2004, 15, 485–490. [Google Scholar] [CrossRef] [PubMed]
- Rahbar, E.; Mori, D.; Moore, J.E., Jr. Three-dimensional analysis of flow disturbances caused by clots in inferior vena cava filters. J. Vasc. Interv. Radiol. 2011, 22, 835–842. [Google Scholar] [CrossRef]
- Stein, P.D.; Sabbah, H.N. Measured turbulence and its effect on thrombus formation. Circ. Res. 1974, 35, 608–614. [Google Scholar] [CrossRef]
- Moradicheghamahi, J. The Role of Wall Mechanics in the Hemodynamics of a Realistic Abdominal Aortic Aneurysm: A Fluid-Structure Interaction Study. J. Eng. 2024, 2024, 3280563. [Google Scholar] [CrossRef]
- Algabri, Y.A.; Altwijri, O.; Chatpun, S. Visualization of Blood Flow in AAA Patient-Specific Geometry: 3-D Reconstruction and Simulation Procedures. Bionanoscience 2019, 9, 966–976. [Google Scholar] [CrossRef]
- Wang, J.; Huang, W.; Zhou, Y.; Han, F.; Ke, D.; Lee, C. Hemodynamic Analysis of VenaTech Convertible Vena Cava Filter Using Computational Fluid Dynamics. Front. Bioeng. Biotechnol. 2020, 8, 556110. [Google Scholar] [CrossRef] [PubMed]
- Cheng, C.P.; Herfkens, R.J.; Taylor, C.A. Inferior vena caval hemodynamics quantified in vivo at rest and during cycling exercise using magnetic resonance imaging. Am. J. Physiol.-Heart Circ. Physiol. 2003, 284, H1161–H1167. [Google Scholar] [CrossRef] [PubMed]
- Ansys Fluent Theory Guide. Release 2021 R2. Available online: https://dl.cfdexperts.net/cfd_resources/Ansys_Documentation/Fluent/Ansys_Fluent_Theory_Guide.pdf (accessed on 27 December 2024).
- Sadeghiseraji, J.; Moradicheghamahi, J.; Sedaghatkish, A. Investigation of a vortex tube using three different RANS-based turbulence models. J. Therm. Anal. Calorim. 2021, 143, 4039–4056. [Google Scholar] [CrossRef]
- Cho, Y.I.; Kensey, K.R. Effects of the non-Newtonian viscosity of blood on flows in a diseased arterial vessel. Part 1: Steady flows. Biorheology 1991, 28, 241–262. [Google Scholar] [CrossRef] [PubMed]
- Jahangiri, M.; Saghafian, M.; Sadeghi, M.R. Numerical simulation of hemodynamic parameters of turbulent and pulsatile blood flow in flexible artery with single and double stenoses. J. Mech. Sci. Technol. 2015, 29, 3549–3560. [Google Scholar] [CrossRef]
- Holzapfel, G.A. Nonlinear Solid Mechanics: A Continuum Approach for Engineering Science; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2002. [Google Scholar]
- Sobin, P. Mechanical Properties of Human Veins. Master’s Thesis, University of California, San Diego, CA, USA, 1977. [Google Scholar]
- Aycock, K.I.; Campbell, R.L.; Manning, K.B.; Sastry, S.P.; Shontz, S.M.; Lynch, F.C.; Craven, B.A. A computational method for predicting inferior vena cava filter performance on a patient-specific basis. J. Biomech. Eng. 2014, 136, 081003. [Google Scholar] [CrossRef]
- Oliva, V.L.; Perreault, P.; Giroux, M.-F.; Bouchard, L.; Therasse, E.; Soulez, G. Recovery G2 Inferior Vena Cava Filter: Technical Success and Safety of Retrieval. J. Vasc. Interv. Radiol. 2008, 19, 884–889. [Google Scholar] [CrossRef]
- Grubman, S.; Kostiuk, V.; Brahmandam, A.; Tonnessen, B.; Mojibian, H.; Schneider, E.; Guzman, R.J.; Chaar, C.I.O. Effect of inferior vena cava filter placement position on device complications. J. Vasc. Surg. Venous Lymphat. Disord. 2023, 11, 1165–1174.e2. [Google Scholar] [CrossRef] [PubMed]
- Sheahan, K.P.; Tong, E.; Lee, M.J. A review of inferior vena cava filters. Br. J. Radiol. 2022, 96, 20211125. [Google Scholar] [CrossRef] [PubMed]
- Muller, L.O. Mathematical Modelling and Simulation of the Human Circulation with Emphasis on The Venous System: Application to the CCSVI Condition. Ph.D. Thesis, University of Trento, Trento, Italy, 2014. [Google Scholar]
- Zore, K.; Sasanapuri, B.; Parkhi, G.; Varghese, A. Ansys mosaic poly-hexcore mesh for high-lift aircraft configuration. In Proceedings of the 21th Annual CFD Symposium, San Diego, CA, USA, 24–27 June 2013; pp. 1–11. [Google Scholar]
- Van Leer, B. Towards the ultimate conservative difference scheme. V. A second-order sequel to Godunov’s method. J. Comput. Phys. 1979, 32, 101–136. [Google Scholar] [CrossRef]
- Jahangiri, M.; Saghafian, M.; Sadeghi, M. Numerical study of hemodynamic parameters in pulsatile turbulent blood flow in flexible artery with stenosis. In Proceedings of the 22st annual international conference on mechanical engineering-ISME2014, Ahvaz, Iran, 22–24 April 2014; Shahid Chamran University: Ahvaz, Iran, 2014. [Google Scholar]
- Philip, N.T.; Patnaik, B.S.V.; Sudhir, B.J. Hemodynamic simulation of abdominal aortic aneurysm on idealised models: Investigation of stress parameters during disease progression. Comput. Methods Programs Biomed. 2022, 213, 106508. [Google Scholar] [CrossRef] [PubMed]
- Moradicheghamahi, J.; Sadeghiseraji, J.; Jahangiri, M. Numerical solution of the Pulsatile, non-Newtonian and turbulent blood flow in a patient specific elastic carotid artery. Int. J. Mech. Sci. 2019, 150, 393–403. [Google Scholar] [CrossRef]
- Pillalamarri, N.R.; Piskin, S.; Patnaik, S.S.; Murali, S.; Finol, E.A. Patient-specific computational analysis of hemodynamics in adult pulmonary hypertension. Ann. Biomed. Eng. 2021, 49, 3465–3480. [Google Scholar] [CrossRef]
- Jahangiri, M.; Saghafian, M.; Sadeghi, M.R. Numerical simulation of non-Newtonian models effect on hemodynamic factors of pulsatile blood flow in elastic stenosed artery. J. Mech. Sci. Technol. 2017, 31, 1003–1013. [Google Scholar] [CrossRef]
- Aryan, H.; Beigzadeh, B.; Siavashi, M. Euler-Lagrange numerical simulation of improved magnetic drug delivery in a three-dimensional CT-based carotid artery bifurcation. Comput. Methods Programs Biomed. 2022, 219, 106778. [Google Scholar] [CrossRef] [PubMed]
- Teymoori, M.; Sadeghi, M.R.; Rabbani, M.; Jahangiri, M. Effect of Extended Lipid Core on the Hemodynamic Parameters: A Fluid-Structure Interaction Approach. Appl. Bionics Biomech. 2022, 2022, 2047549. [Google Scholar] [CrossRef]
- Lee, S.-W.; Antiga, L.; Steinman, D.A. Correlations among indicators of disturbed flow at the normal carotid bifurcation. J. Biomech. Eng. 2009, 131, 061013. [Google Scholar] [CrossRef] [PubMed]
- Ku, D.N.; Giddens, D.P.; Zarins, C.K.; Glagov, S. Pulsatile flow and atherosclerosis in the human carotid bifurcation. Positive correlation between plaque location and low oscillating shear stress. Arteriosclerosis 1985, 5, 293–302. [Google Scholar] [CrossRef]
- Zarins, C.K.; Giddens, D.P.; Bharadvaj, B.; Sottiurai, V.S.; Mabon, R.F.; Glagov, S. Carotid bifurcation atherosclerosis. Quantitative correlation of plaque localization with flow velocity profiles and wall shear stress. Circ. Res. 1983, 53, 502–514. [Google Scholar] [CrossRef] [PubMed]
- Hathcock, J.J. Flow effects on coagulation and thrombosis. Arterioscler. Thromb. Vasc. Biol. 2006, 26, 1729–1737. [Google Scholar] [CrossRef] [PubMed]
- DeRoo, E.; Stranz, A.; Yang, H.; Hsieh, M.; Se, C.; Zhou, T. Endothelial Dysfunction in the Pathogenesis of Abdominal Aortic Aneurysm. Biomolecules 2022, 12, 509. [Google Scholar] [CrossRef]
- Hansen, K.B.; Shadden, S.C. A reduced-dimensional model for near-wall transport in cardiovascular flows. Biomech. Model. Mechanobiol. 2016, 15, 713–722. [Google Scholar] [CrossRef] [PubMed]
- Cecchi, E.; Giglioli, C.; Valente, S.; Lazzeri, C.; Gensini, G.F.; Abbate, R.; Mannini, L. Role of hemodynamic shear stress in cardiovascular disease. Atherosclerosis 2011, 214, 249–256. [Google Scholar] [CrossRef] [PubMed]
- Kleinstreuer, C.; Hyun, S.; Buchanan, J.; Longest, P.; Archie, J.P., Jr.; Truskey, G.A. Hemodynamic parameters and early intimal thickening in branching blood vessels. Crit. Rev. Biomed. Eng. 2001, 29, 1–64. [Google Scholar] [CrossRef]
- Wentzel, J.J.; Janssen, E.; Vos, J.; Schuurbiers, J.C.; Krams, R.; Serruys, P.W.; de Feyter, P.J.; Slager, C.J. Extension of increased atherosclerotic wall thickness into high shear stress regions is associated with loss of compensatory remodeling. Circulation 2003, 108, 17–23. [Google Scholar] [CrossRef] [PubMed]
- Joshi, A.K.; Leask, R.L.; Myers, J.G.; Ojha, M.; Butany, J.; Ethier, C.R. Intimal thickness is not associated with wall shear stress patterns in the human right coronary artery. Arterioscler. Thromb. Vasc. Biol. 2004, 24, 2408–2413. [Google Scholar] [CrossRef] [PubMed]
- Davies, P.F.; Remuzzi, A.; Gordon, E.J.; Dewey, C.F.; Gimbrone, M.A. Turbulent fluid shear stress induces vascular endothelial cell turnover in vitro. Proc. Natl. Acad. Sci. USA 1986, 83, 2114–2117. [Google Scholar] [CrossRef] [PubMed]
- DePaola, N.; Gimbrone, M.A., Jr.; Davies, P.F.; Dewey, C.F., Jr. Vascular endothelium responds to fluid shear stress gradients. Arterioscler. Thromb. A J. Vasc. Biol. 1992, 12, 1254–1257. [Google Scholar] [CrossRef]
- Morel, S.; Schilling, S.; Diagbouga, M.R.; Delucchi, M.; Bochaton-Piallat, M.L.; Lemeille, S.; Hirsch, S.; Kwak, B.R. Effects of Low and High Aneurysmal Wall Shear Stress on Endothelial Cell Behavior: Differences and Similarities. Front. Physiol. 2021, 12, 727338. [Google Scholar] [CrossRef] [PubMed]
- Sunderland, K.; Haferman, C.; Chintalapani, G.; Jiang, J. Vortex Analysis of Intra-Aneurismal Flow in Cerebral Aneurysms. Comput. Math. Methods Med. 2016, 2016, 7406215. [Google Scholar] [CrossRef] [PubMed]
- Turitto, V.T.; Hall, C.L. Mechanical factors affecting hemostasis and thrombosis. Thromb. Res. 1998, 92, S25–S31. [Google Scholar] [CrossRef] [PubMed]
- Barak, O.F.; Mladinov, S.; Hoiland, R.L.; Tremblay, J.C.; Thom, S.R.; Yang, M.; Mijacika, T.; Dujic, Z. Disturbed blood flow worsens endothelial dysfunction in moderate-severe chronic obstructive pulmonary disease. Sci. Rep. 2017, 7, 16929. [Google Scholar] [CrossRef] [PubMed]
- Chiu, J.J.; Chien, S. Effects of disturbed flow on vascular endothelium: Pathophysiological basis and clinical perspectives. Physiol. Rev. 2011, 91, 327–387. [Google Scholar] [CrossRef]
- Dolan, J.M.; Kolega, J.; Meng, H. High wall shear stress and spatial gradients in vascular pathology: A review. Ann. Biomed. Eng. 2013, 41, 1411–1427. [Google Scholar] [CrossRef] [PubMed]
- De Wilde, D.; Trachet, B.; De Meyer, G.; Segers, P. The influence of anesthesia and fluid–structure interaction on simulated shear stress patterns in the carotid bifurcation of mice. J. Biomech. 2016, 49, 2741–2747. [Google Scholar] [CrossRef] [PubMed]
- Box, F.M.; van der Geest, R.J.; Rutten, M.C.; Reiber, J.H. The influence of flow, vessel diameter, and non-newtonian blood viscosity on the wall shear stress in a carotid bifurcation model for unsteady flow. Investig. Radiol. 2005, 40, 277–294. [Google Scholar] [CrossRef]
- Malek, A.M.; Alper, S.L.; Izumo, S. Hemodynamic shear stress and its role in atherosclerosis. JAMA 1999, 282, 2035–2042. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Xie, S.; Li, S.; Pu, F.; Deng, X.; Fan, Y.; Li, D. Flow patterns and wall shear stress distribution in human internal carotid arteries: The geometric effect on the risk for stenoses. J. Biomech. 2012, 45, 83–89. [Google Scholar] [CrossRef]
- Himburg, H.A.; Grzybowski, D.M.; Hazel, A.L.; LaMack, J.A.; Li, X.-M.; Friedman, M.H. Spatial comparison between wall shear stress measures and porcine arterial endothelial permeability. Am. J. Physiol. -Heart Circ. Physiol. 2004, 286, H1916–H1922. [Google Scholar] [CrossRef] [PubMed]
- Papadopoulos, K.P.; Gavaises, M.; Pantos, I.; Katritsis, D.G.; Mitroglou, N. Derivation of flow related risk indices for stenosed left anterior descending coronary arteries with the use of computer simulations. Med. Eng. Phys. 2016, 38, 929–939. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Yu, H.; Shi, Y.; Zhu, M.; Wang, Y.; Hu, X.; Zhang, Y.; Chang, Y.; Xu, M.; Gao, W. Vascular remodelling relates to an elevated oscillatory shear index and relative residence time in spontaneously hypertensive rats. Sci. Rep. 2017, 7, 2007. [Google Scholar] [CrossRef] [PubMed]
- Domanin, M.; Buora, A.; Scardulla, F.; Guerciotti, B.; Forzenigo, L.; Biondetti, P.; Vergara, C. Computational fluid-dynamic analysis after carotid endarterectomy: Patch graft versus direct suture closure. Ann. Vasc. Surg. 2017, 44, 325–335. [Google Scholar] [CrossRef] [PubMed]




| Clot Size | Index | Hyperelastic | Rigid | % Difference | Turbulent | Laminar | % Difference |
|---|---|---|---|---|---|---|---|
| Large Clot | TAWSS | 4.18 | 4.433 | 6.05 | 4.18 | 4.13 | −1.19 |
| OSI | 0.077 | 0.074 | −4.40 | 0.077 | 0.075 | −3.24 | |
| RRT | 2.292 | 2.015 | −12.06 | 2.292 | 2.054 | −10.34 | |
| Small Clot | TAWSS | 0.465 | 0.479 | 3.09 | 0.465 | 0.464 | −0.24 |
| OSI | 0.026 | 0.025 | −1.27 | 0.026 | 0.025 | −1.85 | |
| RRT | 2.314 | 2.255 | −2.55 | 2.314 | 2.305 | −0.40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moradicheghamahi, J.; Goswami, D. Impact of Vein Wall Hyperelasticity and Blood Flow Turbulence on Hemodynamic Parameters in the Inferior Vena Cava with a Filter. Micromachines 2025, 16, 51. https://doi.org/10.3390/mi16010051
Moradicheghamahi J, Goswami D. Impact of Vein Wall Hyperelasticity and Blood Flow Turbulence on Hemodynamic Parameters in the Inferior Vena Cava with a Filter. Micromachines. 2025; 16(1):51. https://doi.org/10.3390/mi16010051
Chicago/Turabian StyleMoradicheghamahi, Jafar, and Debkalpa Goswami. 2025. "Impact of Vein Wall Hyperelasticity and Blood Flow Turbulence on Hemodynamic Parameters in the Inferior Vena Cava with a Filter" Micromachines 16, no. 1: 51. https://doi.org/10.3390/mi16010051
APA StyleMoradicheghamahi, J., & Goswami, D. (2025). Impact of Vein Wall Hyperelasticity and Blood Flow Turbulence on Hemodynamic Parameters in the Inferior Vena Cava with a Filter. Micromachines, 16(1), 51. https://doi.org/10.3390/mi16010051