Metasurface-Coated Liquid Microlens for Super Resolution Imaging
Abstract
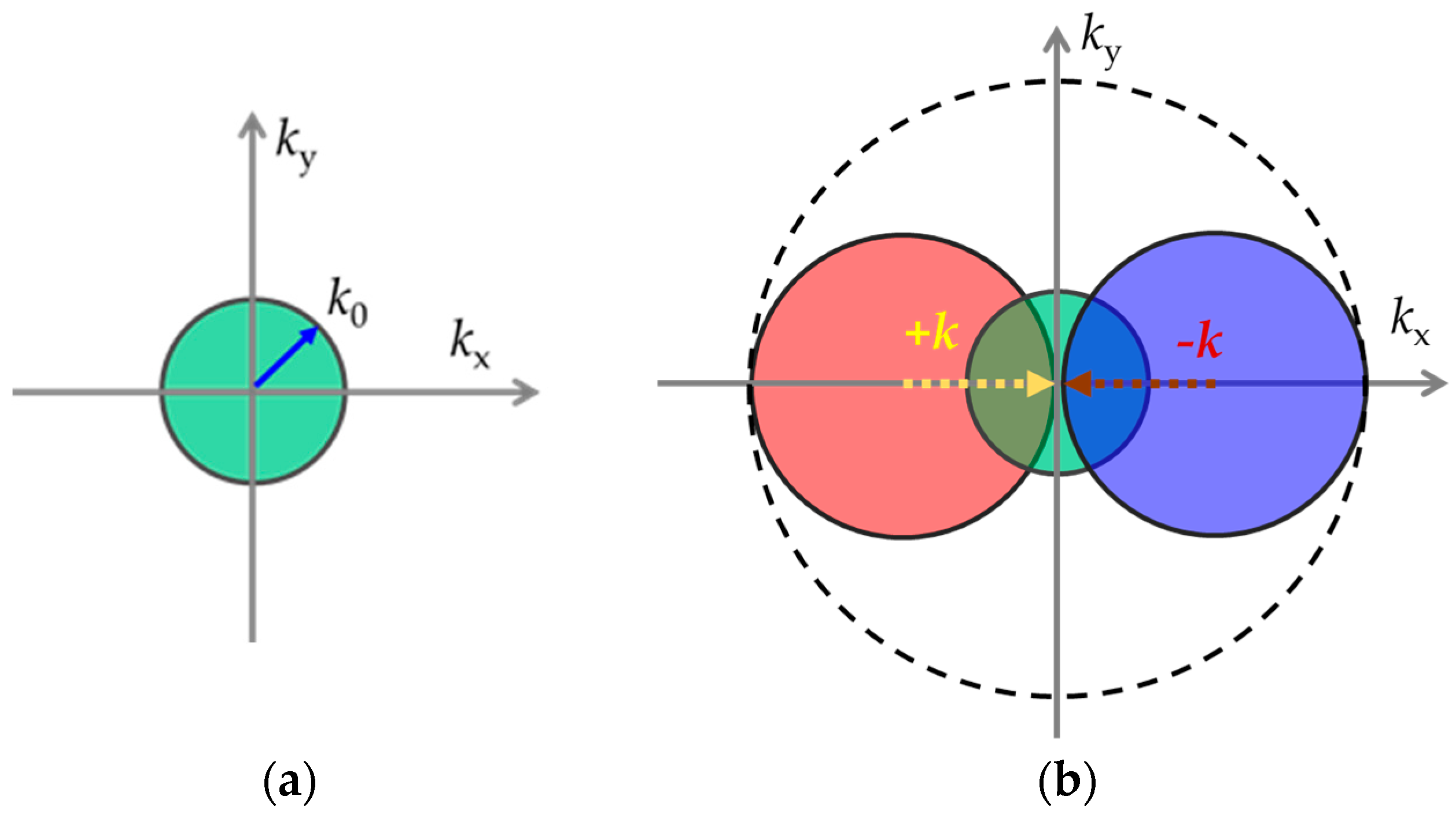
1. Introduction
2. Materials and Methods
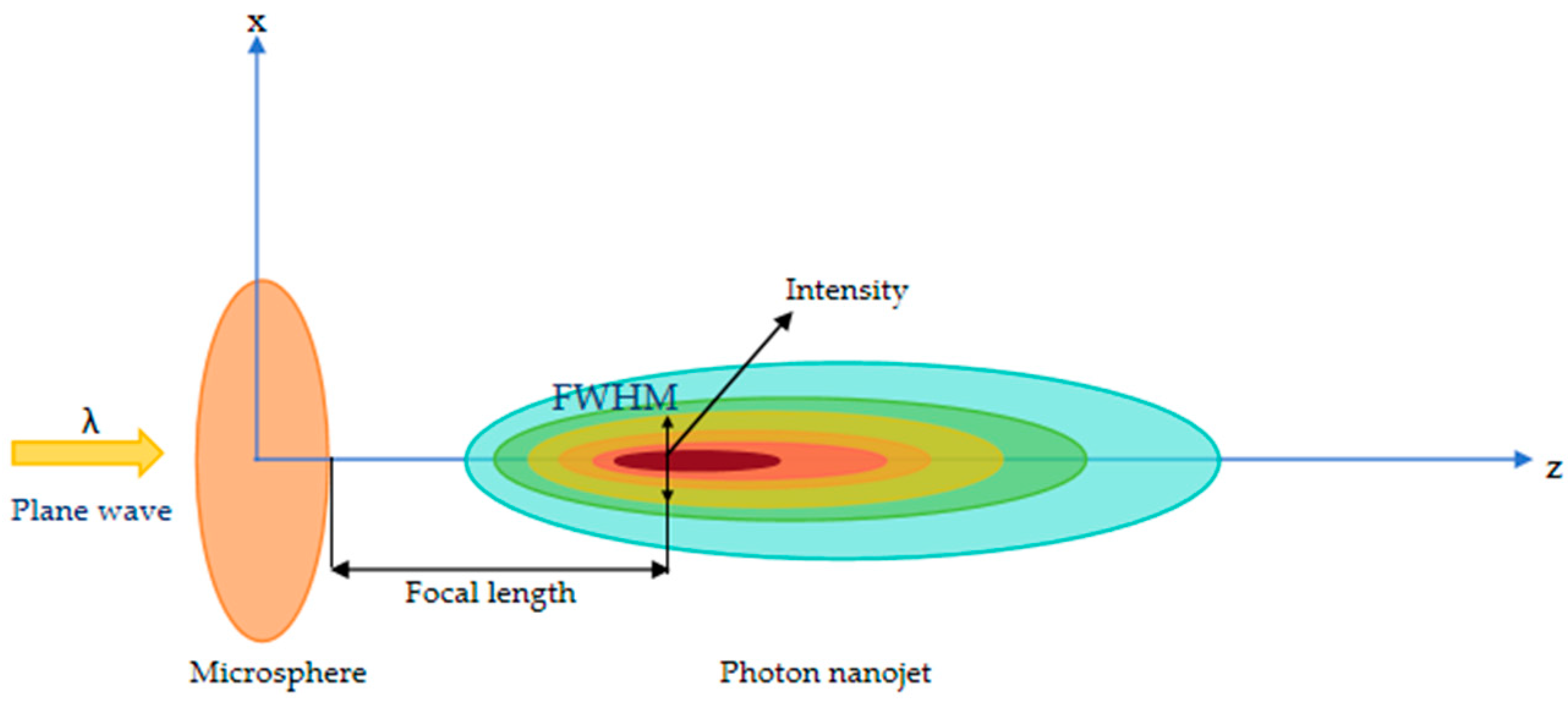
3. Simulation Model
4. Results
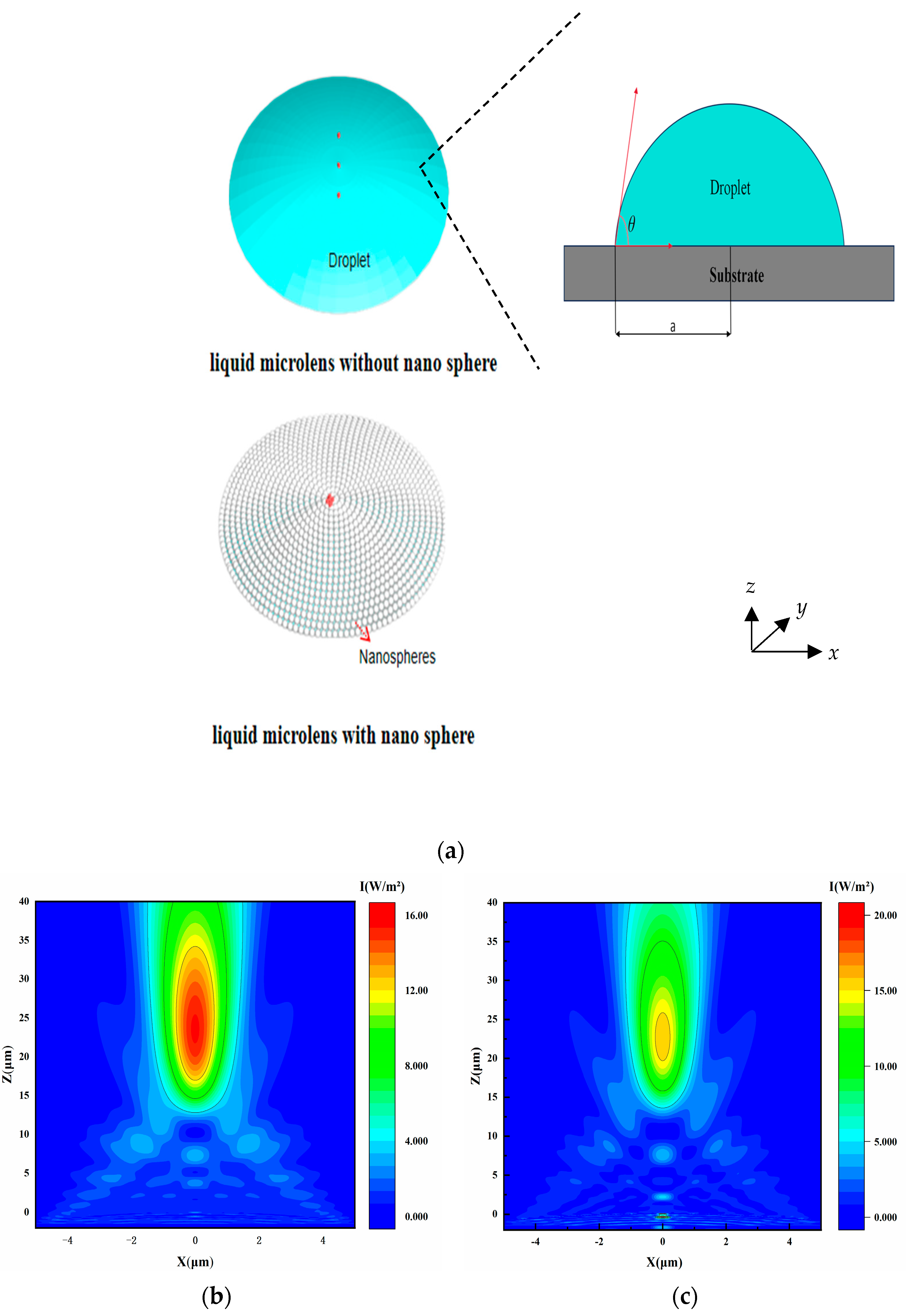
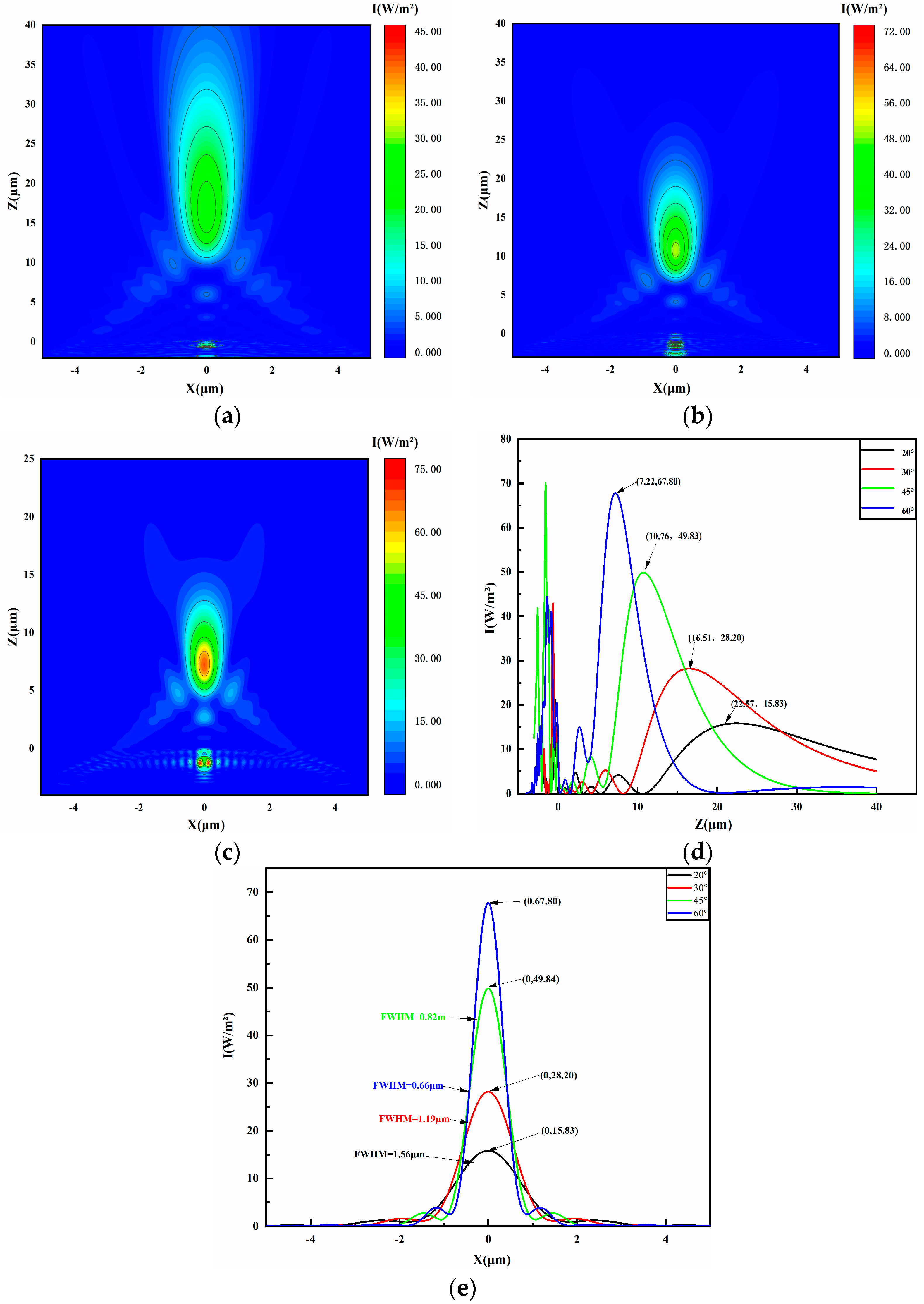
4.1. Initial Contact Angle of Droplets
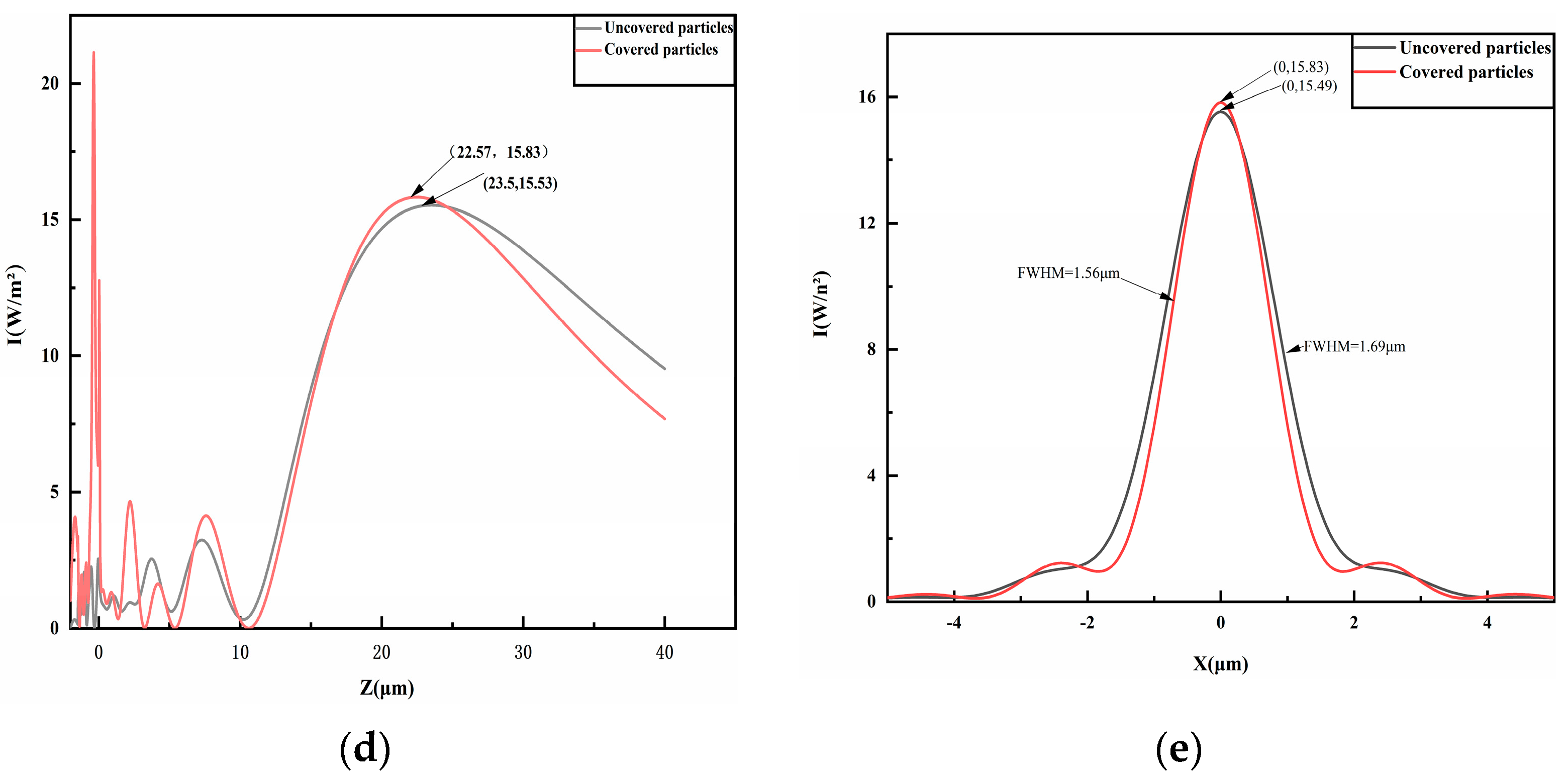
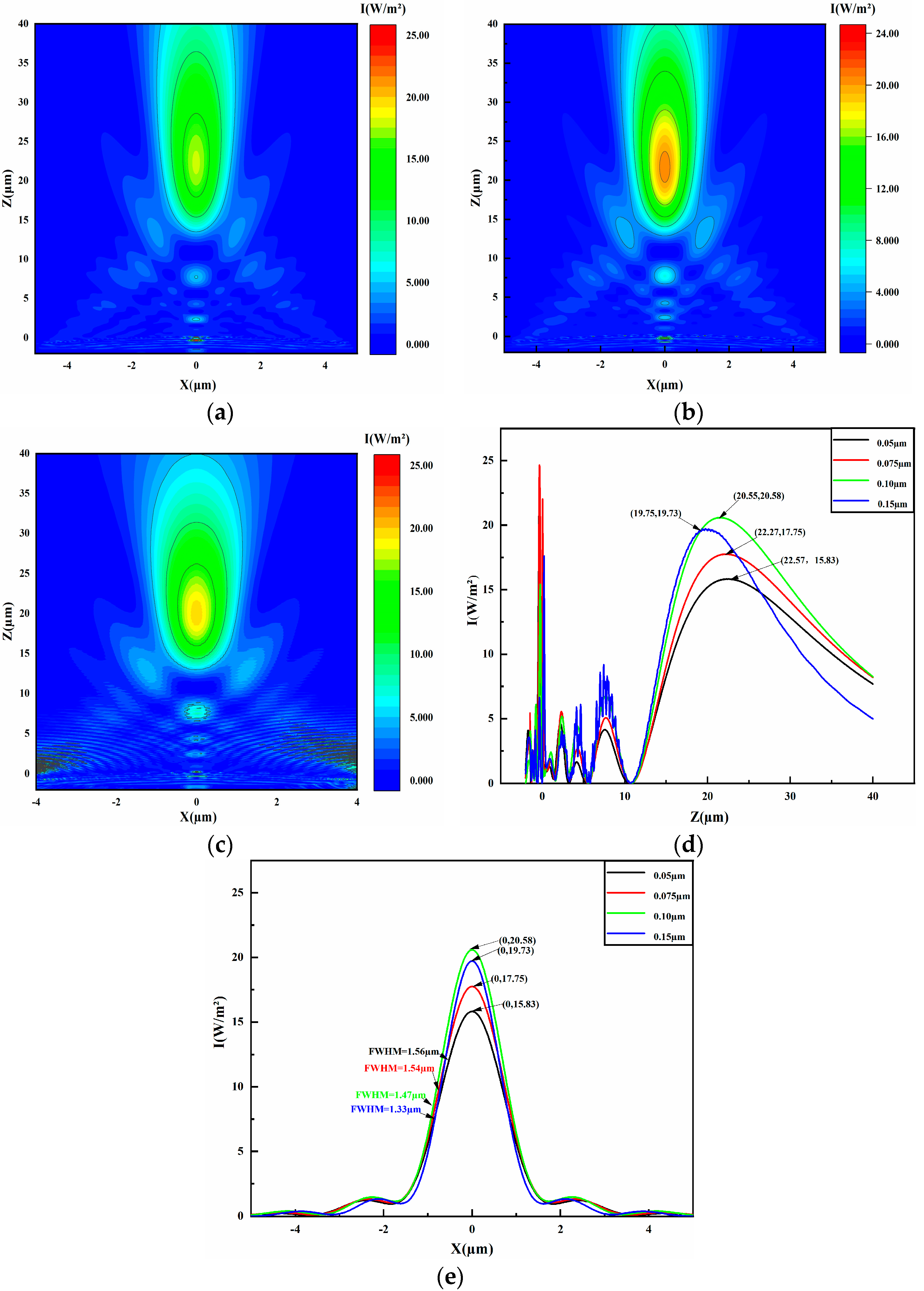
4.2. Radius of Nanospheres
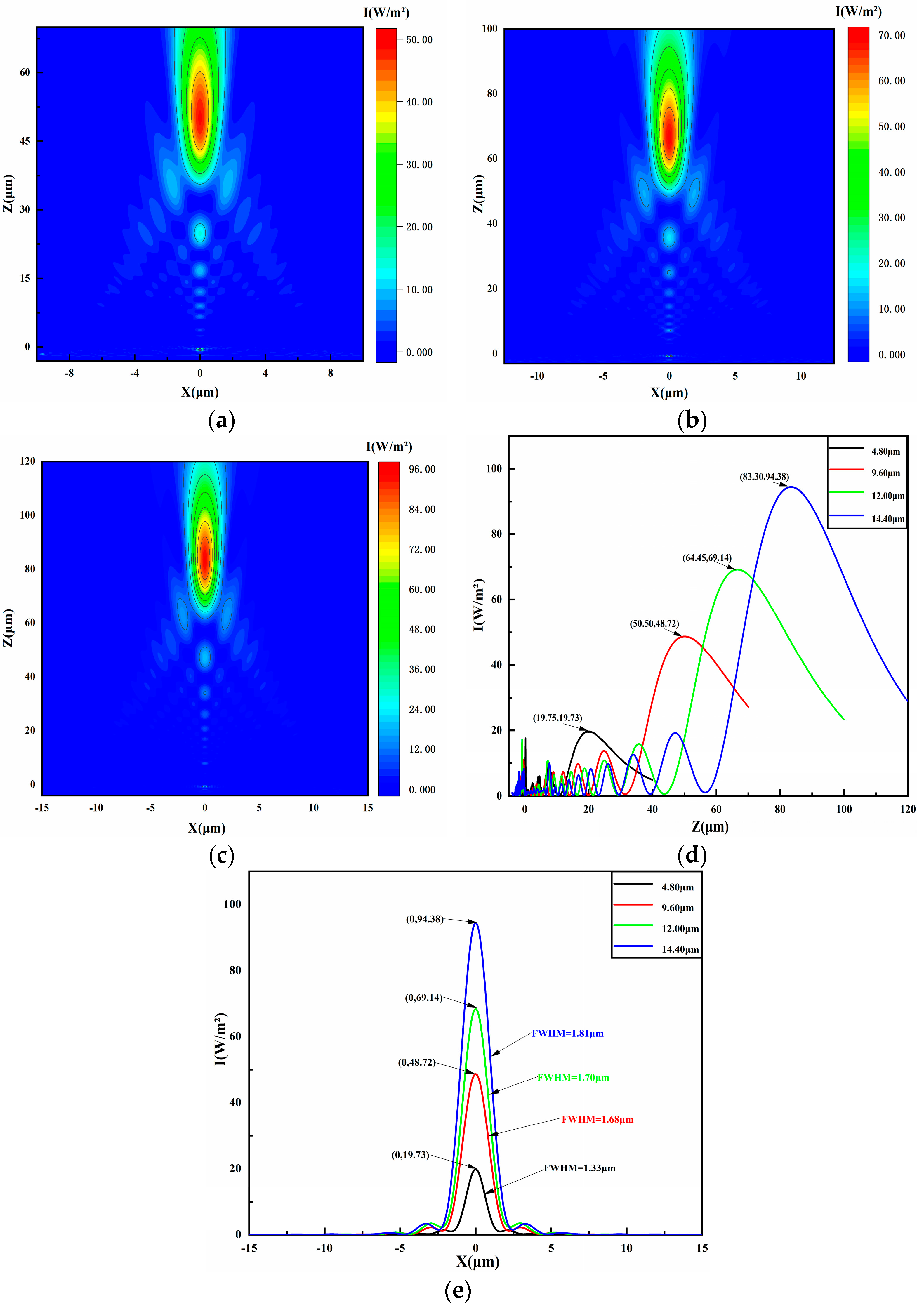
4.3. Diameter of Droplet Bottom
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cao, R.; Li, Y.; Chen, X.; Ge, X.; Li, M.; Guan, M.; Hou, Y.; Fu, Y.; Xu, X.; Leterrier, C.; et al. Open-3DSIM: An open-source three-dimensional structured illumination microscopy reconstruction platform. Nat. Methods 2023, 20, 1183–1186. [Google Scholar] [CrossRef] [PubMed]
- Liang, L.; Feng, Z.; Zhang, Q.; Cong, T.; Wang, Y.; Qin, X.; Ang, M.; Zhou, L.; Feng, H.; Xing, B.; et al. Continuous-wave near-infrared stimulated-emission depletion microscopy using downshifting lanthanide nanoparticles. Nat. Nanotechnol. 2021, 16, 975–980. [Google Scholar] [CrossRef] [PubMed]
- Blom, H.; Widengren, J. Stimulated emission depletion microscopy. Chem. Rev. 2017, 117, 7377–7427. [Google Scholar] [CrossRef]
- O’Holleran, K.; Shaw, M. Optimized approaches for optical sectioning and resolution enhancement in 2D structured illumination microscopy. Biomed. Opt. Express 2014, 5, 2580–2590. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Bates, M.; Jones, S.A.; Zhuang, X. Stochastic optical reconstruction microscopy (STORM): A method for superresolution fluorescence imaging. Cold Spring Harb. Protoc. 2013, 2013, 498–520. [Google Scholar] [CrossRef] [PubMed]
- Balzarotti, F.; Eilers, Y.; Gwosch, C.; Gynnå, A.; Westphal, V.; Stefani, F.; Elf, J.; Hell, S. Nanometer resolution imaging and tracking of fluorescent molecules with minimal photon fluxes. Science 2017, 355, 606–612. [Google Scholar] [CrossRef]
- Dan, D.; Wang, J.; Zhou, X.; Lei, M.; Zhao, T.; Qian, J. Rapid image reconstruction of structured illumination microscopy directly in the spatial domain. IEEE Photonics 2021, 13, 3900411. [Google Scholar] [CrossRef]
- Zheng, Y.; Wang, X.; Jiang, Z.; Xu, J.; Yuan, R.; Zhao, Y.; Zhang, H.; Liu, C.; Wang, Q. Adaptive multiscale microscope with fast zooming, extended working distance, and large field of view. Light Adv. Manuf. 2024, 5, 62–74. [Google Scholar] [CrossRef]
- Betzig, E.; Trautman, K.; Harris, D.; Weiner, S.; Kostelak, L. Breaking the diffraction barrier: Optical microscopy on a nanometric scale. Science 1991, 251, 1468–1470. [Google Scholar] [CrossRef]
- Hecht, B.; Sick, B.; Wild, U.P.; Deckert, V.; Zenobi, R.; Martin, O.J.F.; Pohl, D.W. Scanning near-field optical microscopy with aperture probes: Fundamentals and applications. J. Chem. Phys. 2000, 112, 7761–7774. [Google Scholar] [CrossRef]
- Lereu, A.L.; Passian, A.; Dumas, P. Near field optical microscopy: A brief review. Int. J. Nanotechnol. 2012, 9, 488–501. [Google Scholar] [CrossRef]
- Degtyarev, S.; Khonina, S. T ransmission of focused light signal through an apertured probe of a near-field scanning microscope. Pattern Recognit. Image Anal. 2015, 25, 306–313. [Google Scholar] [CrossRef]
- Gu, G.; Song, M.; Chen, M. Single nanoparticle detection by using photonic nanojet itself. Nanoscale 2018, 10, 14182–14189. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Zhou, Y.; Li, Y.; Hong, M. Microsphere enhanced optical imaging and patterning: From physics to application. Appl. Phys. Rev. 2019, 6, 021304. [Google Scholar] [CrossRef]
- Zhang, P.; Yan, B.; Gu, G.; Yu, Z.; Chen, X.; Wang, Z.; Yang, H. Localized photonic nanojet based sensing platform for highly efficient signal amplification and quantitative biosensing. Sens. Actuat B-Chem 2022, 357, 131401. [Google Scholar] [CrossRef]
- Yang, W.; Hou, L.; Lou, C. When super-resolution microscopy meets microfluidics: Enhanced biological imaging and analysis with unprecedented resolution. Small 2023, 19, 2207341. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Yu, H.; Li, P.; Wang, D.; Wang, F.; Shi, L.; Liu, Z.; Yu, P.; Yang, G.; Wang, C.; et al. Microsphere-based super-resolution imaging for visualized nanomanipulation. ACS Appl. Mater. Interfaces 2020, 12, 48093–48100. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Yu, H.; Shi, J.; Wang, X.; Luo, H.; Lin, D.; Liu, Z.; Su, C.; Wang, Y.; Liu, L. Correlative AFM and scanning microlens microscopy for time-efficient multiscale imaging. Adv. Sci. 2022, 9, 2103902. [Google Scholar] [CrossRef] [PubMed]
- Jin, G.; Bachman, H.; Naquin, T.D.; Rufo, J.; Hou, S.; Tian, Z.; Zhao, C.; Huang, J. Acoustofluidic scanning nanoscope with high resolution and large field of view. ACS Nano 2020, 14, 8624–8633. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Wu, T.; Gong, Z.; Guo, J.; Liu, X.; Zhang, Y.; Li, Y.; Ferraro, P.; Li, B. Lipid droplets as endogenous intracellular microlenses. Light-Sci. Appl. 2021, 10, 242. [Google Scholar] [CrossRef]
- Wu, G.; Zhou, Y.; Hong, M. Sub-50 nm optical imaging in ambient air with 10× objective lens enabled by hyper-hemi-microsphere. Light-Sci. Appl. 2023, 12, 49. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Yan, B.; Wang, H.; Chen, Y.; Nie, X.; Yi, C.; Wang, Z.; Xu, Z.; Zeng, J.; Fan, W. Wide-field and real-time super-resolution optical imaging by titanium dioxide nanoparticle-assembled solid immersion lens. Small 2023, 19, 2207596. [Google Scholar] [CrossRef]
- Zuo, C.; Chen, Q. Resolution, super-resolution and spatial bandwidth product expansion: Some thoughts from the perspective of computation optical imaging. Chin. Opt. 2022, 15, 1105–1166. [Google Scholar]
- Wang, B.; Zuo, Y.; Zhang, L.; Li, Y.; Chen, Q.; Zuo, C. Multimodal super-resolution reconstruction of infrared and visible images via deep learning. Opt. Laser Eng. 2022, 156, 107078. [Google Scholar] [CrossRef]
- Yang, F.; Sun, J.; Shu, Y.; Zhang, Z.; Zheng, G.; Chen, W.; Zhang, J.; Gui, K.; Wang, K.; Chen, Q.; et al. Efficient synthetic aperture for phaseless Fourier Ptychographic microscopy with hybrid coherent and incoherent illumination. Laser Photonics Rev. 2023, 17, 2200201. [Google Scholar]
- Zhang, Y.; Song, X.; Xie, J.; Hu, J.; Chen, J.; Li, X.; Zhang, H.; Zhou, Q.; Yuan, L.; Kong, C.; et al. Large depth-of-field ultra-compact microscope by progressive optimization and deep learning. Nat. Commun. 2023, 14, 4118. [Google Scholar] [CrossRef]
- Wu, J.; Guo, Y.; Chao, D.; Zhang, A.; Qiao, H.; Lu, Z.; Xie, J.; Fang, L.; Dai, Q. An integrated imaging sensor for aberration-corrected 3D photography. Nature 2022, 612, 62–71. [Google Scholar] [CrossRef] [PubMed]
- Pang, H.; Gao, H.; Deng, Q.; Yin, S.; Qiu, Q.; Du, C. Multi-focus plasmonic lens design based on holography. Opt. Express 2013, 21, 18689–18696. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Liu, H.; Hou, X.; Yan, D. Dynamic tunable meta-lens based on a single-layer metal microstructure. Photonics 2022, 9, 917. [Google Scholar] [CrossRef]
- Huang, Y.; Kalyoncu, K.; Zhao, Q.; Torun, R.; Boyraz, O. Silicon-on-sapphire waveguides design for mid-IR evanescent field absorption gas sensors. Opt. Commun. 2014, 313, 186–194. [Google Scholar] [CrossRef]
- Zhou, Y.; Ma, Z.; Liao, D.; Zhang, K.; Wu, S.; Ma, J.; Dai, X.; Shang, Z.; Wen, Z.; Chen, G. Super-resolution imaging via lenses with angular magnification. Adv. Opt. Mater. 2023, 3, 2301362. [Google Scholar] [CrossRef]
- Butt, M.; Kazanskiy, N.; Khonina, S. Highly integrated plasmonic sensor design for the simultaneous detection of multiple analytes. Curr. Appl. Phys. 2020, 20, 1274–1280. [Google Scholar] [CrossRef]
- Lin, Y.; Zhang, X.; Xin, Q.; Zhao, Y.; Song, A.; Zeng, Z.; Yang, F.; Jiang, C. Tunable electrochromic Au nanorod-based metalenses for visible light. Opt. Express 2021, 29, 43011–43021. [Google Scholar] [CrossRef]
- Kogos, L.C.; Li, Y.; Liu, J.; Li, Y.; Tian, L.; Paiella, R. Plasmonic ommatidia for lensless compound-eye vision. Nat. Commun. 2020, 11, 1637. [Google Scholar] [CrossRef]
- Wang, X.; Huang, S.C.; Hu, S.; Yan, S.; Ren, B. Fundamental understanding and applications of plasmon-enhanced Raman spectroscopy. Nat. Rev. Phy. 2022, 2, 253–271. [Google Scholar] [CrossRef]
- Zhang, P.; Zhan, T.; Xue, S.; Yang, H. Microlens-Assisted Light-Scattering Imaging of Plasmonic Nanoparticles at the Single Particle Level. Biosensors 2023, 13, 871. [Google Scholar] [CrossRef]
- Kim, M.; Kwon, H.; Lee, S.; Yoon, S. Effect of nanogap morphology on plasmon coupling. ACS Nano 2019, 13, 12100–12108. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Yu, W.; Li, C.; Zhang, H.; Xu, Z.; Lu, Z.; Sun, Q. Biomimetic compound eye with a high numerical aperture and anti-reflective nanostructures on curved surfaces. Opt. Lett. 2012, 37, 2397–2399. [Google Scholar] [CrossRef]
- Luo, Y.; Wang, L.; Ding, Y.; Li, L.; Shi, J. High light-extracting efficiency for OLED directly fabricated on double-side nanotextured silica substrate. Opt. Lett. 2013, 38, 2394–2396. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Yu, J.; Mao, Y.F.; Chen, J.; Wang, S.; Chen, Z.; Zhang, Y.; Wang, Y.; Chen, X.; Li, T.; et al. Stable, high-performance sodium-based plasmonic devices in the near infrared. Nature 2020, 581, 401–405. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Wang, Z.; Zhong, X.; Che, Y.; Li, X. Photothermal nonlinear scattering of shell-isolated gold nanoparticles and applications in super-resolution imaging. Chin. Opt. Lett. 2023, 21, 103601. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, T.; Wang, K.; Cai, A.; Wu, F.; Chang, Y.; Zhao, H.; Wang, L. Metasurface-Coated Liquid Microlens for Super Resolution Imaging. Micromachines 2025, 16, 25. https://doi.org/10.3390/mi16010025
Gu T, Wang K, Cai A, Wu F, Chang Y, Zhao H, Wang L. Metasurface-Coated Liquid Microlens for Super Resolution Imaging. Micromachines. 2025; 16(1):25. https://doi.org/10.3390/mi16010025
Chicago/Turabian StyleGu, Tongkai, Kang Wang, Anjiang Cai, Fan Wu, Yasheng Chang, Haiyan Zhao, and Lanlan Wang. 2025. "Metasurface-Coated Liquid Microlens for Super Resolution Imaging" Micromachines 16, no. 1: 25. https://doi.org/10.3390/mi16010025
APA StyleGu, T., Wang, K., Cai, A., Wu, F., Chang, Y., Zhao, H., & Wang, L. (2025). Metasurface-Coated Liquid Microlens for Super Resolution Imaging. Micromachines, 16(1), 25. https://doi.org/10.3390/mi16010025






