Operator-Based Triboelectric Nanogenerator Power Management and Output Voltage Control
Abstract
1. Introduction
2. TENG Modeling
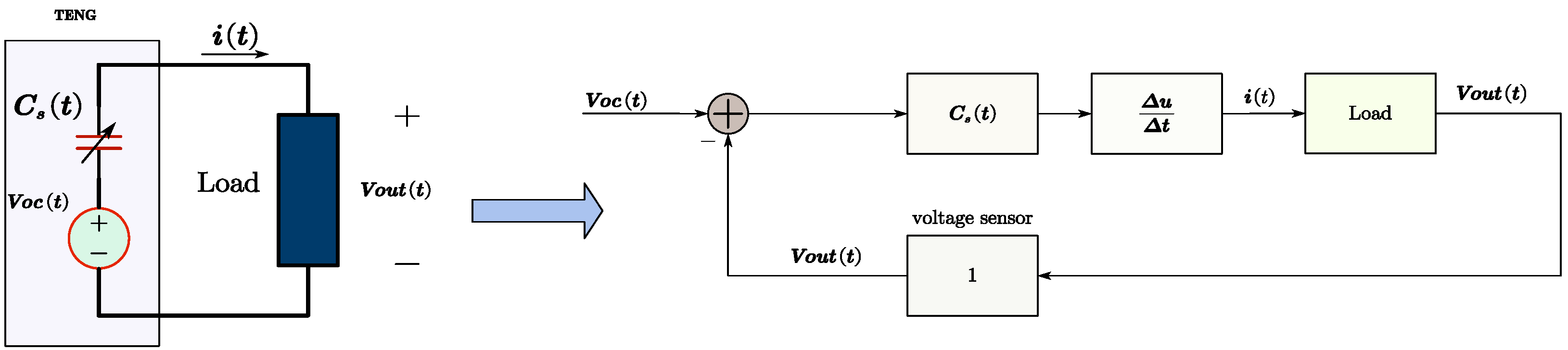
2.1. TENG Model and Analysis of Its Circuit Equation
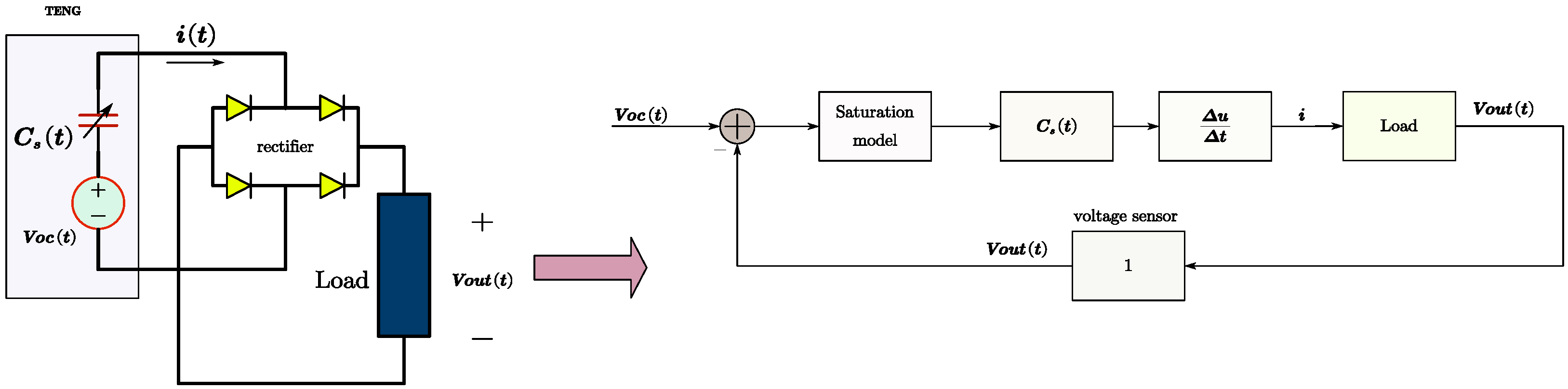
2.2. TENG Simulation Model and Analysis of Its Circuit Equation
3. Proposed TENG’s System and Control
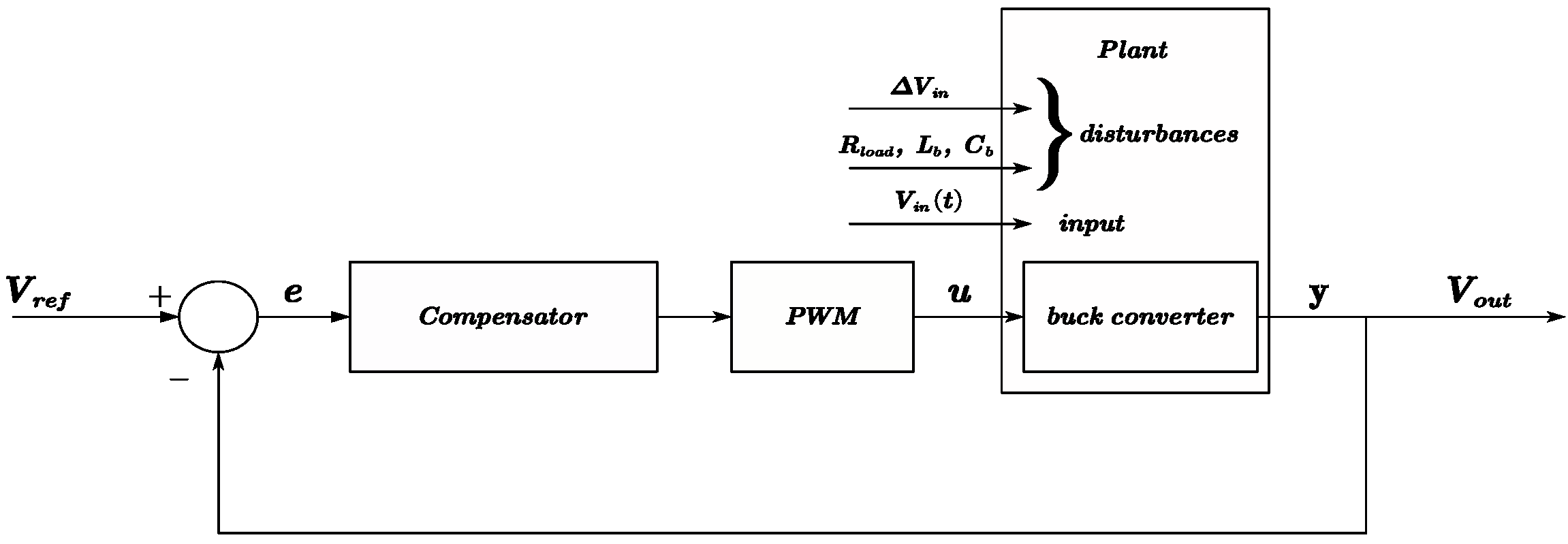
3.1. TENG’s System
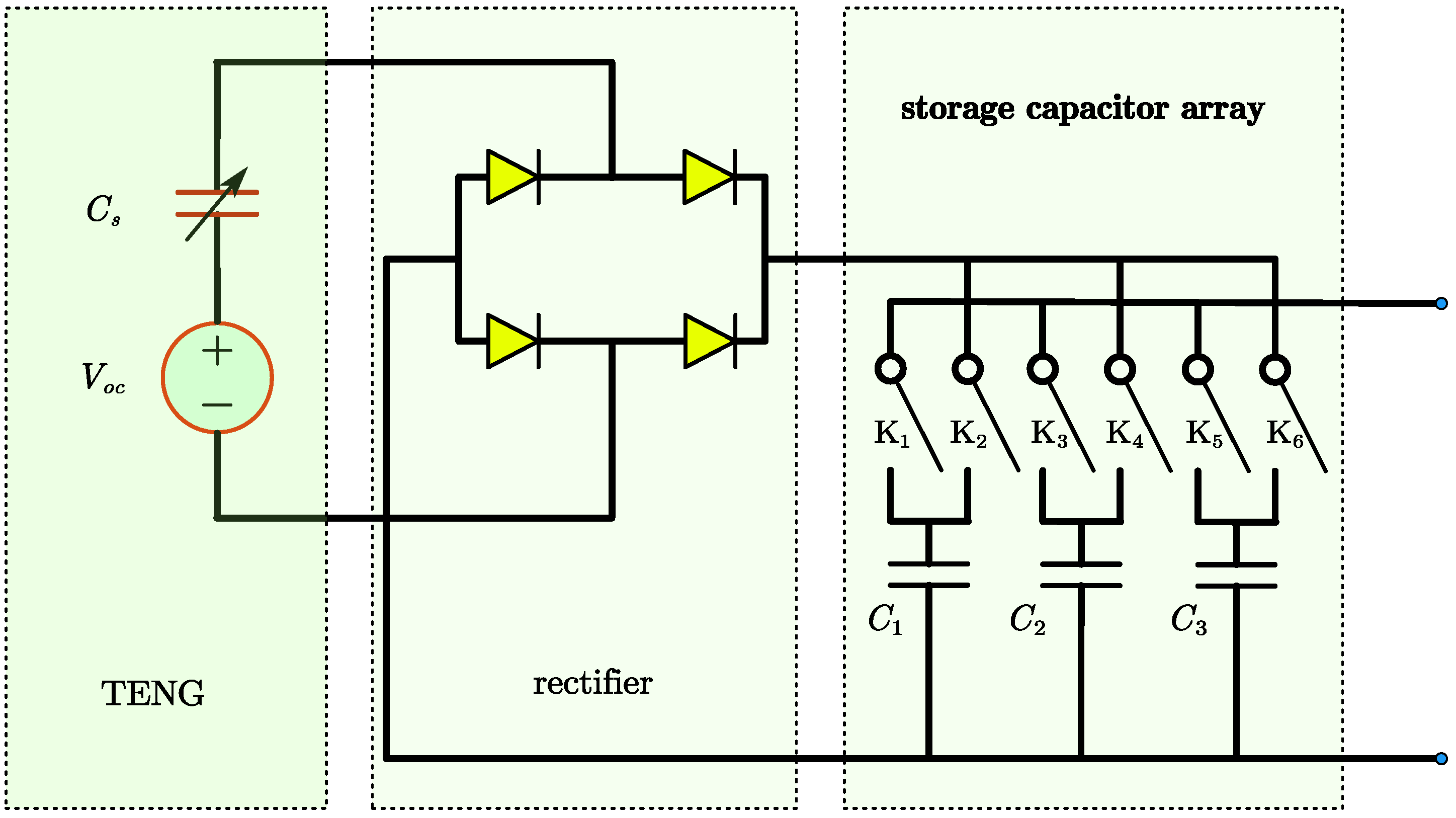
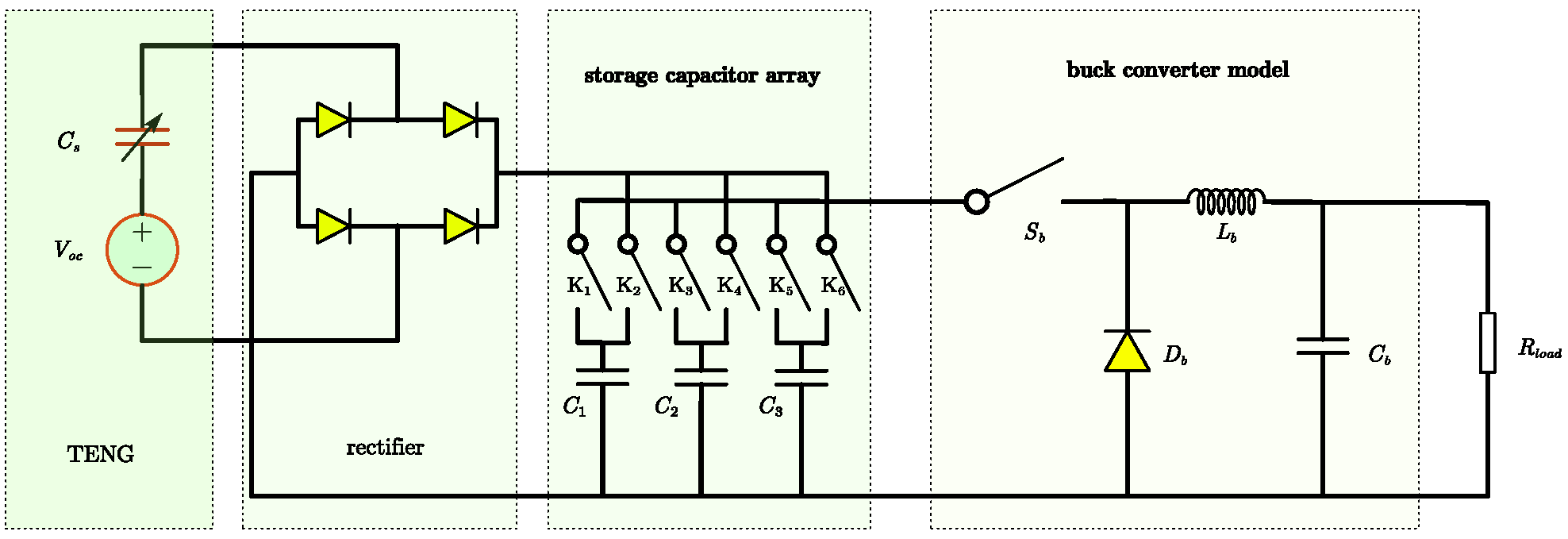
3.1.1. TENG’s PMU with Storage Capacitor Array
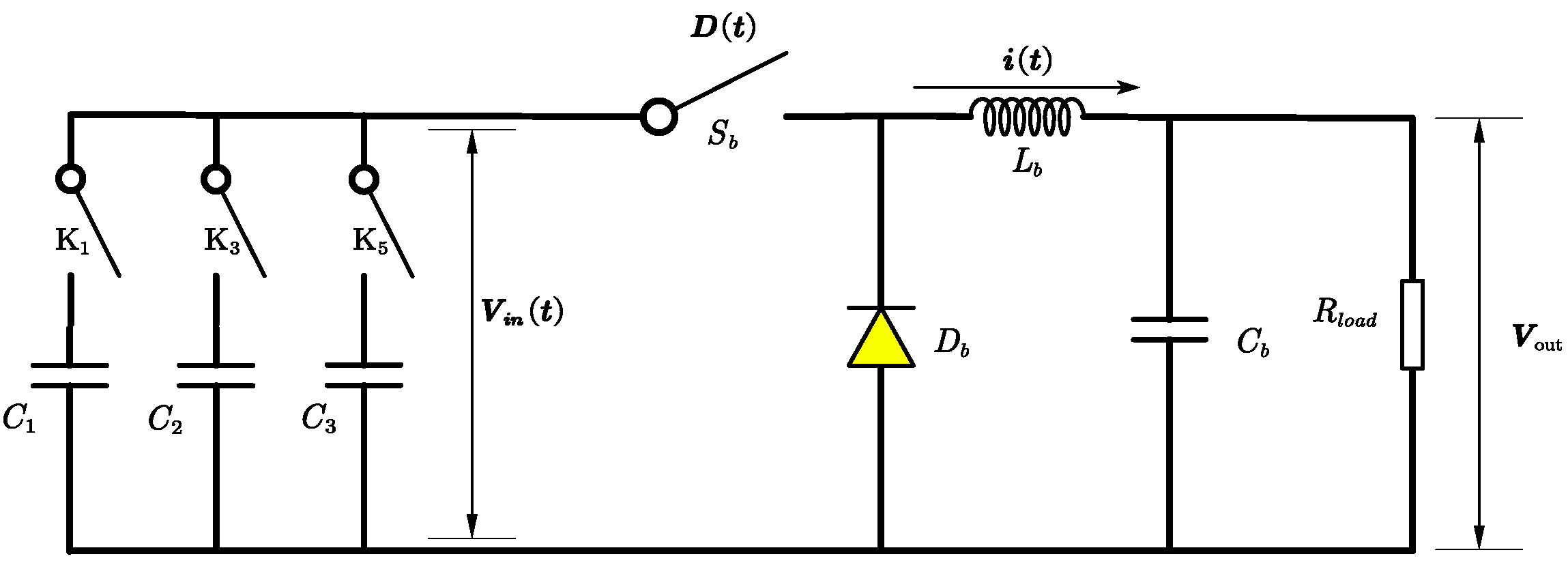
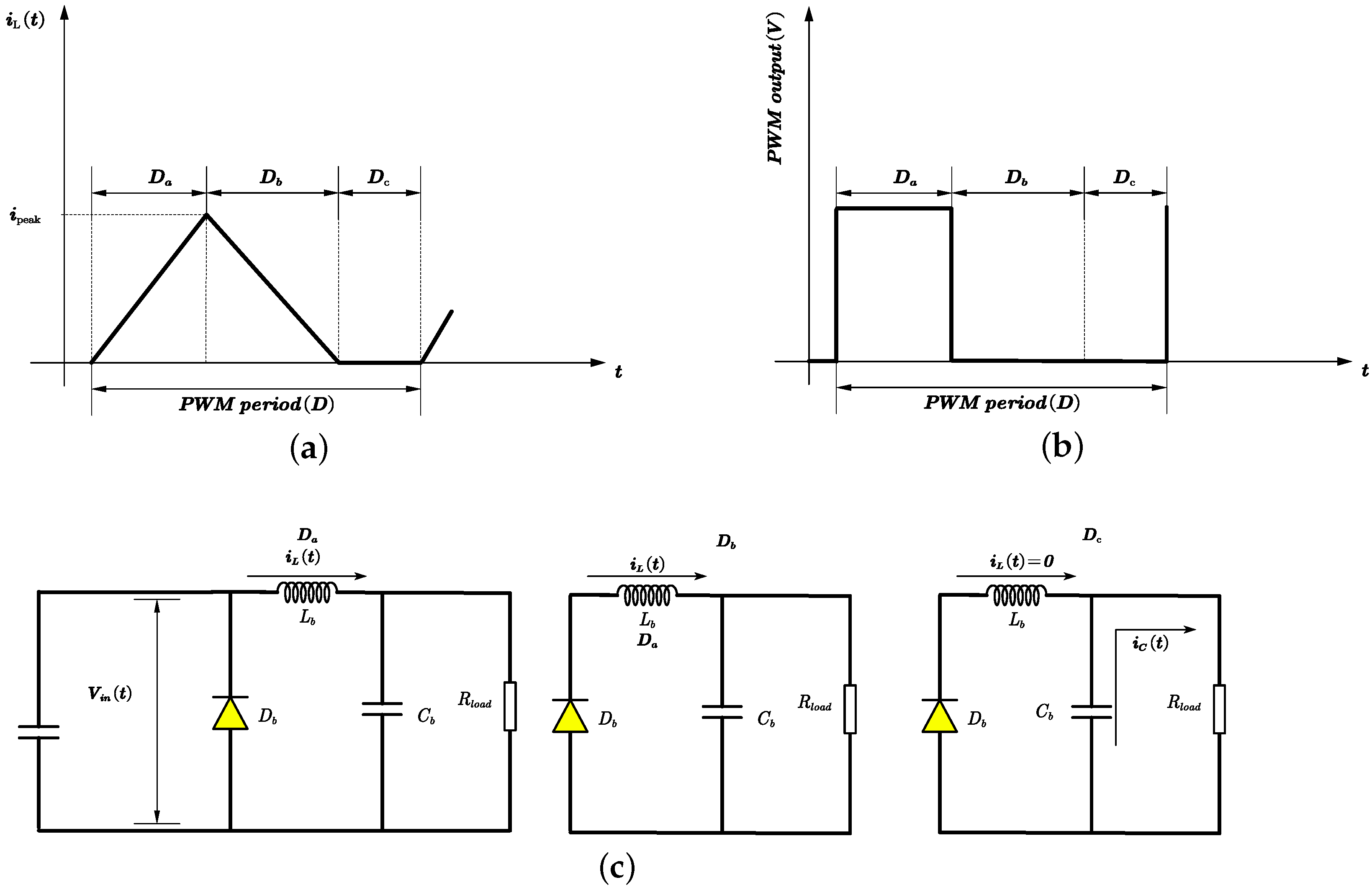
3.1.2. TENG’s DC-DC Converter Structure
3.2. TENG’s System Control
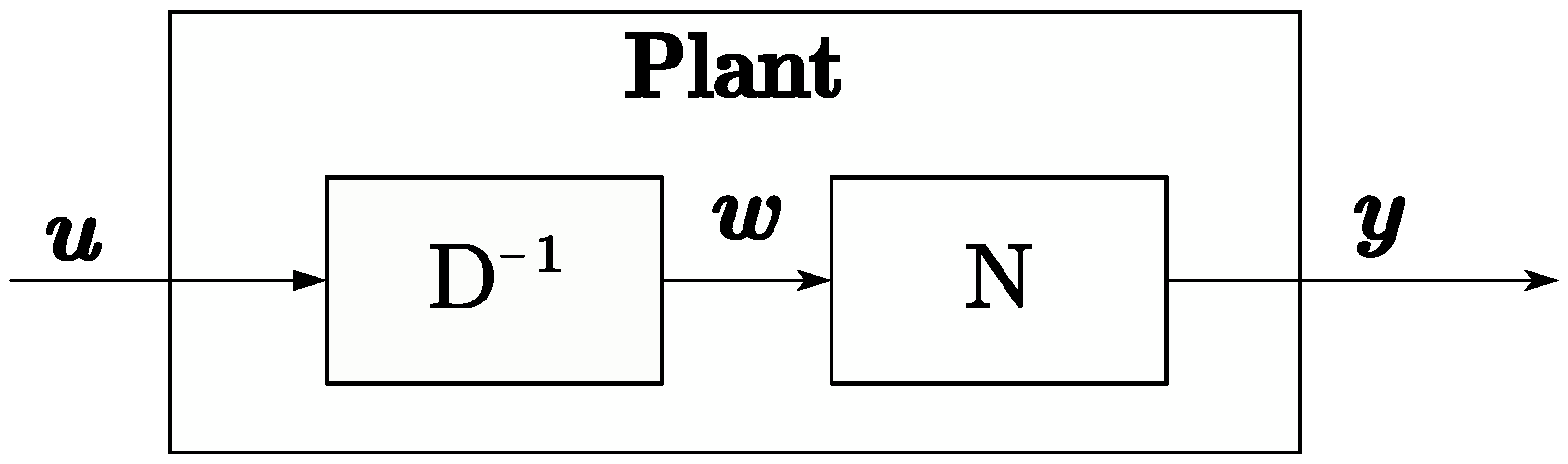
3.2.1. Operator-Based TENG System Decomposition
- -
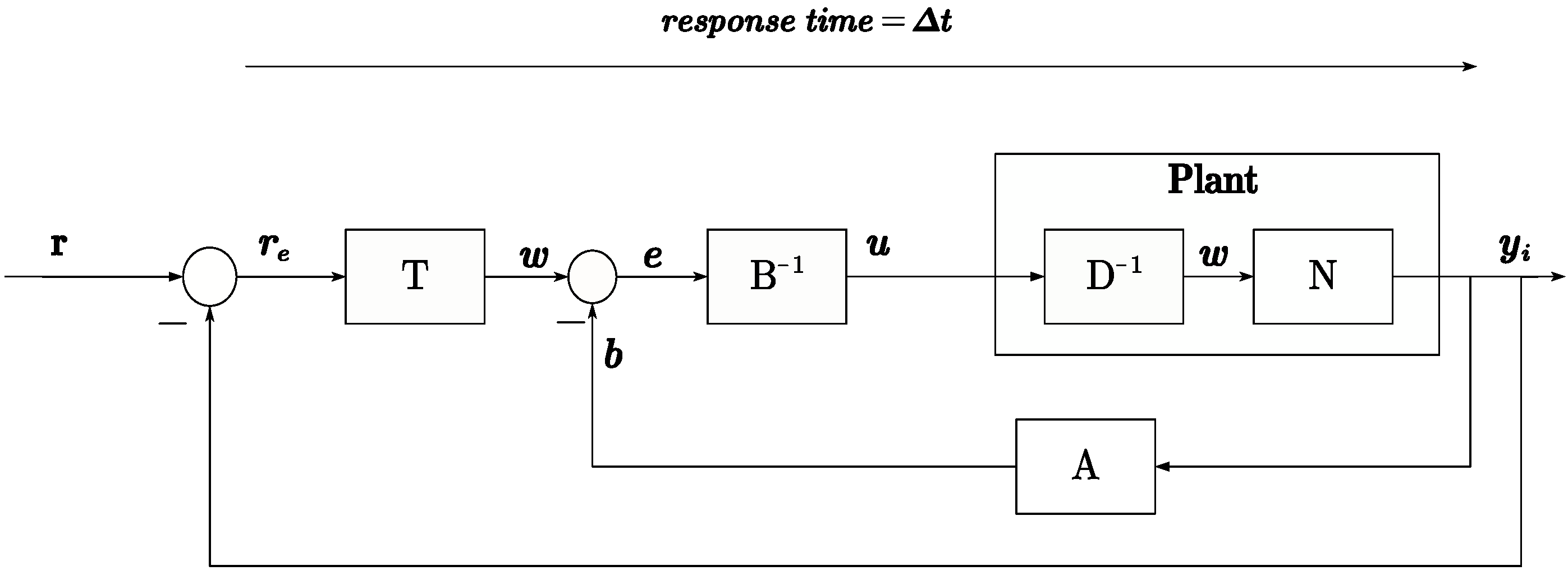
- A implements the mapping from output y to feedback b. Here, b is constructed as , residing in the same space as w, yielding (29).
- -
- implements the mapping from error e to input u. Given that b is structured in the same space as w, e is also designed to reside in this space, specifically , resulting in (30). The construction of B is represented as per the formula, facilitating the mapping from u to e.
3.2.2. Plant Tracking Designed for Reference
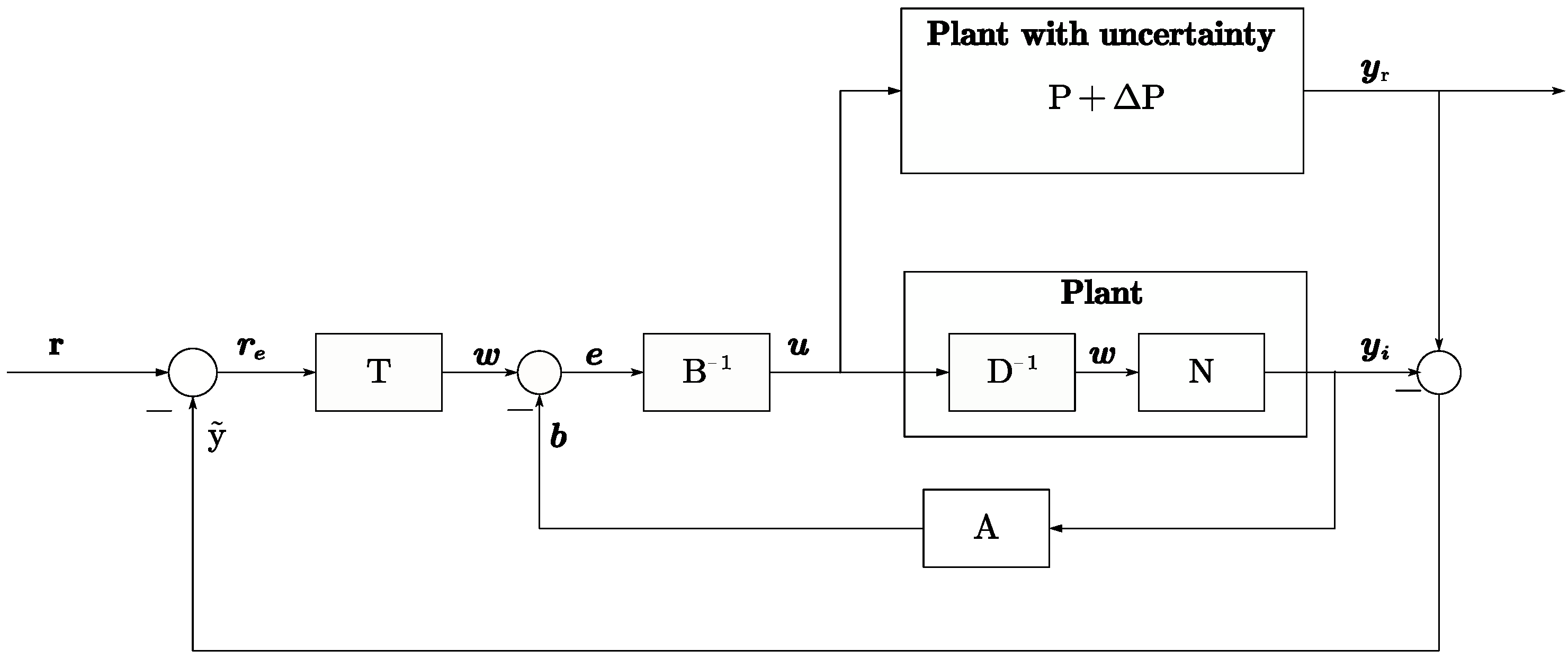
3.2.3. Plant Suppression Designed for Uncertainty
4. Simulation and Verification
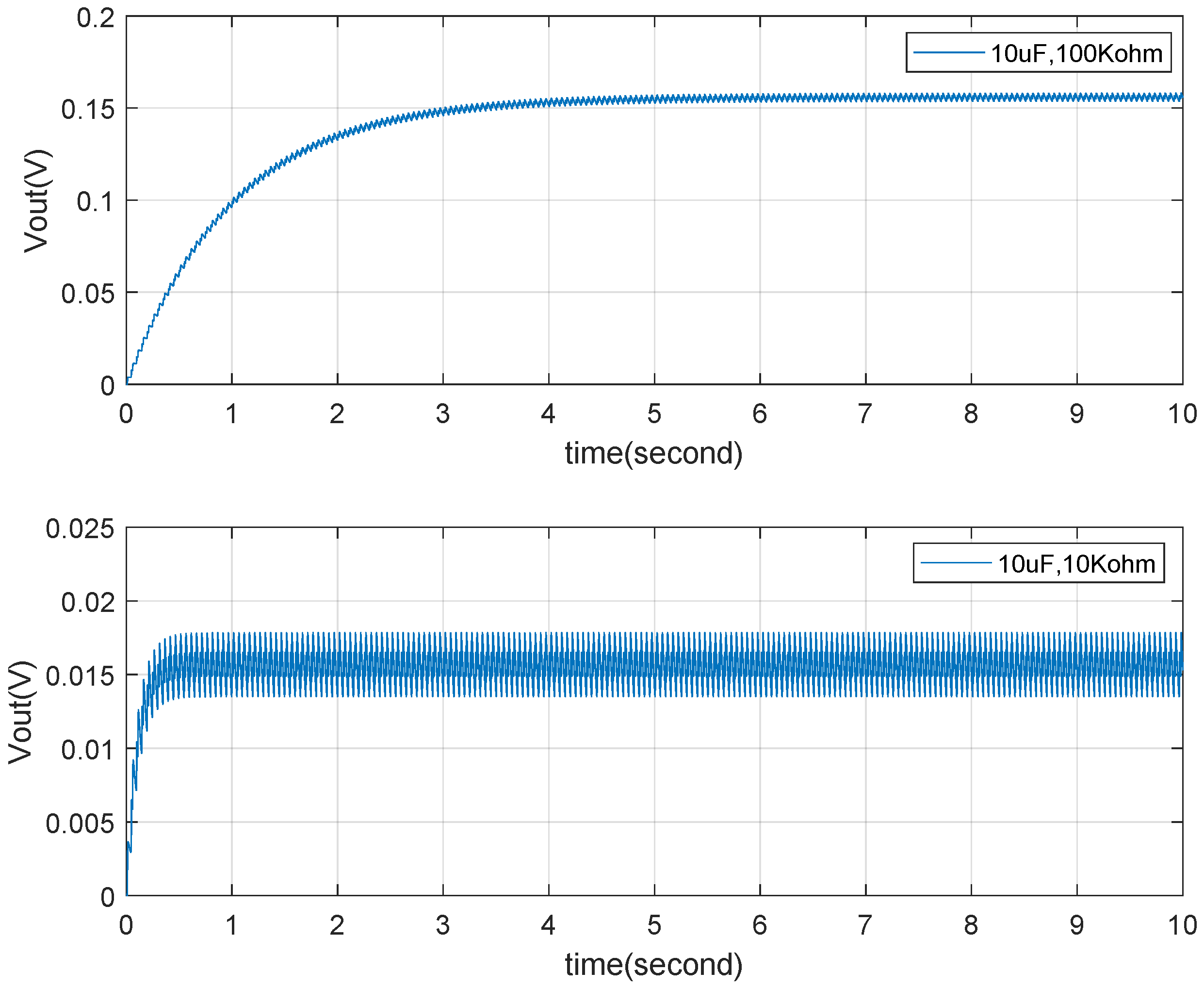
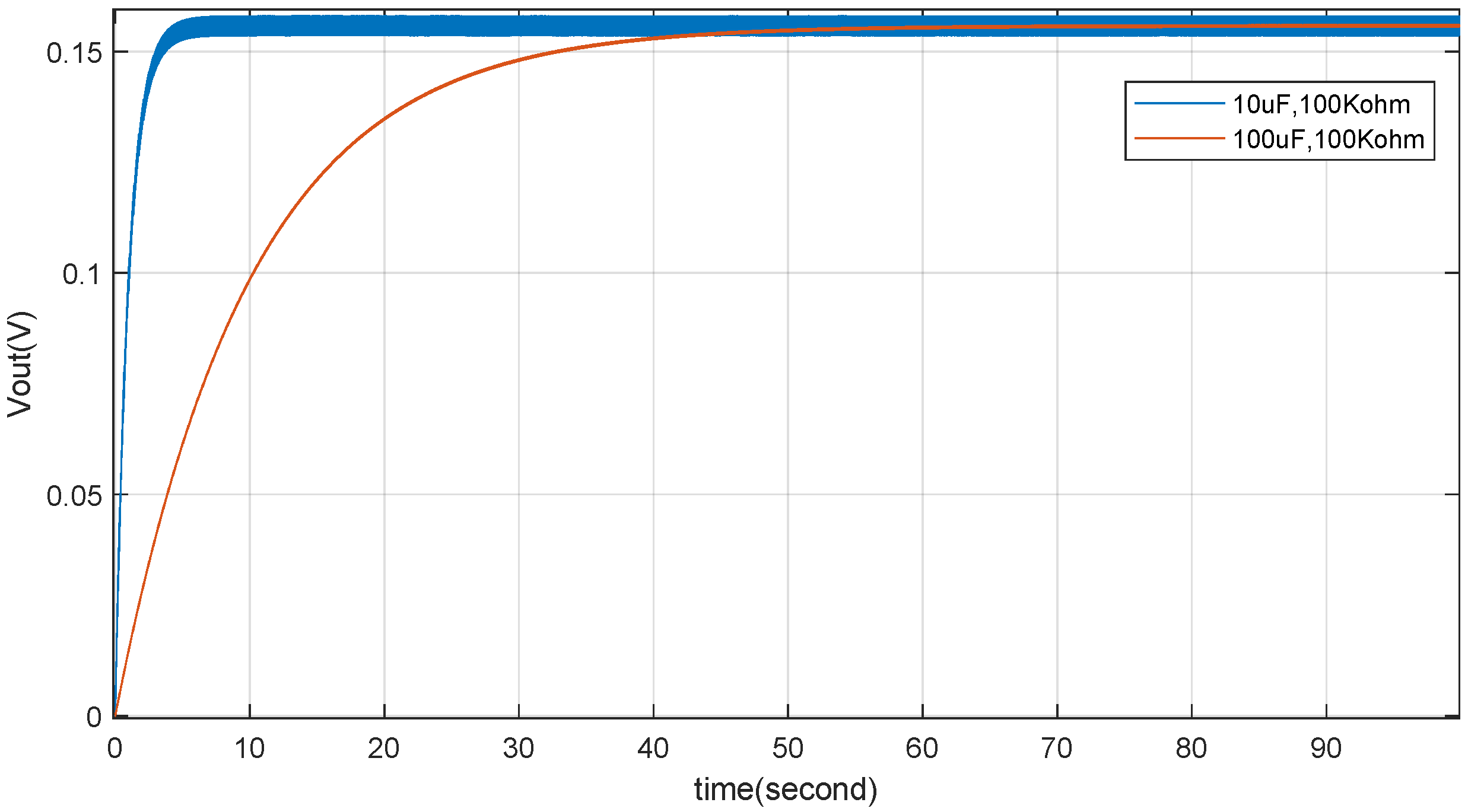
4.1. Simulation of TENG Model
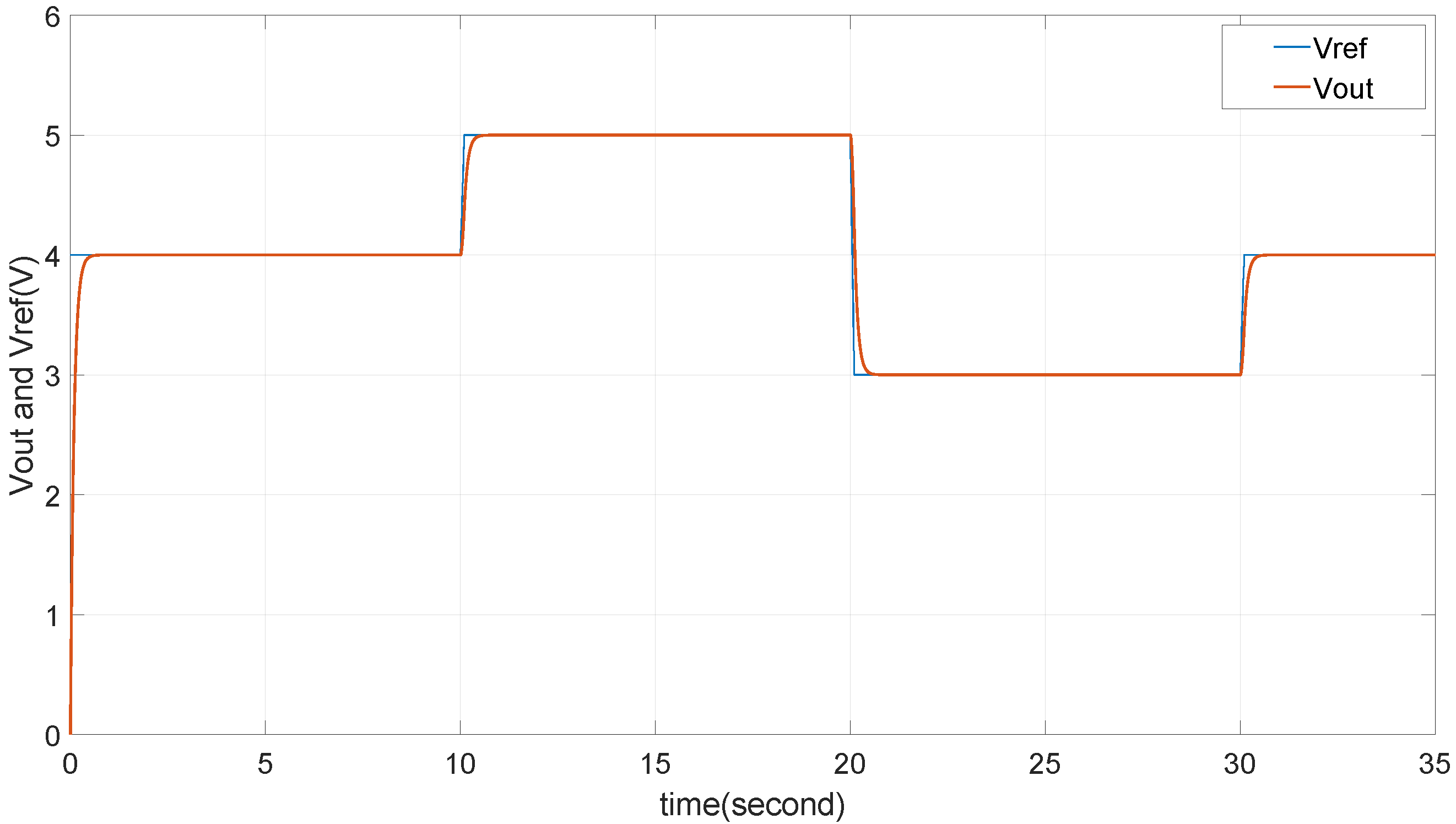
4.2. Simulation of Tracking for Reference
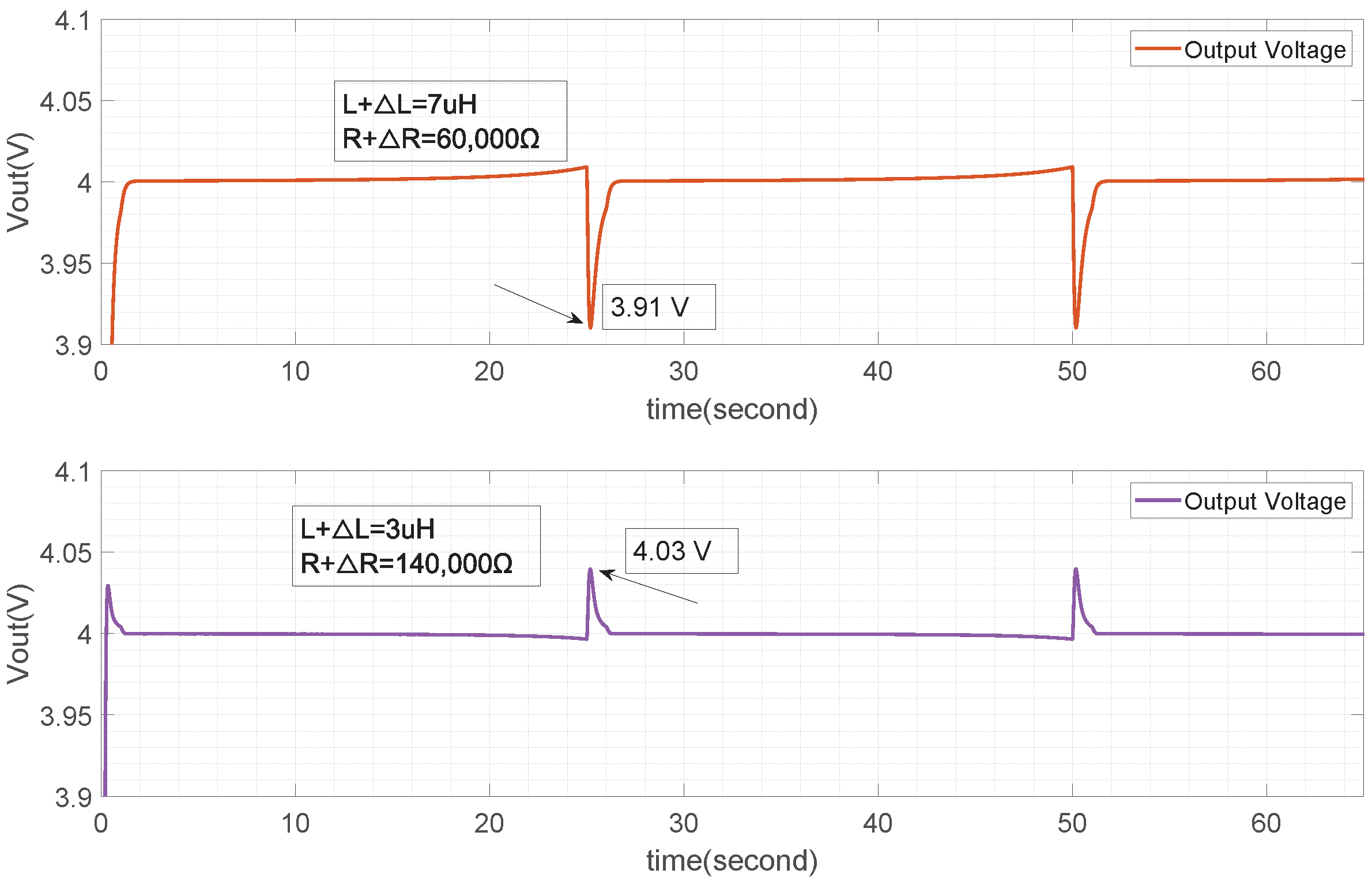
4.3. Simulation of Suppression for Uncertainty
5. Conclusions
- The buck model in DCM is a nonlinear system model with parameters including inductance, capacitance, duty cycle, input voltage, and output voltage. The multi-parameter nature of the model suggests that the control algorithms will be complex, leading to the need for research on output tracking and disturbance suppression based on this model.
- This paper applies the RCF method to the buck model, resulting in a simplified tracking compensator. Based on this, a more complex disturbance suppression algorithm is developed using operator theory and validated through simulations, with favorable results. In practical applications, as shown in Figure 18, represents the actual buck circuit, while other parts of the algorithm are based on the buck model (including parameters). By sampling the output voltage and input voltage parameters of , the algorithm can compute the duty signal. This is because the algorithm has already accounted for the effects of device parameter fluctuations (disturbance sources) within the buck circuit, eliminating the need to focus on parameter variations. This design is characterized by its low dependency on the controlled object and high feasibility.
- Given that TENGs are low-energy-output systems, future research should focus on how to effectively leverage the system’s self-power capability to run the algorithm (based on the controller) while minimizing energy loss and improving the system’s energy utilization efficiency.
- Parasitic parameters and model reconstruction: The mathematical model of the buck converter circuit will be reconstructed to include parasitic parameters of key components such as diodes, inductors, capacitors, resistors, and switches. The uncertainty sources will be expanded to encompass these parasitic parameters. Suppression of such uncertainties will be achieved through compensator design based on operator theory.
- Storage capacitor array model: The design and validation of the storage capacitor array model will be further refined. Testing will be conducted on an experimental platform integrated with the TENG system to ensure that the model accurately reflects real-world performance.
- Comprehensive system modeling: A detailed mathematical model of the external mechanical vibration source for the TENG will be developed and integrated with the TENG and power system models to create a comprehensive system. Research will focus on the efficient conversion of mechanical vibration energy into electrical energy based on this integrated model.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fan, F.R.; Tian, Z.Q.; Wang, Z.L. Flexible triboelectric generator. Nano Energy 2012, 1, 328–334. [Google Scholar] [CrossRef]
- Hu, T.; Wang, H.; Harmon, W.; Bamgboje, D.; Wang, Z.L. Current progress on power management systems for triboelectric nanogenerators. IEEE Trans. Power Electron. 2022, 37, 9850–9864. [Google Scholar] [CrossRef]
- Luo, J.; Wang, Z.L. Recent progress of triboelectric nanogenerators: From fundamental theory to practical applications. EcoMat 2020, 2, e12059. [Google Scholar] [CrossRef]
- Wu, C.; Wang, A.C.; Ding, W.; Guo, H.; Wang, Z.L. Triboelectric nanogenerator: A foundation of the energy for the new era. Adv. Energy Mater. 2019, 9, 1802906. [Google Scholar] [CrossRef]
- Zhu, G.; Pan, C.; Guo, W.; Chen, C.; Zhou, Y.; Yu, R.; Wang, Z. Triboelectric-generator-driven pulse electrodeposition for micropatterning. Nano Lett. 2012, 12, 4960–4965. [Google Scholar] [CrossRef]
- Wang, S.; Lin, L.; Wang, Z. Nanoscale triboelectric-effect-enabled energy conversion for sustainably powering portable electronics. Nano Lett. 2012, 12, 6339–6346. [Google Scholar] [CrossRef]
- Zhu, G.; Lin, Z.; Jing, Q.; Bai, P.; Pan, C.; Yang, Y.; Zhou, Y.; Wang, Z. Toward large-scale energy harvesting by a nanoparticle-enhanced triboelectric nanogenerator. Nano Lett. 2013, 13, 847–853. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Lin, L.; Xie, Y.; Jing, Q.; Niu, S.; Wang, Z. Sliding-triboelectric nanogenerators based on in-plane charge-separation mechanism. Nano Lett. 2013, 13, 2226–2233. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Zhou, Y.; Zhang, H.; Liu, Y.; Lee, S.; Wang, Z. A single-electrode based triboelectric nanogenerator as self-powered tracking system. Adv. Mater. 2013, 25, 6594–6601. [Google Scholar] [CrossRef]
- Wang, S.; Xie, Y.; Niu, S.; Lin, L.; Wang, Z. Freestanding triboelectric-layer-based nanogenerators for harvesting energy from a moving object or human motion in contact and non-contact modes. Adv. Mater. 2014, 26, 2818–2824. [Google Scholar] [CrossRef]
- Li, Q.; Fu, S.; Li, X.; Chen, H.; He, W.; Yang, Q.; Zhang, X.; Yang, H.; Ren, D.; Xi, Y. Overall performance improvement of direct-current triboelectric nanogenerators by charge leakage and ternary dielectric evaluation. Energy Environ. Sci. 2023, 16, 3514–3525. [Google Scholar] [CrossRef]
- Li, Q.; Hu, Y.; Yang, Q.; Li, X.; Zhang, X.; Yang, H.; Ji, P.; Xi, Y.; Wang, Z.L. A robust constant–voltage DC triboelectric nanogenerator using the ternary dielectric triboelectrification effect. Adv. Energy Mater. 2023, 13, 2202921. [Google Scholar] [CrossRef]
- Li, Q.; Liu, W.; Yang, H.; He, W.; Long, L.; Wu, M.; Zhang, X.; Xi, Y.; Hu, C.; Wang, Z.L. Ultra-stability high-voltage triboelectric nanogenerator designed by ternary dielectric triboelectrification with partial soft-contact and non-contact mode. Nano Energy 2021, 90, 106585. [Google Scholar] [CrossRef]
- Li, Q.; Fu, S.; Yang, H.; Li, X.; Zhang, X.; Hu, C.; Xi, Y. Achieving ultrahigh DC-power triboelectric nanogenerators by lightning rRod-inspired field emission modeling. Research 2024, 7, 0437. [Google Scholar] [CrossRef] [PubMed]
- Harmon, W.; Bamgboje, D.; Guo, H.; Hu, T.; Wang, Z.L. Self-driven power management system for triboelectric nanogenerators. Nano Energy 2020, 71, 104642. [Google Scholar] [CrossRef]
- Ha, H.; Qaiser, N.; Yun, T.G.; Cheong, J.Y.; Lim, S.; Hwang, B. Sensing mechanism and application of mechanical strain sensor: A mini-review. Facta Univ. Ser. Mech. Eng. 2023, 21, 751–772. [Google Scholar] [CrossRef]
- Hu, C.; Yang, Y.; Wang, Z.L. Quantitative comparison between the effective energy utilization efficiency of triboelectric nanogenerator and electromagnetic generator post power management. Nano Energy 2022, 103, 107760. [Google Scholar] [CrossRef]
- Cheng, X.; Tang, W.; Song, Y.; Chen, H.; Zhang, H.; Wang, Z.L. Power management and effective energy storage of pulsed output from triboelectric nanogenerator. Nano Energy 2019, 61, 517–532. [Google Scholar] [CrossRef]
- Vauche, G.; Corbier, C. Enhanced performance in energy of low frequency triboelectric-nanogenerator systems. J. Microelectromechanical Syst. 2024, 33, 209–216. [Google Scholar] [CrossRef]
- Walden, R.; Kumar, C.; Mulvihill, D.M.; Pillai, S.C. Opportunities and challenges in triboelectric nanogenerator (TENG) based sustainable energy generation technologies: A mini-review. Chem. Eng. J. Adv. 2022, 9, 100237. [Google Scholar] [CrossRef]
- Bai, Y.; Feng, H.; Li, Z. Theory and applications of high-voltage triboelectric nanogenerators. Cell Rep. Phys. Sci. 2022, 3, 101108. [Google Scholar] [CrossRef]
- Tu, Y.; Xu, Z.; Xiao, Z.; Zheng, D.; Ding, C.; Dai, G.; Chen, S.; Ding, W.; Wang, X.; Xu, S. IC-Compatible high-efficiency power management for triboelectric nanogenerators based on the concept of limit. IEEE Trans. Power Electron. 2023, 39, 6–13. [Google Scholar] [CrossRef]
- Kara, I.; Becermis, M.; Kamar, M.A.A.; Aktan, M.; Dogan, H.; Mutlu, S. A 70-to-2 V triboelectric energy harvesting system utilizing parallel-SSHI rectifier and DC-DC converters. IEEE Trans. Circuits Syst. Regul. Pap. 2020, 68, 210–223. [Google Scholar] [CrossRef]
- Xi, F.; Pang, Y.; Li, W.; Jiang, T.; Zhang, L.; Guo, T.; Liu, G.; Zhang, C.; Wang, Z.L. Universal power management strategy for triboelectric nanogenerator. Nano Energy 2017, 37, 168–176. [Google Scholar] [CrossRef]
- Mumtaz, F.; Yahaya, N.Z.; Meraj, S.T.; Singh, B.; Kannan, R.; Ibrahim, O. Review on non-isolated DC-DC converters and their control techniques for renewable energy applications. Ain Shams Eng. J. 2021, 12, 3747–3763. [Google Scholar] [CrossRef]
- Niu, S.; Zhou, Y.S.; Wang, S.; Liu, Y.; Lin, L.; Bando, Y.; Wang, Z.L. Simulation method for optimizing the performance of an integrated triboelectric nanogenerator energy harvesting system. Nano Energy 2014, 8, 150–156. [Google Scholar] [CrossRef]
- Wang, K.; Liao, Y.; Li, W.; Zhang, Y.; Zhou, X.; Wu, C.; Chen, R.; Kim, T.W. Triboelectric nanogenerator module for circuit design and simulation. Nano Energy 2023, 107, 108139. [Google Scholar] [CrossRef]
- Deng, M.; Inoue, A.; Ishikawa, K. Operator-based nonlinear feedback control design using robust right coprime factorization. IEEE Trans. Autom. Control. 2006, 51, 645–648. [Google Scholar] [CrossRef]
- Wang, A.; Deng, M. Operator-based robust nonlinear tracking control for a human multi-joint arm-like manipulator with unknown time-varying delays. Appl. Math. Inf. Sci. 2012, 6, 459–468. [Google Scholar]
- Deng, M.; Inoue, A.; Goto, S. Operator based thermal control of an aluminum plate with a peltier device. Int. J. Innov. Comput. Inf. Control. 2008, 4, 3219–3229. [Google Scholar]
- Deng, M.; Saijo, N.; Gomi, H.; Inoue, A. A robust real time method for estimating human multijoint arm viscoelasticity. Int. J. Innov. Comput. Inf. Control. 2006, 2, 705–721. [Google Scholar]
- An, Z.; Deng, M.; Morohoshi, Y. Right coprime factorization-based simultaneous control of input hysteresis and output disturbance and its application to soft robotic finger. Electronics 2024, 13, 2025. [Google Scholar] [CrossRef]
- Tan, D.; Wang, K.; Zhou, J.; Peng, J.; Wang, Q. A brief review of nonlinear triboelectric nanogenerator. Int. J. Dyn. Control. 2024, 12, 2072–2092. [Google Scholar] [CrossRef]
- Zou, H.; Zhang, Y.; Guo, L.; Wang, P.; He, X.; Dai, G.; Zheng, H.; Chen, C.; Wang, A.C.; Xu, C.; et al. Quantifying the triboelectric series. Nat. Commun. 2019, 10, 1427. [Google Scholar] [CrossRef]
- Niu, S.; Wang, Z.L. Theoretical systems of triboelectric nanogenerators. Nano Energy 2015, 14, 161–192. [Google Scholar] [CrossRef]
- Niu, S.; Wang, S.; Lin, L.; Liu, Y.; Zhou, Y.S.; Hu, Y.; Wang, Z.L. Theoretical study of contact-mode triboelectric nanogenerators as an effective power source. Energy Environ. Sci. 2013, 6, 3576–3583. [Google Scholar] [CrossRef]
- Niu, S.; Liu, Y.; Zhou, Y.S.; Wang, S.; Lin, L.; Wang, Z.L. Optimization of triboelectric nanogenerator charging systems for efficient energy harvesting and storage. IEEE Trans. Electron Devices 2014, 62, 641–647. [Google Scholar]
- MaksimoviC, D.; Cuk, S. A unified analysis of PWM converters in discontinuous modes. IEEE Trans. Power Electron. 1991, 6, 476–490. [Google Scholar] [CrossRef]
- Leung, K.K.S.; Chung, H.S.h. A comparative study of boundary control with first-and second-order switching surfaces for buck converters operating in DCM. IEEE Trans. Power Electron. 2007, 22, 1196–1209. [Google Scholar] [CrossRef]
- Sun, J.; Mitchell, D.M.; Greuel, M.F.; Krein, P.T.; Bass, R.M. Averaged modeling of PWM converters operating in discontinuous conduction mode. IEEE Trans. Power Electron. 2001, 16, 482–492. [Google Scholar]
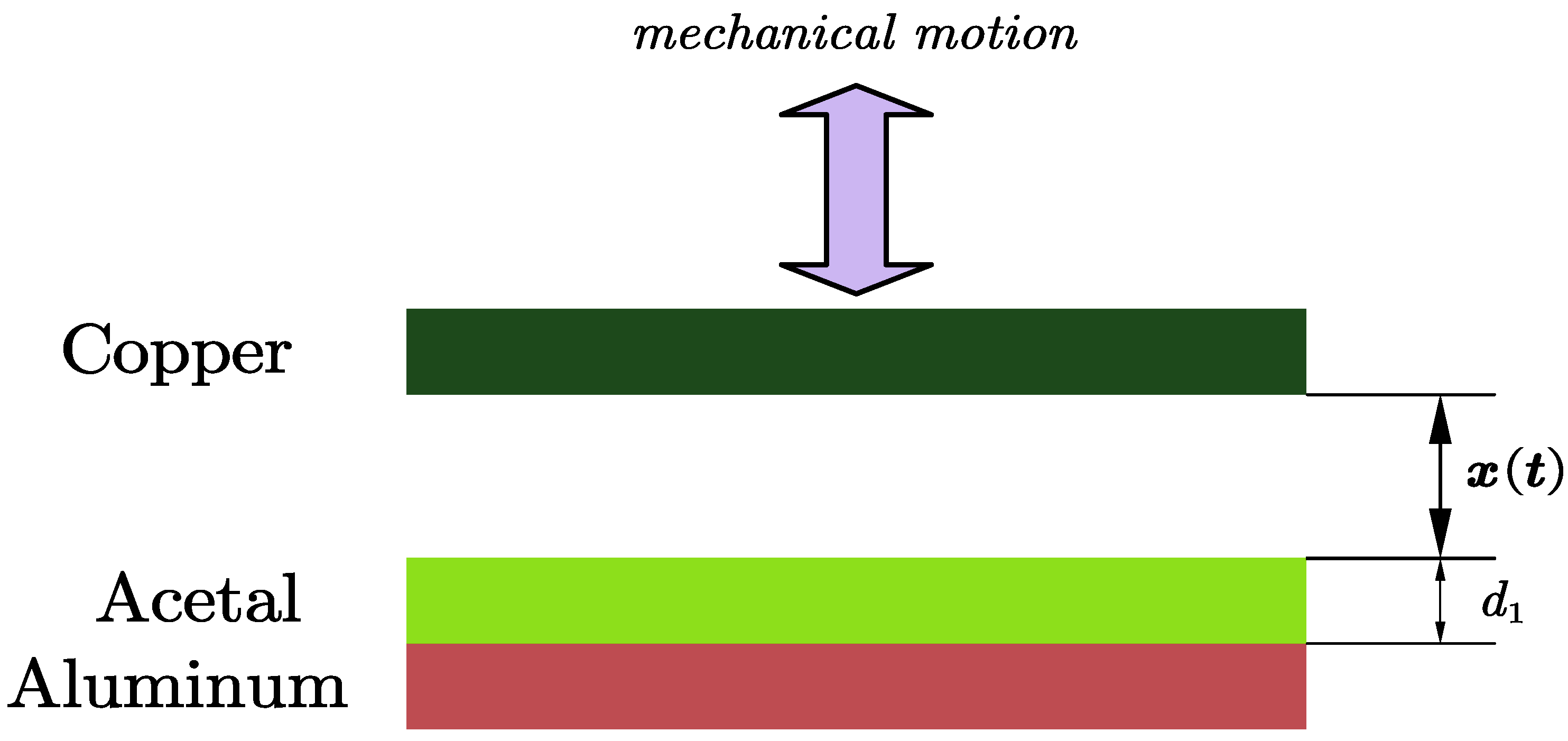
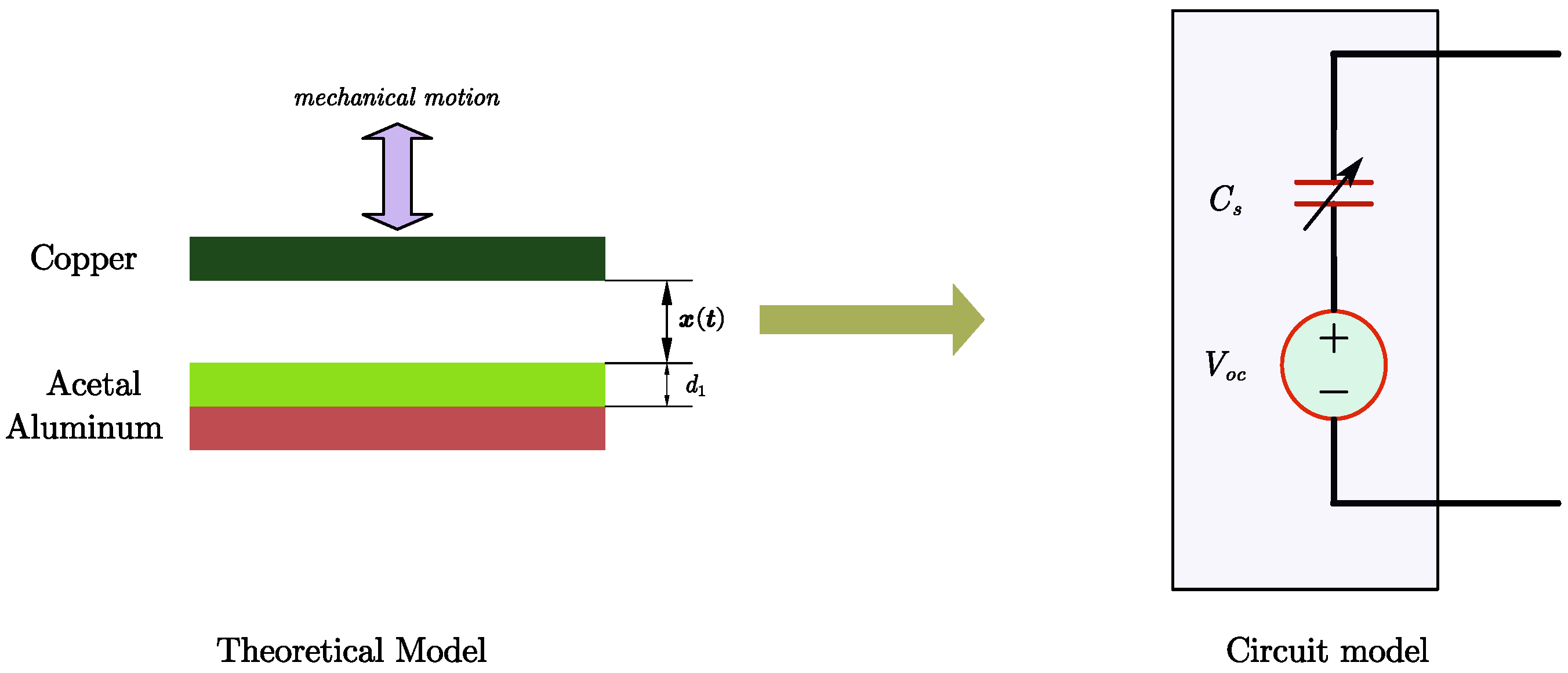
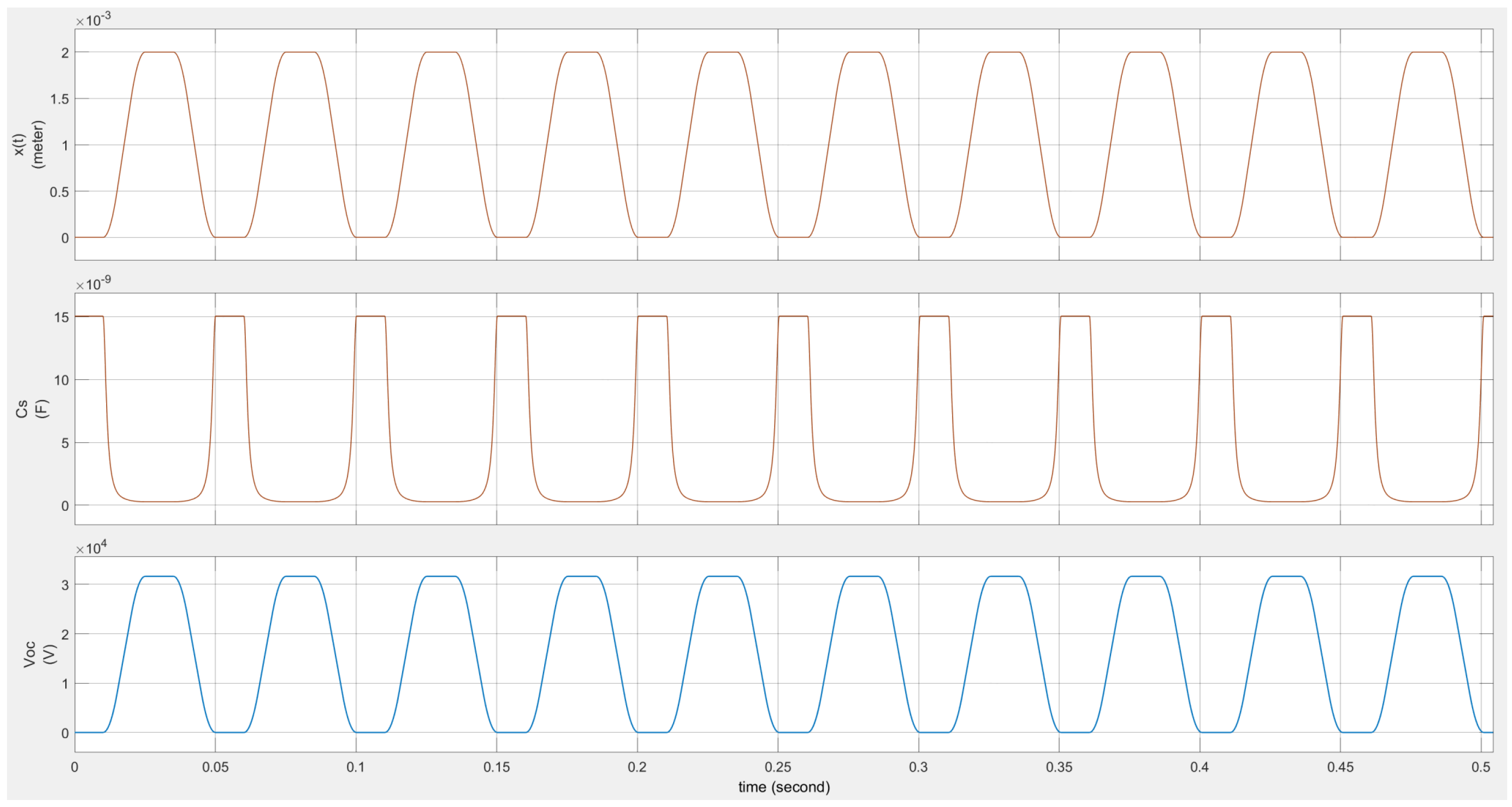
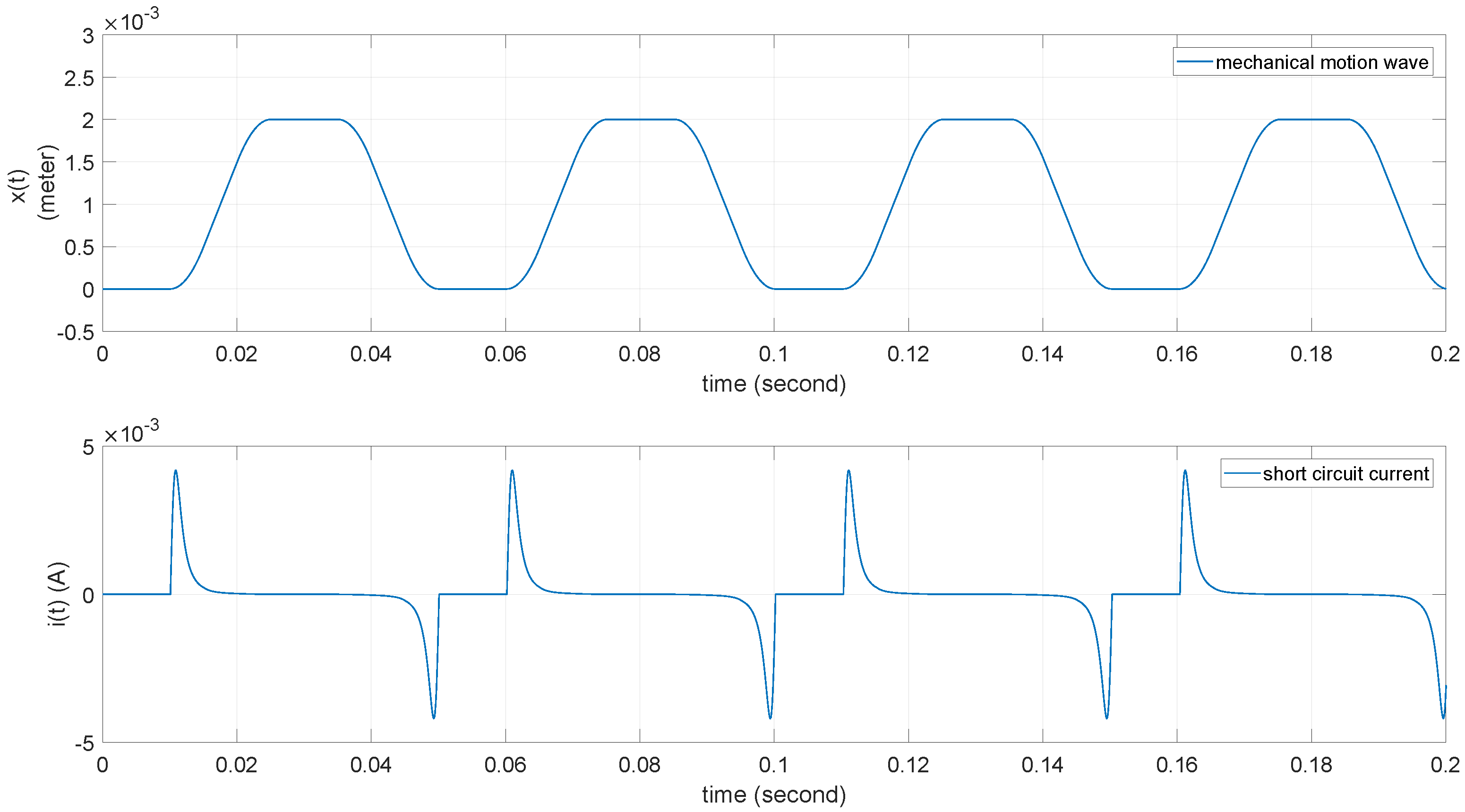
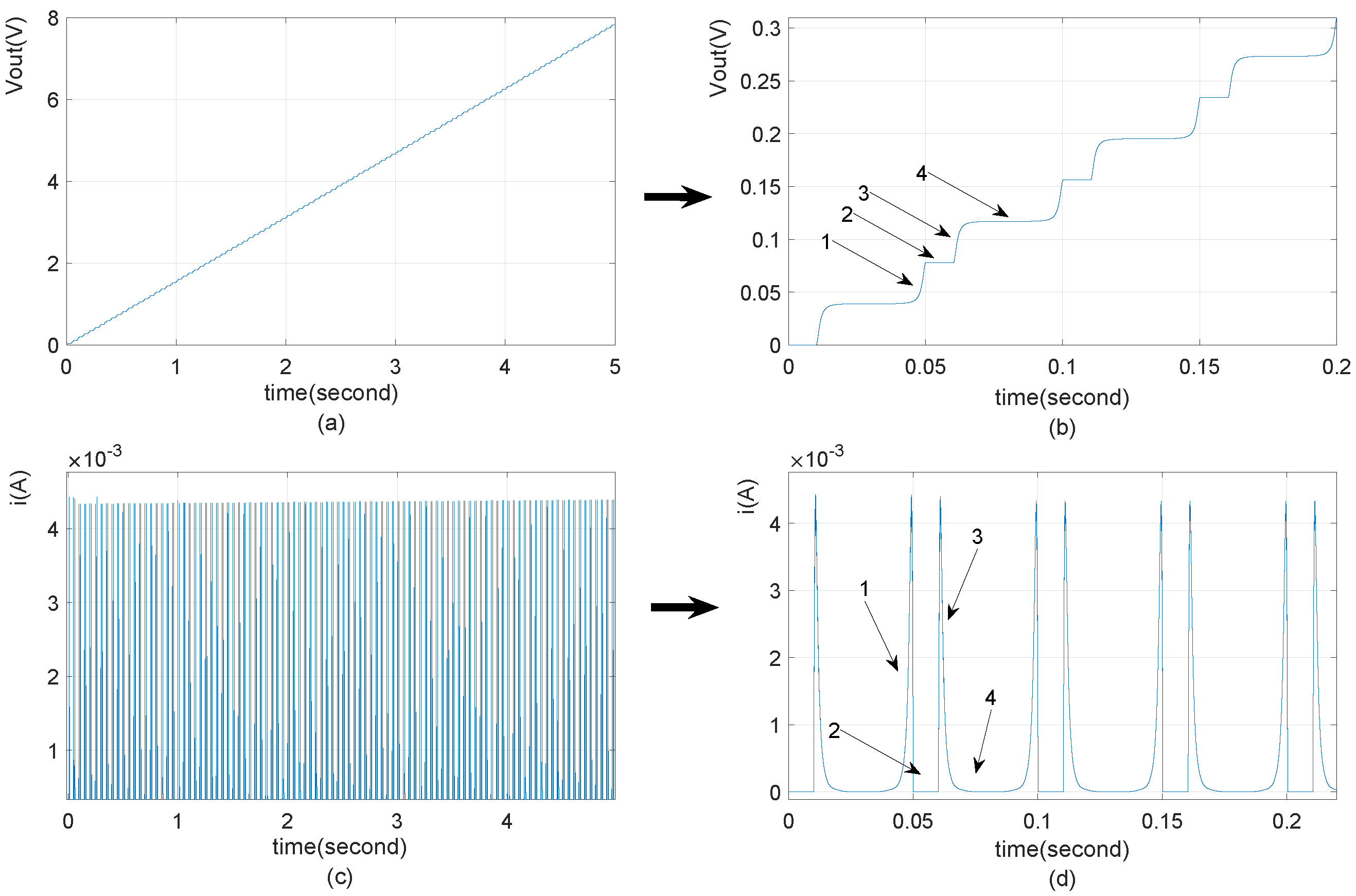







| Parameter | Symbol | Value |
|---|---|---|
| Dielectric thickness | 125 um | |
| Air dielectric constant | 8.85 F/m | |
| Relative dielectric constant | 3.4 | |
| Effective dielectric thickness | um | |
| Width of dielectric | W | m |
| Length of dielectric | L | m |
| Area of dielectric | S | m2 |
| Surface triboelectric charge density | 140 uCm−2 | |
| Maximum separation distance | 0.002 m | |
| Average velocity of mechanical motion | v | 0.133 ms−1 |
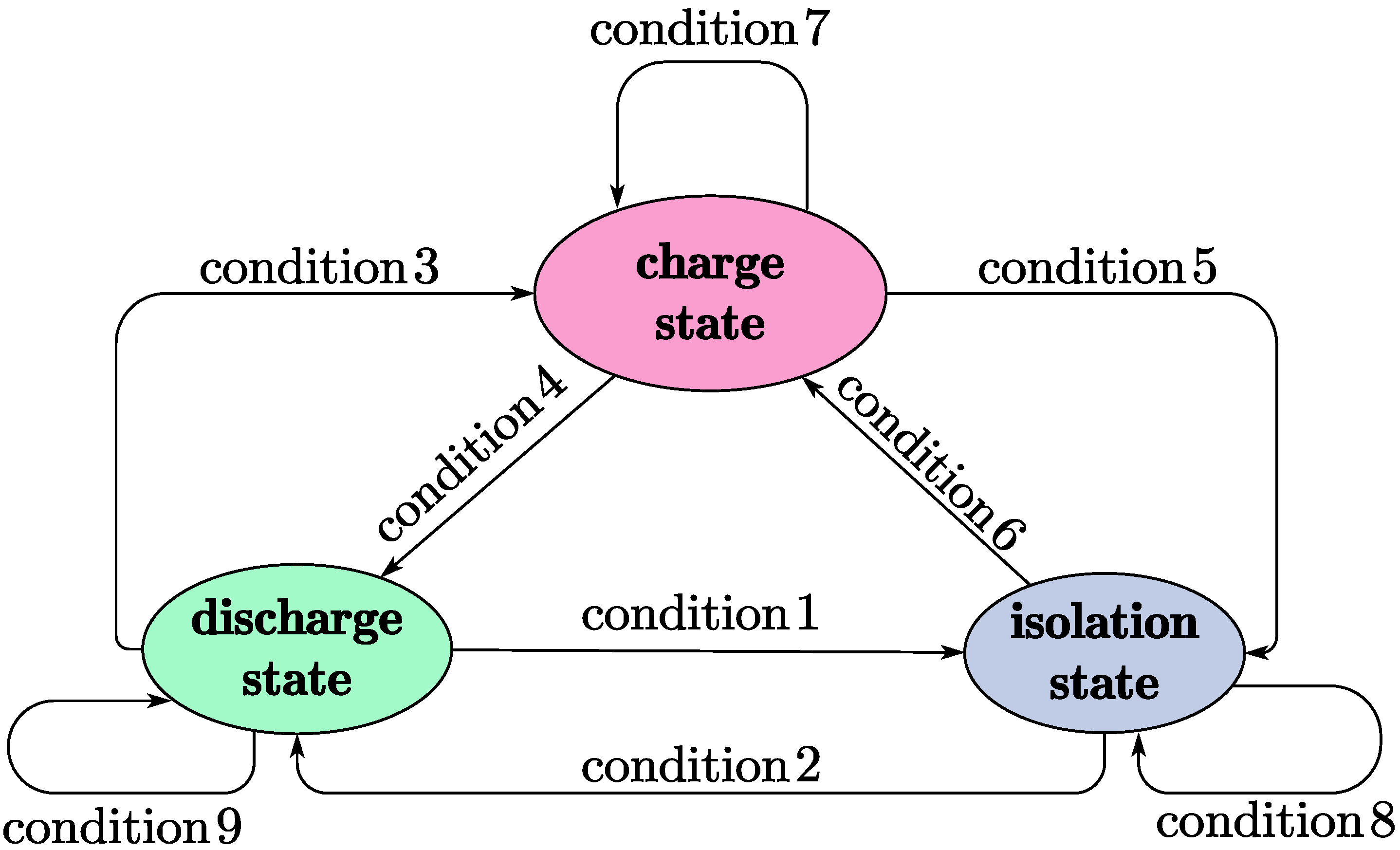
| 1 | State Definition |
|---|---|
| Discharge state | Storage capacitor is used as power source for DC-DC converter |
| Charge state | Storage capacitor is charged by TENG |
| Isolation state | Storage capacitor is not charged and not used as power source |
| 2 | Condition Definition |
| Condition 1 | and TENG is busy |
| Condition 2 | and power source is vacancy |
| Condition 3 | and TENG is idle |
| Condition 4 | and power source is vacancy |
| Condition 5 | and power source is available |
| Condition 6 | and TENG is idle |
| ine Condition 7 | |
| Condition 8 | Power source is available and TENG is busy |
| Condition 9 |
| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Inductor value | 5 | uH | |
| Capacitor value | 1 | uF | |
| Period of PWM | 1 | us | |
| Resistor load | 100 K | ||
| Voltage of output | 4 | V | |
| Voltage of input | See Figure 13 | V |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.; Shimane, R.; Deng, M. Operator-Based Triboelectric Nanogenerator Power Management and Output Voltage Control. Micromachines 2024, 15, 1114. https://doi.org/10.3390/mi15091114
Liu C, Shimane R, Deng M. Operator-Based Triboelectric Nanogenerator Power Management and Output Voltage Control. Micromachines. 2024; 15(9):1114. https://doi.org/10.3390/mi15091114
Chicago/Turabian StyleLiu, Chengyao, Ryusei Shimane, and Mingcong Deng. 2024. "Operator-Based Triboelectric Nanogenerator Power Management and Output Voltage Control" Micromachines 15, no. 9: 1114. https://doi.org/10.3390/mi15091114
APA StyleLiu, C., Shimane, R., & Deng, M. (2024). Operator-Based Triboelectric Nanogenerator Power Management and Output Voltage Control. Micromachines, 15(9), 1114. https://doi.org/10.3390/mi15091114








