Frequency Detection for String Instruments Using 1D-2D Non-Contact Mode Triboelectric Sensors
Abstract
1. Introduction
2. Design of the Sensing Device
3. Operating Modes and Principle of the Device
4. Experimental Results and Discussion
4.1. Measurement of the Electrical Outputs from the TENG and Coding for the Frequency Sensing Application
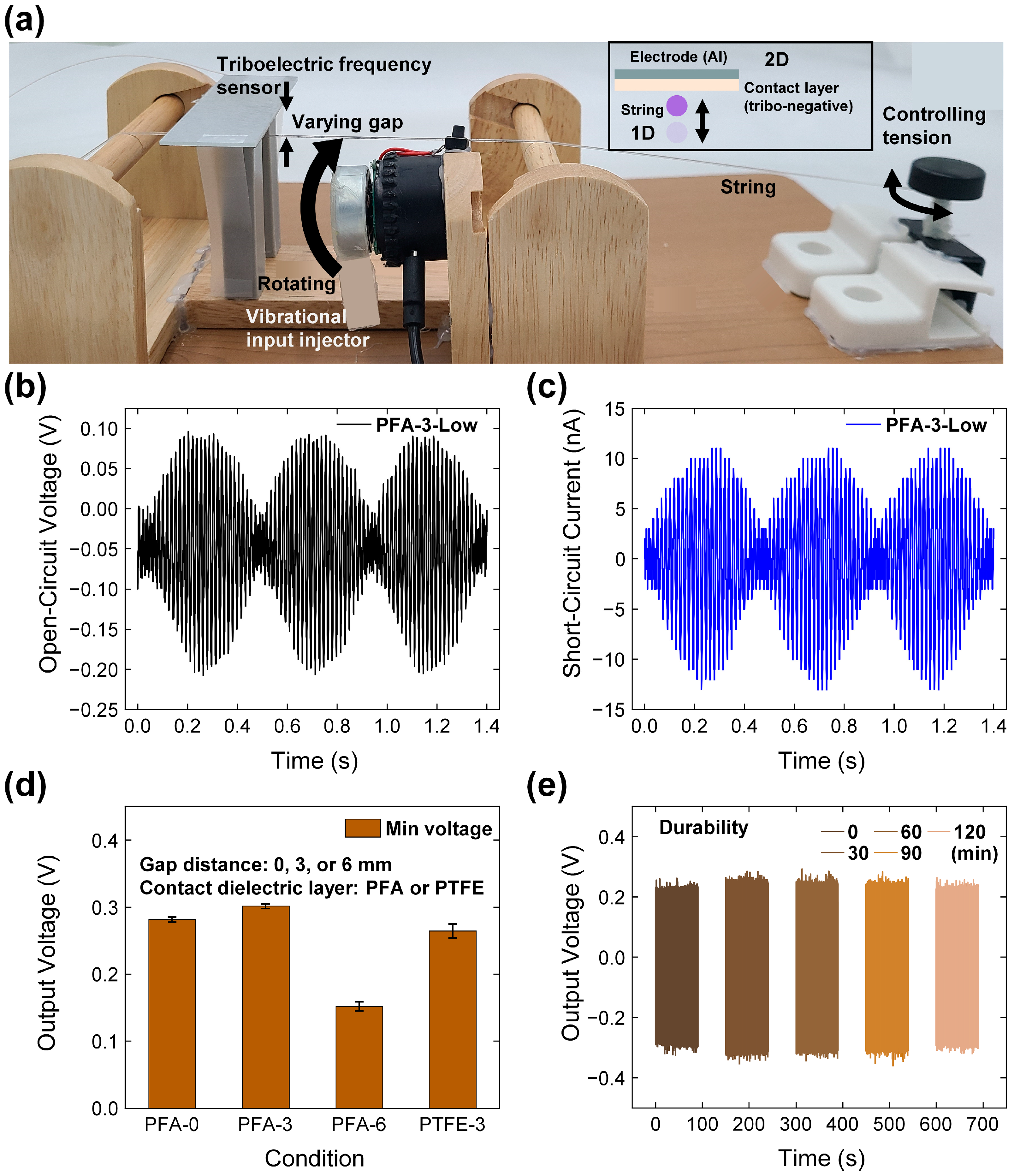
4.2. Setup for Measurement and Basic Electrical Output Characteristics
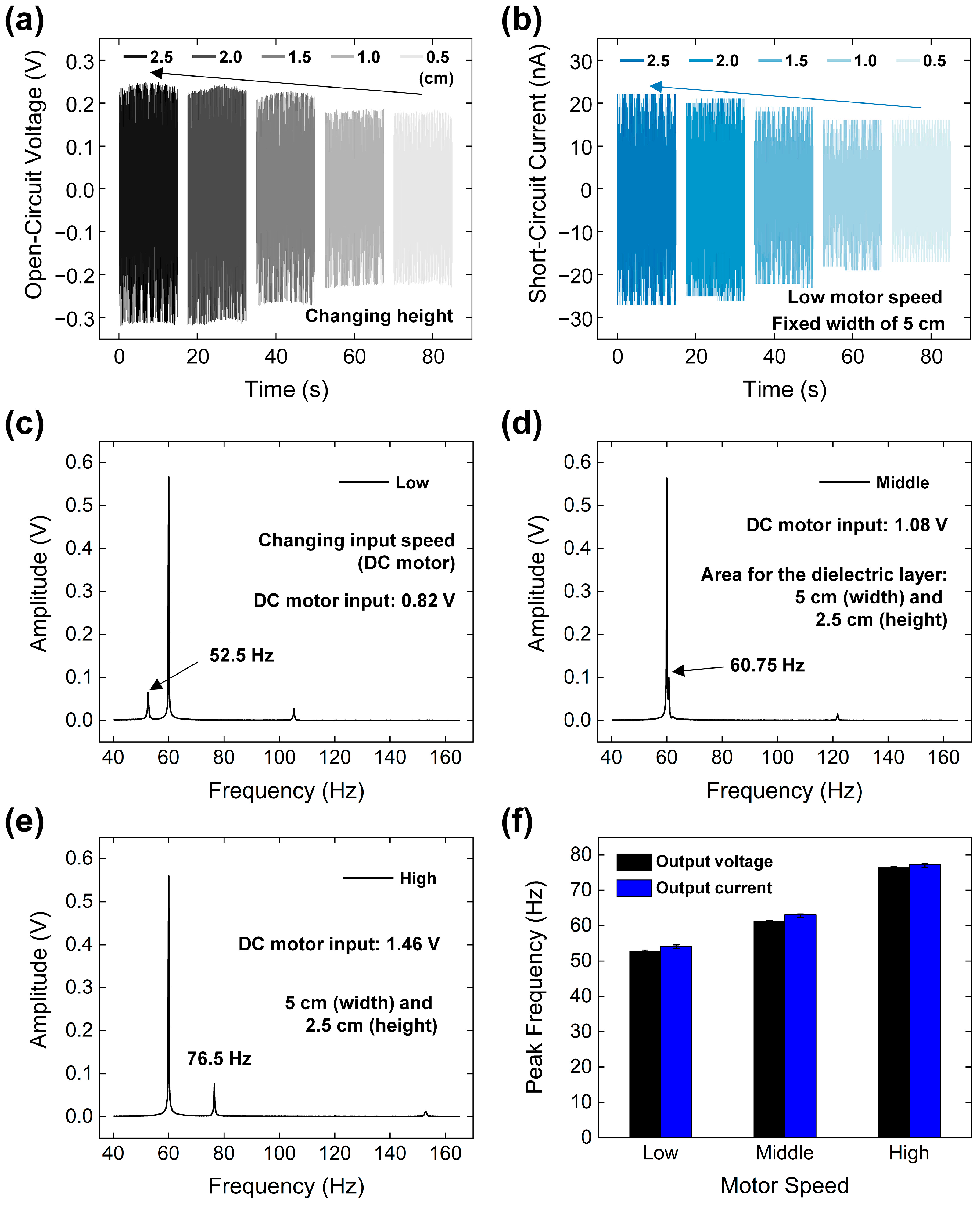
4.3. Electrical Outputs Varying Motor Speed and String Tension with Device Optimization
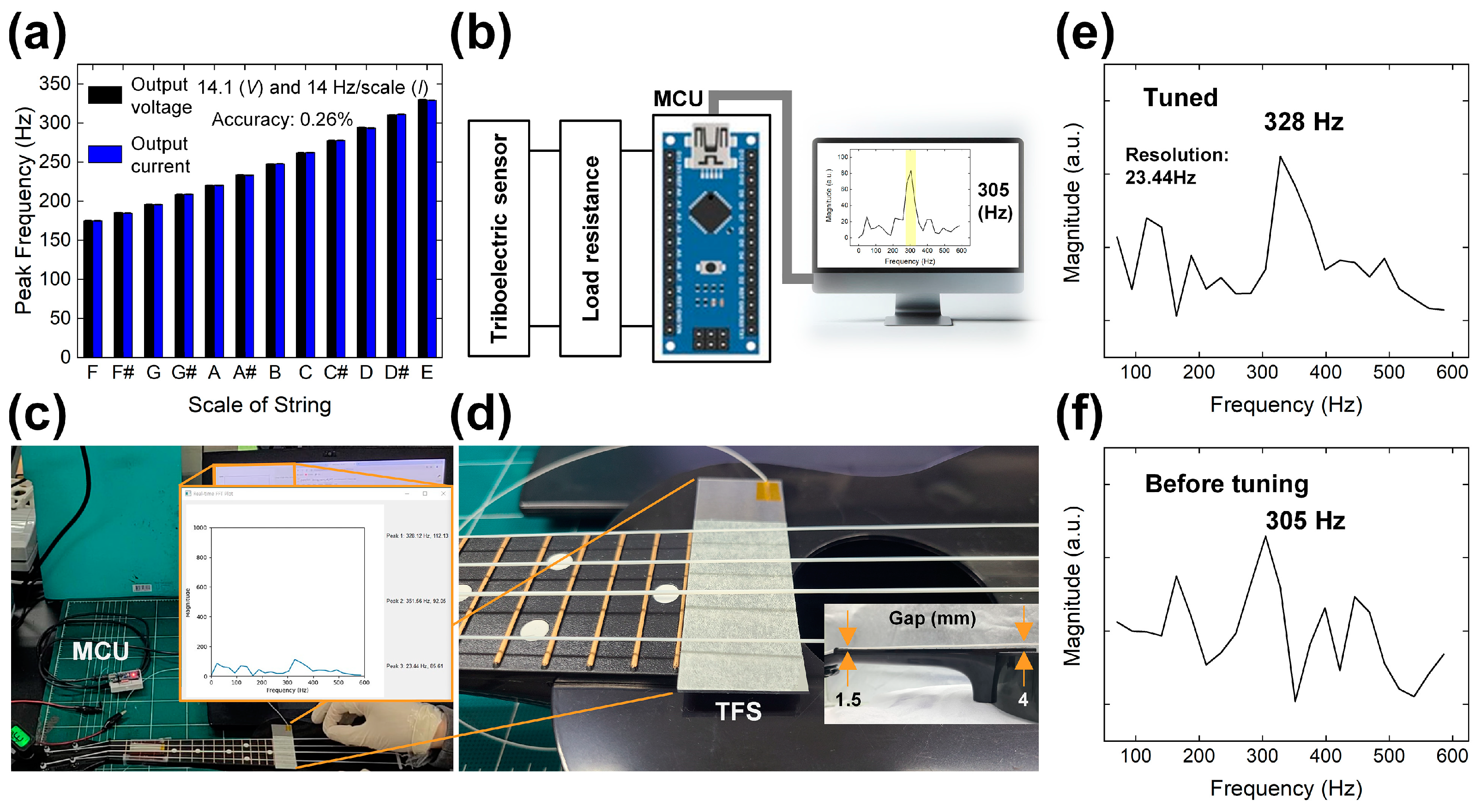
4.4. Integration of MCU and Visualization
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jabbar, H.; Song, Y.S.; Jeong, T.T. RF energy harvesting system and circuits for charging of mobile devices. IEEE Trans. Consum. Electron. 2010, 56, 247–253. [Google Scholar] [CrossRef]
- Mondal, R.; Hasan, M.A.M.; Zhang, R.; Olin, H.; Yang, Y. Nanogenerators-Based Self-Powered Sensors. Adv. Mater. Technol. 2022, 7, 2200282. [Google Scholar] [CrossRef]
- Javaid, S.; Fahim, H.; Zeadally, S.; He, B. Self-Powered Sensors: Applications, Challenges, and Solutions. IEEE Sens. J. 2023, 23, 20483–20509. [Google Scholar] [CrossRef]
- Dai, X.; Liang, Q.; Zhao, Z.-H.; Wu, Y.; Yang, J.; Han, J.; Cao, Y.; Wang, Y.; Li, C.-H.; Zhong, A.; et al. Self-powered sensors for flexible electronic skins capable of self-healing under multiple extreme environments. Nano Energy 2024, 121, 109239. [Google Scholar] [CrossRef]
- Wang, X.; Niu, S.; Yi, F.; Yin, Y.; Hao, C.; Dai, K.; Zhang, Y.; You, Z.; Wang, Z.L. Harvesting Ambient Vibration Energy over a Wide Frequency Range for Self-Powered Electronics. ACS Nano 2017, 11, 1728–1735. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Cui, P.; Zhang, J.; Ge, Y.; Liu, X.; Xuan, N.; Gu, G.; Cheng, G.; Du, Z. A stretchable self-powered triboelectric tactile sensor with EGaIn alloy electrode for ultra-low-pressure detection. Nano Energy 2021, 89, 106320. [Google Scholar] [CrossRef]
- Lei, H.; Xiao, J.; Chen, Y.; Jiang, J.; Xu, R.; Wen, Z.; Dong, B.; Sun, X. Bamboo-inspired self-powered triboelectric sensor for touch sensing and sitting posture monitoring. Nano Energy 2022, 91, 106670. [Google Scholar] [CrossRef]
- Lei, H.; Cao, K.; Chen, Y.; Liang, Z.; Wen, Z.; Jiang, L.; Sun, X. 3D-printed endoplasmic reticulum rGO microstructure based self-powered triboelectric pressure sensor. Chem. Eng. J. 2022, 445, 136821. [Google Scholar] [CrossRef]
- Zhong, Y.; Wang, J.; Han, L.; Dai, S.; Zhu, H.; Hua, J.; Cheng, G.; Ding, J. High-performance flexible self-powered triboelectric pressure sensor based on chemically modified micropatterned PDMS film. Sens. Actuators Phys. 2023, 349, 114013. [Google Scholar] [CrossRef]
- Kim, I.; Ahn, T.Y.; Kim, D. Large-Scale Lever-Based Triboelectric Nanogenerator for Sensing Lateral Vibration and Wrist or Finger Bending for Controlling Shooting Game. Micromachines 2021, 12, 1126. [Google Scholar] [CrossRef]
- Fan, F.-R.; Tian, Z.-Q.; Wang, Z.L. Flexible triboelectric generator. Nano Energy 2012, 1, 328–334. [Google Scholar] [CrossRef]
- Jeon, S.-B.; Nho, Y.-H.; Park, S.-J.; Kim, W.-G.; Tcho, I.-W.; Kim, D.; Kwon, D.-S.; Choi, Y.-K. Self-powered fall detection system using pressure sensing triboelectric nanogenerators. Nano Energy 2017, 41, 139–147. [Google Scholar] [CrossRef]
- Wang, Z.L. On Maxwell’s displacement current for energy and sensors: The origin of nanogenerators. Mater. Today 2017, 20, 74–82. [Google Scholar] [CrossRef]
- Wu, C.; Wang, A.C.; Ding, W.; Guo, H.; Wang, Z.L. Triboelectric Nanogenerator: A Foundation of the Energy for the New Era. Adv. Energy Mater. 2019, 9, 1802906. [Google Scholar] [CrossRef]
- Kim, I.; Roh, H.; Yu, J.; Jayababu, N.; Kim, D. Boron Nitride Nanotube-Based Contact Electrification-Assisted Piezoelectric Nanogenerator as a Kinematic Sensor for Detecting the Flexion–Extension Motion of a Robot Finger. ACS Energy Lett. 2020, 5, 1577–1585. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, P.; Zhang, W. A high-output performance mortise and tenon structure triboelectric nanogenerator for human motion sensing. Nano Energy 2021, 84, 105933. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, B.; Li, W.; Zu, L.; Tang, W.; Wang, Z.L. Bioinspired Triboelectric Soft Robot Driven by Mechanical Energy. Adv. Funct. Mater. 2021, 31, 2104770. [Google Scholar] [CrossRef]
- Seol, M.-L.; Han, J.-W.; Moon, D.-I.; Meyyappan, M. Triboelectric nanogenerator for Mars environment. Nano Energy 2017, 39, 238–244. [Google Scholar] [CrossRef]
- Jeon, S.-B.; Kim, W.-G.; Park, S.-J.; Tcho, I.-W.; Jin, I.-K.; Han, J.-K.; Kim, D.; Choi, Y.-K. Self-powered wearable touchpad composed of all commercial fabrics utilizing a crossline array of triboelectric generators. Nano Energy 2019, 65, 103994. [Google Scholar] [CrossRef]
- Yun, J.; Jayababu, N.; Kim, D. Self-powered transparent and flexible touchpad based on triboelectricity towards artificial intelligence. Nano Energy 2020, 78, 105325. [Google Scholar] [CrossRef]
- Wu, L.; Ren, Z.; Wang, Y.; Tang, Y.; Wang, Z.L.; Yang, R. Miniaturized and High Volumetric Energy Density Power Supply Device Based on a Broad-Frequency Vibration Driven Triboelectric Nanogenerator. Micromachines 2024, 15, 645. [Google Scholar] [CrossRef] [PubMed]
- Wu, P.; Wang, F.; Xu, S.; Liu, T.; Qi, Y.; Zhao, X.; Zhang, C.; Mu, X. A Highly Sensitive Triboelectric Quasi-Zero Stiffness Vibration Sensor with Ultrawide Frequency Response. Adv. Sci. 2023, 10, 2301199. [Google Scholar] [CrossRef] [PubMed]
- Xu, Q.; Qi, Y.; Li, X.; Guo, S.; Huang, X.; Lin, F.; Zhang, C.; Zhang, Q.; Wang, X. Ultrawide-Frequency Vibration Sensor Based on Magnetically Floating Triboelectric Nanogenerator. ACS Appl. Electron. Mater. 2024, 6, 1104–1112. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, C.; Pang, H.; Zhao, Z.; Zhang, Q.; Li, X.; Wang, X.; Lin, F.; Li, B.; Pan, X. Ultra−Wide Range Vibration Frequency Detection Sensors Based on Elastic Steel Triboelectric Nanogenerators for Intelligent Machinery Monitoring. Nanomaterials 2022, 12, 2790. [Google Scholar] [CrossRef]
- Mehamud, I.; Marklund, P.; Björling, M.; Shi, Y. Machine condition monitoring enabled by broad range vibration frequency detecting triboelectric nano-generator (TENG)-based vibration sensors. Nano Energy 2022, 98, 107292. [Google Scholar] [CrossRef]
- Yuan, M.; Tai, Y.; Zhang, W.; Zhang, S.; Xie, Y. A self-powered metamaterial augmented nanogenerator for low-frequency acoustic telecommunication. Sens. Actuators Phys. 2024, 375, 115531. [Google Scholar] [CrossRef]
- Zhao, W.; Xu, S. A facile structural strategy for a wearable strain sensor based on carbon nanotube modified helical yarns. Nanoscale Adv. 2022, 4, 250–257. [Google Scholar] [CrossRef]
- Ghosh, S.K.; Mandal, D. Synergistically enhanced piezoelectric output in highly aligned 1D polymer nanofibers integrated all-fiber nanogenerator for wearable nano-tactile sensor. Nano Energy 2018, 53, 245–257. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, W.; Ye, G.; Tan, Q.; Zhao, Y.; Qiu, J.; Qi, S.; Du, X.; Chen, T.; Liu, N. Core–Sheath Stretchable Conductive Fibers for Safe Underwater Wearable Electronics. Adv. Mater. Technol. 2020, 5, 1900880. [Google Scholar] [CrossRef]
- He, M.; Wang, Y.; Wang, S.; Luo, S. Laser-induced graphene enabled 1D fiber electronics. Carbon 2020, 168, 308–318. [Google Scholar] [CrossRef]
- Carvalho, J.T.; Cunha, I.; Coelho, J.; Fortunato, E.; Martins, R.; Pereira, L. Carbon-Yarn-Based Supercapacitors with In Situ Regenerated Cellulose Hydrogel for Sustainable Wearable Electronics. ACS Appl. Energy Mater. 2022, 5, 11987–11996. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Zhang, L.; Pu, Z.; Bao, B.; Ouyang, W.; Li, D. Fabricating 1D stretchable fiber-shaped electronics based on inkjet printing technology for wearable applications. Nano Energy 2023, 113, 108574. [Google Scholar] [CrossRef]
- Zhao, C.; Du, T.; Ge, B.; Xi, Z.; Qian, Z.; Wang, Y.; Wang, J.; Dong, F.; Shen, D.; Zhan, Z.; et al. Coaxial Flexible Fiber-Shaped Triboelectric Nanogenerator Assisted by Deep Learning for Self-Powered Vibration Monitoring. Small 2024, 20, 2307680. [Google Scholar] [CrossRef] [PubMed]
- Fan, Y.; Zhang, X.; Cheng, E.; Qin, C.; Qin, N.; Wu, J.; Guo, X.; Chen, H.; Guo, T. 1D in-situ convolution system based on vibration signal for real-time structural health monitoring. Nano Energy 2024, 127, 109694. [Google Scholar] [CrossRef]
- Chen, J.; Guo, H.; Pu, X.; Wang, X.; Xi, Y.; Hu, C. Traditional weaving craft for one-piece self-charging power textile for wearable electronics. Nano Energy 2018, 50, 536–543. [Google Scholar] [CrossRef]
- Wang, S.; Tian, M.; Hu, S.; Zhai, W.; Zheng, G.; Liu, C.; Shen, C.; Dai, K. Hierarchical nanofibrous mat via water-assisted electrospinning for self-powered ultrasensitive vibration sensors. Nano Energy 2022, 97, 107149. [Google Scholar] [CrossRef]
- Jung, Y.; Yu, J.; Hwang, H.J.; Bhatia, D.; Chung, K.-B.; Choi, D. Wire-based triboelectric resonator for a self-powered crack monitoring system. Nano Energy 2020, 71, 104615. [Google Scholar] [CrossRef]
- Guan, X.; Xu, B.; Huang, J.; Jing, T.; Gao, Y. Fiber-shaped stretchable triboelectric nanogenerator with a novel synergistic structure of opposite Poisson’s ratios. Chem. Eng. J. 2022, 427, 131698. [Google Scholar] [CrossRef]
- Nawaz, A.; Sarwar, N.; Jeong, D.I.; Yoon, D.H. Energy from discarded graphite-based pencils: Recycling the potential waste material for sensing application. Sens. Actuators Phys. 2022, 336, 113403. [Google Scholar] [CrossRef]
- Sreeja Sadanandan, K.; Saadi, Z.; Murphy, C.; Grikalaite, I.; Craciun, M.F.; Neves, A.I.S. Fabric-based triboelectric nanogenerators with ultrasonic spray coated graphene electrodes. Nano Energy 2023, 116, 108797. [Google Scholar] [CrossRef]
- Lepidi, M.; Gattulli, V.; Vestroni, F. Damage Identification in Elastic Suspended Cables through Frequency Measurement. J. Vib. Control 2009, 15, 867–896. [Google Scholar] [CrossRef]
- Ortiz-Echeverri, C.J.; Rodríguez-Reséndiz, J.; Garduño-Aparicio, M. An approach to STFT and CWT learning through music hands-on labs. Comput. Appl. Eng. Educ. 2018, 26, 2026–2035. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, I.; Cho, H.; Kim, D. Frequency Detection for String Instruments Using 1D-2D Non-Contact Mode Triboelectric Sensors. Micromachines 2024, 15, 1079. https://doi.org/10.3390/mi15091079
Kim I, Cho H, Kim D. Frequency Detection for String Instruments Using 1D-2D Non-Contact Mode Triboelectric Sensors. Micromachines. 2024; 15(9):1079. https://doi.org/10.3390/mi15091079
Chicago/Turabian StyleKim, Inkyum, Hyunwoo Cho, and Daewon Kim. 2024. "Frequency Detection for String Instruments Using 1D-2D Non-Contact Mode Triboelectric Sensors" Micromachines 15, no. 9: 1079. https://doi.org/10.3390/mi15091079
APA StyleKim, I., Cho, H., & Kim, D. (2024). Frequency Detection for String Instruments Using 1D-2D Non-Contact Mode Triboelectric Sensors. Micromachines, 15(9), 1079. https://doi.org/10.3390/mi15091079






