Optical Halo: A Proof of Concept for a New Broadband Microrheology Tool
Abstract
1. Introduction
2. Theoretical Background
2.1. Linear Rheology
2.2. Passive Microrheology
2.3. Range of Accessible Dynamics and Measurable Viscosities
2.4. The Link between Bulk and Micro-Rheology
2.5. Hybrid Microrheology with Optical Tweezers
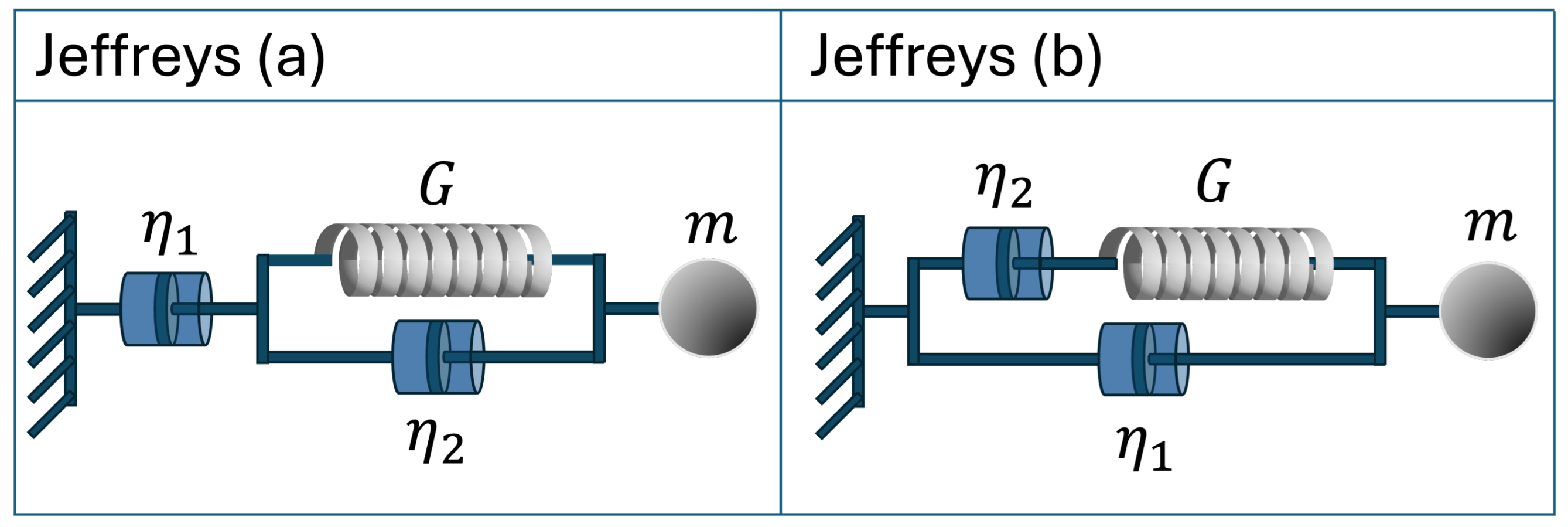
2.6. Jeffreys Model
2.7. Generalized Langevin Equation for an Optically Trapped Particle Moving in a Jeffreys Medium
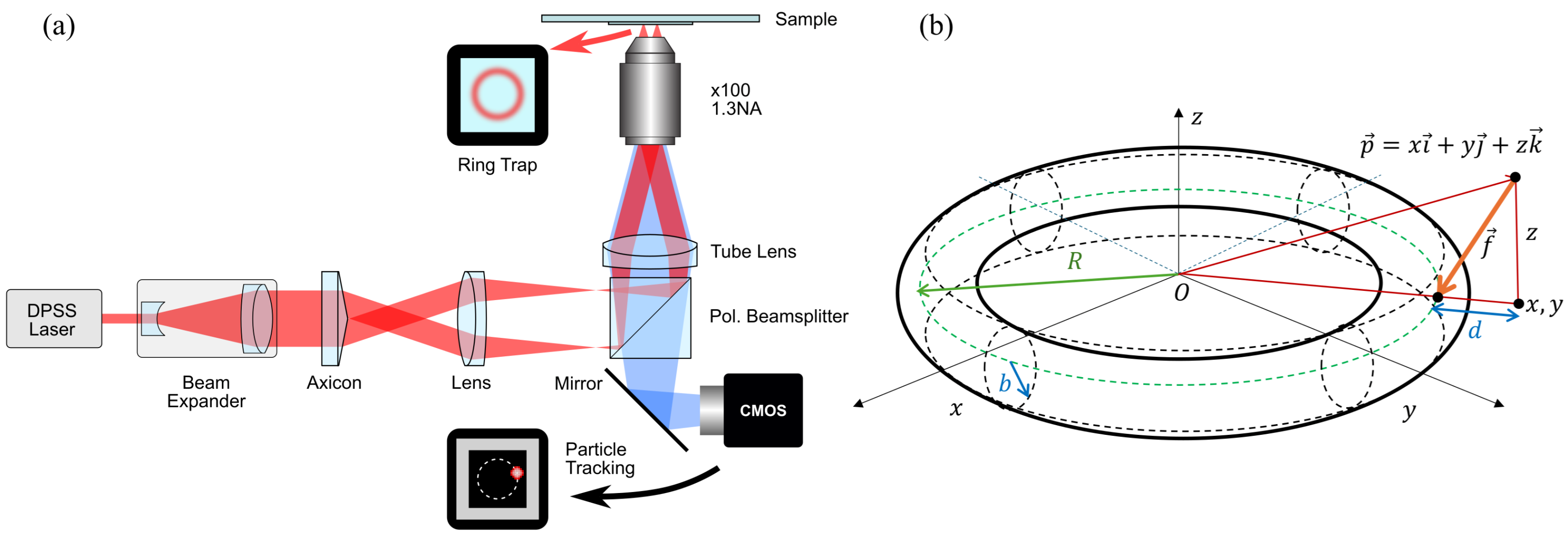
2.8. A Possible Experimental Configuration of an Optical Halo
2.9. Geometrical Representation of an Optical Halo
2.10. Overdamped Particle Moving in a Newtonian Fluid with a Toroidal Optical Trap
3. Results and Discussion
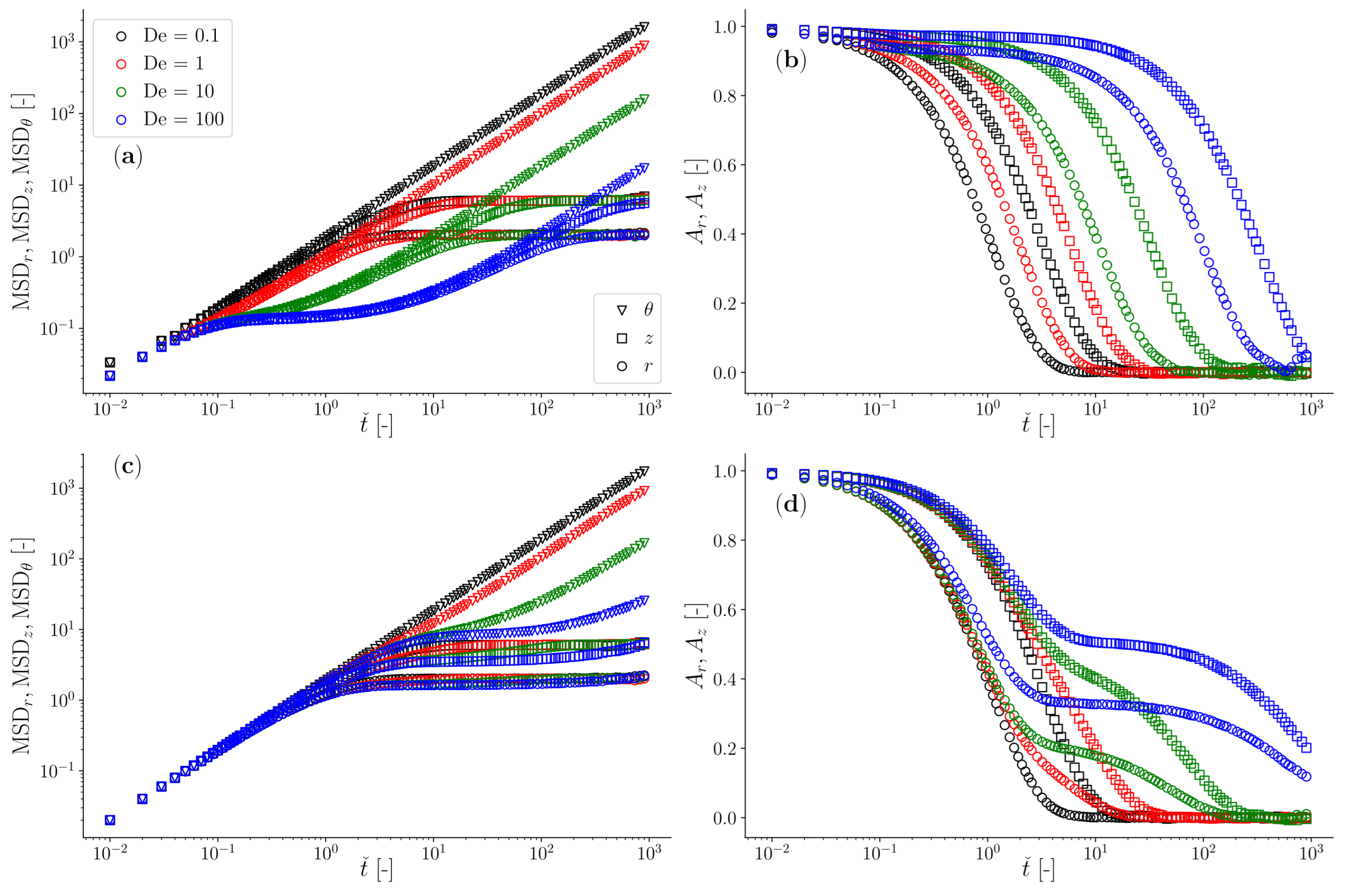
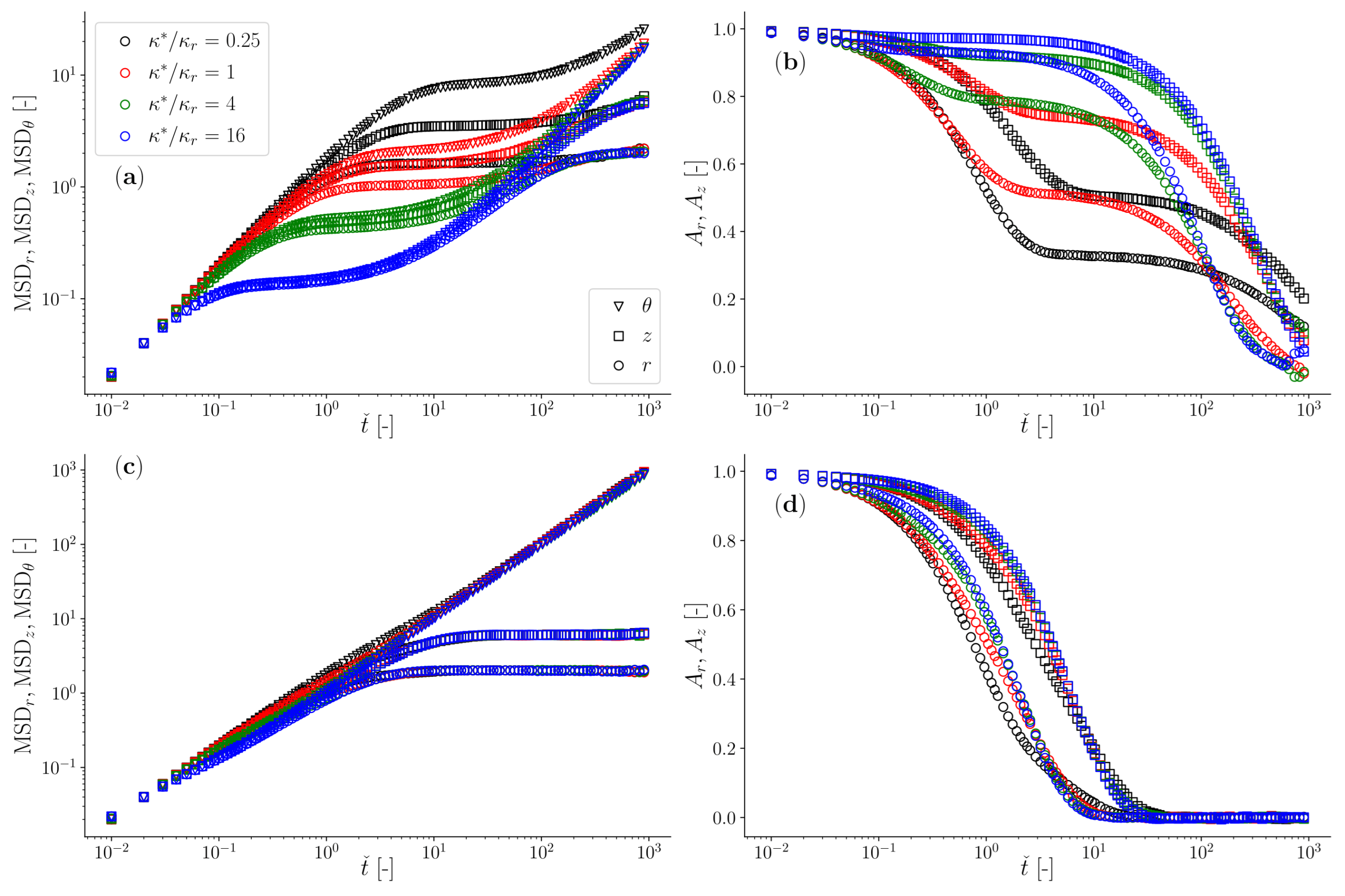
3.1. Overdamped Particle Moving in a Jeffreys Fluid with Toroidal Optical Trap
3.2. Simulation of a Biologically Relevant System with Realistic Numbers
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Einstein, A. Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen. Ann. Phys. 1905, 322, 549–560. [Google Scholar] [CrossRef]
- Perrin, J.B. Discontinuous Structure of Matter. Nobel Lecture 11 December 1926. Available online: https://www.nobelprize.org/prizes/physics/1926/perrin/lecture/ (accessed on 4 July 2024).
- Mason, T.; Weitz, D. Optical measurements of frequency-dependent linear viscoelastic moduli of complex fluids. Phys. Rev. Lett. 1995, 74, 1250–1253. [Google Scholar] [CrossRef]
- Waigh, T.A. Microrheology of complex fluids. Rep. Prog. Phys. 2005, 68, 685. [Google Scholar] [CrossRef]
- Pipe, C.J.; McKinley, G.H. Microfluidic rheometry. Mech. Res. Commun. 2009, 36, 110–120. [Google Scholar] [CrossRef]
- Squires, T.M.; Mason, T.G. Fluid Mechanics of Microrheology. Annu. Rev. Fluid Mech. 2010, 42, 413–438. [Google Scholar] [CrossRef]
- Cicuta, P.; Donald, A.M. Microrheology: A review of the method and applications. Soft Matter 2007, 3, 1449–1455. [Google Scholar] [CrossRef]
- Rizzi, L.G.; Tassieri, M. Microrheology of Biological Specimens. In Encyclopedia of Analytical Chemistry: Applications, Theory and Instrumentation; Wiley Online Library: Hoboken, NJ, USA, 2018; pp. 1–24. [Google Scholar] [CrossRef]
- Bausch, A.; Moller, W.; Sackmann, E. Measurement of local viscoelasticity and forces in living cells by magnetic tweezers. Biophys. J. 1999, 76, 573–579. [Google Scholar] [CrossRef]
- Tassieri, M.; Waigh, T.; Trinick, J.; Aggeli, A.; Evans, R. Analysis of the linear viscoelasticity of polyelectrolytes by magnetic microrheometry-Pulsed creep experiments and the one particle response. J. Rheol. 2010, 54, 117–131. [Google Scholar] [CrossRef]
- Okajima, T.; Tokumoto, H. Nanorheology of living cells investigated by atomic force microscopy. Nihon Reoroji Gakkaishi 2008, 36, 81–86. [Google Scholar] [CrossRef]
- Chim, Y.H.; Mason, L.M.; Rath, N.; Olson, M.F.; Tassieri, M.; Yin, H. A one-step procedure to probe the viscoelastic properties of cells by Atomic Force Microscopy. Sci. Rep. 2018, 8, 14462. [Google Scholar] [CrossRef]
- Brau, R.; Ferrer, J.; Lee, H.; Castro, C.; Tam, B.; Tarsa, P.; Matsudaira, P.; Boyce, M.; Kamm, R.; Lang, M. Passive and active microrheology with optical tweezers. J. Opt. A-Pure Appl. Opt. 2007, 9, S103–S112. [Google Scholar] [CrossRef]
- Fischer, M.; Berg-Sorensen, K. Calibration of trapping force and response function of optical tweezers in viscoelastic media. J. Opt. A-Pure Appl. Opt. 2007, 9, S239–S250. [Google Scholar] [CrossRef]
- Atakhorrami, M.; Sulkowska, J.I.; Addas, K.M.; Koenderink, G.H.; Tang, J.X.; Levine, A.J.; MacKintosh, F.C.; Schmidt, C.F. Correlated fluctuations of microparticles in viscoelastic solutions: Quantitative measurement of material properties by microrheology in the presence of optical traps. Phys. Rev. E 2006, 73, 061501. [Google Scholar] [CrossRef]
- Yao, A.; Tassieri, M.; Padgett, M.; Cooper, J. Microrheology with optical tweezers. Lab Chip 2009, 9, 2568–2575. [Google Scholar] [CrossRef]
- Tassieri, M.; Gibson, G.M.; Evans, R.; Yao, A.M.; Warren, R.; Padgett, M.J.; Cooper, J.M. Measuring storage and loss moduli using optical tweezers: Broadband microrheology. Phys. Rev. E 2010, 81, 026308. [Google Scholar] [CrossRef] [PubMed]
- Preece, D.; Warren, R.; Evans, R.; Gibson, G.M.; Padgett, M.J.; Cooper, J.M.; Tassieri, M. Optical tweezers: Wideband microrheology. J. Opt. 2011, 13, 044022. [Google Scholar] [CrossRef]
- Valentine, M.; Dewalt, L.; OuYang, H. Forces on a colloidal particle in a polymer solution: A study using optical tweezers. J. Phys.-Condens. Matter 1996, 8, 9477–9482. [Google Scholar] [CrossRef]
- Starrs, L.; Bartlett, P. One- and two-point micro-rheology of viscoelastic media. J. Phys.-Condens. Matter 2003, 15, S251–S256. [Google Scholar] [CrossRef]
- Tassieri, M.; Evans, R.M.L.; Yao, A.M.; Lee, M.P.; Phillips, D.B.; Gibson, G.M.; Baule, A.; Papagiannopoulos, A.; Bowman, R.W. Microrheology with Optical Tweezers: Principles and Applications; Pan Stanford: New York, NY, USA, 2015. [Google Scholar]
- Kuo, S.; Gelles, J.; Steuer, E.; Sheetz, M. A model for kinesin movement from nanometer-level movements of kinesin and cytoplasmic dynein and force measurements. J. Cell Sci. 1991, 1991, 135–138. [Google Scholar] [CrossRef]
- Tseng, Y.; Wirtz, D. Mechanics and multiple-particle tracking microheterogeneity of α-actinin-cross-linked actin filament networks. Biophys. J. 2001, 81, 1643–1656. [Google Scholar] [CrossRef]
- Pine, D.; Weitz, D.; Chaikin, P.; Herbolzheimer, E. Diffusing-wave spectroscopy. Phys. Rev. Lett. 1988, 60, 1134–1137. [Google Scholar] [CrossRef]
- Weitz, D.; Zhu, J.; Durian, D.; Gang, H.; Pine, D. Diffusing-wave spectroscopy—The technique and some applications. Phys. Scr. 1993, T49B, 610–621. [Google Scholar] [CrossRef]
- Del Giudice, F.; Tassieri, M.; Oelschlaeger, C.; Shen, A.Q. When Microrheology, Bulk Rheology, and Microfluidics Meet: Broadband Rheology of Hydroxyethyl Cellulose Water Solutions. Macromolecules 2017, 50, 2951–2963. [Google Scholar] [CrossRef]
- Garting, T.; Stradner, A. Optical Microrheology of Protein Solutions Using Tailored Nanoparticles. Small 2018, 14, 1801548. [Google Scholar] [CrossRef]
- Kollmannsberger, P.; Fabry, B. Linear and Nonlinear Rheology of Living Cells. Annu. Rev. Mater. Res. 2011, 41, 75–97. [Google Scholar] [CrossRef]
- Harrison, A.W.; Kenwright, D.A.; Waigh, T.A.; Woodman, P.G.; Allan, V.J. Modes of correlated angular motion in live cells across three distinct time scales. Phys. Biol. 2013, 10, 036002. [Google Scholar] [CrossRef] [PubMed]
- Morse, D.C. Viscoelasticity of concentrated isotropic solutions of semiflexible polymers. 3. nonlinear rheology. Macromolecules 1999, 32, 5934–5943. [Google Scholar] [CrossRef]
- Morse, D.C. Viscoelasticity of concentrated isotropic solutions of semiflexible polymers. 2. Linear response. Macromolecules 1998, 31, 7044–7067. [Google Scholar] [CrossRef]
- Morse, D.C. Viscoelasticity of concentrated isotropic solutions of semiflexible polymers. 1. Model and stress tensor. Macromolecules 1998, 31, 7030–7043. [Google Scholar] [CrossRef]
- Tassieri, M.; Evans, R.; Barbu-Tudoran, L.; Trinick, J.; Waigh, T. The self-assembly, elasticity, and dynamics of cardiac thin filaments. Biophys. J. 2008, 94, 2170–2178. [Google Scholar] [CrossRef][Green Version]
- Tassieri, M.; Evans, R.; Barbu-Tudoran, L.; Khaname, G.N.; Trinick, J.; Waigh, T.A. Dynamics of Semiflexible Polymer Solutions in the Highly Entangled Regime. Phys. Rev. Lett. 2008, 101, 198301. [Google Scholar] [CrossRef] [PubMed]
- Tassieri, M. Dynamics of Semiflexible Polymer Solutions in the Tightly Entangled Concentration Regime. Macromolecules 2017, 50, 5611–5618. [Google Scholar] [CrossRef]
- Schuldt, C.; Schnauß, J.; Händler, T.; Glaser, M.; Lorenz, J.; Golde, T.; Käs, J.A.; Smith, D.M. Tuning Synthetic Semiflexible Networks by Bending Stiffness. Phys. Rev. Lett. 2016, 117, 197801. [Google Scholar] [CrossRef]
- Golde, T.; Huster, C.; Glaser, M.; Händler, T.; Herrmann, H.; Käs, J.A.; Schnauß, J. Glassy dynamics in composite biopolymer networks. Soft Matter 2018, 14, 7970–7978. [Google Scholar] [CrossRef]
- Mours, M.; Winter, H. Time-resolved rheometry. Rheol. Acta 1994, 33, 385–397. [Google Scholar] [CrossRef]
- Berg-Sørensen, K.; Flyvbjerg, H. Power spectrum analysis for optical tweezers. Rev. Sci. Instrum. 2004, 75, 594–612. [Google Scholar] [CrossRef]
- Ferry, J.D. Viscoelastic Properties of Polymers, 3rd ed.; Wiley: Hoboken, NJ, USA, 1980. [Google Scholar]
- Macosko, C.W.; Larson, R.G. Rheology: Principles, Measurements, and Applications; VCH: New York, NY, USA, 1994. [Google Scholar]
- Rubinstein, M.; Colby, R.H. Polymer Physics; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- McLeish, T. Tube theory of entangled polymer dynamics. Adv. Phys. 2002, 51, 1379–1527. [Google Scholar] [CrossRef]
- Tassieri, M.; Ramírez, J.; Karayiannis, N.C.; Sukumaran, S.K.; Masubuchi, Y. i-Rheo GT: Transforming from Time to Frequency Domain without Artifacts. Macromolecules 2018, 51, 5055–5068. [Google Scholar] [CrossRef]
- Russell, B.A.; González-Jiménez, M.; Tukachev, N.V.; Hayes, L.A.; Chowdhury, T.; Javornik, U.; Mali, G.; Tassieri, M.; Farnaby, J.H.; Senn, H.M.; et al. A Second Glass Transition Observed in Single-Component Homogeneous Liquids Due to Intramolecular Vitrification. J. Am. Chem. Soc. 2023, 145, 26061–26067. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Viasnoff, V.; Wirtz, D. Compliance of actin filament networks measured by particle-tracking microrheology and diffusing wave spectroscopy. Rheol. Acta 1998, 37, 387–398. [Google Scholar] [CrossRef]
- Tassieri, M. Comment on “A symmetrical method to obtain shear moduli from microrheology” by K. Nishi, M. L. Kilfoil, C. F. Schmidt, and F. C. MacKintosh, Soft Matter, 2018, 14, 3716. Soft Matter 2018, 14, 8666–8670. [Google Scholar] [CrossRef] [PubMed]
- Ashkin, A. Acceleration and Trapping of Particles by Radiation Pressure. Phys. Rev. Lett. 1970, 24, 156–159. [Google Scholar] [CrossRef]
- Ashkin, A. Optical trapping and manipulation of neutral particles using lasers. Proc. Natl. Acad. Sci. USA 1997, 94, 4853–4860. [Google Scholar] [CrossRef] [PubMed]
- Bird, R.; Curtiss, C.; Armstrong, R.O.H. Dynamics of Polymeric Liquids, 2nd ed.; Wiley: New York, NY, USA, 1987. [Google Scholar]
- Bowman, R.W.; Padgett, M.J. Optical trapping and binding. Rep. Prog. Phys. 2013, 76, 026401. [Google Scholar] [CrossRef]
- Visscher, K.; Gross, S.P.; Block, S.M. Construction of multiple-beam optical traps with nanometer-resolution position sensing. IEEE J. Sel. Top. Quantum Electron. 1996, 2, 1066–1076. [Google Scholar] [CrossRef]
- Grier, D.G. A revolution in optical manipulation. Nature 2003, 424, 810–816. [Google Scholar] [CrossRef] [PubMed]
- Fahrbach, F.O.; Rohrbach, A. Propagation stability of self-reconstructing Bessel beams enables contrast-enhanced imaging in thick media. Nat. Commun. 2012, 3, 632. [Google Scholar] [CrossRef] [PubMed]
- Roichman, Y.; Grier, D.G. Three-dimensional holographic ring traps. In Proceedings of the Complex Light and Optical Forces, San Jose, CA, USA, 24–25 January 2007; SPIE: San Francisco, CA, USA, 2007; Volume 6483, pp. 131–135. [Google Scholar]
- Carstensen, M.S.; Zhu, X.; Iyore, O.E.; Mortensen, N.A.; Levy, U.; Kristensen, A. Holographic resonant laser printing of metasurfaces using plasmonic template. ACS Photonics 2018, 5, 1665–1670. [Google Scholar] [CrossRef]
- Bowman, R.; D’Ambrosio, V.; Rubino, E.; Jedrkiewicz, O.; Trapani, P.D.; Padgett, M.J. Optimisation of a low cost SLM for diffraction efficiency and ghost order suppression. Eur. Phys. J. Spec. Top. 2011, 199, 149–158. [Google Scholar] [CrossRef]
- Shao, B.; Esener, S.C.; Nascimento, J.M.; Botvinick, E.L.; Berns, M.W. Dynamically adjustable annular laser trapping based on axicons. Appl. Opt. 2006, 45, 6421–6428. [Google Scholar] [CrossRef]
- Shao, B.; Esener, S.C.; Nascimento, J.M.; Berns, M.W.; Botvinick, E.L.; Ozkan, M. Size tunable three-dimensional annular laser trap based on axicons. Opt. Lett. 2006, 31, 3375–3377. [Google Scholar] [CrossRef] [PubMed]
- Gibson, G.M.; Bowman, R.W.; Linnenberger, A.; Dienerowitz, M.; Phillips, D.B.; Carberry, D.M.; Miles, M.J.; Padgett, M.J. A compact holographic optical tweezers instrument. Rev. Sci. Instrum. 2012, 83, 113107. [Google Scholar] [CrossRef] [PubMed]
- Öttinger, H.C. Stochastic Processes in Polymeric Fluids: Tools and Examples for Developing Simulation Algorithms; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar] [CrossRef]
- Gardiner, C.W. Stochastic Methods: A Handbook for the Natural and Social Sciences; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Córdoba, A.; Indei, T.; Schieber, J.D. Elimination of inertia from a Generalized Langevin Equation: Applications to microbead rheology modeling and data analysis. J. Rheol. 2012, 56, 185–212. [Google Scholar] [CrossRef]
- Matheson, A.B.; Mendonca, T.; Gibson, G.M.; Dalgarno, P.A.; Wright, A.J.; Paterson, L.; Tassieri, M. Microrheology with an anisotropic optical trap. Front. Phys. 2021, 9, 621512. [Google Scholar] [CrossRef]
- Matheson, A.B.; Mendonca, T.; Smith, M.G.; Sutcliffe, B.; Fernandez, A.J.; Paterson, L.; Dalgarno, P.A.; Wright, A.J.; Tassieri, M. Fully angularly resolved 3D microrheology with optical tweezers. Rheol. Acta 2024, 63, 205–217. [Google Scholar] [CrossRef]
- Tassieri, M. Microrheology with optical tweezers: Peaks & troughs. Curr. Opin. Colloid Interface Sci. 2019, 43, 39–51. [Google Scholar] [CrossRef]
- Smith, M.G.; Radford, J.; Febrianto, E.; Ramírez, J.; O’Mahony, H.; Matheson, A.B.; Gibson, G.M.; Faccio, D.; Tassieri, M. Machine learning opens a doorway for microrheology with optical tweezers in living systems. AIP Adv. 2023, 13, 075315. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramírez, J.; Gibson, G.M.; Tassieri, M. Optical Halo: A Proof of Concept for a New Broadband Microrheology Tool. Micromachines 2024, 15, 889. https://doi.org/10.3390/mi15070889
Ramírez J, Gibson GM, Tassieri M. Optical Halo: A Proof of Concept for a New Broadband Microrheology Tool. Micromachines. 2024; 15(7):889. https://doi.org/10.3390/mi15070889
Chicago/Turabian StyleRamírez, Jorge, Graham M. Gibson, and Manlio Tassieri. 2024. "Optical Halo: A Proof of Concept for a New Broadband Microrheology Tool" Micromachines 15, no. 7: 889. https://doi.org/10.3390/mi15070889
APA StyleRamírez, J., Gibson, G. M., & Tassieri, M. (2024). Optical Halo: A Proof of Concept for a New Broadband Microrheology Tool. Micromachines, 15(7), 889. https://doi.org/10.3390/mi15070889






