A Lego-Like Reconfigurable Microfluidic Stabilizer System with Tunable Fluidic RC Constants and Stabilization Ratios
Abstract
1. Introduction
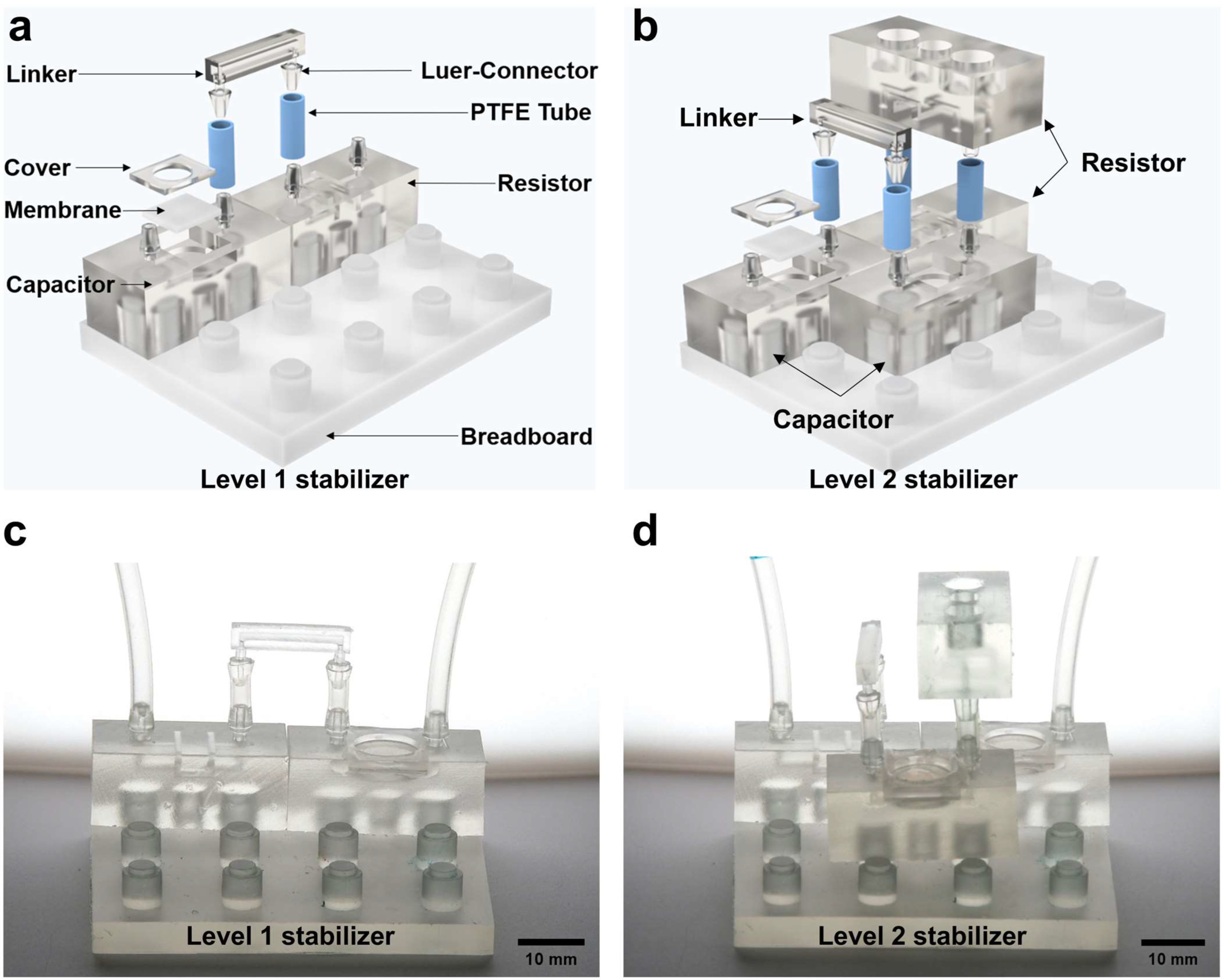
2. Design and Fabrication
3. Experimental Setup and Fluidic Circuit Modelling
4. Results and Discussion
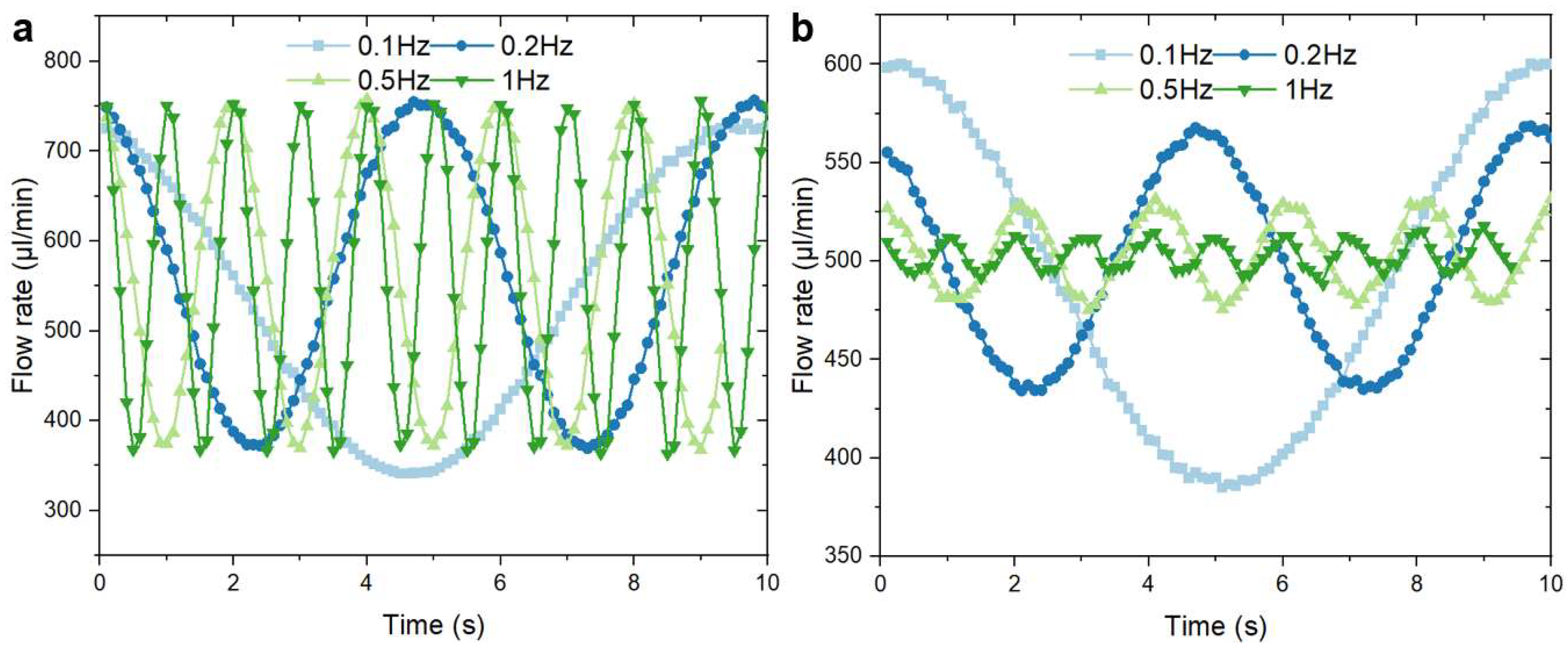
4.1. Model Validation
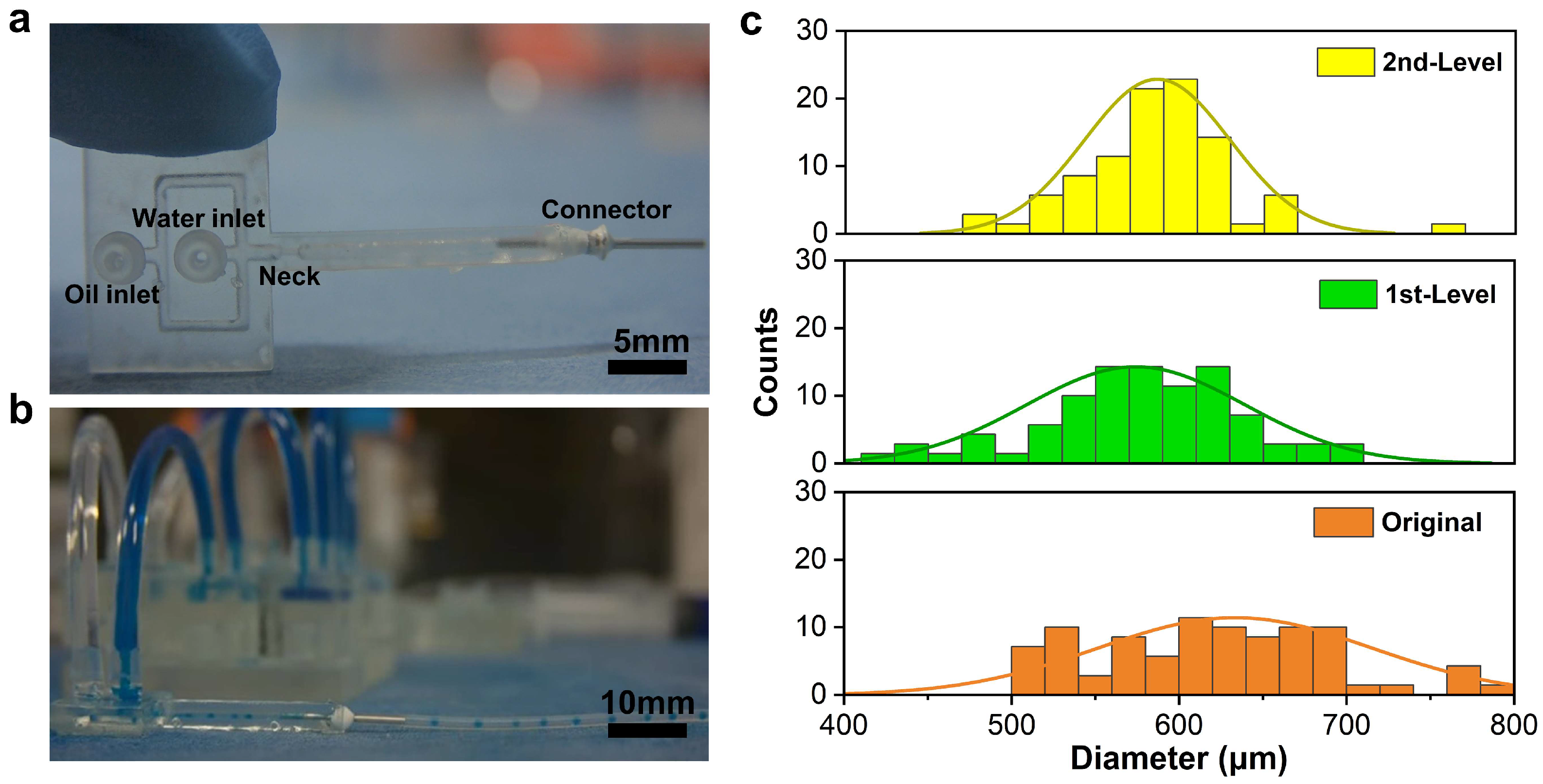
4.2. Droplet Generation
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chong, Z.Z.; Tan, S.H.; Gañán-Calvo, A.M.; Tor, S.B.; Loh, N.H.; Nguyen, N.-T. Active droplet generation in microfluidics. Lab Chip 2016, 16, 35–58. [Google Scholar] [CrossRef] [PubMed]
- Toh, A.G.G.; Wang, Z.P.; Yang, C.; Nguyen, N.-T. Engineering microfluidic concentration gradient generators for biological applications. Microfluid. Nanofluid. 2014, 16, 1–18. [Google Scholar] [CrossRef]
- Xiang, N.; Han, Y.; Jia, Y.; Shi, Z.; Yi, H.; Ni, Z.J. Flow stabilizer on a syringe tip for hand-powered microfluidic sample injection. Lab Chip 2019, 19, 214–222. [Google Scholar] [CrossRef] [PubMed]
- Oh, K.W.; Lee, K.; Ahn, B.; Furlani, E.P. Design of pressure-driven microfluidic networks using electric circuit analogy. Lab Chip 2012, 12, 515–545. [Google Scholar] [CrossRef] [PubMed]
- Araci, I.E.; Agaoglu, S.; Lee, J.Y.; Yepes, L.R.; Diep, P.; Martini, M.; Schmidt, A.J. Flow stabilization in wearable microfluidic sensors enables noise suppression. Lab Chip 2019, 19, 3899–3908. [Google Scholar] [CrossRef] [PubMed]
- Kang, Y.J.; Yang, S. Fluidic low pass filter for hydrodynamic flow stabilization in microfluidic environments. Lab Chip 2012, 12, 1881–1889. [Google Scholar] [CrossRef]
- Yang, B.; Lin, Q. A Compliance-Based Microflow Stabilizer. J. Microelectromechanical Syst. 2009, 18, 539–546. [Google Scholar] [CrossRef]
- Iyer, V.; Raj, A.; Annabattula, R.K.; Sen, A.K. Experimental and numerical studies of a microfluidic device with compliant chambers for flow stabilization. J. Micromech. Microeng. 2015, 25, 075003. [Google Scholar] [CrossRef]
- Zhou, Y.; Liu, J.; Yan, J.; Zhu, T.; Guo, S.; Li, S.; Li, T. Standing Air Bubble-Based Micro-Hydraulic Capacitors for Flow Stabilization in Syringe Pump-Driven Systems. Micromachines 2020, 11, 396. [Google Scholar] [CrossRef]
- Jiao, Z.; Zhao, J.; Chao, Z.; You, Z.; Zhao, J. An air-chamber-based microfluidic stabilizer for attenuating syringe-pump-induced fluctuations. Microfluid. Nanofluid. 2019, 23, 26. [Google Scholar] [CrossRef]
- Lee, J.; Rahman, F.; Laoui, T.; Karnik, R. Bubble-induced damping in displacement-driven microfluidic flows. Phys. Rev. E 2012, 86, 026301. [Google Scholar] [CrossRef] [PubMed]
- Xia, H.M.; Wu, J.W.; Zheng, J.J.; Zhang, J.; Wang, Z.P. Nonlinear microfluidics: Device physics, functions, and applications. Lab Chip 2021, 21, 1241–1268. [Google Scholar] [CrossRef]
- Dincau, B.; Dressaire, E.; Sauret, A. Pulsatile Flow in Microfluidic Systems. Small 2020, 16, e1904032. [Google Scholar] [CrossRef] [PubMed]
- Sochol, R.D.; Sweet, E.; Glick, C.C.; Wu, S.-Y.; Yang, C.; Restaino, M.; Lin, L.J. 3D printed microfluidics and microelectronics. Microelectron. Eng. 2018, 189, 52–68. [Google Scholar] [CrossRef]
- Kanitthamniyom, P.; Zhou, A.; Feng, S.; Liu, A.; Vasoo, S.; Zhang, Y. A 3D-printed modular magnetic digital microfluidic architecture for on-demand bioanalysis. Microsyst. Nanoeng. 2020, 6, 48. [Google Scholar] [CrossRef] [PubMed]
- Bhargava, K.C.; Thompson, B.; Iqbal, D.; Malmstadt, N. Predicting the behavior of microfluidic circuits made from discrete elements. Sci. Rep. 2015, 5, 15609. [Google Scholar] [CrossRef]
- Bhargava, K.C.; Thompson, B.; Malmstadt, N. Discrete elements for 3D microfluidics. Proc. Natl. Acad. Sci. USA 2014, 111, 15013–15018. [Google Scholar] [CrossRef] [PubMed]
- Naderi, A.; Bhattacharjee, N.; Folch, A. Digital manufacturing for microfluidics. Annu. Rev. Biomed. Eng. 2019, 21, 325–364. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, A.V.; Beauchamp, M.J.; Nordin, G.P.; Woolley, A.T. 3D Printed Microfluidics. Annu. Rev. Anal. Chem. 2020, 13, 45–65. [Google Scholar] [CrossRef]
- Tsur, E.E. Computer-Aided Design of Microfluidic Circuits. Annu. Rev. Biomed. Eng. 2020, 22, 285–307. [Google Scholar] [CrossRef]
- Sochol, R.; Sweet, E.; Glick, C.; Venkatesh, S.; Avetisyan, A.; Ekman, K.; Raulinaitis, A.; Tsai, A.; Wienkers, A.; Korner, K. 3D printed microfluidic circuitry via multijet-based additive manufacturing. Lab Chip 2016, 16, 668–678. [Google Scholar] [CrossRef]
- Vittayarukskul, K.; Lee, A.P. A truly Lego®-like modular microfluidics platform. J. Micromech. Microeng. 2017, 27, 035004. [Google Scholar] [CrossRef]
- Phillips, R.H.; Jain, R.; Browning, Y.; Shah, R.; Kauffman, P.; Dinh, D.; Lutz, B.R. Flow control using audio tones in resonant microfluidic networks: Towards cell-phone controlled lab-on-a-chip devices. Lab Chip 2016, 16, 3260–3267. [Google Scholar] [CrossRef]
- Yang, B.; Metier, J.; Lin, Q. Using compliant membranes for dynamic flow stabilization in microfluidic systems. In Proceedings of the 18th IEEE International Conference on Micro Electro Mechanical Systems, Miami Beach, FL, USA, 30 January–3 February 2005; pp. 706–709. [Google Scholar]
- Zhang, X.; Zhu, Z.; Xiang, N.; Ni, Z. A microfluidic gas damper for stabilizing gas pressure in portable microfluidic systems. Biomicrofluidics 2016, 10, 054123. [Google Scholar] [CrossRef]
- Li, Z.; Mak, S.Y.; Sauret, A.; Shum, H.C. Syringe-pump-induced fluctuation in all-aqueous microfluidic system implications for flow rate accuracy. Lab Chip 2014, 14, 744–749. [Google Scholar] [CrossRef]
- Kalantarifard, A.; Alizadeh Haghighi, E.; Elbuken, C. Damping hydrodynamic fluctuations in microfluidic systems. Chem. Eng. Sci. 2018, 178, 238–247. [Google Scholar] [CrossRef]
- Fang, Z.; Li, A.I.; Liu, H.; Pan, T. Digital droplet infusion. Lab Chip 2021, 21, 502–512. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.-H.; Chen, C.-W.; Kuo, L.-S.; Chen, P.-H. A Novel Approach to Measure the Hydraulic Capacitance of a Microfluidic Membrane Pump. Adv. Mater. Sci. Eng. 2014, 2014, 1–8. [Google Scholar] [CrossRef]




| Stabilizer Type | Degree of Modularity | Best Stable Flow | Best Stabilization Ratio |
|---|---|---|---|
| Single-chamber stabilizer [24] | Discrete component | 50 ± 3 µL/min | 6% |
| Multi-chamber Stabilizer [7] | Discrete components with different chamber numbers | 50 ± 1.4 µL/min | 2.8% |
| Fluidic low-pass filter [6] | Discrete components with different membranes | 10 ± 0.21 mL /hour | 2.1% |
| Hand-powered stabilizer [3] | Discrete component with modular connectors | 1214 ± 22 µL/min | 1.8% |
| Air chamber stabilizer [10] | Parallel-connected stabilizers | 60 ± 5 µL/min | 8% |
| Bubble damper stabilizer [25] | Discrete component with controllable dampers | 9.64 ± 0.27 µL/min | 2.8% |
| This work | Modular stabilizer with modular connectors | 504.01 ±1.86 µL/min | 0.93% |
| Configuration | Standard Deviation (µm) | Polydispersity |
|---|---|---|
| Original | 81.8 | 0.13 |
| First Level | 62.9 | 0.11 |
| Second Level | 44.5 | 0.07 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhuge, W.; Li, W.; Wang, K.; Chen, Z.; Wu, C.; Jiang, K.; Ding, J.; Anthony, C.; Cheng, X. A Lego-Like Reconfigurable Microfluidic Stabilizer System with Tunable Fluidic RC Constants and Stabilization Ratios. Micromachines 2024, 15, 843. https://doi.org/10.3390/mi15070843
Zhuge W, Li W, Wang K, Chen Z, Wu C, Jiang K, Ding J, Anthony C, Cheng X. A Lego-Like Reconfigurable Microfluidic Stabilizer System with Tunable Fluidic RC Constants and Stabilization Ratios. Micromachines. 2024; 15(7):843. https://doi.org/10.3390/mi15070843
Chicago/Turabian StyleZhuge, Wuyang, Weihao Li, Kaimin Wang, Zhuodan Chen, Chunhui Wu, Kyle Jiang, Jun Ding, Carl Anthony, and Xing Cheng. 2024. "A Lego-Like Reconfigurable Microfluidic Stabilizer System with Tunable Fluidic RC Constants and Stabilization Ratios" Micromachines 15, no. 7: 843. https://doi.org/10.3390/mi15070843
APA StyleZhuge, W., Li, W., Wang, K., Chen, Z., Wu, C., Jiang, K., Ding, J., Anthony, C., & Cheng, X. (2024). A Lego-Like Reconfigurable Microfluidic Stabilizer System with Tunable Fluidic RC Constants and Stabilization Ratios. Micromachines, 15(7), 843. https://doi.org/10.3390/mi15070843






