Diseased Erythrocyte Enrichment Based on I-Shaped Pillar DLD Arrays
Abstract
1. Introduction
2. Layout Design of the Array in the Chip
2.1. Size Design of Sorting Chip
2.2. Fabrication of Sorting Chip
3. Erythrocyte Enrichment Experiment
3.1. Preparation of the Experiment
3.2. Experimental Results
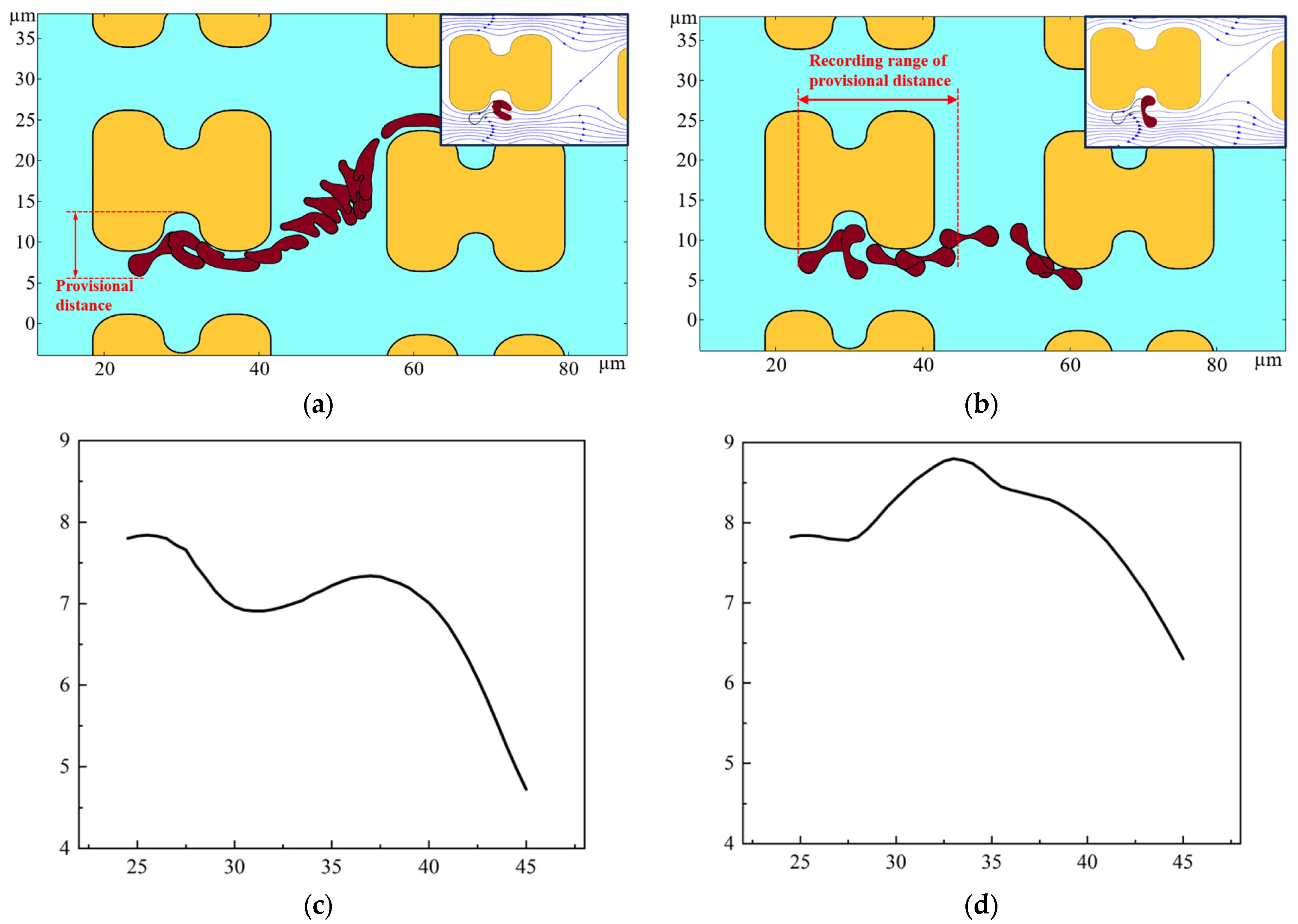
4. Simulation of Erythrocyte Motility Based on the Finite Element Method
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tsubota, K.I.; Wada, S.; Yamaguchi, T. Particle method for computer simulation of red blood cell motion in blood flow. Comput. Methods Programs Biomed. 2006, 83, 139–146. [Google Scholar] [CrossRef] [PubMed]
- Ju, M.; Ye, S.S.; Namgung, B.; Cho, S.; Low, H.T.; Leo, H.L.; Kim, S. A review of numerical methods for red blood cell flow simulation. Comput. Methods Biomech. Biomed. Eng. 2015, 18, 130–140. [Google Scholar] [CrossRef]
- Mendez, S.; Chnafa, C.; Gibaud, E.; Sigueenza, J.; Moureau, V.; Nicoud, F. YALES2BIO: A Computational Fluid Dynamics Software Dedicated to the Prediction of Blood Flows in Biomedical Devices. In Proceedings of the 5th International Conference on the Development of Biomedical Engineering in Vietnam, Ho Chi Minh City, Vietnam, 16–18 June 2014; pp. 7–10. [Google Scholar]
- Huynh, K. Surgery: Restrictive versus liberal red-cell transfusion. Nat. Rev. Cardiol. 2018, 15, 2. [Google Scholar]
- Ulfsdotter Nilsson, C.; Kander, T. Erythrocyte transfusion in critical care. Lakartidningen 2021, 118, 20146. [Google Scholar]
- Blanca, D.; Parrella, G.; Consonni, D.; Villa, S.; Ceriani, G.; Cespiati, A.; Figini, G.; Ghigliazza, G.; Maira, D.; Oberti, G.; et al. Anemia management and transfusion strategy in internal medicine units: Less is more. Eur. J. Intern. Med. 2023, 115, 48–54. [Google Scholar] [CrossRef]
- Bizjak, D.A.; John, L.; Matits, L.; Uhl, A.; Schulz, S.V.W.; Schellenberg, J.; Peifer, J.; Bloch, W.; Weiss, M.; Grüner, B.; et al. SARS-CoV-2 Altered Hemorheological and Hematological Parameters during One-Month Observation Period in Critically Ill COVID-19 Patients. Int. J. Mol. Sci. 2022, 23, 17. [Google Scholar] [CrossRef]
- Niesor, E.J.; Nader, E.; Perez, A.; Lamour, F.; Benghozi, R.; Remaley, A.; Thein, S.L.; Connes, P. Red Blood Cell Membrane Cholesterol May Be a Key Regulator of Sickle Cell Disease Microvascular Complications. Membranes 2022, 12, 15. [Google Scholar] [CrossRef] [PubMed]
- Hareendranath, S.; Sathian, S.P. Dynamic response of red blood cells in health and disease. Soft Matter 2023, 19, 1219–1230. [Google Scholar] [CrossRef] [PubMed]
- Pulliam, K.E.; Joseph, B.; Makley, A.T.; Caldwell, C.C.; Lentsch, A.B.; Goodman, M.D.; Pritts, T.A. Washing packed red blood cells decreases red blood cell storage lesion formation. Surgery 2021, 169, 666–670. [Google Scholar] [CrossRef]
- Zingg, W.; Schuster, R.; Joseph, B.; Caldwell, C.C.; Lentsch, A.B.; Goodman, M.D.; Pritts, T.A. Storage with ethanol attenuates the red blood cell storage lesion. Surgery 2022, 172, 1829–1836. [Google Scholar] [CrossRef]
- Längst, E.; Tissot, J.D.; Prudent, M. Storage of red blood cell concentrates: Clinical impact. Transfu. Clin. Biol. 2021, 28, 397–402. [Google Scholar] [CrossRef]
- Reilly, M.; Bruno, C.D.; Prudencio, T.M.; Ciccarelli, N.; Guerrelli, D.; Nair, R.; Ramadan, M.; Luban, N.L.C.; Posnack, N.G. Potential Consequences of the Red Blood Cell Storage Lesion on Cardiac Electrophysiology. J. Am. Heart Assoc. 2020, 9, 15. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.P.; He, H.; Wang, J.J.; Chen, L.; Xu, Y.; Ge, C.; Li, S.B. Blood quality evaluation via on-chip classification of cell morphology using a deep learning algorithm. Lab Chip 2023, 23, 2113–2121. [Google Scholar] [CrossRef]
- Hochstetter, A.; Vernekar, R.; Austin, R.H.; Becker, H.; Beech, J.P.; Fedosov, D.A.; Gompper, G.; Kim, S.C.; Smith, J.T.; Stolovitzky, G.; et al. Deterministic Lateral Displacement: Challenges and Perspectives. ACS Nano 2020, 14, 10784–10795. [Google Scholar] [CrossRef] [PubMed]
- Davis, J.A. Microfluidic Separation of Blood Components Through Deterministic Lateral Displacement; Princeton University: Princeton, NJ, USA, 2008. [Google Scholar]
- Al-Fandi, M.; Al-Rousan, M.; Jaradat, M.A.K.; Al-Ebbini, L. New design for the separation of microorganisms using microfluidic deterministic lateral displacement. Robot. Comput. Integr. Manuf. 2011, 27, 237–244. [Google Scholar] [CrossRef]
- Zeming, K.K.; Ranjan, S.; Zhang, Y. Rotational separation of non-spherical bioparticles using I-shaped pillar arrays in a microfluidic device. Nat. Commun. 2013, 4, 1625. [Google Scholar] [CrossRef]
- Kabacaoglu, G.; Biros, G. Sorting same-size red blood cells in deep deterministic lateral displacement devices. J. Fluid Mech. 2019, 859, 433–475. [Google Scholar] [CrossRef]
- Zhang, Z.M.; Chien, W.; Henry, E.; Fedosov, D.A.; Gompper, G. Sharp-edged geometric obstacles in microfluidics promote deformability-based sorting of cells. Phys. Rev. Fluids 2019, 4, 18. [Google Scholar] [CrossRef]
- Jiao, Y.Y.; He, Y.Q.; Jiao, F. Two-dimensional Simulation of Motion of Red Blood Cells with Deterministic Lateral Displacement Devices. Micromachines 2019, 10, 15. [Google Scholar] [CrossRef] [PubMed]
- Johnston, I.D.; McCluskey, D.K.; Tan, C.K.L.; Tracey, M.C. Mechanical characterization of bulk Sylgard 184 for microfluidics and microengineering. J. Micromech. Microeng. 2014, 24, 7. [Google Scholar] [CrossRef]
- Johari, S.; Fazmir, H.; Anuar, A.F.M.; Zainol, M.Z.; Nock, V.; Wang, W. PDMS Young’s Modulus Calibration for Micropillar Force Sensor Application. In Proceedings of the IEEE Regional Symposium on Micro and Nanoelectronics (RSM), Kuala Terengganu, Malaysia, 19–21 August 2015; pp. 9–12. [Google Scholar]
- Pulliam, K.E.; Joseph, B.; Veile, R.A.; Friend, L.A.; Makley, A.T.; Caldwell, C.C.; Lentsch, A.B.; Goodman, M.D.; Pritts, T.A. Save it-don’t waste it! Maximizing utilization of erythrocytes from previously stored whole blood. J. Trauma Acute Care Surg. 2020, 89, 665–672. [Google Scholar] [CrossRef]
- van Manen, L.; Maas, A.; Roelofs, J.; Vlaar, A.P.J.; van Bruggen, R.; Juffermans, N.P. The Effect of Washing of Stored Red Blood Cell Transfusion Units on Post Transfusion Recovery and Outcome in a Pneumosepsis Animal Model. Shock 2020, 54, 794–801. [Google Scholar] [CrossRef] [PubMed]
- Pulliam, K.E.; Joseph, B.; Makley, A.T.; Caldwell, C.C.; Lentsch, A.B.; Goodman, M.D.; Pritts, T.A. Improving packed red blood cell storage with a high-viscosity buffered storage solution. Surgery 2022, 171, 833–842. [Google Scholar] [CrossRef]
- Pulliam, K.E.; Joseph, B.; Veile, R.A.; Friend, L.A.; Makley, A.T.; Caldwell, C.C.; Lentsch, A.B.; Goodman, M.D.; Pritts, T.A. Expired but Not Yet Dead: Examining the Red Blood Cell Storage Lesion in Extended-Storage Whole Blood. Shock 2021, 55, 526–535. [Google Scholar] [CrossRef]
- Zhu, Q.; Salehyar, S.; Cabrales, P.; Asaro, R.J. Prospects for Human Erythrocyte Skeleton-Bilayer Dissociation during Splenic Flow. Biophys. J. 2017, 113, 900–912. [Google Scholar] [CrossRef]
- Yamaguchi, T.; Miyazaki, M. Membrane Response of Human Erythrocytes Exposed to a Pressure of 140 MPa. Bull. Chem. Soc. Jpn. 2020, 93, 326–331. [Google Scholar] [CrossRef]
- Wang, H.; Wei, H.W.; Shen, H.C.; Li, Z.Z.; Cheng, Y.; Duan, L.S.; Yin, L.; Yu, J.; Guo, J.R. To study the effect of oxygen carrying capacity on expressed changes of erythrocyte membrane protein in different storage times. Biosci. Rep. 2020, 40, 10. [Google Scholar] [CrossRef] [PubMed]
- Evans, E.; Fung, Y.C. Improved measurements of the erythrocyte geometry. Microvasc. Res. 1972, 4, 335–347. [Google Scholar] [CrossRef]
- Fischer, T.M. The Shape of Human Red Blood Cells Suspended in Autologous Plasma and Serum. Cells 2022, 11, 1941. [Google Scholar] [CrossRef]
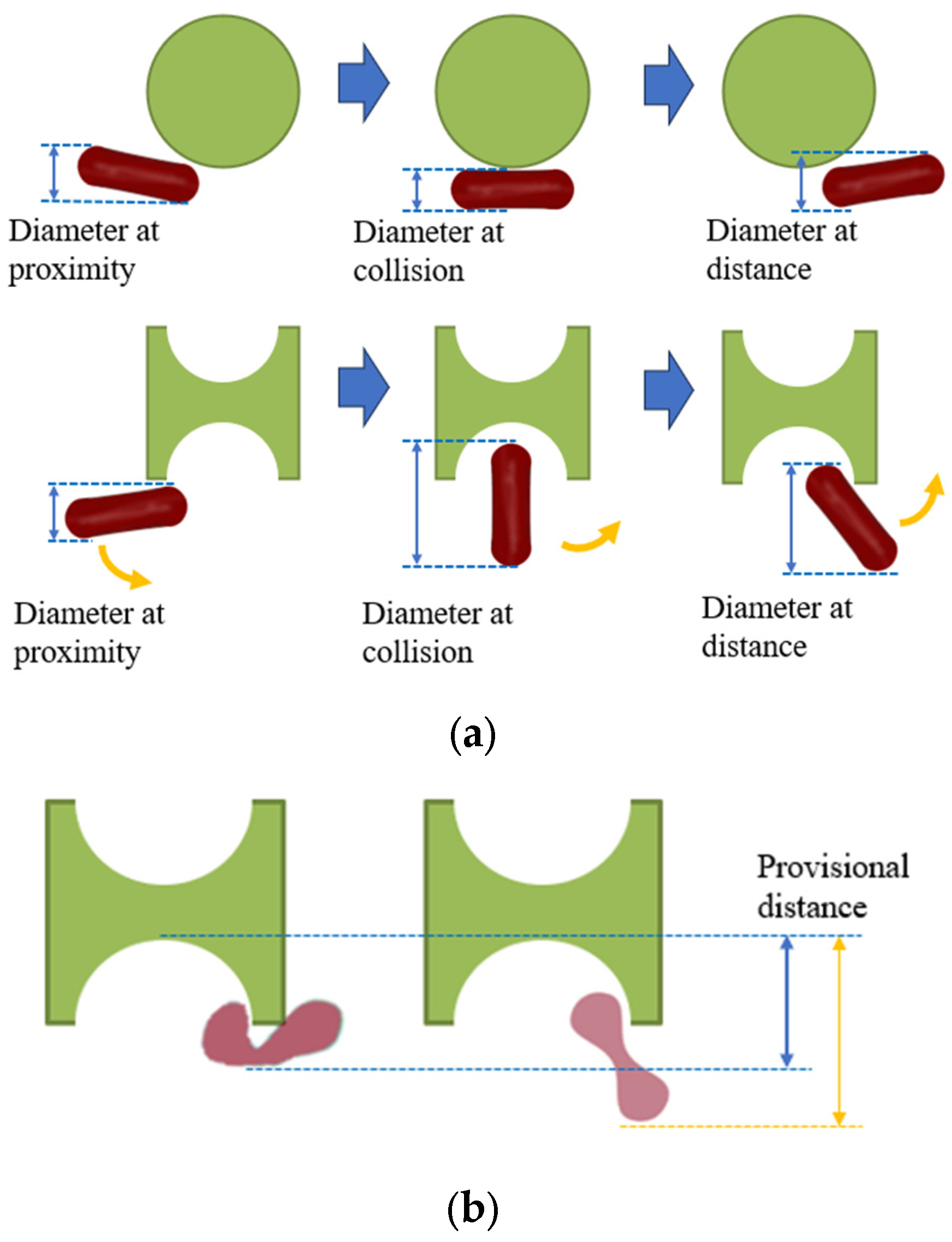
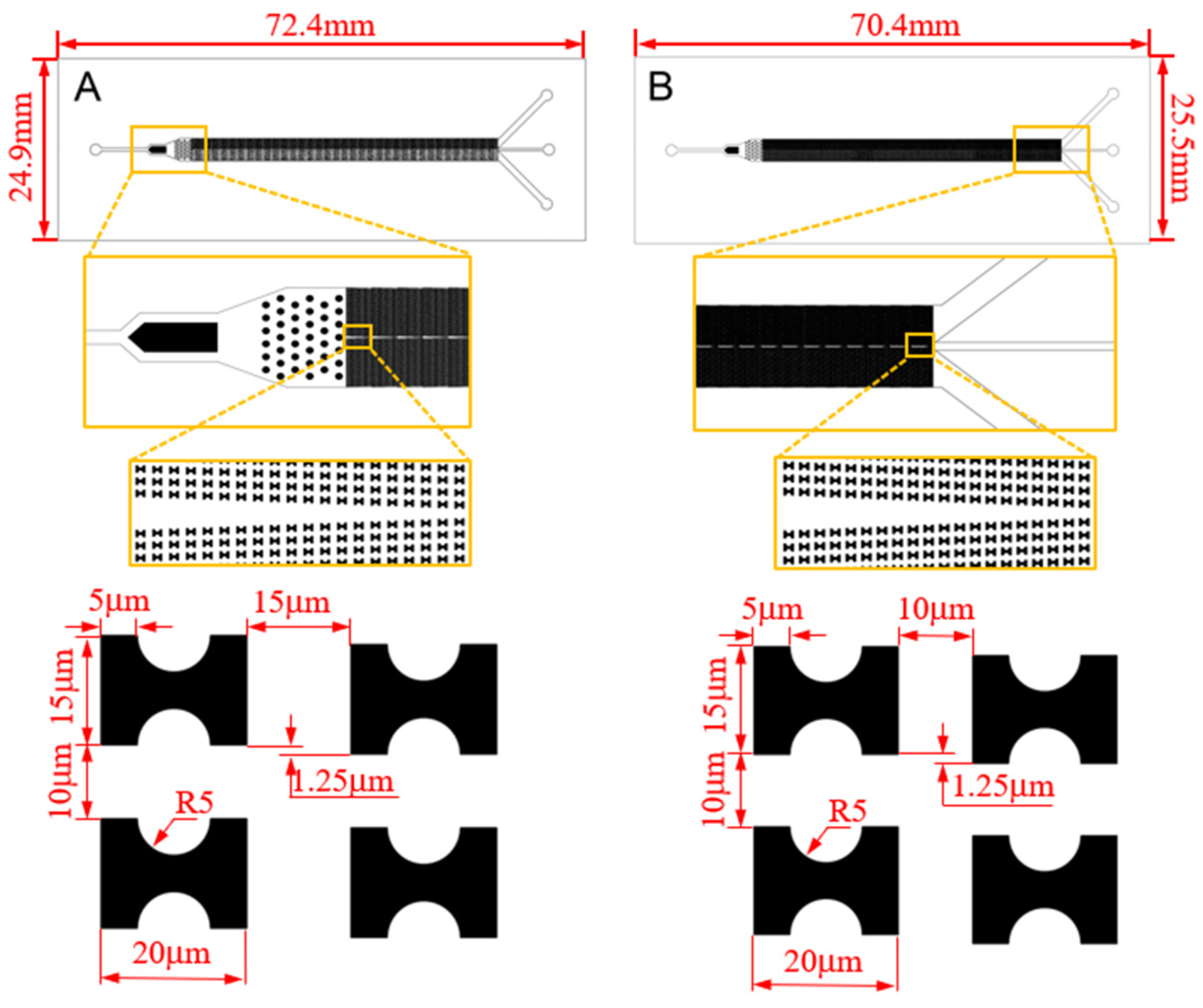









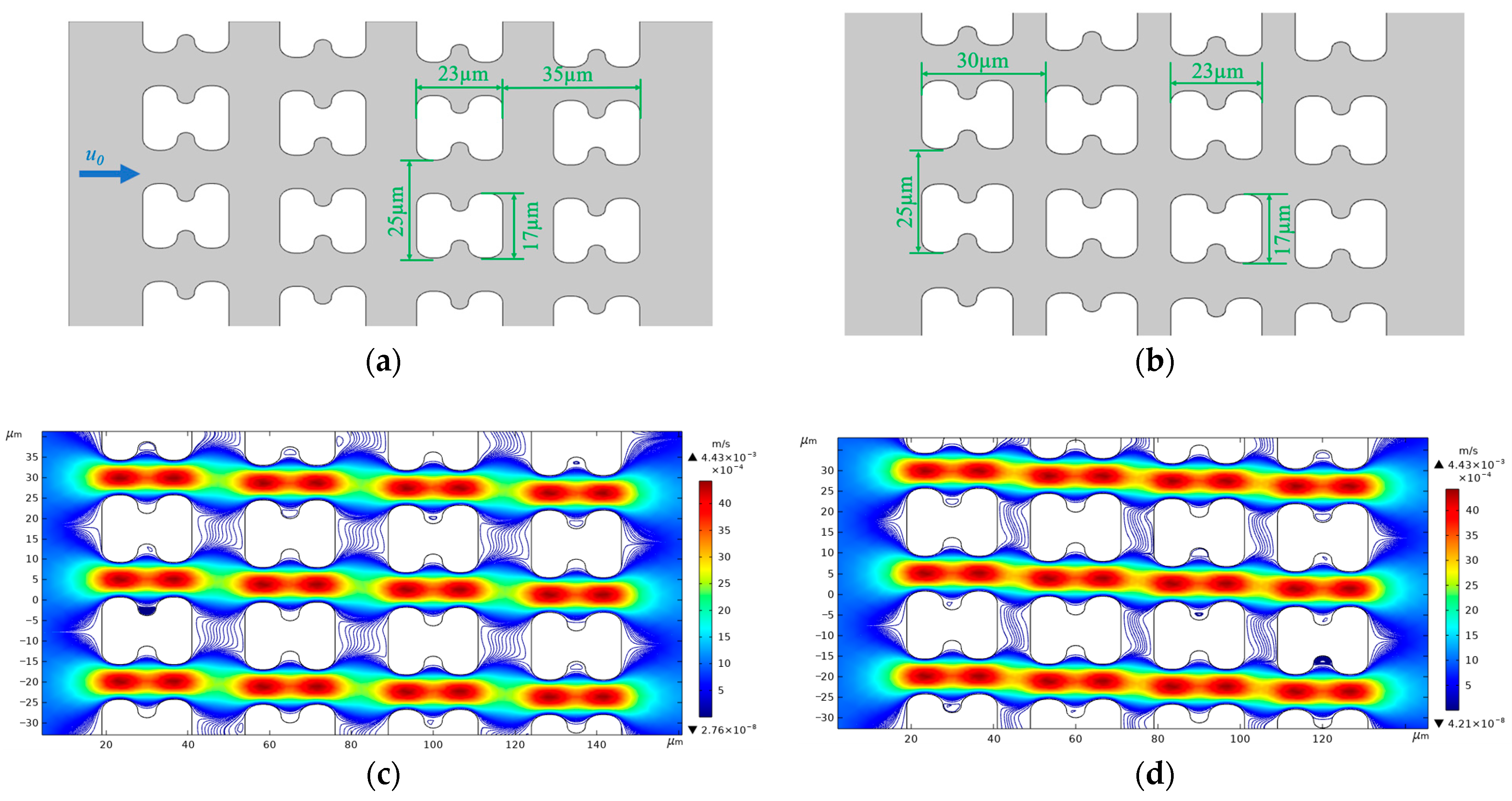
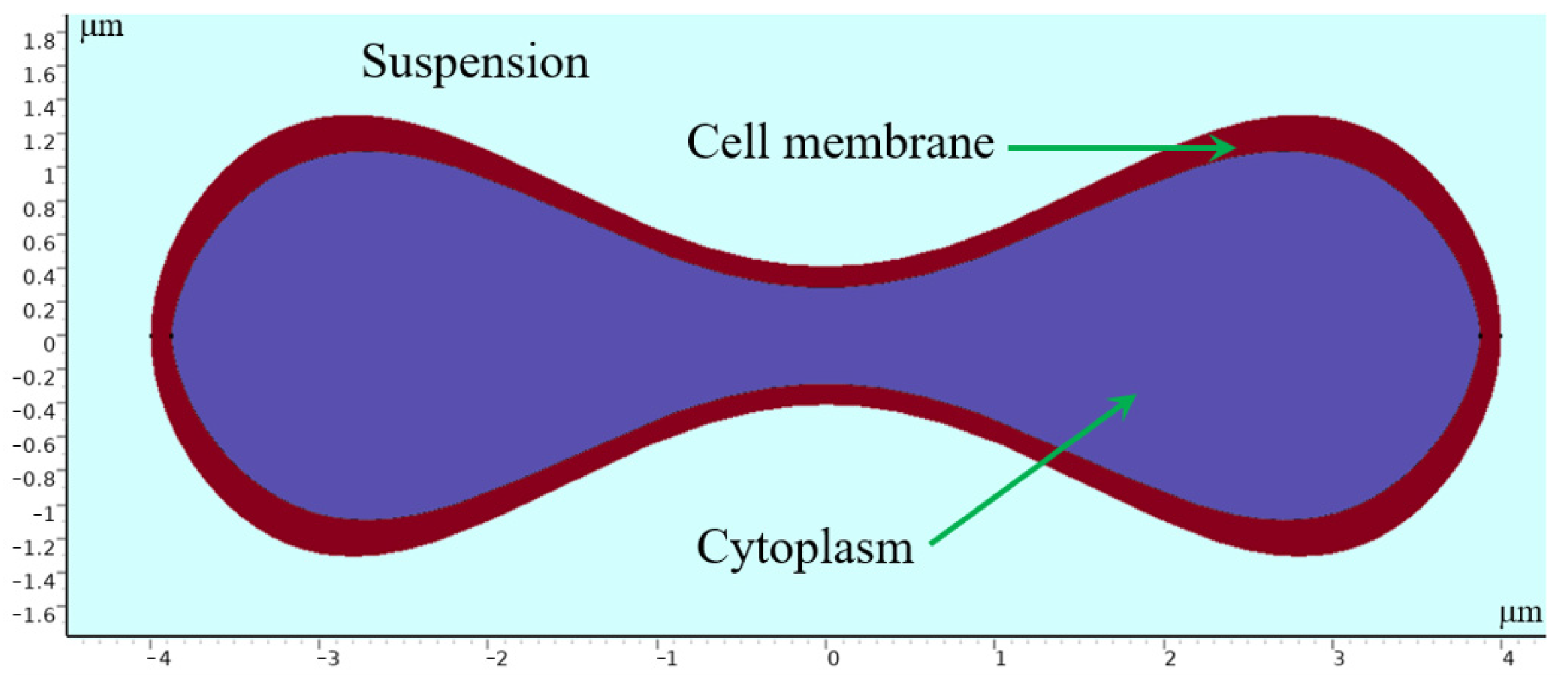
| Syringe Pump Injection Rate | Chip | Deformation and Path of 1D Erythrocytes | Deformation and Path of 7D Erythrocytes |
|---|---|---|---|
| 4.5 μL/min | A | Parachute, displacement mode | String ball, zigzag mode |
| B | Parachute, displacement mode | String ball, displacement mode | |
| 3 μL/min | A | String ball, zigzag mode | String ball, zigzag mode |
| B | String ball, displacement mode | String ball, displacement mode | |
| 1.5 μL/min | A | Pie, zigzag mode | Pie, displacement mode |
| B | Pie, zigzag mode | Pie, displacement mode |
| Erythrocyte Storage Time | Syringe Pump Injection Rate | Chip A Enrichment Ratio | Chip B Enrichment Ratio |
|---|---|---|---|
| 1D erythrocytes | 4.5 μL/min | 12.14 | 15.29 |
| 3 μL/min | 5.26 | 17.55 | |
| 1.5 μL/min | 7.27 | 6.91 | |
| 7D erythrocytes | 4.5 μL/min | 3.89 | 16.17 |
| 3 μL/min | 9.33 | 17.31 | |
| 1.5 μL/min | 14.82 | 19.24 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, Y.; Wu, J.; He, Y.; Liu, J.; Zhang, W.; Yan, Z. Diseased Erythrocyte Enrichment Based on I-Shaped Pillar DLD Arrays. Micromachines 2024, 15, 214. https://doi.org/10.3390/mi15020214
Lv Y, Wu J, He Y, Liu J, Zhang W, Yan Z. Diseased Erythrocyte Enrichment Based on I-Shaped Pillar DLD Arrays. Micromachines. 2024; 15(2):214. https://doi.org/10.3390/mi15020214
Chicago/Turabian StyleLv, Yao, Jiangbo Wu, Yongqing He, Jie Liu, Wenyu Zhang, and Zihan Yan. 2024. "Diseased Erythrocyte Enrichment Based on I-Shaped Pillar DLD Arrays" Micromachines 15, no. 2: 214. https://doi.org/10.3390/mi15020214
APA StyleLv, Y., Wu, J., He, Y., Liu, J., Zhang, W., & Yan, Z. (2024). Diseased Erythrocyte Enrichment Based on I-Shaped Pillar DLD Arrays. Micromachines, 15(2), 214. https://doi.org/10.3390/mi15020214






