Design of a Half-Mode Substrate-Integrated Waveguide (HMSIW) Multimode Resonator Bandpass Filter Using the Minkowski Fractal for C-Band Applications
Abstract
1. Introduction
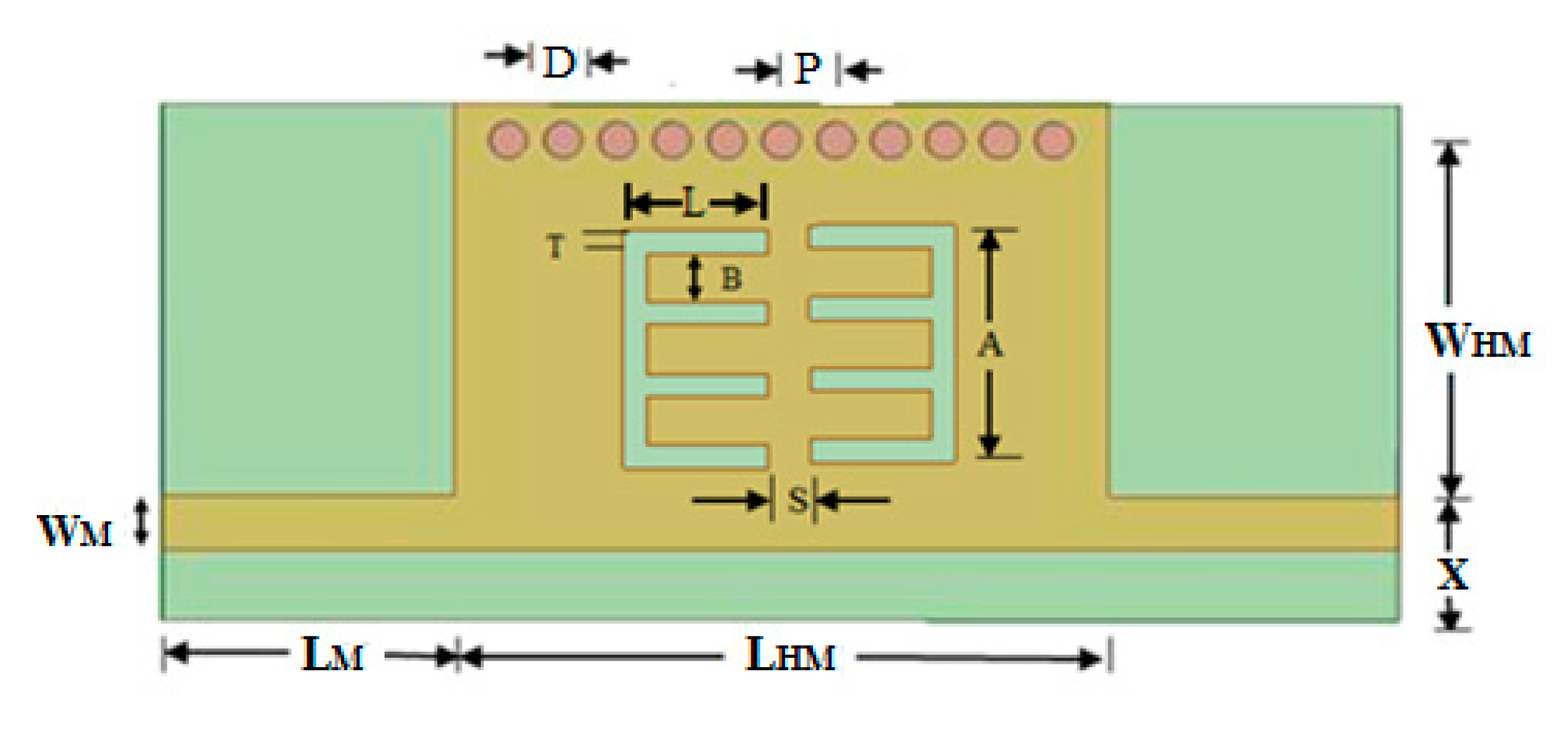
2. Design of a Comb-Shaped Half-Mode SIW (HMSIW) with Comb Slots
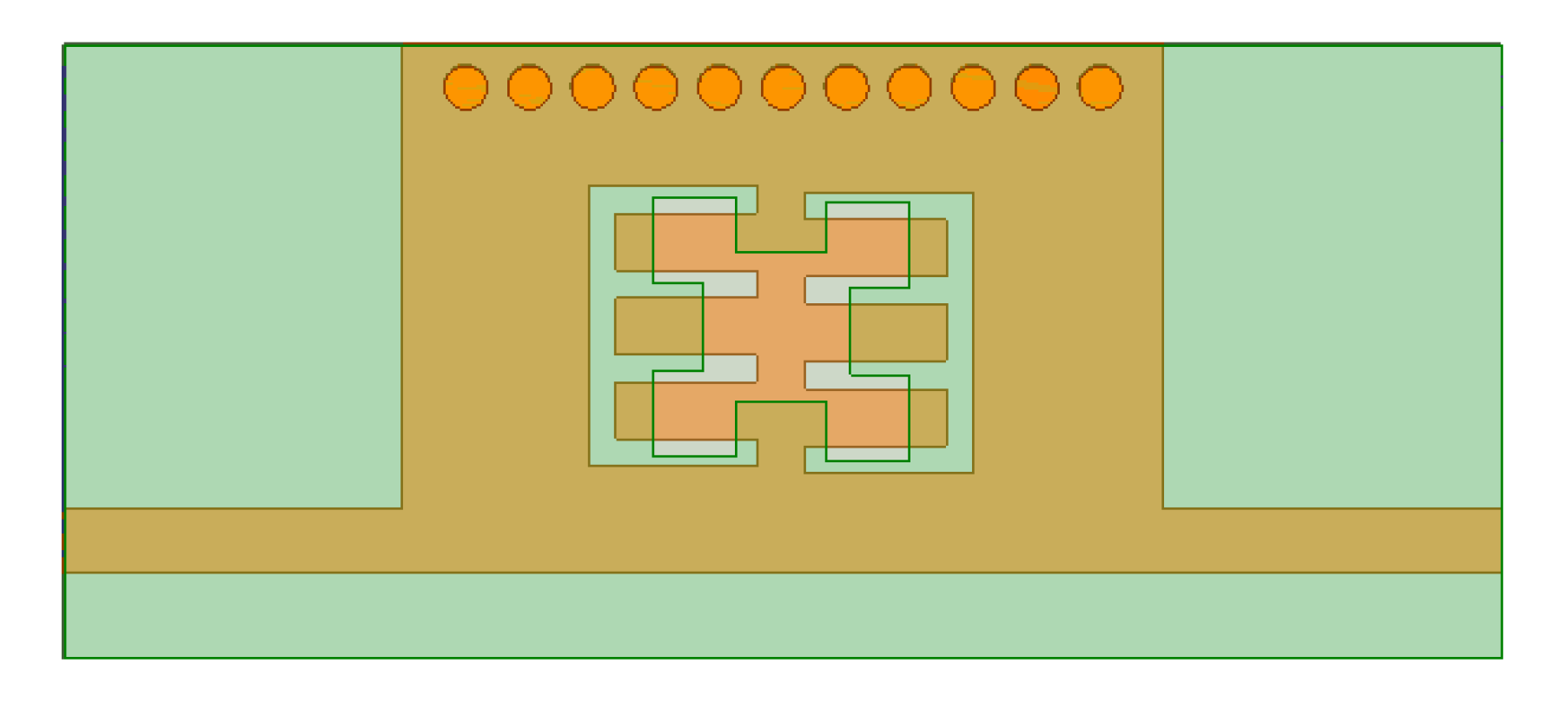
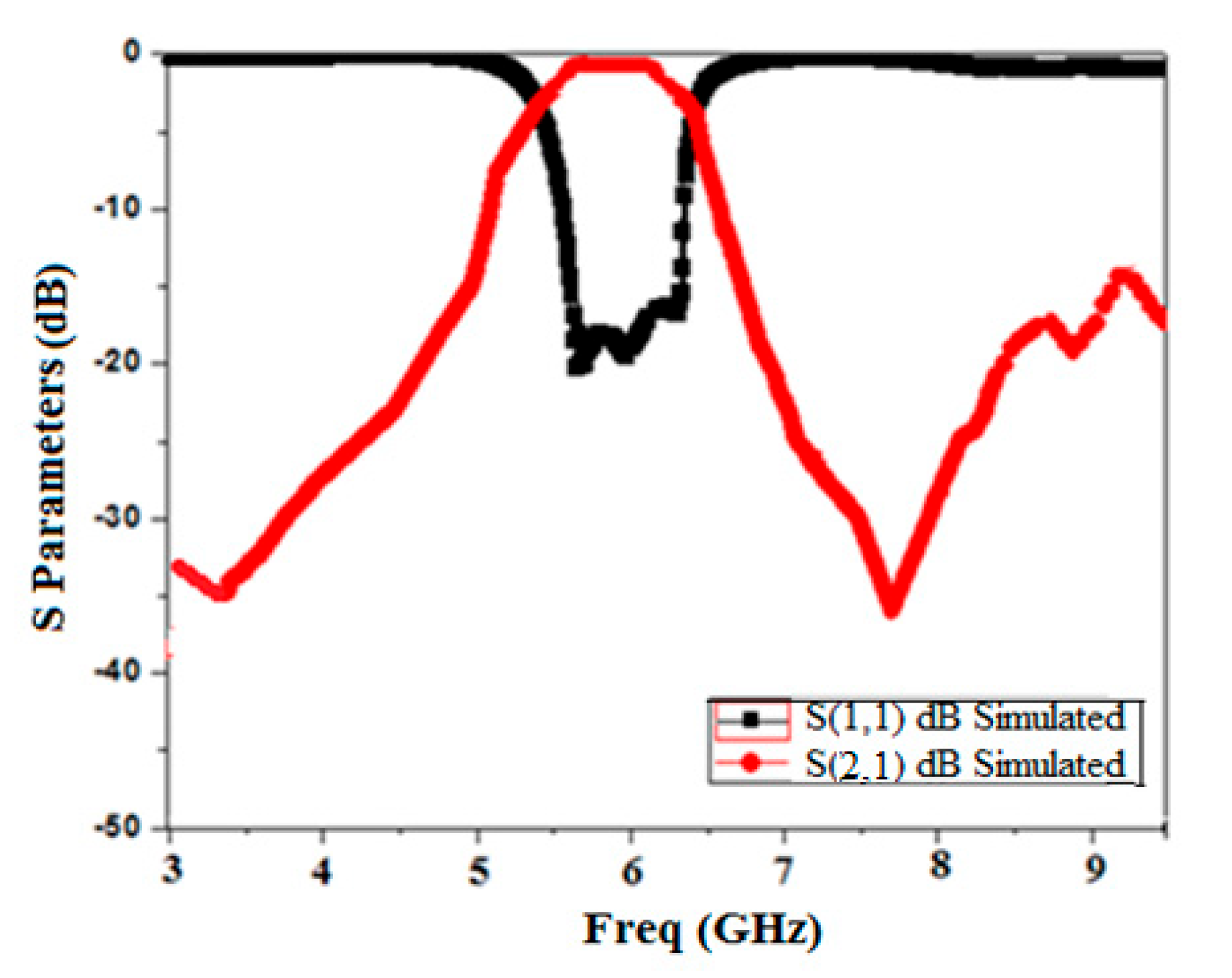
3. Band Pass Filter Based on the First Iteration of the Minkowski Fractal Curve
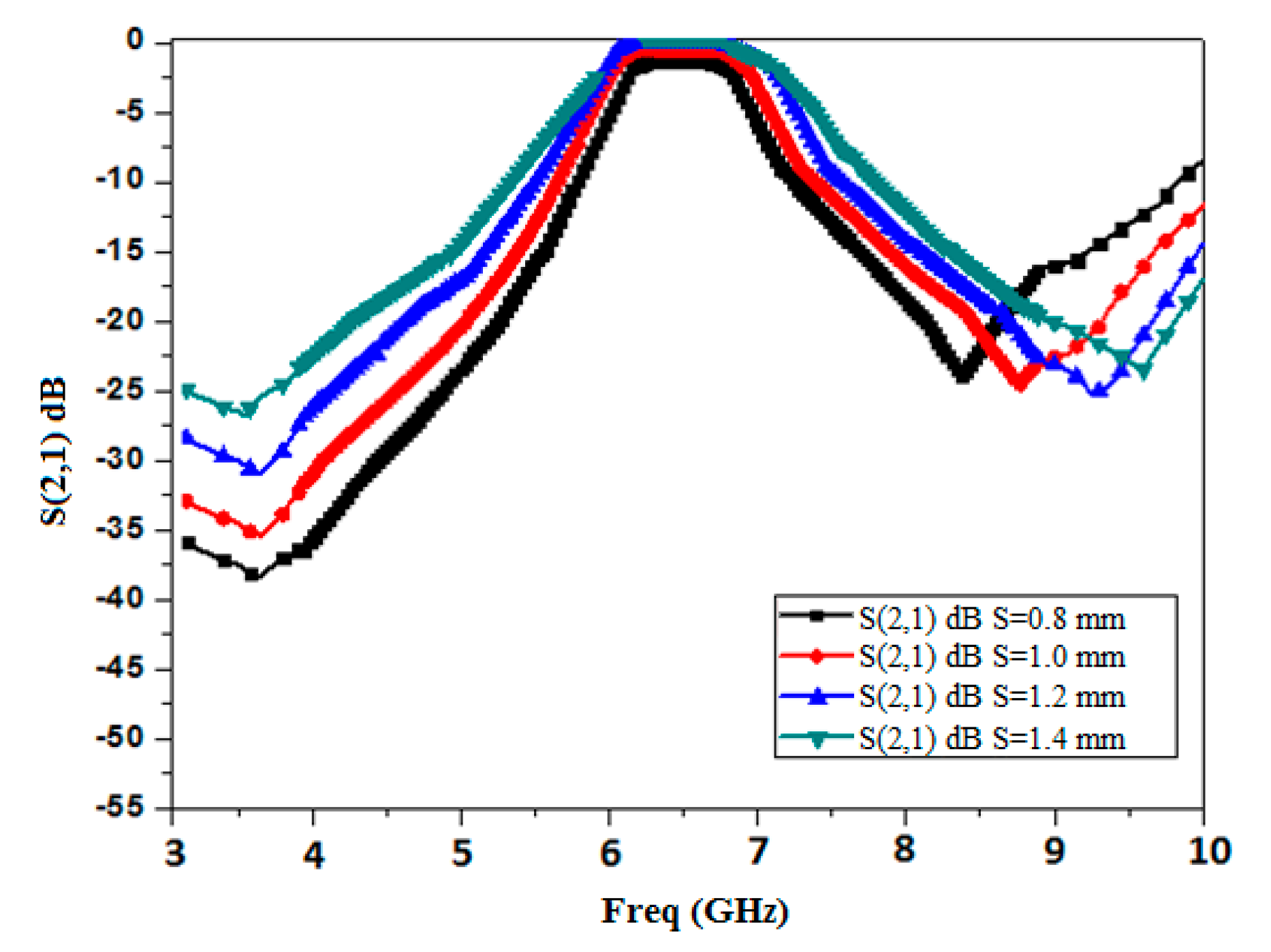
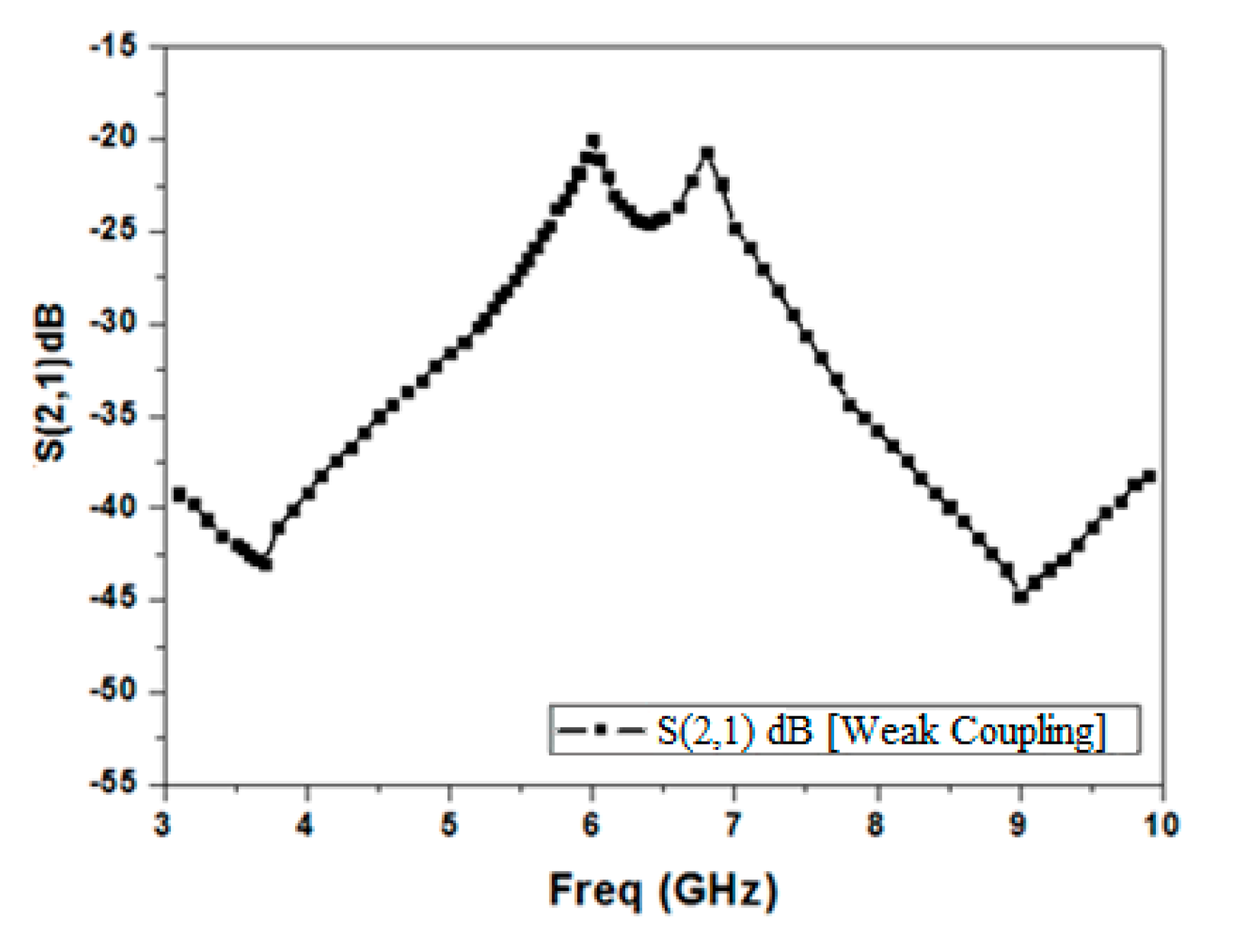
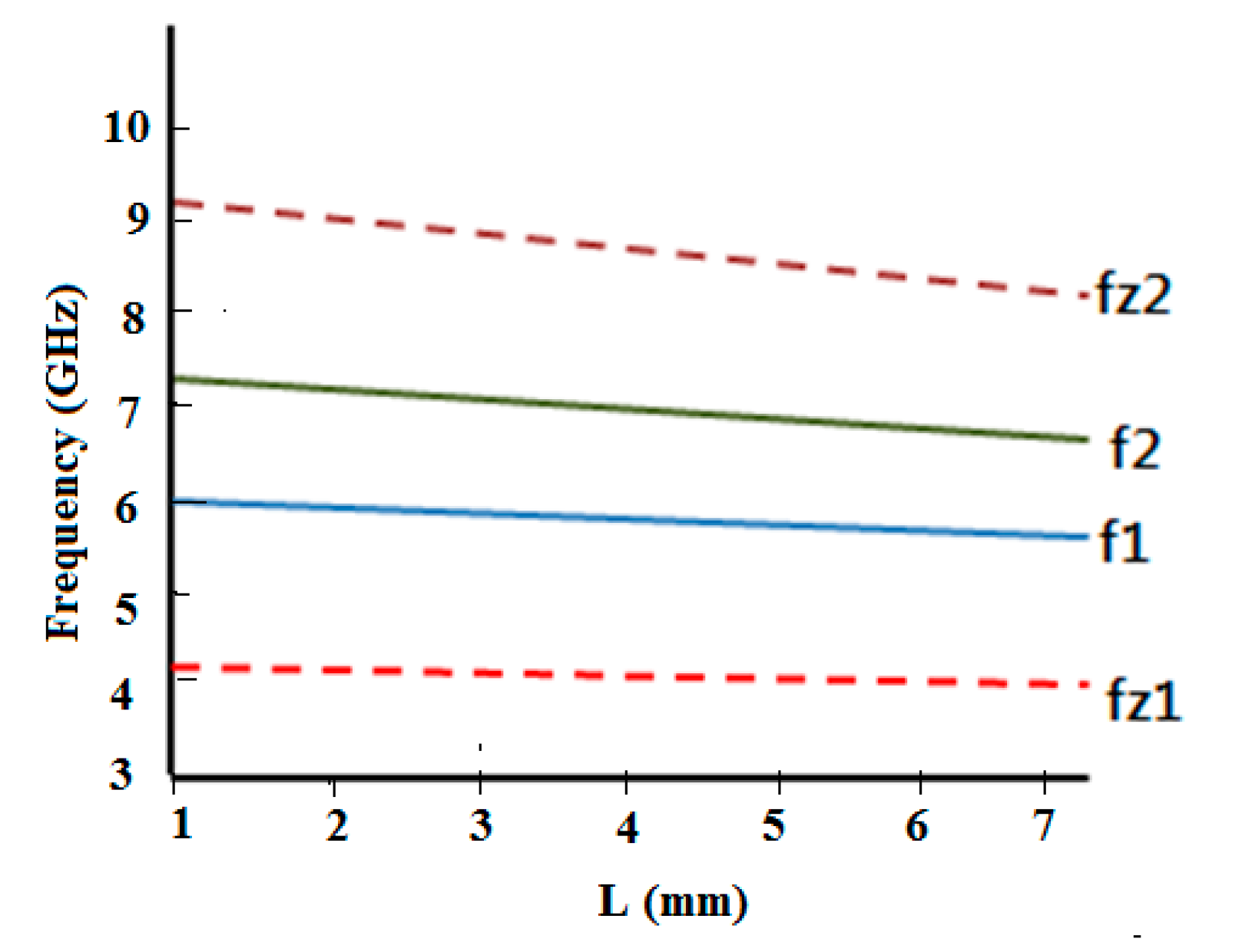
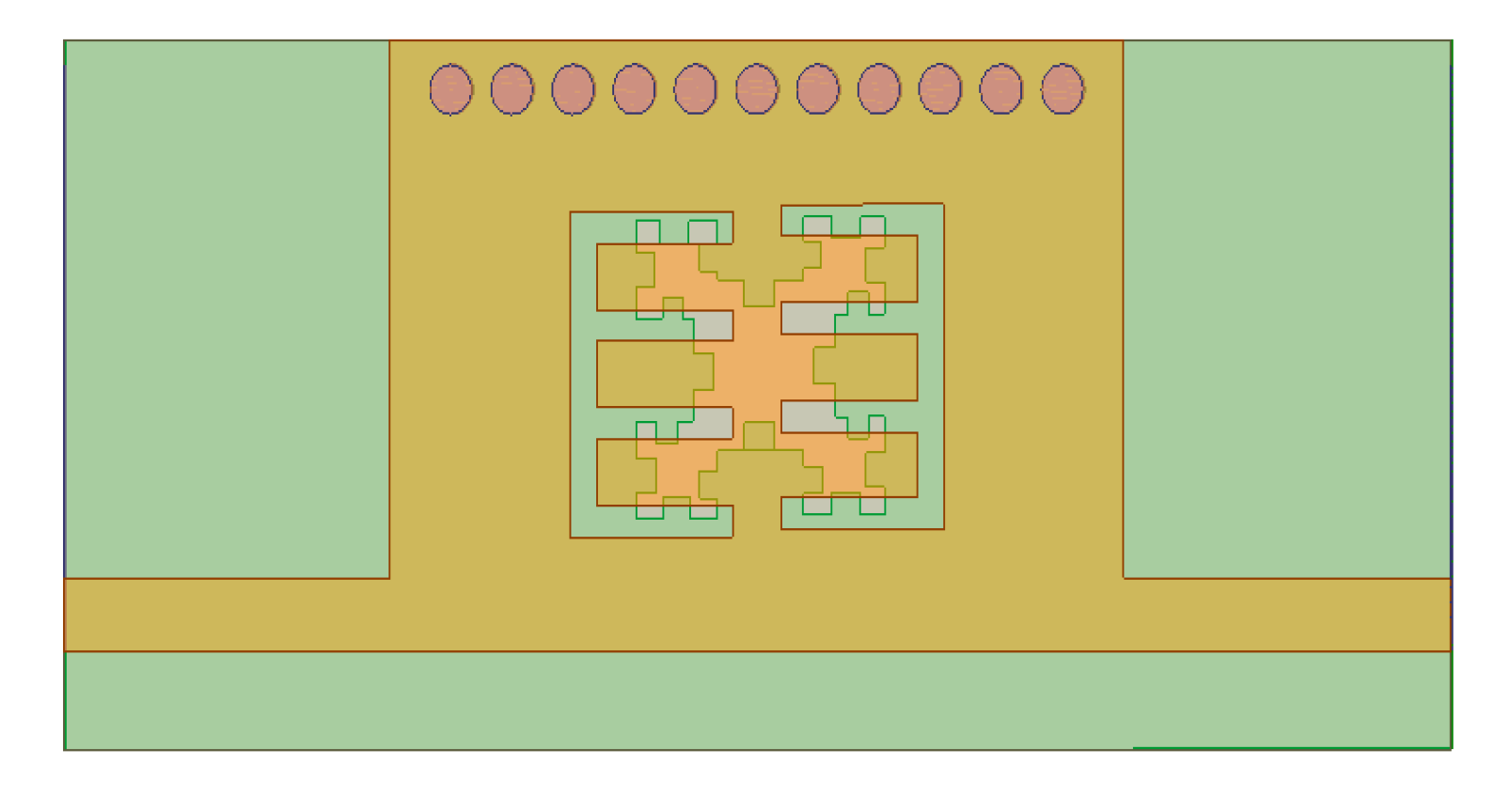
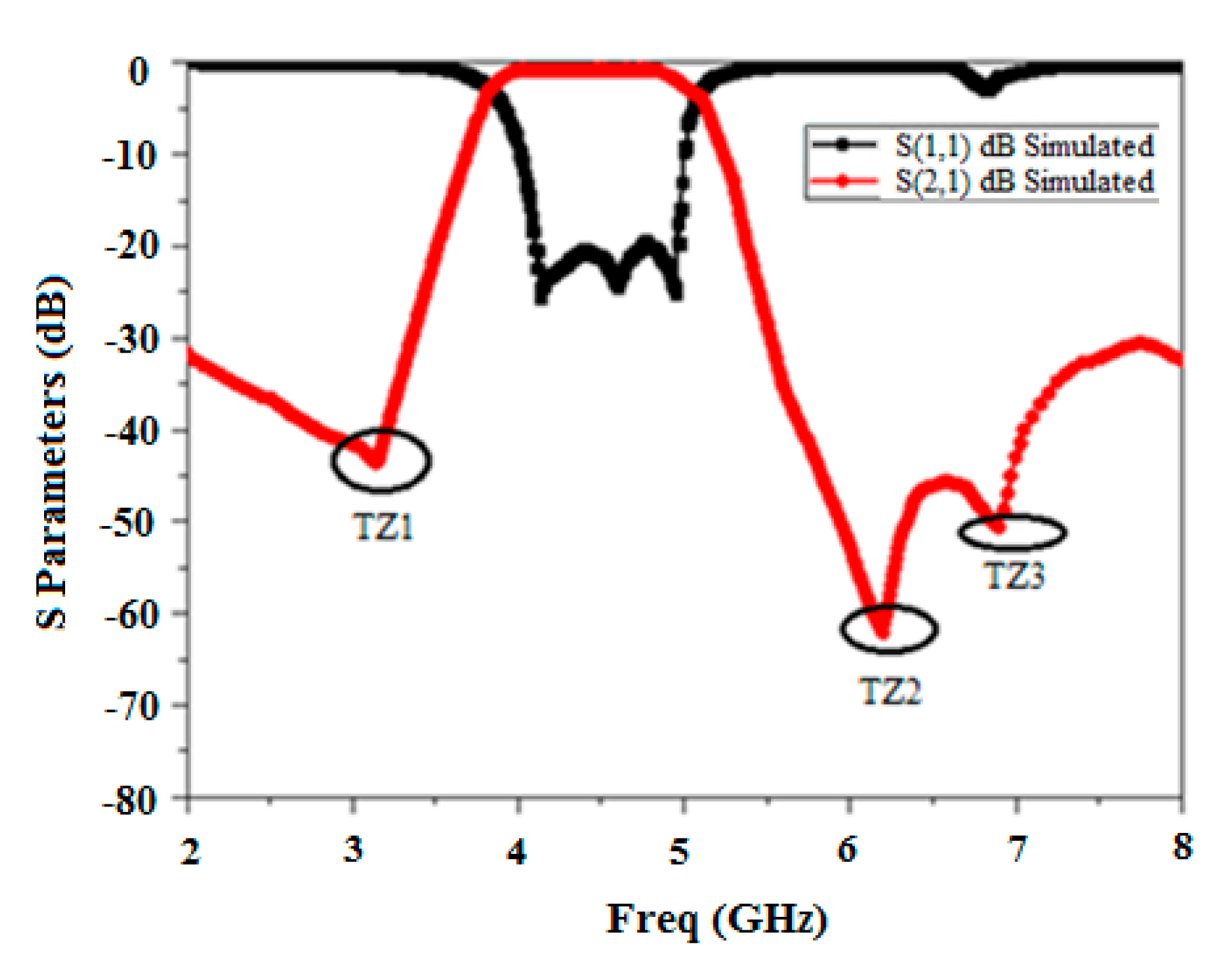
4. Band Pass Filter Based on the Second Iteration of the Minkowski Fractal Curve as DGS
5. Fabrication and Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hong, J.S.; Lancaster, M.J. Microstrip Filters for RF/Microwave Applications, 2nd ed.; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2011. [Google Scholar]
- Deslandes, D.; Wu, K. Single-substrate integration technique of planar circuits and waveguide filters. IEEE Trans. Microw. Theory Tech. 2003, 51, 593–596. [Google Scholar] [CrossRef]
- Muchhal, N.; Srivastava, S. Review of recent trends on miniaturization of substrate integrated waveguide (SIW) components. In Proceedings of the 2017 3rd International Conference on Computational Intelligence & Communication Technology (CICT), Ghaziabad, India, 9–10 February 2017; pp. 1–6. [Google Scholar]
- Tharani, D.; Kamakshy, S.; Karthikeyan, S. Miniaturized SIW filter using D-shaped resonators with wide out-of-band rejection for 5G applications. J. Electromagn. Waves Appl. 2020, 34, 2397–2409. [Google Scholar]
- Vala, A.; Patel, A. Half-mode substrate-integrated waveguide based band-pass filter for C band application. Microw. Opt. Technol. Lett. 2019, 61, 1468–1472. [Google Scholar] [CrossRef]
- Huang, L.; Robertson, I.D.; Wu, W.; Yuan, N. Substrate integrated waveguide filters with broadside-coupled complementary split ring resonators. IET Microw. Antennas Propag. 2013, 7, 795–801. [Google Scholar] [CrossRef]
- Noura, A.; Benaissa, M.; Abri, M.; Badaoui, H.; Vuong, T.H.; Tao, J. Miniaturized half-mode SIW band-pass filter design integrating dumbbell DGS cells. Microw. Opt. Technol. Lett. 2019, 61, 1473–1479. [Google Scholar] [CrossRef]
- Guo, Z.; Chin, K.-S.; Che, W.; Chang, C.-C. Cross-coupled bandpass filters using QMSIW cavities and S-shaped slot coupling structures. J. Electromagn. Waves Appl. 2013, 27, 160–167. [Google Scholar] [CrossRef]
- Muchhal, N.; Chakraborty, A.; Manoj, V.; Srivastava, S. Slotted Folded Substrate Integrated Waveguide Band Pass Filter with Enhanced Bandwidth for Ku/K Band Applications. Prog. Electromagn. Res.-M 2018, 70, 51–60. [Google Scholar] [CrossRef]
- Vallerotonda, P.; Pelliccia, L.; Tomassoni, C.; Cacciamani, F.; Sorrentino, R.; Galdeano, J.; Ernst, C. Compact Waveguide Bandpass Filters for Broadband Space Applications in C and Ku-Bands. In Proceedings of the 2019 European Microwave Conference in Central Europe (EuMCE), Prague, Czech Republic, 13–15 May 2019; pp. 116–119. [Google Scholar]
- Muchhal, N.; Elkhouly, M.; Fares, Y.; Vintimilla, R.Z. Design of Highly Selective Band Pass Filter with Wide Stop-band using Open Stubs and Spurlines for Satellite Communication (SATCOM) Applications. In Proceedings of the Fourteen International Conference on Advances in Satellite and Space Communications SPACOMM, Barcelona, Spain, 24–28 April 2022; pp. 6–11. [Google Scholar]
- Yang, X.-L.; Zhu, X.-W.; Wang, X. Dual-Band Substrate Integrated Waveguide Filters Based on Multi-Mode Resonator Overlapping Mode Control. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 1971–1975. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, G.; Zheng, J.; Tang, W.; Yang, J. SIW Filter With Adjustable Number of Passbands Using Assembled Multimode Resonant PCBs. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 3386–3389. [Google Scholar] [CrossRef]
- Wang, Y.; Hong, W.; Dong, Y.; Liu, B.; Tang, H.J.; Chen, J.; Yin, X.; Wu, K. Half mode substrate integrated waveguide (HMSIW) bandpass filter. IEEE Microw. Compon. Lett. 2007, 17, 265–267. [Google Scholar] [CrossRef]
- Ziboon, T.H.; Ali, J.K. Fractal geometry: An attractive choice for miniaturized planar microwave filter design, fractal analysis. In Fractal Analysis; Intech Open: London, UK, 2018. [Google Scholar]
- Kordiboroujeni, Z.; Bornemann, J. Designing the width of substrate integrated waveguide structures. IEEE Microw. Compon. Lett. 2003, 23, 518–522. [Google Scholar] [CrossRef]
- Lai, Q.; Fumeaux, C.; Hong, W.; Vahldieck, R. Characterization of the propagation properties of the Half-mode substrate integrated waveguide. IEEE Trans. Microw. Theory Tech. 2009, 57, 1996–2004. [Google Scholar]
- Balanis, C.A. Antenna Theory: Analysis and Design, 3rd ed.; Wiley and Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Mandelbort, B.B. The Fractal Geometry of Nature; W.H. Freeman and Company: San Francisco, CA, USA, 1983. [Google Scholar]
- Nagaraju, V.; Madhav, P.V.; Kumar, M. Optimization of patch size of fractal hybrid antenna for GPS application. Int. J. Eng. Res. Appl. 2013, 3, 2003–2008. [Google Scholar]
- Khandelwal, M.K.; Kanuaujia, B.K.; Kumar, S. Defected Ground Structure: Fundamentals, Analysis, and Applications in Modern Wireless Trends. Int. J. Antennas Propag. 2017, 2017, 2018527. [Google Scholar] [CrossRef]
- Ohi, M.A.R.; Hasan, Z.; Faruquee, S.F.B.; Kawsar, A.A.M.; Ahmed, A. Wideband Minkowski fractal antenna using complementary split ring resonator in modified ground plane for 5G wireless communications. Eng. Rep. 2021, 3, e1238. [Google Scholar] [CrossRef]
- Kumar, S.; Das, S. A new defected ground structure for different microstrip circuit applications. Radioengineering 2007, 16, 16–22. [Google Scholar]
- Aditomo, W.; Munir, A. Bandwidth enhancement of ultra-wideband microstrip bandpass filter using defected ground structure. In Proceedings of the 2013 International Conference on QiR, Yogyakarta, Indonesia, 25–28 June 2013; pp. 64–67. [Google Scholar]
- Ahn, D.; Park, J.-S.; Kim, C.-S.; Kim, J.; Qian, Y.; Itoh, T. A design of the low-pass filter using the novel microstrip defected ground structure. IEEE Trans. Microw. Theory Tech. 2001, 49, 86–93. [Google Scholar] [CrossRef]
- A-Rahman, A.; Ali, A.R.; Amari, S.; Omar, A.S. Compact bandpass filters using Defected Ground Structure (DGS) coupled resonators. In Proceedings of the IEEE MTT-S International Microwave Symposium Digest, Long Beach, CA, USA, 17 June 2005; pp. 1479–1482. [Google Scholar]
- Ali, J.K.; Ziboon, H.T. Design of Compact Bandpass Filters based on Fractal Defected Ground Structure (DGS) Resonators. Indian J. Sci. Technol. 2016, 9, 1–9. [Google Scholar]
- Bhat, R.U.; Jha, R.K.; Singh, G. Wide stopband harmonic suppressed lowpass filter with novel DGS. Int. J. RF Microw. Comput.-Aided Eng. 2017, 28, e21235. [Google Scholar]
- Hong, J.G.; Lancaster, M.J. Microstrip Filters for RF/Microwave Applications; John Wiley & Sons: New York, NY, USA, 2001. [Google Scholar]






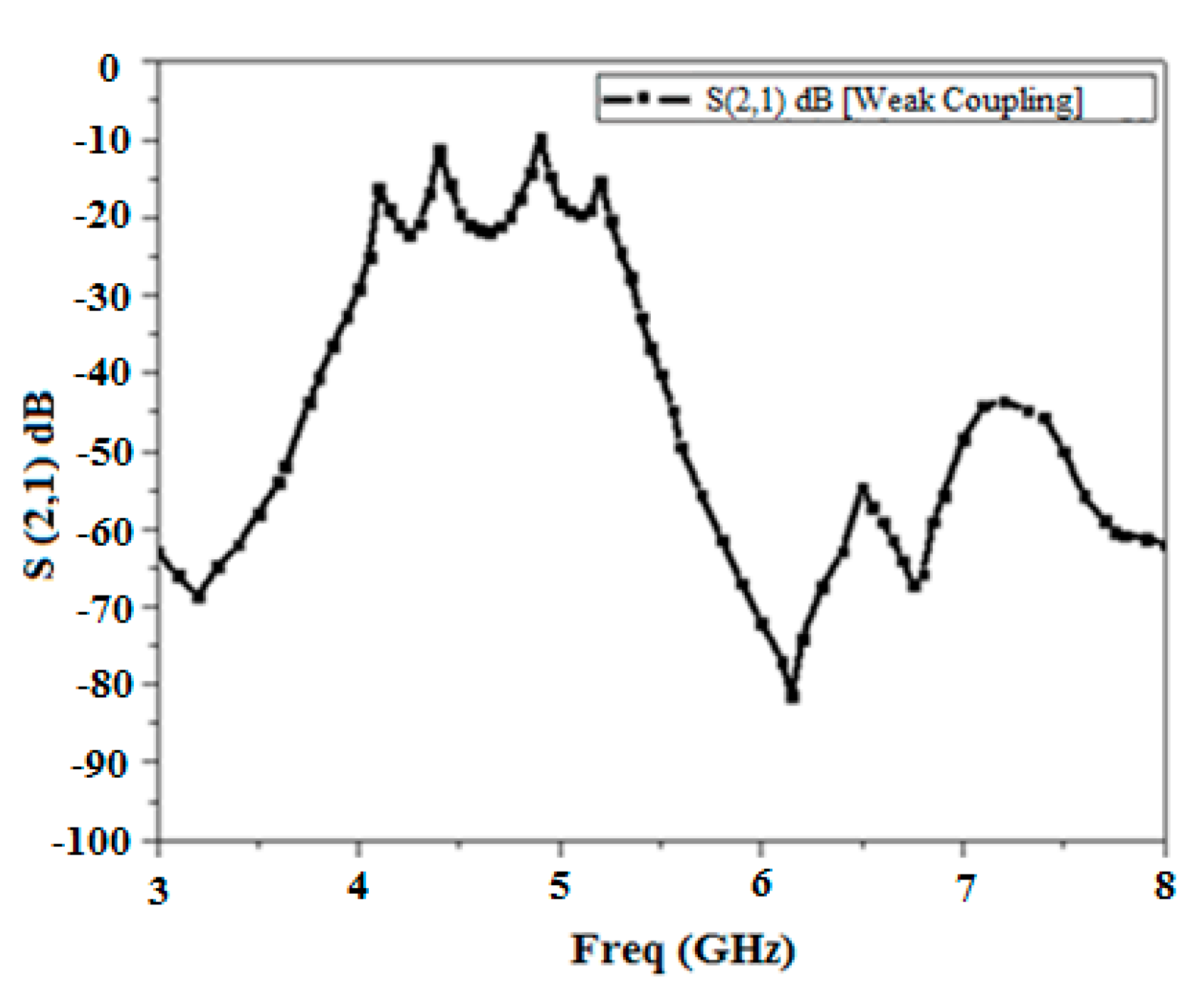

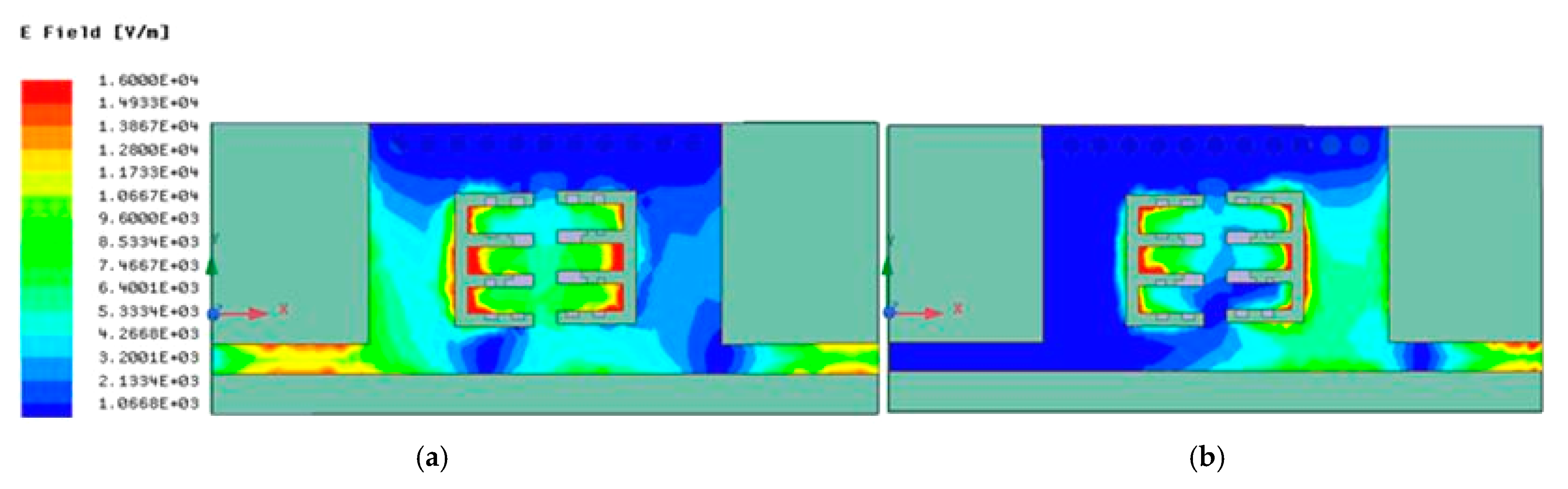


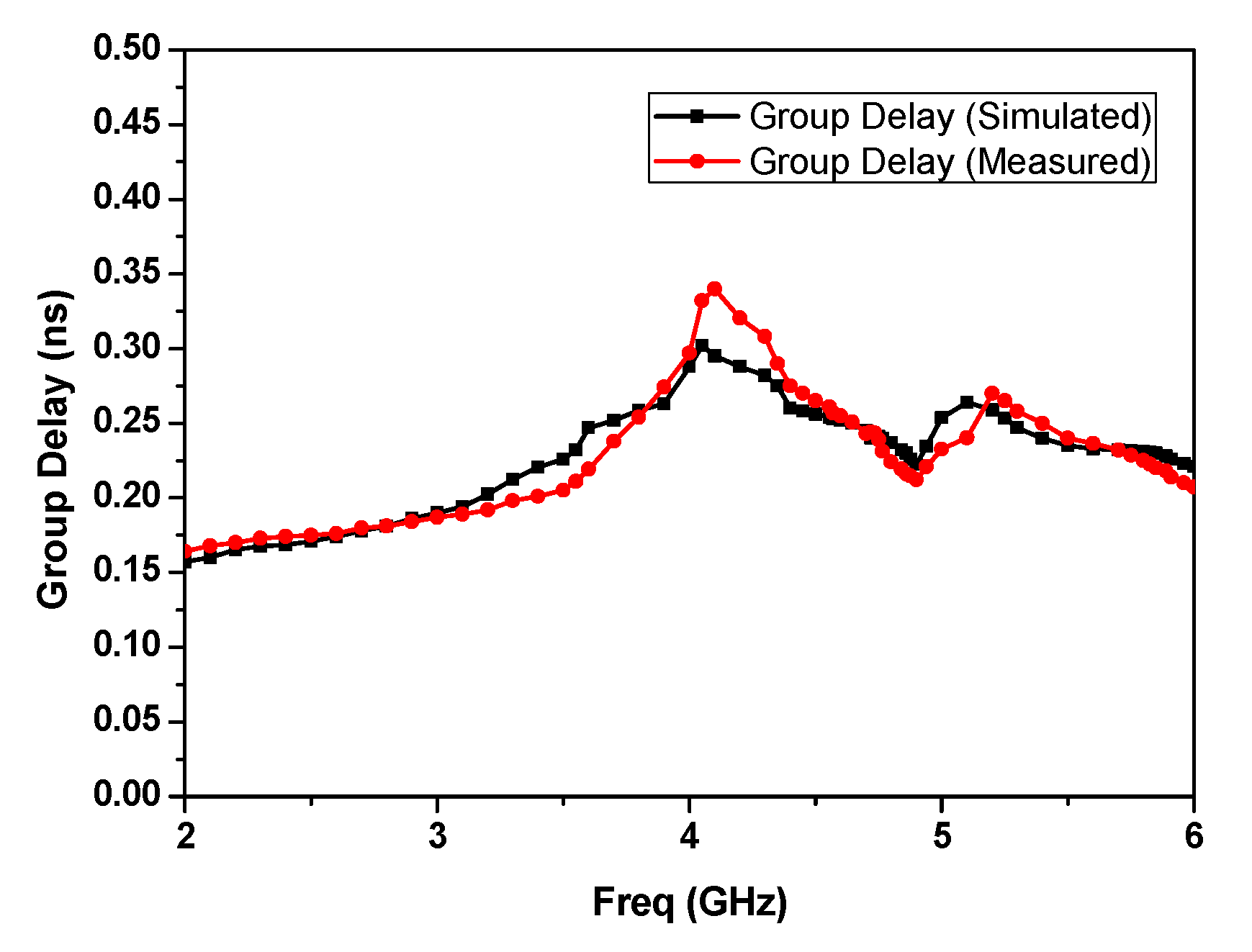
| Ref. No. | Center Freq. fo (GHz) | IL (dB)/RL (dB) | 3 db-FBW (%) | Avg. Roll Off Rate (dB/GHz) | Out-of-Band Rejection (>−20 dB) | Q Factor | Area Size in mm2 (in λ02) |
|---|---|---|---|---|---|---|---|
| [4] | 6.11 | 1.1/20.5 | 8.9 | 45 | 3f0 | 58.5 | 25.5 × 9.6 (0.086) |
| [5] | 7.15 | 2/25 | 1.55 | 28.4 | Not Given | 45.4 | 13.5 × 40 (0.32) |
| [6] | 5.1 | 4/19 | 5.8 | 68.5 | 1.5fo | 14.5 | 20 × 13 (0.075) |
| [7] | 6.5 | 2.6/34 | 24.2 | 24.5 | 1.3fo | 10.8 | 38.1 × 7.5 (0.21) |
| [8] | 5.57 | 2/18 | 7.44 | 45.5 | 2fo | 26.2 | 22.6 × 22.6 (0.16) |
| [This work] | 4.7 | 1.05/18.5 | 21.4 | 66.5 | >2fo | 11.4 | 19.5 mm × 6.5 mm (0.038) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muchhal, N.; Kumar, A.; Tewari, N.; Kalia, S.; Srivastava, S. Design of a Half-Mode Substrate-Integrated Waveguide (HMSIW) Multimode Resonator Bandpass Filter Using the Minkowski Fractal for C-Band Applications. Micromachines 2024, 15, 1440. https://doi.org/10.3390/mi15121440
Muchhal N, Kumar A, Tewari N, Kalia S, Srivastava S. Design of a Half-Mode Substrate-Integrated Waveguide (HMSIW) Multimode Resonator Bandpass Filter Using the Minkowski Fractal for C-Band Applications. Micromachines. 2024; 15(12):1440. https://doi.org/10.3390/mi15121440
Chicago/Turabian StyleMuchhal, Nitin, Abhay Kumar, Nidhi Tewari, Samriti Kalia, and Shweta Srivastava. 2024. "Design of a Half-Mode Substrate-Integrated Waveguide (HMSIW) Multimode Resonator Bandpass Filter Using the Minkowski Fractal for C-Band Applications" Micromachines 15, no. 12: 1440. https://doi.org/10.3390/mi15121440
APA StyleMuchhal, N., Kumar, A., Tewari, N., Kalia, S., & Srivastava, S. (2024). Design of a Half-Mode Substrate-Integrated Waveguide (HMSIW) Multimode Resonator Bandpass Filter Using the Minkowski Fractal for C-Band Applications. Micromachines, 15(12), 1440. https://doi.org/10.3390/mi15121440






