A Novel MZI Fiber Sensor with Enhanced Curvature and Strain Sensitivity Based on Four-Core Fiber
Abstract
1. Introduction
2. Manufacturing and Sensing Principles
3. Experiments and Measurement
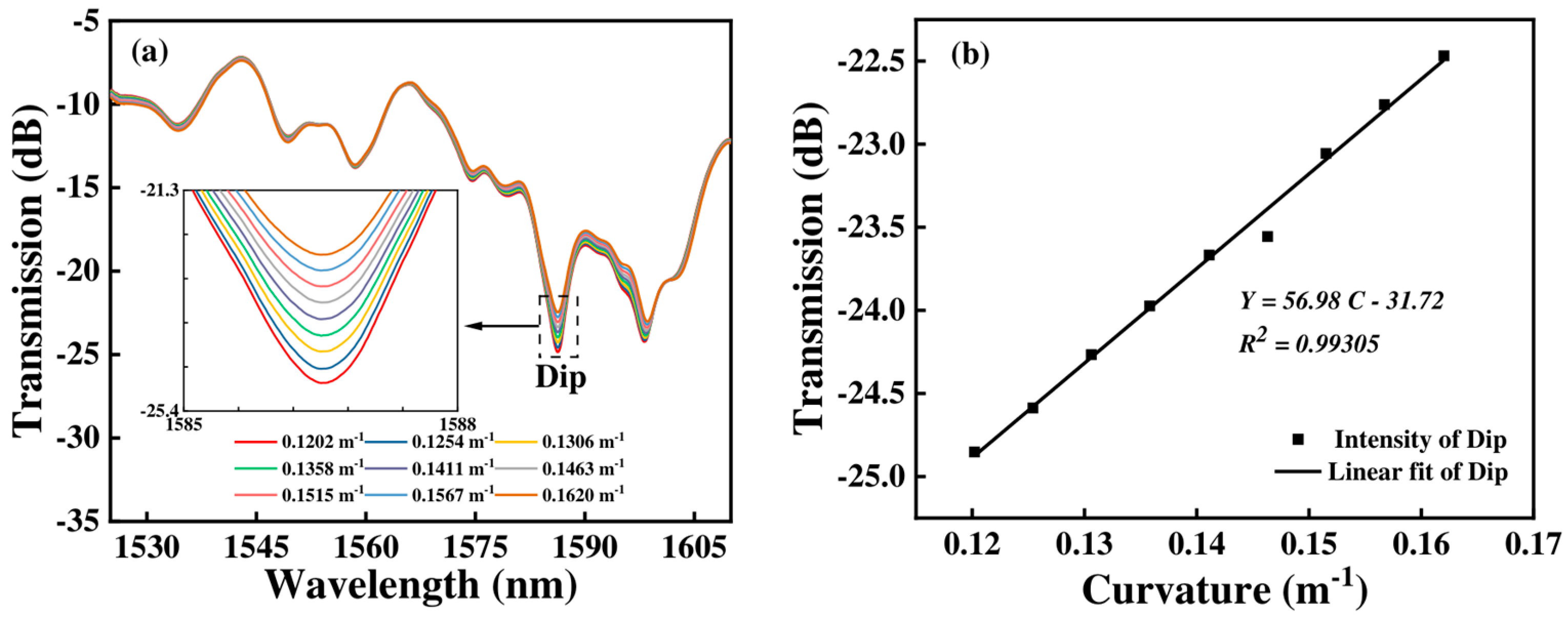
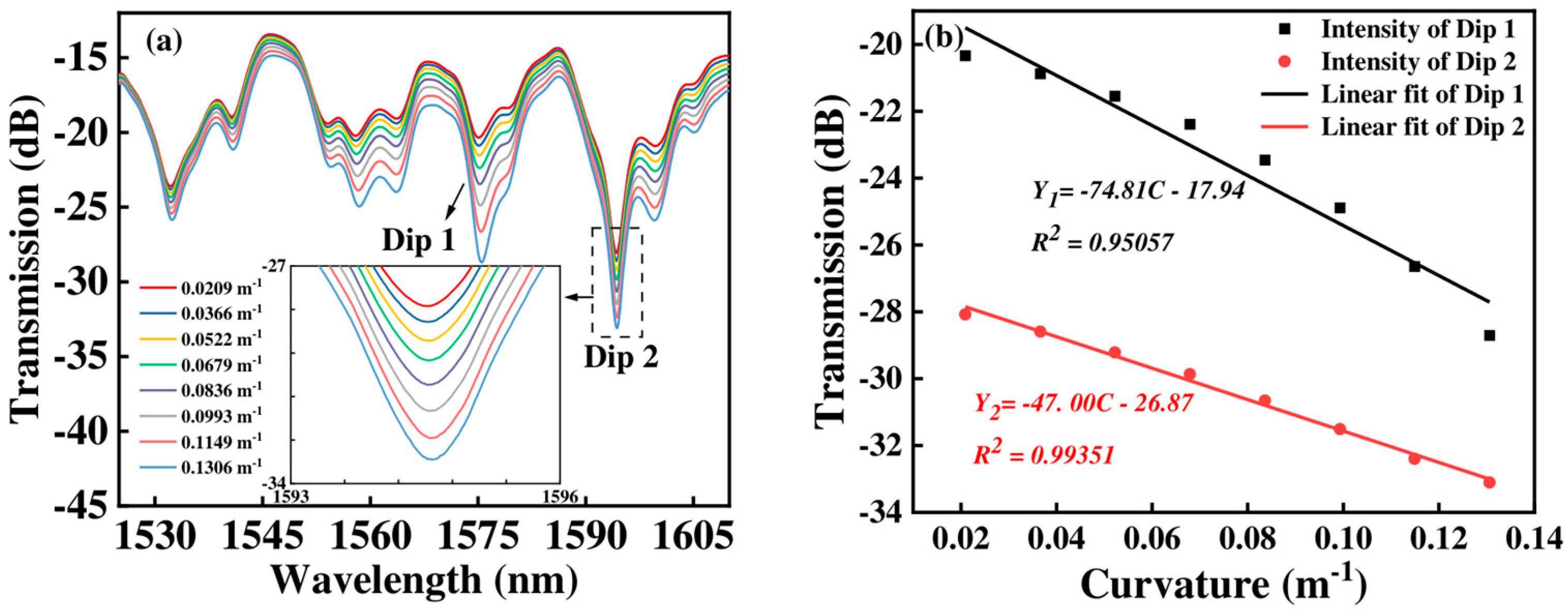
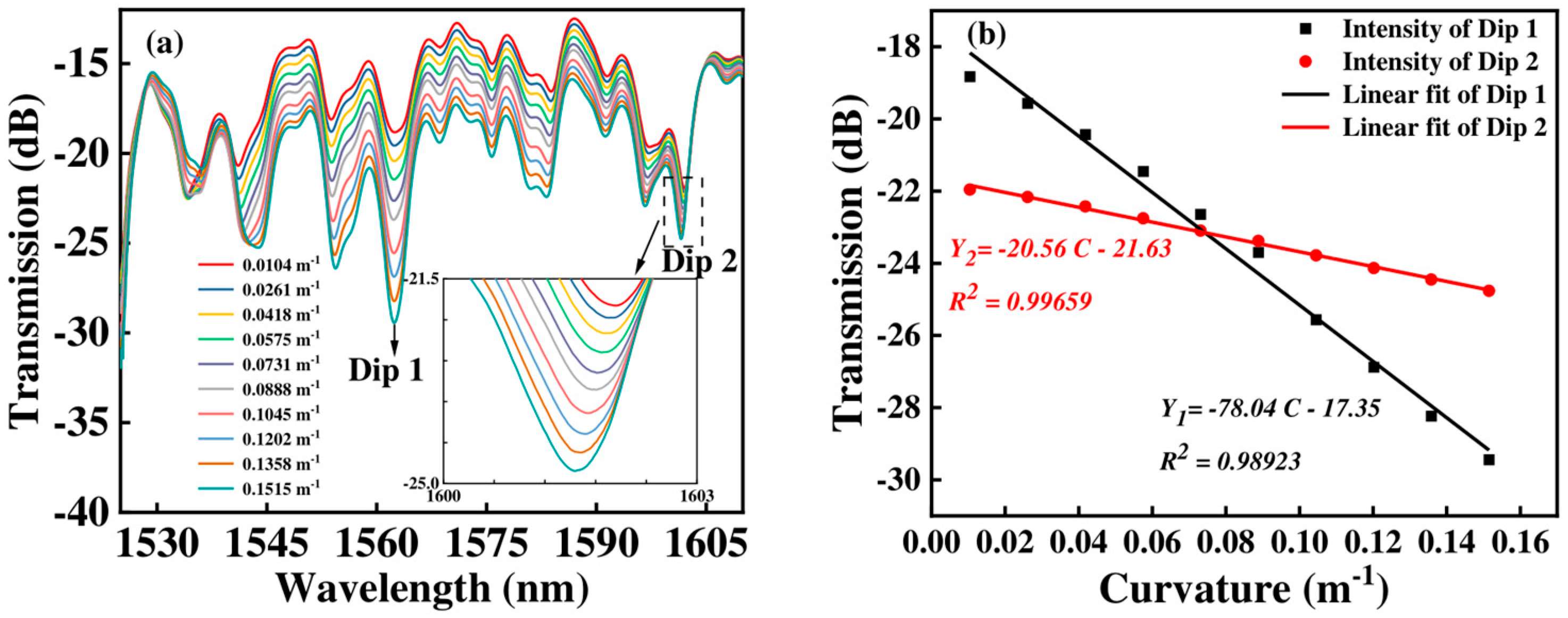
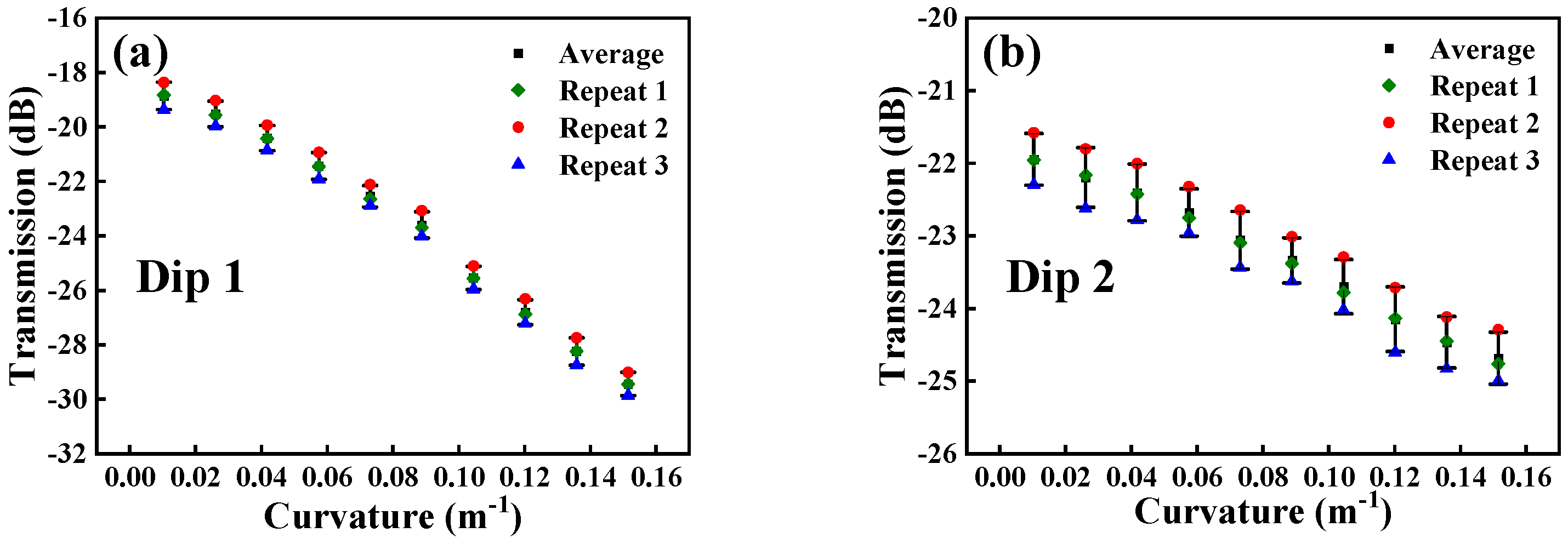
3.1. Curvature Measurement
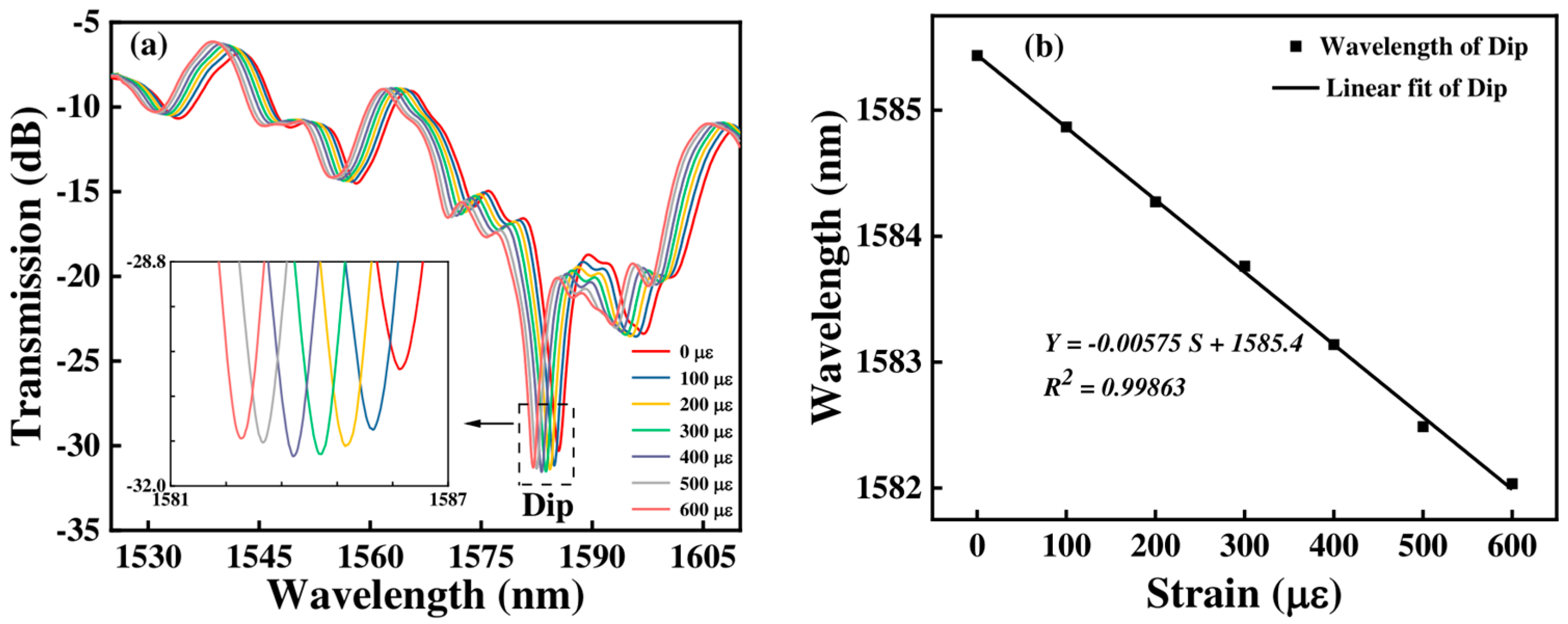
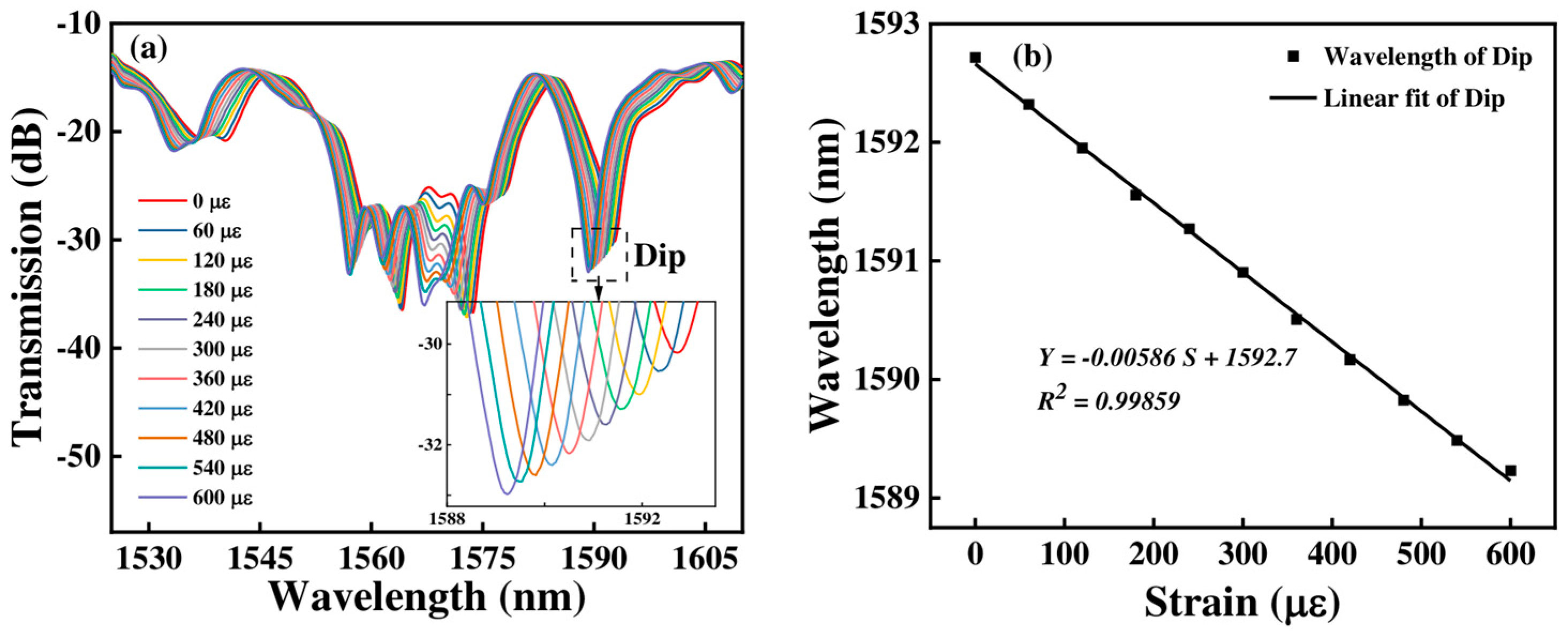
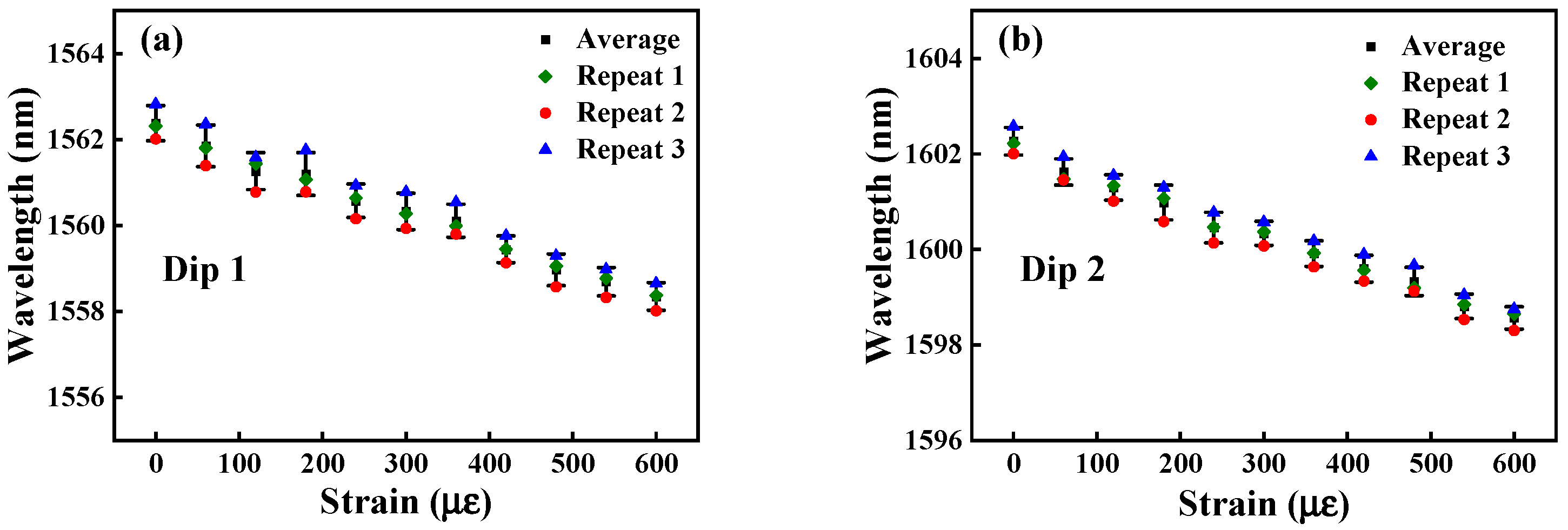
3.2. Strain Measurement
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ruan, J. Fiber curvature sensor based on concave-heterotypic cascaded fiber Sagnac interferometer. Microw. Opt. Technol. Lett. 2020, 62, 3645–3649. [Google Scholar] [CrossRef]
- Jauregui-Vazquez, D.; Korterik, J.P.; Osornio-Martinez, C.E.; Estudillo-Ayala, J.M.; Offerhaus, H.L.; Alvarez-Chavez, J.A. A strain reflection-based fiber optic sensor using thin core and standard single-mode fibers. Opt. Commun. 2022, 522, 128659. [Google Scholar] [CrossRef]
- Wang, F.; Wei, Y.; Han, Y. High Sensitivity and Wide Range Refractive Index Sensor Based on Surface Plasmon Resonance Photonic Crystal Fiber. Sensors 2023, 23, 6617. [Google Scholar] [CrossRef] [PubMed]
- Xiao, S.; Wu, B.; Wang, Z.; Jiang, Y. A peanut taper based Mach-Zehnder interferometric sensor for strain and temperature discrimination. Opt. Fiber Technol. 2022, 70, 102871. [Google Scholar] [CrossRef]
- Shao, M.; Zang, Y.; Qiao, X.; Fu, H.; Jia, Z.A. Humidity Sensor Based on Hybrid Fiber Bragg Grating/Abrupt Fiber Taper. IEEE Sens. J. 2017, 17, 1302–1305. [Google Scholar] [CrossRef]
- Gao, J.W.; Xia, Q.K.; Wang, D.N. Fiber In-Line Mach-Zehnder Interferometer Based on a Pair of Optical Fiber Diffraction Gratings. IEEE Photonics Technol. Lett. 2022, 34, 1096–1099. [Google Scholar] [CrossRef]
- Jauregui-Vazquez, D.; Herrera-Piad, L.A.; Tentori, D.; Castro-Toscano, J.D.; Escalante-Sanchez, K.C.; Gallegos-Arellano, E.; Sierra-Hernandez, J.M. Visible range curvature fiber-optic sensor with low strain-temperature dependence. Opt. Commun. 2024, 563, 130601. [Google Scholar] [CrossRef]
- Dong, L.; Gang, T.; Bian, C.; Tong, R.; Wang, J.; Hu, M. A high sensitivity optical fiber strain sensor based on hollow core tapering. Opt. Fiber Technol. 2020, 56, 102179. [Google Scholar] [CrossRef]
- Xu, s.; Chen, H.; Feng, W. Fiber-optic curvature and temperature sensor based on the lateral-offset spliced SMF-FCF-SMF interference structure. Opt. Laser Technol. 2021, 141, 107174. [Google Scholar] [CrossRef]
- Zhao, R.; Shu, X. Curvature sensor based on femtosecond laser-inscribed straight waveguide in FMF. Opt. Laser Technol. 2022, 152, 108154. [Google Scholar] [CrossRef]
- Zhao, T.; Lou, S.; Wang, X.; Zhang, W.; Wang, Y. Simultaneous measurement of curvature, strain and temperature using a twin-core photonic crystal fiber-based sensor. Sensors 2018, 18, 2145. [Google Scholar] [CrossRef]
- Liu, Z.; Zhu, L.; Lu, L.; Shangguan, C.; Zhang, D.; Wang, J. Determination of temperature and strain by a compact optical fiber Mach-Zehnder interferometer (MZI) composed of a single-mode fiber (SMF), seven core fiber (SCF), and multimode fiber (MMF) with a fiber Bragg grating (FBG). Instrum. Sci. Technol. 2021, 49, 457–469. [Google Scholar] [CrossRef]
- Liu, Y.; Dong, J.; Huang, L.; Song, X.; Li, B. Investigations on seven-core fiber based interferometric all-fiber sensor for curvature and temperature measurements. Optik 2022, 254, 168638. [Google Scholar] [CrossRef]
- Li, C.; Ning, T.; Li, J.; Pei, L.; Zhang, C.; Zhang, C.B.; Lin, H.; Wen, X. Simultaneous measurement of refractive index, strain, and temperature based on a four-core fiber combined with a fiber Bragg grating. Opt. Laser Technol. 2017, 90, 179–184. [Google Scholar] [CrossRef]
- Yang, R.; Zhu, L.; Li, J.; Xu, T.; Sun, G. High fringe visibility Mach-Zehnder interferometric sensor based on a Four-Core fiber. Instrum. Sci. Technol. 2020, 48, 326–337. [Google Scholar] [CrossRef]
- Fu, X.; Zhang, Y.; Zhou, J.; Li, Q.; Fu, G.; Jin, W.; Bi, W.; Hu, Q. A Temperature and Strain Dual-Parameter Sensor Based on Conical Four-Core Fiber Combined with a Multimode Fiber. IEEE Sens. J. 2022, 22, 23990–23996. [Google Scholar] [CrossRef]
- Sun, J.; Wang, T.; Wang, X.; Chang, J.; Ke, W. Multiparameter measurement sensor based on no-core fiber. Appl. Opt. 2022, 61, 3247. [Google Scholar] [CrossRef]
- Zhao, Y.; Cai, L.; Li, X.-G. Temperature-Insensitive Optical Fiber Curvature Sensor Based on SMF-MMF-TCSMF-MMF-SMF Structure. IEEE Trans. Instrum. Meas. 2017, 66, 141–147. [Google Scholar] [CrossRef]
- Dong, X.; Du, H.; Sun, X.; Luo, Z.; Duan, J. A novel strain sensor with large measurement range based on all fiber mach-zehnder interferometer. Sensors 2018, 18, 1549. [Google Scholar] [CrossRef]
- Zhu, C.; Zhuang, Y.; Huang, J. Machine Learning Assisted High-Sensitivity and Large-Dynamic-Range Curvature Sensor Based on No-Core Fiber and Hollow-Core Fiber. J. Light. Technol. 2022, 40, 5762–5767. [Google Scholar] [CrossRef]
- Li, C.; Ning, T.; Zhang, C.; Li, J.; Zhang, C.B.; Wen, X.; Lin, H.; Pei, L. All-fiber multipath Mach–Zehnder interferometer based on a four-core fiber for sensing applications. Sens. Actuators A Phys. 2016, 248, 148–154. [Google Scholar] [CrossRef]
- Yu, j.; Xu, S.; Jiang, Y.; Chen, H.; Feng, W. Multi-parameter sensor based on the fiber Bragg grating combined with triangular-lattice four-core fiber. Optik 2020, 208, 164094. [Google Scholar] [CrossRef]
- Marrujo-Garcia, S.; Hernandez-Romano, I.; Torres-Cisneros, M.; May-Arrioja, D.A.; Minkovich, V.P.; Monzon-Hernandez, D. Temperature-independent curvature sensor based on in-fiber mach-zehnder interferometer using hollow-core fiber. J. Light. Technol. 2020, 38, 4166–4173. [Google Scholar] [CrossRef]







| Structure | Sensitivity of Curvature | Sensitivity of Strain | Reference |
|---|---|---|---|
| SMF-FCF-SMF | 18.75 nm/m−1 | -- | [9] |
| SMF-NCF-SCF-NCF-SMF | 10.22 dB/m−1 | -- | [13] |
| SMF-FCF-SMF | 20.18 nm/m−1 | 1.78 pm/με | [21] |
| FBG-SMF-FCF-SMF | 15.57 pm/m−1 | -- | [22] |
| SMF-MMF-HCF-MMF-SMF | 19.58 dB/m−1 | -- | [23] |
| SMF-NCF-FCF-NCF-SMF | −78.04 dB/m−1 | −6.49 pm/με | This Work |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, X.; Chen, F.; Zhuang, H.; Qian, J.; Liu, H.; Cao, J.; Shi, Y.; Wang, X.; Wu, W. A Novel MZI Fiber Sensor with Enhanced Curvature and Strain Sensitivity Based on Four-Core Fiber. Micromachines 2024, 15, 1427. https://doi.org/10.3390/mi15121427
Zhu X, Chen F, Zhuang H, Qian J, Liu H, Cao J, Shi Y, Wang X, Wu W. A Novel MZI Fiber Sensor with Enhanced Curvature and Strain Sensitivity Based on Four-Core Fiber. Micromachines. 2024; 15(12):1427. https://doi.org/10.3390/mi15121427
Chicago/Turabian StyleZhu, Xiaojun, Feijie Chen, Haoran Zhuang, Jiayi Qian, Hai Liu, Juan Cao, Yuechun Shi, Xia Wang, and Wuming Wu. 2024. "A Novel MZI Fiber Sensor with Enhanced Curvature and Strain Sensitivity Based on Four-Core Fiber" Micromachines 15, no. 12: 1427. https://doi.org/10.3390/mi15121427
APA StyleZhu, X., Chen, F., Zhuang, H., Qian, J., Liu, H., Cao, J., Shi, Y., Wang, X., & Wu, W. (2024). A Novel MZI Fiber Sensor with Enhanced Curvature and Strain Sensitivity Based on Four-Core Fiber. Micromachines, 15(12), 1427. https://doi.org/10.3390/mi15121427






