IR-Drop-Based Temperature Distribution in Large-Size AMOLED Panel
Abstract
1. Introduction
2. Modeling IR-Drop of Large-Size and High-Resolution AMOLED
2.1. IR-Drop Model
2.2. Sparse Representation of the IR-Drop Model
2.3. IR-Drop Model Solution
3. Temperature Distribution Analysis of AMOLED Panel
3.1. IR-Drop-Based Power Model
3.2. AMOLED Thermal Simulation Model
4. Simulation Results
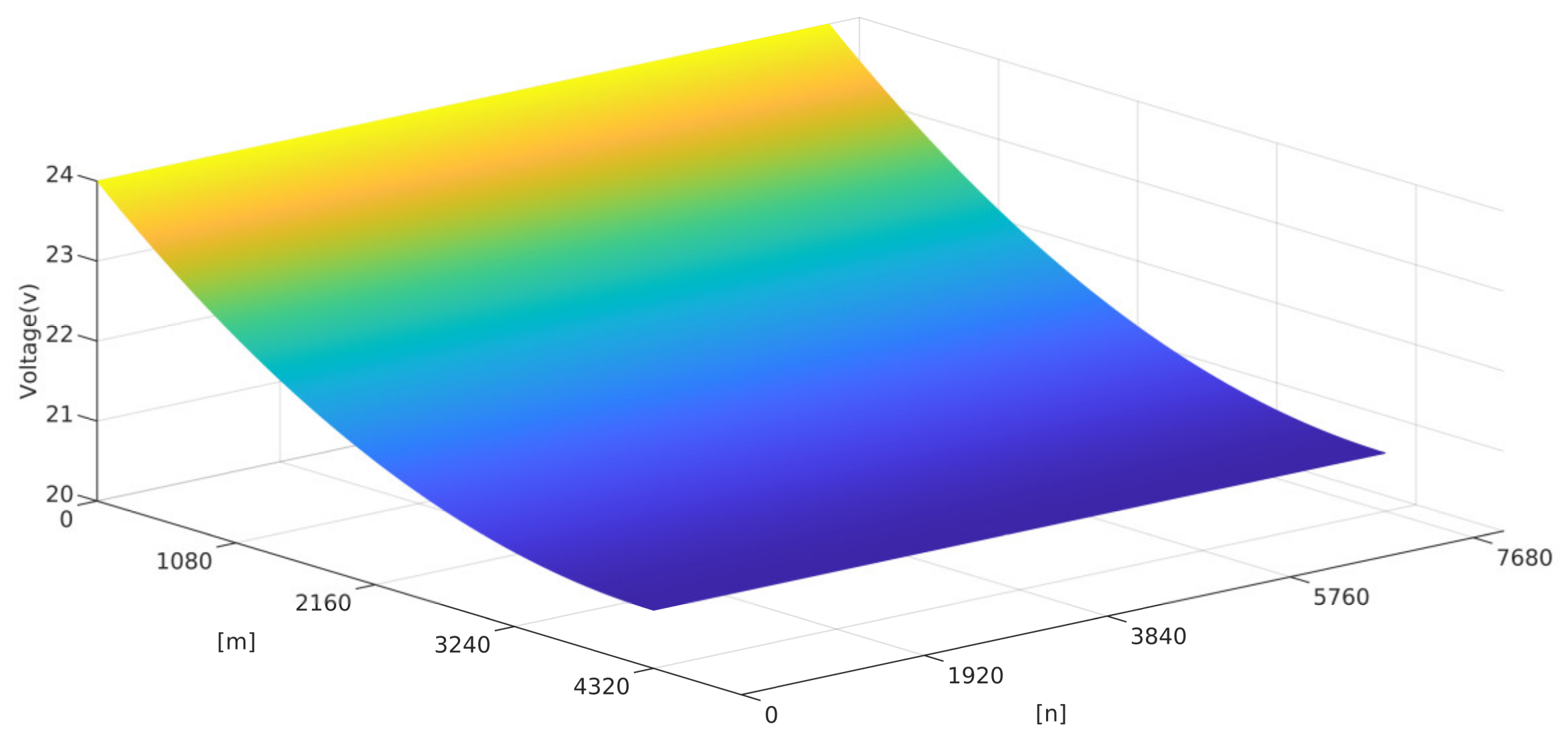
4.1. Results of IR-Drop
4.2. Results of Temperature Distribution Simulation of AMOLED Panel
5. Experimental Results and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cheng, Y. Process in display technologies and their application. Chin. Opt. 2010, 3, 31–36. [Google Scholar]
- Guan, Y.X.; Chen, L.J.; Chen, P. Organic light-emitting device based on LSMO. Infrared Laser Eng. 2015, 44, 2105–2109. [Google Scholar]
- Yum, J.; Yu, Y.-H.; Park, H.; Lim, H. A Novel Method to Reduce Luminance Variation Due to IR-drop in Active Matrix OLED Displays. In Proceedings of the 2020 IEEE International Conference on Consumer Electronics (ICCE), Las Vegas, NV, USA, 4–6 January 2020; pp. 1–4. [Google Scholar]
- Kohno, T.; Kageyama, H.; Miyamoto, M.; Ishii, M.; Kasai, N.; Nakamura, N.; Akimoto, H. High-Speed Programming Architecture and Image-Sticking Cancellation Technology for High-Resolution Low-Voltage AMOLEDs. IEEE Trans. Electron Devices 2011, 58, 3444–3452. [Google Scholar] [CrossRef]
- Zhang, J.P.; Wen, S.S. Simulation of thermal properties for polymer light-emitting diodes. Acta Polym. Sin. 2010, 12, 1458–1463. [Google Scholar] [CrossRef]
- Gärditz, C.; Winnacker, A. Impact of Joule heating on the brightness homogeneity of organic light emitting devices. Appl. Phys. Lett. 2007, 90, 103506. [Google Scholar] [CrossRef]
- Fenter, P.; Schreiber, F.; Bulovi, V. Thermally induced failure mechanisms of organic light emitting device structures probed by X-ray specular reflectivity. Chem. Phys. Lett. 1997, 277, 521–526. [Google Scholar] [CrossRef]
- Kim, J.; Lee, H.H. Wave formation by heating in thin metal film on an elastomer. J. Polym. Sci. Part B Polym. Phys. 2001, 39, 1122–1128. [Google Scholar] [CrossRef]
- Lee, Y.J.; Lee, H.; Byun, Y.; Song, S.; Kim, J.E.; Eom, D.; Cha, W.; Park, S.S.; Kim, J.; Kim, H. Study of thermal degradation of organic light emitting device structures by X-ray scattering. Thin Solid Film. 2007, 515, 5674–5677. [Google Scholar] [CrossRef]
- Zhou, X.; He, J. Real -time observation of temperature rise and thermal breakdown processes in organic LEDs using an IR imaging and analysis system. Adv. Mater. 1997, 12, 265–269. [Google Scholar] [CrossRef]
- Xiang, N.; Gao, Z. Novel fluorene/indole-based hole transport materials with high thermal stability for efficient OLEDs. Dye. Pigment. 2017, 137, 36–42. [Google Scholar] [CrossRef]
- Boroumand, F.A.; Hammiche, A. Characterizing joule heating in polymer light-emitting diodes using a scanning thermal microscope. Adv. Mater. 2004, 16, 252–256. [Google Scholar] [CrossRef]
- Zhang, W.W.; Wu, Z.X.; Liu, Y.W. Thermal analysis of organic light emitting diodes based on basic heat transfer theory. Chin. Phys. Lett. 2015, 32, 143–147. [Google Scholar] [CrossRef]
- Li, Y.T.; Song, X.F.; Chen, J.L. Encapsulation’s thermal characteristics for organic electroluminescent devices. Acta Photonica Sin. 2011, 40, 1630–1635. [Google Scholar]
- Lin, S.F.; Nguyen, D.H. Prediction of OLED temperature distribution based on a neural network model. Microsyst. Technol. 2022, 28, 2215–2222. [Google Scholar] [CrossRef]
- Chao, P.C.-P.; Cheng, S.-S.; Chen, C.-H. A New IR-Drop Model That Improves Effectively the Brightness Uniformity of an AMOLED Panel. IEEE J. Electron Devices Soc. 2022, 10, 627–636. [Google Scholar] [CrossRef]
- Lim, S.-G.; Lee, K.; Kim, Y.-J. Mobile AMOLED Display Power Model Considering I–R Drop in Smartphones. IEEE Trans. Ind. Electron. 2021, 68, 2694–2702. [Google Scholar] [CrossRef]
- Chesterman, F.; Muliuk, G.; Piepers, B.; Kimpe, T.; De Visschere, P.; Neyts, K. Power Consumption and Temperature Distribution in WRGB Active-Matrix OLED Displays. J. Disp. Technol. 2016, 12, 616–625. [Google Scholar] [CrossRef]
- Su, Y.F. Analysis of IR-Drop Voltage Drop and Thermal Reliability of P/G Network. Master’s Thesis, Xi’an University of Electronic Science and Technology, Xi’an, China, 2009. [Google Scholar]


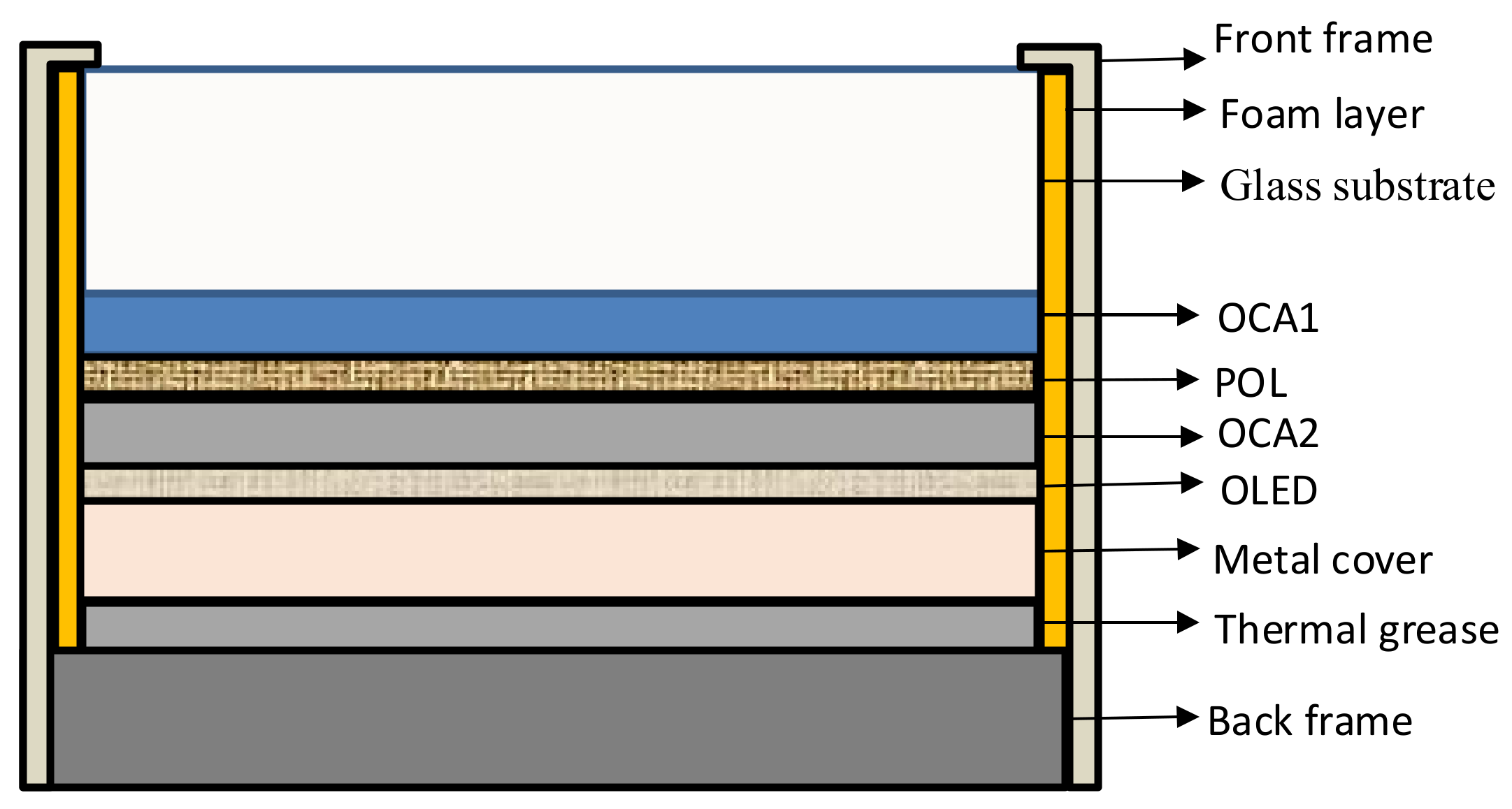





| Structure | Material | |
|---|---|---|
| Glass substrate | Glass | 1.1 |
| OCA1 | Olefin film | 0.24 |
| POL | Polymer film | 0.2 |
| OCA2 | Olefin film | 0.24 |
| OLED | Nichrome film | 43.8 |
| Metal cover | Stainless steel | 26.3 |
| Thermal grease | Aluminum | 1 |
| Back frame | ABS | 0.24 |
| Front frame | ABS | 0.24 |
| Bumper | EPE | 0.04 |
| Method | Time (s) |
|---|---|
| CG | 10,173.64 |
| ICCG | 3379.66 |
| BCG | 3635.39 |
| Proposed algorithm | 120.72 |
| No | Cases | Current) |
|---|---|---|
| 1 | All-white image | |
| 2 | Checkerboard image | |
| 3 | Checkerboard image |
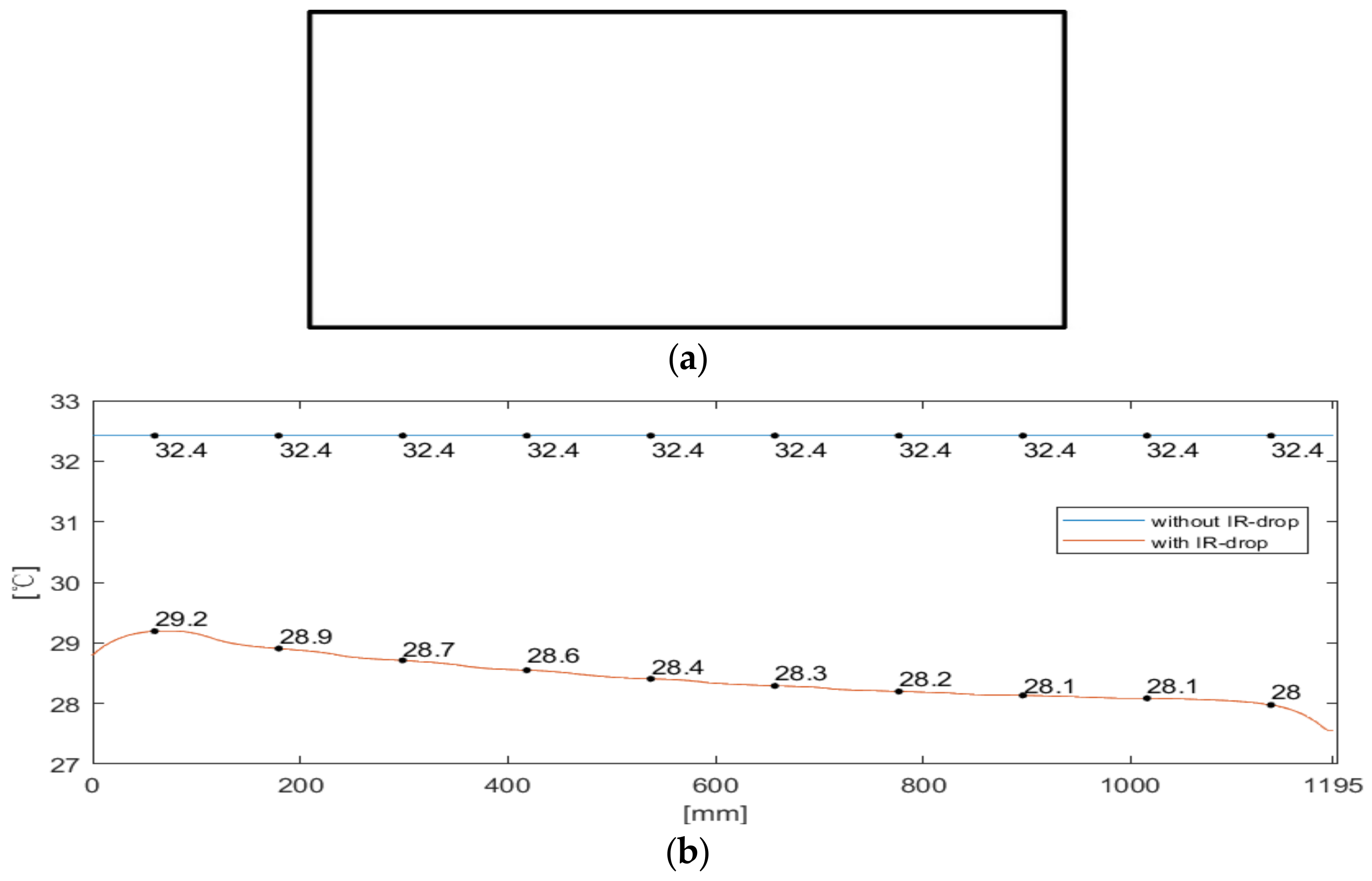
| Temperature of the Test Points (°C) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Case 1 | Actual measurement | 32 | 29 | 31 | 30 | 29 | 29 | 30 | 29 | 29 | 29 |
| With IR-drop | 29.2 | 28.9 | 28.7 | 28.6 | 28.4 | 28.3 | 28.2 | 28.1 | 28.1 | 28 | |
| Error | 2.8 | 0.1 | 2.3 | 1.4 | 0.6 | 0.7 | 1.8 | 0.9 | 0.9 | 1 | |
| Without IR-drop | 32.4 | 32.4 | 32.4 | 32.4 | 32.4 | 32.4 | 32.4 | 32.4 | 32.4 | 32.4 | |
| Error | 0.4 | 3.4 | 1.4 | 2.4 | 3.4 | 3.4 | 2.4 | 3.4 | 3.4 | 3.4 | |
| Case 2 | Actual measurement | 41.3 | 23.8 | 41.8 | 23.2 | 39.3 | 22.3 | 39.6 | 21.7 | 39.6 | / |
| With IR-drop | 40.9 | 23.1 | 38.9 | 22.9 | 38 | 22.8 | 37.5 | 22.7 | 38 | / | |
| Error | 0.4 | 0.7 | 2.9 | 0.3 | 1.3 | 0.5 | 2.1 | 1 | 1.6 | / | |
| Without IR-drop | 50.4 | 21.9 | 48.8 | 21.9 | 48.8 | 21.9 | 48.8 | 21.9 | 50.4 | / | |
| Error | 9.1 | 1.9 | 7 | 1.3 | 9.5 | 0.4 | 9.2 | 0.2 | 10.8 | / | |
| Case 3 | Actual measurement | 50 | 26 | 49.2 | 24.5 | 46.6 | 22.8 | 42.7 | 22.2 | 43.3 | / |
| With IR-drop | 52.7 | 24.8 | 48.4 | 24.4 | 46.3 | 24.1 | 45 | 23.9 | 45.5 | / | |
| Error | 2.7 | 1.2 | 0.8 | 0.1 | 0.3 | 1.3 | 2.3 | 1.7 | 2.2 | / | |
| Without IR-drop | 62.5 | 21.7 | 61.9 | 21.7 | 61.9 | 21.7 | 61.9 | 21.7 | 62.5 | / | |
| Error | 11.9 | 2.6 | 11.5 | 1.1 | 14.1 | 0.6 | 18 | 1.2 | 18.6 | / | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, Q.; Ren, H.; Dong, Z.; Wang, Z.; Lv, G. IR-Drop-Based Temperature Distribution in Large-Size AMOLED Panel. Micromachines 2024, 15, 1236. https://doi.org/10.3390/mi15101236
Feng Q, Ren H, Dong Z, Wang Z, Lv G. IR-Drop-Based Temperature Distribution in Large-Size AMOLED Panel. Micromachines. 2024; 15(10):1236. https://doi.org/10.3390/mi15101236
Chicago/Turabian StyleFeng, Qibin, Hongtao Ren, Zhe Dong, Zi Wang, and Guoqiang Lv. 2024. "IR-Drop-Based Temperature Distribution in Large-Size AMOLED Panel" Micromachines 15, no. 10: 1236. https://doi.org/10.3390/mi15101236
APA StyleFeng, Q., Ren, H., Dong, Z., Wang, Z., & Lv, G. (2024). IR-Drop-Based Temperature Distribution in Large-Size AMOLED Panel. Micromachines, 15(10), 1236. https://doi.org/10.3390/mi15101236






