Electromagnetohydrodynamic (EMHD) Flow in a Microchannel with Random Surface Roughness
Abstract
:1. Introduction
2. Materials and Methods
3. Dirichlet’s Condition and Applications
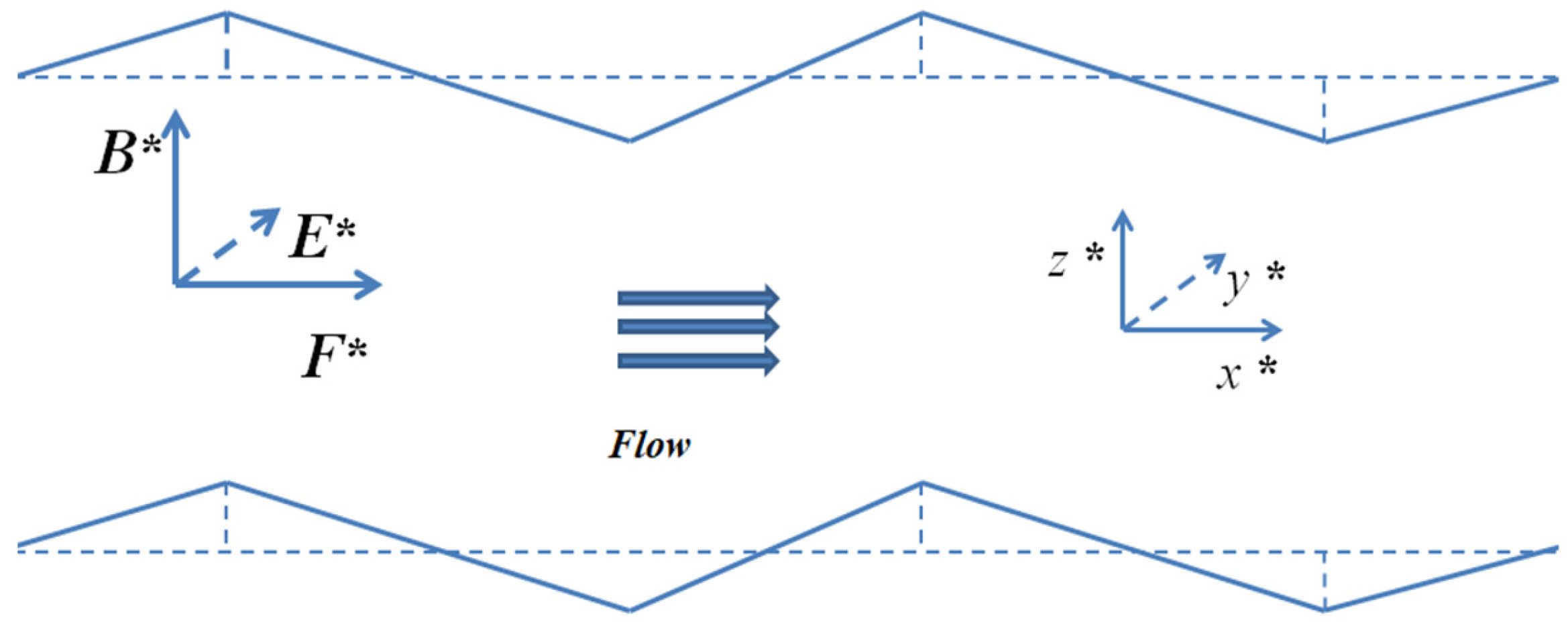
3.1. Sinusoidal Corrugations
3.2. Triangular Corrugations
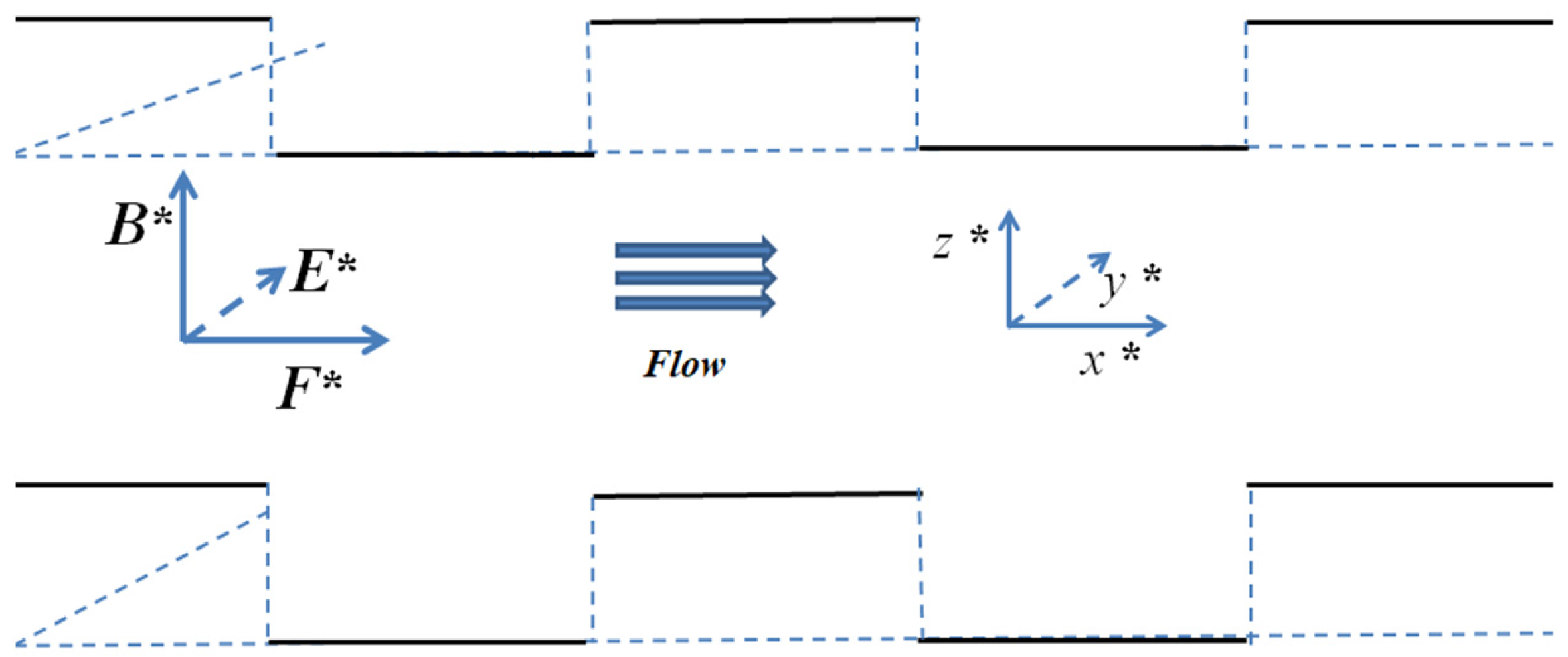
3.3. Rectangular Corrugations
3.4. Sawtooth Corrugations
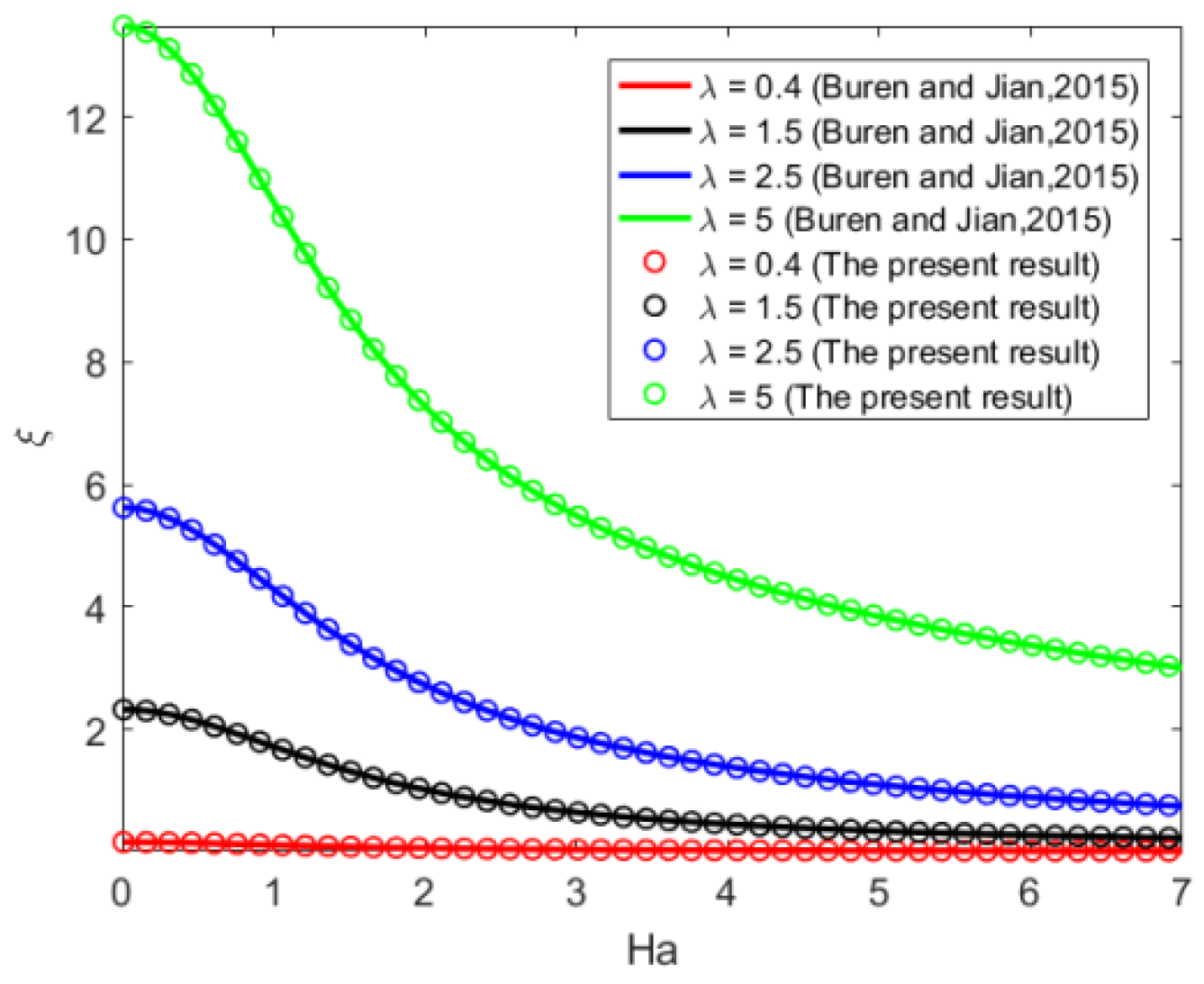
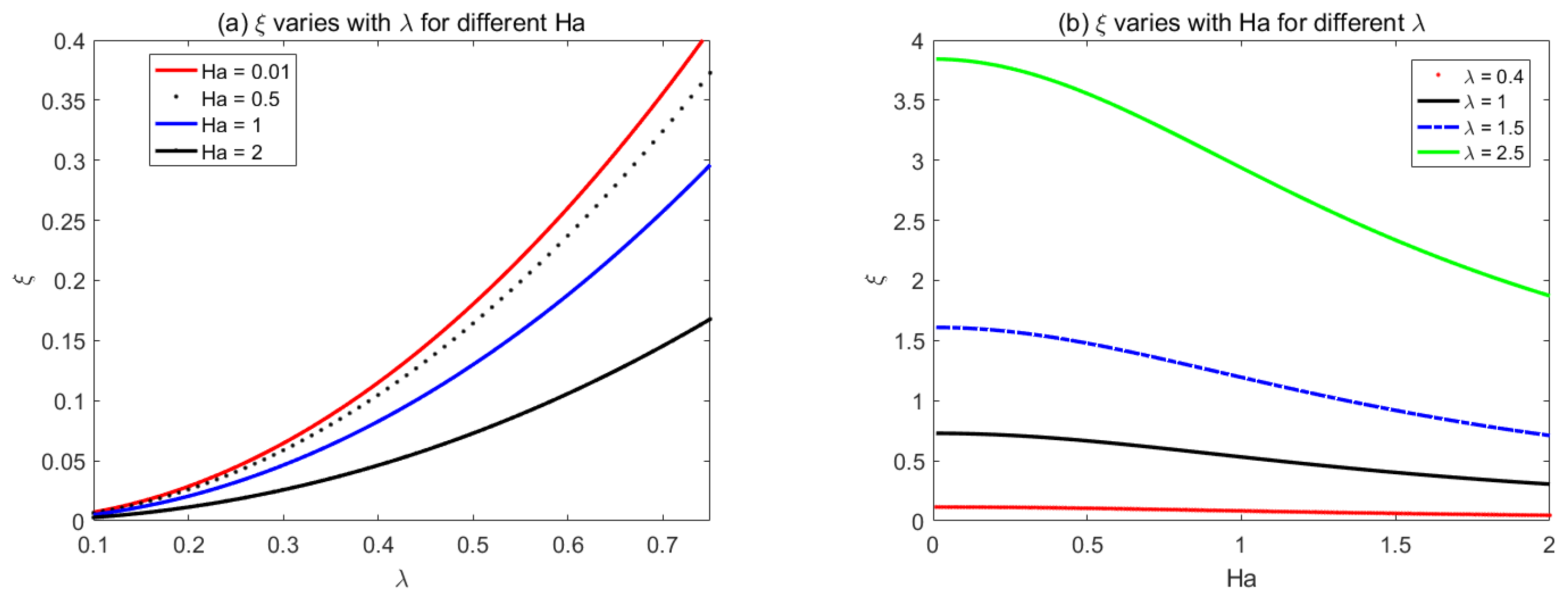
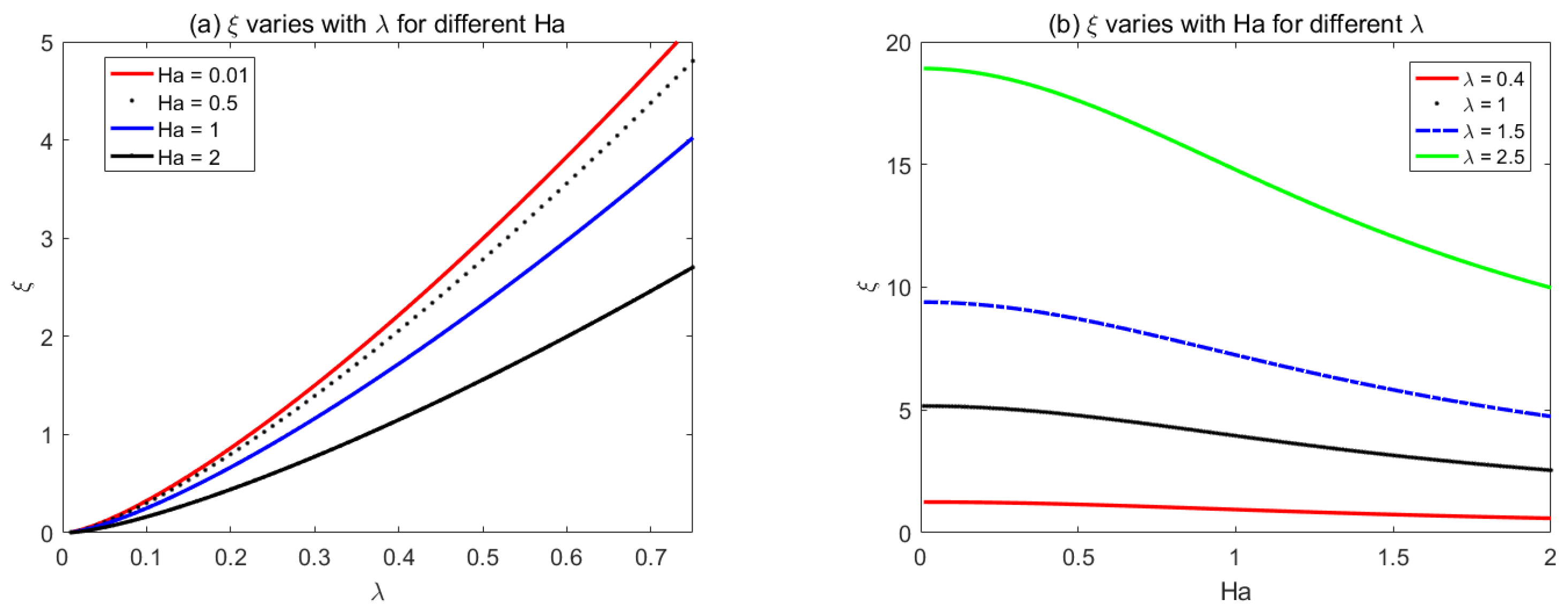
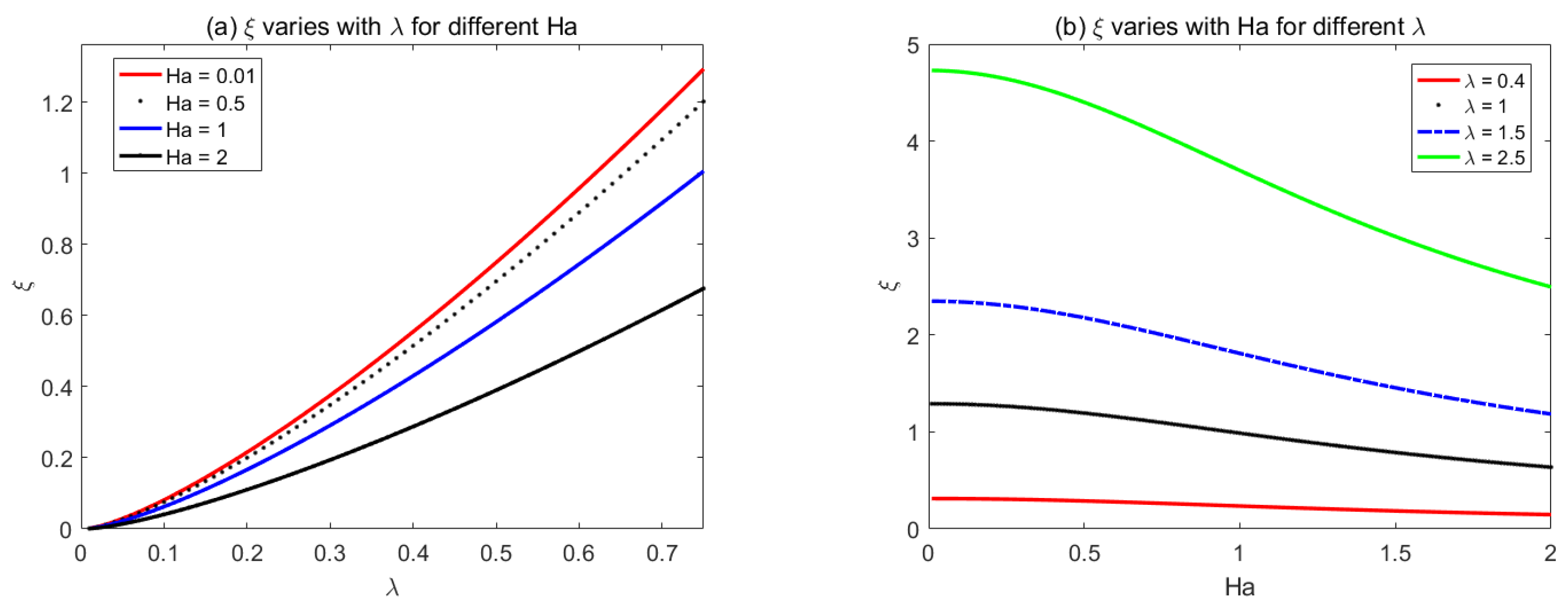
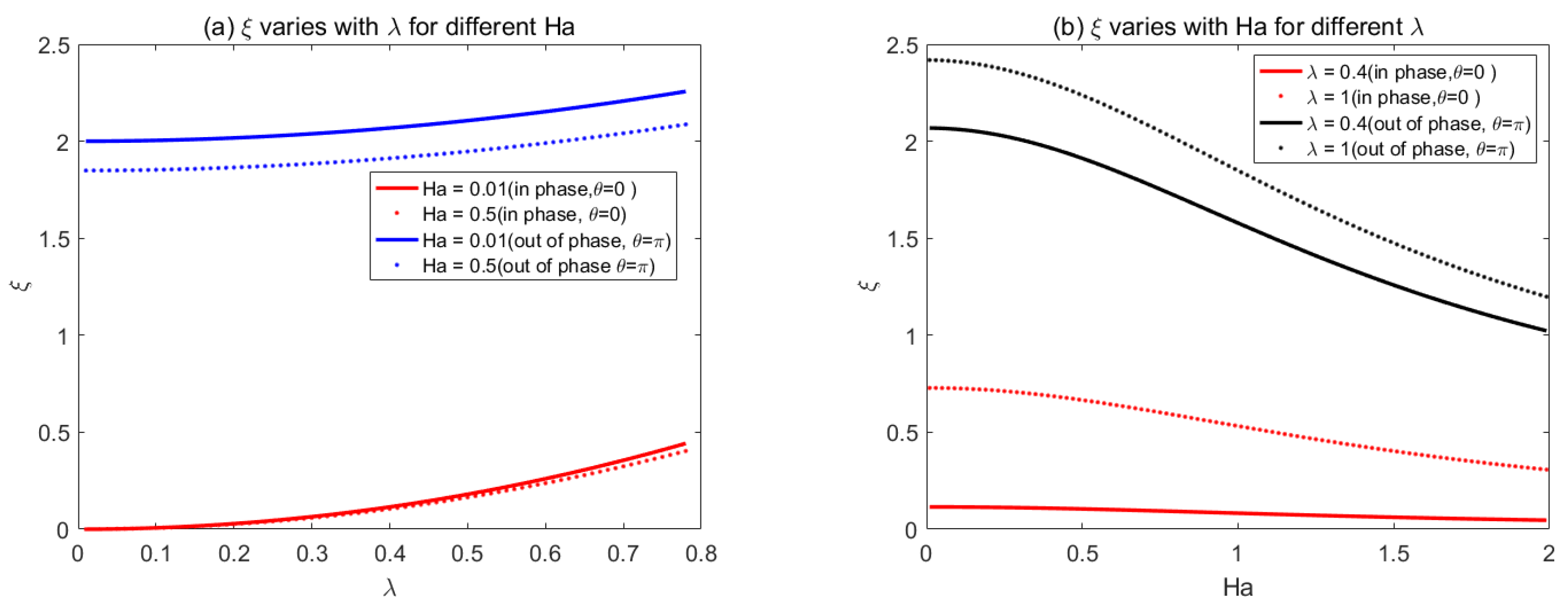
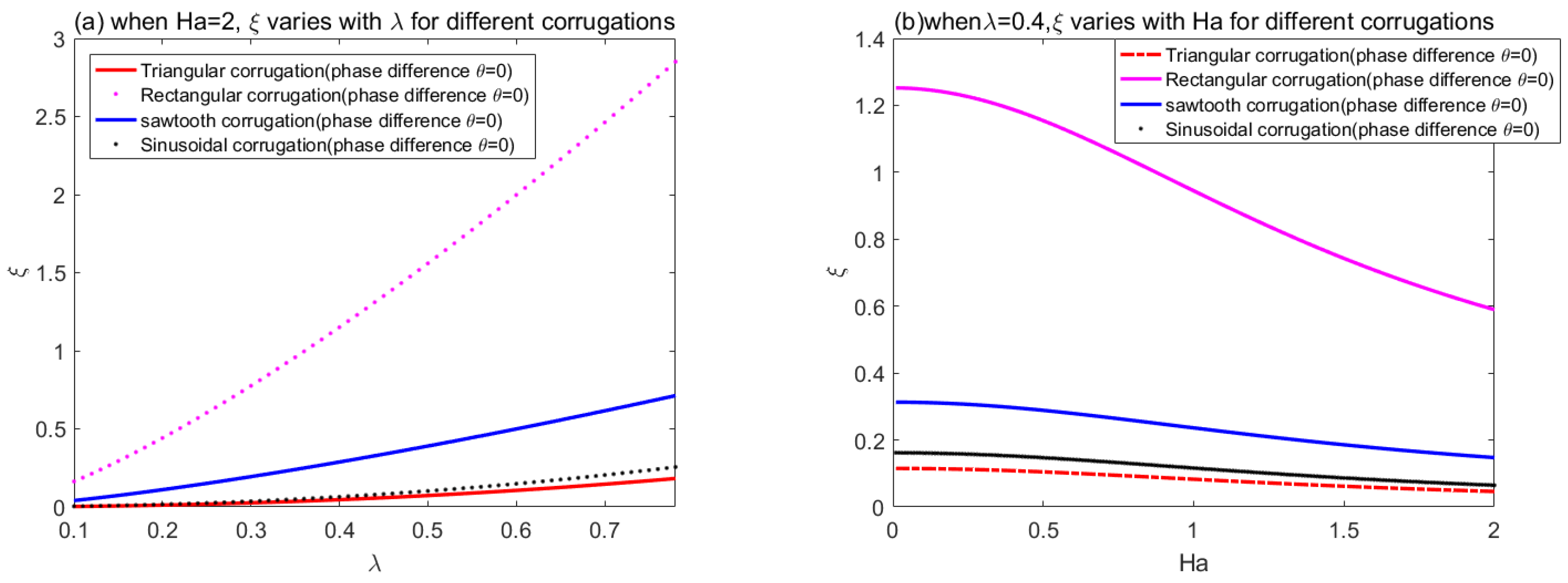
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| (x, y, z) | cartesian coordinate system |
| u | velocity vector |
| L | channel length |
| W | channel width |
| B | magnetic field |
| E | electric field |
| J | electrical current density |
| Σ | electrical conductivity |
| u, v, w | components of velocity vector u |
| p | pressure of the liquid |
| μ | dynamic viscosity |
| ρ | density |
| ∇ | gradient operator |
| ε | amplitude of the corrugation |
| m(x), n(x) | stationary random functions |
| dZi(λ)(i = 1, 2) | interval random function |
| δij (j, k = 1, 2) | Kronecker delta |
| Fij (j, k = 1, 2) | real non-decreasing bounded functions |
| |Rij(s)|(j,k = 1, 2) | correlation function |
| Ωjk (j, k = 1, 2) | spectral densities of m(x) and n(x). |
| Ψ | stream function |
| Q | flow rate per unit width |
| Ha | Hartmann number |
| S | dimensionless electric field strength |
| n | normal vector |
| nx, nz | the x-and z-components of the unit normal |
| A1 | coefficient of the zero-order solution |
| αj, βj, γj, δj (j = 1, 2) | coefficients of first-order solutions |
| ajk, bjk, cjk, djk (j, k = 1, 2) | coefficients of second-order solutions |
| ξ | corrugation function |
| λ | wave number |
| δ | the Dirac generalized function |
| θ | phase difference |
| an, bn | Fourier coefficient |
References
- Stephen, C.; Jakeway, J.; de Mello, L. Miniaturized total analysis systems for biological analysis. Fresnius J. Anal. Chem. 2000, 366, 525–539. [Google Scholar]
- Dash, A.K.; Cudworth, G.C. Therapeutic applications of implantable drug delivery systems. J. Pharmacol. Toxicol. Methods. 1998, 40, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Jiang, L.; James, M.; Jae, M.K.; David, H.; Yao, S.H.; Zhang, L.; Zhou, P.; James, G.M.; Ravi, P.; Juan, G.S.; et al. Closed-loop electroosmotic microchannel cooling system for VLSI circuits IEEE Trans. Compon. Packag. Technol. 2002, 25, 347–355. [Google Scholar] [CrossRef]
- Bruschi, P.; Diligenti, A.; Piotto, M. Micromachined gas flow regulator for ion propulsion systems. IEEE. Trans. Aerosp. Electron. Syst. 2002, 38, 982–988. [Google Scholar] [CrossRef]
- Jang, J.; Lee, S.S. Theoretical and experimental study of MHD (magnetohydrodynamic) micropump. Sensor Actuat. A-Phys. 2000, 80, 84–89. [Google Scholar] [CrossRef]
- Ko, H.J.; Dulikravich, G.S. Non-reflective boundaryconditions for a consistent two-dimensional planar model of electro-magneto-hydrodynamics(EMHD). Int. J. Nonlinear Mech. 2001, 36, 155–163. [Google Scholar] [CrossRef]
- Chakraborty, S.; Paul, D. Microchannel flow control through a combined electromagnetohydrodynamic transport. J. Phys. D Appl. Phys. 2006, 39, 5364. [Google Scholar] [CrossRef]
- Awatif, J.A.; Abo-Elkhair, R.E.; Essam, M.E.; Abdel, H.A.; Mohamed, S.A. Effect of magnetic force and moderate Reynolds number on MHD Jeffrey hybrid nanofluid through peristaltic channel: Application of cancer treatment. Eur. Phys. J. Plus. 2023, 138, 137. [Google Scholar]
- Qian, S.; Bau, H.H. Magneto-hydrodynamics based microfluidics. Mech. Res. Commun. 2009, 36, 10–21. [Google Scholar] [CrossRef]
- Asterios, P.; Eugen, M. EMHD free-convection boundary-layer flow from a Riga-plate. J. Eng. Math. 2009, 64, 303–315. [Google Scholar]
- Buren, M.; Jian, Y.J.; Chang, L. Electromagnetohydrodynamic flow through a microparallel channel with corrugated walls. J. Phys. D Appl. Phys. 2014, 47, 425501. [Google Scholar] [CrossRef]
- Tso, C.P.; Sundaravadivelu, K. Capillary flow between parallel plates in the presence of an electromagnetic field. J. Phys. D Appl. Phys. 2001, 34, 3522–3527. [Google Scholar] [CrossRef]
- Si, D.Q.; Jian, Y.J. Electromagnetohydrodynamic (EMHD) micropump of Jeffrey fluids through two parallel microchannels with corrugated walls. J. Phys. D Appl. Phys. 2015, 48, 085501. [Google Scholar] [CrossRef]
- Jamshed, W.; Mohd Nasir, N.A.A.; Qureshi, M.A.; Shahzad, F.; Banerjee, R.; Eid, M.R.; Nisar, K.S.; Ahmad, S. Dynamical irreversible processes analysis of Poiseuille magneto-hybrid nanofluid flow in microchannel: A novel case study. Waves Random Complex Media 2022. [Google Scholar] [CrossRef]
- Faisal, S.; Wasim, J.; Mohamed, R.E.; Rabha, W.I.; Farheen, A.; Siti, S.P.M.I.; Kamel, G. The effect of pressure gradient on MHD flow of a tri-hybrid Newtonian nanofluid in a circular channel. J. Magn. Magn. Mater. 2023, 568, 170320. [Google Scholar]
- Bhatti, M.M.; Bég, O.A.; Ellahi, R.; Abbas, T. Natural Convection Non-Newtonian EMHD dissipative flow through a microchannel containing a non-darcy porous medium: Homotopy perturbation method study. Qual. Theory Dyn. Syst. 2022, 21, 97. [Google Scholar] [CrossRef]
- Wang, M.; Kang, Q. Electrokinetic transport in microchannels with random roughness. Anal. Chem. 2009, 81, 2953–2961. [Google Scholar] [CrossRef]
- Chen, C.K.; Cho, C.C. Electrokinetically-driven flow mixing in microchannels with wavy surface. J. Colloid Interface Sci. 2007, 312, 470–480. [Google Scholar] [CrossRef]
- Parsa, M.K.; Hormozi, F. Experimental and CFD modeling of fluid mixing in sinusoidal microchannels with different phase shift between side walls. J. Micromech. Microeng. 2014, 24, 065018. [Google Scholar] [CrossRef]
- Wang, C.Y. On Stokes flow between corrugated Plates. J. Appl. Mech. 1979, 46, 462–464. [Google Scholar] [CrossRef]
- Chu, Z.K.H. Slip flow in an annulus with corrugated walls. J. Phys. D Appl. Phys. 2000, 33, 627. [Google Scholar] [CrossRef]
- Tashtoush, B.; Al-Odat, M. Magnetic field effect on heat and fluid flow over a wavy surface with a variable heat flux. J. Magn. Magn. Mater. 2004, 268, 357–363. [Google Scholar] [CrossRef]
- Chang, L.; Jian, Y.J.; Buren, M.; Liu, Q.S.; Sun, Y.J. Electroosmotic flow through a microtube with sinusoidal roughness. J. Mol. Liq. 2016, 220, 258–264. [Google Scholar] [CrossRef]
- Lei, J.C.; Chang, C.C.; Wang, C.Y. Electro-osmotic pumping through a bumpy microtube: Boundary perturbation and detection of roughness. Phys. Fluids 2019, 31, 012001. [Google Scholar] [CrossRef]
- Su, J.; Jian, Y.J.; Chang, L.; Liu, Q.S. Transient electro-osmotic and pressure driven flows of two-layer fluids through a slit microchannel. Acta Mech. Sin. 2013, 29, 534–542. [Google Scholar] [CrossRef]
- Ng, C.O.; Wang, C.Y. Darcy–Brinkman flow through a corrugated channel. Transp. Porous Media 2010, 85, 605–618. [Google Scholar] [CrossRef]
- Bujurke, N.M.; Kudenatti, R.B. MHD lubrication flow between rough rectangular plates. Fluid Dyn. Res. 2007, 39, 334–345. [Google Scholar] [CrossRef]
- Ashmawy, E.A. Effects of surface roughness on a couple stress fluid flow through corrugated tube. Eur. J. Mech. B-Fluid 2019, 76, 365–374. [Google Scholar] [CrossRef]
- Phan-Thien, N. On Stokes flow between parallel plates with stationary random surface roughness. Z. Angew. Math. Mech. 1980, 60, 675–679. [Google Scholar] [CrossRef]
- Phan-Thien, N. On Stokes flows in channels and pipes with parallel stationary random surface roughness. Z. Angew. Math. Mech. 1981, 61, 193–199. [Google Scholar] [CrossRef]
- Faltas, M.S.; Sherief, H.H.; Mansour, M.A. Slip-brinkman flow through corrugated channel with stationary random model. J. Porous Media 2017, 20, 723–748. [Google Scholar] [CrossRef]
- Faltas, M.S.; Sherief, H.H.; Ibrahim, M.A. Darcy–Brinkman micropolar fluid flow through corrugated micro-tube with stationary random model. Colloid J. 2020, 82, 604–616. [Google Scholar] [CrossRef]
- Yaglom, A.M. An Introduction to the Theory of Stationary Random Functions; Dover Publication: Englewood Cliffs, NJ, USA, 1962. [Google Scholar]
- Buren, M.; Jian, Y.J. Electromagnetohydrodynamic (EMHD) flow between two transversely wavy microparallel plates. Electrophoresis 2015, 36, 1539–1548. [Google Scholar] [CrossRef] [PubMed]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, N.; Sun, Y.; Jian, Y. Electromagnetohydrodynamic (EMHD) Flow in a Microchannel with Random Surface Roughness. Micromachines 2023, 14, 1617. https://doi.org/10.3390/mi14081617
Ma N, Sun Y, Jian Y. Electromagnetohydrodynamic (EMHD) Flow in a Microchannel with Random Surface Roughness. Micromachines. 2023; 14(8):1617. https://doi.org/10.3390/mi14081617
Chicago/Turabian StyleMa, Nailin, Yanjun Sun, and Yongjun Jian. 2023. "Electromagnetohydrodynamic (EMHD) Flow in a Microchannel with Random Surface Roughness" Micromachines 14, no. 8: 1617. https://doi.org/10.3390/mi14081617
APA StyleMa, N., Sun, Y., & Jian, Y. (2023). Electromagnetohydrodynamic (EMHD) Flow in a Microchannel with Random Surface Roughness. Micromachines, 14(8), 1617. https://doi.org/10.3390/mi14081617






