Self-Propulsion of Two Contacting Bubbles Due to the Radiation Interaction Force
Abstract
:1. Introduction
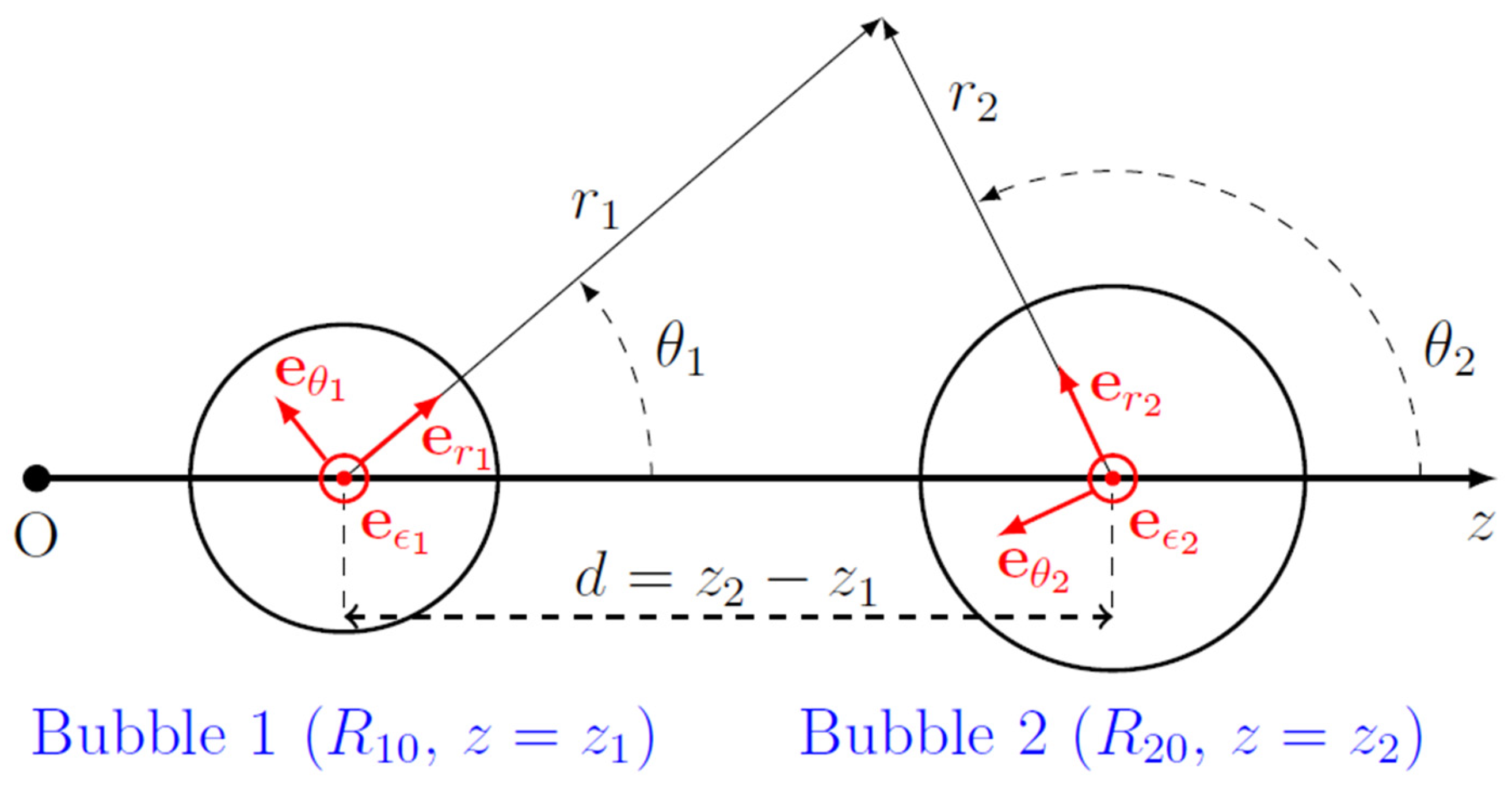
2. Theory
2.1. Interaction Force between Two Bubbles in an Acoustic Field
2.2. Linear Scattering Coefficients When Parametric Excitation Is Absent
2.3. Net Force Experienced by Two Contacting Bubbles
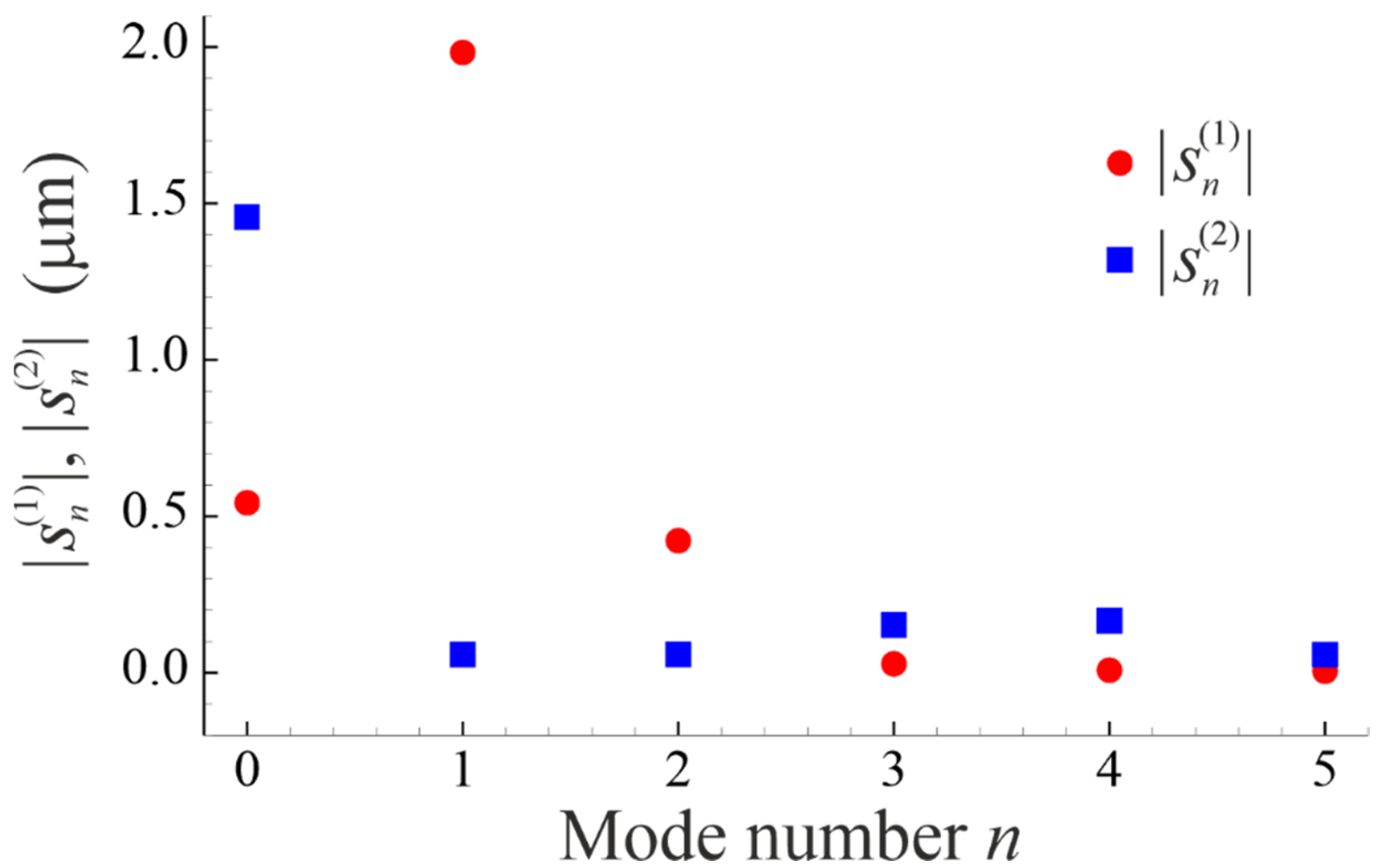
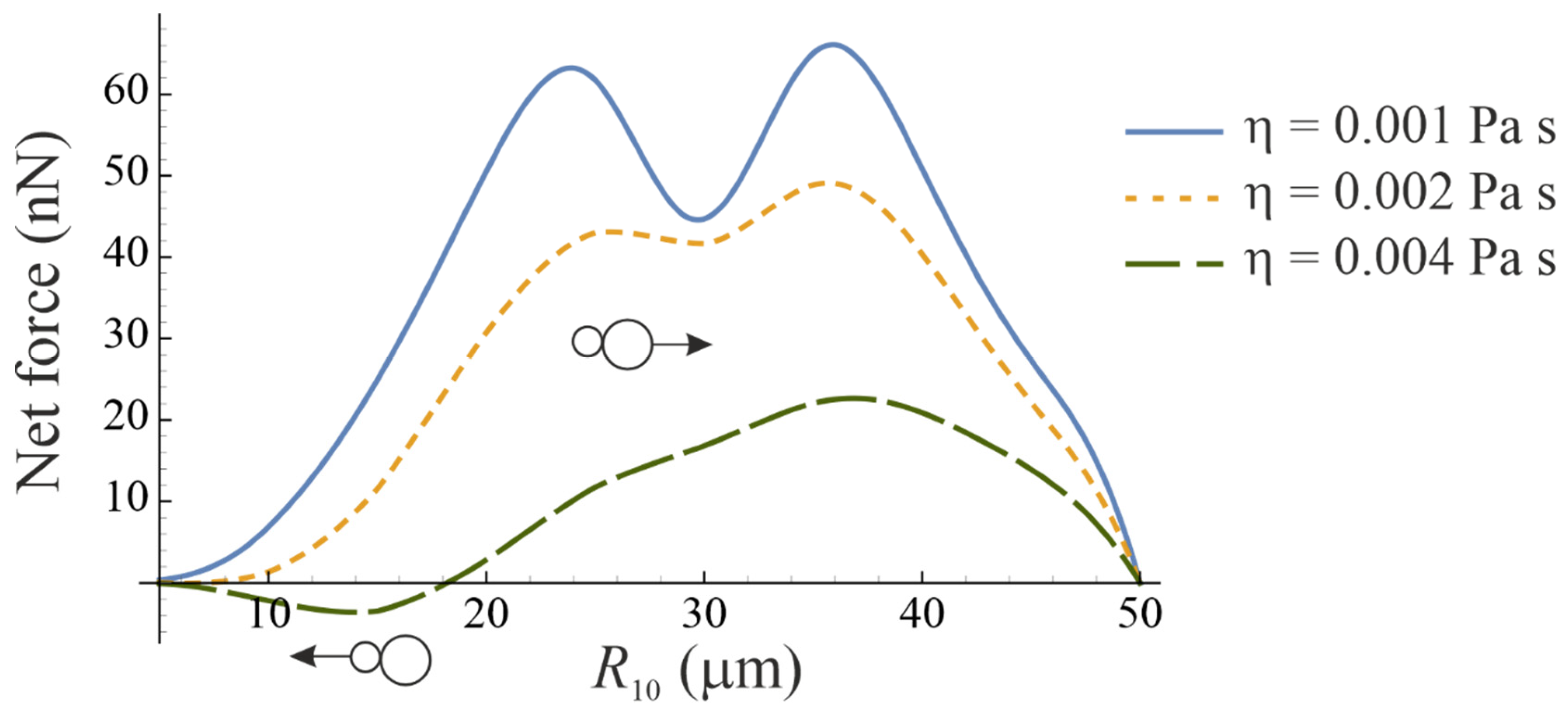
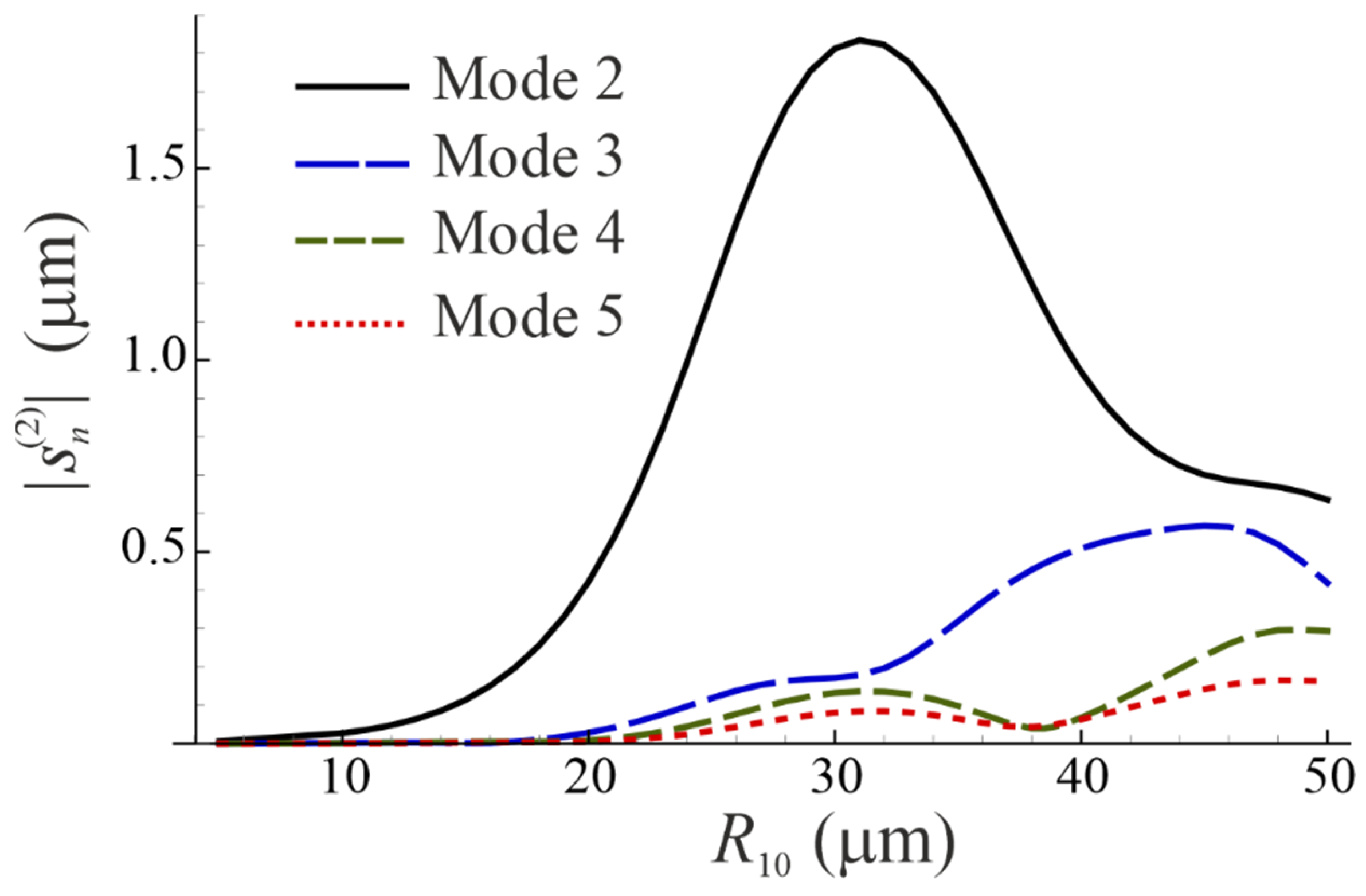
3. Numerical Simulations
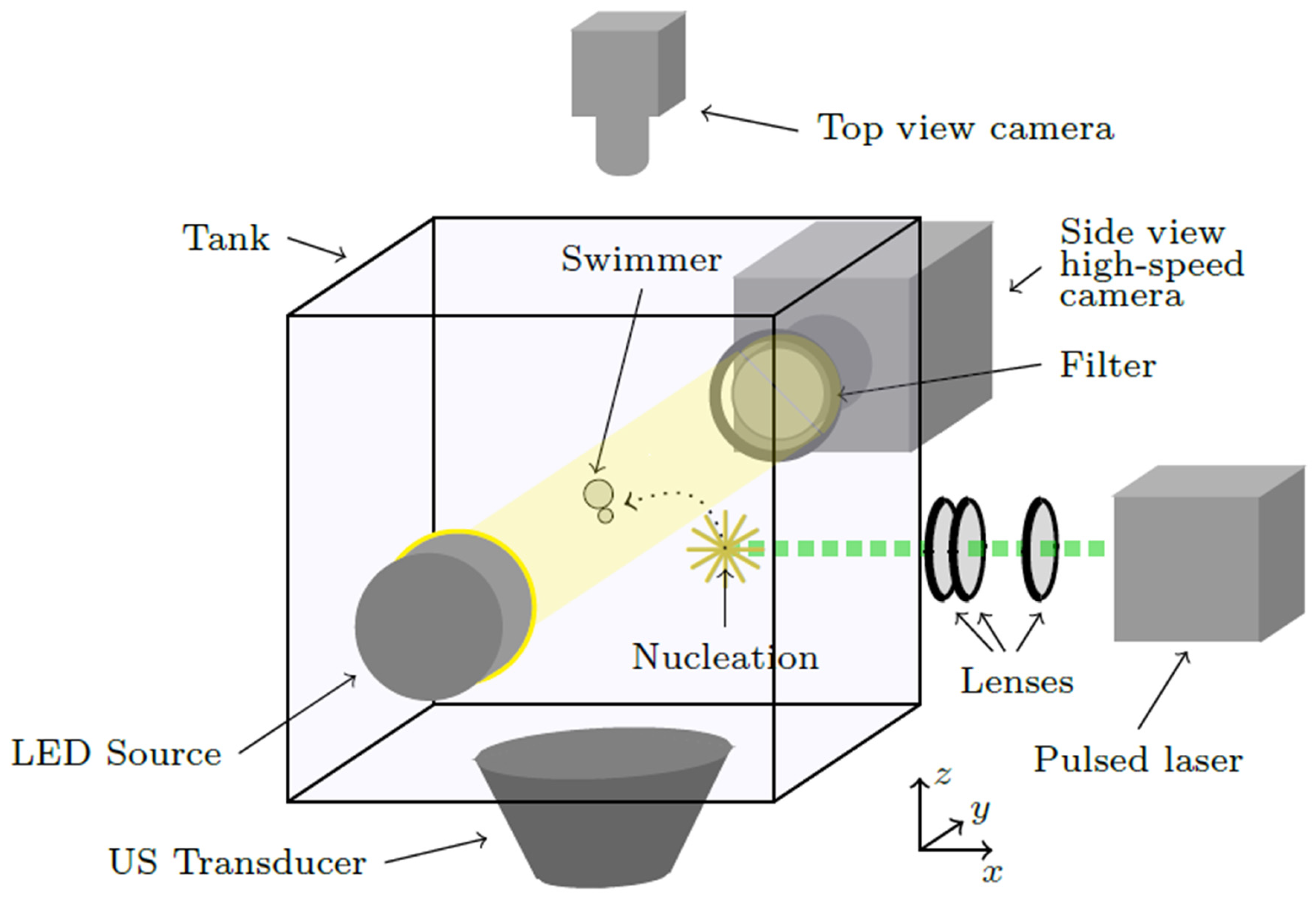
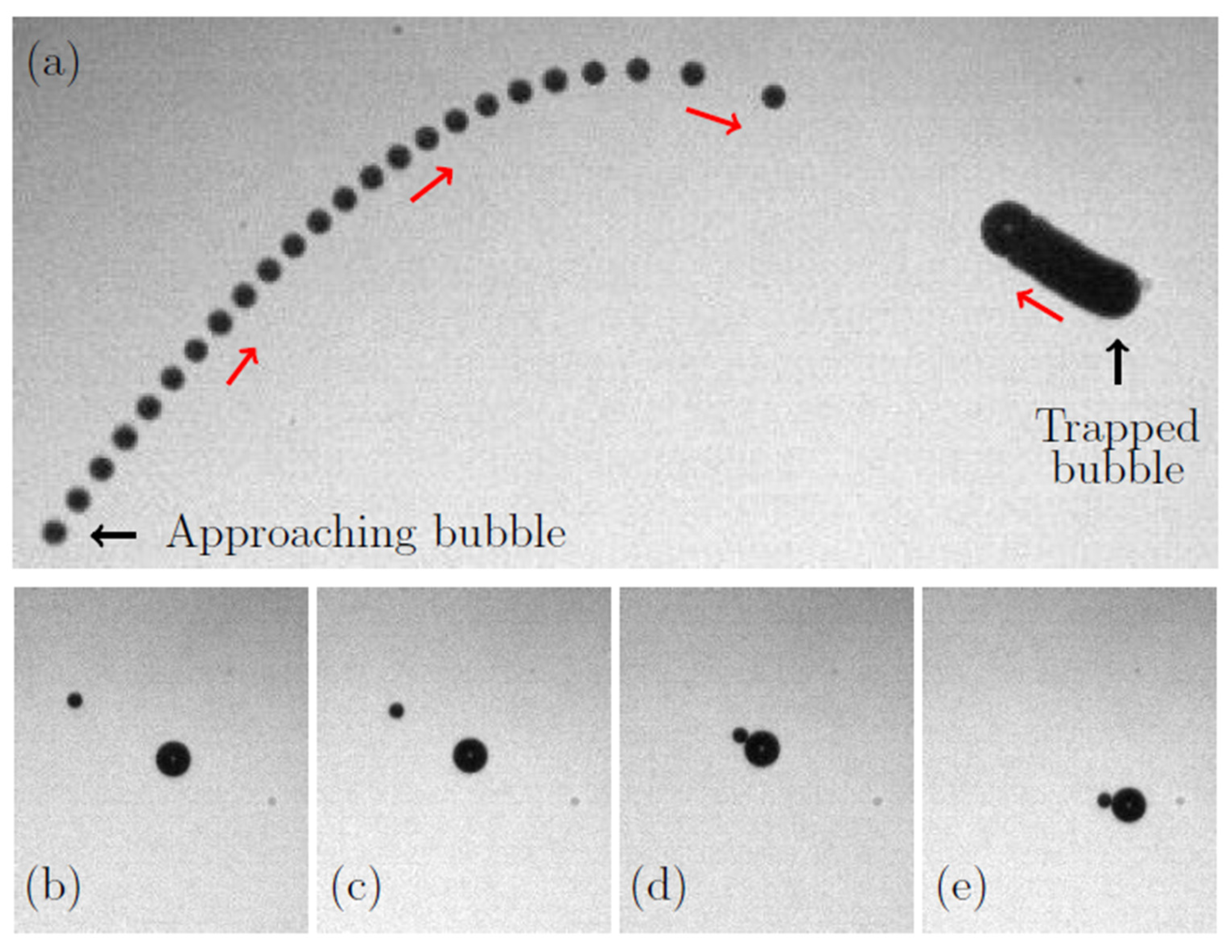
4. Experiments
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Mathematical Formulas Used in Calculations
References
- Bunea, A.-I.; Taboryski, R. Recent advances in microswimmers for biomedical applications. Micromachines 2020, 11, 1048. [Google Scholar] [CrossRef]
- Sridhar, V.; Park, B.-W.; Sitti, M. Light-driven Janus hollow mesoporous TiO2-Au microswimmers. Adv. Funct. Mater. 2018, 28, 1704902. [Google Scholar] [CrossRef]
- Alapan, Y.; Yigit, B.; Beker, O.; Demirörs, A.F.; Sitti, M. Shape-encoded dynamic assembly of mobile micromachines. Nat. Mater. 2019, 18, 1244–1251. [Google Scholar] [CrossRef]
- Ceylan, H.; Yasa, I.C.; Yasa, O.; Tabak, A.F.; Giltinan, J.; Sitti, M. 3D-printed biodegradable microswimmer for theranostic cargo delivery and release. ACS Nano 2019, 13, 3353–3362. [Google Scholar] [CrossRef]
- Louf, J.F.; Bertin, N.; Dollet, B.; Stephan, O.; Marmottant, P. Hovering microswimmers exhibit ultrafast motion to navigate under acoustic forces. Adv. Mater. Interfaces 2018, 5, 1800425. [Google Scholar] [CrossRef]
- Bertin, N.; Spelman, T.A.; Stephan, O.; Gredy, L.; Bouriau, M.; Lauga, E.; Marmottant, P. Propulsion of bubble-based acoustic microswimmers. Phys. Rev. Appl. 2015, 4, 064012. [Google Scholar] [CrossRef]
- Feng, J.; Yuan, J.; Cho, S.K. Micropropulsion by an acoustic bubble for navigating microfluidic spaces. Lab Chip 2015, 15, 1554–1562. [Google Scholar] [CrossRef]
- Ahmed, D.; Lu, M.; Nourhani, A.; Lammert, P.E.; Stratton, Z.; Muddana, H.S.; Crespi, V.H.; Huang, T.J. Selectively manipulable acoustic-powered microswimmers. Sci. Rep. 2015, 5, 9744. [Google Scholar] [CrossRef]
- Jeong, J.; Jang, D.; Kim, D.; Lee, D.; Chung, S.K. Acoustic bubble-based drug manipulation: Carrying, releasing and penetrating for targeted drug delivery using an electromagnetically actuated microrobot. Sens. Actuators A 2020, 306, 111973. [Google Scholar] [CrossRef]
- Ahmed, D.; Mao, X.; Shi, J.; Juluri, B.K.; Huang, T.J. A millisecond micromixer via single-bubble-based acoustic streaming. Lab Chip 2009, 9, 2738–2741. [Google Scholar] [CrossRef]
- Gao, Y.; Wu, M.; Luan, Q.; Papautsky, I.; Xu, J. Acoustic bubble for spheroid trapping, rotation and culture: A tumor-on-a-chip platform (ABSTRACT platform). Lab Chip 2022, 22, 805–813. [Google Scholar] [CrossRef]
- Luo, T.; Wu, M. Biologically inspired micro-robotic swimmers remotely controlled by ultrasound waves. Lab Chip 2021, 21, 4095–4103. [Google Scholar] [CrossRef]
- Pak, O.S.; Zhu, L.; Brandt, L.; Lauga, E. Micropropulsion and microrheology in complex fluids via symmetry breaking. Phys. Fluids 2012, 24, 103102. [Google Scholar] [CrossRef]
- Bjerknes, V.F.K. Fields of Force; Columbia U. P.: New York, NY, USA, 1906. [Google Scholar]
- Crum, L.A. Bjerknes forces on bubbles in a stationary sound field. J. Acoust. Soc. Am. 1975, 57, 1363–1370. [Google Scholar] [CrossRef]
- Doinikov, A.A. Acoustic radiation forces: Classical theory and recent advances. In Recent Research Developments in Acoustics; Transworld Research Network: Trivandrum, India, 2003; Volume 1, pp. 39–67. [Google Scholar]
- Doinikov, A.A. Dissipative effects on Bjerknes forces between two bubbles. J. Acoust. Soc. Am. 1997, 102, 747–751. [Google Scholar] [CrossRef]
- Doinikov, A.A. Bjerknes forces between two bubbles in a viscous fluid. J. Acoust. Soc. Am. 1999, 106, 3305–3312. [Google Scholar] [CrossRef]
- Doinikov, A.A.; Regnault, G.; Mauger, C.; Blanc-Benon, P.; Inserra, C. Acoustic microstreaming produced by two interacting gas bubbles undergoing axisymmetric shape oscillations. J. Fluid Mech. 2022, 931, A19. [Google Scholar] [CrossRef]
- Shaw, S.J. Translation and oscillation of a bubble under axisymmetric deformation. Phys. Fluids 2006, 18, 072104. [Google Scholar] [CrossRef]
- Guédra, M.; Inserra, C. Bubble shape oscillations of finite amplitude. J. Fluid Mech. 2018, 857, 681–703. [Google Scholar] [CrossRef]
- Doinikov, A.A. Acoustic radiation pressure on a compressible sphere in a viscous fluid. J. Fluid Mech. 1994, 267, 1–21. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs and Mathematical Tables, 10th ed.; Dover: New York, NY, USA, 1972. [Google Scholar]
- Varshalovich, D.A.; Moskalev, A.N.; Khersonskii, V.K. Quantum Theory of Angular Momentum; World Scientific: Teaneck, NJ, USA, 1988. [Google Scholar]
- Zwillinger, D. Standard Mathematical Tables and Formulae, 31st ed.; CRC: Boca Raton, FL, USA, 2003. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Fluid Mechanics, 2nd ed.; Pergamon Press: Oxford, UK, 1987. [Google Scholar]
- Doinikov, A.A.; Cleve, S.; Regnault, G.; Mauger, C.; Inserra, C. Acoustic microstreaming produced by nonspherical oscillations of a gas bubble. I. Case of modes 0 and m. Phys. Rev. E 2019, 100, 033104. [Google Scholar] [CrossRef]
- Prosperetti, A. Viscous effects on perturbed spherical flows. Quart. Appl. Math. 1977, 34, 339–352. [Google Scholar] [CrossRef]
- Cleve, S.; Guédra, M.; Inserra, C.; Mauger, C.; Blanc-Benon, P. Surface modes with controlled axisymmetry triggered by bubble coalescence in a high-amplitude acoustic field. Phys. Rev. E 2018, 98, 033115. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Doinikov, A.A.; Micol, T.; Mauger, C.; Blanc-Benon, P.; Inserra, C. Self-Propulsion of Two Contacting Bubbles Due to the Radiation Interaction Force. Micromachines 2023, 14, 1615. https://doi.org/10.3390/mi14081615
Doinikov AA, Micol T, Mauger C, Blanc-Benon P, Inserra C. Self-Propulsion of Two Contacting Bubbles Due to the Radiation Interaction Force. Micromachines. 2023; 14(8):1615. https://doi.org/10.3390/mi14081615
Chicago/Turabian StyleDoinikov, Alexander A., Thomas Micol, Cyril Mauger, Philippe Blanc-Benon, and Claude Inserra. 2023. "Self-Propulsion of Two Contacting Bubbles Due to the Radiation Interaction Force" Micromachines 14, no. 8: 1615. https://doi.org/10.3390/mi14081615
APA StyleDoinikov, A. A., Micol, T., Mauger, C., Blanc-Benon, P., & Inserra, C. (2023). Self-Propulsion of Two Contacting Bubbles Due to the Radiation Interaction Force. Micromachines, 14(8), 1615. https://doi.org/10.3390/mi14081615





