Composite Diffraction-Free Beam Formation Based on Iteratively Calculated Primitives
Abstract
1. Introduction
2. Methods
2.1. Theoretical Background
2.2. Iterative Algorithm
3. Calculation Results
3.1. Simple Primitives
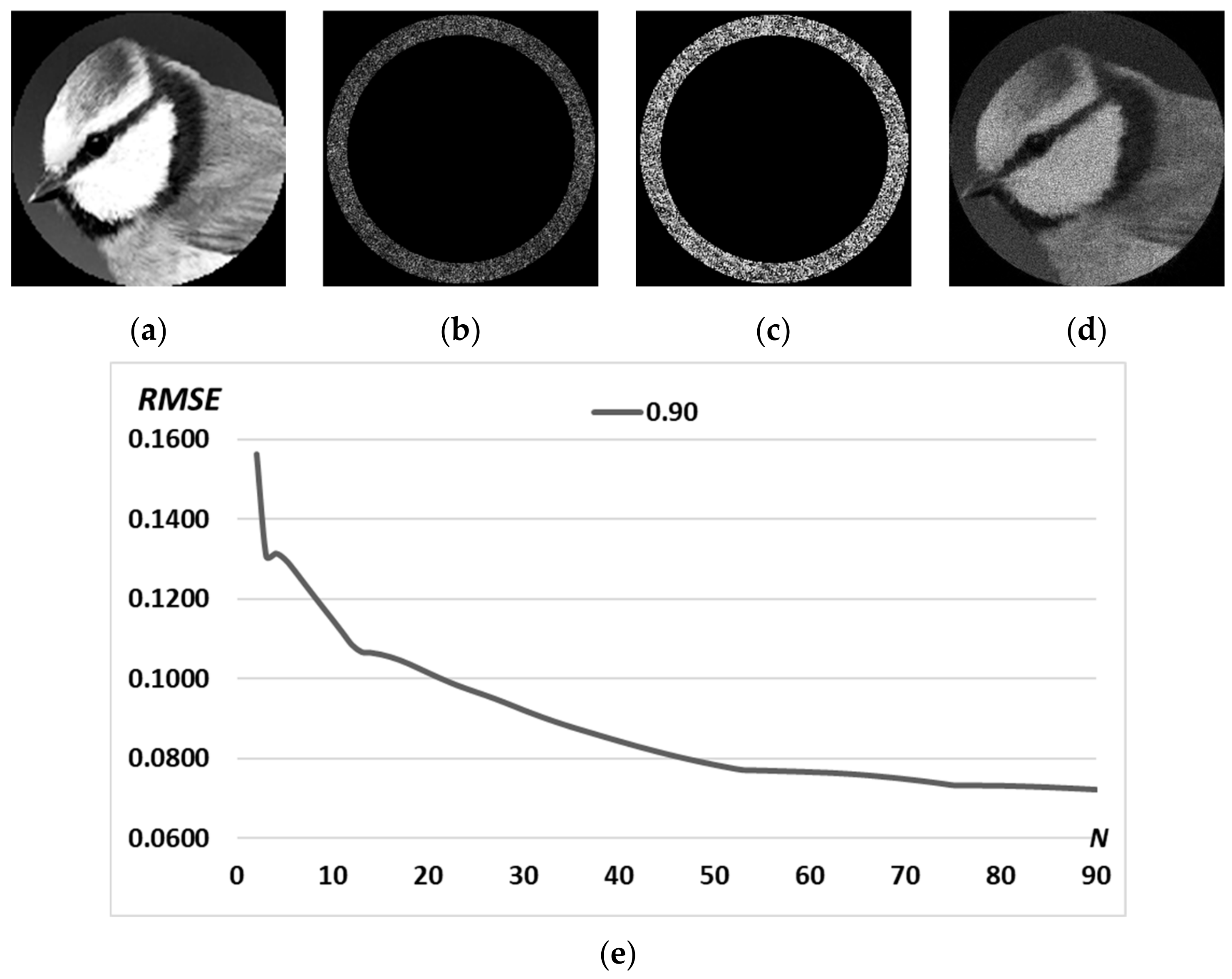
3.2. Complex Patterns
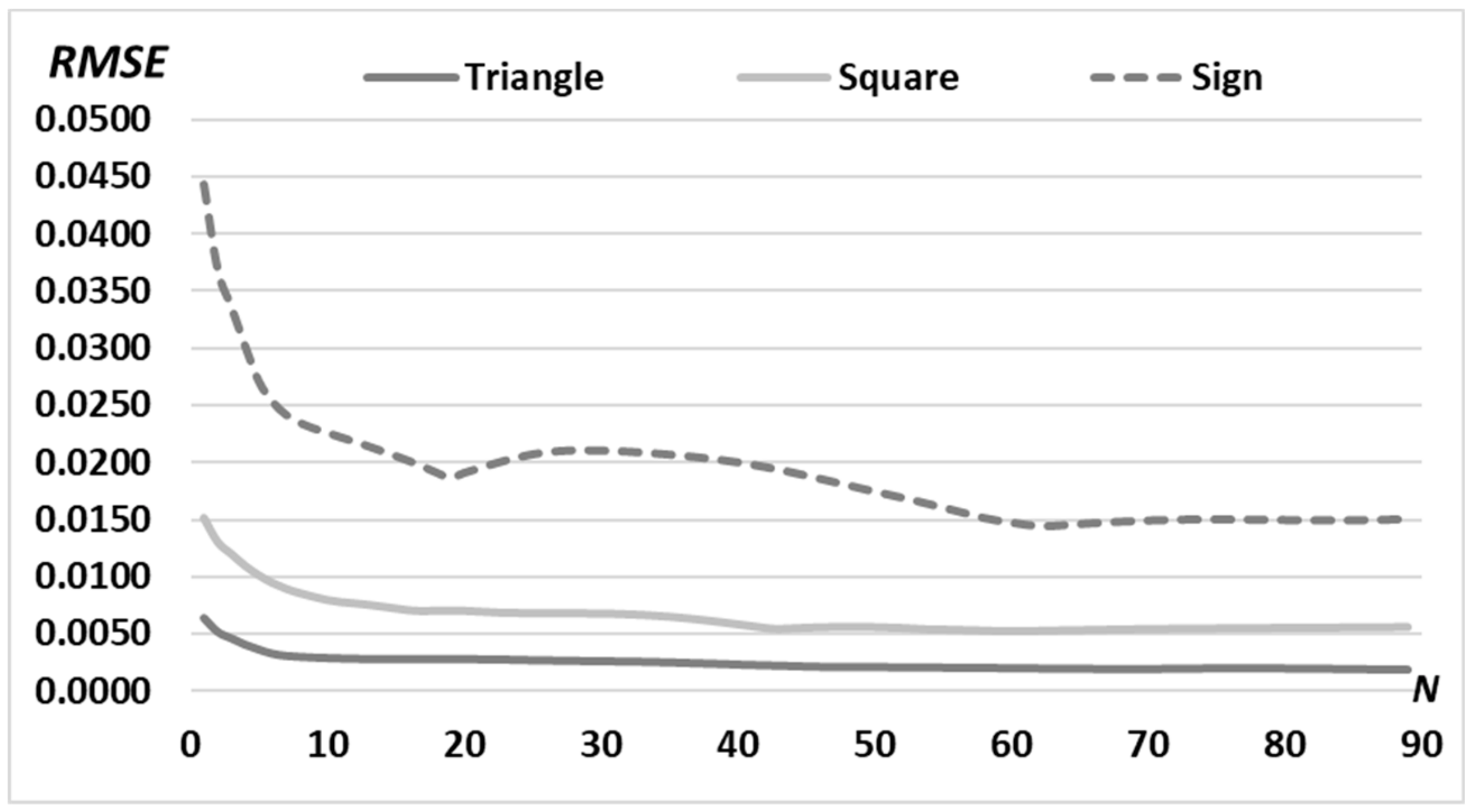
3.3. Superposition of Simple Primitives
4. Simulation and Experimental Results
4.1. Diffraction-Free Properties
4.2. Experimental Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Berezny, A.E.; Prokhorov, A.M.; Sisakian, I.N.; Soifer, V.A. Bessel Optics. Dokl. Akad. Nauk. SSSR 1984, 29, 115–117. [Google Scholar]
- Durnin, J.; Miceli, J.J.; Eberly, J.H. Diffraction-Free Beams. Phys. Rev. Lett. 1987, 58, 1499–1501. [Google Scholar] [CrossRef]
- Khonina, S.N.; Kazanskiy, N.L.; Karpeev, S.V.; Butt, M.A. Bessel Beam: Significance and Applications—A Progressive Review. Photonics 2020, 11, 997. [Google Scholar] [CrossRef]
- Gutierrez-Vega, J.C.; Iturbe-Castillo, M.D.; Chavez-Cerda, S. Alternative Formulation for Invariant Optical Fields: Mathieu Beams. Opt. Lett. 2000, 25, 1493–1495. [Google Scholar] [CrossRef]
- Gutiérrez-Vega, J.C.; Iturbe-Castillo, M.D.; Ramırez, G.A.; Tepichın, E.; Rodrıguez-Dagnino, R.M.; Chávez-Cerda, S.; New, G.H.C. Experimental Demonstration of Optical Mathieu Beams. Opt. Commun. 2001, 195, 35–40. [Google Scholar] [CrossRef]
- Bandres, M.A.; Gutierrez-Vega, J.C.; Chavez-Cerda, S. Parabolic Nondiffracting Optical Wave Fields. Opt. Lett. 2004, 29, 44–46. [Google Scholar] [CrossRef] [PubMed]
- López-Mariscal, C.; Bandres, M.A.; Gutiérrez-Vega, J.C.; Chávez-Cerda, S. Observation of Parabolic Nondiffracting Optical Fields. Opt. Express 2005, 13, 2364–2369. [Google Scholar] [CrossRef] [PubMed]
- Gutierrez-Vega, J.C.; Rodrıguez-Masegosa, R.; Chavez-Cerda, S. Focusing Evolution of Generalized Propagation Invariant Optical Fields. J. Opt. A 2003, 5, 276–282. [Google Scholar] [CrossRef]
- Zhang, P.; Hu, Y.; Li, T.; Cannan, D.; Yin, X.; Morandotti, R.; Chen, Z.; Zhang, X. Nonparaxial Mathieu and Weber Accelerating Beams. Phys. Rev. Lett. 2012, 109, 193901. [Google Scholar] [CrossRef] [PubMed]
- Khonina, S.N.; Ustinov, A.V.; Chávez-Cerda, S. Generalized Parabolic Nondiffracting Beams of Two Orders. J. Opt. Soc. Am. A 2018, 35, 1511–1517. [Google Scholar] [CrossRef]
- Ziolkowski, R.W.; Besieris, I.M.; Shaarawi, A.M. Aperture Realizations of Exact Solutions to Homogeneous-Wave Equations. J. Opt. Soc. Am. A 1993, 10, 75–87. [Google Scholar] [CrossRef]
- Siviloglou, G.A.; Broky, J.; Dogariu, A.; Christodoulides, D.N. Observation of Accelerating Airy Beams. Phys. Rev. Lett. 2007, 99, 213901. [Google Scholar] [CrossRef] [PubMed]
- Davis, J.A.; Mitry, M.J.; Bandres, M.A.; Ruiz, I.; McAuley, K.P.; Cottrell, D.M. Generation of Accelerating Airy and Accelerating Parabolic Beams Using Phase-Only Patterns. Appl. Opt. 2009, 48, 3170–3176. [Google Scholar] [CrossRef] [PubMed]
- Belafhal, A.; Ez-Zariy, L.; Hennani, S.; Nebdi, H. Theoretical Introduction and Generation Method of a Novel Nondiffracting Waves: Olver Beams. Opt. Photon. J. 2015, 5, 234–246. [Google Scholar] [CrossRef]
- Khonina, S.N.; Ustinov, A.V. Fractional Airy Beams. J. Opt. Soc. Am. A 2017, 34, 1991–1999. [Google Scholar] [CrossRef]
- McLeod, J.H. The axicon: A New Type of Optical Element. J. Opt. Soc. Am. 1954, 44, 592–597. [Google Scholar] [CrossRef]
- Arlt, J.; Dholakia, K. Generation of High-Order Bessel Beams by Use of an Axicon. Opt. Commun. 2000, 177, 297–301. [Google Scholar] [CrossRef]
- Khonina, S.N.; Kazanskiy, N.L.; Khorin, P.A.; Butt, M.A. Modern Types of Axicons: New Functions and Applications. Sensors 2021, 21, 6690. [Google Scholar] [CrossRef]
- Turunen, J.; Vasara, A.; Friberg, A.T. Holographic Generation of Diffraction-Free Beams. Appl. Opt. 1988, 27, 3959–3962. [Google Scholar]
- Vasara, A.; Turunen, J.; Friberg, A.T. Realization of General Nondiffracting Beams with Computer Generated Holograms. J. Opt. Soc. Am. A. 1989, 6, 1748–1754. [Google Scholar] [CrossRef] [PubMed]
- Paterson, C.; Smith, R. Higher-Order Bessel Waves Produced by Axicon-Type Computer-Generated Holograms. Opt. Commun. 1996, 124, 121–130. [Google Scholar] [CrossRef]
- Chattrapiban, N.; Rogers, E.A.; Cofield, D.; Hill, W.T., III; Roy, R. Generation of Nondiffracting Bessel Beams by Use of a Spatial Light Modulator. Opt. Lett. 2003, 28, 2183–2185. [Google Scholar] [CrossRef]
- Zhai, Z.; Cheng, Z.; Lv, Q.; Wang, X. Tunable Axicons Generated by Spatial Light Modulator with High-Level Phase Computer Generated Holograms. Appl. Sci. 2020, 10, 5127. [Google Scholar] [CrossRef]
- Khonina, S.N.; Ustinov, A.V.; Porfirev, A.P. Fractional Two-Parameter Parabolic Diffraction-Free Beams. Opt. Commun. 2019, 450, 103–111. [Google Scholar] [CrossRef]
- Thomson, L.C.; Courtial, J. Holographic Shaping of Generalized Self-Reconstructing Light Beams. Opt. Commun. 2008, 281, 1217–1221. [Google Scholar] [CrossRef]
- Goorden, S.A.; Bertolotti, J.; Mosk, A.P. Superpixel-Based Spatial Amplitude and Phase Modulation Using a Digital Micromirror Device. Opt. Express 2014, 22, 17999–18009. [Google Scholar] [CrossRef]
- Anguiano-Morales, M.; Martinez, A.; Iturbe-Castillo, M.D.; Chavez-Cerda, S. Different Field Distributions Obtained with an Axicon and an Amplitude Mask. Opt. Commun. 2008, 281, 401–407. [Google Scholar] [CrossRef]
- Khonina, S.N. Simple Way for Effective Formation Various Nondiffractive Laser Beams. Comput. Opt. 2009, 33, 70–78. [Google Scholar]
- Fedotowsky, A.; Lehovec, K. Far Field Diffraction Patterns of Circular Gratings. Appl. Opt. 1974, 13, 2638–2642. [Google Scholar] [CrossRef]
- Vaity, P.; Rusch, L. Perfect Vortex Beam: Fourier Transformation of a Bessel Beam. Opt. Lett. 2015, 40, 597–600. [Google Scholar] [CrossRef]
- Quemener, M.; Guenette, J.; Borne, J.; Thibault, S. Toric Lens Analysis as a Focal Ring and Bessel Beam Generator. J. Opt. Soc. Am. A 2020, 37, 1657–1661. [Google Scholar] [CrossRef]
- Khonina, S.N.; Kharitonov, S.I.; Volotovskiy, S.G.; Soifer, V.A. Caustics of Non-Paraxial Perfect Optical Vortices Generated by Toroidal Vortex Lenses. Photonics 2021, 8, 259. [Google Scholar] [CrossRef]
- Padgett, M.; Bowman, R. Tweezers with a Twist. Nat. Photon. 2011, 5, 343–348. [Google Scholar] [CrossRef]
- Porfirev, A.P.; Skidanov, R.V. Dark-Hollow Optical Beams with a Controllable Shape for Optical Trapping in Air. Opt. Express 2015, 23, 8373–8382. [Google Scholar] [CrossRef]
- Rodrigo, J.A.; Alieva, T. Freestyle 3D Laser Traps: Tools for Studying Light-Driven Particle Dynamics and Beyond. Optica 2015, 2, 812–815. [Google Scholar] [CrossRef]
- Suarez, R.A.; Neves, A.A.; Gesualdi, M.R. Optical Trapping with Non-Diffracting Airy Beams Array Using a Holographic Optical Tweezers. Opt. Laser Technol. 2021, 135, 106678. [Google Scholar] [CrossRef]
- Courvoisier, F.; Stoian, R.; Couairon, A. Ultrafast Laser Micro- and Nano-Processing With Nondiffracting and Curved Beams: Invited Paper for the Section: Hot Topics in Ultrafast Lasers. Opt. Laser Technol. 2016, 80, 125–137. [Google Scholar] [CrossRef]
- Syubaev, S.; Zhizhchenko, A.; Vitrik, O.; Porfirev, A.; Fomchenkov, S.; Khonina, S.N.; Kudryashov, S.; Kuchmizhak, A. Chirality of Laser-Printed Plasmonic Nanoneedles Tunable by Tailoring Spiral Shape Pulses. Appl. Surf. Sci. 2019, 470, 526–534. [Google Scholar] [CrossRef]
- Flamm, D.; Chen, K.; Jenne, M.; Schäfer, M.; Grossmann, D.G.; Hellstern, J.; Tillkorn, C.; Kumkar, M. Generalized Non-Diffracting Beams for Ultrafast Materials Processing. Proc. SPIE 2020, 11270, 112700Y. [Google Scholar]
- Vetter, C.; Steinkopf, R.; Bergner, K.; Ornigotti, M.; Nolte, S.; Gross, H.; Szameit, A. Realization of Free-Space Long-Distance Self-Healing Bessel Beams. Laser Photon. Rev. 2019, 13, 1900103. [Google Scholar] [CrossRef]
- Saadati-Sharafeh, F.; Borhanifar, A.; Porfirev, A.; Amiri, P.; Akhlaghi, E.; Khonina, S.N.; Azizian Kalandaragh, Y. The Superposition of the Bessel and Mirrored Bessel Beams and Investigation of Their Self-Healing Characteristics. Optik 2020, 208, 164057. [Google Scholar] [CrossRef]
- Chen, X.; Yuan, Y.; Yan, B.; Zhang, R.; Liu, H.; Lu, Z.; Liu, B. Propagation and Self-Healing Properties of Lommel-Gaussian Beam Through Atmospheric Turbulence. Optoelectron. Lett. 2021, 17, 572–576. [Google Scholar] [CrossRef]
- Sun, P.C.; Mazurenko, Y.; Fainman, Y. Long-Distance Frequency-Division Interferometer for Communication and Quantum Cryptography. Opt. Lett. 1995, 20, 1062–1064. [Google Scholar] [CrossRef]
- Khonina, S.N.; Golub, I. Creating Order with the Help of Randomness: Generating Transversely Random, Longitudinally Invariant Vector Optical Fields. Opt. Lett. 2015, 40, 4070–4073. [Google Scholar] [CrossRef]
- Wang, T.-L.; Gariano, J.A.; Djordjevic, I.B. Employing Bessel-Gaussian Beams to Improve Physical-Layer Security in Free-Space Optical Communications. IEEE Photon. J. 2018, 10, 7907113. [Google Scholar] [CrossRef]
- Hu, Y.; Chen, Z.; Xiang, L.; Xing, D. Extended Depth-of-Field All-Optical Photoacoustic Microscopy with a Dual Non-Diffracting Bessel Beam. Opt. Lett. 2019, 44, 1634–1637. [Google Scholar] [CrossRef]
- Khonina, S.N.; Ustinov, A.V.; Porfirev, A.P. Dynamic Focal Shift and Extending Depth of Focus Based on the Masking of the Illuminating Beam and Using an Adjustable Axicon. J. Opt. Soc. Am. A 2019, 36, 1039–1047. [Google Scholar] [CrossRef]
- Ren, Y.X.; He, H.; Tang, H.; Wong, K.K. Non-Diffracting Light Wave: Fundamentals and Biomedical Applications. Front. Phys. 2021, 9, 698343. [Google Scholar] [CrossRef]
- Grier, D.G. A Revolution in Optical Manipulation. Nature 2003, 424, 810–816. [Google Scholar] [CrossRef]
- Curtis, J.E.; Koss, B.A.; Grier, D.G. Dynamic Holographic Optical Tweezers. Opt. Commun. 2002, 207, 169175. [Google Scholar] [CrossRef]
- Rodrigo, P.J.; Daria, V.R.; Gluckstad, J. Real-Time Three-Dimensional Optical Micromanipulation of Multiple Particles and Living Cells. Opt. Lett. 2004, 29, 2270–2272. [Google Scholar] [CrossRef] [PubMed]
- Rodrigo, J.A.; Alieva, T.; Abramochkin, E.; Castro, I. Shaping of Light Beams Along Curves in Three Dimensions. Opt. Express 2013, 21, 20544–20555. [Google Scholar] [CrossRef] [PubMed]
- Rodrigo, J.A.; Alieva, T. Polymorphic Beams and Nature Inspired Circuits for Optical Current. Sci. Rep. 2016, 6, 35341. [Google Scholar] [CrossRef]
- Khonina, S.N.; Porfirev, A.P. Generation of Multi-Contour Plane Curves Using Vortex Beams. Optik 2021, 229, 166299. [Google Scholar] [CrossRef]
- Zhang, Y.; Belić, M.R.; Sun, J.; Zheng, H.; Chen, H.; Li, C.; Wang, Z.; Zhang, Y. Three-Dimensional Nonparaxial Accelerating Beams from the Transverse Whittaker Integral. Europhys. Let. 2014, 107, 34001. [Google Scholar] [CrossRef]
- Suarez, R.A.; Neves, A.A.; Gesualdi, M.R. Generation and Characterization of an Array of Airy-Vortex Beams. Opt. Commun. 2019, 458, 124846. [Google Scholar] [CrossRef]
- Frolov, A.O.; Khonina, S.N. Modeling the Propagation of Sets of Autofocusing Laser Beams. Proc. SPIE 2021, 11793, 117930I. [Google Scholar]
- Khonina, S.N. Mirror and Circular Symmetry of Autofocusing Beams. Symmetry 2021, 13, 1794. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Khonina, S.N.; Soifer, V.A. Calculation of Phase Formers of Non-Diffracting Images and a Set of Concentric Rings. Optik 1996, 102, 45–50. [Google Scholar]
- Whyte, G.; Courtial, J. Experimental Demonstration of Holographic Three-Dimensional Light Shaping Using a Gerchberg–Saxton Algorithm. New J. Phys. 2005, 7, 117. [Google Scholar] [CrossRef]
- Lopez-Aguayo, S.; Kartashov, Y.V.; Vysloukh, V.A.; Torner, L. Method to Generate Complex Quasi Nondiffracting Optical Lattices. Phys. Rev. Lett. 2010, 105, 013902. [Google Scholar] [CrossRef]
- Kachalov, D.G.; Pavelyev, V.S.; Khonina, S.N.; Skidanov, R.V.; Moiseev, O.Y. Application of the Direct Search in Solving a Problem of Forming Longitudinal Distribution of Intensity. J. Mod. Opt. 2011, 58, 69–76. [Google Scholar] [CrossRef]
- Hsu, W.-F.; Lin, S.-C. Iterative Pixelwise Approach Applied to Computer-Generated Holograms and Diffractive Optical Elements. Appl. Opt. 2018, 57, A189–A196. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.; Seka, W.; Eberly, J.H.; Huang, H.; Brown, D.L. Experimental Investigation of Bessel Beam Characteristics. Appl. Opt. 1992, 31, 2708. [Google Scholar] [CrossRef] [PubMed]
- Whittaker, E.T.; Watson, G.N. A Course of Modern Analysis, 4th ed.; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Durnin, J. Exact Solutions for Nondiffracting Beams. I. The Scalar Theory. J. Opt. Soc. Am. A 1987, 4, 651–654. [Google Scholar] [CrossRef]
- McGloin, D.; Dholakia, K. Bessel Beams: Diffraction in a New Light. Contemp. Phys. 2005, 46, 15–28. [Google Scholar] [CrossRef]
- Courtial, J.; Whyte, G.; Bouchal, Z.; Wagner, J. Iterative Algorithms for Holographic Shaping of Non-Diffracting and Self-Imaging Light Beams. Opt. Express 2006, 140, 2108–2116. [Google Scholar] [CrossRef] [PubMed]
- Mukhametgaleev, I.V.; Khonina, S.N. An Iterative Algorithm for Calculating Images with Diffraction-Free Properties Based on the Selection of a Narrow Spectral Ring. Bull. Samara State Aerosp. Univ. 2010, 4, 238–246. [Google Scholar]
- Khorin, P.A.; Ustinov, A.V. The Formation of Diffraction-Free Beams with a Given Distribution Based on the Whittaker Integral. In Proceedings of the 2020 International Conference on Information Technology and Nanotechnology (ITNT), Samara, Russia, 26–29 May 2020; pp. 1–5. [Google Scholar]
- Chafiq, A.; Belafhal, A. Optical Fourier Transform of Pseudo-Nondiffracting Beams. J. Quant. Spectrosc. Radiat. Transf. 2021, 258, 107357. [Google Scholar] [CrossRef]
- Khorin, P.A. Calculation of Diffractive Optical Elements for the Formation of Thin Light Sheet. Jour. Phys. Conf. Series. 2019, 1368, 022014. [Google Scholar] [CrossRef]
- Vettenburg, T.; Dalgarno, H.I.C.; Nylk, J.; Coll-Llado, C.; Ferrier, D.E.K.; Čižmár, T.; Gunn-Moore, F.J.; Dholakia, K. Light-Sheet Microscopy Using an Airy Beam. Nat. Methods 2014, 11, 541–544. [Google Scholar] [CrossRef] [PubMed]
- Piksarv, P.; Marti, D.; Le, T.; Unterhuber, A.; Forbes, L.H.; Andrews, M.R.; Stingl, A.; Drexler, W.; Andersen, P.E.; Dholakia, K. Integrated Single- and Two-Photon Light Sheet Microscopy Using Accelerating Beams. Sci. Rep. 2017, 7, 1435. [Google Scholar] [CrossRef] [PubMed]
- Khonina, S.N.; Balalayev, S.A.; Skidanov, R.V.; Kotlyar, V.V.; Päivänranta, B.; Turunen, J. Encoded Binary Diffractive Element to Form Hyper-Geometric Laser Beams. J. Opt. A Pure Appl. Opt. 2009, 11, 065702. [Google Scholar] [CrossRef]
- Khonina, S.N.; Karpeev, S.V.; Paranin, V.D. A Technique for Simultaneous Detection of Individual Vortex States of Laguerre—Gaussian Beams Transmitted Through an Aqueous Suspension of Microparticles. Opt. Laser. Eng. 2018, 105, 68. [Google Scholar] [CrossRef]






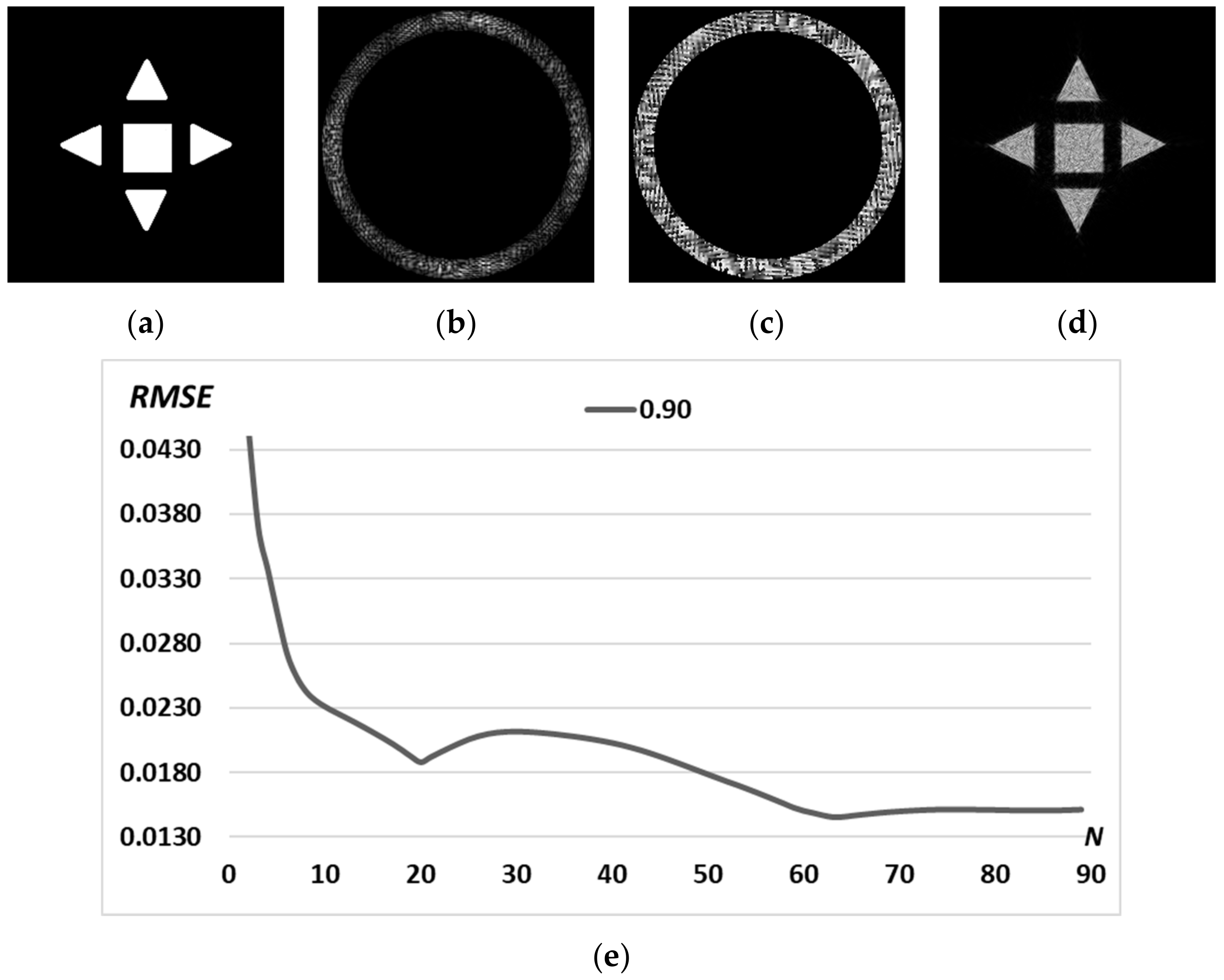






| Iteration, n | 2 | 4 | 10 | 50 | 90 |
|---|---|---|---|---|---|
| Intensity |  |  |  |  |  |
| RMSE | 0.0064 | 0.0046 | 0.0029 | 0.0021 | 0.0019 |
| The Variable Width Δd | 0.20 R0 | 0.25 R0 | 0.30 R0 | 0.35 R0 | 0.40 R0 |
|---|---|---|---|---|---|
| DOE phase |  |  |  |  |  |
| Focal intensity |  |  |  |  |  |
| RMSE | 0.0019 | 0.0015 | 0.0012 | 0.0009 | 0.0005 |
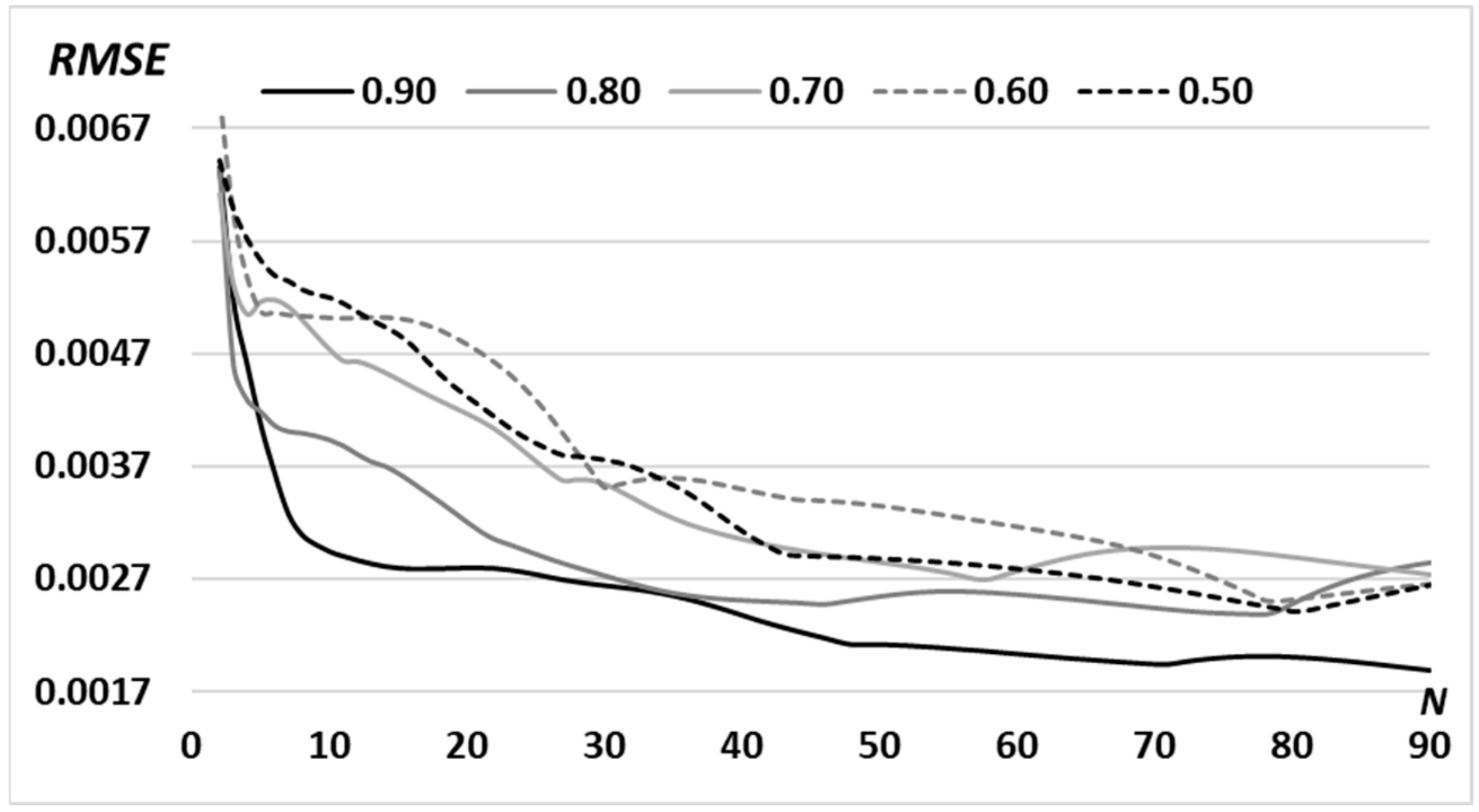
| The Middle Radius of the Ring d | 0.5 R0 | 0.6 R0 | 0.7 R0 | 0.8 R0 | 0.9 R0 |
|---|---|---|---|---|---|
| DOE phase |  |  |  |  |  |
| Focal intensity |  |  |  |  |  |
| RMSE | 0.0028 | 0.0027 | 0.0027 | 0.0026 | 0.0019 |
| Type of Beam | Distance to the Focal Plane Δz, mm | ||||
|---|---|---|---|---|---|
| −75 | −50 | −25 | −15 | 0 | |
| Primitive Triangle with Δd = 0.2 R0 |  |  |  |  |  |
| Primitive Triangle with Δd = 0.4 R0 |  |  |  |  |  |
| Superposition of simple primitives with Δd = 0.2 R0 |  |  |  |  |  |
| Type of Beam | Distance to the Focal Plane Δz, mm | ||||
|---|---|---|---|---|---|
| −75 | −50 | −25 | −15 | 0 | |
| Complex pattern D(u,v) of the “bird” image with Δd = 0.2 R0 |  | 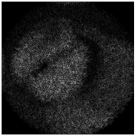 | 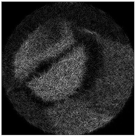 | 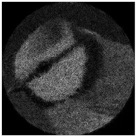 | 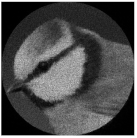 |
| Complex pattern D(u,v) of the “bird” image with Δd = 0.4 R0 | 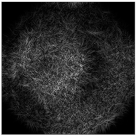 | 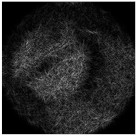 |  | 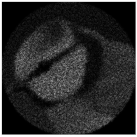 | 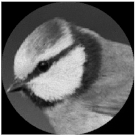 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khorin, P.A.; Porfirev, A.P.; Khonina, S.N. Composite Diffraction-Free Beam Formation Based on Iteratively Calculated Primitives. Micromachines 2023, 14, 989. https://doi.org/10.3390/mi14050989
Khorin PA, Porfirev AP, Khonina SN. Composite Diffraction-Free Beam Formation Based on Iteratively Calculated Primitives. Micromachines. 2023; 14(5):989. https://doi.org/10.3390/mi14050989
Chicago/Turabian StyleKhorin, Pavel A., Alexey P. Porfirev, and Svetlana N. Khonina. 2023. "Composite Diffraction-Free Beam Formation Based on Iteratively Calculated Primitives" Micromachines 14, no. 5: 989. https://doi.org/10.3390/mi14050989
APA StyleKhorin, P. A., Porfirev, A. P., & Khonina, S. N. (2023). Composite Diffraction-Free Beam Formation Based on Iteratively Calculated Primitives. Micromachines, 14(5), 989. https://doi.org/10.3390/mi14050989









