Modeling of MEMS Transducers with Perforated Moving Electrodes
Abstract
1. Introduction
2. Analytical Solution
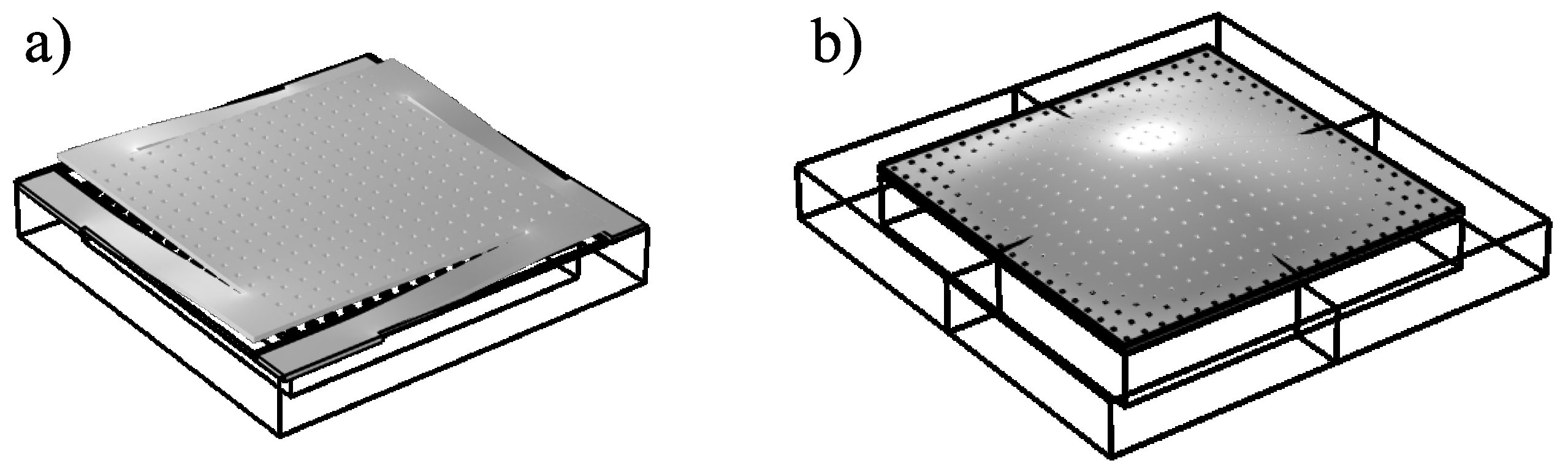
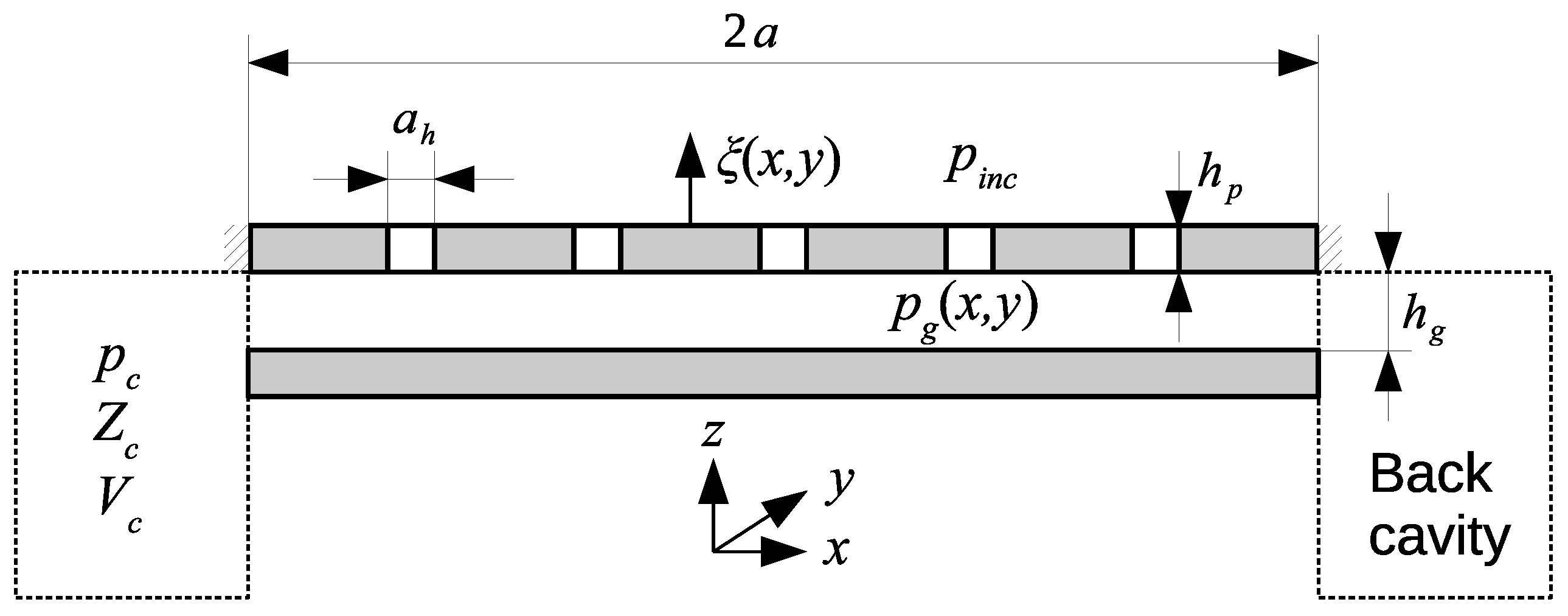
2.1. Description of the Device
2.2. The Acoustic Pressure Field inside the Transducer
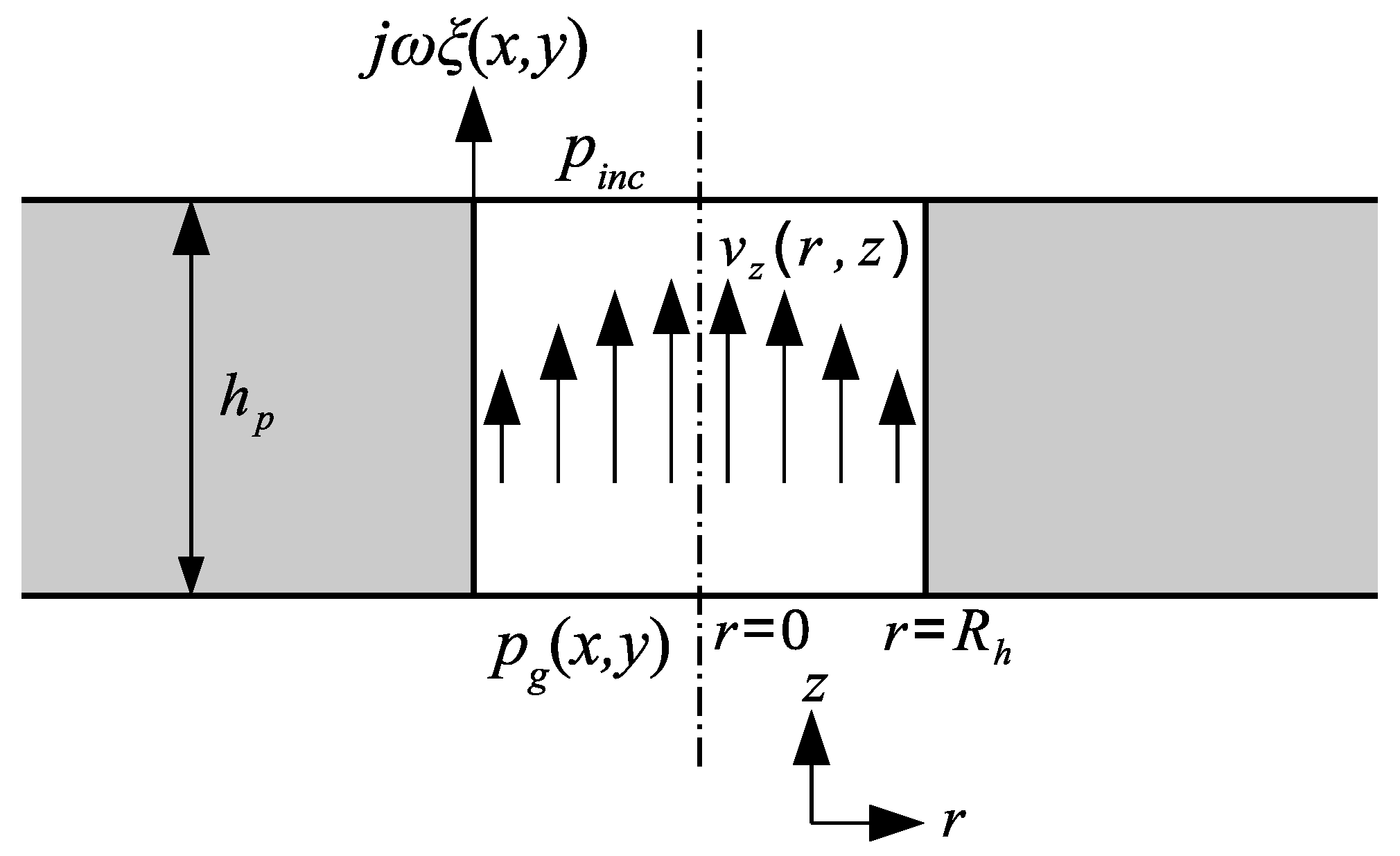
2.2.1. Viscous Effects Originating in the Holes in the Perforated Moving Electrode
2.2.2. Wave Equation Governing the Acoustic Pressure in the Air Gap
- Change of the mass per unit of time in both x and y directions , where w designates x and y.
- Contribution from the moving electrode .
- Contribution form the holes , where is given by Equation (6).
2.2.3. Solution for the Acoustic Pressure in the Air Gap in Case of Piston-like Movement of the Moving Electrode
2.2.4. Solution for the Acoustic Pressure in the Air Gap in Case of Nonuniform Movement of the Moving Electrode
2.3. Coupling of the Moving Electrode Displacement Field and the Acoustic Pressure Field
2.3.1. Elastically Supported Rigid Perforated Plate
2.3.2. Flexible Perforated Plate Clamped at All Edges
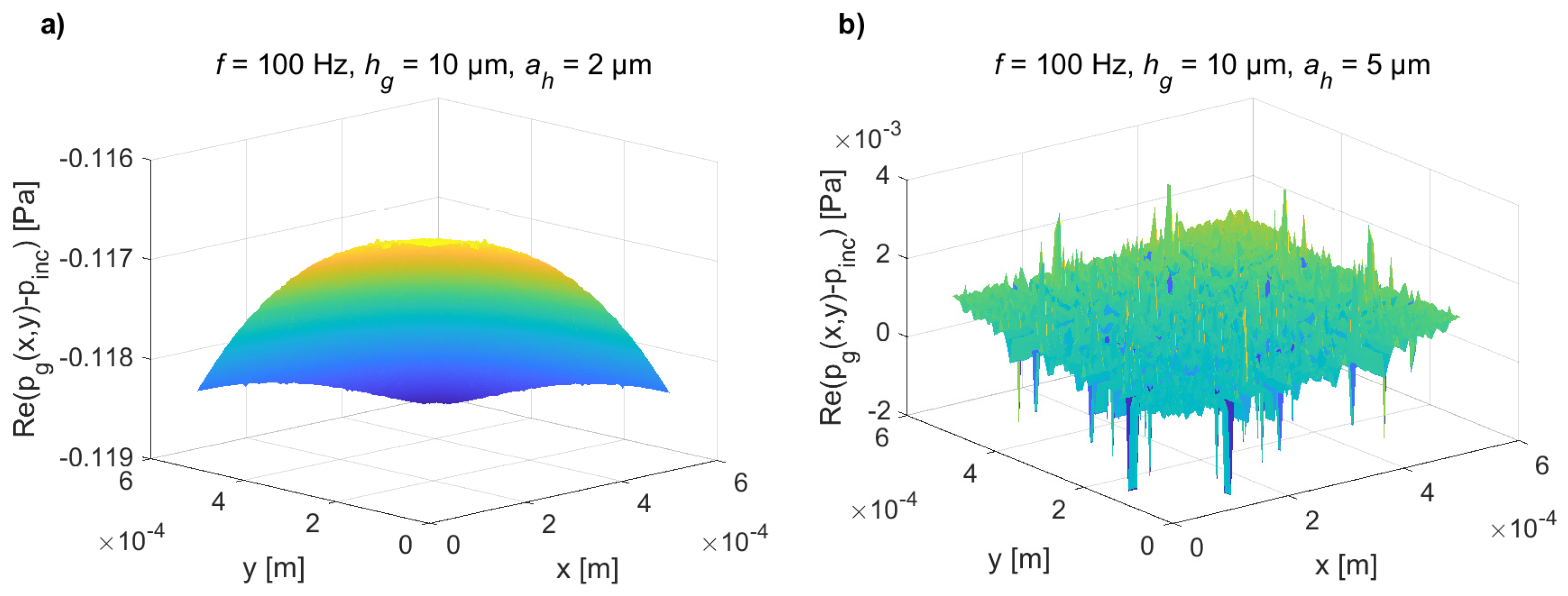
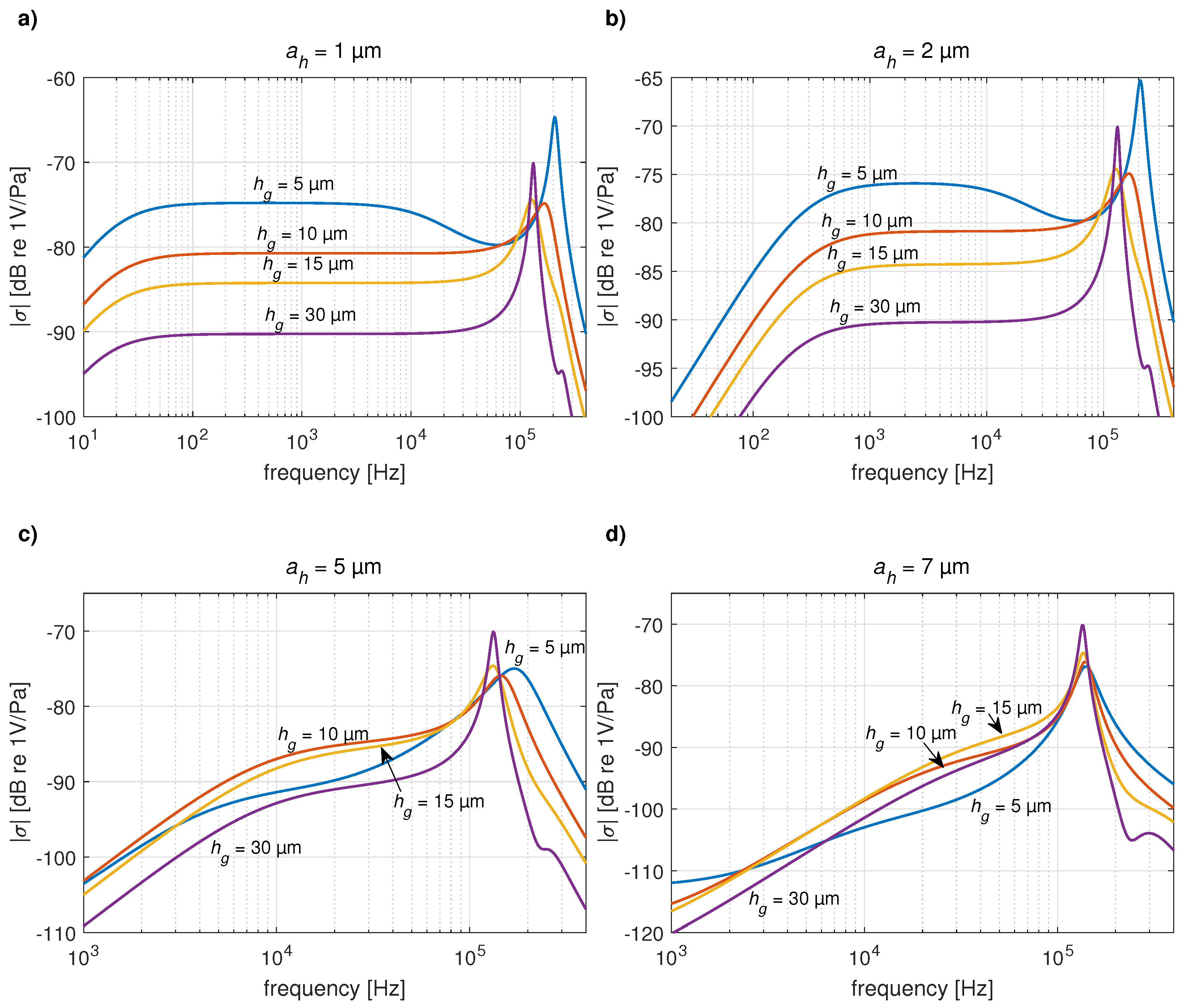
3. Analytical Results and Comparisons with the Numerical (FEM) Ones
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Approximate Eigenfunctions of the Perforated Flexible Square Plate Clamped at All Edges [32]
References
- Malcovati, P.; Baschirotti, A. The Evolution of Integrated Interfaces for MEMS Microphones. Micromachines 2018, 9, 323. [Google Scholar] [CrossRef] [PubMed]
- Ali, W.R.; Prasad, M. Piezoelectric MEMS based acoustic sensors: A review. Sens. Actuator A Phys. 2020, 301, 111756. [Google Scholar] [CrossRef]
- Dehé, A. Silicon microphone development and application. Sens. Actuator A Phys. 2007, 133, 283–287. [Google Scholar] [CrossRef]
- Bergqvist, J.; Rudolf, F. A silicon condenser microphone using bond and etch-back technology. Sens. Actuator A Phys. 1994, 45, 115–124. [Google Scholar] [CrossRef]
- Iguchi, Y.; Goto, M.; Iwaki, M.; Ando, A.; Tanioka, K.; Tajima, T.; Takeshi, F.; Matsunaga, S.; Yasuno, Y. Silicon microphone with wide frequency range and high linearity. Sens. Actuator A Phys. 2007, 135, 420–425. [Google Scholar] [CrossRef]
- Scheeper, P.R.; Nordstrand, B.; Gulløv, J.O.; Liu, B.; Clausen, T.; Midjord, L.; Storgaard-Larsen, T. A new measurement microphone based on MEMS technology. J. Microelectromech. Syst. 2003, 12, 880–891. [Google Scholar] [CrossRef]
- Füldner, M.; Dehé, A. Dual Back Plate Silicon MEMS microphone: Balancing High Performance! In Proceedings of the DAGA 2015, Nürnberg, Germany, 16–19 March 2015; pp. 41–43. [Google Scholar]
- Peña-García, N.N.; Aguilera-Cortés, L.A.; Gonzáles-Palacios, M.A.; Raskin, J.-P.; Herrera-May, A.L. Design and Modeling of a MEMS Dual-Backplate Capacitive Microphone with Spring-Supported Diaphragm for Mobile Device Applications. Sensors 2018, 18, 3545. [Google Scholar] [CrossRef]
- Rong, Z.; Zhang, M.; Ning, Y.; Pang, W. An ultrasound-induced wireless power supply based on AlN piezoelectric micromachined ultrasonic transducers. Sci. Rep. 2022, 12, 16174. [Google Scholar] [CrossRef]
- Pinto, R.M.R.; Gund, V.; Dias, R.A.; Nagaraja, K.K.; Vinayakumar, K.B. CMOS-Integrated Aluminum Nitride MEMS: A Review. J. Microelectromech. Syst. 2022, 31, 500–523. [Google Scholar] [CrossRef]
- Lynes, D.D.; Chandrahalim, H. Influence of a Tailored Oxide Interface on the Quality Factor of Microelectromechanical Resonators. Adv. Mater. Interfaces 2023, 10, 2202446. [Google Scholar] [CrossRef]
- Verdot, T.; Redon, E.; Ege, K.; Czarny, J.; Guianvarc’h, C.; Guyader, J.-L. Microphone with planar nano-gauge detection: Fluid-structure coupling including thermo-viscous effects. Acta Acust. United Acust. 2016, 102, 517–529. [Google Scholar] [CrossRef]
- Rufer, L.; De Pasquale, G.; Esteves, J.; Randazzo, F.; Basrour, S.; Somà, A. Micro-acoustic source for hearing applications fabricated with 0.35 μm CMOS-MEMS process. Procedia Eng. 2015, 120, 944–947. [Google Scholar] [CrossRef]
- Ganji, B.A.; Sedaghat, S.B.; Roncaglia, A.; Belsito, L. Design and fabrication of very small MEMS microphone with silicon diaphragm supported by Z-shape arms using SOI wafer. Solid State Electron. 2018, 148, 27–34. [Google Scholar] [CrossRef]
- Ganji, B.A.; Majlis, B.Y. Design and fabrication of a new MEMS capacitive microphone using a perforated aluminum diaphragm. Sens. Actuator A Phys. 2009, 149, 29–37. [Google Scholar] [CrossRef]
- Ganji, B.A.; Sedaghat, S.B.; Roncaglia, A.; Belsito, L. Design and fabrication of high performance condenser microphone using C-slotted diaphragm. Microsyst. Technol. 2018, 24, 3133–3140. [Google Scholar] [CrossRef]
- Sedaghat, S.B.; Ganji, B.A.; Ansari, R. Design and modeling of a frog-shape MEMS capacitive microphone using SOI technology. Microsyst. Technol. 2018, 24, 1061–1070. [Google Scholar] [CrossRef]
- Škvor, Z. On the Acoustical Resistance due to Viscous Losses in the Air Gap of Electrostatic Transducers. Acustica 1967, 19, 295–299. [Google Scholar]
- Estèves, J.; Rufer, L.; Ekeom, D.; Basrour, S. Lumped-parameters equivalent circuit for condenser microphones modeling. J. Acoust. Soc. Am. 2017, 142, 2121–2132. [Google Scholar] [CrossRef]
- Zuckerwar, A.J. Theoretical response of condenser microphones. J. Acoust. Soc. Am. 1978, 64, 1278–1285. [Google Scholar] [CrossRef]
- Lavergne, T.; Durand, S.; Bruneau, M.; Joly, N. Dynamic Behavior of Circular Membrane and An Electrostatic Microphone: Effect of Holes In The Backing Electrode. J. Acoust. Soc. Am. 2010, 128, 3459–3477. [Google Scholar] [CrossRef]
- Lavergne, T.; Durand, S.; Bruneau, M.; Joly, N. Analytical Modeling of Electrostatic Transducers in Gases: Behavior of Their Membrane and Sensitivity. Acta Acust. United Acust. 2014, 100, 440–447. [Google Scholar] [CrossRef]
- Naderyan, V.; Raspet, R.; Hickey, C. Thermo-viscous acoustic modeling of perforated micro-electro-mechanical systems (MEMS). J. Acoust. Soc. Am. 2020, 148, 2376–2385. [Google Scholar] [CrossRef] [PubMed]
- Pedersen, M.; Olthuis, W.; Bergveld, P. On the electromechanical behaviour of thin perforated backplates in silicon condenser microphones. In Proceedings of the 8th International Conference on Solid-state Sensors ancl Actuators, and Eurosensors IX, Stockholm, Sweden, 25–29 June 1995; p. 234 A7. [Google Scholar]
- Novak, A.; Honzík, P.; Bruneau, M. Dynamic behaviour of a planar micro-beam loaded by a fluid-gap: Analytical and numerical approach in a high frequency range, benchmark solutions. J. Sound Vib. 2017, 401, 36–53. [Google Scholar] [CrossRef]
- Honzík, P.; Bruneau, M. Acoustic fields in thin fluid layers between vibrating walls and rigid boundaries: Integral method. Acta Acust. United Acust. 2015, 101, 859–862. [Google Scholar] [CrossRef]
- Šimonová, K.; Honzík, P.; Bruneau, M.; Gatignol, P. Modelling approach for MEMS transducers with rectangular clamped plate loaded by a thin fluid layer. J. Sound Vib. 2020, 473, 115246. [Google Scholar] [CrossRef]
- Herring Jensen, M.J.; Sandermann Olsen, E. Virtual prototyping of condenser microphone using the finite element method for detailed electric, mechanic, and acoustic characterisation. Proc. Meet. Acoust. 2013, 19, 030039. [Google Scholar]
- Bruneau, M.; Scelo, T. Fundamentals of Acoustics; ISTE: London, UK, 2006. [Google Scholar]
- Leissa, A.W. Vibration of Plates; Scientific and Technical Information Division, National Aeronautics and Space Administration: Washington, DC, USA, 1969. [Google Scholar]
- Šimonová, K.; Honzík, P.; Joly, N.; Durand, S.; Bruneau, M. Modelling of a MEMS transducer using approximate eigenfunctions of a square clamped plate. In Proceedings of the 23rd International Congress on Acoustics, Aachen, Germany, 9–13 September 2019; pp. 7361–7368. [Google Scholar]
- Šimonová, K.; Honzík, P.; Joly, N.; Durand, S.; Bruneau, M. Modelling of a MEMS Transducer with a Moving Electrode in Form of Perforated Square Plate. Proceedings of Forum Acusticum 2020, Lyon, France, 7–11 December 2020; pp. 2539–2542. [Google Scholar]
- COMSOL Multiphysics. Acoustics Module User’s Guide. 2022. Available online: https://doc.comsol.com/6.1/doc/com.comsol.help.aco/AcousticsModuleUsersGuide.pdf (accessed on 23 March 2023).
- COMSOL Multiphysics. Structural Mechanics Module User’s Guide. 2022. Available online: https://doc.comsol.com/6.1/doc/com.comsol.help.sme/StructuralMechanicsModuleUsersGuide.pdf (accessed on 23 March 2023).
- Le Van Suu, T.; Durand, S.; Bruneau, M. On the modelling of a clamped plate loaded by a squeeze fluid film: Application to miniaturized sensors. Acta Acust. United Acust. 2010, 96, 923–935. [Google Scholar] [CrossRef]



| Parameter | Value | Unit |
|---|---|---|
| Adiabatic sound speed | 343.2 | m s |
| Air density | 1.2 | kg m |
| Shear dynamic viscosity | Pa s | |
| Thermal conductivity | W m K | |
| Specific heat coefficient at constant pressure per unit of mass | 1005 | J kg K |
| Ratio of specific heats | 1.4 | - |
| Parameter | Value | Unit |
|---|---|---|
| Plate density | 2330 | kg m |
| Young’s modulus E | 160 | G Pa |
| Poisson’s ratio | 0.27 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Šimonová, K.; Honzík, P. Modeling of MEMS Transducers with Perforated Moving Electrodes. Micromachines 2023, 14, 921. https://doi.org/10.3390/mi14050921
Šimonová K, Honzík P. Modeling of MEMS Transducers with Perforated Moving Electrodes. Micromachines. 2023; 14(5):921. https://doi.org/10.3390/mi14050921
Chicago/Turabian StyleŠimonová, Karina, and Petr Honzík. 2023. "Modeling of MEMS Transducers with Perforated Moving Electrodes" Micromachines 14, no. 5: 921. https://doi.org/10.3390/mi14050921
APA StyleŠimonová, K., & Honzík, P. (2023). Modeling of MEMS Transducers with Perforated Moving Electrodes. Micromachines, 14(5), 921. https://doi.org/10.3390/mi14050921






