Parameter Identification of Model for Piezoelectric Actuators
Abstract
1. Introduction
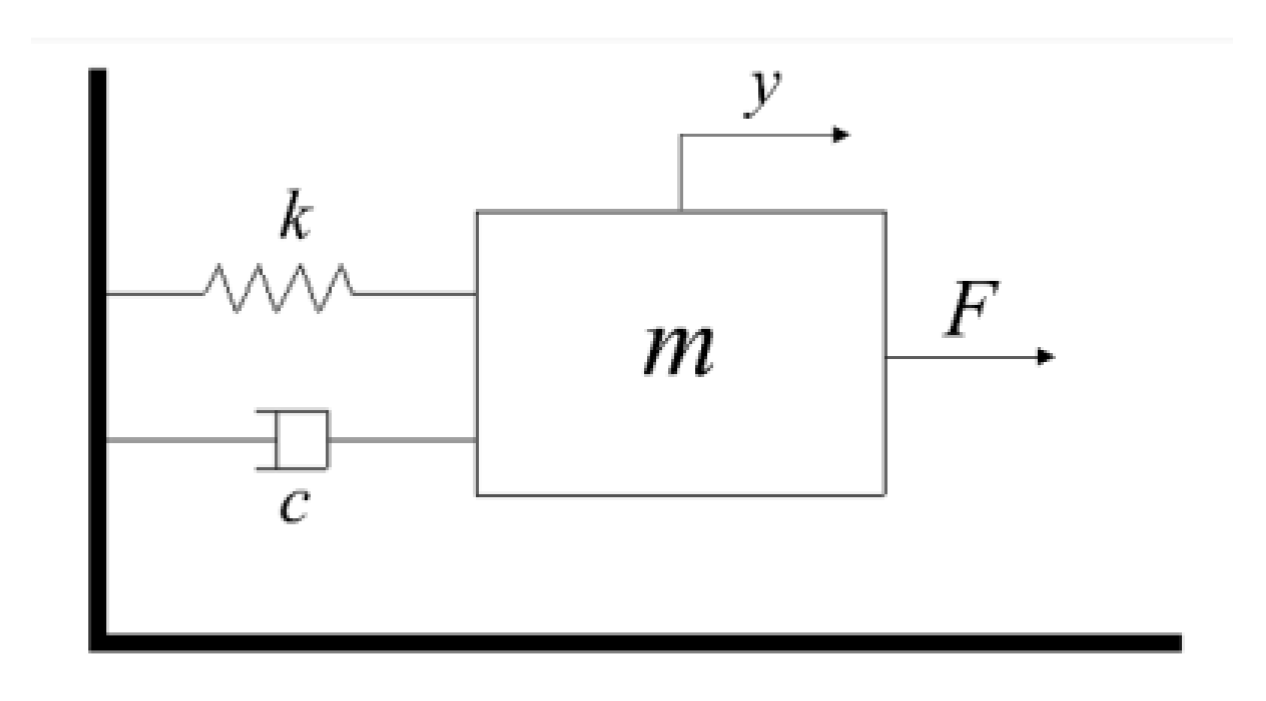
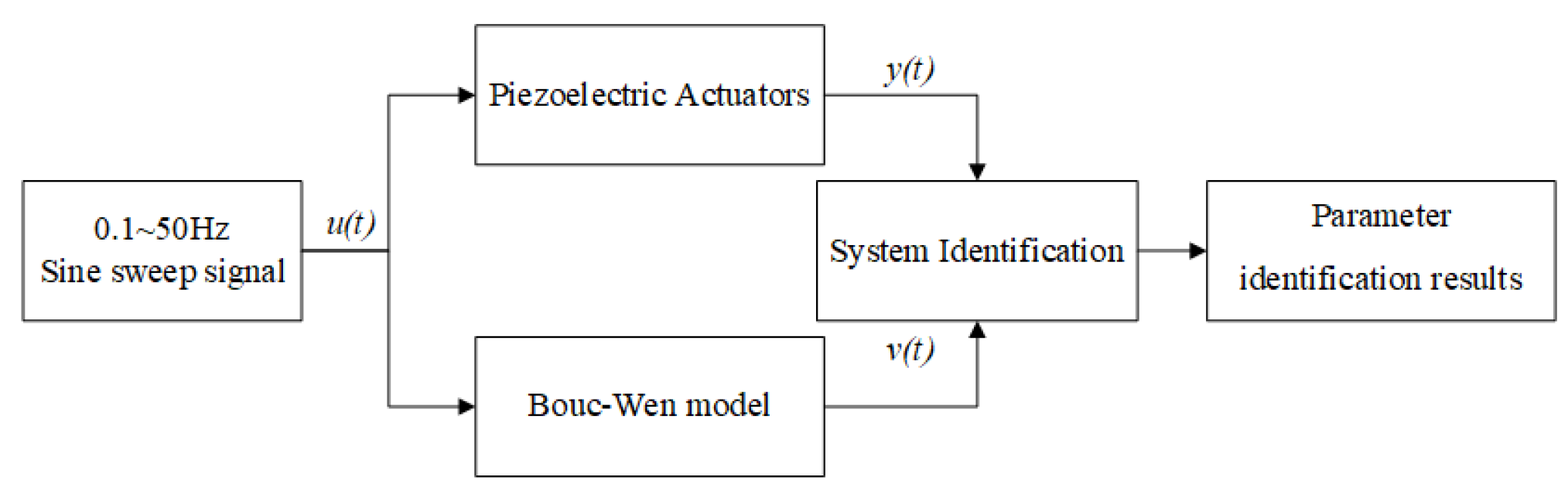
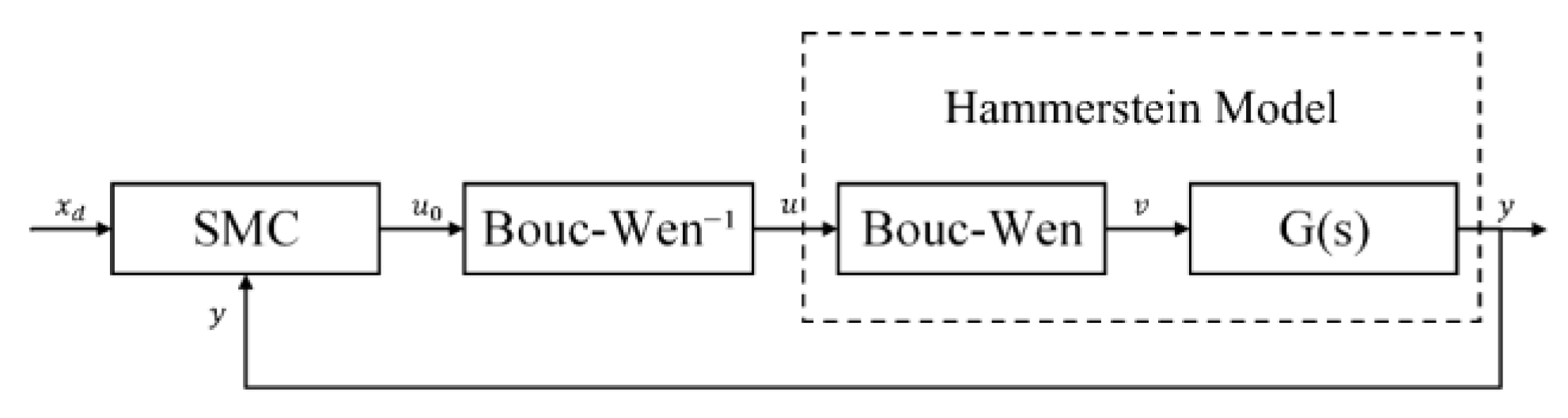
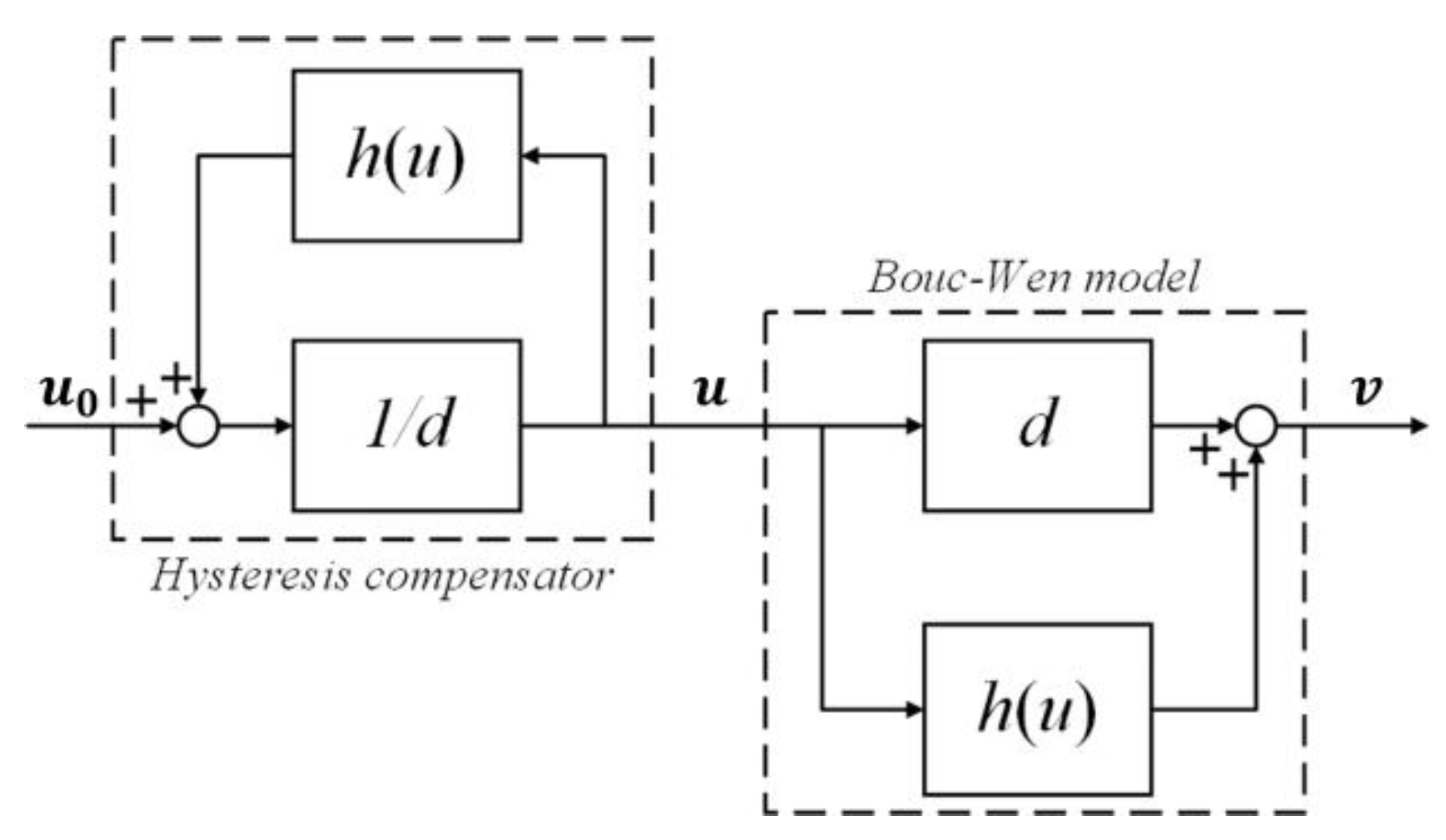
2. Hammerstein Model
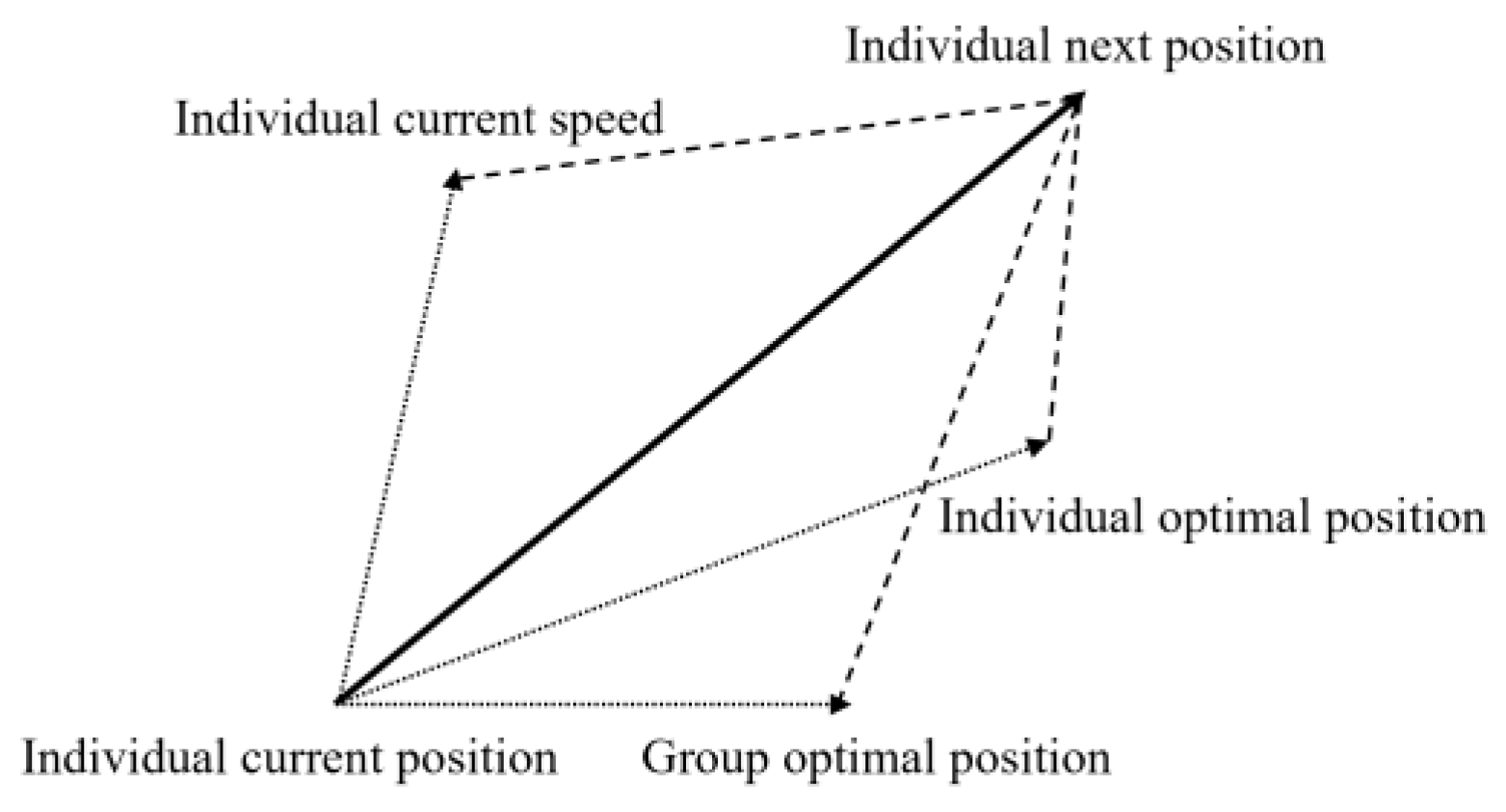
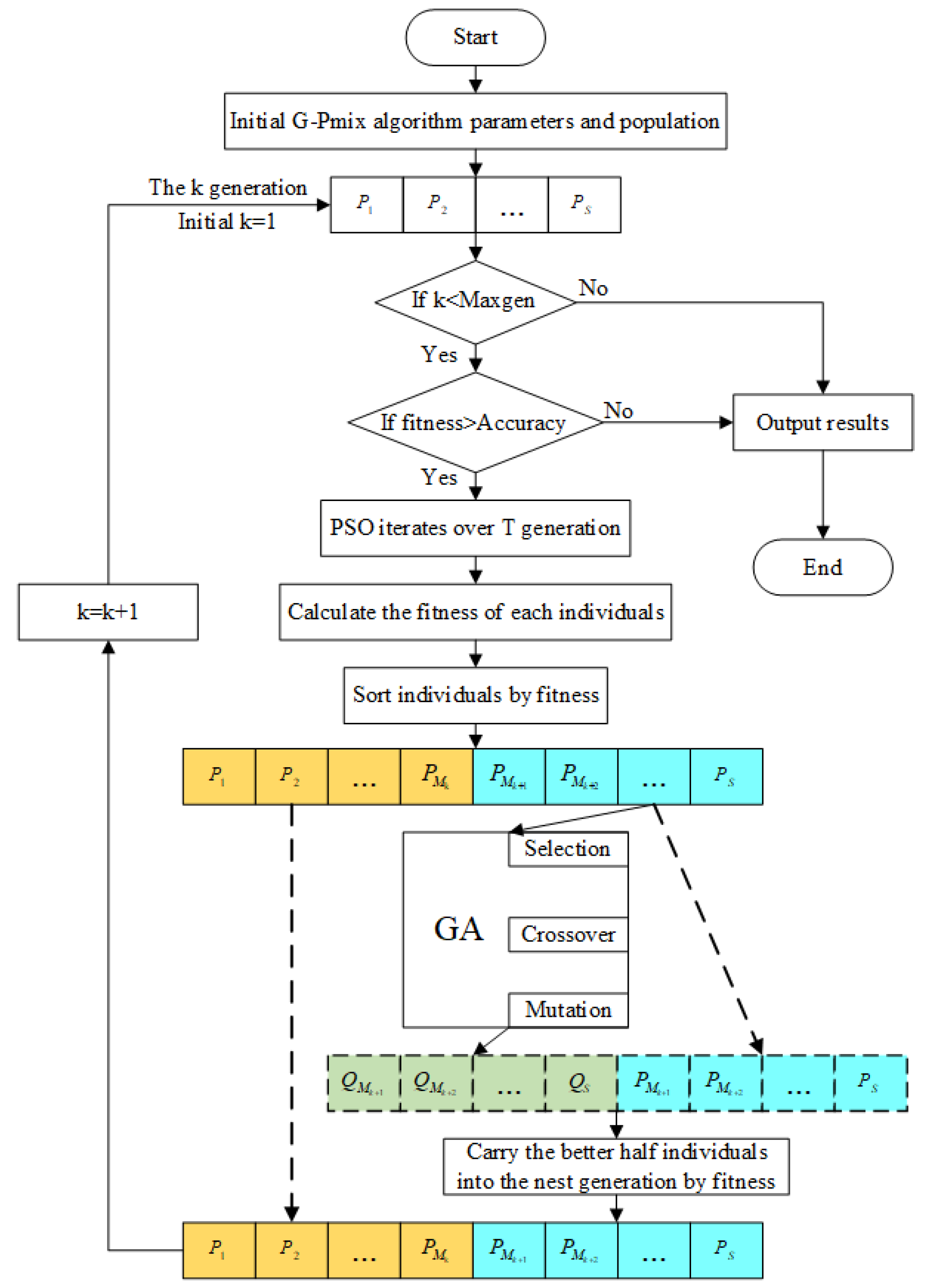
3. Particle Swarm Genetic Hybrid Parameter Identification Method
3.1. Parameter Identification of Static Nonlinear Section
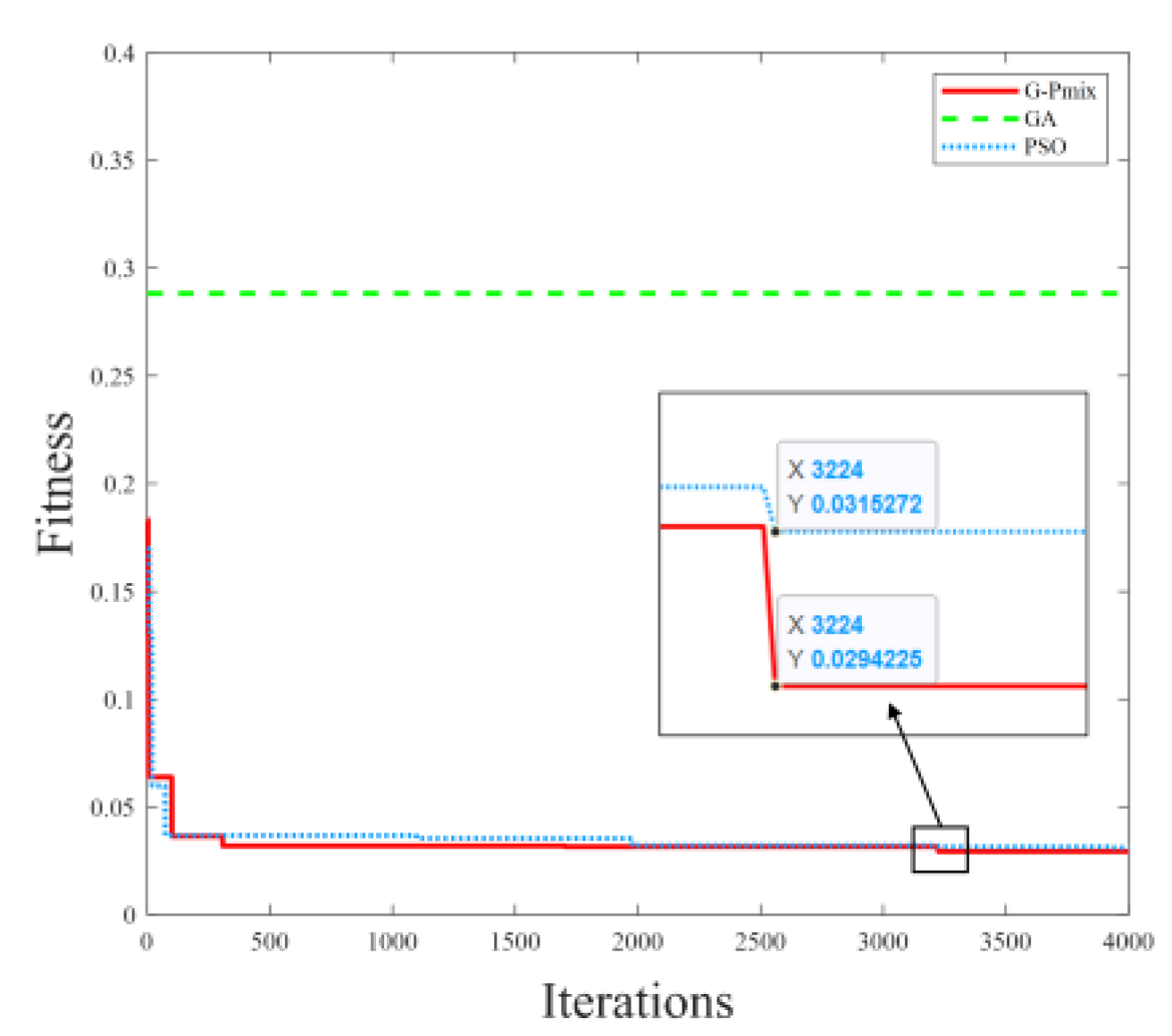
3.2. Parameter Identification of Dynamic Linear Section
4. Modeling Based on G-Pmix Algorithm
4.1. Experiment Equipment
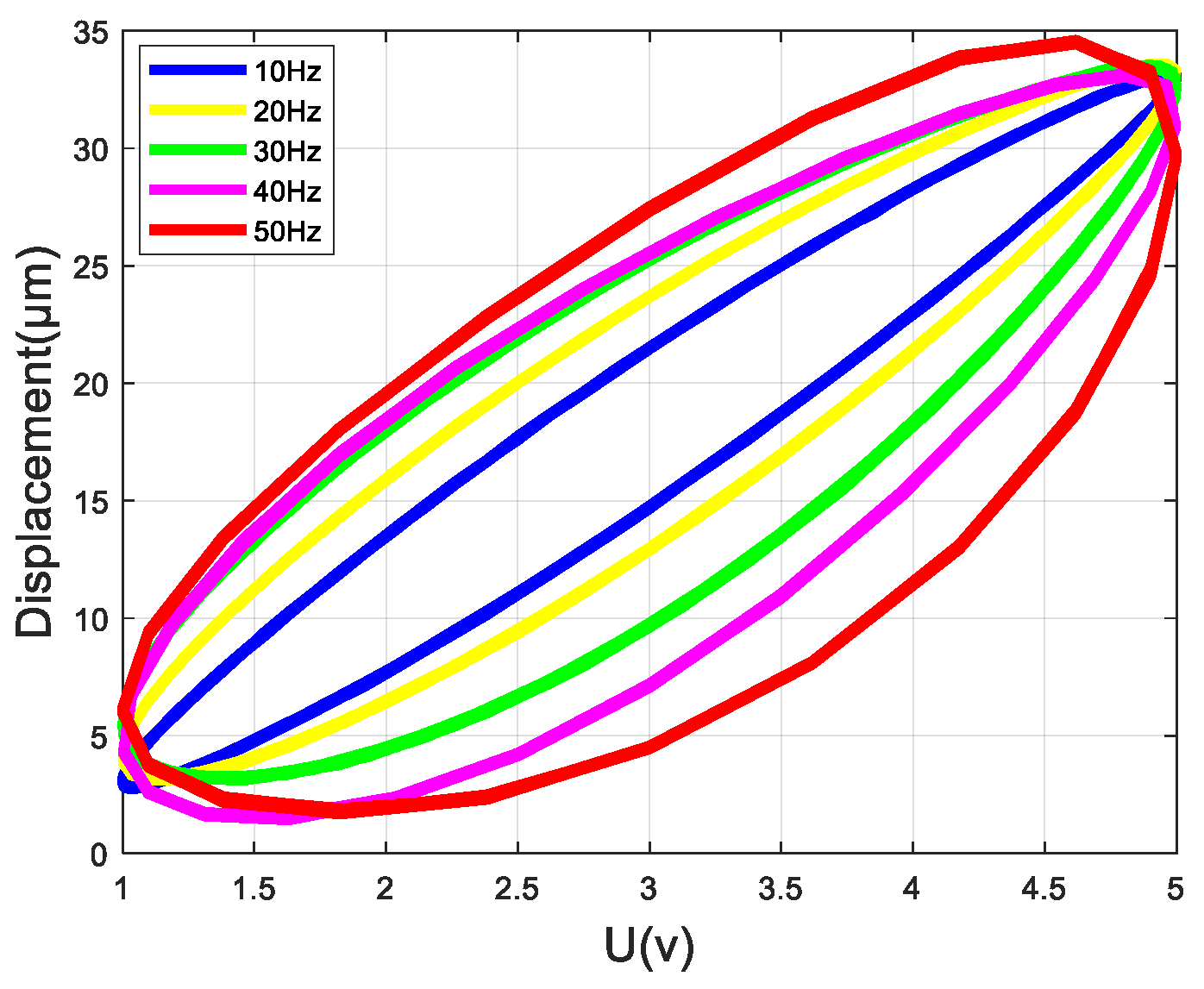
4.2. Experiments of Static Nonlinear Section
4.3. Experiments of Dynamic Linear Section
5. Model Verification
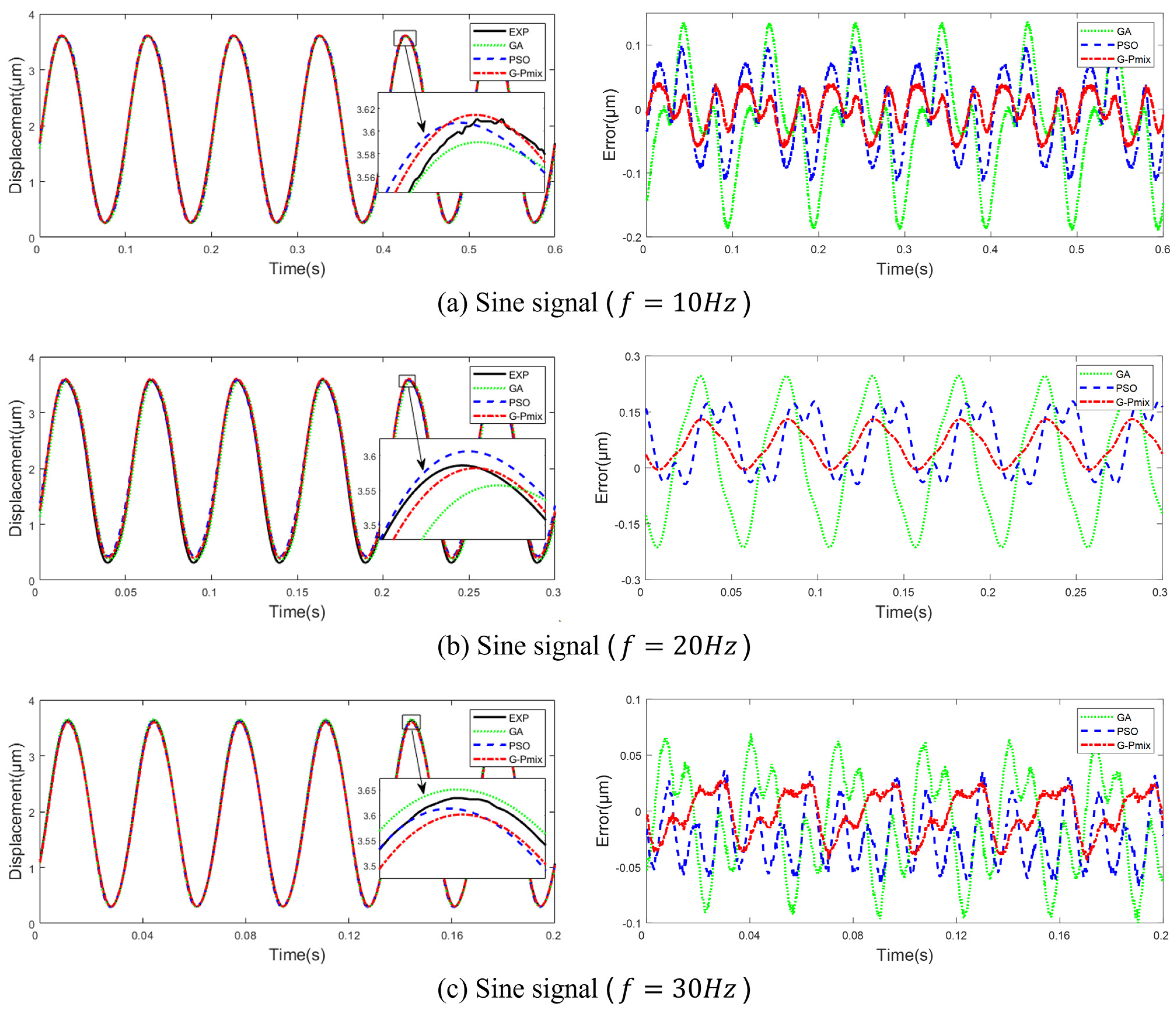
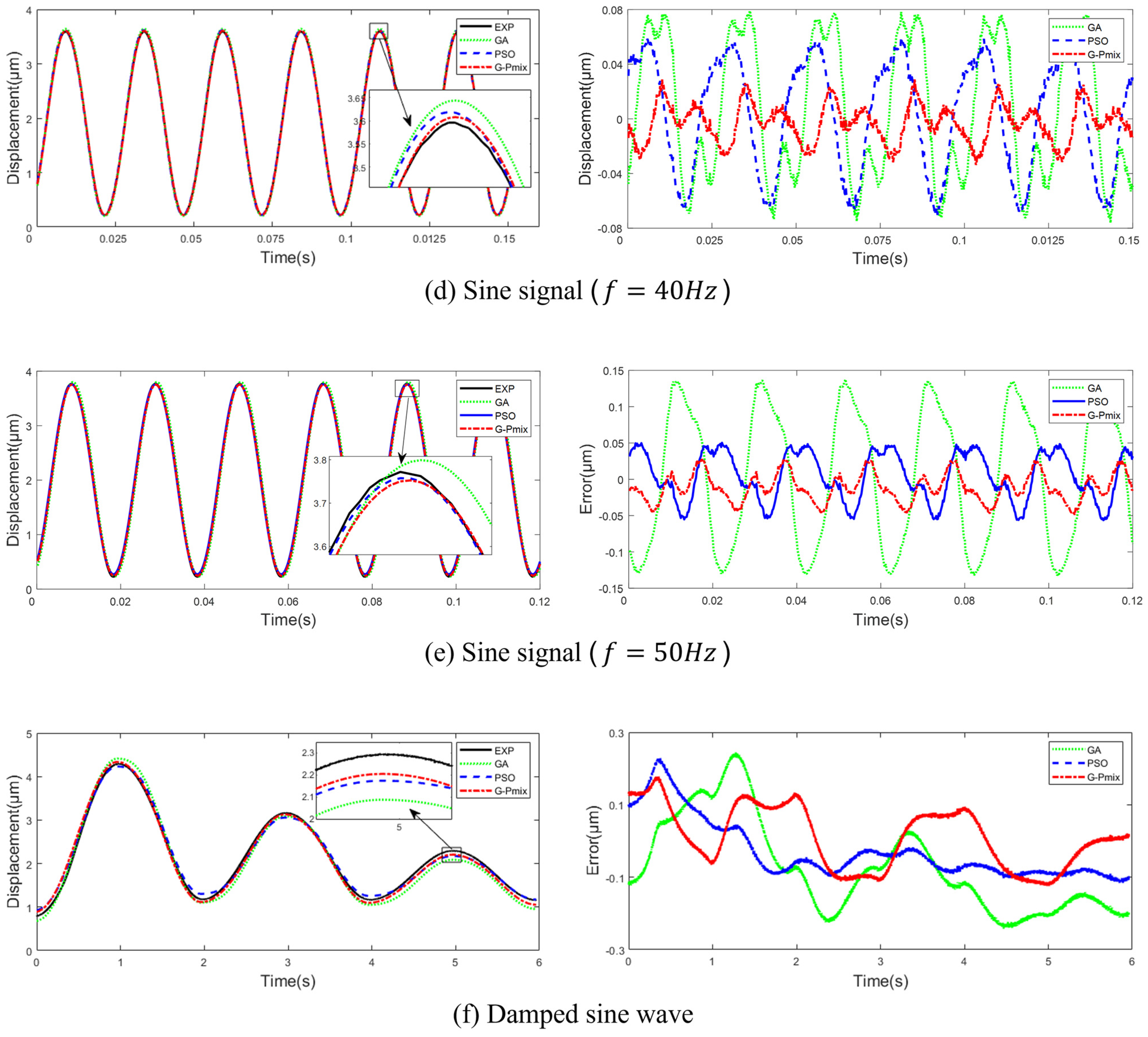
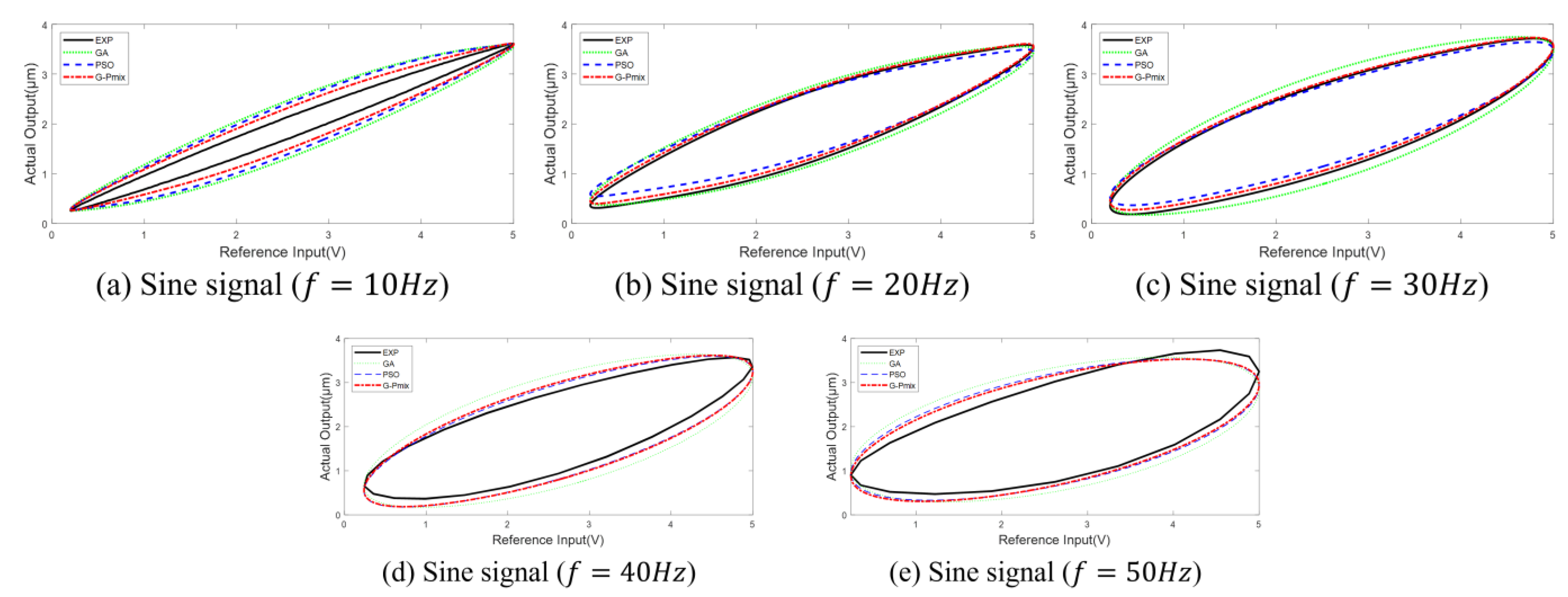
5.1. Model Fitting Experiment
5.2. Feed-Forward and Feedback Control Experiment
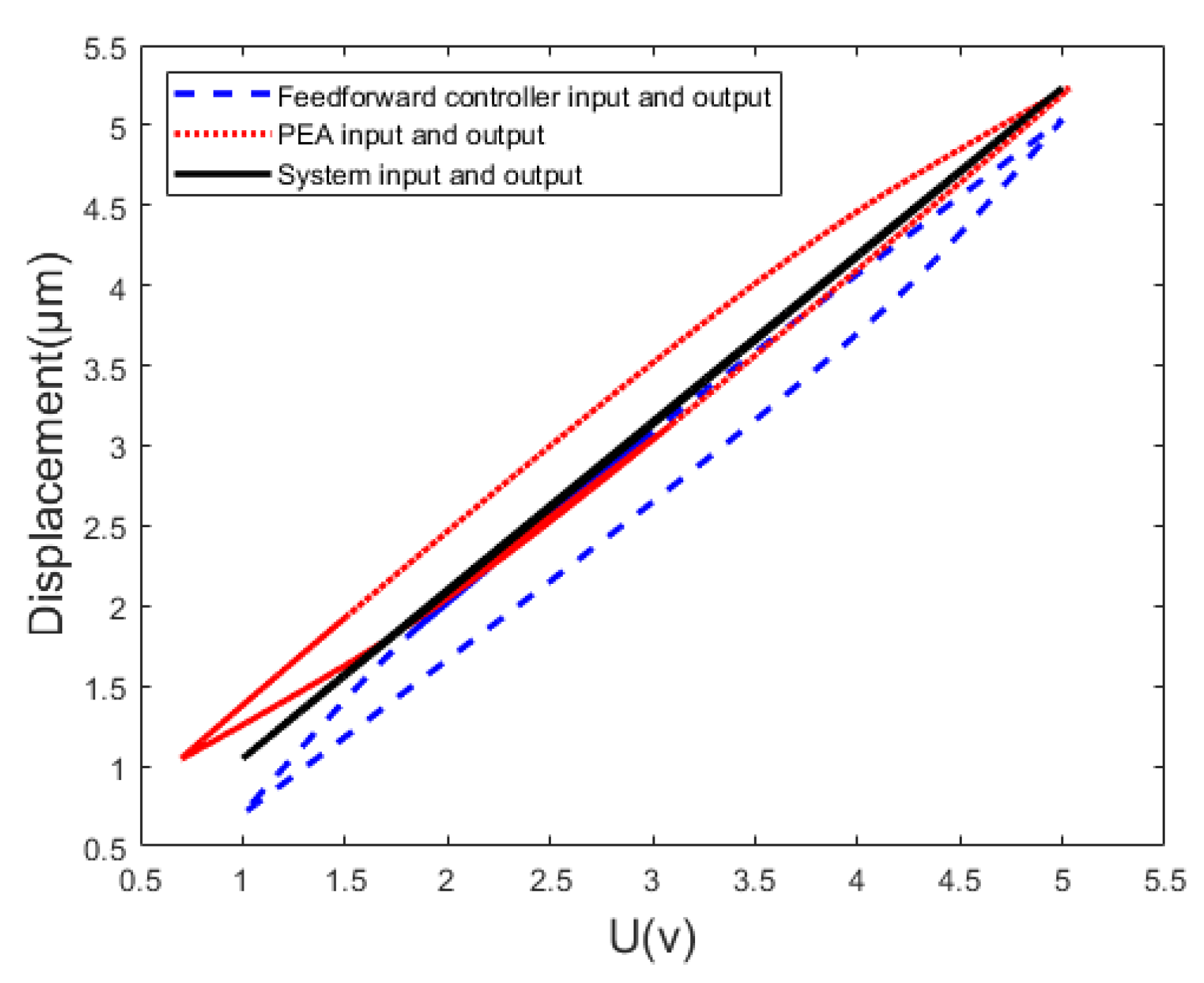
5.2.1. Feed-Forward Control
5.2.2. Feedback Control
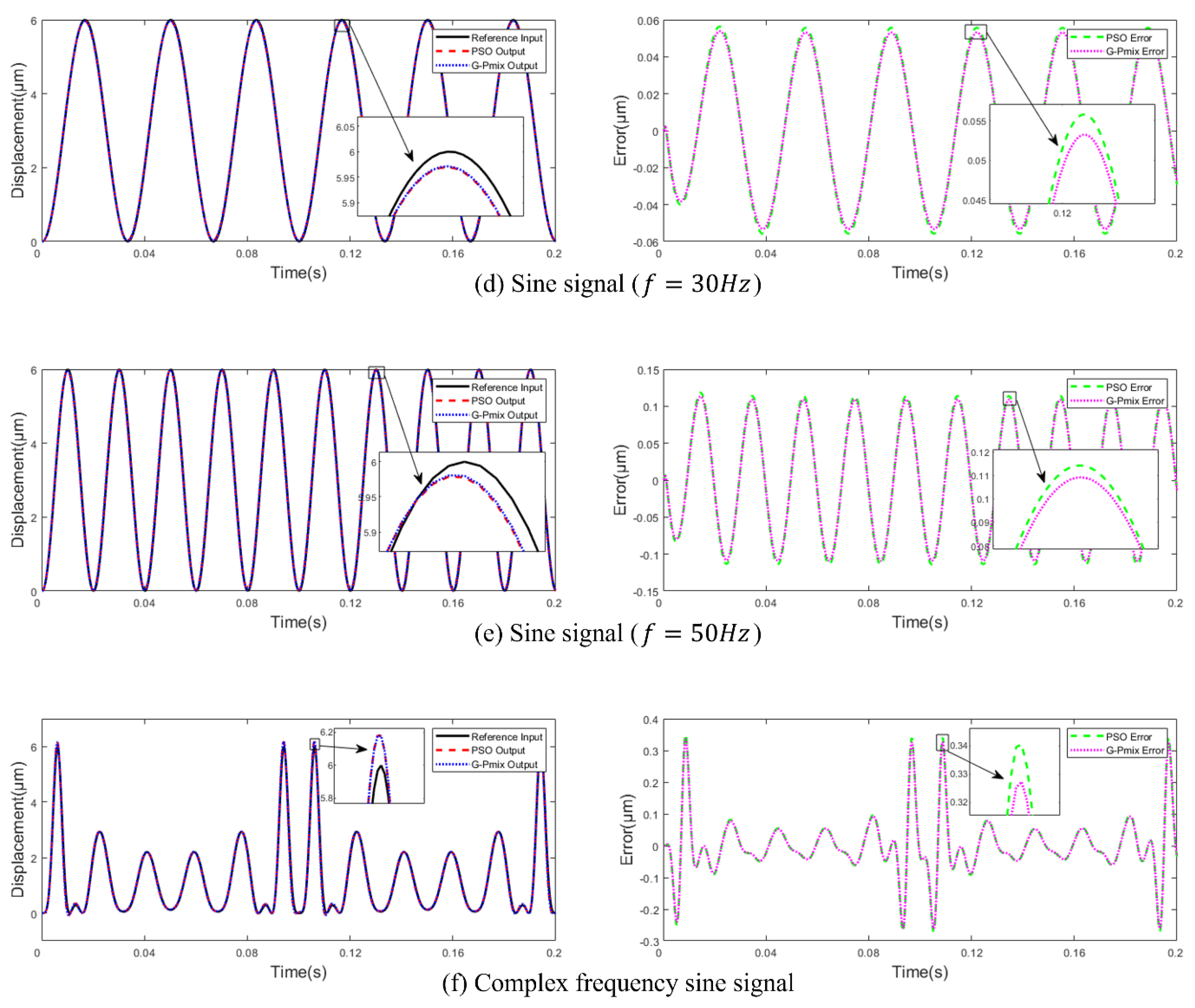
5.2.3. Signal Tracking Experiment
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, J.-L.; Zhao, X.-L.; Ma, L. Adaptive control for hysteretic system with unknown control direction. In Proceedings of the 11th World Congress on Intelligent Control and Automation, Shenyang, China, 29 June–4 July 2014. [Google Scholar]
- El Harti, K.; Rahmoune, M.; Sanbi, M.; Saadani, R.; Bentaleb, M.; Rahmoune, M. Finite Element Model of Vibration Control for an Exponential Functionally Graded Timoshenko Beam with Distributed Piezoelectric Sensor/Actuator. Actuators 2019, 8, 19. [Google Scholar] [CrossRef]
- Wang, G.; Zhou, K.; Zhou, H. Integrated Design and Performance Test for Strain Type Piezoelectric Optical Deflector. Laser Optoelectron. Prog. 2017, 54, 82301. [Google Scholar] [CrossRef]
- Cao, Q.; Tan, Y. Online Optimization Method for Nonlinear Model-Predictive Control in Angular Tracking for MEMS Micromirror. Micromachines 2022, 13, 1867. [Google Scholar] [CrossRef] [PubMed]
- Yu, Z.; Jiang, X.; Cao, K.; Li, S. Hysteresis Characteristics of Steering Mirror Driven by Piezoelectric Actuator and Its Experimental Research. Acta Opt. Sin. 2018, 38, 0814002. [Google Scholar]
- Wang, S.; Wu, X.; Zhu, W.; Li, M. Fluorescence Detection of Polycyclic Aromatic Hydrocarbons by Parallel Factor Combined with Support Vector Machine. Acta Opt. Sin. 2019, 39, 397–405. [Google Scholar]
- Zhao, J.; Mu, G.; Dong, H.; Sun, T.; Grattan, K.T.V. Study of the Velocity and Direction of Piezoelectric Robot Driven by Traveling Waves. IEEE Trans. Ind. Electron. 2022, 70, 9260–9269. [Google Scholar] [CrossRef]
- Mu, G.; Zhao, J.; Dong, H.; Wu, J.; Grattan, K.T.V.; Sun, T. Structural parameter study of dual transducers-type ultrasonic levitation-based transportation system. Smart Mater. Struct. 2021, 30, 045009. [Google Scholar] [CrossRef]
- Wu, J.; Niu, J.; Liu, Y.; Rong, X.; Song, R.; Dong, H.; Zhao, J.; Li, Y. Development of a Self-Moving Ultrasonic Actuator with High Carrying/Towing Capability Driven by Longitudinal Traveling Wave. IEEE-ASME Trans. 2022, 28, 267–279. [Google Scholar] [CrossRef]
- Deng, J.; Liu, Y.; Li, J.; Zhang, S.; Li, K. Displacement Linearity Improving Method of Stepping Piezoelectric Platform Based on Leg Wagging Mechanism. IEEE Trans. 2022, 69, 6429–6432. [Google Scholar] [CrossRef]
- Zhang, L.-J.; Yang, L.-X.; Guo, L.-D.; Sun, L.-N. Adaptive Output Feedback Control for Piezoactuator-driven Stage. Acta Autom. Sin. 2012, 38, 1550. [Google Scholar] [CrossRef]
- Xue, G.; Bai, H.; Li, T. Numerical Solving Method for Jiles-Atherton Model and Influence Analysis of the Initial Magnetic Field on Hysteresis. Mathematics 2022, 10, 4431. [Google Scholar] [CrossRef]
- Wang, S.-X. Study on Multi-requirement Points Vehicle Scheduling Model and Its Swarm Mix Algorithm. Acta Autom. Sin. 2008, 34, 102–104. [Google Scholar] [CrossRef]
- Wang, W.; Wang, R.; Chen, Z. A new hysteresis modeling and optimization for piezoelectric actuators based on asymmetric Prandtl-Ishlinskii model. Sens. Actuators A Phys. 2020, 12, 112431. [Google Scholar] [CrossRef]
- Ang, W.T.; Khosla, P.K.; Riviere, C.N. Riviere. Feedforward controller with inverse rate-dependent model for piezoelectric actuators in trajectorytracking applications. IEEE/ASME Trans. Mechatron. 2007, 12, 134–142. [Google Scholar] [CrossRef]
- Delibas, B.; Arockiarajan, A.; Seemann, W. A nonlinear model of piezoelectric polcrystalline ceramics under quasi-static electromechanical loading. J. Mater. Sci. Mater. Electron 2005, 16, 507–515. [Google Scholar] [CrossRef]
- Wong, P.K.; Xu, Q.; Vong, C.M.; Wong, H.C. Rate-dependent hysteresis modeling and control of a piezostage using online support vector machine and relevance vector machine. IEEE Trans. Ind. Electron. 2011, 59, 1988–2001. [Google Scholar] [CrossRef]
- Xie, Y.; Fu, J.-l.; Chen, B.-y. Solutions of Symmetries for Piezoelectric Stack Actuators. Appl. Math. Mech. 2016, 37, 778–790. [Google Scholar]
- Yang, L.; Zhao, Z.; Zang, Y.; Li, D. Rate-Dependent Modeling of Piezoelectric Actuators for Nano Manipulation Based on Fractional Hammerstein Model. Micromachines 2022, 13, 42. [Google Scholar] [CrossRef]
- Tao, Y.-D.; Li, H.-X.; Zhu, L.-M. Rate-dependent hysteresis modeling and compensation of piezoelectric actuators using Gaussian process. Sens. Actuators A Phys. 2019, 8, 295. [Google Scholar] [CrossRef]
- Yang, Z.; Li, W.; Peng, T.; Cui, Y.; Ma, J. Performance of Closed-Loop Correction with Hysteresis Compensation for Unimorph Deformable Mirror. Acta Opt. Sin. 2019, 39, 0522001. [Google Scholar] [CrossRef]
- Sabarianand, D.V.; Karthikeyan, P.; Muthuramalingam, T. A review on control strategies for compensation of hysteresis and creep on piezoelectric actuators based micro systems. Mech. Syst. Signal Process. 2020, 7, 106634. [Google Scholar] [CrossRef]
- Gan, J.; Zhang, X.-m. A review of nonlinear hysteresis modeling and control of piezoelectric actuators. AIP Adv. 2019, 9, 040702. [Google Scholar] [CrossRef]
- Gan, J.; Zhang, X. Nonlinear Hysteresis Modeling of Piezoelectric Actuators Using a Generalized Bouc-Wen Model. Micromachines 2019, 10, 183. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Li, S.; Wang, X. Source Optimization Using Particle Swarm Optimization Algorithm in Optical Lithography. Acta Opt. Sin. 2015, 35, 0422002. [Google Scholar] [CrossRef]
- Xia, C.; Zhang, Y.; Gong, D.; Sun, X. Quantum particle swarm algorithm for Many-objective optimization problem. In Proceedings of the 11th World Congress on Intelligent Control and Automation, Shenyang, China, 29 June–4 July 2014. [Google Scholar]
- Zhang, D.; Liu, W.; Wang, A.; Jin, H. Parameter Optimization for SVR Based on Genetic Algorithm and Simplex Method. In Proceedings of the 2010 Chinese Conference on Pattern Recognition (CCPR), Chongqing, China, 21–23 October 2010. [Google Scholar]
- Shi, G.; Wu, F.; Zhang, L.; Zhang, S.; Guo, C. An Airborne Multi-Sensor Task Allocation Method Based on Improved Particle Swarm Optimization Algorithm. Xibei Gongye Daxue Xuebao/J. Northwestern Polytech. Univ. 2018, 36, 722–727. [Google Scholar] [CrossRef]
- Yang, J.; Liu, Y. Design of Radar Orthogonal Waveform Based on Hybrid Genetic Chicken Swarm Optimization Algorithm. Laser Optoelectron. Prog. 2018, 55, 80702. [Google Scholar] [CrossRef]
- Qin, Y.; Zhang, Y.; Duan, H.; Han, J. High-Bandwidth Hysteresis Compensation of Piezoelectric Actuators via Multilayer Feedforward Neural Network Based Inverse Hysteresis Modeling. Micromachines 2021, 12, 1325. [Google Scholar] [CrossRef]
- Feng, Y. Hysteretic Nolinearity Modeling and Control of Micro-Positioning Stage Driven by Piezoelectric Actuators. Master’s Thesis, Jilin University, Changchun, China, 2019. [Google Scholar]
- Yu, X.; Gu, H.; Yu, X. Flexible job-shop scheduling study based on multi-swarm hybrid particle swarm arithmetic. In Proceedings of the 2010 International Conference on Future Information Technology and Management Engineering, Changzhou, China, 9–10 October 2010. [Google Scholar]
- Guo, W.-Z.; Chen, G.-L.; Xiong, N.; Peng, S.-J. Hybrid Particle Swarm Optimization Algorithm for VLSI Circuit Partitioning. J. Softw. 2011, 22, 833–842. [Google Scholar] [CrossRef]
- Wang, P.; Zhang, J.; Cui, G. Research on particle filtering based on genetic algorithm. In Proceedings of the 8th World Congress on Intelligent Control and Automation, Jinan, China, 7–9 July 2010. [Google Scholar]
- Song, J.; Zhang, A.; Yang, L. Trajectory tracking control of micro positioning platform based on dynamic sliding mode. J. Shanghai Univ. Eng. Sci. 2022, 36, 261–266. [Google Scholar]




| Parameter | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Value | 4000 | 50 | 4 | 1 | 1 | 4 | 0.4 | 0.9 | 0.2 | 0.2 |
| Parameter | G-Pmix | PSO | GA |
|---|---|---|---|
| 0.304225 | 0.262017 | 0.132514 | |
| 0.675313 | 0.675520 | 0.409838 | |
| 0.497724 | 0.368105 | 1.048550 | |
| 1.045814 | 1.048355 | 0.947412 | |
| Minimum fitness | 0.029423 | 0.031505 | 0.288188 |
| Parameter | G-Pmix | GA | PSO |
|---|---|---|---|
| 267,700 | 327,100 | 228,900 | |
| 510.1069 | 683.914 | 386.7 | |
| 255,700 | 284,790 | 225,200 |
| Signal | G-Pmix | PSO | GA |
|---|---|---|---|
| 10 | 0.0617/0.0284 | 0.1134/0.0601 | 0.1910/0.0865 |
| 20 | 0.1306/0.0775 | 0.1781/0.1047 | 0.2463/0.1531 |
| 30 | 0.0434/0.0192 | 0.0688/0.0345 | 0.1000/0.0457 |
| 40 | 0.0336/0.0141 | 0.0706/0.0413 | 0.0791/0.0515 |
| 50 | 0.1547/0.0232 | 0.0684/0.0399 | 0.1547/0.1056 |
| Damped sine wave | 0.1784/0.1501 | 0.2301/0.1868 | 0.2451/0.2553 |
| Mean of / | 0.0823/0.0519 | 0.1216/0.0779 | 0.1694/0.1163 |
| Parameters | ||||
|---|---|---|---|---|
| Value | 0.304225 | 0.675313 | 0.497724 | 1.045814 |
| Signal | G-Pmix | G-Pmix | PSO | PSO |
|---|---|---|---|---|
| Ramp | 2.4739 × 10−4 | 0.0011 | 2.5372 × 10−4 | 0.0011 |
| Damped sine wave | 1.2311 × 10−5 | 9.8599 × 10−4 | 1.3309 × 10−5 | 0.0010 |
| 0.0078 | 0.0053 | 0.0081 | 0.0055 | |
| 0.0539 | 0.0368 | 0.0564 | 0.0385 | |
| 0.1134 | 0.0763 | 0.1187 | 0.0798 | |
| Complex frequency | 0.3375 | 0.0910 | 0.3512 | 0.0948 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, D.; Dong, J.; Guo, S.; Tan, L.; Yu, S. Parameter Identification of Model for Piezoelectric Actuators. Micromachines 2023, 14, 1050. https://doi.org/10.3390/mi14051050
Liu D, Dong J, Guo S, Tan L, Yu S. Parameter Identification of Model for Piezoelectric Actuators. Micromachines. 2023; 14(5):1050. https://doi.org/10.3390/mi14051050
Chicago/Turabian StyleLiu, Dongmei, Jingqu Dong, Shuai Guo, Li Tan, and Shuyou Yu. 2023. "Parameter Identification of Model for Piezoelectric Actuators" Micromachines 14, no. 5: 1050. https://doi.org/10.3390/mi14051050
APA StyleLiu, D., Dong, J., Guo, S., Tan, L., & Yu, S. (2023). Parameter Identification of Model for Piezoelectric Actuators. Micromachines, 14(5), 1050. https://doi.org/10.3390/mi14051050





