Full Solutions to Flow and Heat Transfer from Slip-Induced Microtube Shapes
Abstract
1. Introduction
2. Equations of Momentum and Energy
3. Full and Perturbation Solutions
3.1. Full Velocity Solution and Pipe Surface Formation
3.2. Perturbative Temperature Solution
4. Results and Discussions
5. Conclusions
- For small aspect ratios, the slip increases the volumetric flow rate continuously and it decreases the skin friction factor, leading to a reduction in the Poiseuille number.
- For large aspect ratios, the Poiseuille number increases with slip.
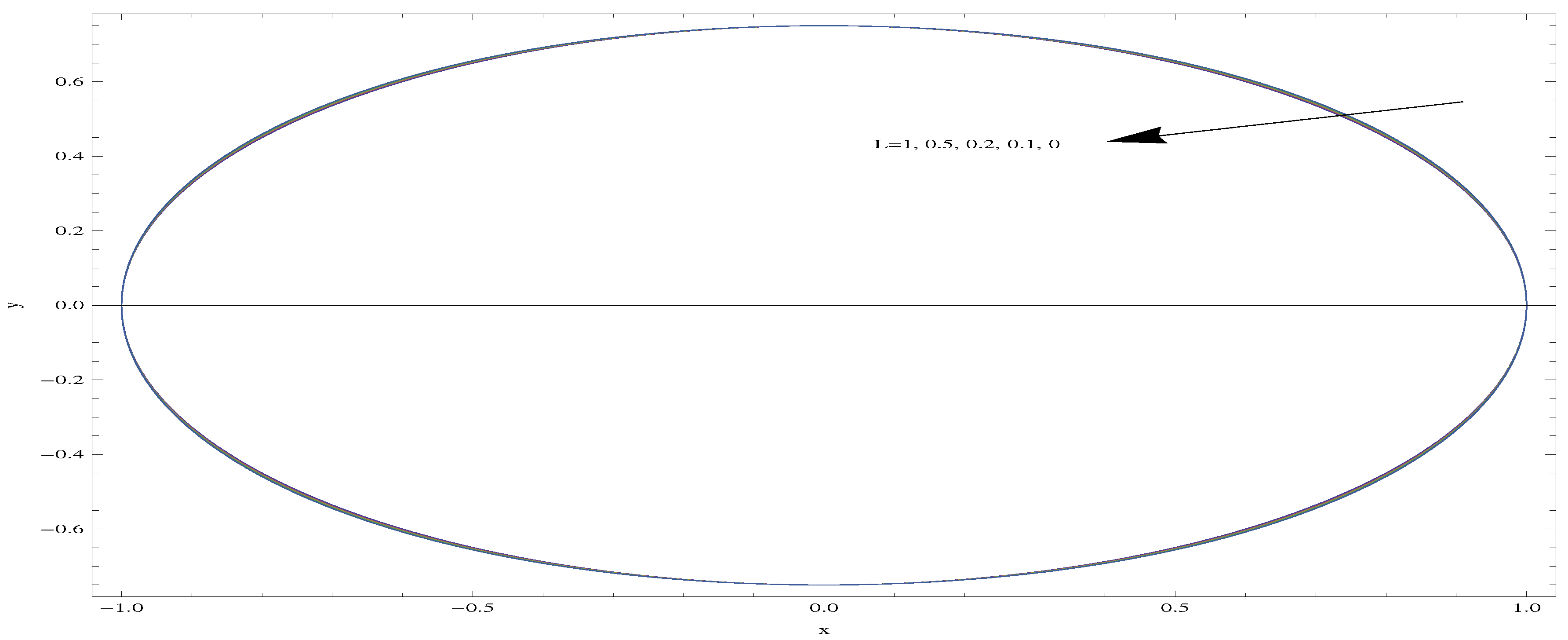
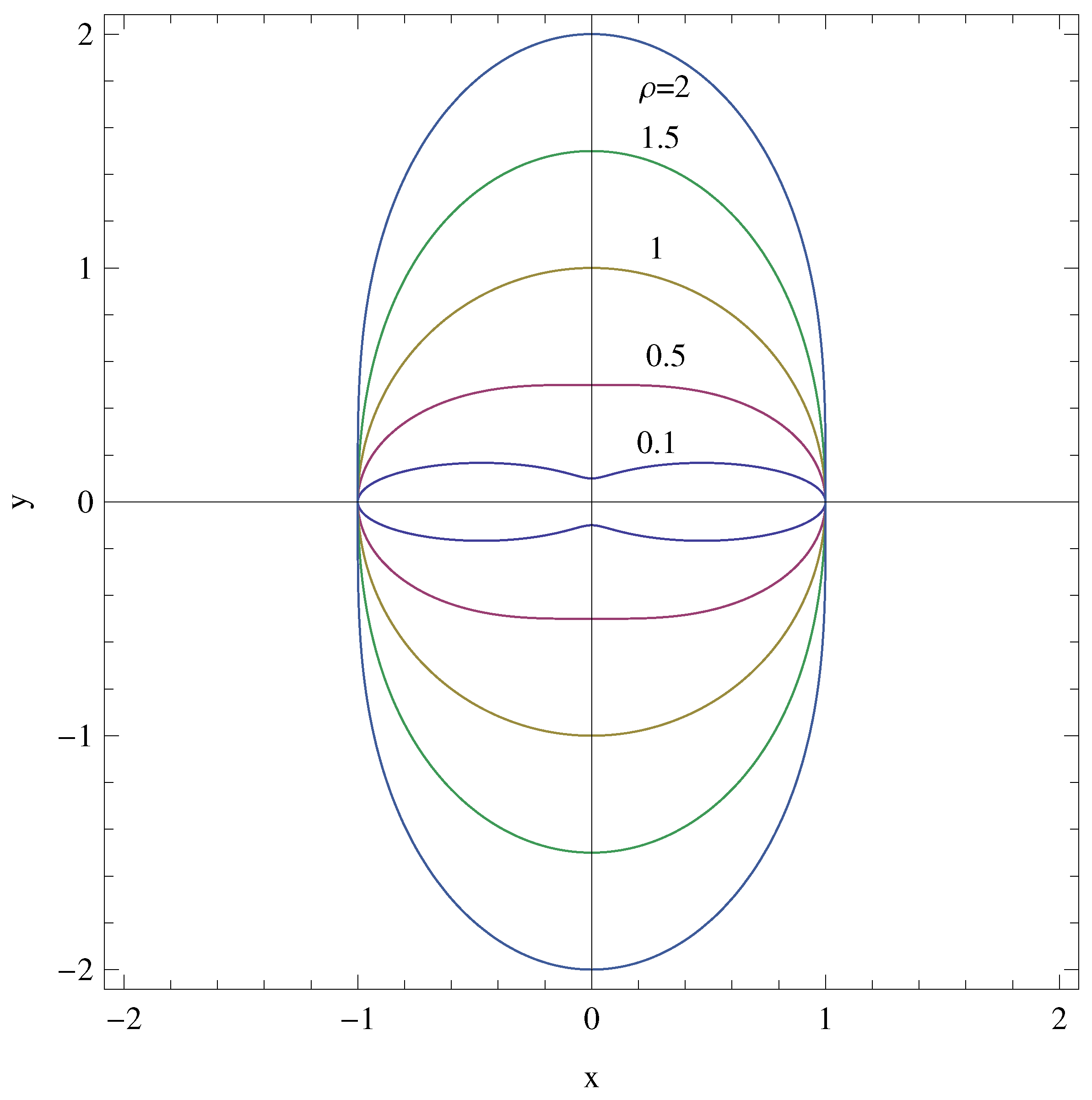
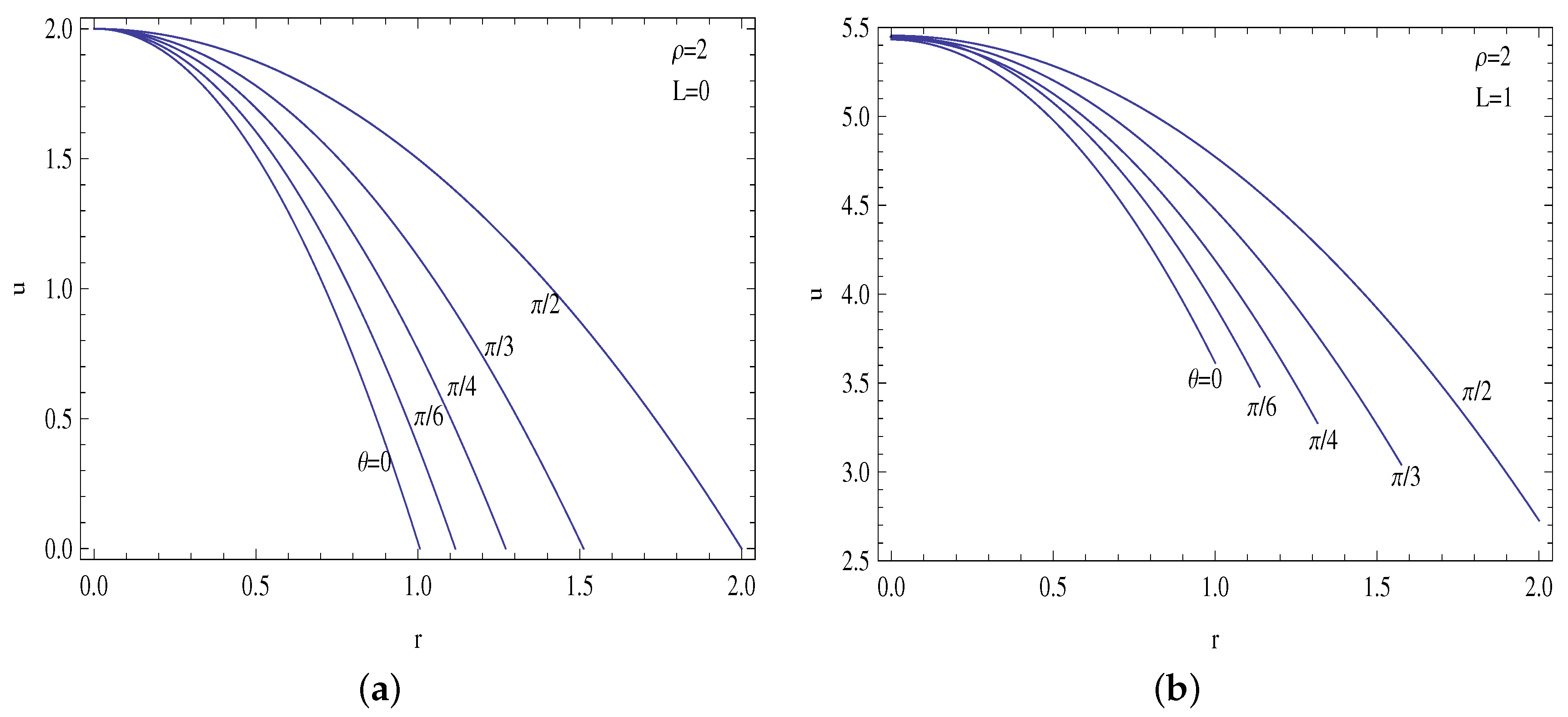
- For aspect ratios less than unity, the slip velocity becomes larger on the minor axis, with a maximum on the major axis for larger aspect ratios.
- The total shear stress helps the surface to achieve a lower drag force under the influence of the slip mechanism.
- In the presence of a stronger slip, the maximum/minimum shear is off the minor axis.
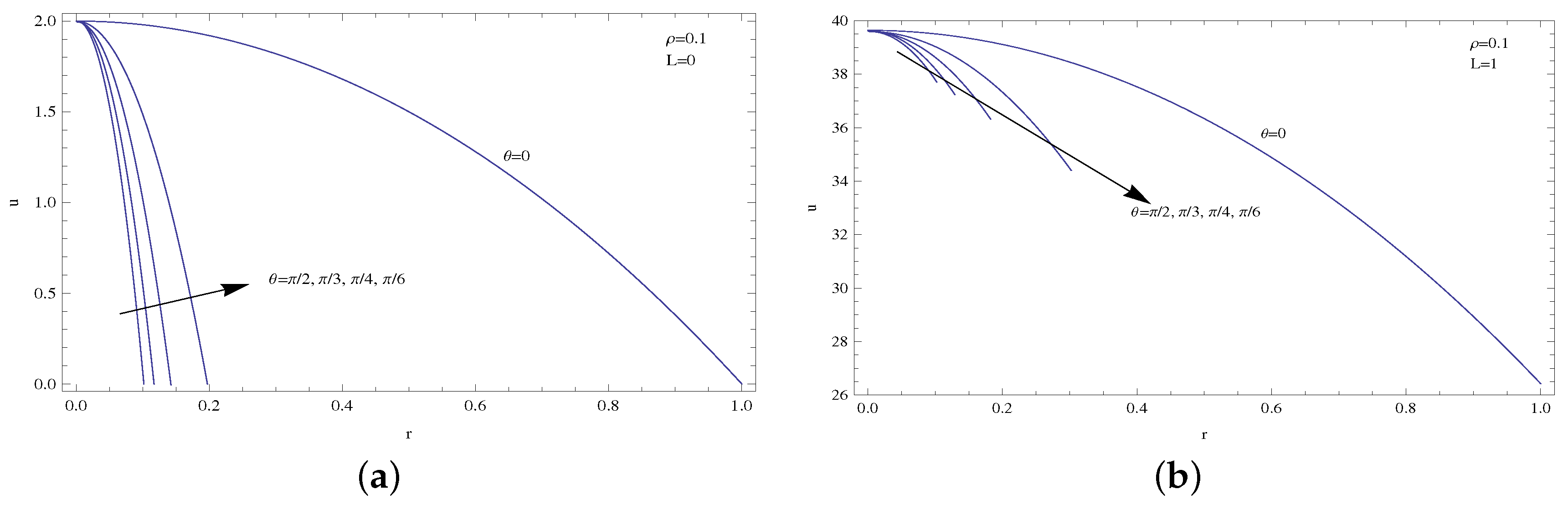
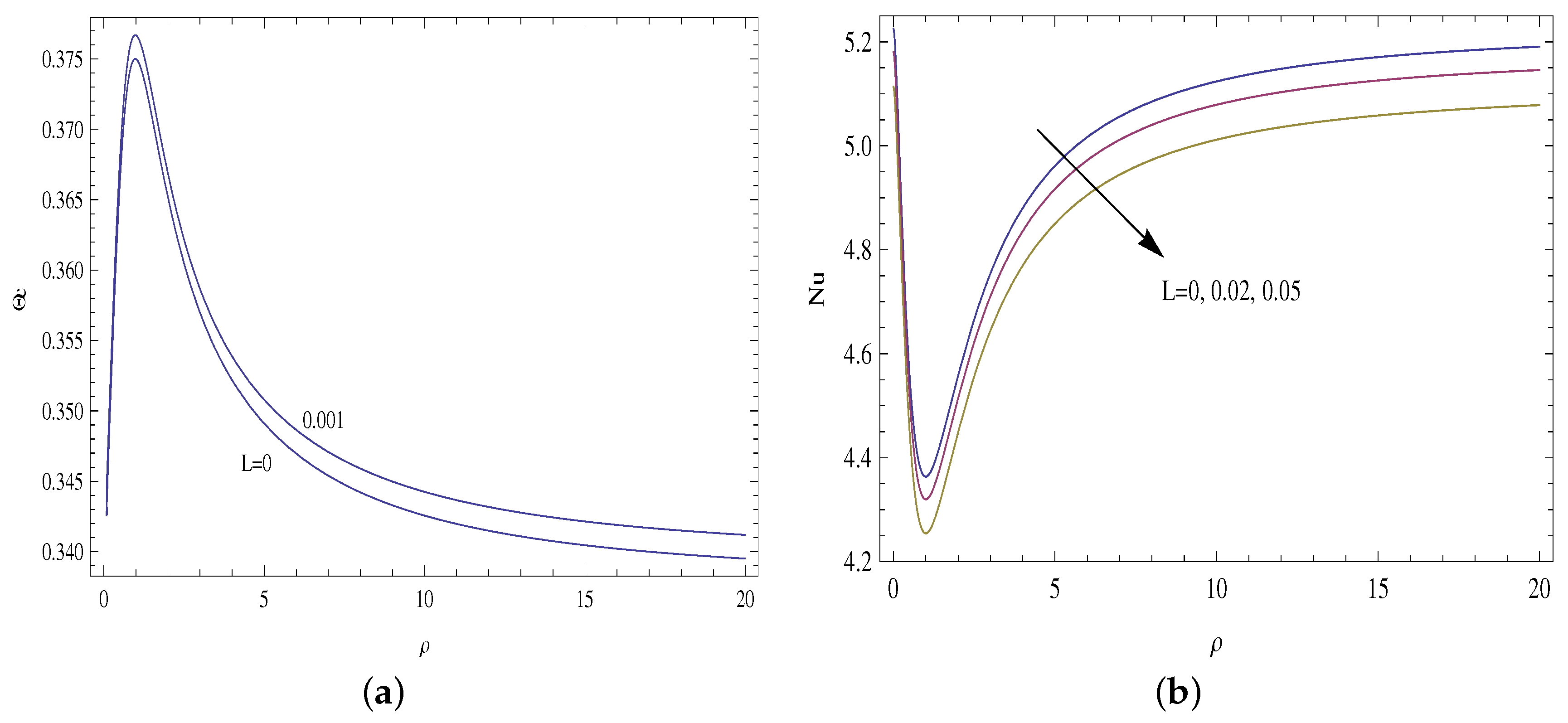
- The centerline temperature is reduced by the presence of slip, which results in lower heat transfer rates compared to no slip profiles.
Author Contributions
Funding
Conflicts of Interest
References
- Timoshenko, S.P.; Gere, J.M. Theory of Elastic Stability; McGraw-Hill: New York, NY, USA, 1961. [Google Scholar]
- Harley, J.; Huang, Y.; Bau, H.; Zemel, J.N. Gas flows in microchannels. J. Fluid Mech. 1995, 284, 257–274. [Google Scholar] [CrossRef]
- Karniadakis, G.E.; Beskok, A.; Aluru, N. Microflows and Nanoflows: Fundamentals and Simulation; Springer: New York, NY, USA, 2005. [Google Scholar]
- Lienhard, J.H. A Heat Transfer Textbook, 3rd ed.; Phlogiston Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Kakac, S.; Yener, Y.; Pramuanjaroenkij, A. Convective Heat Transfer, 3rd ed.; CRC Press, Taylor & Francis: Abingdon, UK, 2014. [Google Scholar]
- Higgins, T.J. A comprehensive review of Saint-Venant’s torsion problem. Am. J. Phys. 1942, 10, 248–259. [Google Scholar] [CrossRef]
- Shah, R.K.; London, A.L. Laminar Flow Forced Convection in Ducts: A Source Book for Compact Heat Exchanger Analytical Data; Academic Press: Cambridge, MA, USA, 1978. [Google Scholar]
- Zhang, H.; Ebadian, M.; Campo, A. An analytical/numerical solution of convective heat transfer in the thermal entrance region of irregular ducts. Int. Heat Mass Transf. 1991, 18, 273–291. [Google Scholar] [CrossRef]
- Sakalis, V.; Hatzikonstantinou, P.; Kafousias, N. Thermally developing flow in elliptic ducts with axially variable wall temperature distribution. Int. J. Heat Mass Transfer. 2002, 45, 25–35. [Google Scholar] [CrossRef]
- Tunc, G.; Bayazitoglu, Y. Heat transfer in rectangular microchannels. Int. J. Heat Mass Transfer. 2002, 45, 765–773. [Google Scholar] [CrossRef]
- Duan, Z.; Muzychka, Y.S. Slip flow in elliptic microchannels. Int. J. Therm. Sci. 2007, 46, 1104–1111. [Google Scholar] [CrossRef]
- Lekner, J. Viscous flow through pipes of various cross-sections. Eur. J. Phys. 2007, 28, 521–527. [Google Scholar] [CrossRef]
- Muzychka, Y.S.; Yovanovich, M.M. Pressure drop in laminar developing flow in noncircular ducts: A scaling and modeling approach. J. Fluids Eng. 2009, 131, 111105. [Google Scholar] [CrossRef]
- Akbari, M.; Sinton, D.; Bahrami, M. Viscous flow in variable cross-section microchannels of arbitrary shapes. J. Heat Mass Transf. 2011, 54, 3970–3978. [Google Scholar] [CrossRef]
- Shahmardan, M.M.; Norouzi, M.; Kayhani, M.H.; Delouei, A.A. An exact analytical solution for convective heat transfer in rectangular ducts. J. Zhejiang Univ. Sci. A 2012, 13, 768–781. [Google Scholar] [CrossRef]
- Shahmardan, M.; Sedaghat, M.; Norouzi, M. An analytical solution for fully developed forced convection in triangular ducts. Heat Transf. Res. 2015, 44, 489–498. [Google Scholar] [CrossRef]
- Kozlovsky, P.; Zaretsky, U.; Jaffa, A.J.; Elad, D. General tube law for collapsible thin and thick wall tubes. J. Biomech. 2014, 47, 2378–2384. [Google Scholar] [CrossRef] [PubMed]
- Tahmouresi, F.; Das, S.K. Analytical modeling of gaseous slip flow in parabolic microchannels. ASME J. Fluids Eng. 2014, 136, 071201. [Google Scholar] [CrossRef]
- Weigand, B.; Eisenschmidt, K. The extended Graetz problem with piecewise constant wall temperature for laminar and turbulent flows through a concentric annulus. Int. J. Therm. Sci. 2012, 54, 89–97. [Google Scholar] [CrossRef]
- Ryzhkov, I.I. The extended Graetz problem with specified heat flux for multicomponent fluids with Soret and Dufour effects. Int. J. Heat Mass Transf. 2013, 66, 461–471. [Google Scholar] [CrossRef]
- Cetin, B.; Zeinali, S. Analysis of heat transfer and entropy generation for a low-Peclet-number microtube flow using a second-order slip model: An extended-Graetz problem. J. Eng. Math. 2014, 89, 13–25. [Google Scholar] [CrossRef]
- Barrera, C.; Letelier, M.; Siginer, D.; Stockle, J. The Graetz problem in tubes of arbitrary cross section. Acta Mech. 2016, 227, 3239–3246. [Google Scholar] [CrossRef]
- Letelier, M.F.; Hinojosa, C.B.; Siginer, D.A. Analytical solution of the Graetz problem for non-linear viscoelastic fluids in tubes of arbitrary cross-section. Int. J. Therm. Sci. 2017, 111, 369–378. [Google Scholar] [CrossRef]
- Ali, N.; Khan, M.W.S. The Graetz problem for the Ellis fluid model. Z. Naturforsch. 2019, 74, 15–24. [Google Scholar] [CrossRef]
- Navardi, S.; Bhattacharya, S. Dispersion in channels of arbitrary cross-sections in presence of active surfaces. Chem. Eng. Sci. 2015, 130, 197–206. [Google Scholar] [CrossRef]
- Rana, S.K.; Jena, A. A BEM formulation of two dimensional steady state heat conduction in exchanger tubes of arbitrary cross sections. Int. J. Heat Mass Transf. 2017, 106, 195–211. [Google Scholar] [CrossRef]
- Gay-Balmaz, F.; Georgievskii, D.; Putkaradze, V. Stability of helical tubes conveying fluid. J. Fluids Struct. 2018, 78, 146–174. [Google Scholar] [CrossRef]
- Zhang, Z. Modeling and simulation for cross-sectional ovalization of thin-walled tubes in continuous rotary straightening process. Int. J. Mech. Sci. 2019, 153–154, 83–102. [Google Scholar] [CrossRef]
- Bilston, D.; Ruan, D.; Candido, A.; Durandet, Y. Parametric study of the cross-section shape of aluminium tubes in dynamic three-point bending. Thin-Walled Struct. 2019, 136, 315–322. [Google Scholar] [CrossRef]
- Minko, K.B.; Yankov, G.G.; Artemov, V.I.; Milman, O.O. A mathematical model of forced convection condensation of steam on smooth horizontal tubes and tube bundles in the presence of noncondensables. Int. J. Heat Mass Transfer. 2019, 140, 41–50. [Google Scholar] [CrossRef]
- Qian-bei, Y.; Liu, G.R.; Ju-bao, L.; Liu, G.Z.; Ri-zhi, D. Analyses of fluid-solid coupling dynamics of elastic tubes vibrating in cross flows. Eur. Mech. A Solids 2019, 73, 248–259. [Google Scholar] [CrossRef]
- Mirjavadi, S.S.; Forsat, M.; Badnava, S. Nonlinear modeling and dynamic analysis of bioengineering hyper-elastic tubes based on different material models. Biomech. Model. Mechanobiol. 2020, 19, 971–983. [Google Scholar] [CrossRef]
- Rostamzadeh, A.; Razavi, S.E.; Mirsajedi, S.M. Towards Multidimensional Artificially Characteristic-Based Scheme for Incompressible Thermo-Fluid Problems. Mechanika 2017, 23, 826–834. [Google Scholar] [CrossRef]
- Rahbarshahlan, S.; Esmaeilzadeh, E.; Khosroshahi, A.R.; Bakhshayesh, A.G. Numerical simulation of fluid flow and heat transfer in microchannels with patterns of hydrophobic/hydrophilic walls. Eur. Phys. J. Plus 2020, 135, 157. [Google Scholar] [CrossRef]
- Arciniegas, A.; Amaya, L.E.; Puccini, M. Mathematical model of geometry of the eye. Ann. Ophthalmol. 1985, 17, 502–505. [Google Scholar]
- Aletti, M.C.M. Mathematical Modelling and Simulations of the Hemodynamics in the Eye. Ph.D. Thesis, Universite Pierre et Marie Curie, Paris, France, 2017. [Google Scholar]
- Kays, W.; Crawford, M.; Weigand, B. Convective Heat and Mass Transfer, 4th ed.; Mc Graw-Hill Publishing Co., Ltd.: New York, NY, USA, 2005. [Google Scholar]
- Fernandez, E.D. Analysis of Newtonian Viscous Flows through Tubes of Arbitrary Varying Cross Sections. Ph.D. Thesis, Lehigh University, Bethlehem, PA, USA, 2017. [Google Scholar]
- Turkyilmazoglu, M. Laminar slip wall jet of Glauert type and heat transfer. Int. J. Heat Mass Transf. 2019, 134, 1153–1158. [Google Scholar] [CrossRef]

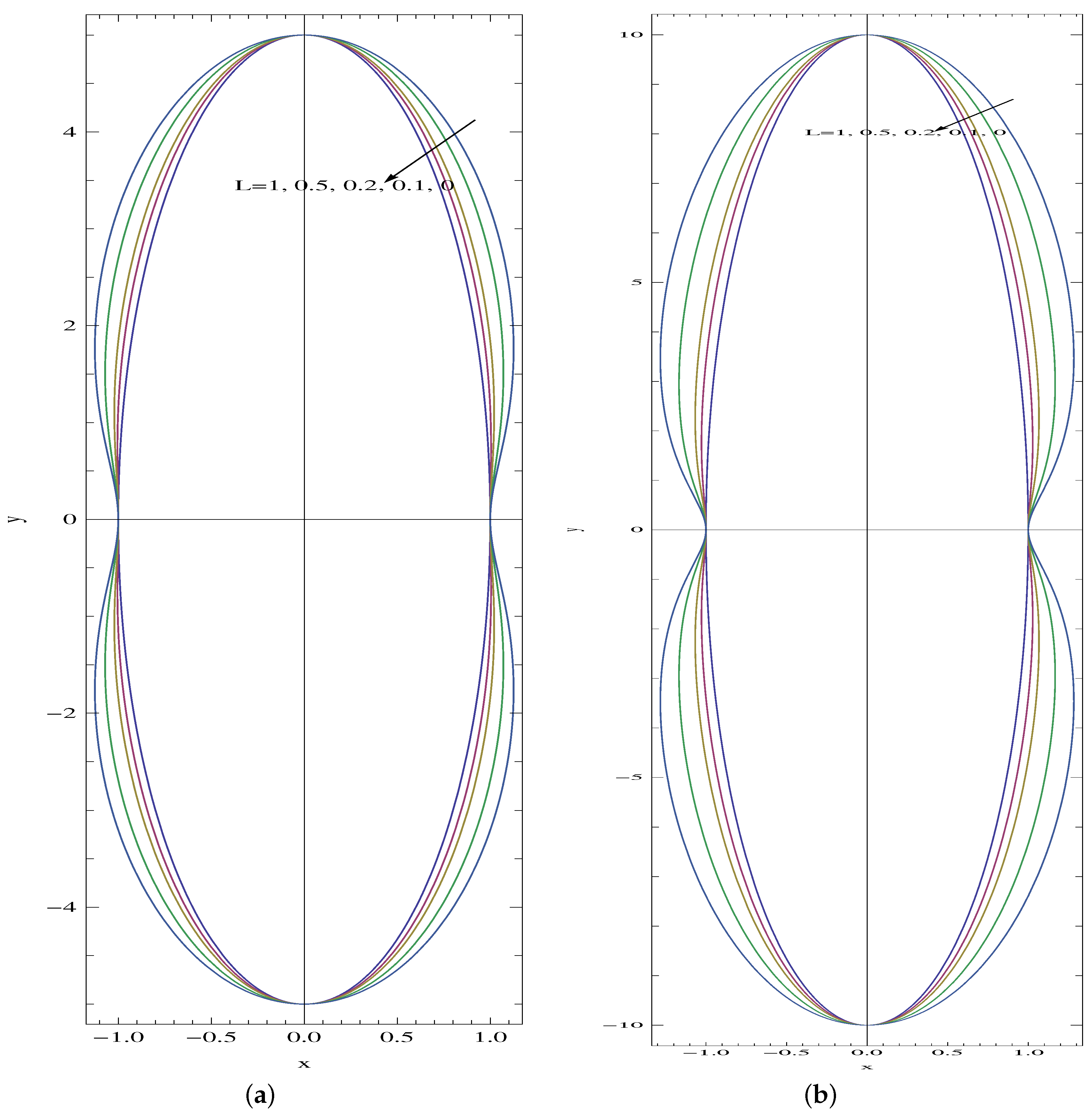


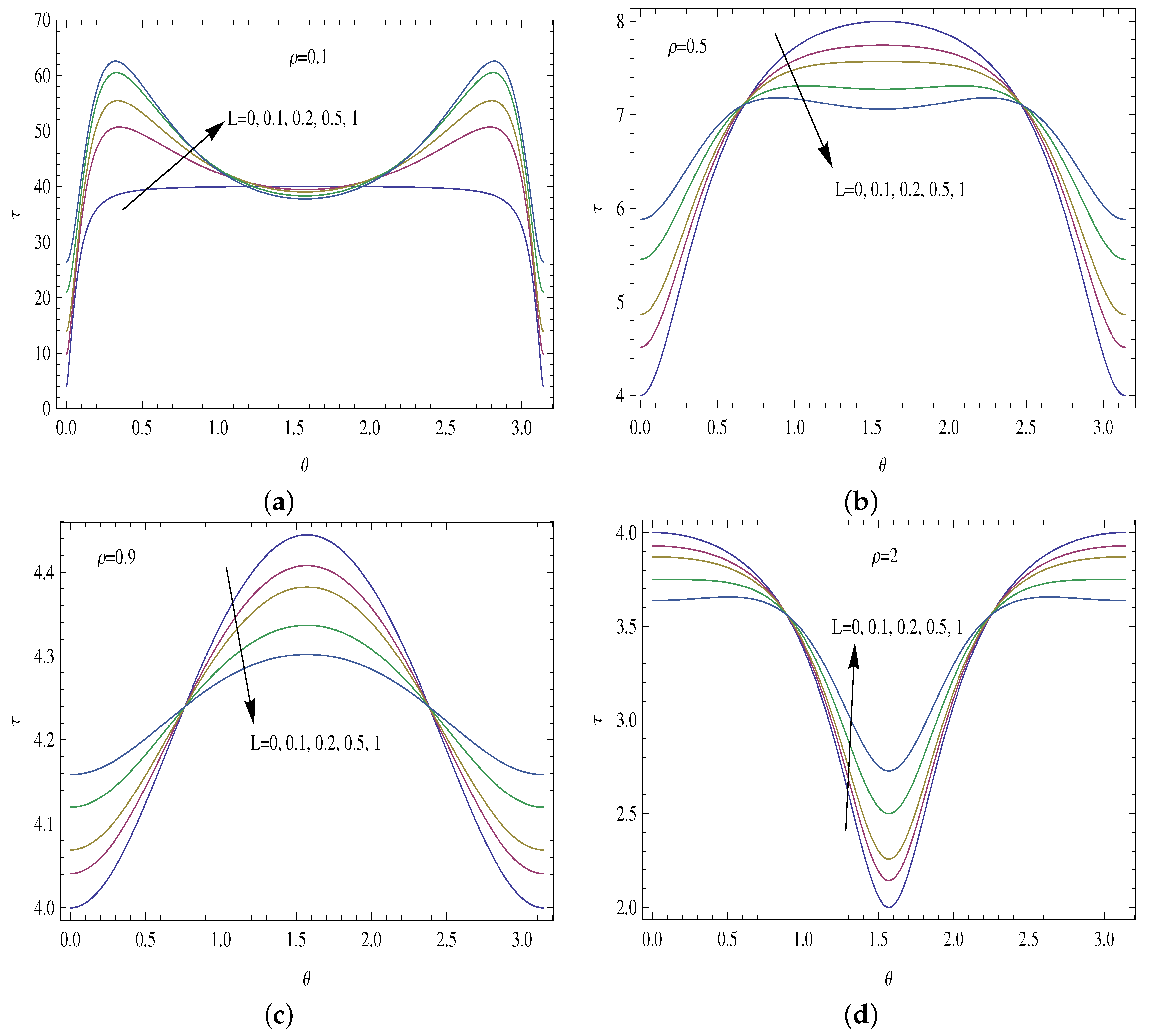
| A | P | Q | ||
|---|---|---|---|---|
| 0.31416 | 4.06397 | 0.00078 | 19.3139 | |
| 0.53260 | 4.23009 | 0.04548 | 1.48516 | |
| 1.57080 | 4.84422 | 0.07854 | 16.8233 | |
| 1.65528 | 4.94139 | 0.62797 | 2.36630 | |
| 3.14159 | 6.28319 | 0.39270 | 16.0000 | |
| 3.14159 | 6.28319 | 1.96350 | 3.20000 | |
| 15.7080 | 21.0100 | 3.77595 | 18.6024 | |
| 18.9085 | 21.5626 | 18.1058 | 6.42452 | |
| 31.4159 | 40.6397 | 7.77622 | 19.3139 | |
| 42.2733 | 41.2846 | 38.9915 | 9.09372 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Turkyilmazoglu, M.; Duraihem, F.Z. Full Solutions to Flow and Heat Transfer from Slip-Induced Microtube Shapes. Micromachines 2023, 14, 894. https://doi.org/10.3390/mi14040894
Turkyilmazoglu M, Duraihem FZ. Full Solutions to Flow and Heat Transfer from Slip-Induced Microtube Shapes. Micromachines. 2023; 14(4):894. https://doi.org/10.3390/mi14040894
Chicago/Turabian StyleTurkyilmazoglu, Mustafa, and Faisal Z. Duraihem. 2023. "Full Solutions to Flow and Heat Transfer from Slip-Induced Microtube Shapes" Micromachines 14, no. 4: 894. https://doi.org/10.3390/mi14040894
APA StyleTurkyilmazoglu, M., & Duraihem, F. Z. (2023). Full Solutions to Flow and Heat Transfer from Slip-Induced Microtube Shapes. Micromachines, 14(4), 894. https://doi.org/10.3390/mi14040894





