Finger-Actuated Micropump of Constant Flow Rate without Backflow
Abstract
1. Introduction
- Easy to fabricate by using the Embedded Scaffold Removing Open Technology (ESCARGOT) method.
- Controlling the total deformation of the flexible diaphragm until the bottom chamber of a finger-actuated micropump allows for indirect regulation of the volume of fluid moving.
- A combination of Tesla valves, serpentine microchannels, and hydrogel-assisted reservoirs can increase the reverse flow resistance, in other words, no backflow can be obtained. This can reduce the risk of hygiene and make sensing reading redundant.
1.1. Proposed Concept Design
- Take note that the extraction rate should not go above 1–2 mL/min to prevent discomfort, pain, distortion, and tearing of the tissue [67,68,69]. Hence, the low extraction rate (from 10 µL/min to a few hundred microliters) is painless [69] and suitable for transdermal application [70,71]. 1 μL/min flow rate is appropriate flow rate for maximizing recovery factor (RF) and obtaining high accuracy measurement in detection biosensor [72]. The recovery factor (RF), which is the ratio of the glucose concentration in the extracted ISF to the fresh ISF in the skin, can be calculated using Equation (1). In cases where the flow rate is less than 1 μL/min, although the recovery factor is greater, a longer time is taken to reach the sensor, and a higher sensitivity of the sensor is required [73]. At high flow rates, the working electrodes of the sensor cannot fully interact with the glucose, making the sensor less accurate at detecting glucose [74,75,76].
- The ability to maintain a consistent flow rate enables stable sensing signals and data transmission for real-time analysis, judgement, and treatment decision-making.
- It should be consumed in the smallest possible volume for diagnosis within the desired flow rate range. Continuous monitoring, such as measuring glucose levels in a diabetic patient, is challenging to carry out since it requires a sampling process at a high frequency within a day, and a large sample size is impractical. As long as the sensor is able to analyze the relevant analytes of interest and produce a sensing signal using a minimal sampling size that is applied to the sensing reaction area, it is appropriate for the overall system. Laboratory techniques may require a sample volume of >100 μL for precise analysis and lengthy testing times. However, in practice, most diagnosis devices extract a small volume of 1–10 μL of ISF [17,77] and 0.6–1.1 μL of blood sampling size for biosensors [78], respectively, within a minute [79]. A adequate of ISF sample can produce an accurate and reliable measurement, so a larger volume of sample fluid than is necessary to fully saturate the sensing region’s reaction area is recommended. Incorrect measurements can lead to wrong diagnoses and ineffective treatments.
- It should have robust performance under various conditions and be economical. High manufacturing costs are a barrier to the widespread use of microfluidic devices since they are required to integrate multiple components to achieve desired results. Single-use devices (disposables) have had an overwhelmingly large impact on society and the economy compared to applications that consider continuous long-term monitoring strategies.
- No backflow to avoid hygiene or incorrect analysis due to repeated use of the same sample
- Leakage-free
1.2. Theoretical Analysis
1.2.1. Consistent Flow Rate Analysis
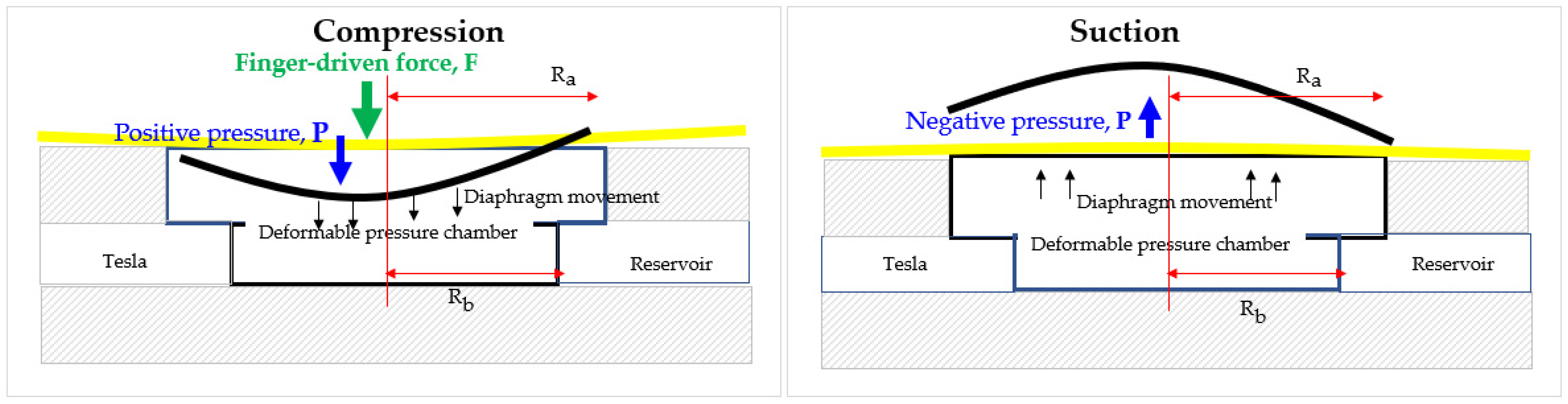
1.2.2. Backflow Analysis
- ISF used as working fluid is Newtonian fluid
- The fluid flow is laminar (Re < 2300) [89], incompressible fluid flow in which the fluid properties, such as its density and viscosity, are constant; steady flow in which density does not change as a function of time
- There will be no leakage or additional fluid in the system; in other words, the volumetric mass flow rate will be the same everywhere in the system ()
- Isothermal (Temperature = constant)
- Fully developed . A constant velocity profile is maintained by the flow when the pressure gradient and shear forces are equalized. The z-axis pressure gradient remains constant [96].
- Velocity along z-axis is function of x and y. (, w
- Fluid flow moving horizontally, thus gravity effect is negligible (g = 0)
2. Materials and Methods
2.1. Material
2.2. Simulation and Their Boundary Condition
2.3. Swelling Ratio Profile, Absorption Rate and Water Retention of Hydrogel
2.4. Fabrication of Microfluidic Device
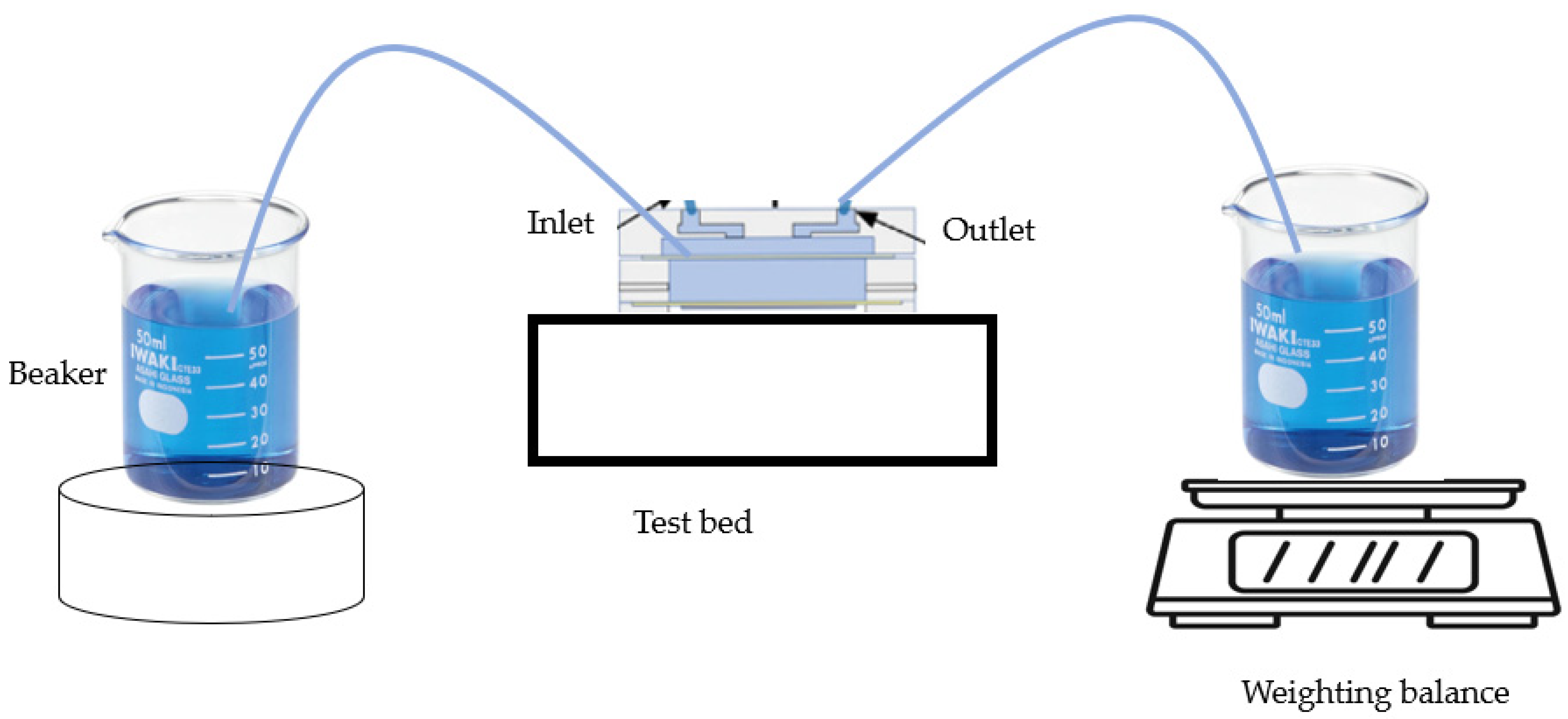
2.5. Experimental Microfluidic System Versatility Confirmation
3. Result and Discussion
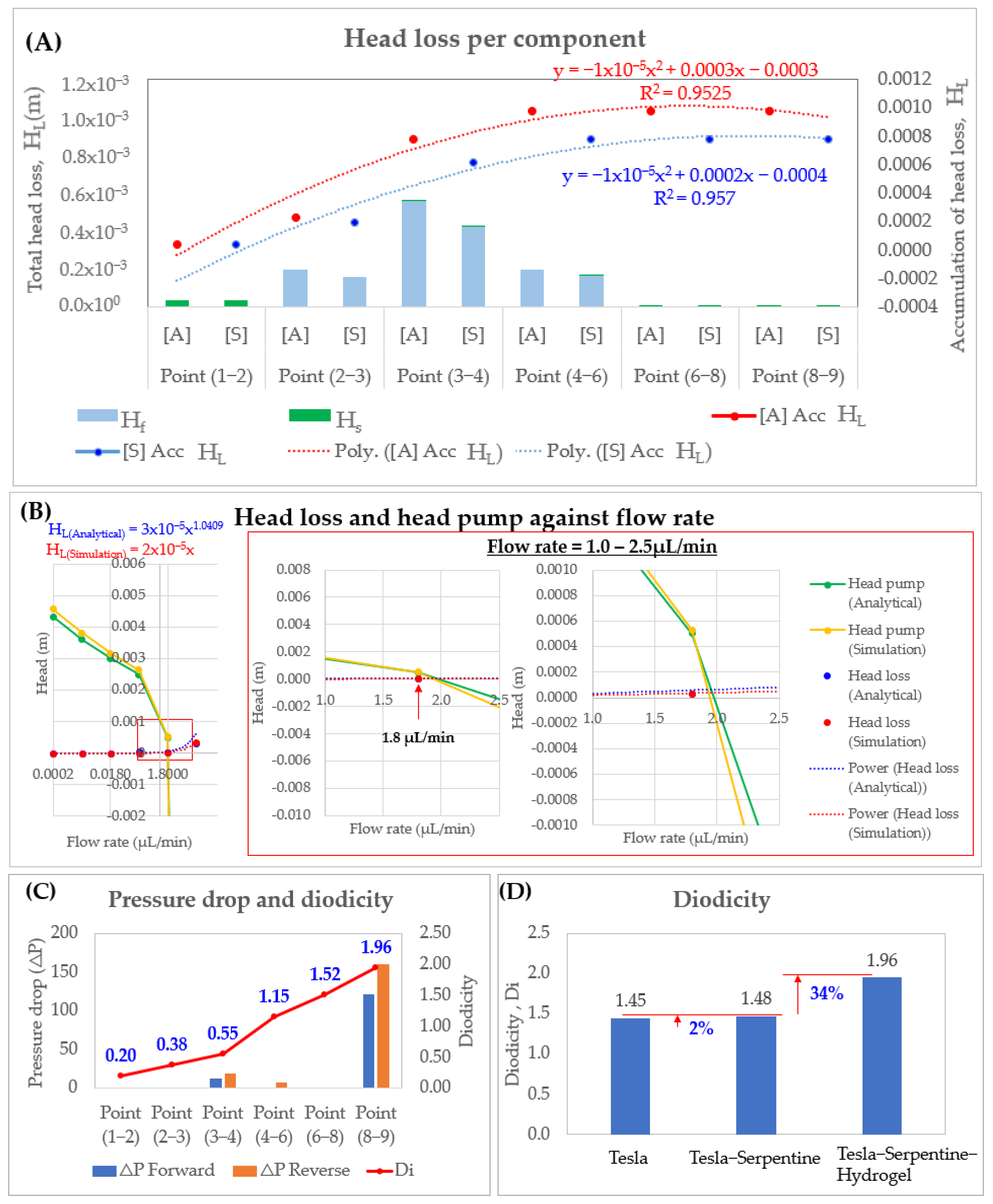
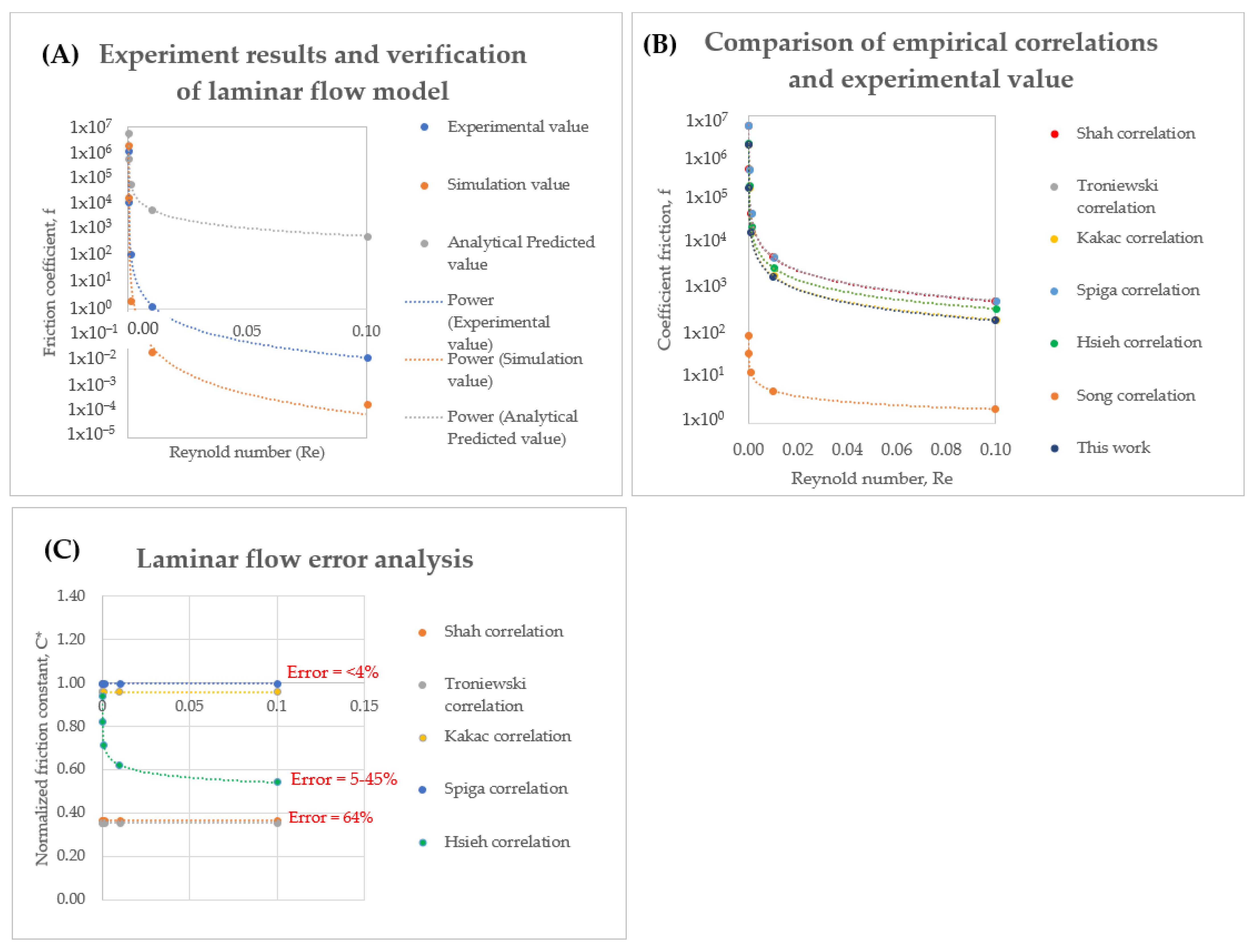
3.1. Head Loss, Pressure Drop and Diodicity Analysis
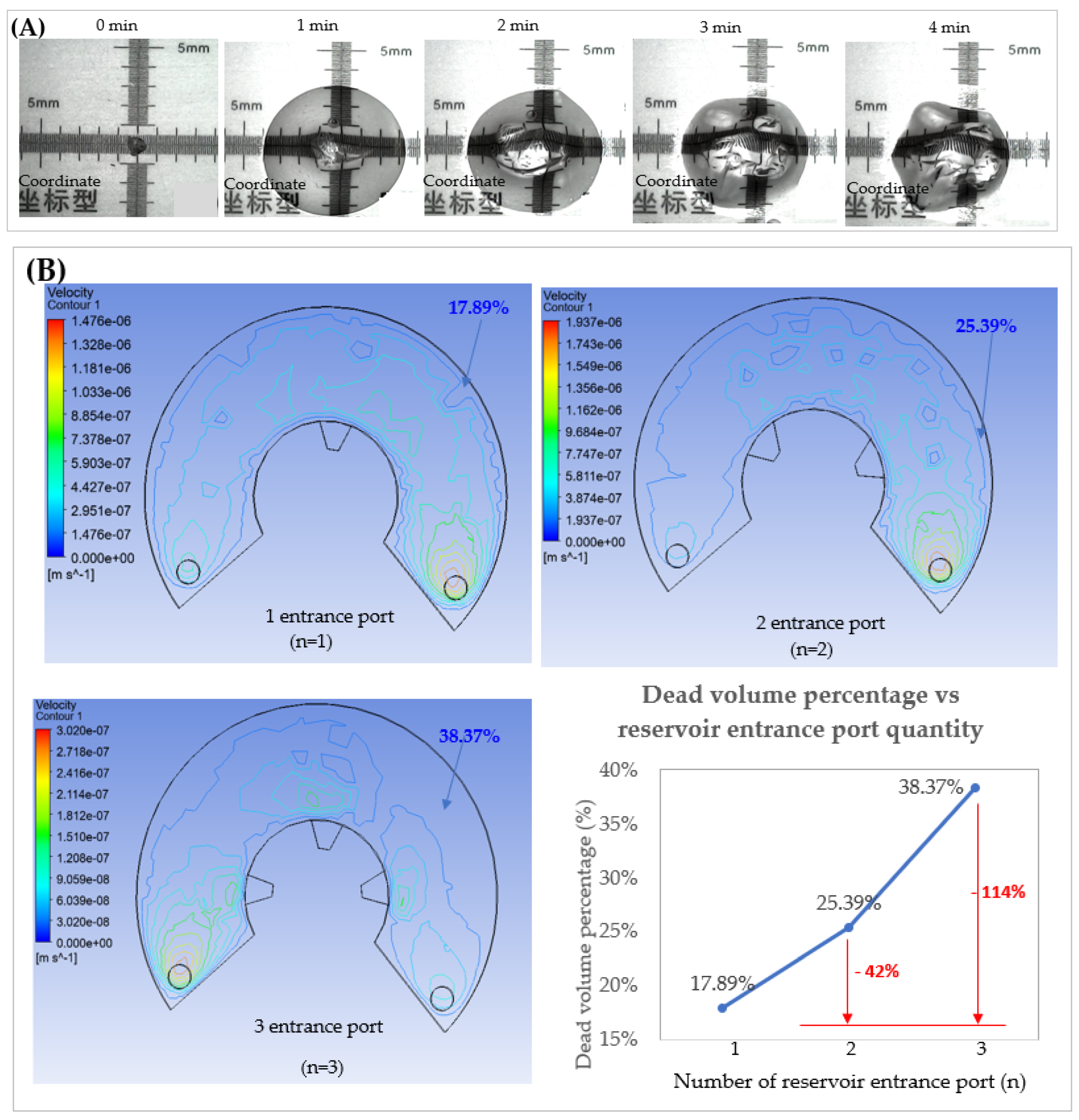
3.2. Hydrogel-Assisted Reservoir for Interstitial Fluid Collector and Backflow Reduction
- Effect of reservoir entrance quantity on the static area
- 2.
- Effect of diffuser width, b on the static area
3.3. Characterization of Microfluidic Fabrication in the ESCARGOT Process
3.4. Experimental Versatility
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Squires, T.; Quake, S. Microfluidics: Fluid physics at the nanoliter scale. Rev. Mod. Phys. 2005, 77, 977. [Google Scholar] [CrossRef]
- Gale, B.K.; Jafek, A.R.; Lambert, C.J.; Goenner, B.L.; Moghimifam, H.; Nze, U.C.; Kamarapu, S.K. A Review of Current Methods in Microfluidic Device Fabrication and Future Commercialization Prospects. Inventions 2018, 3, 60. [Google Scholar] [CrossRef]
- Wang, C.; Liu, M.; Wang, Z.; Li, S.; Deng, Y.; He, N. Point-of-care diagnostics for infectious diseases: From methods to devices. Nano Today 2021, 37, 101092. [Google Scholar] [CrossRef] [PubMed]
- Njoku, K.; Chiasserini, D.; Jones, E.R.; Barr, C.E.; O’Flynn, H.; Whetton, A.D.; Crosbie, E.J. Urinary Biomarkers and Their Potential for the Non-Invasive Detection of Endometrial Cancer. Front. Oncol. 2020, 10, 559016. [Google Scholar] [CrossRef] [PubMed]
- Jing, J.; Gao, Y. Urine biomarkers in the early stages of diseases: Current status and perspective. Discov. Med. 2018, 25, 57–65. [Google Scholar]
- Jordaens, S.; Zwaenepoel, K.; Tjalma, W.; Deben, C.; Beyers, K.; Vankerckhoven, V.; Pauwels, P.; Vorsters, A. Urine biomarkers in cancer detection: A systematic review of preanalytical parameters and applied methods. Int. J. Cancer 2023, 152, 2186–2205. [Google Scholar] [CrossRef]
- Nunes, L.; Mussavira, S.; Bindhu, O.S. Clinical and diagnostic utility of saliva as a non-invasive diagnostic fluid: A systematic review. Biochem. Med. 2015, 25, 177–192. [Google Scholar] [CrossRef]
- Swetha, P.; Balijapalli, U.; Feng, S.P. Wireless accessing of salivary biomarkers based wearable electrochemical sensors: A mini-review. Electrochem. Commun. 2022, 140, 107314. [Google Scholar] [CrossRef]
- Saha, T.; Del Caño, R.; la De Paz, E.; Sandhu, S.S.; Wang, J. Access and Management of Sweat for Non-Invasive Biomarker Monitoring: A Comprehensive Review. Small 2022, 2206064. [Google Scholar] [CrossRef]
- Ravishankar, P.; Daily, A. Tears as the Next Diagnostic Biofluid: A Comparative Study between Ocular Fluid and Blood. Appl. Sci. 2022, 12, 2884. [Google Scholar] [CrossRef]
- Amorim, M.; Martins, B.; Caramelo, F.; Gonçalves, C.; Trindade, G.; Simão, J.; Barreto, P.; Marques, I.; Leal, E.C.; Carvalho, E.; et al. Putative Biomarkers in Tears for Diabetic Retinopathy Diagnosis. Front. Med. 2022, 9, 873483. [Google Scholar] [CrossRef] [PubMed]
- Bruen, D.; Delaney, C.; Florea, L.; Diamond, D. Glucose Sensing for Diabetes Monitoring: Recent Developments. Sensors 2017, 17, 1866. [Google Scholar] [CrossRef] [PubMed]
- Tang, L.; Chang, S.; Chen, C.J.; Liu, J.T. Non-Invasive Blood Glucose Monitoring Technology: A Review. Sensors 2020, 20, 6925. [Google Scholar] [CrossRef] [PubMed]
- Sim, D.; Brothers, M.C.; Slocik, J.M.; Islam, A.E.; Maruyama, B.; Grigsby, C.C.; Naik, R.R.; Kim, S.S. Biomarkers and Detection Platforms for Human Health and Performance Monitoring: A Review. Adv. Sci. 2022, 9, 2104426. [Google Scholar] [CrossRef] [PubMed]
- Kolluru, C.; Williams, M.; Chae, J.; Prausnitz, M.R. Recruitment and Collection of Dermal Interstitial Fluid Using a Microneedle Patch. Adv. Healthc. Mater. 2019, 8, 1801262. [Google Scholar] [CrossRef]
- Samant, P.P.; Niedzwiecki, M.M.; Raviele, N.; Tran, V.; Mena-Lapaix, J.; Walker, D.I.; Felner, E.I.; Jones, D.P.; Miller, G.W.; Prausnitz, M.R. Sampling interstitial fluid from human skin using a microneedle patch. Sci. Transl. Med. 2020, 12, eaaw0285. [Google Scholar] [CrossRef]
- Friedel, M.; Thompson, I.A.P.; Kasting, G.; Polsky, R.; Cunningham, D.; Soh, H.T.; Heikenfeld, J. Opportunities and challenges in the diagnostic utility of dermal interstitial fluid. Nat. Biomed. Eng. 2023. [Google Scholar] [CrossRef]
- Tran, B.Q.; Miller, P.R.; Taylor, R.M.; Boyd, G.; Mach, P.M.; Rosenzweig, C.N.; Baca, J.T.; Polsky, R.; Glaros, T. Proteomic Characterization of Dermal Interstitial Fluid Extracted Using a Novel Microneedle-Assisted Technique. J. Proteome Res. 2018, 17, 479–485. [Google Scholar] [CrossRef]
- Rebrin, K.; Steil, G.M. Can interstitial glucose assessment replace blood glucose measurements? Diabetes Technol. 2000, 2, 461–472. [Google Scholar] [CrossRef]
- Sharma, S.; Zapatero-Rodríguez, J.; Estrela, P.; O’Kennedy, R. Point-of-Care Diagnostics in Low Resource Settings: Present Status and Future Role of Microfluidics. Biosensors 2015, 5, 577–601. [Google Scholar] [CrossRef]
- Damhorst, G.L.; Murtagh, M.; Rodriguez, W.R.; Bashir, R. Microfluidics and Nanotechnology for Detection of Global Infectious Diseases. Proc. IEEE 2015, 103, 150–160. [Google Scholar] [CrossRef]
- Damiati, S.; Kompella, U.B.; Damiati, S.A.; Kodzius, R. Microfluidic Devices for Drug Delivery Systems and Drug Screening. Genes 2018, 9, 103. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.M.; Lv, S.; Zhang, W.; Cui, Y. Microfluidic Point-of-Care (POC) Devices in Early Diagnosis: A Review of Opportunities and Challenges. Sensors 2022, 22, 1620. [Google Scholar] [CrossRef] [PubMed]
- Simsek, M.; Aijaz, A.; Dohler, M.; Sachs, J.; Fettweis, G. 5G-Enabled Tactile Internet. IEEE J. Sel. Areas Commun. 2016, 34, 460–473. [Google Scholar] [CrossRef]
- Woo, M.W.; Lee, J.; Park, K. A reliable IoT system for Personal Healthcare Devices. Future Gener. Comput. Syst. 2018, 78, 626–640. [Google Scholar] [CrossRef]
- Sheikh, N.; Sheikh, O. Forecasting of Biosensor Technologies for Emerging Point of Care and Medical IoT Applications Using Bibliometrics and Patent Analysis. In Proceedings of the Portland International Conference on Management of Engineering and Technology (PICMET), Honolulu, HI, USA, 4–8 September 2016; pp. 3082–3093. [Google Scholar]
- Pradhan, B.; Bhattacharyya, S.; Pal, K. IoT-Based Applications in Healthcare Devices. J. Healthc. Eng. 2021, 2021, 6632599. [Google Scholar] [CrossRef] [PubMed]
- Mejía-Salazar, J.R.; Rodrigues Cruz, K.; Materón Vásques, E.M.; Novais de Oliveira, O., Jr. Microfluidic Point-of-Care Devices: New Trends and Future Prospects for eHealth Diagnostics. Sensors 2020, 20, 1951. [Google Scholar] [CrossRef]
- Sweet, E.C.; Mehta, R.R.; Lin, R.; Lin, L. Finger-powred, 3D printed microfluidic pumps. In Proceedings of the 19th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS), Kaohsiung, China, 18–22 June 2017; pp. 1766–1769. [Google Scholar]
- Fathi, S.; Mohseni, S.S.; Mehrizi, A.A. Flow rate controlling by capillary micropumps in open biomicrofluidic devices. In Proceedings of the 27th National and 5th International Iranian Conference on Biomedical Engineering (ICBME), Tehran, Iran, 26–27 November 2020; pp. 187–191. [Google Scholar]
- Xu, L.; Wang, A.; Li, X.; Oh, K.W. Passive micropumping in microfluidics for point-of-care testing. Biomicrofluidics 2020, 14, 031503. [Google Scholar] [CrossRef]
- Iwai, K.; Shih, K.C.; Lin, X.; Brubaker, T.A.; Sochol, R.D.; Lin, L. Finger-powered microfluidic systems using multilayer soft lithography and injection molding processes. Lab A Chip 2014, 14, 3790–3799. [Google Scholar] [CrossRef]
- Park, J.; Park, J.K. Finger-Actuated Microfluidic Display for Smart Blood Typing. Anal. Chem. 2019, 91, 11636–11642. [Google Scholar] [CrossRef]
- Eluru, G.; Adhikari, J.V.; Chanda, P.; Gorthi, S.S. Hand-Powered Elastomeric Pump for Microfluidic Point-of-Care Diagnostics. Micromachines 2020, 11, 67. [Google Scholar] [CrossRef] [PubMed]
- Ruiz, C.; Kadimisetty, K.; Yin, K.; Mauk, M.G.; Zhao, H.; Liu, C. Fabrication of Hard–Soft Microfluidic Devices Using Hybrid 3D Printing. Micromachines 2020, 11, 567. [Google Scholar] [CrossRef] [PubMed]
- Sarabi, M.R.; Ahmadpour, A.; Yetisen, A.K.; Tasoglu, S. Finger-Actuated Microneedle Array for Sampling Body Fluids. Appl. Sci. 2021, 11, 5329. [Google Scholar] [CrossRef]
- Park, J.; Park, J.K. Finger-actuated microfluidic device for the blood cross-matching test. Lab A Chip 2018, 18, 1215–1222. [Google Scholar] [CrossRef] [PubMed]
- Park, J.; Park, J.K. Integrated microfluidic pumps and valves operated by finger actuation. Lab A Chip 2019, 19, 2973–2977. [Google Scholar] [CrossRef]
- Park, J.; Kim, H.; Park, J.K. Microfluidic channel-integrated hanging drop array chip operated by pushbuttons for spheroid culture and analysis. Analyst 2020, 145, 6974–6980. [Google Scholar] [CrossRef]
- Park, J.; Roh, H.; Park, J.K. Finger-Actuated Microfluidic Concentration Gradient Generator Compatible with a Microplate. Micromachines 2019, 10, 174. [Google Scholar] [CrossRef]
- Park, J.; Lee, K.G.; Han, D.H.; Lee, J.S.; Lee, S.J.; Park, J.K. Pushbutton-activated microfluidic dropenser for droplet digital PCR. Biosens. Bioelectron. 2021, 181, 113159. [Google Scholar] [CrossRef]
- Jo, Y.; Park, J.; Park, J.K. Colorimetric Detection of Escherichia coli O157:H7 with Signal Enhancement Using Size-Based Filtration on a Finger-Powered Microfluidic Device. Sensors 2020, 20, 2267. [Google Scholar] [CrossRef]
- Park, J.; Han, D.H.; Hwang, S.H.; Park, J.K. Reciprocating flow-assisted nucleic acid purification using a finger-actuated microfluidic device. Lab A Chip 2020, 20, 3346–3353. [Google Scholar] [CrossRef]
- Li, W.; Chen, T.; Chen, Z.; Fei, P.; Yu, Z.; Pang, Y.; Huang, Y. Squeeze-chip: A finger-controlled microfluidic flow network device and its application to biochemical assays. Lab A Chip 2012, 12, 1587–1590. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.; Kim, H.; Lee, W.; Kim, J. Finger-triggered portable PDMS suction cup for equipment-free microfluidic pumping. Micro Nano Syst. Lett. 2018, 6, 1–5. [Google Scholar] [CrossRef]
- Ju, T. Working Principle and Applications of Active and Passive Microfluidic Valves. J. Phys. Conf. Ser. 2022, 2230, 012013. [Google Scholar] [CrossRef]
- Stemme, E.; Stemme, G. A valveless diffuser/nozzle-based fluid pump. Sens. Actuators A-Phys. 1993, 39, 159–167. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, X.; Chen, Z.; Dai, J.; Zhang, F.; Ma, M.; Huo, Y.; Gui, Z. A valveless piezoelectric pump with novel flow path design of function of rectification to improve energy efficiency. Front. Mech. Eng. 2022, 17, 29. [Google Scholar] [CrossRef]
- Li, H.; Liu, J.; Li, K.; Liu, Y. A review of recent studies on piezoelectric pumps and their applications. Mech. Syst. Signal Process. 2021, 151, 107393. [Google Scholar] [CrossRef]
- Yan, Q.; Yin, Y.; Sun, W.; Fu, J. Advances in Valveless Piezoelectric Pumps. Appl. Sci. 2021, 11, 7061. [Google Scholar] [CrossRef]
- Yao, Y.; Zhou, Z.; Liu, H.; Li, T.; Gao, X. Valveless Piezoelectric Pump with Reverse Diversion Channel. Electronics 2021, 10, 1712. [Google Scholar] [CrossRef]
- Morris, C.; Forster, F. Improvements in Fixed-Valve Micropump Performance Through Shape Optimization of Valves. J. Fluids Eng. 2005, 127, 339–346. [Google Scholar]
- Porwal, P.R.; Thompson, S.M.; Walters, D.K.; Jamal, T. Heat transfer and fluid flow characteristics in multistaged Tesla valves. Numer. Heat Transf. Part A Appl. 2018, 73, 347–365. [Google Scholar] [CrossRef]
- Khodayari Bavil, A.; Coltisor, V.; Estlack, Z.; Kim, J. A pneumatically controlled microfluidic rectifier enabling zero backflow under pulsatile flow regime. J. Micromech. Microeng. 2021, 31, 095009. [Google Scholar] [CrossRef]
- Fadl, A.; Zhang, Z.; Geller, S.; Tölke, J.; Krafczyk, M.; Meyer, D. The effect of the microfluidic diodicity on the efficiency of valve-less rectification micropumps using Lattice Boltzmann Method. Microsyst. Technol. 2009, 15, 1379–1387. [Google Scholar] [CrossRef]
- Sochol, R.; Lu, A.; Lei, J.; Iwai, K.; Lee, L.; Lin, L. Microfluidic bead-based diodes with targeted circular microchannels for low Reynolds number applications. Lab A Chip 2014, 14, 1585–1594. [Google Scholar] [CrossRef]
- Park, J.Y.; Kim, D.J.; Kim, S.R.; Baek, J.Y.; Sun, K.; Lee, S.H. Microfluidic Valve Employing the pH-Responsive Hydrogel Microsphere as an Actuating Element. In Proceedings of the International Conference on Microtechnologies in Medicine and Biology, Okinawa, Japan, 9–12 May 2006; pp. 35–38. [Google Scholar]
- Toda, H.; Iwasaki, W.; Morita, N.; Motomura, T.; Takemura, K.; Nagano, M.; Nakanishi, Y.; Nakashima, Y. Reversible Thermo-Responsive Valve for Microfluidic Paper-Based Analytical Devices. Micromachines 2022, 13, 690. [Google Scholar] [CrossRef] [PubMed]
- Seo, J.; Wang, C.; Chang, S.; Park, J.; Kim, W. A hydrogel-driven microfluidic suction pump with a high flow rate. Lab A Chip 2019, 19, 1790–1796. [Google Scholar] [CrossRef] [PubMed]
- Liu, G.S.; Kong, Y.; Wang, Y.; Luo, Y.; Fan, X.; Xie, X.; Yang, B.R.; Wu, M.X. Microneedles for transdermal diagnostics: Recent advances and new horizons. Biomaterials 2020, 232, 119740. [Google Scholar] [CrossRef] [PubMed]
- Kashaninejad, N.; Munaz, A.; Moghadas, H.; Yadav, S.; Umer, M.; Nguyen, N.T. Microneedle Arrays for Sampling and Sensing Skin Interstitial Fluid. Chemosensors 2021, 9, 83. [Google Scholar] [CrossRef]
- Ma, S.; Li, J.; Pei, L.; Feng, N.; Zhang, Y. Microneedle-based interstitial fluid extraction for drug analysis: Advances, challenges, and prospects. J. Pharm. Anal. 2023, 13, 111–126. [Google Scholar] [CrossRef]
- Ahmad, N.N.; Ghazali, N.N.N.; Wong, Y.H. Concept Design of Transdermal Microneedles for Diagnosis and Drug Delivery: A Review. Adv. Eng. Mater. 2021, 23, 2100503. [Google Scholar] [CrossRef]
- Samant, P.P.; Prausnitz, M.R. Mechanisms of sampling interstitial fluid from skin using a microneedle patch. Proc. Natl. Acad. Sci. USA 2018, 115, 4583–4588. [Google Scholar] [CrossRef]
- Guyton, A.C.; Scheel, K.; Murphree, D. Interstitial fluid pressure. 3. Its effect on resistance to tissue fluid mobility. Circ. Res. 1966, 19, 412–419. [Google Scholar] [CrossRef] [PubMed]
- Wiig, H.; Swartz, M.A. Interstitial Fluid and Lymph Formation and Transport: Physiological Regulation and Roles in Inflammation and Cancer. Physiol. Rev. 2012, 92, 1005–1060. [Google Scholar] [CrossRef]
- Gupta, J. Microneedles for Transdermal Drug Delivery in Human Subjects. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 2009. [Google Scholar]
- Gupta, J.; Felner, E.I.; Prausnitz, M.R. Minimally invasive insulin delivery in subjects with type 1 diabetes using hollow microneedles. Diabetes Technol. Ther. 2009, 11, 329–337. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.C.; Park, J.H.; Prausnitz, M.R. Microneedles for drug and vaccine delivery. Adv. Drug Deliv. Rev. 2012, 64, 1547–1568. [Google Scholar] [CrossRef] [PubMed]
- Nuxoll, E. BioMEMS in drug delivery. Adv. Drug Deliv. Rev. 2013, 65, 1611–1625. [Google Scholar] [CrossRef]
- Ashraf, M.W.; Tayyaba, S.; Afzulpurkar, N. Micro Electromechanical Systems (MEMS) Based Microfluidic Devices for Biomedical Applications. Int. J. Mol. Sci. 2011, 12, 3648–3704. [Google Scholar] [CrossRef] [PubMed]
- Najmi, A.; Saidi, M.S.; Kazemzadeh Hannani, S. Design of the micropump and mass-transfer compartment of a microfluidic system for regular nonenzymatic glucose measurement. Biotechnol. Rep. 2022, 34, e00723. [Google Scholar] [CrossRef]
- Najmi, A.; saidi, M.s.; Shahrokhian, S. Numerical simulation of a microfluidic system for regular glucose measurement. In Proceedings of the 26th National and 4th International Iranian Conference on Biomedical Engineering (ICBME), Tehran, Iran, 27–28 November 2019; pp. 60–65. [Google Scholar]
- Lamberti, F.; Luni, C.; Zambon, A.; Andrea Serra, P.; Giomo, M.; Elvassore, N. Flow biosensing and sampling in indirect electrochemical detection. Biomicrofluidics 2012, 6, 24114. [Google Scholar] [CrossRef]
- Keenan, D.B.; Mastrototaro, J.J.; Voskanyan, G.; Steil, G.M. Delays in minimally invasive continuous glucose monitoring devices: A review of current technology. J. Diabetes Sci. Technol. 2009, 3, 1207–1214. [Google Scholar] [CrossRef]
- Chou, J.C.; Huang, Y.H.; Kuo, P.Y.; Lai, C.H.; Nien, Y.H.; Chen, Y.Y.; Kang, Z.X.; Lee, K.T. Application of the Non-Enzymatic Glucose Sensor Combined with Microfluidic System and Calibration Readout Circuit. Chemosensors 2021, 9, 351. [Google Scholar] [CrossRef]
- Chinnadayyala, S.R.; Park, K.D.; Cho, S. Editors’ Choice—Review—In Vivo and In Vitro Microneedle Based Enzymatic and Non-Enzymatic Continuous Glucose Monitoring Biosensors. ECS J. Solid State Sci. Technol. 2018, 7, Q3159–Q3171. [Google Scholar] [CrossRef]
- Pfützner, A.; Schipper, C.; Ramljak, S.; Flacke, F.; Sieber, J.; Forst, T.; Musholt, P.B. Evaluation of the effects of insufficient blood volume samples on the performance of blood glucose self-test meters. J. Diabetes Sci. Technol. 2013, 7, 1522–1529. [Google Scholar] [CrossRef] [PubMed]
- Bhalla, N.; Jolly, P.; Formisano, N.; Estrela, P. Introduction to biosensors. Essays Biochem. 2016, 60, 1–8. [Google Scholar] [PubMed]
- Ahmad, N.N.; Ghazali, N.N.N.; Wong, Y.H. Mechanical and fluidic analysis of hollow side-open and outer-grooved design of microneedles. Mater. Today Commun. 2021, 29, 102940. [Google Scholar] [CrossRef]
- Griss, P.; Stemme, G. Side-opened out-of-plane microneedles for microfluidic transdermal liquid transfer. J. Microelectromech. Syst. 2003, 12, 296–301. [Google Scholar] [CrossRef]
- Zhang, H. Fabrication of Hollow Silicon Microneedle Arrays for Transdermal Biological Fluid Extraction. Master’s Thesis, University of Waterloo, UWSpace, Waterloo, ON, Canada, 2018. [Google Scholar]
- Roxhed, N.; Gasser, T.C.; Griss, P.; Holzapfel, G.A.; Stemme, G. Penetration-Enhanced Ultrasharp Microneedles and Prediction on Skin Interaction for Efficient Transdermal Drug Delivery. J. Microelectromech. Syst. 2007, 16, 1429–1440. [Google Scholar] [CrossRef]
- Bodhale, D.W.; Nisar, A.; Afzulpurkar, N. Structural and microfluidic analysis of hollow side-open polymeric microneedles for transdermal drug delivery applications. Microfluid. Nanofluidics 2010, 8, 373–392. [Google Scholar] [CrossRef]
- Trautmann, A.; Roth, G.-L.; Nujiqi, B.; Walther, T.; Hellmann, R. Towards a versatile point-of-care system combining femtosecond laser generated microfluidic channels and direct laser written microneedle arrays. Microsyst. Nanoeng. 2019, 5, 6. [Google Scholar] [CrossRef]
- Maaden, K.V.D.; Jiskoot, W.; Bouwstra, J. Microneedle technologies for (trans)dermal drug and vaccine delivery. J. Control. Release 2012, 161, 645–655. [Google Scholar] [CrossRef]
- Ita, K. Transdermal Delivery of Drugs with Microneedles-Potential and Challenges. Pharmaceutics 2015, 7, 90–105. [Google Scholar] [CrossRef]
- Bankar, R.; Godase, A.; Mule, A.; Gaikwad, N.; Gidde, R. Computational Analysis of a Piezo-electrically Actuated Valve-less Micropump for Micro-fluidic Applications. Int. J. New Technol. Res. 2019, 5, 51–55. [Google Scholar] [CrossRef]
- Mahesh, K.; Vaidya, S. Microfluidics: A boon for biological research. Curr. Sci. 2017, 112, 2021–2028. [Google Scholar] [CrossRef]
- Begolo, S.; Zhukov, D.; Selck, D.; Li, L.; Ismagilov, R. The pumping lid: Investigating multi-material 3D printing for equipment-free, programmable generation of positive and negative pressures for microfluidic applications. Lab A Chip 2014, 14, 4616–4628. [Google Scholar] [CrossRef] [PubMed]
- Guo-Hua, F.; Eun Sok, K. Piezoelectrically actuated dome-shaped diaphragm micropump. J. Microelectromech. Syst. 2005, 14, 192–199. [Google Scholar] [CrossRef]
- Ebah, L. Extraction and Analysis of Interstitial Fluid, and Characterisation of the Interstitial Compartment in Kidney Disease. Ph.D. Thesis, University of Manchester, Manchester, UK, 2012. [Google Scholar]
- Yao, W.; Li, Y.; Ding, G. Interstitial Fluid Flow: The Mechanical Environment of Cells and Foundation of Meridians. Evid.-Based Complement. Altern. Med. 2012, 2012, 853516. [Google Scholar] [CrossRef]
- Petersen, O.H. Human Physiology, 5th ed.; Blackwell Pub.: Malden, MA, USA, 2007; p. 664. [Google Scholar]
- Xiao Chao, T.; Hai Gang, W.; Hu, W.; Zhi Gong, W.; Yu Ze, S.; Jin Zhi, Z.; Jian, Z.; Si Da, Z.; Zhi Gang, Y. Design and test of a piezoelectric micropump based on hydraulic amplification. AIP Adv. 2021, 11, 065230. [Google Scholar]
- Song, G.; Sun, R.; Zhang, D.; Su, G.H.; Tian, W.; Qiu, S. Experimental study on flow characteristics of rectangular narrow channel. Int. J. Adv. Nucl. React. Des. Technol. 2020, 2, 60–68. [Google Scholar] [CrossRef]
- Nobakht, A.Y.; Shahsavan, M.; Paykani, A. Numerical Study of Diodicity Mechanism in Different Tesla-Type Microvalves. J. Appl. Res. Technol. 2013, 11, 876–885. [Google Scholar] [CrossRef]
- Hamidi, I.; Ouederni, A. Single phase flow characteristics in rectangular microchannel: Entrance length and friction factor. Int. J. Innov. Appl. Stud. 2014, 8, 819–826. [Google Scholar]
- Papautsky, I.; Ameel, T. A review of laminar single-phase flow in microchannels. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, New York, NY, USA, 11–16 November 2001. [Google Scholar]
- Lin, S.; Zhao, L.; Guest, J.; Weihs, T.; Liu, Z. Topology Optimization of Fixed-Geometry Fluid Diodes. J. Mech. Des. 2015, 137, 81402. [Google Scholar] [CrossRef]
- Bohm, S.; Phi, H.B.; Moriyama, A.; Runge, E.; Strehle, S.; König, J.; Cierpka, C.; Dittrich, L. Highly efficient passive Tesla valves for microfluidic applications. Microsyst. Nanoeng. 2022, 8, 97. [Google Scholar] [CrossRef]
- Wang, Y.; He, Y.; Xie, X.; Huang, Z.; Xu, H.; Hu, Q.; Ma, C. Design and Simulation of a New Near Zero-Wear Non-Contact Self-Impact Seal Based on the Tesla Valve Structure. Lubricants 2023, 11, 102. [Google Scholar] [CrossRef]
- Nguyen, Q.M.; Abouezzi, J.; Ristroph, L. Early turbulence and pulsatile flows enhance diodicity of Tesla’s macrofluidic valve. Nat. Commun. 2021, 12, 2884. [Google Scholar] [CrossRef] [PubMed]
- Bao, Y.; Wang, H. Numerical study on flow and heat transfer characteristics of a novel Tesla valve with improved evaluation method. Int. J. Heat Mass. Transf. 2022, 187, 122540. [Google Scholar] [CrossRef]
- Baghelani, M.; Abbasi, Z.; Daneshmand, M.; Light, P.E. Non-invasive continuous-time glucose monitoring system using a chipless printable sensor based on split ring microwave resonators. Sci. Rep. 2020, 10, 12980. [Google Scholar] [CrossRef] [PubMed]
- Singh, S.; Kumar, N.; George, D.; Sen, A.K. Analytical modeling, simulations and experimental studies of a PZT actuated planar valveless PDMS micropump. Sens. Actuators A Phys. 2015, 225, 81–94. [Google Scholar] [CrossRef]
- Kumar, V.; Paraschivoiu, M.; Nigam, K.D.P. Single-phase fluid flow and mixing in microchannels. Chem. Eng. Sci. 2011, 66, 1329–1373. [Google Scholar] [CrossRef]
- Zhang, K.; Feng, W.; Jin, C. Protocol efficiently measuring the swelling rate of hydrogels. MethodsX 2020, 7, 100779. [Google Scholar] [CrossRef]
- Jayaramudu, T.; Ko, H.U.; Kim, H.C.; Kim, J.W.; Kim, J. Swelling Behavior of Polyacrylamide–Cellulose Nanocrystal Hydrogels: Swelling Kinetics, Temperature, and pH Effects. Materials 2019, 12, 2080. [Google Scholar] [CrossRef]
- Zhu, J.; Zhou, X.; Kim, H.J.; Qu, M.; Jiang, X.; Lee, K.; Ren, L.; Wu, Q.; Wang, C.; Zhu, X.; et al. Gelatin Methacryloyl Microneedle Patches for Minimally Invasive Extraction of Skin Interstitial Fluid. Small 2020, 16, 1905910. [Google Scholar] [CrossRef]
- Donnelly, R.F.; McCrudden, M.T.; Zaid Alkilani, A.; Larrañeta, E.; McAlister, E.; Courtenay, A.J.; Kearney, M.C.; Singh, T.R.; McCarthy, H.O.; Kett, V.L.; et al. Hydrogel-forming microneedles prepared from “super swelling” polymers combined with lyophilised wafers for transdermal drug delivery. PLoS ONE 2014, 9, e111547. [Google Scholar] [CrossRef] [PubMed]
- Omidian, H.; Hashemi, S.A.; Sammes, P.G.; Meldrum, I. A model for the swelling of superabsorbent polymers. Polymer 1998, 39, 6697–6704. [Google Scholar] [CrossRef]
- Mamidi, N.; González-Ortiz, A.; Lopez Romo, I.; Barrera, E.V. Development of Functionalized Carbon Nano-Onions Reinforced Zein Protein Hydrogel Interfaces for Controlled Drug Release. Pharmaceutics 2019, 11, 621. [Google Scholar] [CrossRef] [PubMed]
- Tang, W.; Liu, H.; Zhu, L.; Shi, J.; Li, Z.; Xiang, N.; Yang, J. Fabrication of Different Microchannels by Adjusting the Extrusion Parameters for Sacrificial Molds. Micromachines 2019, 10, 544. [Google Scholar] [CrossRef] [PubMed]
- Rehmani, M.A.A.; Jaywant, S.A.; Arif, K.M. Study of Microchannels Fabricated Using Desktop Fused Deposition Modeling Systems. Micromachines 2021, 12, 14. [Google Scholar] [CrossRef] [PubMed]
- Šustková, A.; Konderlová, K.; Drastíková, E.; Sützl, S.; Hárendarčíková, L.; Petr, J. Rapid Production of PDMS Microdevices for Electrodriven Separations and Microfluidics by 3D-Printed Scaffold Removal. Separations 2021, 8, 67. [Google Scholar] [CrossRef]
- Abidin, U.; Daud, N.A.S.M.; Brun, V.L. Replication and leakage test of polydimethylsiloxane (PDMS) microfluidics channel. AIP Conf. Proc. 2019, 2062, 020064. [Google Scholar]
- Rasljic, M.; Gadjanski, I.; Smiljanić, M.; Jankovic, N.; Lazić, Ž.; Cvetanovic, K. Microfabrication of bifurcated microchannels with PDMS and ABS. In Proceedings of the 4th International Conference on Electrical, Electronics and Computing Engineering (IcETRAN), Kladovo, Serbia, 5–8 June 2017; pp. MOI2.1.1–MOI2.1.4. [Google Scholar]
- Rusli, M.Q.; Abidin, U. Polydimethylsiloxane Microchannel Fabrication from 3D Printed Mold. J. Mek. 2019, 41, 16–22. [Google Scholar]
- Kalpattu, A. PDMS Shrinkage. Protoc. Rep. 2017, 42, 1–3. [Google Scholar]
- Saggiomo, V.; Velders, A.H. Simple 3D Printed Scaffold-Removal Method for the Fabrication of Intricate Microfluidic Devices. Adv. Sci. 2015, 2, 1500125. [Google Scholar] [CrossRef]
- Goh, W.H.; Hashimoto, M. Fabrication of 3D Microfluidic Channels and In-Channel Features Using 3D Printed, Water-Soluble Sacrificial Mold. Macromol. Mater. Eng. 2018, 303, 1700484. [Google Scholar] [CrossRef]
- Ranjan, P. Investigations on the flow behaviour in microfluidic device due to surface roughness: A computational fluid dynamics simulation. Microsyst. Technol. 2019, 25, 3779–3789. [Google Scholar] [CrossRef]
- Troniewski, L.; Ulbrich, R. Two-phase gas-liquid flow in rectangular channels. Chem. Eng. Sci. 1984, 39, 751–765. [Google Scholar] [CrossRef]
- Shah, R.K. Laminar flow friction and forced convection heat transfer in ducts of arbitrary geometry. Int. J. Heat Mass Transf. 1975, 18, 849–862. [Google Scholar] [CrossRef]
- Kakac, S.; Shah, R.K.; Aung, W. Handbook of Single-Phase Convective Heat Transfer; John Wiley and Sons Inc.: New York, NY, USA, 1987. [Google Scholar]
- Spiga, M.; Morino, G.L. A symmetric solution for velocity profile in laminar flow through rectangular ducts. Int. Commun. Heat Mass Transf. 1994, 21, 469–475. [Google Scholar] [CrossRef]
- Hsieh, S.S.; Lin, C.Y.; Huang, C.F.; Tsai, H.H. Liquid flow in a micro-channel. J. Micromech. Microeng. 2004, 14, 436. [Google Scholar] [CrossRef]
- Kandlikar, S.G.; Li, D.; Colin, S.; Garimella, S.S.; King, M. Heat Transfer and Fluid Flow in Minichannels and Microchannels; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Zhai, Y.; Xia, G.; Li, Z.; Wang, H. Experimental investigation and empirical correlations of single and laminar convective heat transfer in microchannel heat sinks. Exp. Therm. Fluid Sci. 2017, 83, 207–214. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, Y.; Zhu, M.; Zhang, Y.; Liu, X.; Yu, H.; Jiang, Y.; Chen, Y.; Kuckling, D.; Adler, H.J.P. Surprising conversion of nanocomposite hydrogels with high mechanical strength by posttreatment: From a low swelling ratio to an ultrahigh swelling ratio. J. Polym. Sci. Part A Polym. Chem. 2006, 44, 6640–6645. [Google Scholar] [CrossRef]
- Cheng, W.M.; Hu, X.M.; Zhao, Y.Y.; Wu, M.Y.; Hu, X.M.; Yu, X.T. Preparation and swelling properties of poly(acrylic acid-co-acrylamide) composite hydrogels. e-Polymers 2017, 17, 95–106. [Google Scholar] [CrossRef]
- Kazeminejadfard, F.; Hojjati, M.R. Preparation of superabsorbent composite based on acrylic acid-hydroxypropyl distarch phosphate and clinoptilolite for agricultural applications. J. Appl. Polym. Sci. 2019, 136, 47365. [Google Scholar] [CrossRef]
- Wang, X.; Hou, H.; Li, Y.; Wang, Y.; Chen, H.; Ge, C. A novel semi-IPN hydrogel: Preparation, swelling properties and adsorption studies of Co (II). J. Ind. Eng. Chem. 2016, 41, 82–90. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Y.; He, S.; Hou, H.; Hao, C. Ultrasonic-assisted synthesis of superabsorbent hydrogels based on sodium lignosulfonate and their adsorption properties for Ni2+. Ultrason. Sonochem. 2018, 40, 221–229. [Google Scholar] [CrossRef] [PubMed]
- Lv, Q.; Wu, M.; Shen, Y. Enhanced swelling ratio and water retention capacity for novel super-absorbent hydrogel. Colloids Surf. A Physicochem. Eng. Asp. 2019, 583, 123972. [Google Scholar] [CrossRef]
- Al-Nasra, M. Self-sealing concrete mortar, concrete mortar mixed with super absorbent polymer. In Proceedings of the International Conference on Advances in Sustainable Construction Materials & Civil Engineering Systems (ASCMCES-17), Sharjah, United Arab Emirates, 18–20 April 2017; p. 02002. [Google Scholar]
- Mun, G.; Suleimenov, I.; Park, K.; Omidian, H. Superabsorbent Hydrogels. In Biomedical Applications of Hydrogels Handbook; Springer: New York, NY, USA, 2010; pp. 375–391. [Google Scholar]
- Chen, P.C.; Chou, C.C.; Chiang, C.H. Systematically Studying Dissolution Process of 3D Printed Acrylonitrile Butadiene Styrene (ABS) Mold for Creation of Complex and Fully Transparent Polydimethylsiloxane (PDMS) Fluidic Devices. BioChip J. 2021, 15, 144–151. [Google Scholar] [CrossRef]
- Yamashita, T.; Yasukawa, K.; Yunoki, E. Fabrication of a Polydimethylsiloxane Fluidic Chip Using a Sacrificial Template Made by Fused Deposition Modeling 3D Printing and Application for Flow-injection Analysis. Anal. Sci. 2019, 35, 769–775. [Google Scholar] [CrossRef]
- Chen, P.C.; Chou, C.C. Fabrication of a Nonplanar Microfluidics by Using Sonication-Assisted Dissolution Technique. In Proceedings of the 2018 IEEE 13th Annual International Conference on Nano/Micro Engineered and Molecular Systems (NEMS), Singapore, 22–26 April 2018; pp. 421–424. [Google Scholar]
- Haldkar, R.K.; Gupta, V.K.; Sheorey, T.; Parinov, I.A. Design, Modeling, and Analysis of Piezoelectric-Actuated Device for Blood Sampling. Appl. Sci. 2021, 11, 8449. [Google Scholar] [CrossRef]
- Kumar Das, S.; Nayak, K.K.; Krishnaswamy, P.R.; Kumar, V.; Bhat, N. Review—Electrochemistry and Other Emerging Technologies for Continuous Glucose Monitoring Devices. ECS Sens. Plus 2022, 1, 031601. [Google Scholar] [CrossRef]
- Zarifi, M.H.; Sadabadi, H.; Hejazi, S.H.; Daneshmand, M.; Sanati-Nezhad, A. Noncontact and Nonintrusive Microwave-Microfluidic Flow Sensor for Energy and Biomedical Engineering. Sci. Rep. 2018, 8, 139. [Google Scholar] [CrossRef]
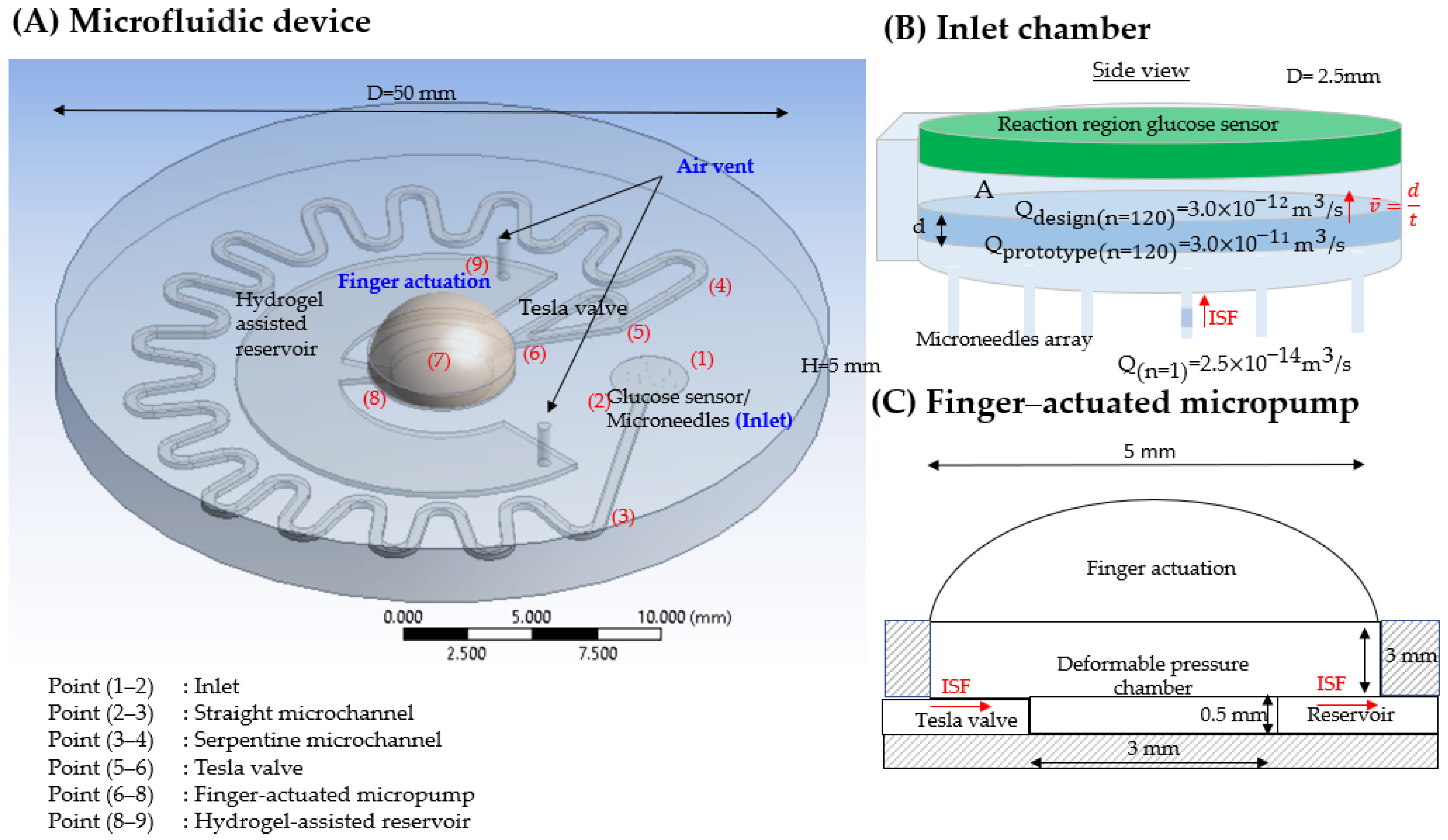
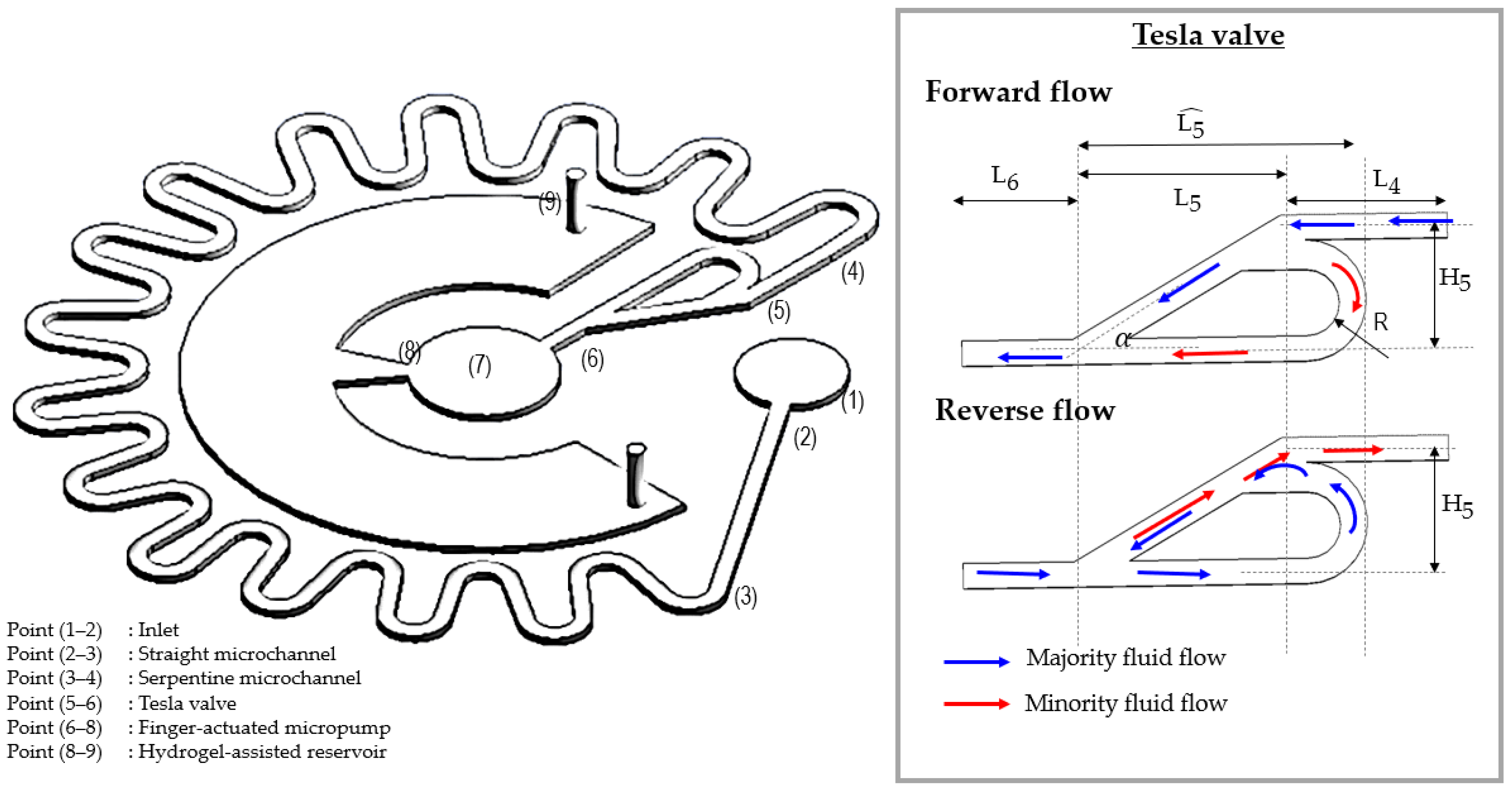



| Part | Parameter | Design | Prototype |
|---|---|---|---|
| Inlet | Inlet diameter, Di | 0.25 mm | 2.5 mm |
| Inlet height, hi | 0.05 mm | 0.5 mm | |
| Microchannel cross-sectional geometry | Width, w | 0.10 mm | 1.0 mm |
| Height, h | 0.05 mm | 0.5 mm | |
| Microchannel | Length, L(2→3) | 0.84 mm | 8.42 mm |
| Length, L(3→4) | 2.8 mm | 28 mm | |
| Length, L(4→5) | 0.3 mm | 3 mm | |
| Tesla | Length, L(5→6) | 0.38 mm | 3.8 mm |
| Pump chamber | Top diameter, Dp(T) | 0.5 mm | 5 mm |
| Top height, Hp(T) | 0.3 mm | 3 mm | |
| Bottom diameter, Dp(B) | 0.3 mm | 3 mm | |
| Bottom height, HP(B) | 0.05 mm | 0.5 mm | |
| Diffuser | Width, a | 0.05 mm | 0.5 mm |
| Width, b | 0.15 mm | 1.5 mm | |
| Length, L(8) | 0.15 mm | 1.5 mm | |
| Reservoir | Outer Diameter, DR1 | 1.6 mm | 16 mm |
| Inner Diameter, DR2 | 0.8 mm | 8 mm | |
| Air vent | Diameter, Do | 0.1 mm | 1.0 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmad, N.N.; Ghazali, N.N.N.; Abdul Rani, A.T.; Othman, M.H.; Kee, C.C.; Jiwanti, P.K.; Rodríguez-Gómez, A.; Wong, Y.H. Finger-Actuated Micropump of Constant Flow Rate without Backflow. Micromachines 2023, 14, 881. https://doi.org/10.3390/mi14040881
Ahmad NN, Ghazali NNN, Abdul Rani AT, Othman MH, Kee CC, Jiwanti PK, Rodríguez-Gómez A, Wong YH. Finger-Actuated Micropump of Constant Flow Rate without Backflow. Micromachines. 2023; 14(4):881. https://doi.org/10.3390/mi14040881
Chicago/Turabian StyleAhmad, NurFarrahain Nadia, Nik Nazri Nik Ghazali, Ahmad Taufiq Abdul Rani, Mohammad Hafiz Othman, Chia Ching Kee, Prastika Krisma Jiwanti, Arturo Rodríguez-Gómez, and Yew Hoong Wong. 2023. "Finger-Actuated Micropump of Constant Flow Rate without Backflow" Micromachines 14, no. 4: 881. https://doi.org/10.3390/mi14040881
APA StyleAhmad, N. N., Ghazali, N. N. N., Abdul Rani, A. T., Othman, M. H., Kee, C. C., Jiwanti, P. K., Rodríguez-Gómez, A., & Wong, Y. H. (2023). Finger-Actuated Micropump of Constant Flow Rate without Backflow. Micromachines, 14(4), 881. https://doi.org/10.3390/mi14040881







