A Predictive Model of Capillary Forces and Contact Diameters between Two Plates Based on Artificial Neural Network
Abstract
1. Introduction
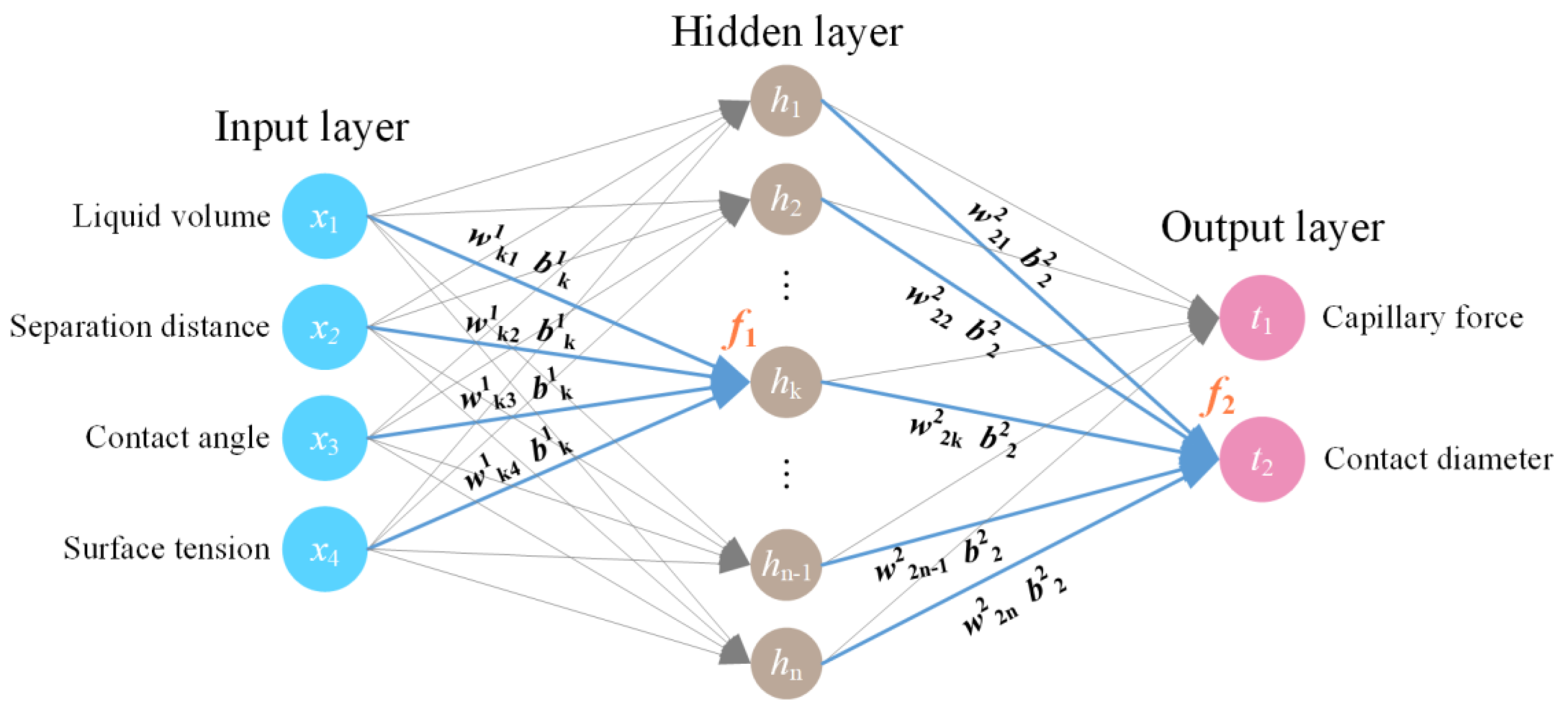
2. ANN Model and GA Optimization
2.1. ANN Model
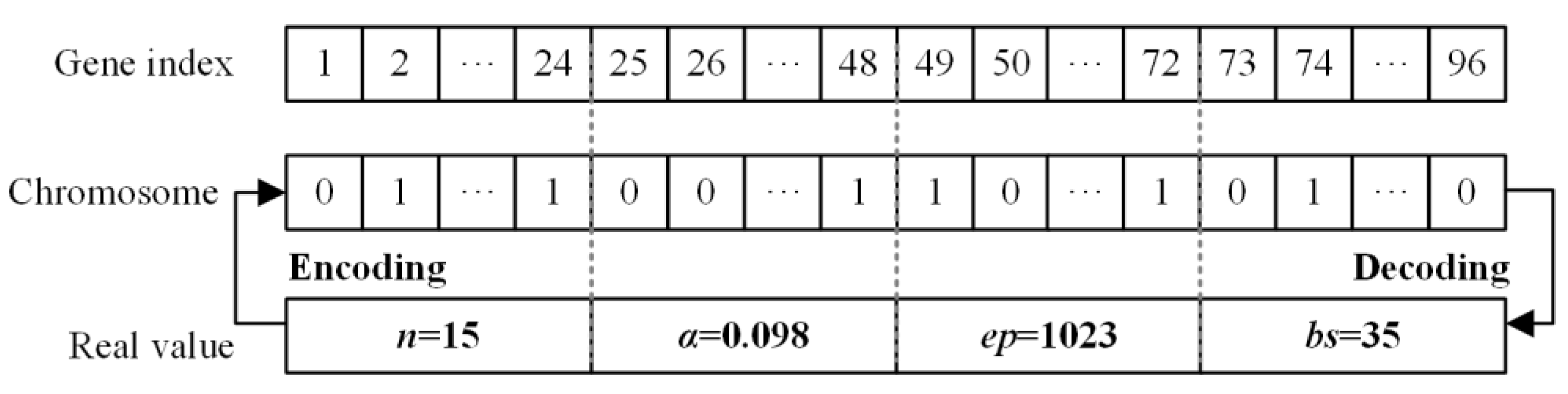
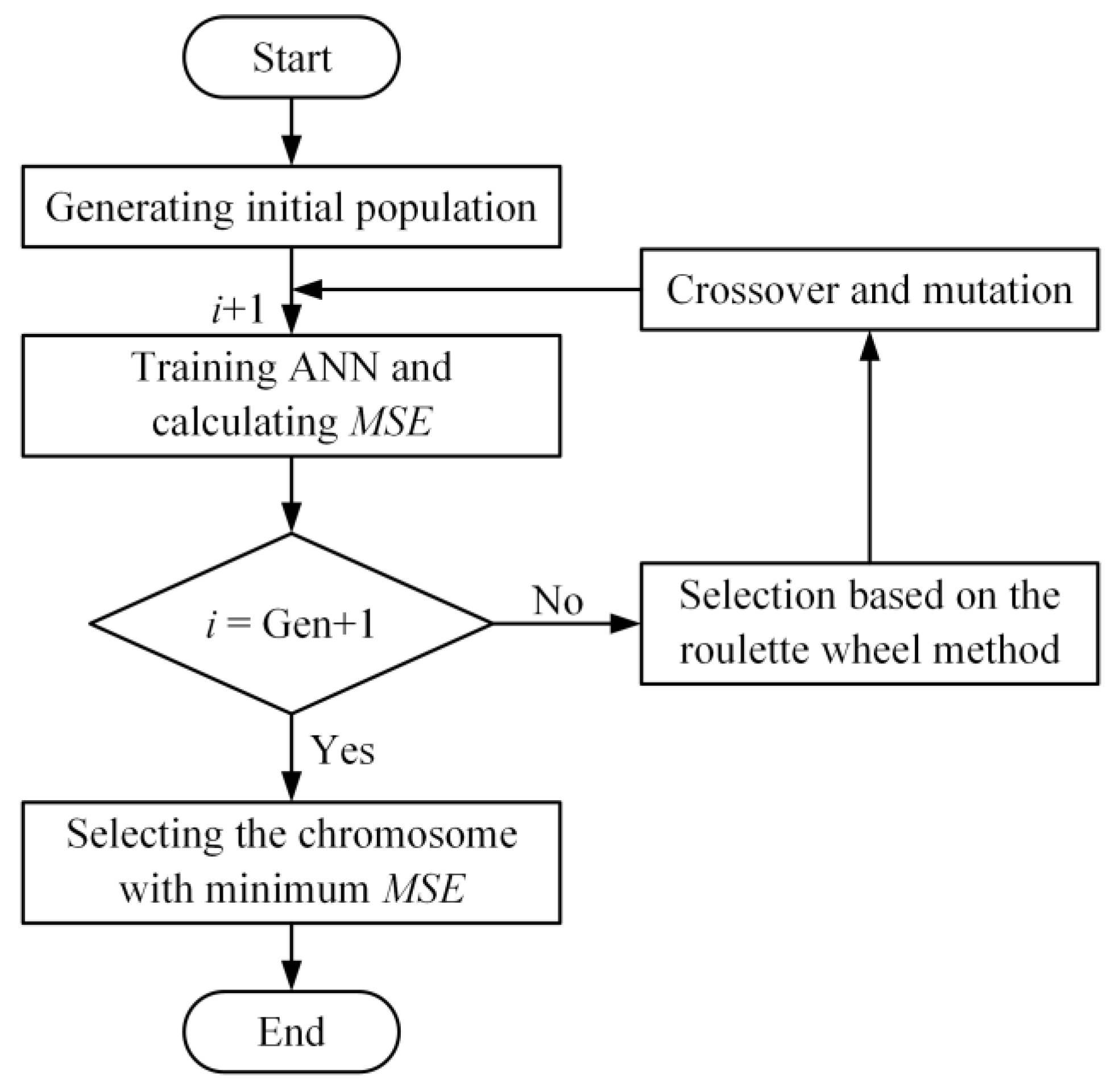
2.2. Optimization of ANN Using GA
- Step 1
- Generating initial population. The initial population consisting of 20 chromosomes is randomly generated. Each chromosome represents a set of values of n, α, ep and bs. The present generation i is initially set to 0. The total generation number Gen is set to 100.
- Step 2
- Training ANN. i adds one. ANN is trained and MSE is calculated under the condition that each chromosome is represented.
- Step 3
- Optimization. The processes of selection, crossover and mutation are conducted as i is not equal to Gen+1.
- Step 4
- Generation of the best ANN parameters. Step 2 and step 3 are repeated until i is equal to Gen+1. The chromosome with minimum MSE is selected as the optimal set of values of n, α, ep and bs.
3. Experiments
3.1. Experimental Setup
3.2. Experimental Data
4. Results and Discussions
4.1. ANN Training
4.2. Modeling
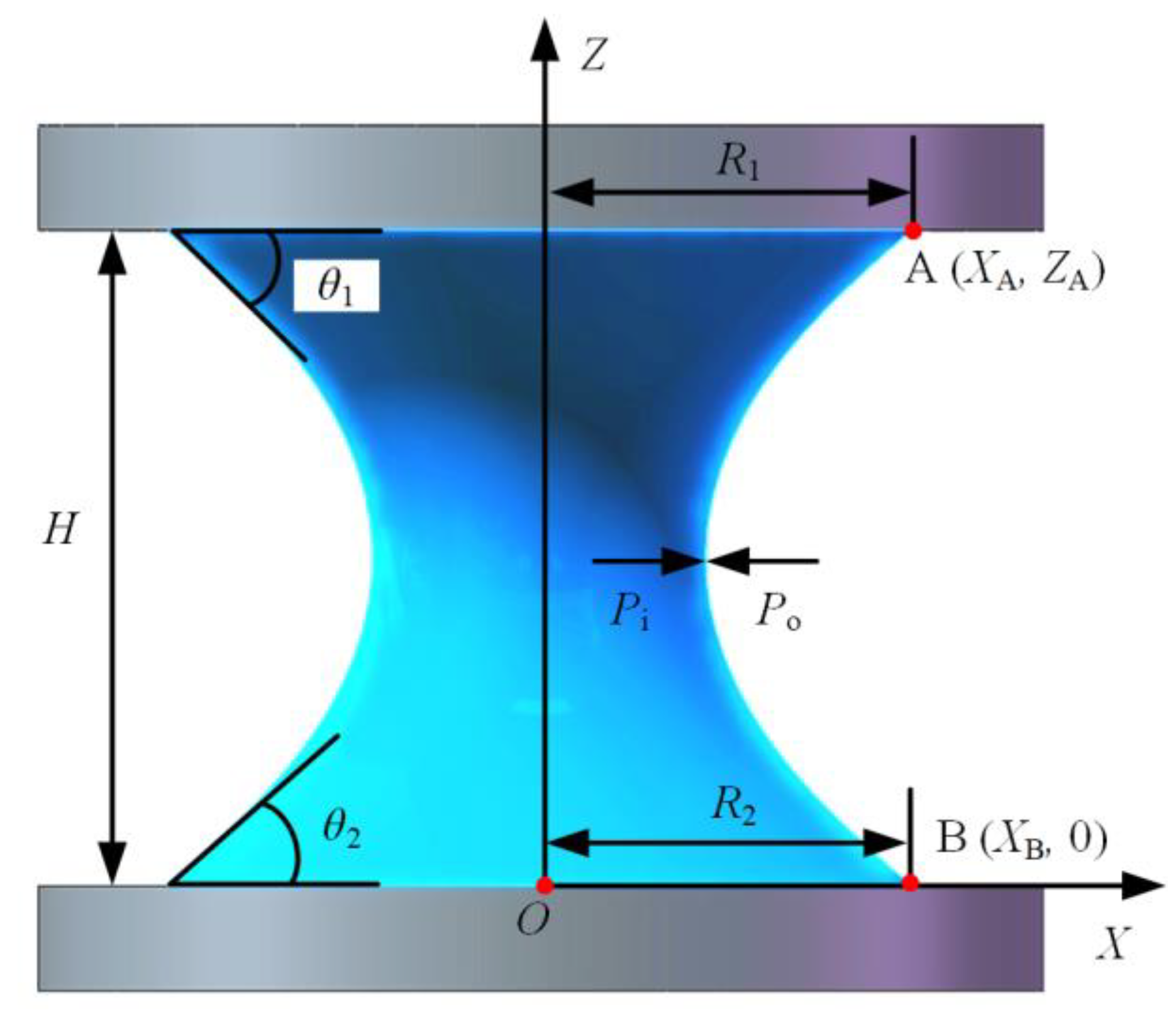
4.2.1. Theoretical Model
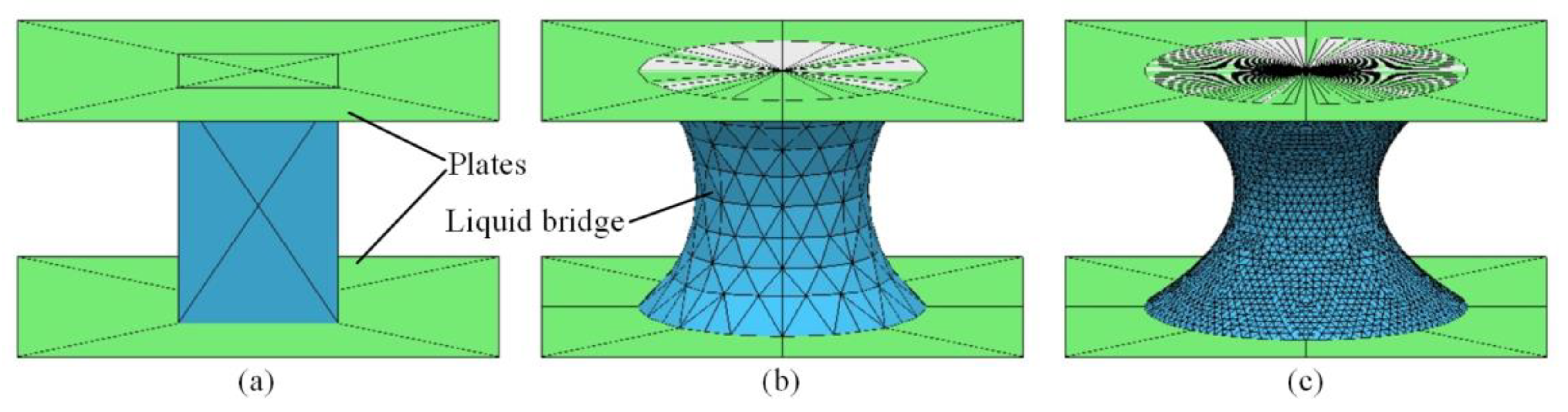
4.2.2. Simulation Model
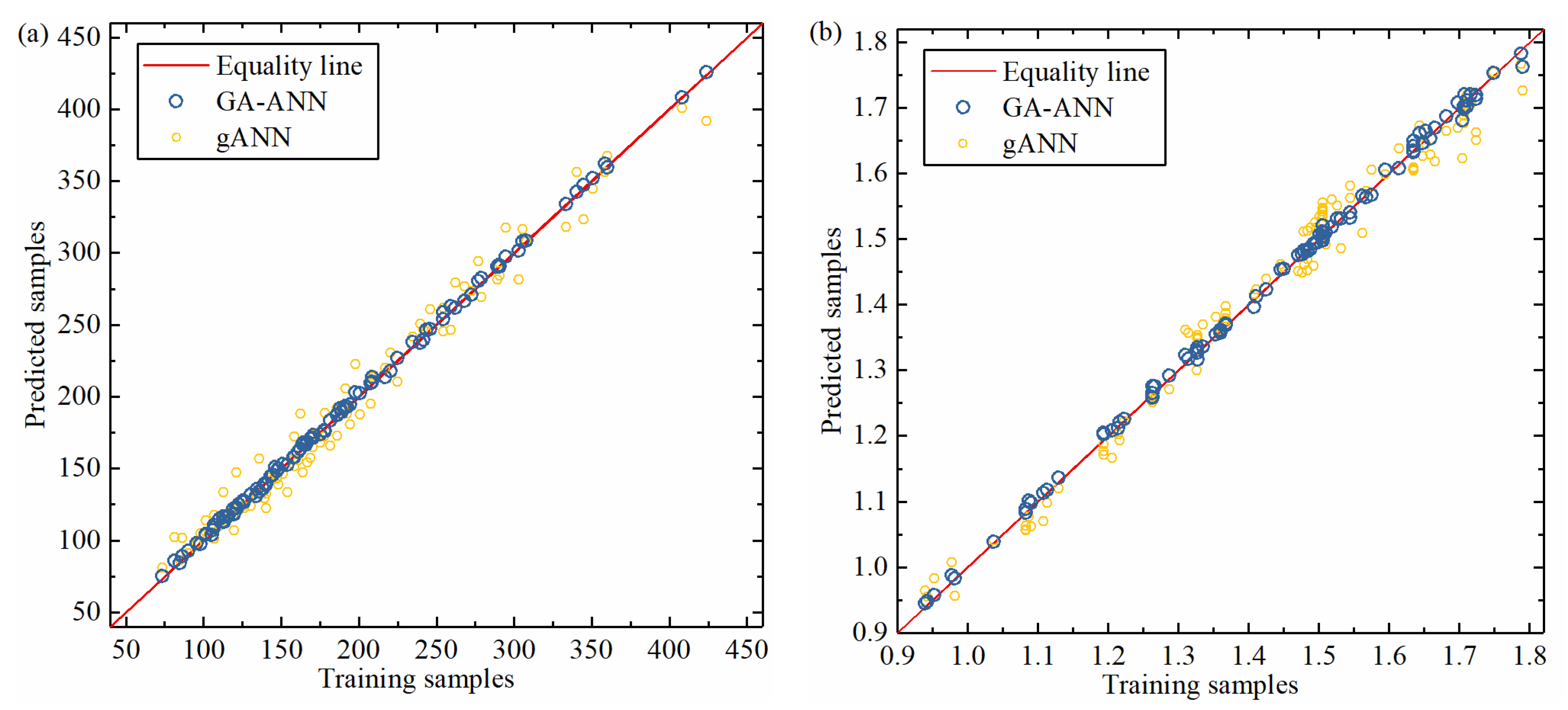
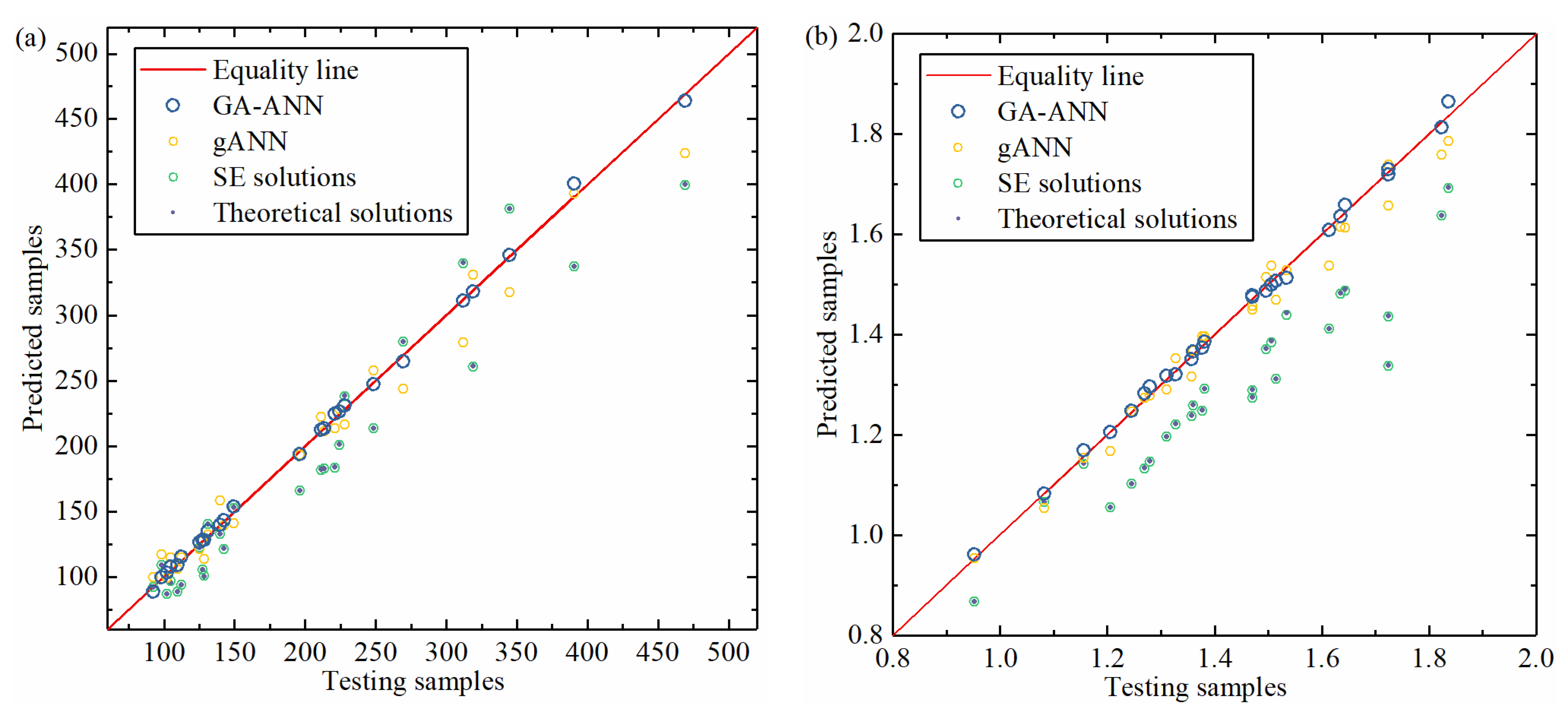
4.3. Comparison of GA-ANN, gANN, Simulation and Theoretical Solutions
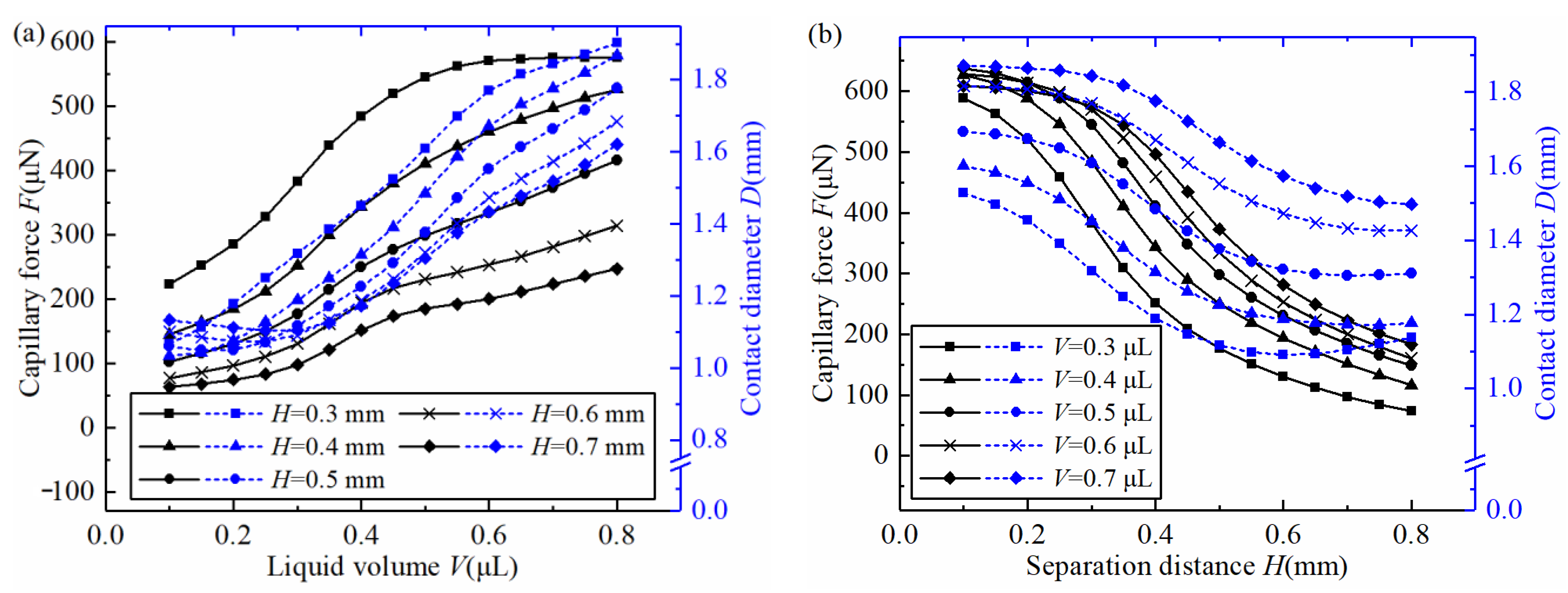
4.4. Effects of Input Parameters on Capillary Force and Contact Diameter
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | Name |
| n | Number of neurons in the hidden layer |
| f | Activation function |
| w | Weight |
| b | Bias |
| h | Output of hidden layer |
| t | Predicted value of ANN |
| y | Actual value of dataset |
| R2 | Correlation coefficient |
| α | Initial learning rate |
| ep | Number of epochs |
| bs | Number of samples passed to ANN at once |
| p | Selected probability in the GA optimization process |
| pop | Population size in GA |
| Gen | Total generation number |
| μ | Viscosity |
| γ | Surface tension |
| ρ | Density |
| θs | Static contact angle |
| θr | Receding contact angle |
| U | Stretching speed |
| λc | Capillary length |
| L | Characteristic length of system |
| V | Liquid volume |
| H | Separation distance |
| F | Capillary force |
| D | Contact diameter |
| GA-ANN | ANN optimized by GA |
| gANN | ANN employing general parameters |
| Abbreviation | Name |
| CAH | Contact angle hysteresis |
| ANN | Artificial neural network |
| GA | Genetic algorithm |
| MSE | Mean square error |
| EG | Ethylene Glycol |
| Ca | Capillary number |
| We | Weber number |
References
- Liu, J.; Zhao, J.; Deng, X.; Yang, S.; Xue, C.; Wu, Y.; Tai, R.; Hu, X.; Dai, G.; Li, T. Hybrid application of laser-focused atomic deposition and extreme ultraviolet interference lithography methods for manufacturing of self-traceable nanogratings. Nanotechnology 2021, 32, 175301. [Google Scholar] [CrossRef]
- Berthier, J.; Brakke, K.; Grossi, F.; Sanchez, L.; Di Cioccio, L. Self-alignment of silicon chips on wafers: A capillary approach. J. Appl. Phys. 2010, 108, 054905. [Google Scholar] [CrossRef]
- Tan, H.W.; An, J.; Chua, C.K.; Tran, T. Metallic nanoparticle inks for 3D printing of electronics. Adv. Electron. Mater. 2019, 5, 1800831. [Google Scholar] [CrossRef]
- Oggianu, M.; Monni, N.; Mameli, V.; Cannas, C.; Ashoka Sahadevan, S.; Mercuri, M.L. Designing Magnetic NanoMOFs for Biomedicine: Current Trends and Applications. Magnetochemistry 2020, 6, 39. [Google Scholar] [CrossRef]
- Yan, H.; Qin, Z.; Ciwen, M.; Zhiming, O. Self-calibration of micro-components based on manipulator guidance. J. Micromech. Microeng. 2022, 32, 085005. [Google Scholar] [CrossRef]
- Fan, Z.; Rong, W.; Tian, Y.; Wei, X.; Gao, J. Micro-scale droplet deposition for micro-object self-alignment release based on water condensation. Appl. Phys. Lett. 2019, 114, 013703. [Google Scholar] [CrossRef]
- Tanikawa, T.; Hashimoto, Y.; Arai, T. Micro drops for adhesive bonding of micro assemblies and making a 3-D structure “micro scarecrow”. In Proceedings of the 1998 IEEE/RSJ International Conference on Intelligent Robots and Systems. Innovations in Theory, Practice and Applications (Cat. No. 98CH36190), Victoria, BC, Canada, 17 October 1998; Volume 2, pp. 776–781. [Google Scholar]
- Saito, S.; Motokado, T.; Obata, K.J.; Takahashi, K. Capillary force with a concave probe-tip for micromanipulation. Appl. Phys. Lett. 2005, 87, 234103. [Google Scholar] [CrossRef]
- Vasudev, A.; Zhe, J. A capillary microgripper based on electrowetting. Appl. Phys. Lett. 2008, 93, 103503. [Google Scholar] [CrossRef]
- Wang, L.F.; Guan, N.N.; Rong, W.B.; Sun, L.N. Microobjects gripping with controllable menisci based on pressure adjustment. Appl. Mech. Mater. 2013, 373, 116–121. [Google Scholar] [CrossRef]
- Hagiwara, W.; Ito, T.; Tanaka, K.; Tokui, R.; Fuchiwaki, O. Capillary force gripper for complex-shaped micro-objects with fast droplet forming by on–off control of a piston slider. IEEE Robot. Autom. Lett. 2019, 4, 3695–3702. [Google Scholar] [CrossRef]
- Fan, Z.; Wang, L.; Rong, W.; Sun, L. Dropwise condensation on a hydrophobic probe-tip for manipulating micro-objects. Appl. Phys. Lett. 2015, 106, 084105. [Google Scholar] [CrossRef]
- Shigeta, T.; Aoyama, H.; Hirata, S. Development of multi-needle-type capillary; high DOF micromanipulator using surface tension. In Proceedings of the 2012 IEEE International Conference on Mechatronics and Automation, Chengdu, China, 5–8 August 2012; IEEE: Piscataway, NJ, USA; pp. 819–824. [Google Scholar]
- Zhang, Q.; Wang, H.; Gan, Y.; Huang, W.; Aoyama, H. Method of orientation control and experimental investigation using a liquid-drop micromanipulator. J. Micromech. Microeng. 2017, 27, 045006. [Google Scholar] [CrossRef]
- Tanaka, K.; Ito, T.; Nishiyama, Y.; Fukuchi, E.; Fuchiwaki, O. Double-nozzle capillary force gripper for cubical, triangular prismatic, and helical 1-mm-Sized-Objects. IEEE Robot. Autom. Let. 2021, 7, 1324–1331. [Google Scholar] [CrossRef]
- Chang, B.; Shah, A.; Routa, I.; Lipsanen, H.; Zhou, Q. Low-height sharp edged patterns for capillary self-alignment assisted hybrid microassembly. J. Micro-Bio. Robot. 2014, 9, 1–10. [Google Scholar] [CrossRef]
- Orr, F.; Scriven, L.; Rivas, A.P. Pendular rings between solids: Meniscus properties and capillary force. J. Fluid Mech. 1975, 67, 723–742. [Google Scholar] [CrossRef]
- Willett, C.D.; Adams, M.J.; Johnson, S.A.; Seville, J.P. Capillary bridges between two spherical bodies. Langmuir 2000, 16, 9396–9405. [Google Scholar] [CrossRef]
- Zhao, C.-F.; Kruyt, N.P.; Millet, O. Capillary bridges between unequal-sized spherical particles: Rupture distances and capillary forces. Powder Technol. 2019, 346, 462–476. [Google Scholar] [CrossRef]
- De Souza, E.; Gao, L.; McCarthy, T.; Arzt, E.; Crosby, A. Effect of contact angle hysteresis on the measurement of capillary forces. Langmuir 2008, 24, 1391–1396. [Google Scholar] [CrossRef]
- Shi, Z.; Zhang, Y.; Liu, M.; Hanaor, D.A.; Gan, Y. Dynamic contact angle hysteresis in liquid bridges. Colloids Surf. A Physicochem. Eng. Asp. 2018, 555, 365–371. [Google Scholar] [CrossRef]
- Chen, J.; Wang, P.; Li, M.; Shen, J.; Howes, T.; Wang, G. Rupture distance and shape of the liquid bridge with rough surface. Miner. Eng. 2021, 167, 106888. [Google Scholar] [CrossRef]
- Xu, A.; Chang, H.; Xu, Y.; Li, R.; Li, X.; Zhao, Y. Applying artificial neural networks (ANNs) to solve solid waste-related issues: A critical review. Waste Manag. 2021, 124, 385–402. [Google Scholar] [CrossRef] [PubMed]
- Hsieh, M.C.; Maurya, S.N.; Luo, W.J.; Li, K.Y.; Hao, L.; Bhuyar, P. Coolant volume prediction for spindle cooler with adaptive neuro-fuzzy inference system control method. Sens. Mater. 2022, 34, 2447–2466. [Google Scholar] [CrossRef]
- Liu, Y.-L.; Nisa, E.C.; Kuan, Y.-D.; Luo, W.-J.; Feng, C.-C. Combining deep neural network with genetic algorithm for axial flow fan design and development. Processes 2023, 11, 122. [Google Scholar] [CrossRef]
- Shahbazi, A.; Monfared, M.S.; Thiruchelvam, V.; Fei, T.K.; Babasafari, A.A. Integration of knowledge-based seismic inversion and sedimentological investigations for heterogeneous reservoir. J. Asian Earth Sci. 2020, 202, 104541. [Google Scholar] [CrossRef]
- Khayer, K.; Roshandel Kahoo, A.; Soleimani Monfared, M.; Tokhmechi, B.; Kavousi, K. Target-Oriented fusion of attributes in data level for salt dome geobody delineation in seismic data. Nat. Resour. Res. 2022, 31, 2461–2481. [Google Scholar] [CrossRef]
- Abdou, M.A. Literature review: Efficient deep neural networks techniques for medical image analysis. Neural. Comput. Appl. 2022, 34, 5791–5812. [Google Scholar] [CrossRef]
- Ahadian, S.; Moradian, S.; Sharif, F.; Tehran, M.A.; Mohseni, M. An artificial neural network approach to capillary rise in porous media. Chem. Eng. Commun. 2007, 195, 435–448. [Google Scholar] [CrossRef]
- Taghipour-Gorjikolaie, M.; Motlagh, N.V. Predicting wettability behavior of fluorosilica coated metal surface using optimum neural network. Surf. Sci. 2018, 668, 47–53. [Google Scholar] [CrossRef]
- Zhang, J.; Lin, G.; Yin, X.; Zeng, J.; Wen, S.; Lan, Y. Application of artificial neural network (ANN) and response surface methodology (RSM) for modeling and optimization of the contact angle of rice leaf surfaces. Acta Physiol. Plant. 2020, 42, 51. [Google Scholar] [CrossRef]
- Esfe, M.H.; Bahiraei, M.; Mahian, O. Experimental study for developing an accurate model to predict viscosity of CuO–ethylene glycol nanofluid using genetic algorithm based neural network. Powder Technol. 2018, 338, 383–390. [Google Scholar] [CrossRef]
- Ji, W.; Yang, L.; Chen, Z.; Mao, M.; Huang, J.-N. Experimental studies and ANN predictions on the thermal properties of TiO2-Ag hybrid nanofluids: Consideration of temperature, particle loading, ultrasonication and storage time. Powder Technol. 2021, 388, 212–232. [Google Scholar] [CrossRef]
- Afrand, M.; Najafabadi, K.N.; Sina, N.; Safaei, M.R.; Kherbeet, A.S.; Wongwises, S.; Dahari, M. Prediction of dynamic viscosity of a hybrid nano-lubricant by an optimal artificial neural network. Int. Commun. Heat Mass Transfer 2016, 76, 209–214. [Google Scholar] [CrossRef]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, Sardinia, Italy, 13–15 May 2010; pp. 249–256. [Google Scholar]
- Shin, Y.; Kim, Z.; Yu, J.; Kim, G.; Hwang, S. Development of NOx reduction system utilizing artificial neural network (ANN) and genetic algorithm (GA). J. Cleaner Prod. 2019, 232, 1418–1429. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef]
- Chen, H.; Tang, T.; Amirfazli, A. Fast liquid transfer between surfaces: Breakup of stretched liquid bridges. Langmuir 2015, 31, 11470–11476. [Google Scholar] [CrossRef]
- Bai, S.E.; Shim, J.S.; Lee, C.H.; Bai, C.H.; Shin, K.Y. Dynamic effect of surface contact angle on liquid transfer in a low speed printing process. Jpn. J. Appl. Phys. 2014, 53, 05HC05. [Google Scholar] [CrossRef]
- Fan, Z.; Liu, Z.; Huang, C.; Zhang, W.; Lv, Z.; Wang, L. Capillary Forces between Concave Gripper and Spherical Particle for Micro-Objects Gripping. Micromachines 2021, 12, 285. [Google Scholar] [CrossRef] [PubMed]



| Liquids | μ (Pa s) | γ (mN/m) | ρ (g/cm3) | θs (°) | θr (°) |
|---|---|---|---|---|---|
| Ethylene glycol | 0.021 | 48.4 | 1.11 | 41.7 | 34.4 |
| 50 wt% ethylene glycol | 0.004 | 57 | 1.07 | 50.3 | 40.4 |
| Glycerol | 0.243 | 63.4 | 1.26 | 42.6 | 33.3 |
| Liquids | λc (mm) | Ca | We |
|---|---|---|---|
| Ethylene glycol | 2.109 | 4.34 × 10−6 | 5.28 × 10−4 |
| 50 wt% ethylene glycol | 2.331 | 7.02 × 10−7 | 2.67 × 10−3 |
| Glycerol | 2.266 | 3.83 × 10−5 | 5.18 × 10−5 |
| Models | MSE of Capillary Force | MSE of Contact Diameter | R2 of Capillary Force | R2 of Contact Diameter |
|---|---|---|---|---|
| GA-ANN | 10.3 | 0.0001 | 0.9989 | 0.9977 |
| gANN | 244.706 | 0.0011 | 0.9748 | 0.9764 |
| SE solutions | 865.883 | 0.0268 | 0.9109 | 0.4389 |
| Theoretical solutions | 860.581 | 0.0265 | 0.9114 | 0.4468 |
| Neuron Number | Weight | |||||
|---|---|---|---|---|---|---|
| Liquid Volume (x1) | Separation Distance (x2) | Contact Angle (x3) | Surface Tension (x4) | Capillary Force (t1) | Contact Diameter (t2) | |
| 1 | 0.272 | 2.657 | 3.642 | −1.608 | −0.34 | 1.218 |
| 2 | −0.234 | −3.530 | −0.280 | 1.944 | 0.073 | −1.300 |
| 3 | 0.702 | −1.779 | 1.869 | −1.682 | 0.450 | −0.802 |
| 4 | 1.818 | −1.430 | 0.163 | −1.043 | −0.801 | 0.219 |
| 5 | 1.769 | −1.570 | −0.290 | −0.597 | −0.060 | 0.425 |
| 6 | −3.487 | 1.240 | −0.307 | 0.159 | 2.647 | 0.817 |
| 7 | −2.176 | 1.248 | 0.141 | 0.214 | 2.013 | 1.052 |
| 8 | 2.566 | −4.556 | 0.490 | 1.668 | 0.039 | −0.464 |
| 9 | 1.481 | −1.650 | 0.520 | 1.775 | −0.811 | 0.865 |
| 10 | 0.593 | 2.880 | −0.978 | −1.805 | −0.639 | −0.288 |
| 11 | 0.978 | −4.842 | −0.817 | −0.700 | −0.909 | −0.123 |
| 12 | −1.150 | 2.577 | 0.790 | −0.118 | 0.489 | 0.409 |
| 13 | 0.614 | −0.858 | 3.061 | −1.881 | −0.120 | −0.636 |
| Sum of products for capillary force | −17.970 | 10.159 | −0.076 | 2.239 | - | - |
| Importance of capillary force | 1 | 2 | 4 | 3 | - | - |
| Percentage | 59.0% | 33.3% | 2.4% | 7.3% | - | - |
| Sum of products for contact diameter | −4.975 | 12.646 | 2.093 | −0.747 | - | - |
| Importance of contact diameter | 2 | 1 | 3 | 4 | - | - |
| Percentage | 24.3% | 61.8% | 10.2% | 3.7% | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, C.; Fan, Z.; Fan, M.; Xu, Z.; Gao, J. A Predictive Model of Capillary Forces and Contact Diameters between Two Plates Based on Artificial Neural Network. Micromachines 2023, 14, 754. https://doi.org/10.3390/mi14040754
Huang C, Fan Z, Fan M, Xu Z, Gao J. A Predictive Model of Capillary Forces and Contact Diameters between Two Plates Based on Artificial Neural Network. Micromachines. 2023; 14(4):754. https://doi.org/10.3390/mi14040754
Chicago/Turabian StyleHuang, Congcong, Zenghua Fan, Ming Fan, Zhi Xu, and Jun Gao. 2023. "A Predictive Model of Capillary Forces and Contact Diameters between Two Plates Based on Artificial Neural Network" Micromachines 14, no. 4: 754. https://doi.org/10.3390/mi14040754
APA StyleHuang, C., Fan, Z., Fan, M., Xu, Z., & Gao, J. (2023). A Predictive Model of Capillary Forces and Contact Diameters between Two Plates Based on Artificial Neural Network. Micromachines, 14(4), 754. https://doi.org/10.3390/mi14040754






