Molecular Dynamics Simulation Study on the Influence of the Abrasive Flow Process on the Cutting of Iron-Carbon Alloys (α-Fe)
Abstract
1. Introduction
2. Materials and Methods
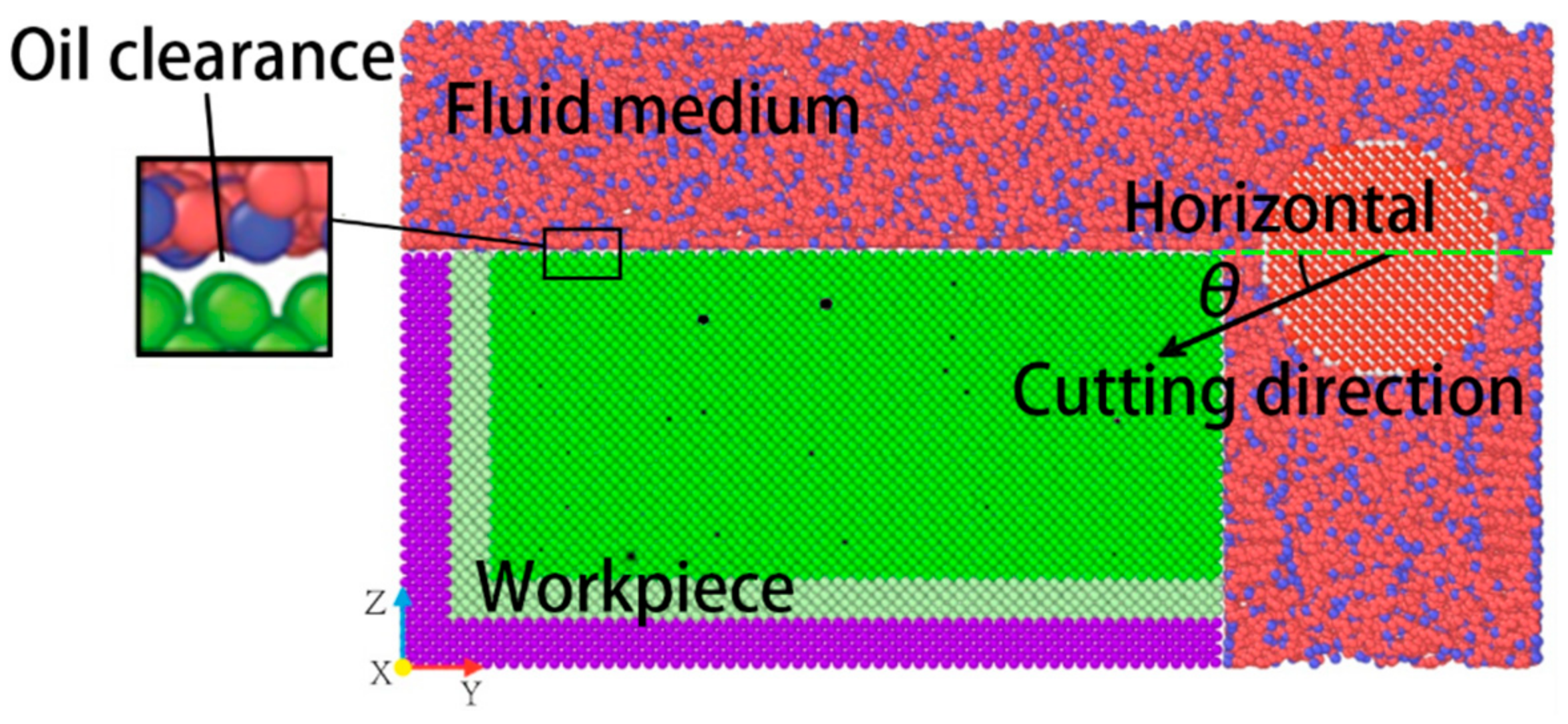
2.1. Model Building
2.2. Interatomic Potentials
2.3. Simulation Environment
3. Results and Discussion
3.1. Analysis of Liquid Phase Flow State and Effect
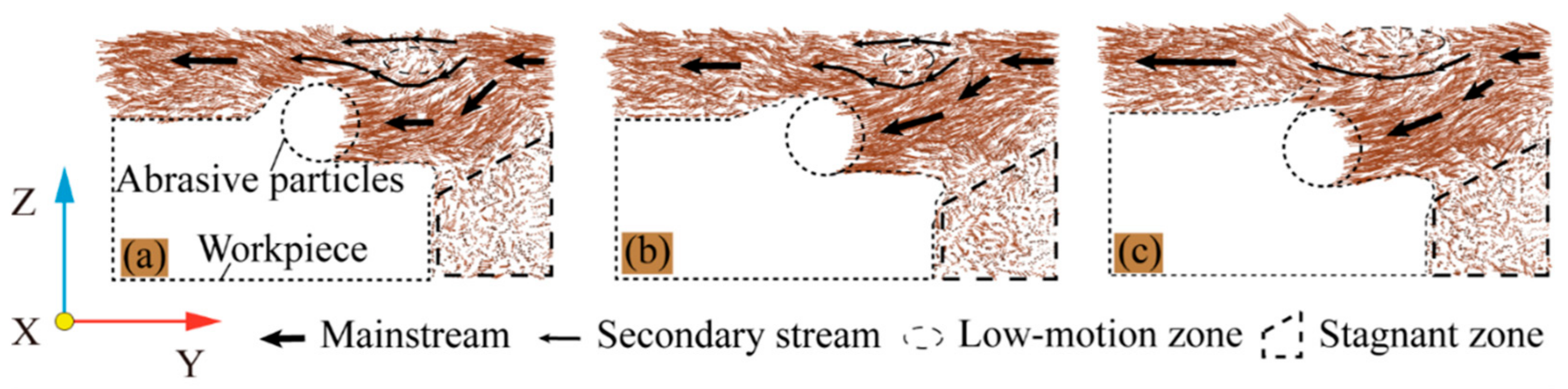
3.1.1. Analysis of Fluid Medium Flow State
3.1.2. Effect of Fluid Medium on Workpiece Temperature
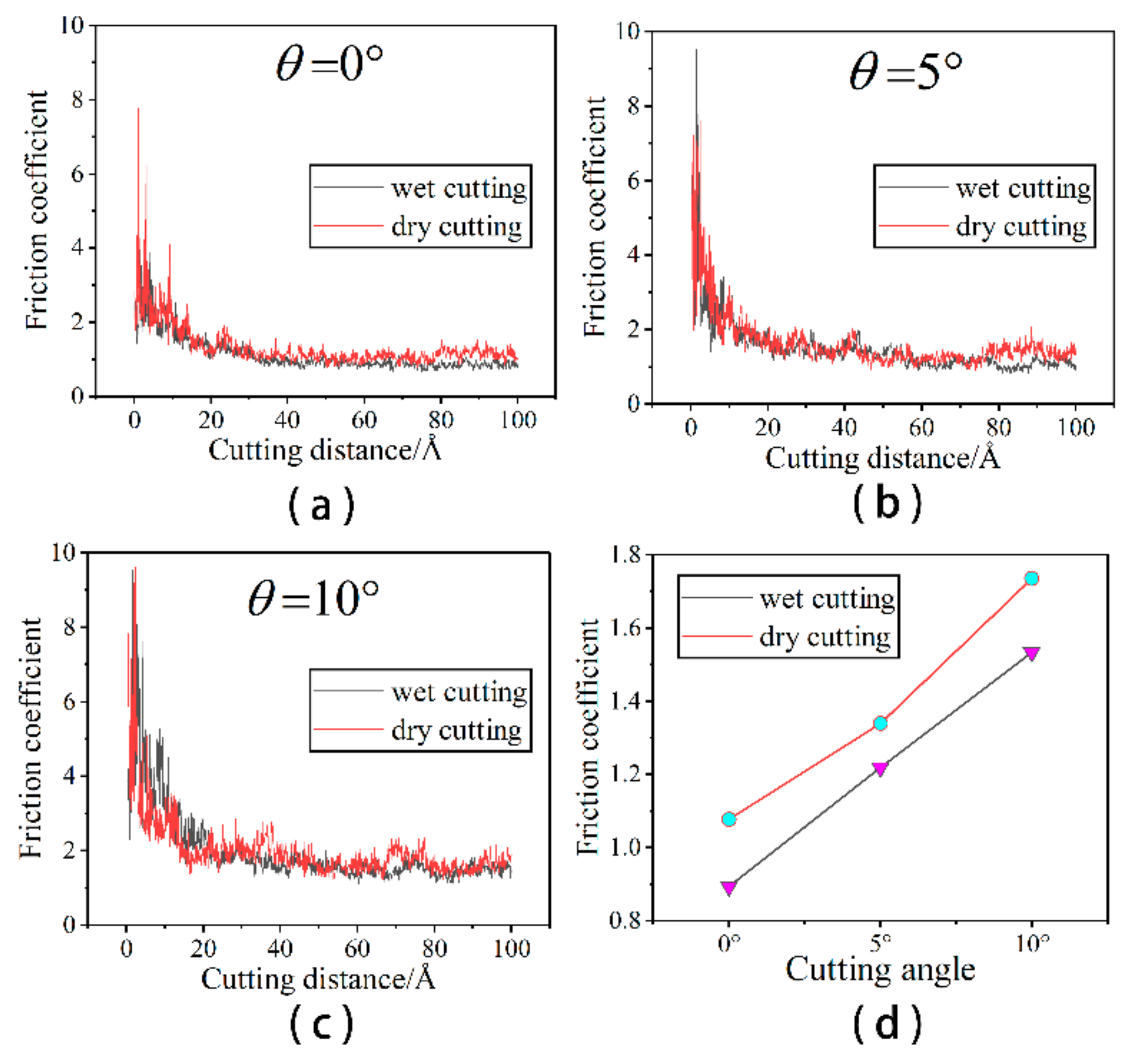
3.1.3. Effect of Fluid Medium on Friction Coefficient
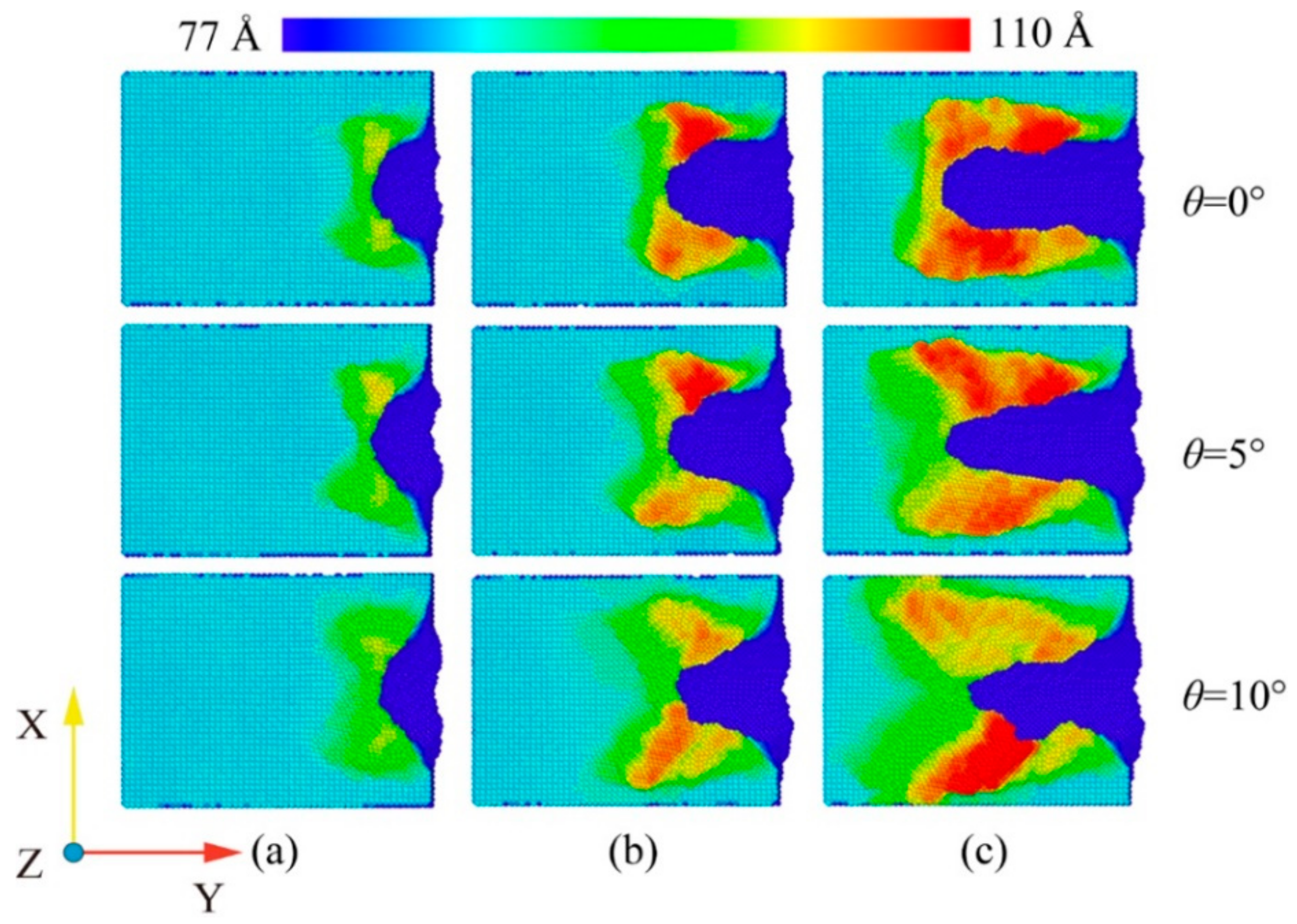
3.2. Evolution of Workpiece Surface Morphology
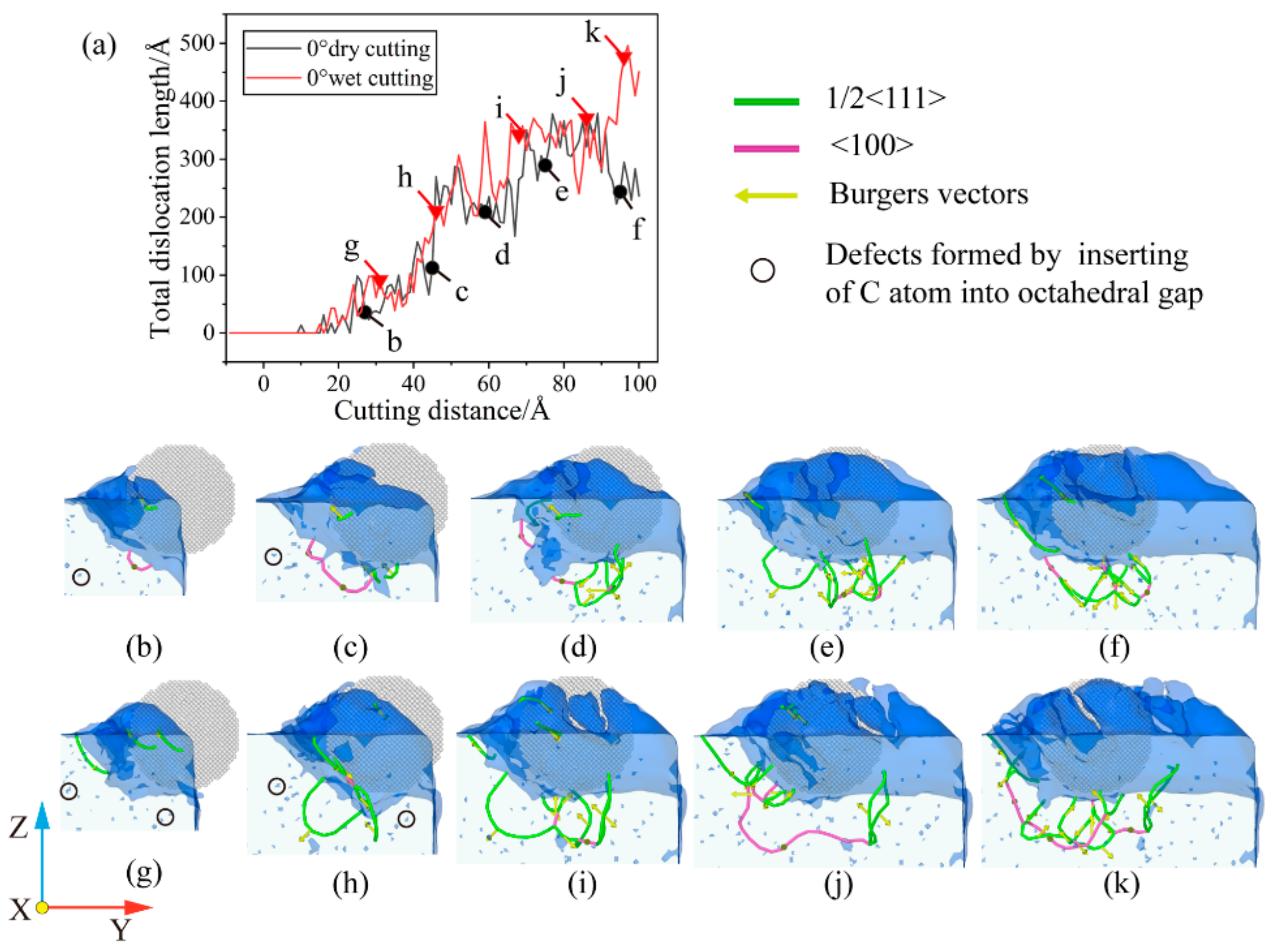
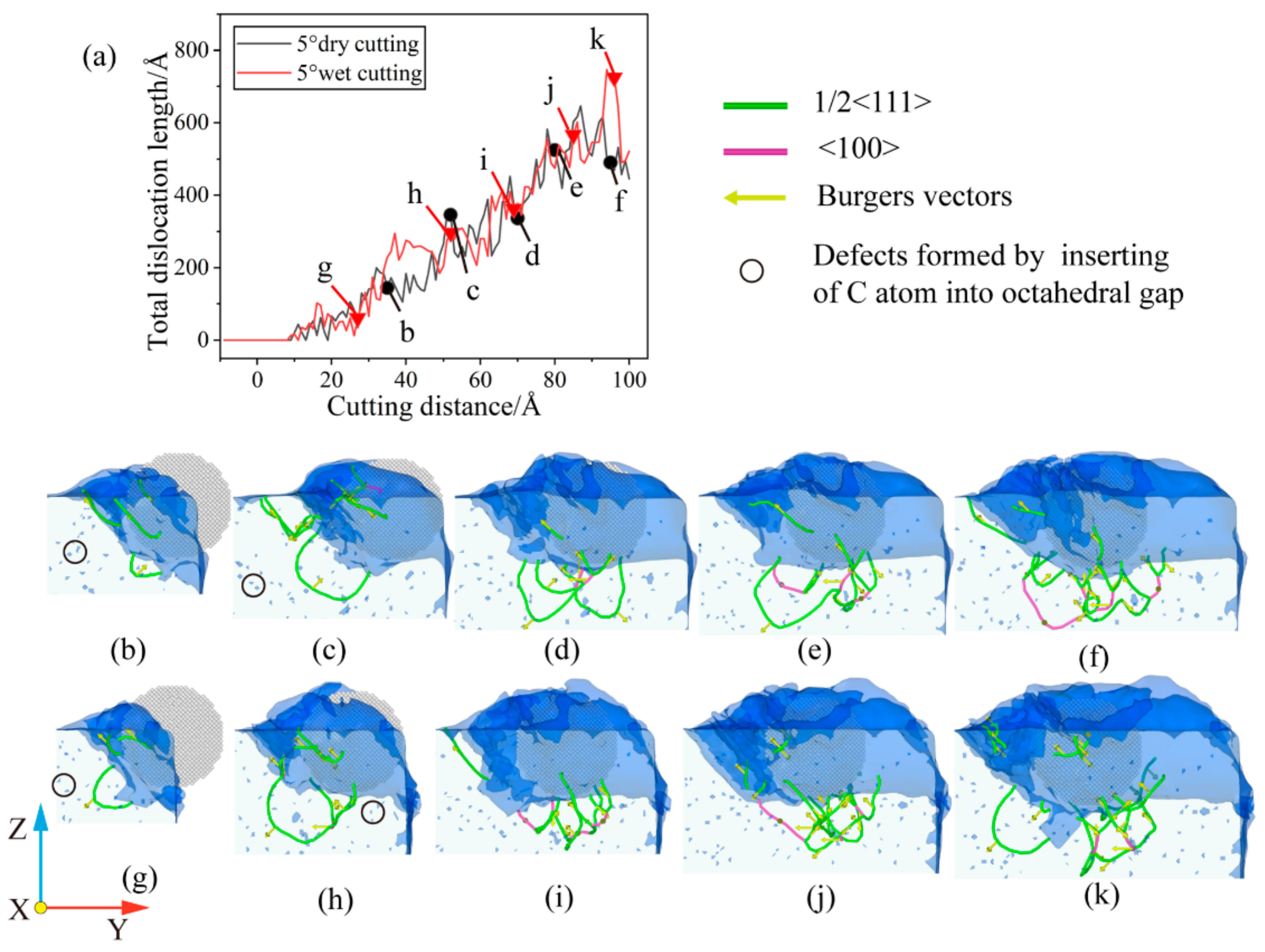
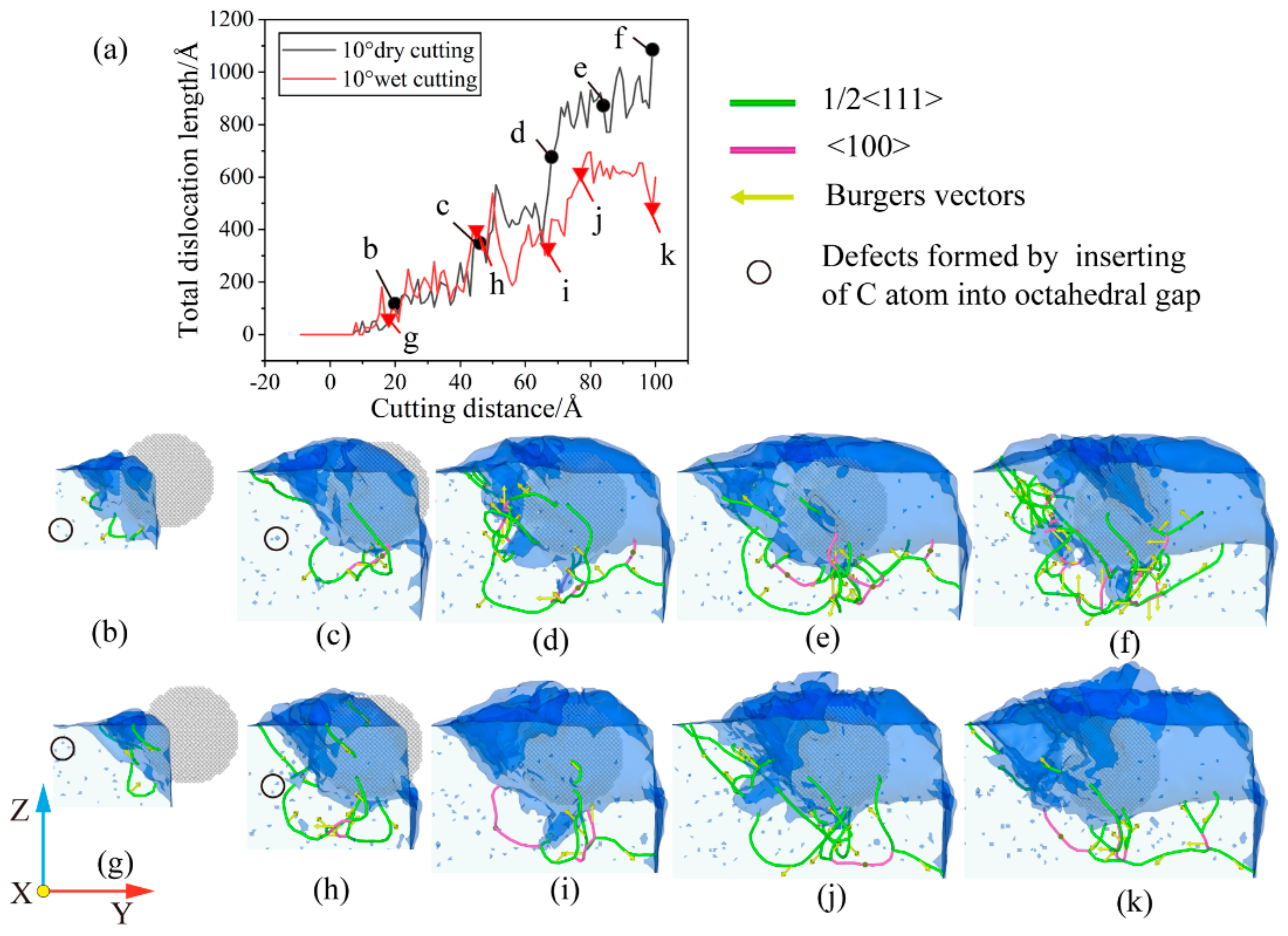
3.3. Analysis of Dislocation Evolution
4. Conclusions
- In comparison to machining without a fluid medium, machining using a fluid medium () lowers the machining temperature and the coefficient of friction.
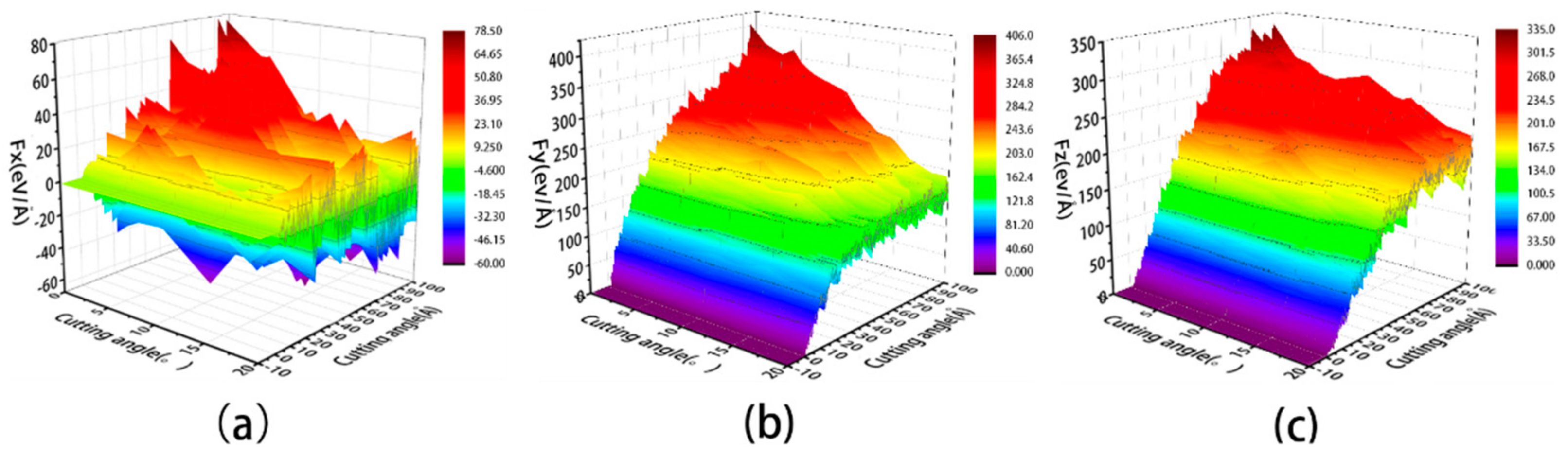
- Temperature and coefficient of friction increase with increasing cutting angle during abrasive flow machining.
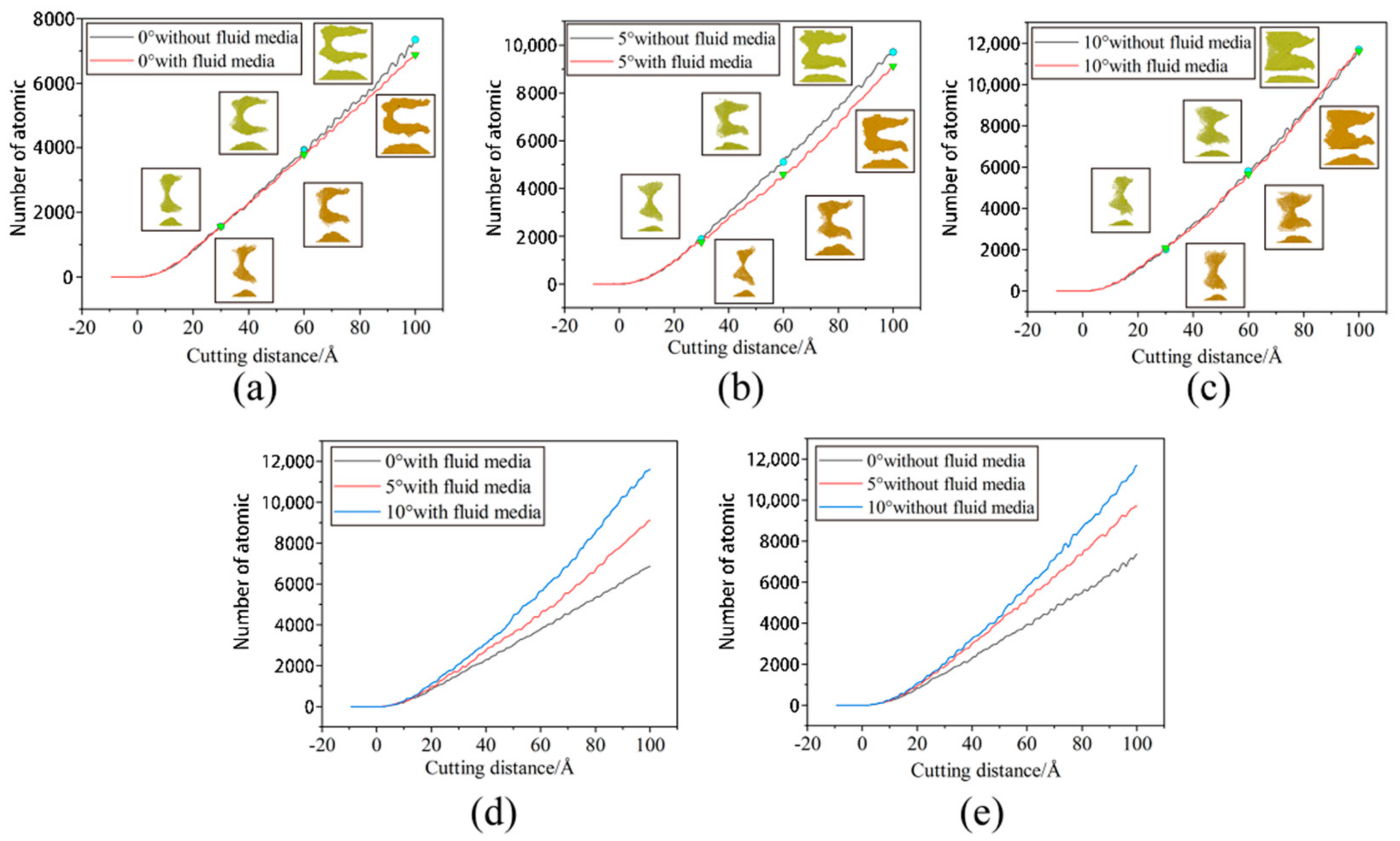
- The cutting angle has a greater influence on the formation of the workpiece’s surface profile and the manner in which the workpiece atoms are displaced, whereas the fluid medium has a lesser influence. When the cutting angle is 0°, 5° and 10°, respectively, the workpiece’s surface profile flows at 45° to both sides. The height of the atomic accumulation on the workpiece’s surface gradually decreases, but at the same time the area where displacement changes occur becomes larger. As the cutting angle increases, so does the depth of cut, resulting in more material damage.
- The area of displacement gradually expands towards the interior of the workpiece as the cutting angle increases. The number of atoms displaced to the workpiece’s surface decreases and remains within the workpiece. The atoms that accumulate inside the workpiece squeeze the uncut area, causing a bulge in the workpiece’s surface, which degrades the workpiece’s quality, but is beneficial for the removal of large burrs.
- During the cutting process, a large number of dislocations were discovered at b = 1/2 <1 1 1> and b = <1 0 0>. The b = 1/2 <1 1 1> dislocations dominate, with b = <1 0 0> connecting the dislocations in different areas. The dislocation reaction network is formed by the presence of a large number of single and double-branched structures within the workpiece. During large-angle cutting, the fluid medium can reduce the number of dislocations and the total dislocation length, which in turn reduces the generation of sub-surface defect structures, resulting in better machining quality.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Guo, P. Research on the Evaluation of Nano-Surface Roughness in Ultra-Precision Machining. Master’s Thesis, Nanchang University, Nanchang, China, 2022. [Google Scholar] [CrossRef]
- Wang, Y.; Yuan, Z.W.; Zhang, Y.J. Overview of material removal theory in ultra-precision machining. Mech. Des. Manuf. 2022, 147–150+155. [Google Scholar] [CrossRef]
- Gou, Y. Research on Sub-Surface Damage of Single Crystal Tungsten Cutting Based on Molecular Dynamics. Master’s Thesis, Dalian University of Technology, Dalian, China, 2021. [Google Scholar] [CrossRef]
- Yang, S.; Cao, H.; Liu, Y.; Yao, P.; Feng, R. Molecular dynamics simulation of the effect of rough surface on material removal and subsurface defects during γ-TiAl processing. Rare Met. Mater. Eng. 2022, 51, 3236–3243. [Google Scholar]
- Du, M. Fundamental Study on the Evolution of Subsurface Defects in Ultra-Precision-Cut Single-Crystal Copper Based on Molecular Dynamics Simulation. Master’s Thesis, Huaqiao University, Quanzhou, China, 2022. [Google Scholar] [CrossRef]
- Liu, H.; Guo, Y.; Li, D.; Wang, J. Material Removal Mechanism of FCC Single-Crystalline Materials at Nano-Scales: Chip Removal & Ploughing. J. Mater. Process. Technol. 2021, 294, 117106. [Google Scholar] [CrossRef]
- Yue, H. Study on the Removal Mechanism of Monocrystalline Silicon by Three-Body Polishing with Diamond Abrasive Based on Molecular Dynamics. Master’s Thesis, Guizhou University, Guiyang, China, 2022. [Google Scholar] [CrossRef]
- Ma, Z.; Liang, G.; Lu, M. Molecular dynamics research on anisotropic nano-cutting of monocrystalline silicon. Mech. Des. Manuf. 2021, 8, 99–102. [Google Scholar] [CrossRef]
- Gao, Y.; Urbassek, H.M. Evolution of plasticity in nanometric cutting of Fe single crystals. Appl. Surf. Sci. 2014, 317, 6–10. [Google Scholar] [CrossRef]
- Ma, T.; Xie, H. Mechanism of formation of face-centered cubic phase in single crystal iron along [101] during crystal orientation impact. J. Phys. 2020, 69, 111–121. [Google Scholar]
- Lian, T. Research on Nano-Mechanical Properties and Deformation Mechanism of Single Crystal Iron Carbide. Master’s Thesis, Huaqiao University, Quanzhou, China, 2022. [Google Scholar] [CrossRef]
- Li, X.; Yin, Y.; Zhang, Y. Point defect types and concentration pairs Molecular dynamics simulation of the effect of plastic deformation behavior of α-Fe. Rare Met. Mater. Eng. 2022, 51, 2881–2889. [Google Scholar]
- Wei, W.; Yu, X. Molecular dynamics study on the effect of lithium on the tensile mechanical behavior of ferrite. J. Univ. Chin. Acad. Sci. 2022, 39, 13–20. [Google Scholar]
- Alhafez, I.A.; Urbassek, H.M. Influence of the Rake Angle on Nanocutting of Fe Single Crystals: A Molecular-Dynamics Study. Crystals 2020, 10, 516. [Google Scholar] [CrossRef]
- Zamzamian, S.M.; Feghhi, S.A.H.; Samadfam, M. A study on the mobility of ½<111> {011} edge dislocation in low-carbon α-Fe and its interactions with damage cascade: On picosecond time scale using molecular dynamics simulations. J. Nucl. Mater. 2019, 527, 151806. [Google Scholar] [CrossRef]
- Jiao, Y.; Dan, W.; Zhang, W. The strain-induced martensitic phase transformation of Fe–C alloys considering C addition: A molecular dynamics study. J. Mater. Res. 2020, 35, 1803–1816. [Google Scholar] [CrossRef]
- Luu, H.-T.; Gunkelmann, N. Pressure-induced phase transformations in Fe-C: Molecular dynamics approach. Comput. Mater. Sci. 2019, 162, 295–303. [Google Scholar] [CrossRef]
- Martin, M.G.; Siepmann, J.I. Transferable Potentials for Phase Equilibria. 1. United-Atom Description of n-Alkanes. J. Phys. Chem. B 1998, 102, 2569–2577. [Google Scholar] [CrossRef]
- Zheng, X.; Zhu, H.; Kosasih, B.; Tieu, A.K. A molecular dynamics simulation of boundary lubrication: The effect of n-alkanes chain length and normal load. Wear 2013, 301, 62–69. [Google Scholar] [CrossRef]
- Liyanage, L.S.I.; Kim, S.-G.; Houze, J.; Kim, S.; Tschopp, M.A.; Baskes, M.I.; Horstemeyer, M.F. Structural, elastic, and thermal properties of cementite (Fe3C) calculated using a modified embedded atom method. Phys. Rev. B 2014, 89, 094102. [Google Scholar] [CrossRef]
- Girifalco, L.A.; Weizer, V.G. Application of the Morse Potential Function to Cubic Metals. Phys. Rev. 1959, 114, 687–690. [Google Scholar] [CrossRef]
- Hegab, H.; Umer, U.; Soliman, M.; Kishawy, H.A. Effects of nano-cutting fluids on tool performance and chip morphology during machining Inconel 718. Int. J. Adv. Manuf. Technol. 2018, 96, 3449–3458. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Stukowski, A.; Albe, K. Extracting dislocations and non-dislocation crystal defects from atomistic simulation data. Model. Simul. Mater. Sci. Eng. 2010, 18, 085001. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Ruda, M.; Farkas, D.; Garcia, G. Atomistic simulations in the Fe–C system. Comput. Mater. Sci. 2009, 45, 550–560. [Google Scholar] [CrossRef]
- Cao, H.; Zhang, T.; Chen, Y. Research on Cooling Methods for Cutting Fluids. Equip. Manag. Maint. 2021, 5, 144–145. [Google Scholar] [CrossRef]
- Yang, Y. Study on the Characteristics of Coolant Temperature Field Change during High Speed Cutting. Master’s Thesis, Yanshan University, Qinhuangdao, China, 2018. [Google Scholar]
- Doan, D.-Q.; Fang, T.-H.; Chen, T.-H. Nanotribological characteristics and strain hardening of amorphous Cu64Zr36/ crystalline Cu nanolaminates. Tribol. Int. 2020, 147, 106275. [Google Scholar] [CrossRef]
- Pan, C.; Wang, C.; Li, W.; Wang, Y.; Yuan, Y.; Wu, H. Development and practical testing of a special micro-lubrication cutting fluid for titanium alloy. Mould. Manuf. 2022, 22, 70–75. [Google Scholar]
- Yang, Y. Research on the Application of Micro-Lubrication Technology of Green Nano Cutting Fluid. Master’s Thesis, Hangzhou University of Electronic Science and Technology, Hangzhou, China, 2020. [Google Scholar] [CrossRef]
- Wang, H. Cutting Numerical Simulation and Cutter Roller Optimization Design of Drum Chipper. Master’s Thesis, Northeast Forestry University, Harbin, China, 2019. [Google Scholar] [CrossRef]
- Smith, R.; Christopher, D.; Kenny, S.D.; Richter, A.; Wolf, B. Defect generation and pileup of atoms during nanoindentation of Fe single crystals. Phys. Rev. B 2003, 67, 245405. [Google Scholar] [CrossRef]
- Katzarov, I.H.; Drenchev, L.B. Unveiling the Mechanisms of High-Temperature 1/2[111] Screw Dislocation Glide in Iron–Carbon Alloys. Crystals 2022, 12, 518. [Google Scholar] [CrossRef]
- Li, S.; Chen, Z.; Yun, J.; Zhang, J. Phase-field crystal method investigated the dislocation annihilation and grain boundary migration in grain shrink process. Acta Phys. Sin. 2014, 63, 128101. [Google Scholar] [CrossRef]







| Parameters | Values |
|---|---|
| Workpiece | Iron–carbon alloy |
| Lattice structure | BCC |
| Workpiece orientation | [100], [010], [001] |
| Workpiece size | 114.52 Å × 171.78 Å × 85.89 Å |
| Abrasive particle | SiC |
| Radius of abrasive particle | 25 Å |
| Atomic number of workpiece | 147,773 |
| Atomic number of abrasive particle | 6287 |
| Molecular number of fluid medium | 62,064 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Zhao, Z.; Li, J.; Xiao, F.; Qiu, R.; Xie, H.; Meng, W. Molecular Dynamics Simulation Study on the Influence of the Abrasive Flow Process on the Cutting of Iron-Carbon Alloys (α-Fe). Micromachines 2023, 14, 703. https://doi.org/10.3390/mi14030703
Li J, Zhao Z, Li J, Xiao F, Qiu R, Xie H, Meng W. Molecular Dynamics Simulation Study on the Influence of the Abrasive Flow Process on the Cutting of Iron-Carbon Alloys (α-Fe). Micromachines. 2023; 14(3):703. https://doi.org/10.3390/mi14030703
Chicago/Turabian StyleLi, Junye, Zhenguo Zhao, Junwei Li, Fujun Xiao, Rongxian Qiu, Hongcai Xie, and Wenqing Meng. 2023. "Molecular Dynamics Simulation Study on the Influence of the Abrasive Flow Process on the Cutting of Iron-Carbon Alloys (α-Fe)" Micromachines 14, no. 3: 703. https://doi.org/10.3390/mi14030703
APA StyleLi, J., Zhao, Z., Li, J., Xiao, F., Qiu, R., Xie, H., & Meng, W. (2023). Molecular Dynamics Simulation Study on the Influence of the Abrasive Flow Process on the Cutting of Iron-Carbon Alloys (α-Fe). Micromachines, 14(3), 703. https://doi.org/10.3390/mi14030703






