RC Bridge Oscillation Memristor Chaotic Circuit for Electrical and Electronic Technology Extended Simulation Experiment
Abstract
:1. Introduction
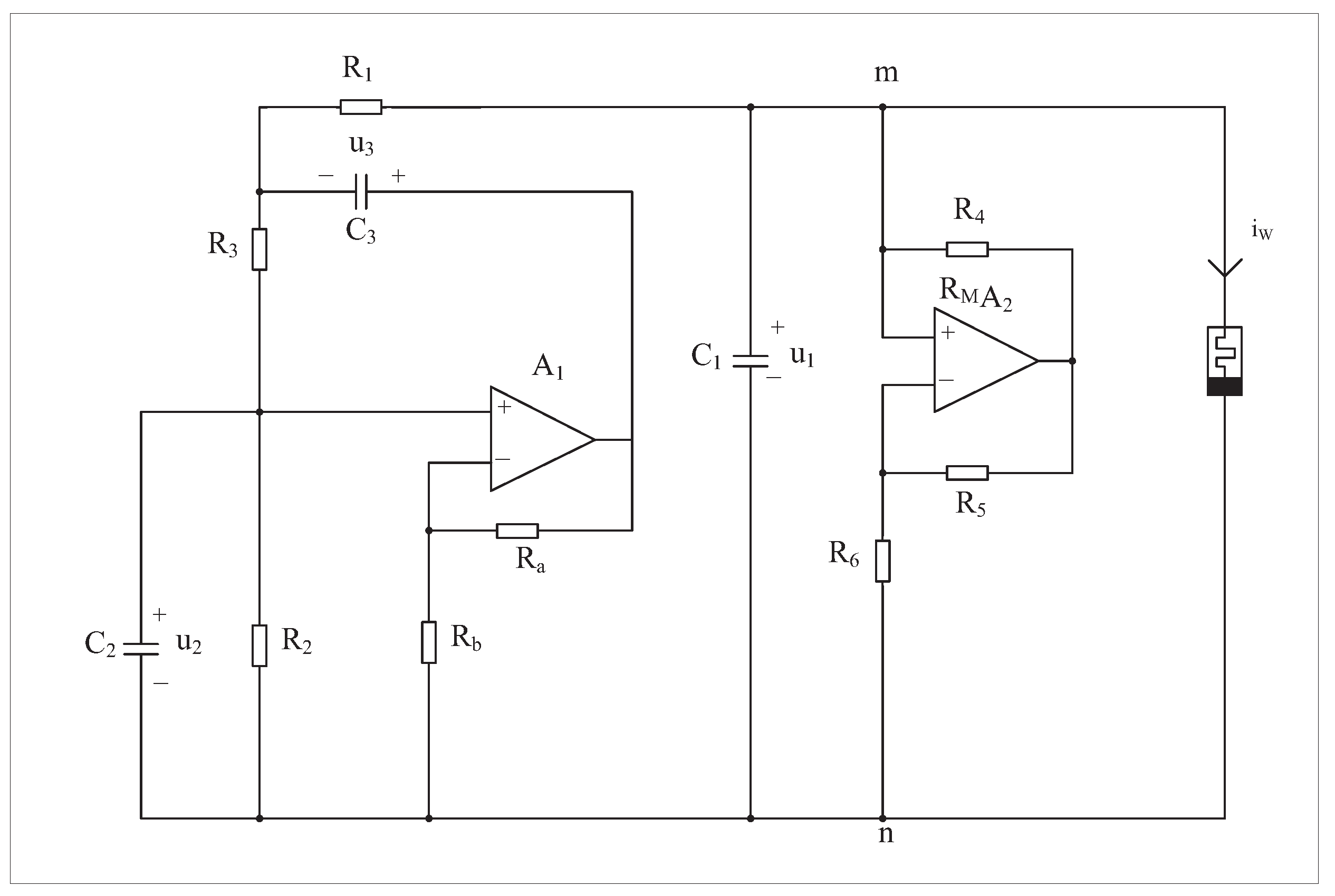
2. Chaotic Circuit Based on Quadratic Smooth Model of Memristor
3. Dynamical Behavior of Chaotic System
3.1. Equilibrium Point and Stability Analysis
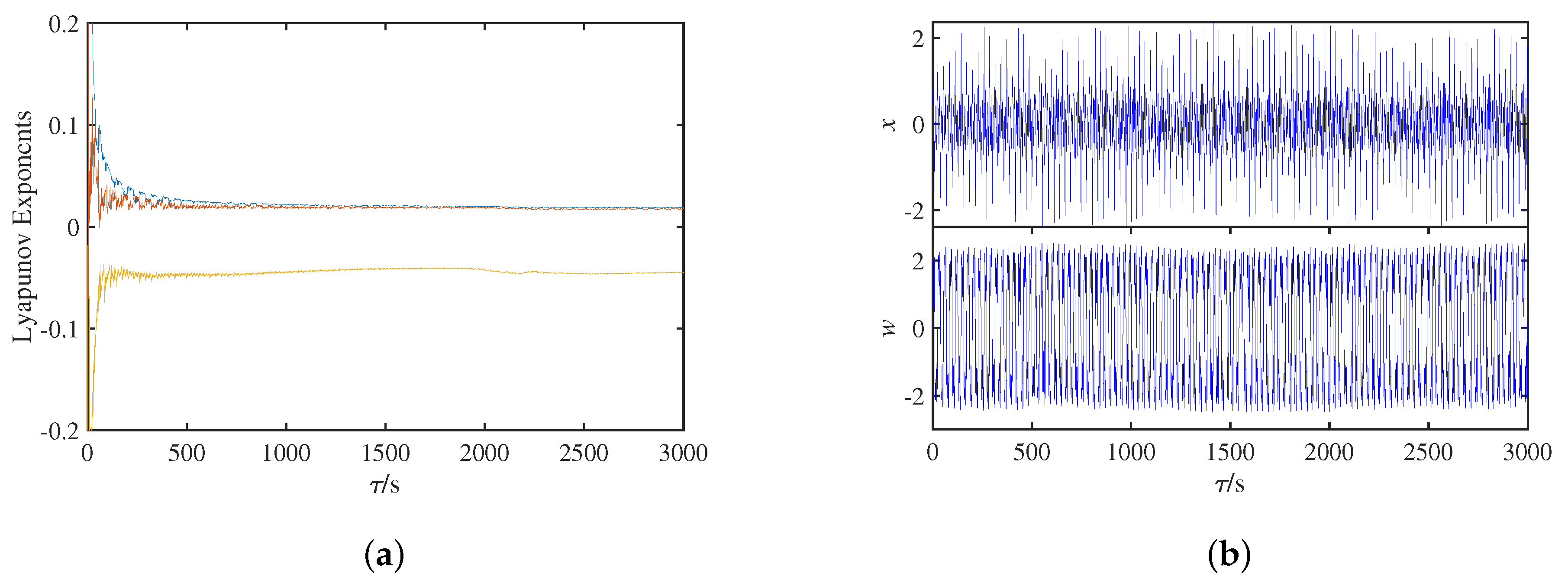
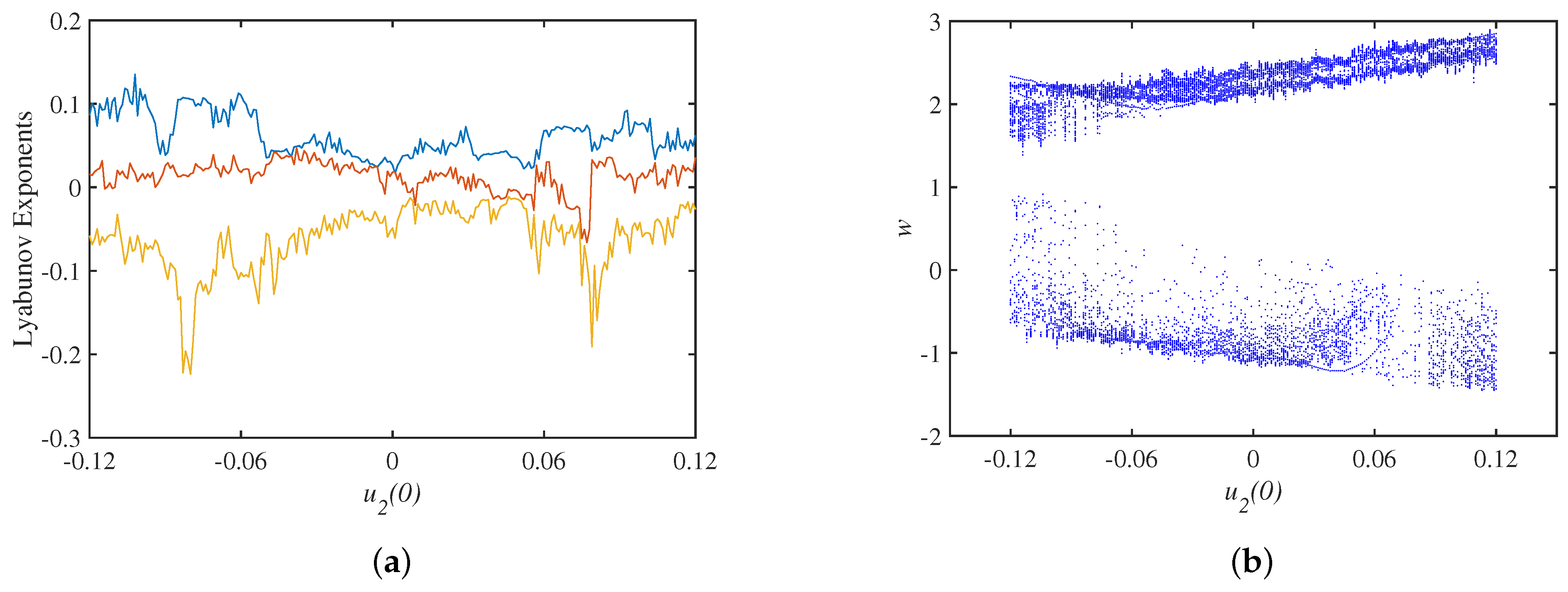
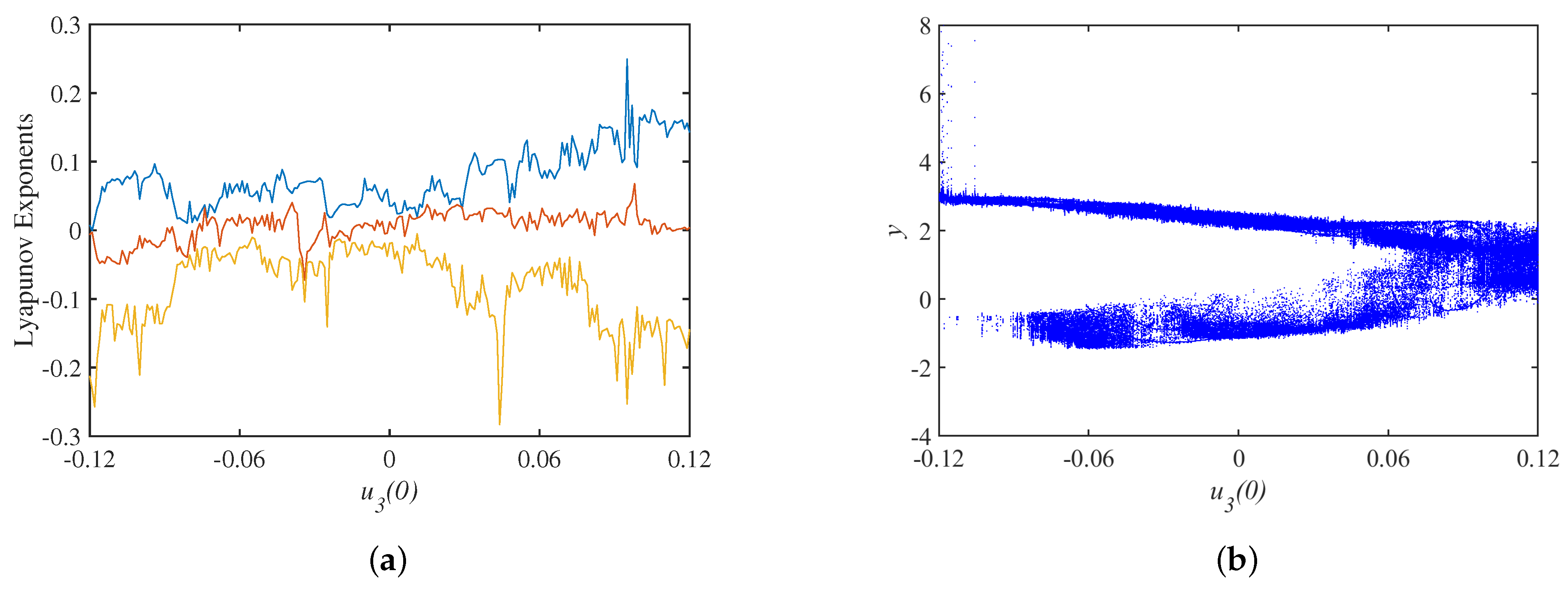
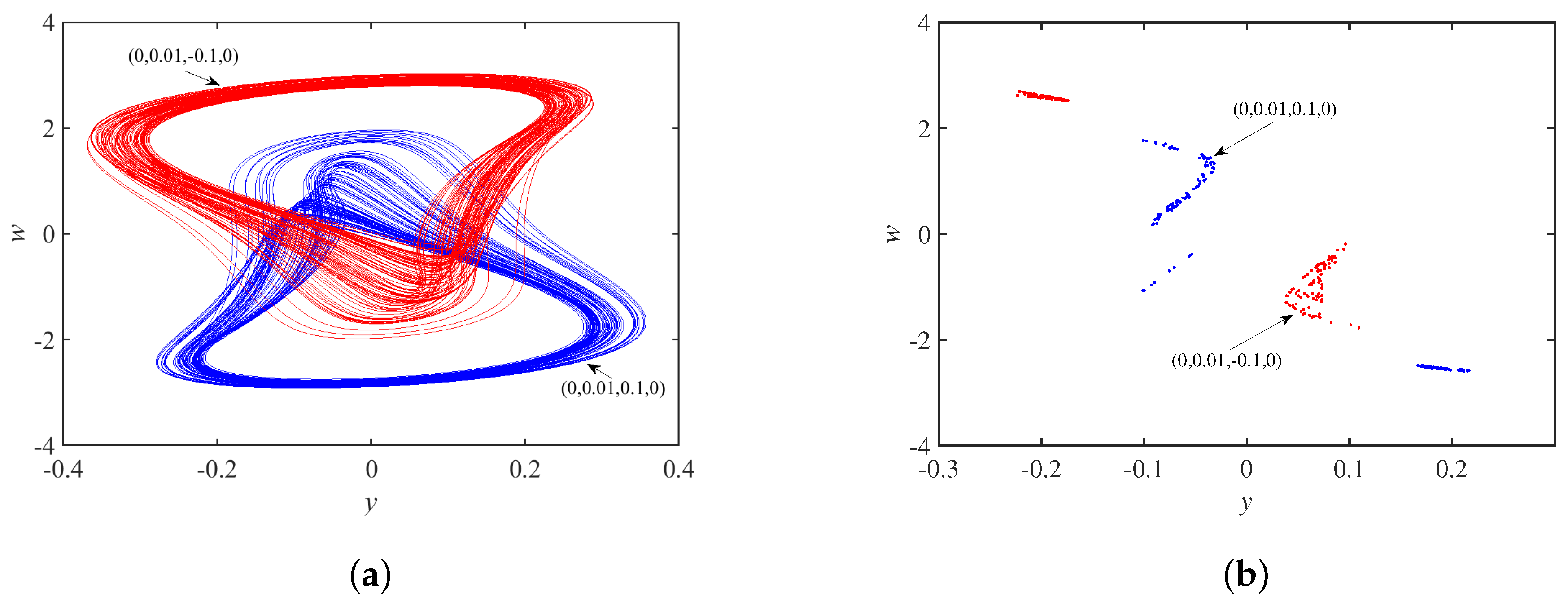
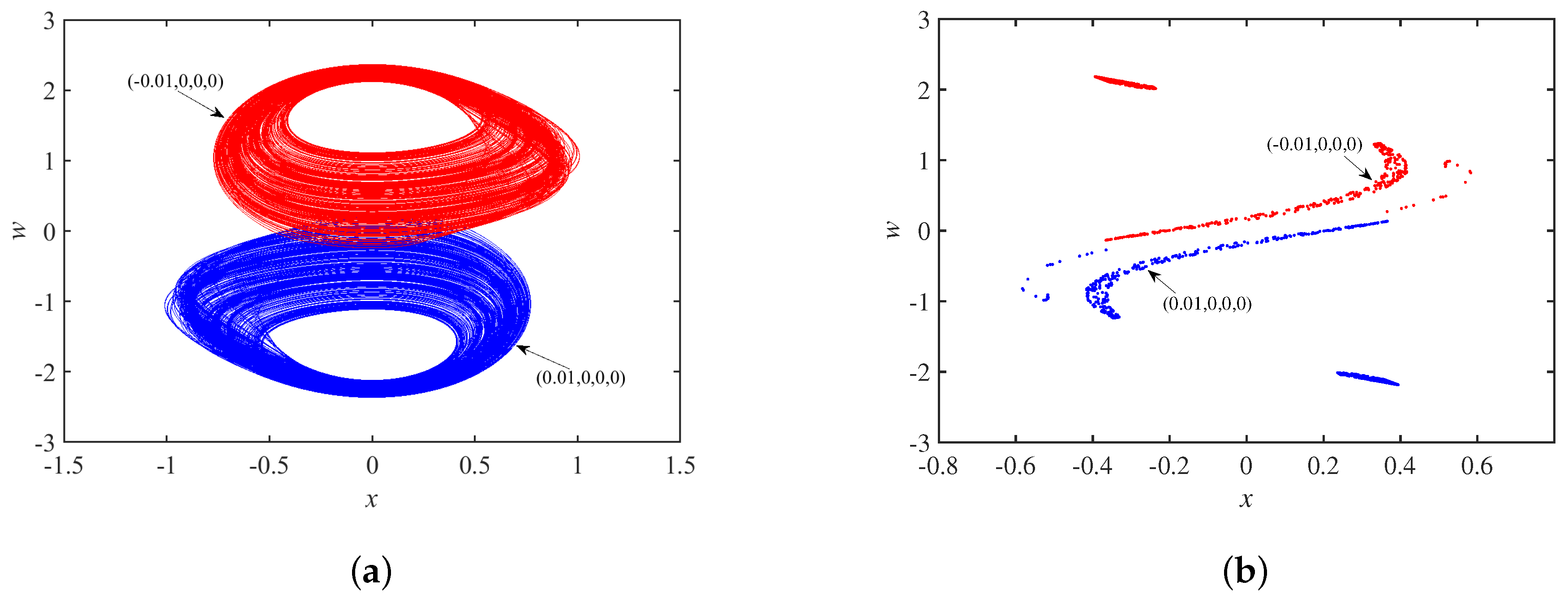
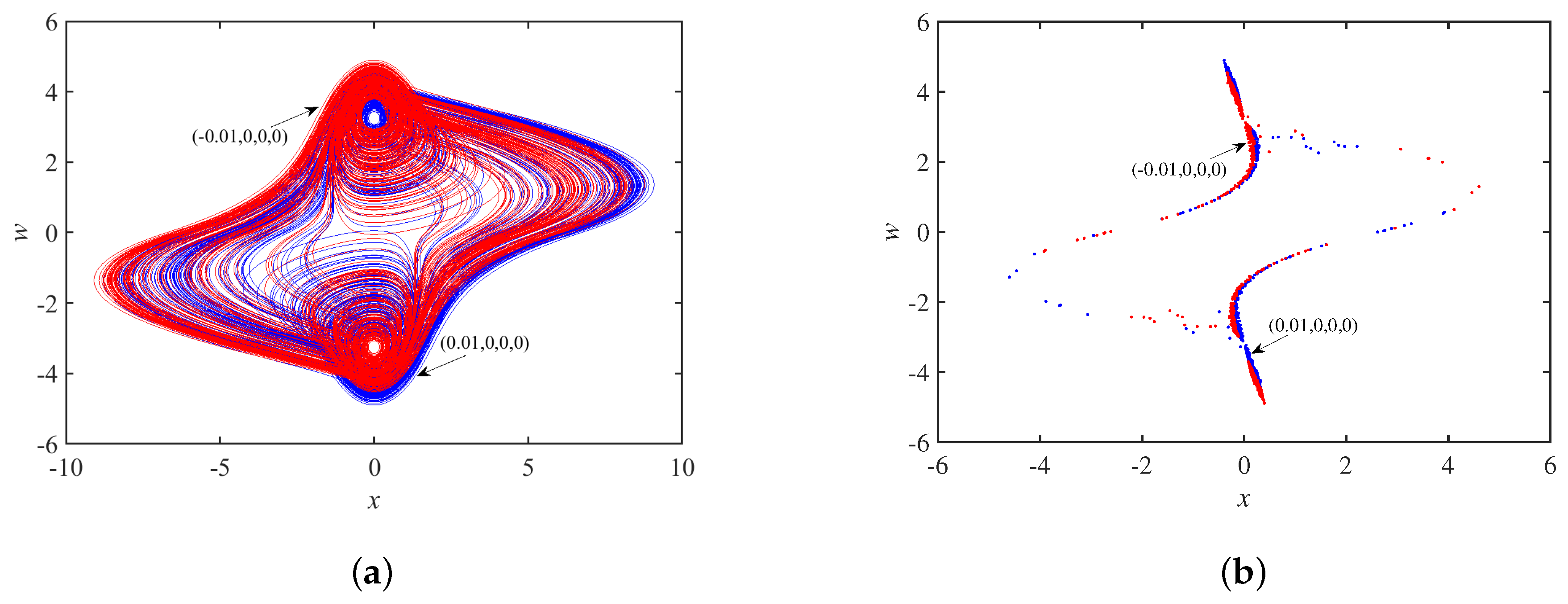
3.2. Dynamics Analysis with Initial Values
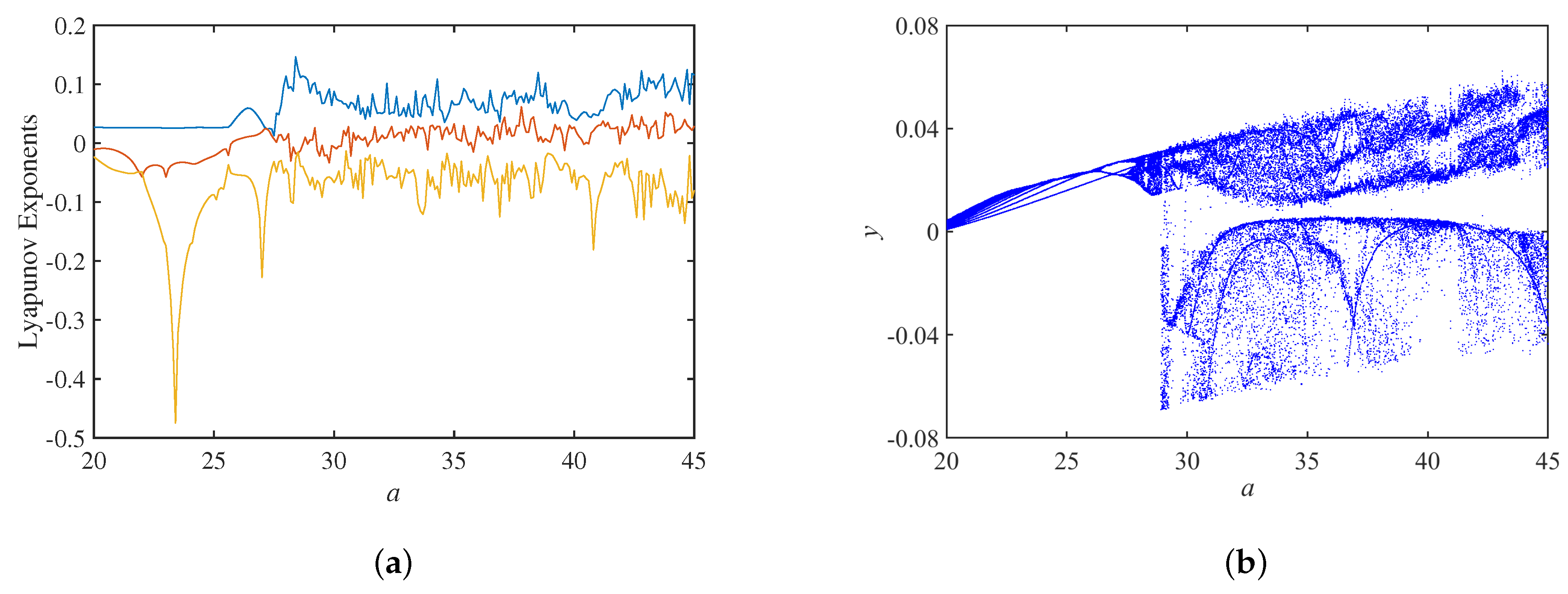
3.3. Dynamic Analysis of Circuit Parameter Variation
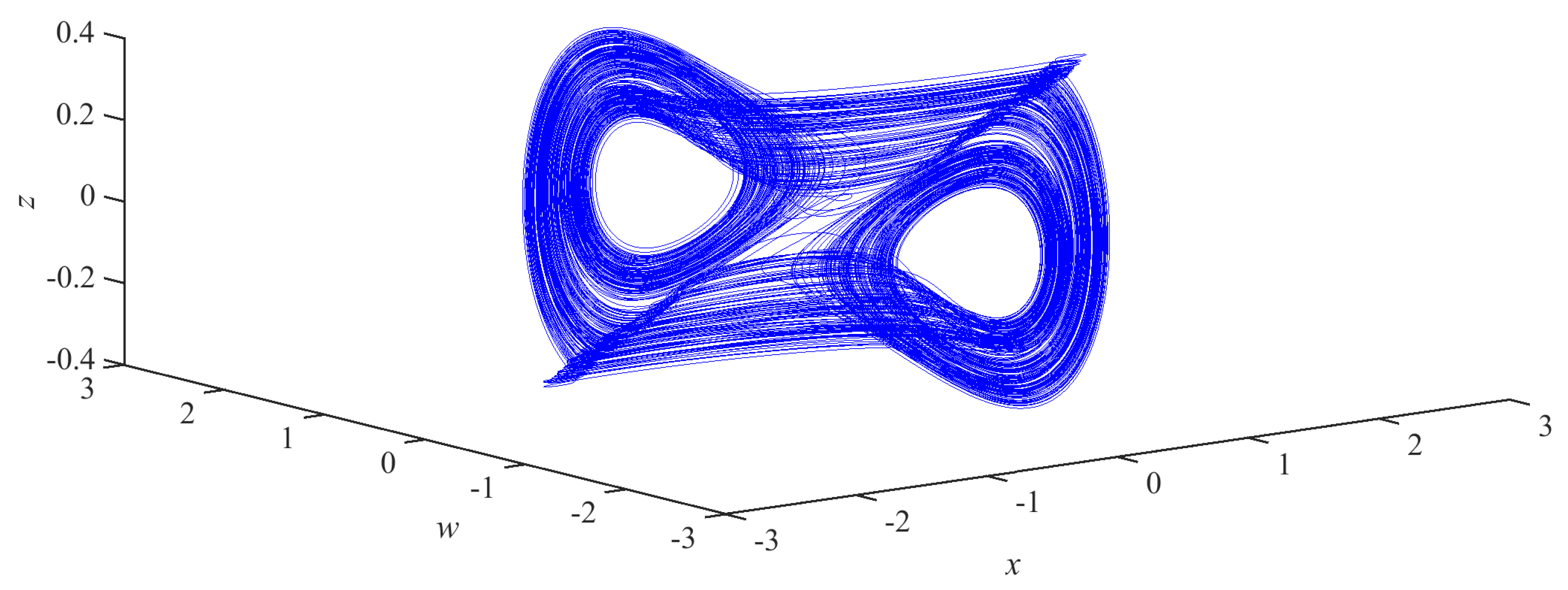
3.4. Coexistence Phenomenon
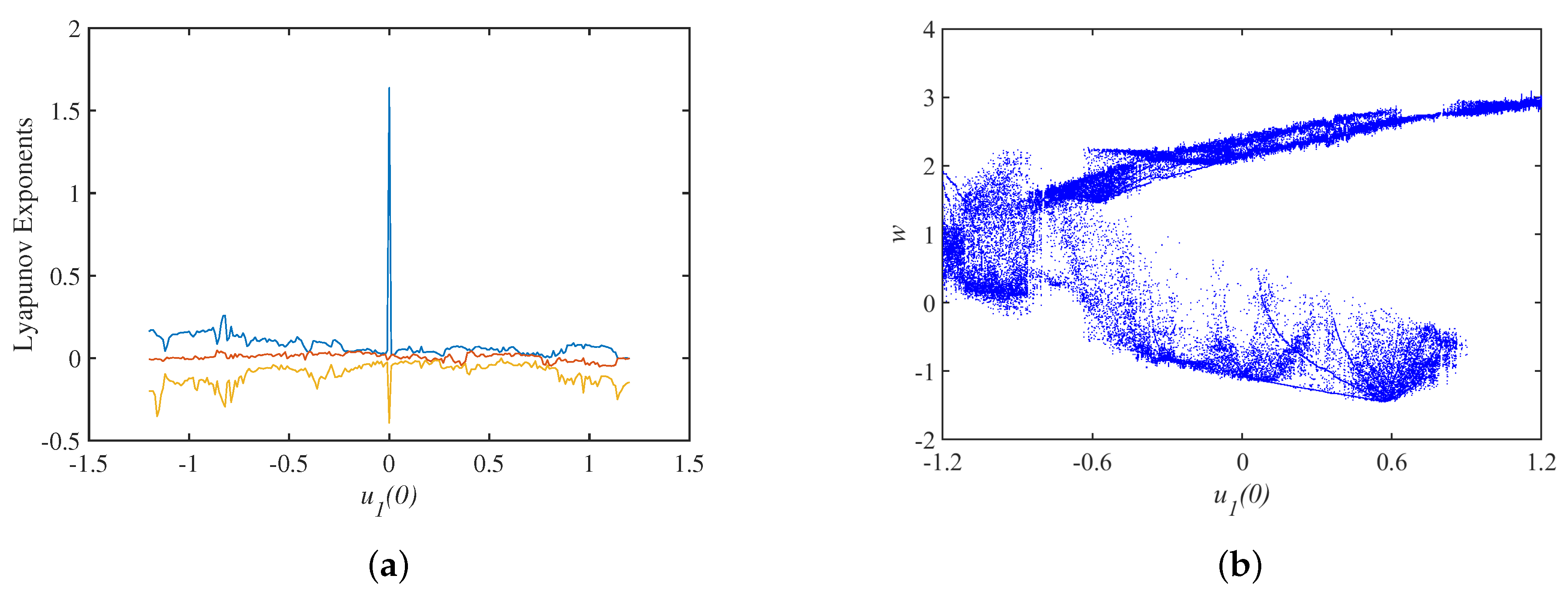
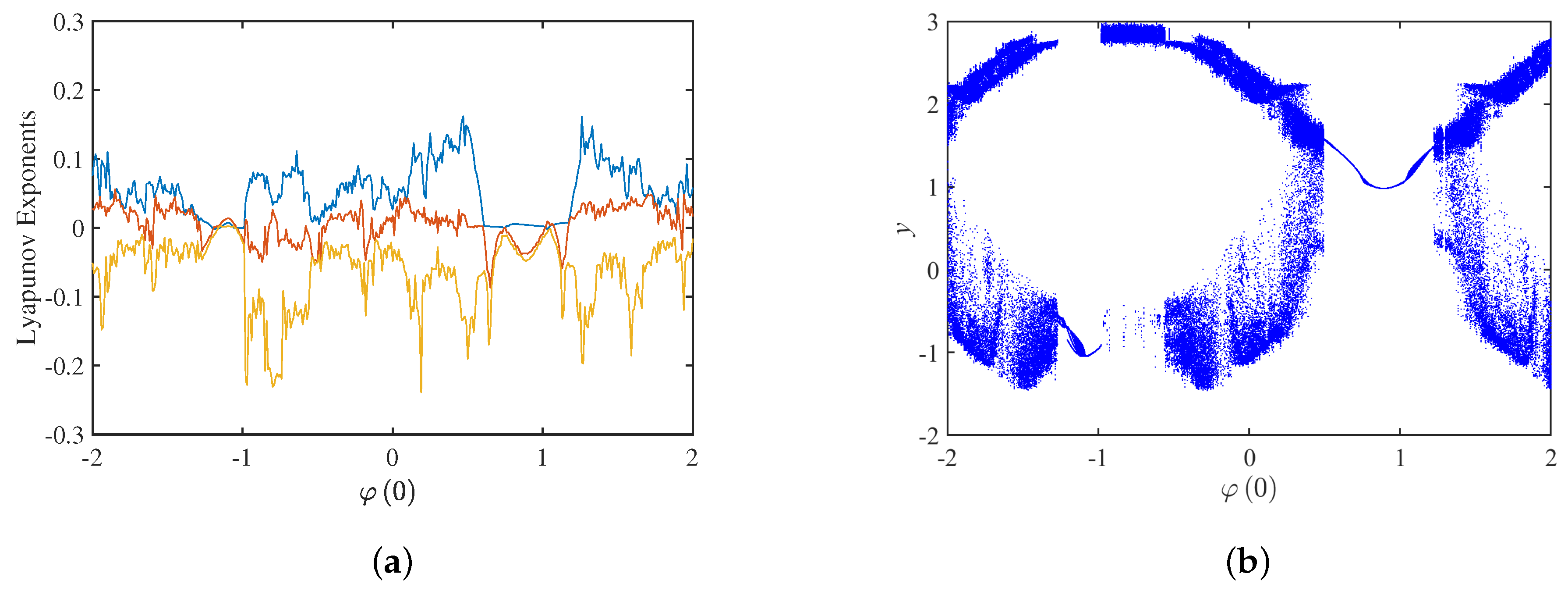
4. The Complex Dynamical Behavior Exhibited by the Change of Initial State φ(0)
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Name | Implication |
| SBT | |
| The amplification of OP-AMP1 | |
| a | |
| b | |
| c | |
| The voltage of the capacitor | |
| The voltage of the capacitor | |
| The voltage of the capacitor | |
| The internal flux of the SBT memristor |
References
- Chua, L. Memristor-The missing circuit element. IEEE Trans. Circuit Theory 1971, 18, 507–519. [Google Scholar] [CrossRef]
- Strukov, D.B.; Snider, G.S.; Stewart, D.R.; Williams, R.S. The missing memristor found. Nature 2008, 453, 80–83. [Google Scholar] [CrossRef] [PubMed]
- Torrezan, A.C.; Strachan, J.P.; Medeiros, R.G.; Williams, R.S. Sub-nanosecond switching of a tantalum oxide memristor. Nanotechnology 2011, 22, 485203. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Choi, M.J.; Suh, J.M.; Han, J.S.; Kim, S.G.; Jang, H.W. Quasi-2D halide perovskites for resistive switching devices with ON/OFF ratios above 109. NPG Asia Mater. 2020, 12, 21. [Google Scholar]
- Almadhoun, M.N.; Speckbacher, M.; Olsen, B.C.; Luber, E.J.; Sayed, S.Y.; Tornow, M.; Buriak, J.M. Bipolar resistive switching in junctions of gallium Oxide and p-type silicon. Nano Lett. 2021, 21, 2666–2674. [Google Scholar] [CrossRef]
- Jiao, M.; Wang, D. The Savitzky-Golay filter based bidirectional long short-term memory network for SOC estimation. Int. J. Energy Res. 2021, 45, 19467–19480. [Google Scholar] [CrossRef]
- Qian, W.; Xing, W.; Fei, S. H∞ state estimation for neural networks with general activation function and mixed time-varying delays. IEEE Trans. Neural Netw. Learn Syst. 2021, 32, 3909–3918. [Google Scholar] [CrossRef]
- Jiao, M.; Wan, G.; Guo, Y.; Wang, D.; Liu, H.; Xiang, J.; Liu, F. A graph Fourier transform based bidirectional long short-term memory neural network for electrophysiological source imaging. Front. Neurosci. 2022, 16, 867466. [Google Scholar] [CrossRef]
- Dou, G.; Zhao, K.; Guo, M.; Mou, J. Memristor-based LSTM Network for Text Classification. Fractals, 2023; accepted papers. [Google Scholar] [CrossRef]
- Ma, T.; Mou, J.; Yan, H.; Cao, Y. A New Class of Hopfield Neural Network with Double Memristive Synapses and Its DSP Implementation. Eur. Phys. J. Plus 2022, 137, 1135. [Google Scholar] [CrossRef]
- Chua, L. Everything you wish to know about memristors but are afraid to ask. Radioengineering 2015, 24, 319–368. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, W.; Liu, Q.; Zhao, X.; Wei, J.; Cao, R.; Yao, Z.; Zhu, X.; Zhang, F.; Lv, H.; et al. An artificial neuron based on a threshold switching memristor. IEEE Electron. Device Lett. 2018, 39, 308–311. [Google Scholar]
- Zhou, G.; Wang, Z.; Sun, B.; Zhou, F.; Sun, L.; Zhao, H.; Hu, X.; Peng, X.; Yan, J.; Wang, H.; et al. Volatile and nonvolatile memristive devices for neuromorphic computing. Adv. Electron. Mater. 2022, 8, 2101127. [Google Scholar] [CrossRef]
- Li, C.; Yang, Y.; Yang, X.; Zi, X.; Xiao, F. A tristable locally active memristor and its application in Hopfield neural network. Nonlinear Dyn. 2022, 108, 1697–1717. [Google Scholar]
- Yao, L.; Liu, P.; Wu, J.; Han, Y.; Zhong, Y.; You, Z. Integrating Two Logics Into One Crossbar Array for Logic Gate Design. IEEE Trans. Circuits Syst. II Express Briefs. 2021, 68, 2987–2991. [Google Scholar]
- Wang, X.; Dong, C.; Zhou, P.; Nandi, S.K.; Nath, S.K.; Elliman, R.G.; Lu, H.H.C. Kang, S.; Eshraghian, J.K. Low-Variance Memristor-based Multi-Level Ternary Combinational Logic. IEEE Trans. Circuits Syst. I Regul. Pap. 2022, 69, 2423–2434. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, P.; Eshraghian, J.K.; Li, C.; Iu, H.H.C.; Chang, T.; Kang, S. High-Density Memristor-CMOS Ternary Logic Family. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 264–274. [Google Scholar]
- Liu, G.; Zheng, L.; Wang, G.; Shen, Y.; Liang, Y. A Carry Lookahead Adder Based on Hybrid CMOS-Memristor Logic Circuit. IEEE Access 2019, 7, 43691–43696. [Google Scholar]
- Guo, M.; Liu, R.; Dou, M.; Dou, G. An SBT-memristor-based crossbar memory circuit. Chin. Phys. B 2021, 30, 068402. [Google Scholar] [CrossRef]
- Guo, M.; Zhu, Y.; Liu, R.; Zhao, K.; Dou, G. An associative memory circuit based on physical memristors. Neurocomputing 2022, 472, 12–23. [Google Scholar]
- Hong, Q.; Chen, H.; Sun, J. Memristive Circuit Implementation of a Self-Repairing Network Based on Biological Astrocytes in Robot Application. IEEE Trans. Neural Netw. Learn Syst. 2022, 33, 2106–2120. [Google Scholar] [CrossRef] [PubMed]
- Bao, B.; Zhu, Y.; Ma, M.; Bao, H.; Wu, H.; Chen, M. Memristive neuron model with an adapting synapse and its hardware experiments. Sci. China Technol. Sci. 2021, 64, 1107–1117. [Google Scholar] [CrossRef]
- Dou, G.; Dou, M.; Liu, R.; Guo, M. Artifificial synaptic behavior of the SBT-memristor. Chin. Phys. B 2021, 30, 078401. [Google Scholar] [CrossRef]
- Yang, J.; Chen, G.; Wen, S. Finite-time dissipative control for bidirectional associative memory neural networks with state-dependent switching and time-varying delays. Knowl. Based Syst. 2022, 252, 109338. [Google Scholar]
- Guo, M.; Sun, Y.; Zhu, Y.; Han, M.; Dou, G.; Wen, S. Pruning and Quantization Algorithm with Applications in Memristor-based Convolutional Neural Network. Cogn. Neurodyn. 2023, 1–13. [Google Scholar] [CrossRef]
- Lai, Q.; Wan, Z.; Kengne, L.K.; Kuate, P.D.K.; Chen, C. Two-Memristor-Based Chaotic System With Infinite Coexisting Attractors. IEEE Trans. Circuits Syst. II Express Briefs. 2021, 68, 2197–2201. [Google Scholar]
- Peng, Y.; He, S.; Sun, K. A higher dimensional chaotic map with discrete memristor. Int. J. Electron. Commun. 2021, 129, 153539. [Google Scholar] [CrossRef]
- Vadivel, R.; Sabarathinam, S.; Wu, Y.; Chaisena, K.; Gunasekaran, N. New results on T–S fuzzy sampled-data stabilization for switched chaotic systems with its applications. Chaos Solitons Fractals 2022, 164, 112741. [Google Scholar] [CrossRef]
- Han, X.; Mou, J.; Jahanshahi, H.; Cao, Y.; Bu, F. A New Set of Hyperchaotic Maps Based on Modulation and Coupling. Eur. Phys. J. Plus 2022, 137, 523. [Google Scholar] [CrossRef]
- Sha, Y.; Sun, B.; Chen, X.; Mou, J.; Jahanshahi, H. A Chaotic Image Encryption Scheme Based on Genetic Central Dogma and KMP Method. Int. J. Bifurcat. Chaos 2022, 32, 2250186. [Google Scholar] [CrossRef]
- Liu, X.; Mou, J.; Yan, H.; Bi, X. Memcapacitor-Coupled Chebyshev Hyperchaotic Map. Int. J. Bifurcat. Chaos 2022, 32, 2250180. [Google Scholar] [CrossRef]
- Guo, M.; Gao, Z.; Xue, Y.; Dou, G.; Li, Y. Dynamics of a physical SBT memristor-based Wien-bridge circuit. Nonlinear Dyn. 2018, 93, 1681–1693. [Google Scholar] [CrossRef]
- Wu, H.; Zhou, J.; Chen, M.; Xu, Q.; Bao, B. DC-offset induced asymmetry in memristive diode-bridge-based Shinriki oscillator. Chaos Solitons Fractals 2022, 154, 111624. [Google Scholar] [CrossRef]
- Dou, G.; Duan, H.; Yang, W.; Yang, H.; Guo, M.; Li, Y. Effects of initial conditions and circuit parameters on the SBT-memristor-based chaotic circuit. Int. J. Bifurcat. Chaos 2019, 29, 1950171. [Google Scholar]
- Dou, G.; Yang, H.; Gao, Z.; Li, P.; Dou, M.; Yang, W.; Guo, M.; Li, Y. Coexisting Multi-Dynamics of a Physical SBT Memristor-Based Chaotic Circuit. Int. J. Bifurcat. Chaos 2020, 30, 2030043. [Google Scholar] [CrossRef]
- Ren, L.; Mou, J.; Banerjee, S.; Zhang, Y. A Hyperchaotic Map with A New Discrete Memristor Model: Design, Dynamical Analysis, Implementation and Application. Chaos Solitons Fractals 2023, 167, 113024. [Google Scholar] [CrossRef]
- Li, C.; Li, H.; Xie, W.; Du, J. A S-type bistable locally active memristor model and its analog implementation in an oscillator circuit. Nonlinear Dyn. 2021, 106, 1041–1058. [Google Scholar] [CrossRef]
- Li, H.; Li, C.; Du, J. Discretized locally active memristor and application in logarithmic map. Nonlinear Dyn. 2023, 111, 2895–2915. [Google Scholar] [CrossRef]
- Guo, M.; Yang, W.; Xue, Y.; Gao, Z.; Yuan, F.; Dou, G.; Li, Y. Multistability in a physical memristor-based modified Chua’s circuit. Chaos 2019, 29, 043114. [Google Scholar] [CrossRef] [PubMed]
- Bao, B.; Jiang, P.; Wu, H.; Hu, F. Complex transient dynamics in periodically forced memristive Chua’s circuit. Nonlinear Dyn. 2015, 79, 2333–2343. [Google Scholar]
- Fitch, A.L.; Yu, D.; Herbert, H.C.I.; Sreeram, V. Hyperchaos in a memristor-based modified canonical Chua’s circuit. Int. J. Bifurcat. Chaos 2012, 22, 1250133. [Google Scholar] [CrossRef]
- Simmons, D.R.; Clegorne, N.; Polmear, M. Uncovering the Hidden Curriculum of Leadership Education in Civil Engineering. Int. J. Eng. Educ. 2022, 38, 224–236. [Google Scholar]
- Rajagopal, K.; Karthikeyan, A.; Srinivasan, A. Dynamical analysis and FPGA implementation of a chaotic oscillator with fractional-order memristor components. Nonlinear Dyn. 2018, 91, 1491–1512. [Google Scholar]
- Dou, G.; Yu, Y.; Guo, M.; Zhang, Y.; Sun, Z.; Li, Y. Memristive Behavior Based on Ba-Doped SrTiO3 Films. Chin. Phys. Lett. 2017, 34, 038502. [Google Scholar] [CrossRef]
- Guo, M.; Zhu, Y.; Yang, R.; Zhang, M.; Zhao, K.; Yang, H.; Dou, G. A single-T chaotic circuit based on a physical memristor. Eur. Phys. J. Spec. Top. 2022, 231, 3163–3170. [Google Scholar] [CrossRef]



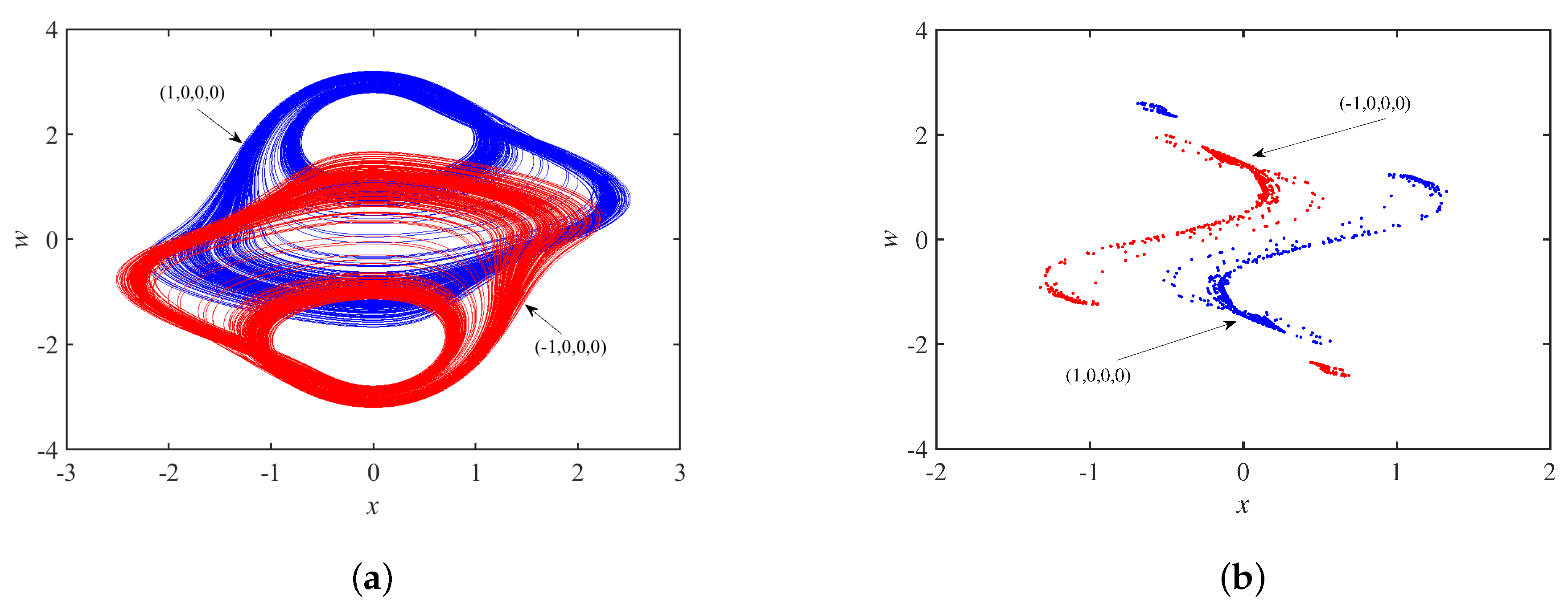

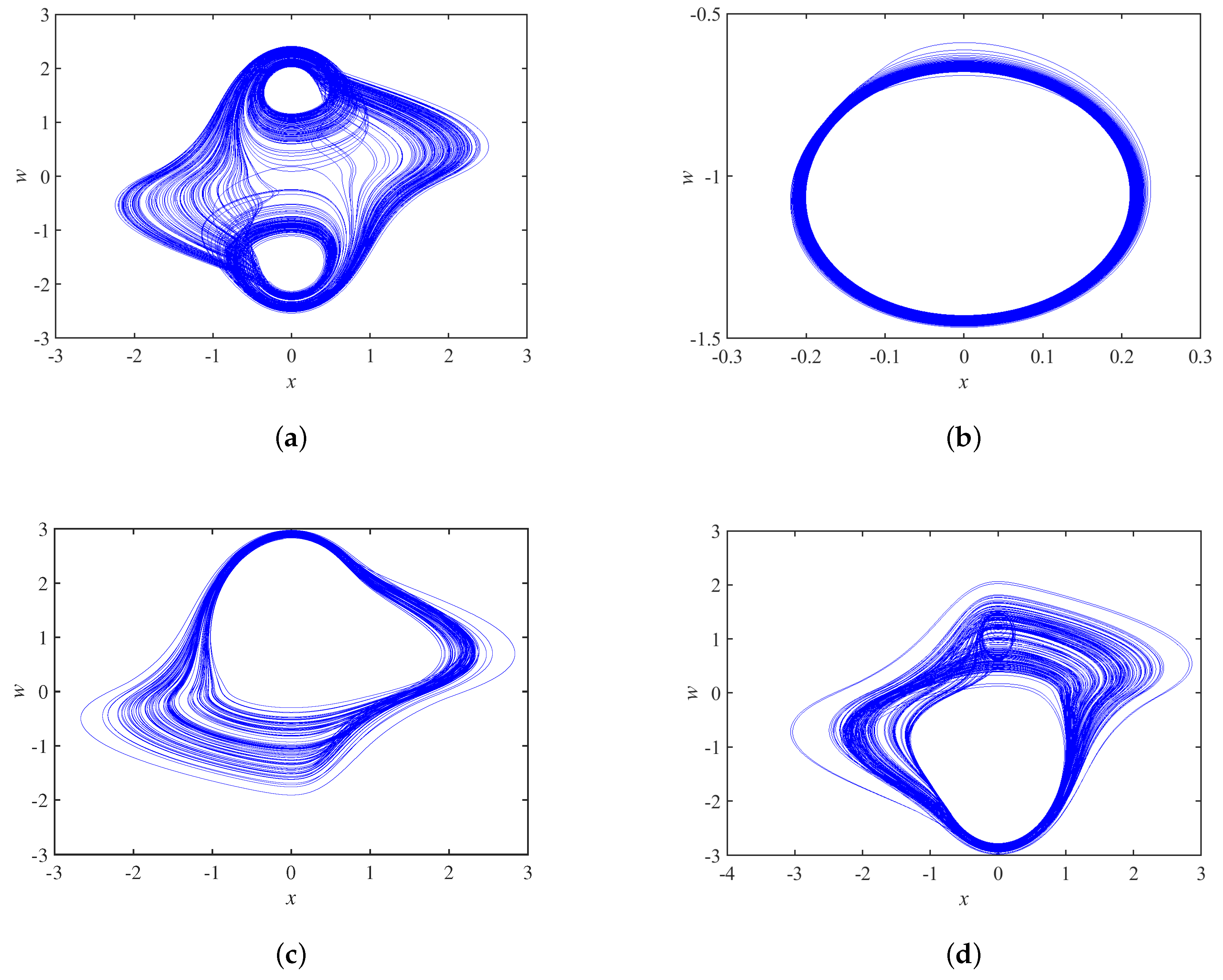
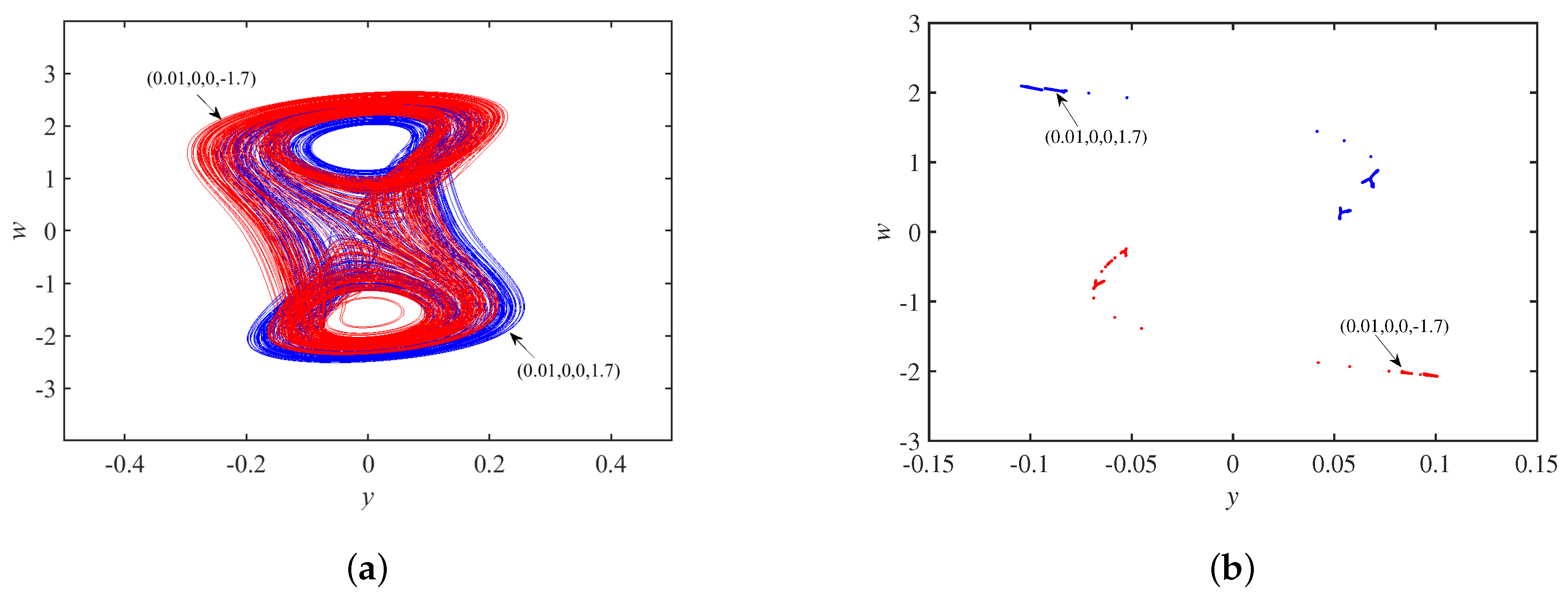
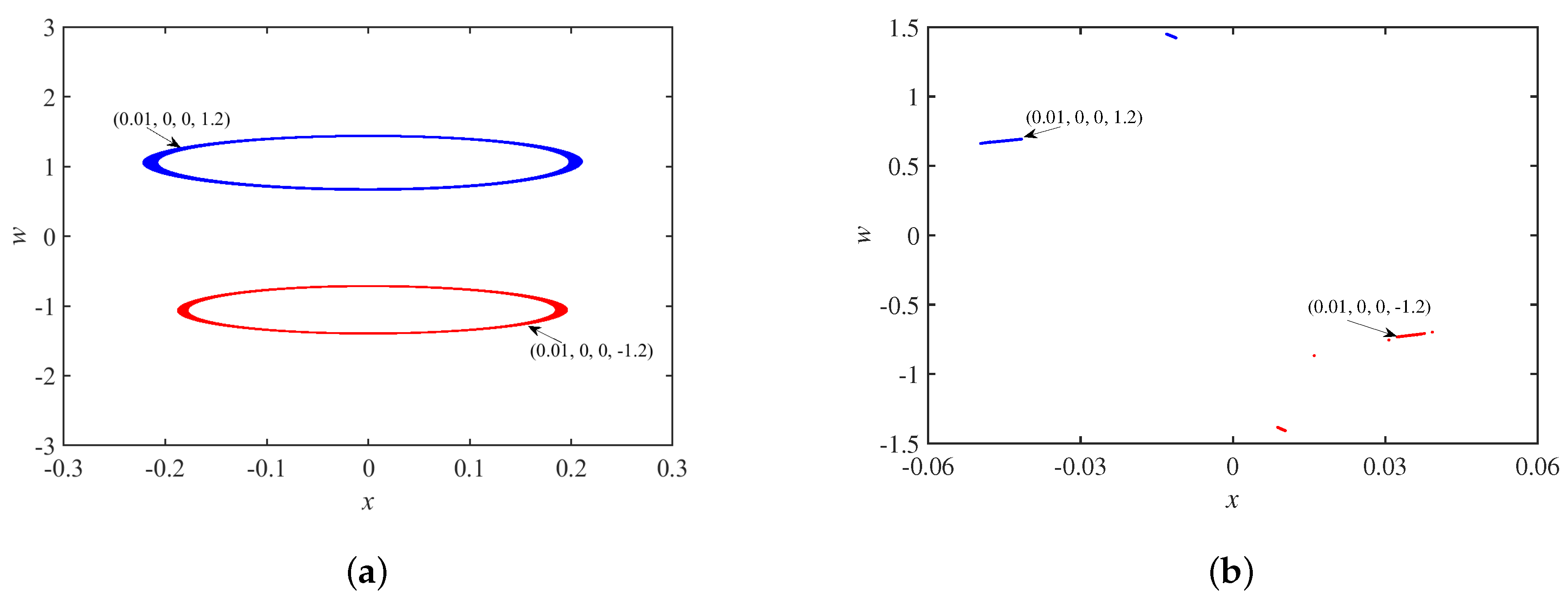
| Values of Circuits Parameters | Dynamical Behaviors |
|---|---|
| , , , | Coexisting single-scroll attractors |
| , , , | Coexisting double-scroll attractors |
| , , , | Coexisting double-scroll attractors |
| The Initial State | Interval | Dynamics |
|---|---|---|
| Double-scroll attractor | ||
| Periodic limit cycle | ||
| Single-scroll attractor | ||
| Double-scroll attractor | ||
| Periodic limit cycle | ||
| Single-scroll attractor | ||
| Period-window | ||
| Periodic limit cycle | ||
| Single-scroll attractor | ||
| Double-scroll attractor |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dou, G.; Zhang, Y.; Yang, H.; Han, M.; Guo, M.; Gai, W. RC Bridge Oscillation Memristor Chaotic Circuit for Electrical and Electronic Technology Extended Simulation Experiment. Micromachines 2023, 14, 410. https://doi.org/10.3390/mi14020410
Dou G, Zhang Y, Yang H, Han M, Guo M, Gai W. RC Bridge Oscillation Memristor Chaotic Circuit for Electrical and Electronic Technology Extended Simulation Experiment. Micromachines. 2023; 14(2):410. https://doi.org/10.3390/mi14020410
Chicago/Turabian StyleDou, Gang, Yongcheng Zhang, Hai Yang, Mingqiao Han, Mei Guo, and Wendong Gai. 2023. "RC Bridge Oscillation Memristor Chaotic Circuit for Electrical and Electronic Technology Extended Simulation Experiment" Micromachines 14, no. 2: 410. https://doi.org/10.3390/mi14020410
APA StyleDou, G., Zhang, Y., Yang, H., Han, M., Guo, M., & Gai, W. (2023). RC Bridge Oscillation Memristor Chaotic Circuit for Electrical and Electronic Technology Extended Simulation Experiment. Micromachines, 14(2), 410. https://doi.org/10.3390/mi14020410







