Towards Optimizing Width Modulation for Maximum Thermoelectric Efficiency
Abstract
:1. Introduction
2. Theoretical Model and Methodology
3. Results and Discussion
3.1. The Effect of a Two-QD Modulation
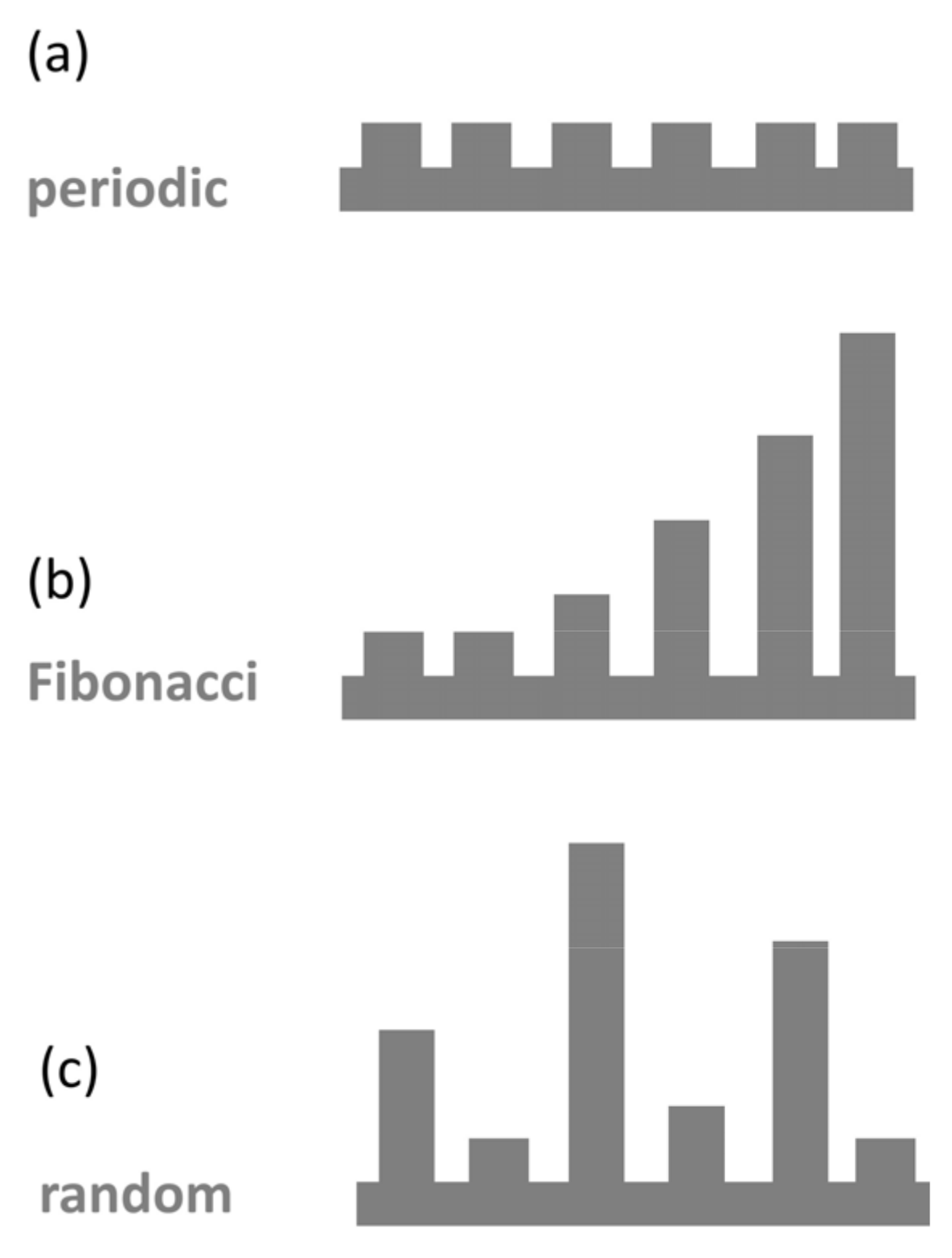
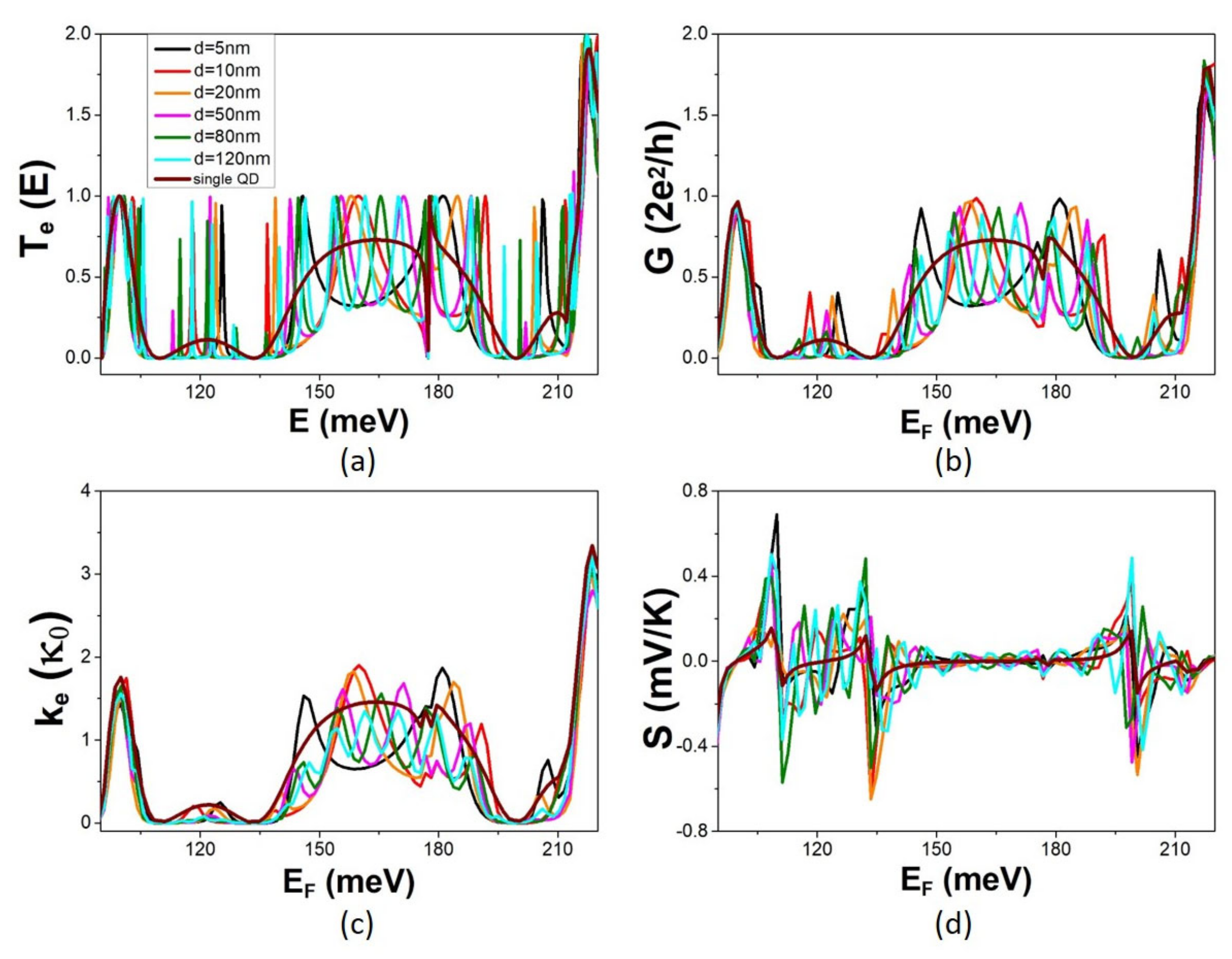
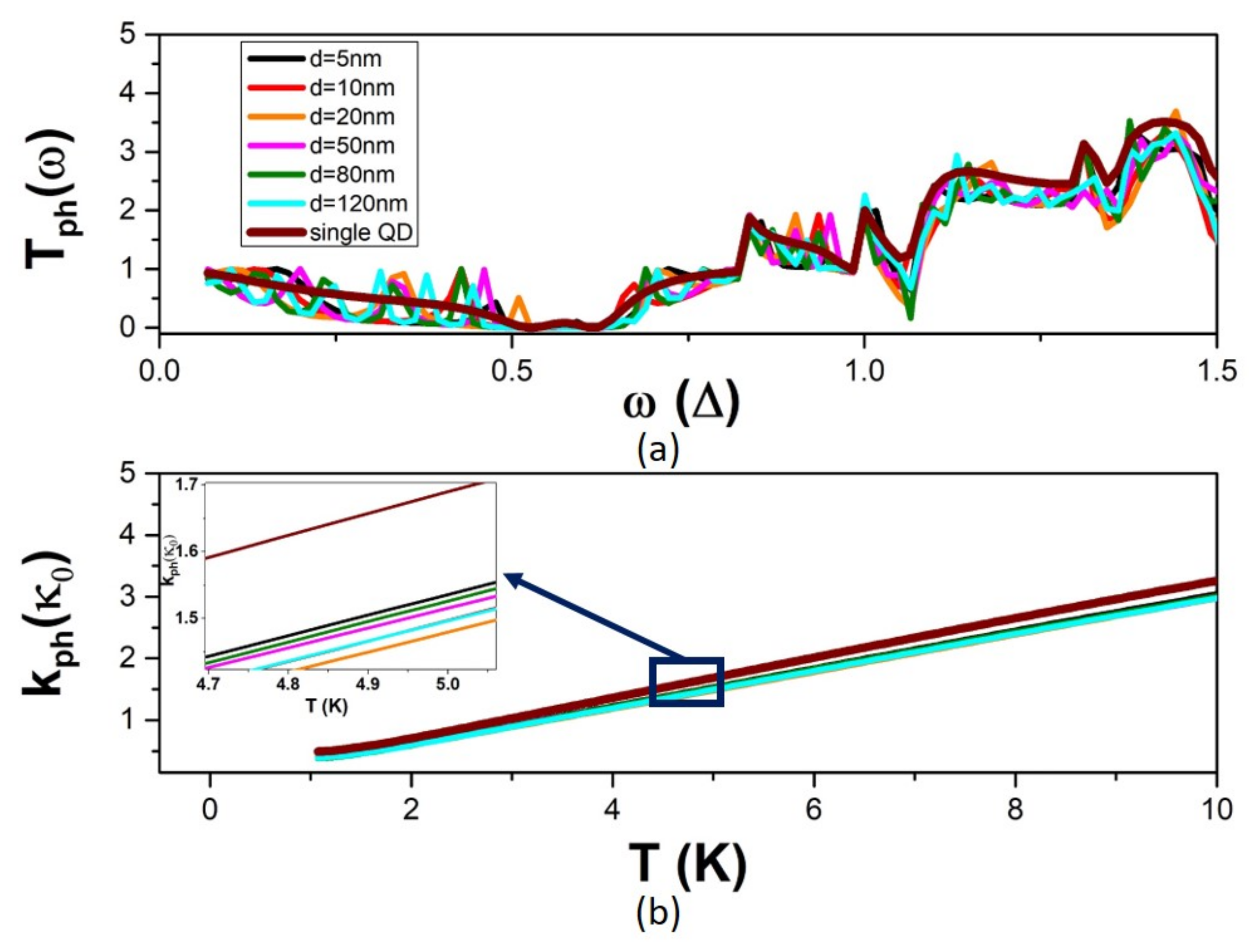
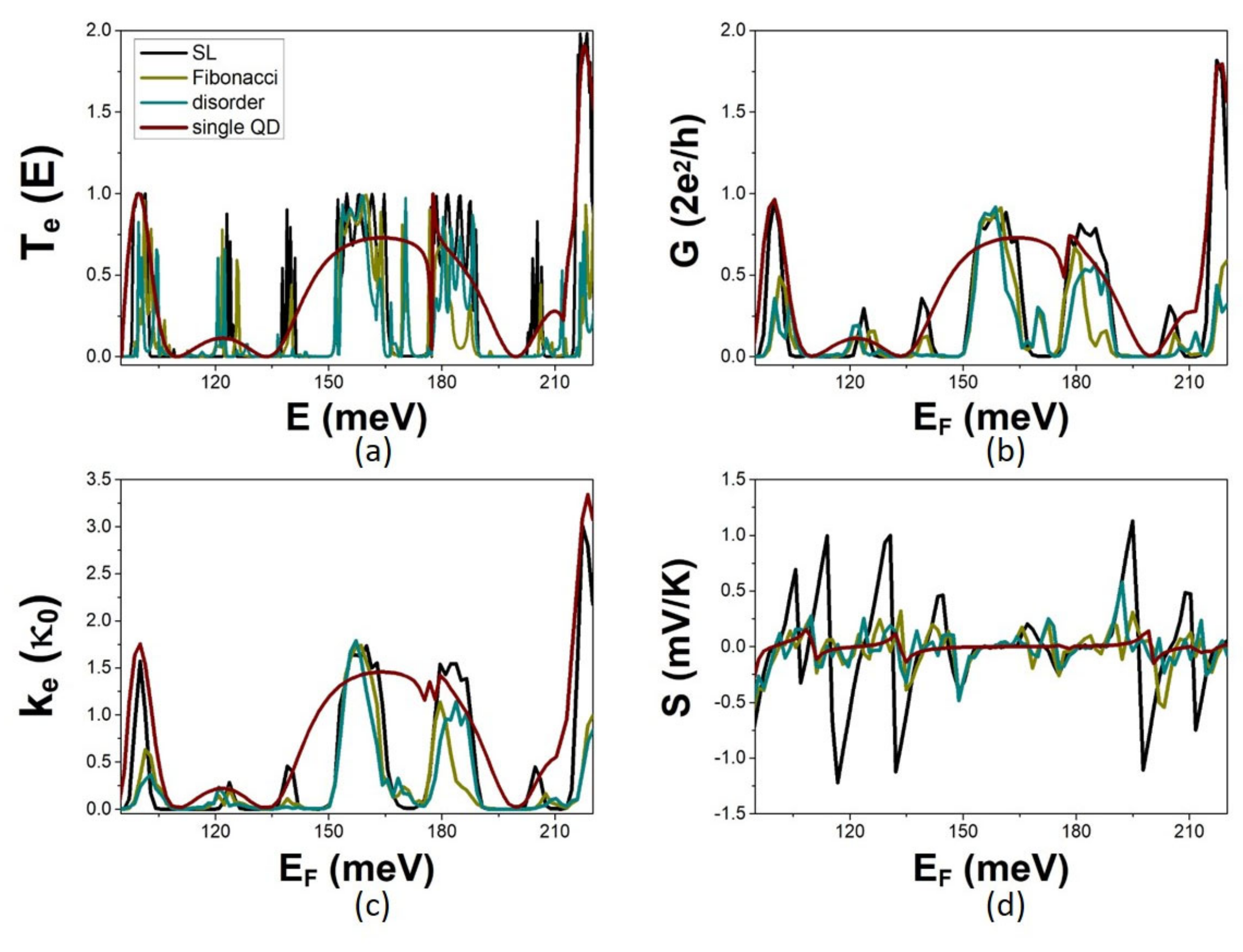
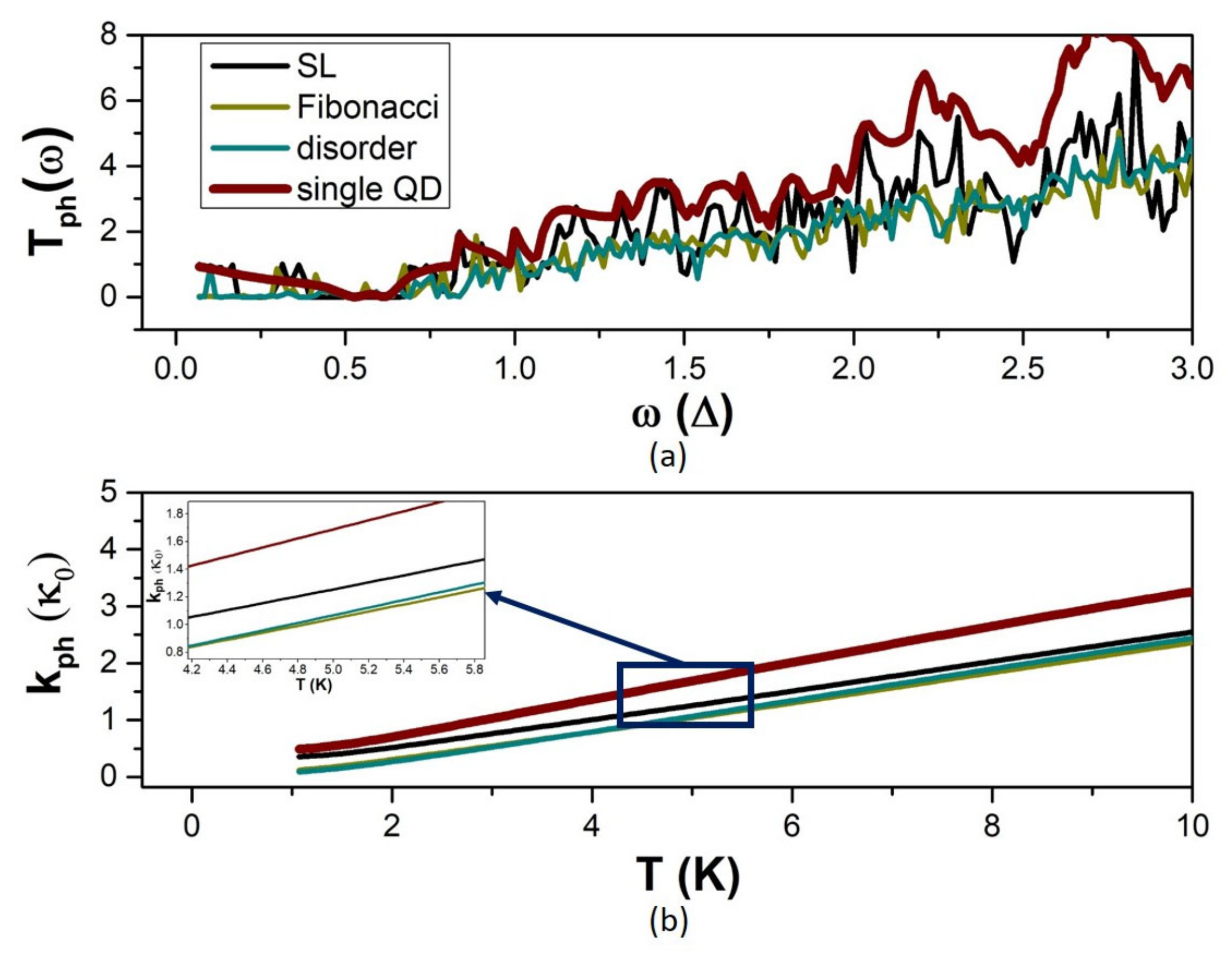
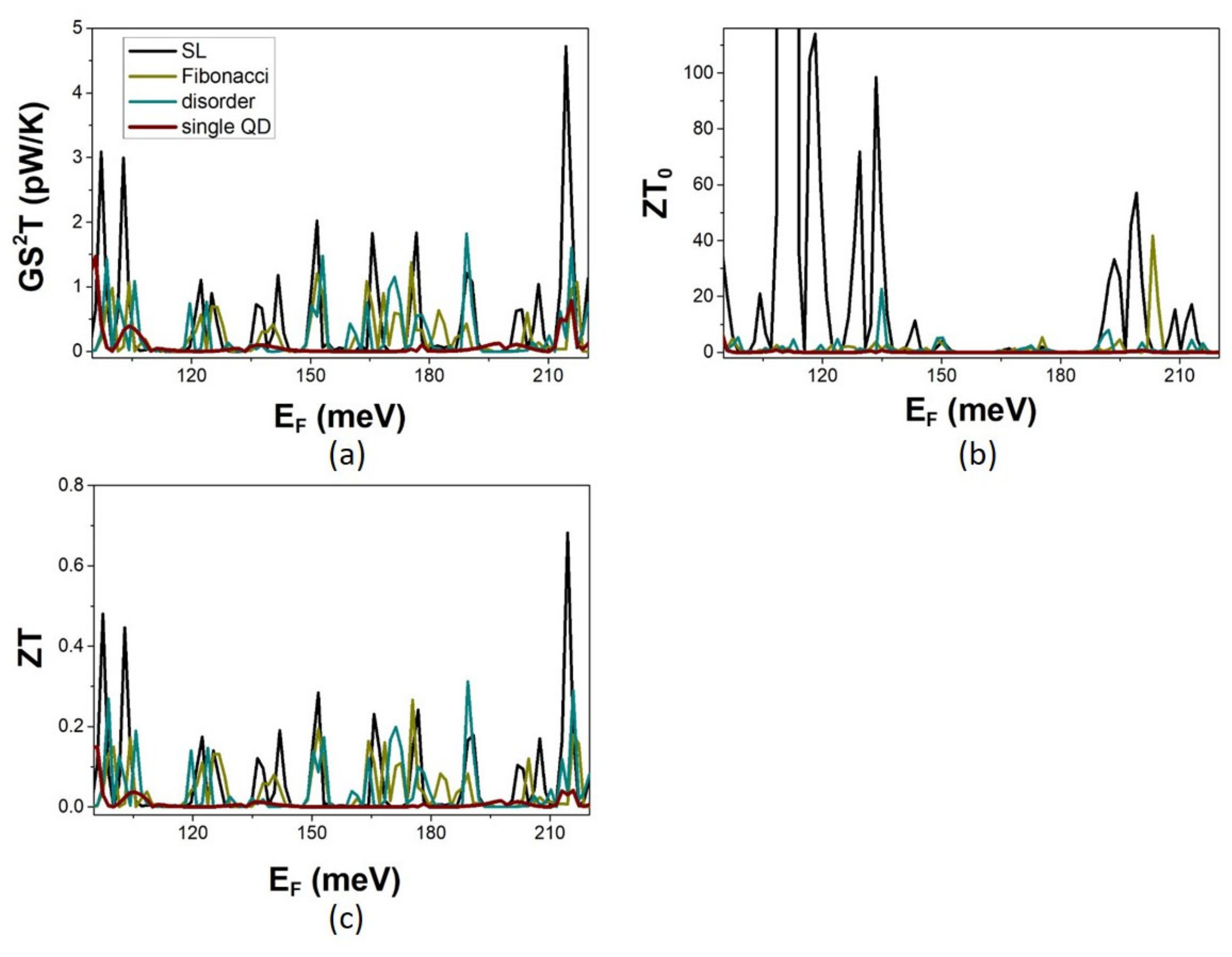
3.2. The Effect of Multiple-QD Modulation
4. Overview and Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zianni, X. Diameter-modulated nanowires as candidates for high thermoelectric energy conversion efficiency. Appl. Phys. Lett. 2010, 97, 233106. [Google Scholar] [CrossRef]
- Pendry, J. Metamaterials in the sunshine. Nat. Mater. 2006, 5, 599–600. [Google Scholar] [CrossRef]
- Kadic, M.; Milton, G.; van Hecke, M.; Wegener, M. 3D metamaterials. Nat. Rev. 2019, 1, 198–210. [Google Scholar] [CrossRef]
- Zhang, J.; Hu, B.; Wang, S. Review and perspective on acoustic metamaterials: From fundamentals to applications. Appl. Phys. Lett. 2023, 123, 010502. [Google Scholar] [CrossRef]
- Zianni, X. The effect of the modulation shape in the ballistic thermal conductance of modulated nanowires. J. Solid State Chem. 2012, 193, 53–57. [Google Scholar] [CrossRef]
- Zianni, X. Disorder-induced enhancement of the thermoelectric efficiency in diameter- modulated nanowires. Microelectron. Eng. 2013, 112, 235–240. [Google Scholar] [CrossRef]
- Butcher, P.; March, N.; Tosi, M. Physics of Low-Dimensional Semiconductor Structures; Plenum Press: New York, NY, USA, 1993. [Google Scholar]
- Kelly, M. Low-Dimensional Semiconductors: Materials, Physics, Technology, Devices; Clarendon Press: Oxford, UK, 1995. [Google Scholar]
- Davies, J. The Physics of Low-Dimensional Semiconductors—An Introduction; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Mensah, S.Y.; Kangah, G.K. The thermoelectric effect in a semiconductor superlattice in a non-quantized electric field. J. Phys. Condens. Matter 1992, 4, 919. [Google Scholar] [CrossRef]
- Hicks, L.D.; Dresselhaus, M. Effect of quantum-well structures on the thermoelectric figure of merit. Phys. Rev. B 1993, 47, 12727. [Google Scholar] [CrossRef] [PubMed]
- Hicks, L.D.; Dresselhaus, M. Thermoelectric figure of merit of a one-dimensional conductor. Phys. Rev. B 1993, 47, 16631. [Google Scholar] [CrossRef] [PubMed]
- Mahan, G.D.; Lyon, H.B. Thermoelectric devices using semiconductor quantum wells. J. Appl. Phys. 1994, 76, 1899–1901. [Google Scholar] [CrossRef]
- Sofo, J.O.; Mahan, G.D. Thermoelectric figure of merit of superlattices. Appl. Phys. Lett. 1994, 65, 2690–2692. [Google Scholar] [CrossRef]
- Stefanou, A.-D.; Zianni, X. The Effect of Width-Mismatch of Modulated Nanowaveguides on the Thermoelectric Efficiency. Micromachines 2023, 14, 1912. [Google Scholar] [CrossRef] [PubMed]
- Datta, S. Electron Transport in Mesoscopic Systems; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Chen, G. Thermal conductivity and ballistic-phonon transport in the cross-plane direction of superlattices. Phys. Rev. B 1998, 57, 14958. [Google Scholar] [CrossRef]
- Cross, M.C.; Lifshitz, R. Elastic wave transmission at an abrupt junction in a thin plate with application to heat transport and vibrations in mesoscopic systems. Phys. Rev. B 2001, 64, 085324. [Google Scholar] [CrossRef]
- Li, W.-X.; Chen, K.-Q.; Duan, W.; Wu, J.; Gu, B.-L. Acoustic phonon transport through a T-shaped quantum waveguide. J. Phys. Condens. Matter 2004, 16, 5049–5059. [Google Scholar] [CrossRef]
- Li, W.-X.; Liu, T.; Liu, C. Phonon transport through a three-dimensional abrupt junction. Appl. Phys. Lett. 2006, 89, 163104. [Google Scholar] [CrossRef]
- Yang, P.; Sun, Q.-F.; Guo, H.; Hu, B. Thermal transport in a dielectric T-shaped quantum wire. Phys. Rev. B 2007, 75, 235319. [Google Scholar] [CrossRef]
- Weisshaar, A.J.; Lary, J.; Goodnick, S.M.; Tripathi, V.K. Analysis and modeling of quantum waveguide structures and devices. J. Appl. Phys. 1991, 70, 355. [Google Scholar] [CrossRef]
- Heron, J.S.; Fournier, T.; Mingo, N.; Bourgeois, O. Mesoscopic Size Effects on the Thermal Conductance of Silicon Nanowire. Nano Lett. 2009, 9, 1861–1865. [Google Scholar] [CrossRef] [PubMed]
- Ziman, B.J. Electrons and Phonons, Reprint Ed.; Oxford University Press: Oxford, UK, 2001; pp. 431–434. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stefanou, A.-D.; Zianni, X. Towards Optimizing Width Modulation for Maximum Thermoelectric Efficiency. Micromachines 2023, 14, 2176. https://doi.org/10.3390/mi14122176
Stefanou A-D, Zianni X. Towards Optimizing Width Modulation for Maximum Thermoelectric Efficiency. Micromachines. 2023; 14(12):2176. https://doi.org/10.3390/mi14122176
Chicago/Turabian StyleStefanou, Antonios-Dimitrios, and Xanthippi Zianni. 2023. "Towards Optimizing Width Modulation for Maximum Thermoelectric Efficiency" Micromachines 14, no. 12: 2176. https://doi.org/10.3390/mi14122176
APA StyleStefanou, A.-D., & Zianni, X. (2023). Towards Optimizing Width Modulation for Maximum Thermoelectric Efficiency. Micromachines, 14(12), 2176. https://doi.org/10.3390/mi14122176





