Phase-Controlled Tunable Unconventional Photon Blockade in a Single-Atom-Cavity System
Abstract
:1. Introduction
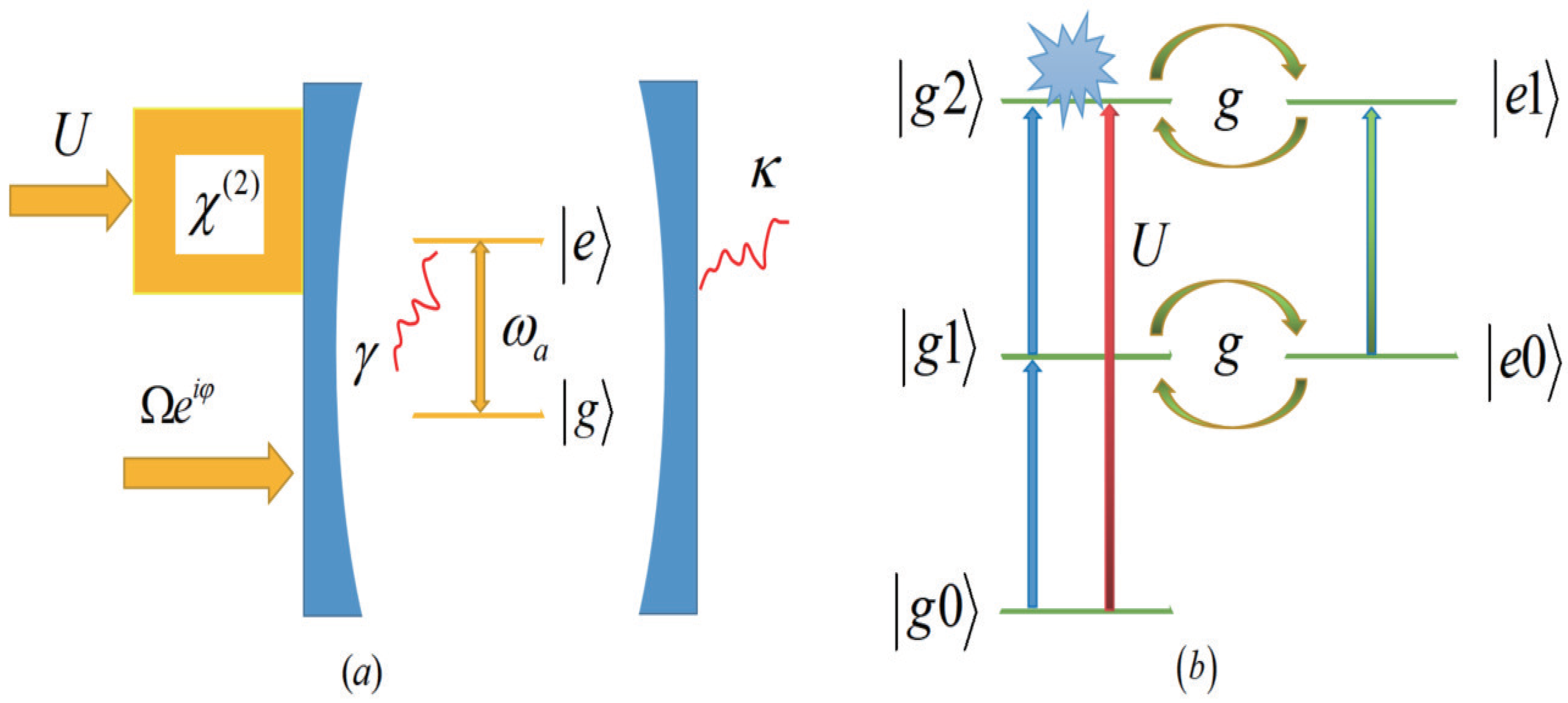
2. Model and Dynamical Equations of the System
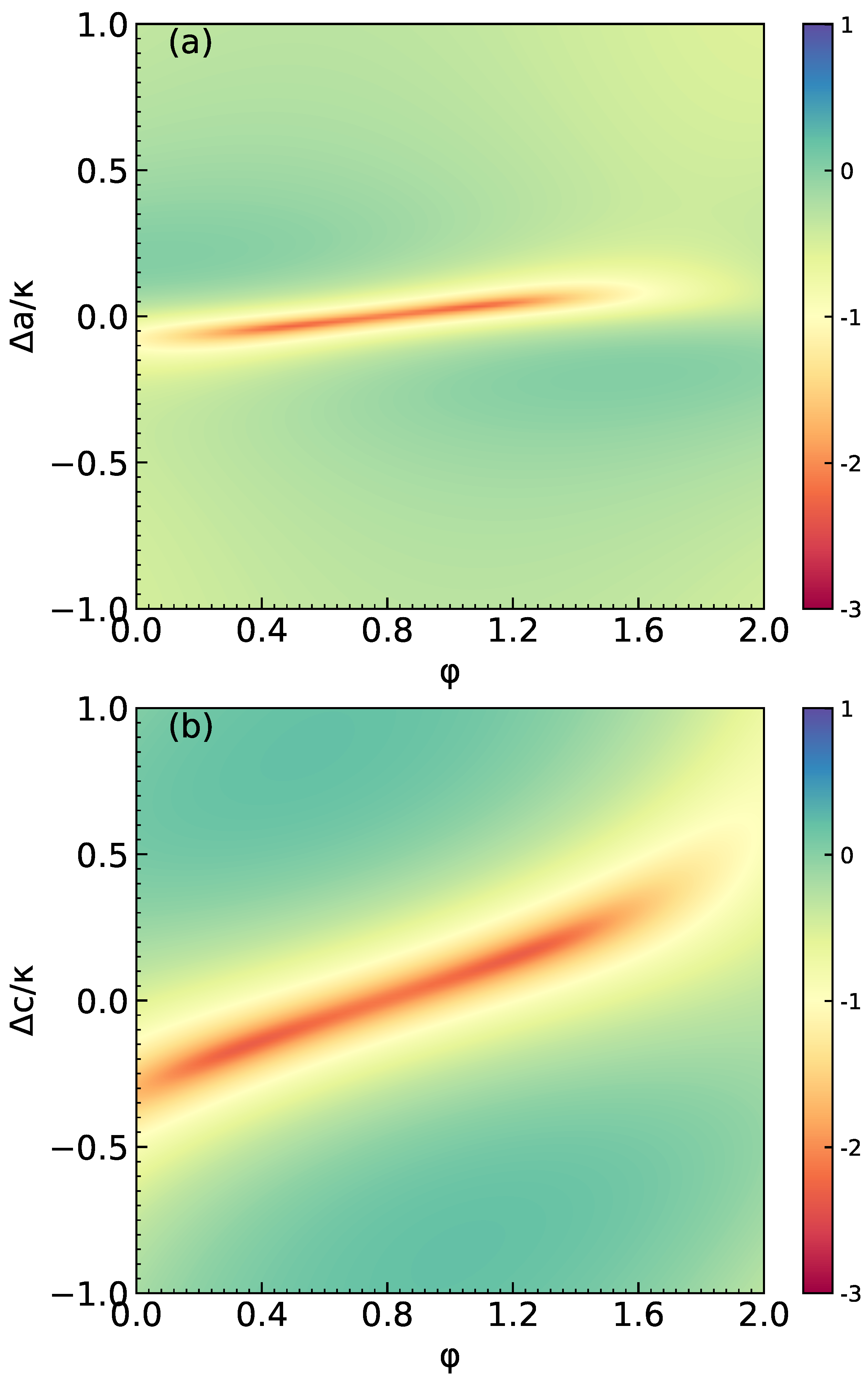
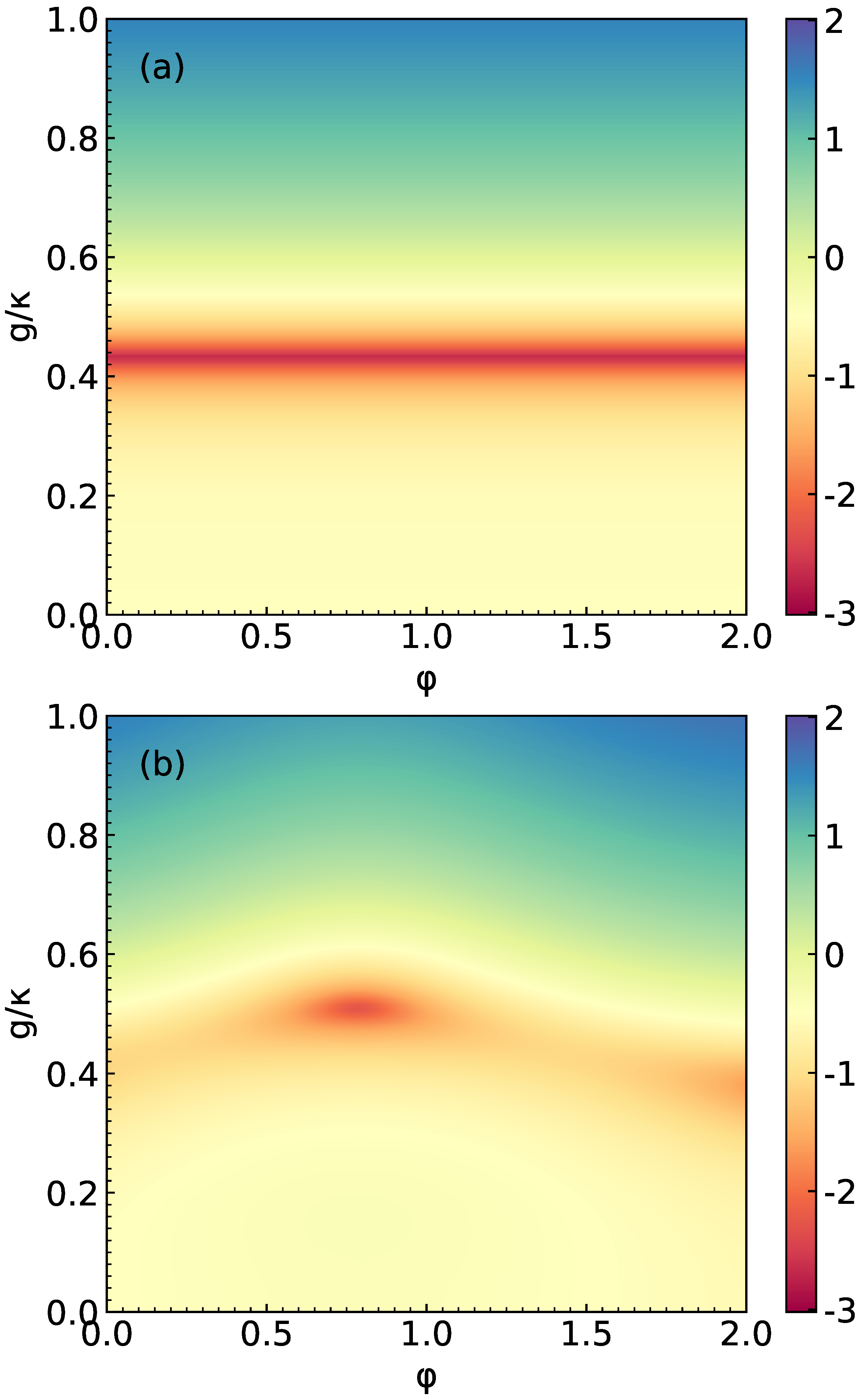
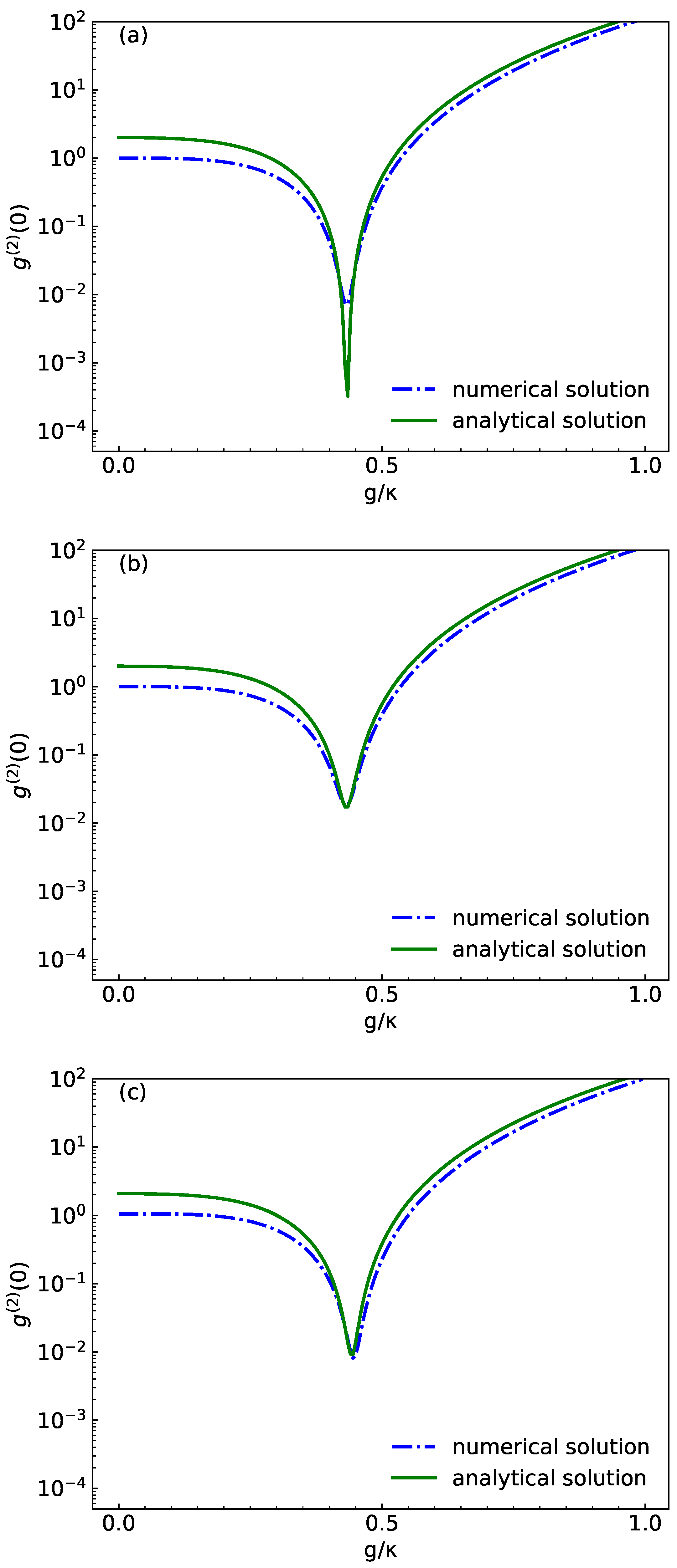
3. Numerical Simulation and Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Blair, D.G.; Caves, C.M. The detection of gravitational waves. Phys. Today 1992, 45, 59–60. [Google Scholar] [CrossRef]
- Braginskii, V.B.; Manukin, A.B. Ponderomotive effects of electromagnetic radiation. J. Exp. Theor. Phys. 1967, 25, 653–655. [Google Scholar]
- Caves, C.M.; Thorne, K.S.; Drever, R.W.P.; Sandberg, V.D.; Zimmermann, M. On the measurement of a weak classical force coupled to a quantum-mechanical oscillator. I. Issues of principle. Rev. Mod. Phys. 1980, 52, 341–392. [Google Scholar]
- Aspelmeyer, M.; Kippenberg, T.J.; Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 2014, 86, 1391. [Google Scholar]
- Kippenberg, T.J.; Vahala, K.J. Cavity optomechanics: Back-action at the mesoscale. Science 2008, 321, 1172. [Google Scholar]
- Metcalfe, M. Applications of cavity optomechanics. Appl. Phys. Rev. 2014, 1, 031105. [Google Scholar]
- Genes, C.; Vitali, D.; Tombesi, P.; Aspelmeyer, M. Ground-State Cooling of a Micromechanical Oscillator: Comparing Cold Damping and Cavity-Assisted Cooling Schemes. Phys. Rev. A 2008, 77, 033804. [Google Scholar]
- Ojanen, T.; Brkje, K. Ground-State Cooling of Mechanical Motion in the Unresolved Sideband Regime by Use of Optomechanically Induced Transparency. Phys. Rev. A 2014, 90, 013824. [Google Scholar]
- Vitali, D.; Gigan, S.; Ferreira, A.; Böhm, H.R.; Tombesi, P.; Guerreiro, A.; Vedral, V.; Zeilinger, A.; Aspelmeyer, M. Optomechanical Entanglement between a Movable Mirror and a Cavity Field. Phys. Rev. Lett. 2007, 98, 030405. [Google Scholar]
- Paz, J.P.; Roncaglia, A.J. Dynamics of the Entanglement between Two Oscillators in the Same Environment. Phys. Rev. Lett. 2008, 100, 220401. [Google Scholar] [CrossRef]
- Rabl, P. Photon Blockade Effect in Optomechanical Systems. Phys. Rev. Lett. 2014, 107, 063601. [Google Scholar] [CrossRef]
- Agarwal, G.S.; Huang, S. Electromagnetically Induced Transparency in Mechanical Effects of Light. Phys. Rev. A 2010, 81, 041803. [Google Scholar] [CrossRef]
- Safavi-Naeini, A.H.; Alegre, T.P.M.; Chan, J.; Eichenfield, M.; Winger, M.; Lin, Q.; Hill, J.T.; Chang, D.E.; Painter, O. Electromagnetically Induced Transparency and Slow Light with Optomechanics. Nature 2011, 472, 69–73. [Google Scholar]
- Wang, J.; Sciarrino, F.; Laing, A.; Thompson, M.G. Integrated photonic quantum technologies. Nat. Photonics 2020, 14, 273. [Google Scholar]
- O’Brien, J.L.; Furusawa, A.; Vučković, J. Photonic quantum technologies. Nat. Photonics 2009, 3, 687. [Google Scholar] [CrossRef]
- Faraon, A.; Majumdar, A.; Vučković, J. Generation of nonclassical states of light via photon blockade in optical nanocavities. Phys. Rev. A 2010, 81, 033838. [Google Scholar] [CrossRef]
- Wang, X.; Miranowicz, A.; Li, H.R.; Nori, F. Multiple-output microwave single-photon source using superconducting circuits with longitudinal and transverse couplings. Phys. Rev. A 2016, 9, 053858. [Google Scholar] [CrossRef]
- Gu, X.; Kockum, A.F.; Miranowicz, A.; Liu, Y.X.; Nori, F. Microwave photonics with superconducting quantum circuits. Phys. Rep. 2017, 1, 718–719. [Google Scholar]
- Imamoḡlu, A.; Schmidt, H.; Woods, G.; Deutsch, M. Strongly Interacting Photons in a Nonlinear Cavity. Phys. Rev. Lett. 1997, 79, 1467–1470. [Google Scholar]
- Fulton, T.A.; Dolan, G.J. Observation of Single-Electron Charging Effects in Small Tunnel Junctions. Phys. Rev. Lett. 1987, 59, 109–112. [Google Scholar] [CrossRef]
- Birnbaum, K.M.; Boca, A.; Miller, R.; Boozer, A.D.; Northup, T.E.; Kimble, H.J. Photon Blockade in an Optical Cavity with One Trapped Atom. Nature 2005, 436, 87. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.H.; Li, G.; Tian, Y.L.; Zhang, T.C. Quantum state manipulation of single-Cesium-atom qubit in a micro-optical trap. Front. Phys. 2014, 9, 634–639. [Google Scholar] [CrossRef]
- Shan, G.C.; Yin, Z.Q.; Shek, C.H.; Huang, W. Single photon sources with single semiconductor quantum dots. Front. Phys. 2014, 9, 170–193. [Google Scholar] [CrossRef]
- Tian, L.; Shi, S.P.; Tian, Y.H.; Wang, Y.J.; Zheng, Y.H.; Peng, K.C. Resource reduction for simultaneous generation of two types of continuous variable nonclassical states. Front. Phys. 2021, 16, 1–6. [Google Scholar] [CrossRef]
- Fan, L. Squeezed light goes flexible. Front. Phys. 2021, 16, 1. [Google Scholar] [CrossRef]
- Stefanatos, D.; Paspalakis, E. Dynamical blockade in a bosonic Josephson junction using optimal coupling. Phys. Rev. A 2020, 102, 013716. [Google Scholar] [CrossRef]
- Xu, X.W.; Li, Y. Strongly interacting photons in a nonlinear cavity. Phys. Rev. Lett. 2014, 90, 033809. [Google Scholar]
- Kyriienko, O.; Shelykh, I.A.; Liew, T.C.H. Tunable single-photon emission from dipolaritons. Phys. Rev. A 2014, 90, 033807. [Google Scholar] [CrossRef]
- Dayan, B.; Parkins, A.S.; Aoki, T.; Ostby, E.P.; Vahala, K.J.; Kimble, H.J. A photon turnstile dynamically regulated by one atom. Science 2008, 319, 1062–1065. [Google Scholar] [CrossRef]
- Reinhard, A.; Volz, T.; Winger, M.; Badolato, A.; Hennessy, K.J.; Hu, E.L.; Imamoğlu, A. Strongly correlated photons on a chip. Nat. Photonics 2012, 6, 93–96. [Google Scholar] [CrossRef]
- Lang, C.; Bozyigit, D.; Eichler, C.; Steffen, L.; Fink, J.M.; Abdumalikov, A.A., Jr.; Baur, M.; Filipp, S.; da Silva, M.P.; Blais, A.; et al. Observation of resonant photon blockade at microwave frequencies using correlation function measurements. Phys. Rev. Lett. 2011, 106, 243601. [Google Scholar] [CrossRef]
- Carmichael, H.J. Breakdown of photon blockade: A dissipative quantum phase transition in zero dimensions. Phys. Rev. X 2015, 5, 031028. [Google Scholar] [CrossRef]
- Vaneph, C.; Morvan, A.; Aiello, G.; Féchant, M.; Aprili, M.; Gabelli, J.; Estéve, J. Observation of the unconventional photon blockade in the microwave domain. Phys. Rev. Lett. 2018, 121, 043602. [Google Scholar] [CrossRef] [PubMed]
- Su, S.L.; Tian, Y.; Shen, H.Z.; Zang, H.; Liang, E.; Zhang, S. Applications of the modified Rydberg antiblockade regime with simultaneous driving. Phys. Rev. A 2017, 96, 042335. [Google Scholar] [CrossRef]
- Su, S.L.; Gao, Y.; Liang, E.; Zhang, S. Fast Rydberg antiblockade regime and its applications in quantum logic gates. Phys. Rev. A 2017, 95, 022319. [Google Scholar] [CrossRef]
- Miranowicz, A.; Bajer, J.; Paprzycka, M.; Liu, Y.; Zagoskin, A.M.; Nori, F. State-dependent photon blockade via quantum-reservoir engineering. Phys. Rev. A 2014, 90, 033831. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, X.W.; Miranowicz, A.; Nori, F. From blockade to transparency: Controllable photon transmission through a circuit-QED system. Phys. Rev. A 2014, 89, 043818. [Google Scholar] [CrossRef]
- Wu, Q.C.; Zhou, Y.H.; Ye, B.L.; Liu, T.; Yang, C.P. Nonadiabatic quantum state engineering by time-dependent decoherence-free subspaces in open quantum systems. New J. Phys. 2021, 23, 113005. [Google Scholar] [CrossRef]
- Chang, D.E.; Gritsev, V.; Morigi, G.; Vuletić, V.; Lukin, M.D.; Demler, E.A. Photon blockade in an optical cavity with one trapped atom. Nat. Phys. 2008, 4, 884. [Google Scholar] [CrossRef]
- Miranowicz, A.; Bajer, J.; Paprzycka, M.; Liu, Y.; Zagoskin, A.M.; Nori, F. Two-photon and three-photon blockades in driven nonlinear systems. Phys. Rev. A 2011, 83, 021802. [Google Scholar] [CrossRef]
- Hartmann, M.J.; Brandao, F.G.S.L.; Plenio, M.B. Strongly interacting polaritons in coupled arrays of cavities. Nat. Phys. 2006, 2, 849. [Google Scholar] [CrossRef]
- Greentree, A.D.; Tahan, C.; Cole, J.H.; Hollenberg, L.C.L. Quantum phase transitions of light. Nat. Phys. 2006, 2, 856. [Google Scholar] [CrossRef]
- Angelakis, D.G.; Santos, M.F.; Bose, S. Photon-blockade-induced Mott transitions and X Y spin models in coupled cavity arrays. Phys. Rev. A 2007, 76, 031805. [Google Scholar] [CrossRef]
- Wu, H.Z.; Yang, Z.B.; Zheng, S.B. Implementation of a multiqubit quantum phase gate in a neutral atomic ensemble via the asymmetric Rydberg blockade. Phys. Rev. A 2010, 82, 034307. [Google Scholar] [CrossRef]
- Zhou, Y.H.; Shen, H.Z.; Yi, X.X. Unconventional photon blockade with second-order nonlinearity. Phys. Rev. A 2015, 92, 023838. [Google Scholar] [CrossRef]
- Zhou, Y.H.; Zhang, X.Y.; Wu, Q.C.; Ye, B.L.; Zhang, Z.Q.; Zou, D.D.; Shen, H.Z.; Yang, C.P. Conventional photon blockade with a three-wave mixing. Phys. Rev. A 2020, 102, 033713. [Google Scholar] [CrossRef]
- Shen, H.Z.; Zhou, Y.H.; Yi, X.X. Quantum optical diode with semiconductor microcavities. Phys. Rev. A 2014, 90, 023849. [Google Scholar] [CrossRef]
- Zhou, Y.H.; Shen, H.Z.; Shao, X.Q.; Yi, X.X. Strong photon antibunching with weak second-order nonlinearity under dissipation and coherent driving. Opt. Express 2016, 24, 17332–17344. [Google Scholar] [CrossRef]
- Majumdar, A.; Gerace, D. Single-photon blockade in doubly resonant nanocavities with second-order nonlinearity. Phys. Rev. B 2013, 87, 235319. [Google Scholar] [CrossRef]
- Bamba, M.; Imamoğlu, A.; Carusotto, I.; Ciuti, C. Origin of Strong Photon Antibunching in Weakly Nonlinear Photonic Molecules. Phys. Rev. A 2011, 83, 021802. [Google Scholar] [CrossRef]
- Carusotto, I.; Ciuti, C. Quantum fluids of light. Rev. Mod. Phys. 2013, 85, 299–366. [Google Scholar] [CrossRef]
- Snijders, H.J.; Frey, J.A.; Norman, J.; Flayac, H.; Savona, V.; Gossard, A.C.; Bowers, J.E.; van Exter, M.P.; Bouwmeester, D.; Löffler, W. Observation of the Unconventional Photon Blockade. Phys. Rev. Lett. 2018, 121, 043601. [Google Scholar] [CrossRef] [PubMed]
- Liew, T.C.H.; Savona, V. Single photons from coupled quantum modes. Phys. Rev. Lett. 2010, 104, 183601. [Google Scholar] [CrossRef]
- Bayer, M.; Gutbrod, T.; Reithmaier, J.P.; Forchel, A.; Forchel, T.L.; Knipp, P.A.; Dremin, A.A.; Dremin, V.D. Optical modes in photonic molecules. Phys. Rev. Lett. 1998, 81, 2582. [Google Scholar] [CrossRef]
- Rakovich, Y.P.; Donegan, J.F. Photonic atoms and molecules. Laser Photonics Rev. 2010, 4, 179–191. [Google Scholar] [CrossRef]
- Xu, X.W.; Li, Y. Tunable photon statistics in weakly nonlinear photonic molecules. Phys. Rev. A 2014, 90, 043822. [Google Scholar] [CrossRef]
- Xu, X.W.; Li, Y. Strongly correlated two-photon transport in a one-dimensional waveguide coupled to a weakly nonlinear cavity. Phys. Rev. A 2014, 90, 033832. [Google Scholar] [CrossRef]
- Xu, X.W.; Li, Y. Strong photon antibunching of symmetric and antisymmetric modes in weakly nonlinear photonic molecules. Phys. Rev. A 2014, 90, 033809. [Google Scholar] [CrossRef]
- Liew, T.C.H.; Savona, V. Multimode entanglement in coupled cavity arrays. New J. Phys. 2013, 15, 025015. [Google Scholar] [CrossRef]
- Flayac, H.; Savona, V. Unconventional photon blockade. Phys. Rev. A 2017, 96, 053810. [Google Scholar] [CrossRef]
- Ganthya, D.; Parai, A.; Jana, P.C. Unconventional photon blockade in four mode coupled optomechanical system. Phys. Lett. A 2023, 462, 128653. [Google Scholar] [CrossRef]
- Zhang, W.; Yu, Z.Y.; Liu, Y.M.; Peng, Y.W. Optimal photon antibunching in a quantum-dot-bimodal-cavity system. Phys. Rev. A 2014, 89, 043832. [Google Scholar] [CrossRef]
- Vukics, A.; Dombi, A.; Fink, J.M.; Domokos, P. Finite-size scaling of the photon-blockade breakdown dissipative quantum phase transition. Quantum 2019, 3, 150. [Google Scholar] [CrossRef]
- Gao, Y.P.; Cao, C.; Lu, P.F.; Wang, C. Phase-controlled photon blockade in optomechanical systems. Fundam. Res. 2023, 3, 30–36. [Google Scholar] [CrossRef]
- Yin, T.S.; Jin, G.R.; Chen, A.X. Enhanced Phonon Antibunching in a Circuit Quantum Acoustodynamical System Containing Two Surface Acoustic Wave Resonators. Micromachines 2022, 13, 591. [Google Scholar] [CrossRef] [PubMed]
- Jabri, H.; Eleuch, H. Enhanced Unconventional photon blockade effect in one- and two-qubit cavities interacting with nonclassical light. Phys. Rev. A 2022, 106, 023704. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Liu, M.; Yang, F.; Zhang, S.; Ruan, S. Phase-Controlled Tunable Unconventional Photon Blockade in a Single-Atom-Cavity System. Micromachines 2023, 14, 2123. https://doi.org/10.3390/mi14112123
Li H, Liu M, Yang F, Zhang S, Ruan S. Phase-Controlled Tunable Unconventional Photon Blockade in a Single-Atom-Cavity System. Micromachines. 2023; 14(11):2123. https://doi.org/10.3390/mi14112123
Chicago/Turabian StyleLi, Hong, Ming Liu, Feng Yang, Siqi Zhang, and Shengping Ruan. 2023. "Phase-Controlled Tunable Unconventional Photon Blockade in a Single-Atom-Cavity System" Micromachines 14, no. 11: 2123. https://doi.org/10.3390/mi14112123
APA StyleLi, H., Liu, M., Yang, F., Zhang, S., & Ruan, S. (2023). Phase-Controlled Tunable Unconventional Photon Blockade in a Single-Atom-Cavity System. Micromachines, 14(11), 2123. https://doi.org/10.3390/mi14112123




