Numerical Study of the Time–Periodic Electroosmotic Flow of Viscoelastic Fluid through a Short Constriction Microchannel
Abstract
:1. Introduction
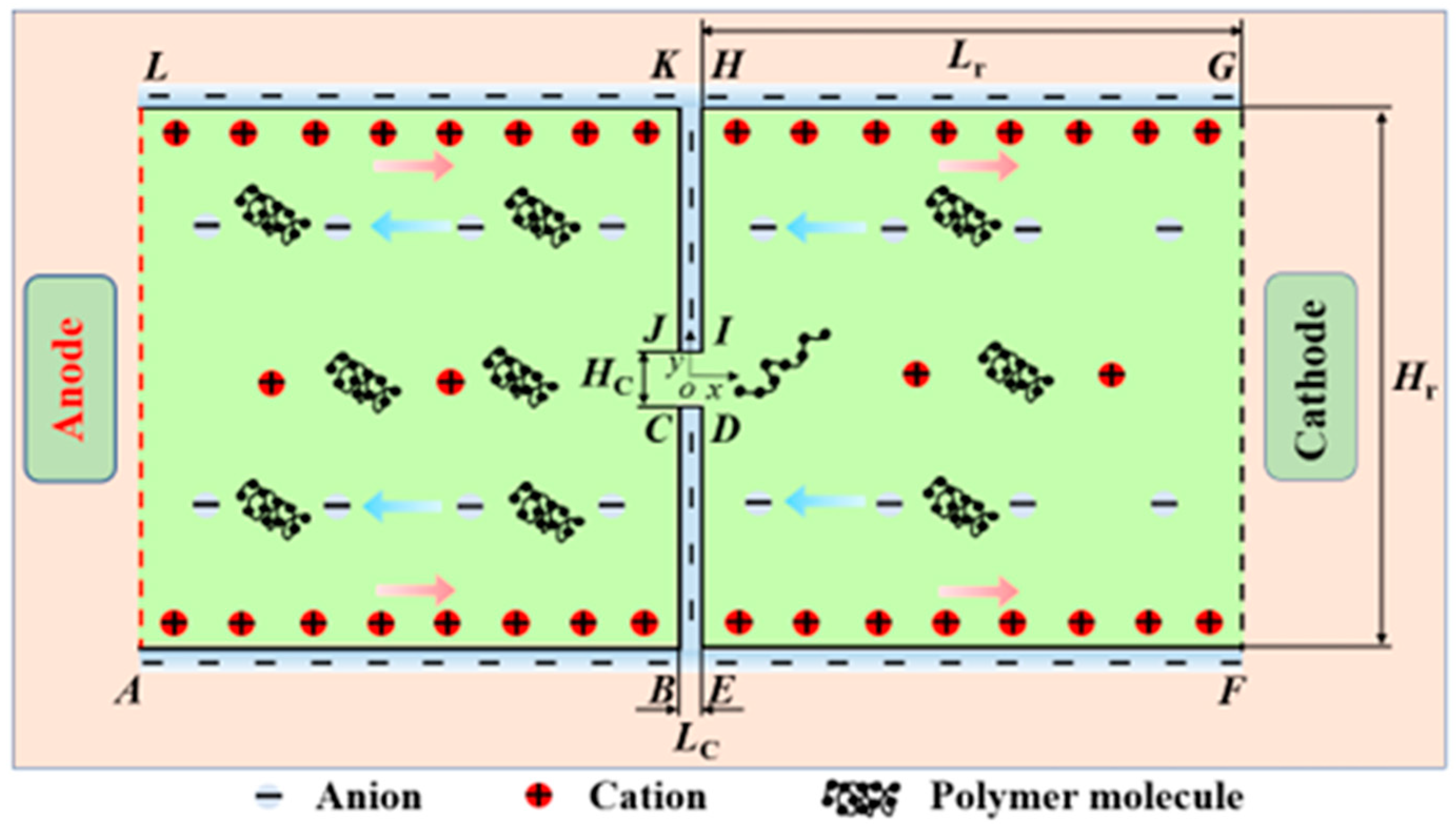
2. Mathematical Model
- (1)
- At the Anode (edge AL in Figure 1): n∙u = 0; p = 0; τ = 0; ϕExt = U0 + UAsin(2fEπt); n∙ψ = 0; Θ = 0; where n denotes the normal unit vector on the surface;
- (2)
- (3)
3. Numerical Method and Code Validation
4. Results and Discussion
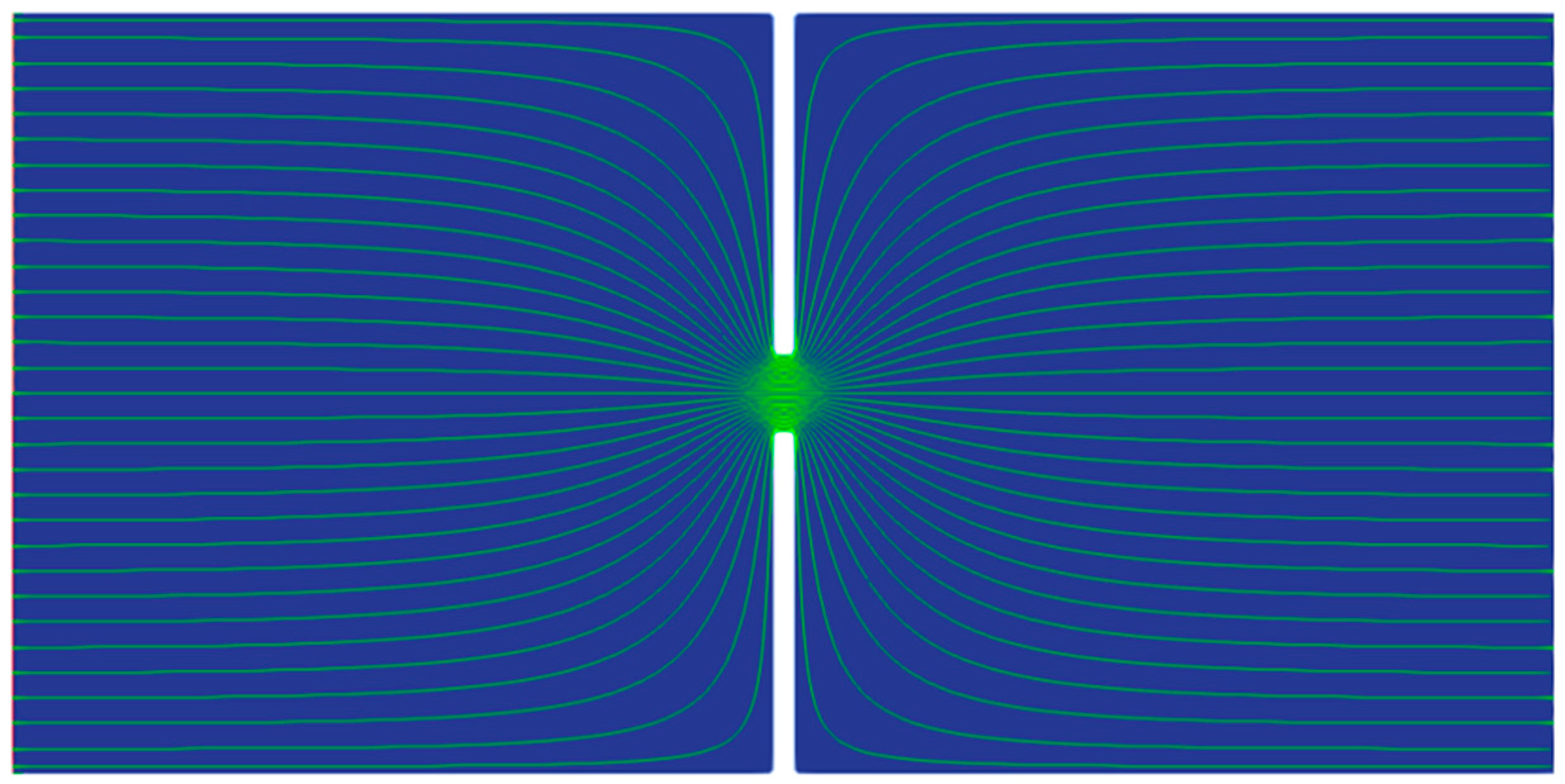
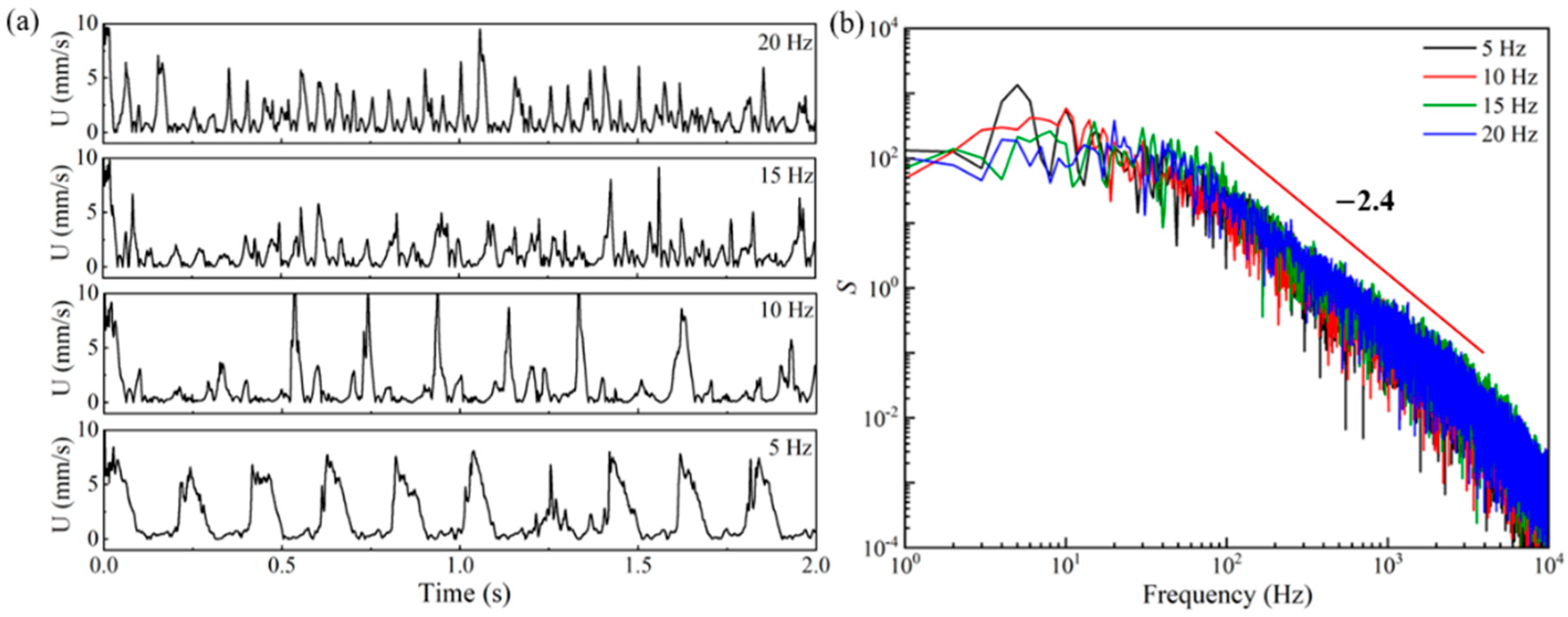
4.1. Characteristic Frequency of the EOF under a Constant Electric Field
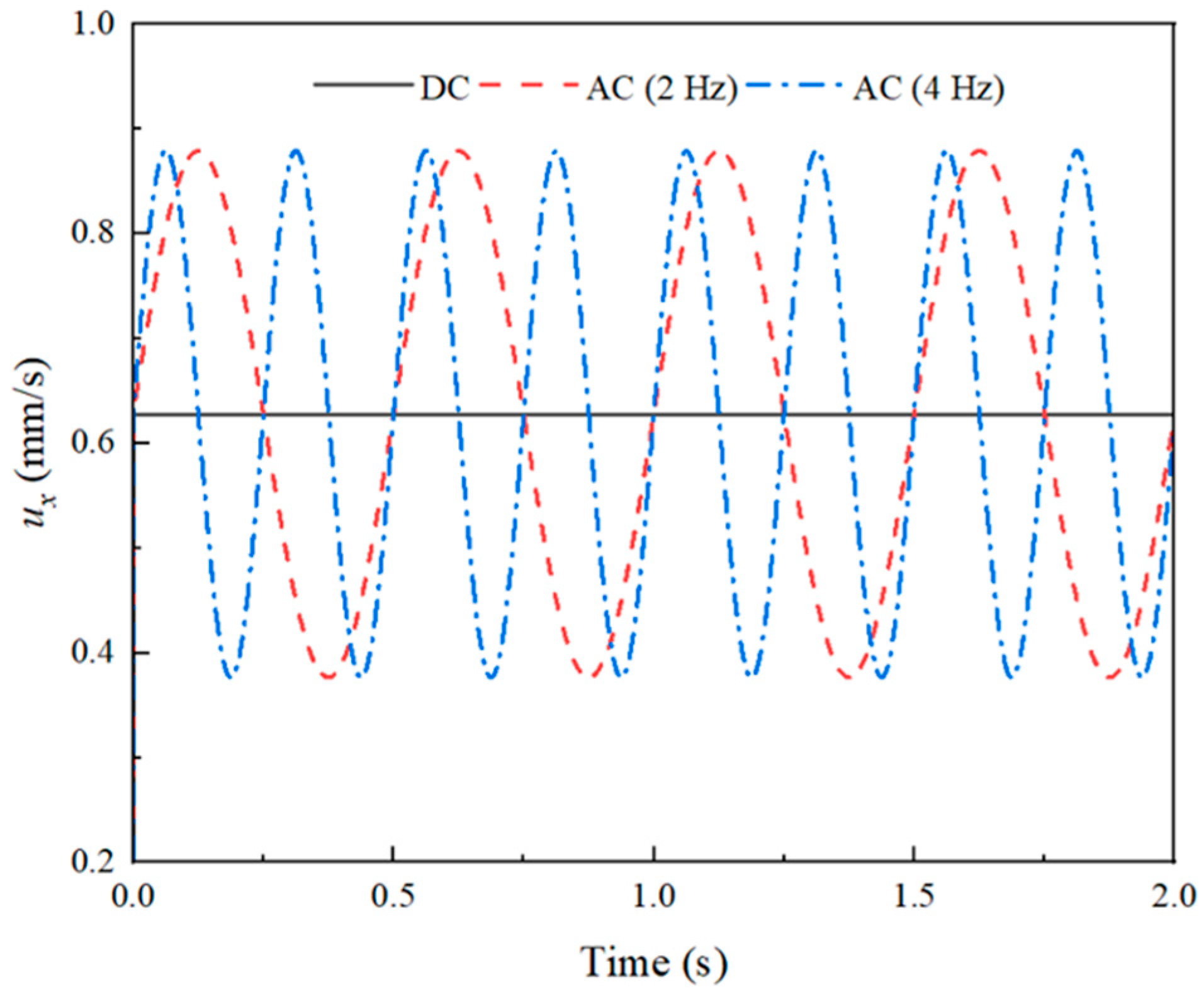
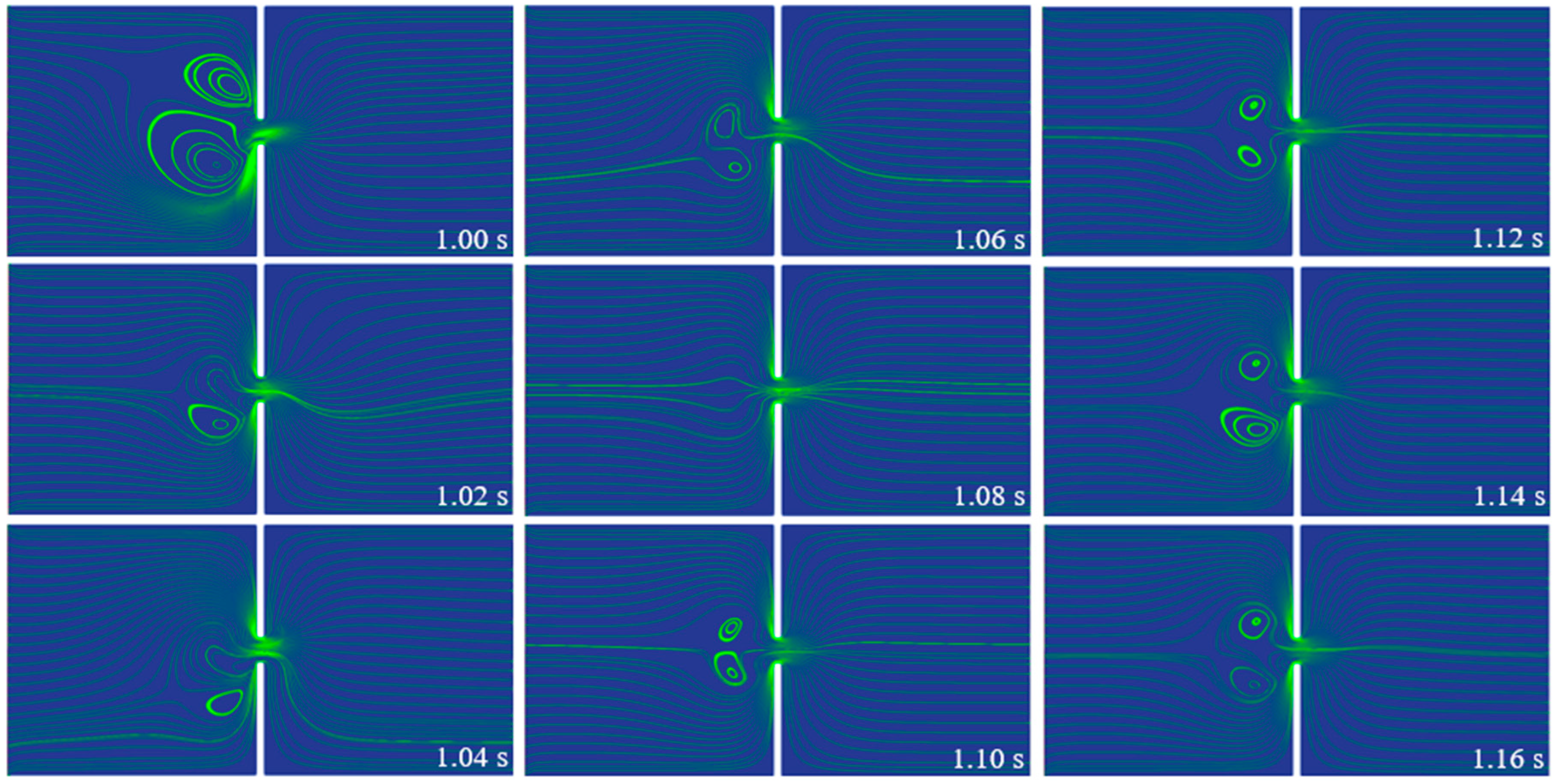
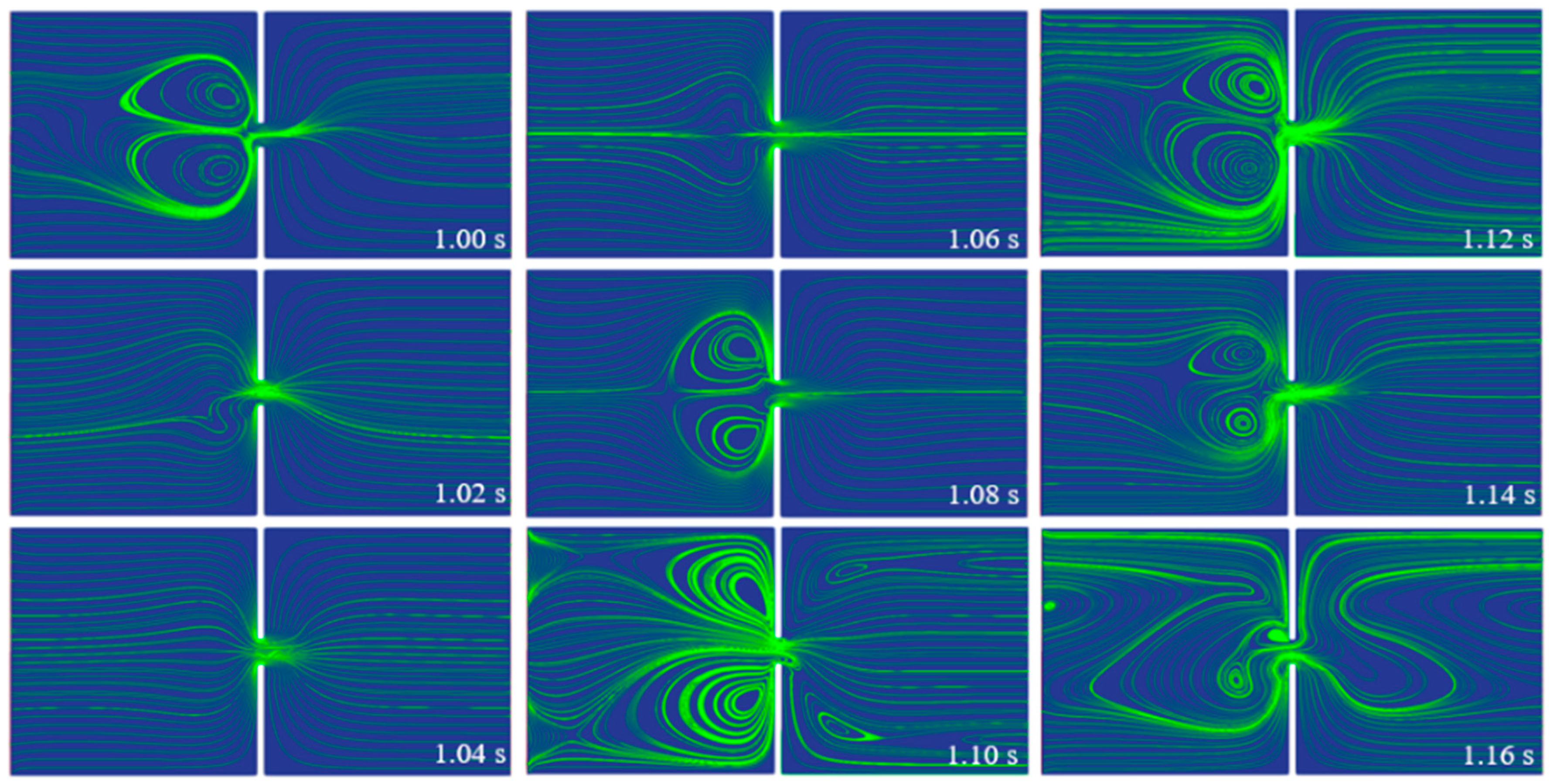
4.2. Frequency Study of the Viscoelastic EOF under a Pulsating Electric Field
5. Conclusions
- (1)
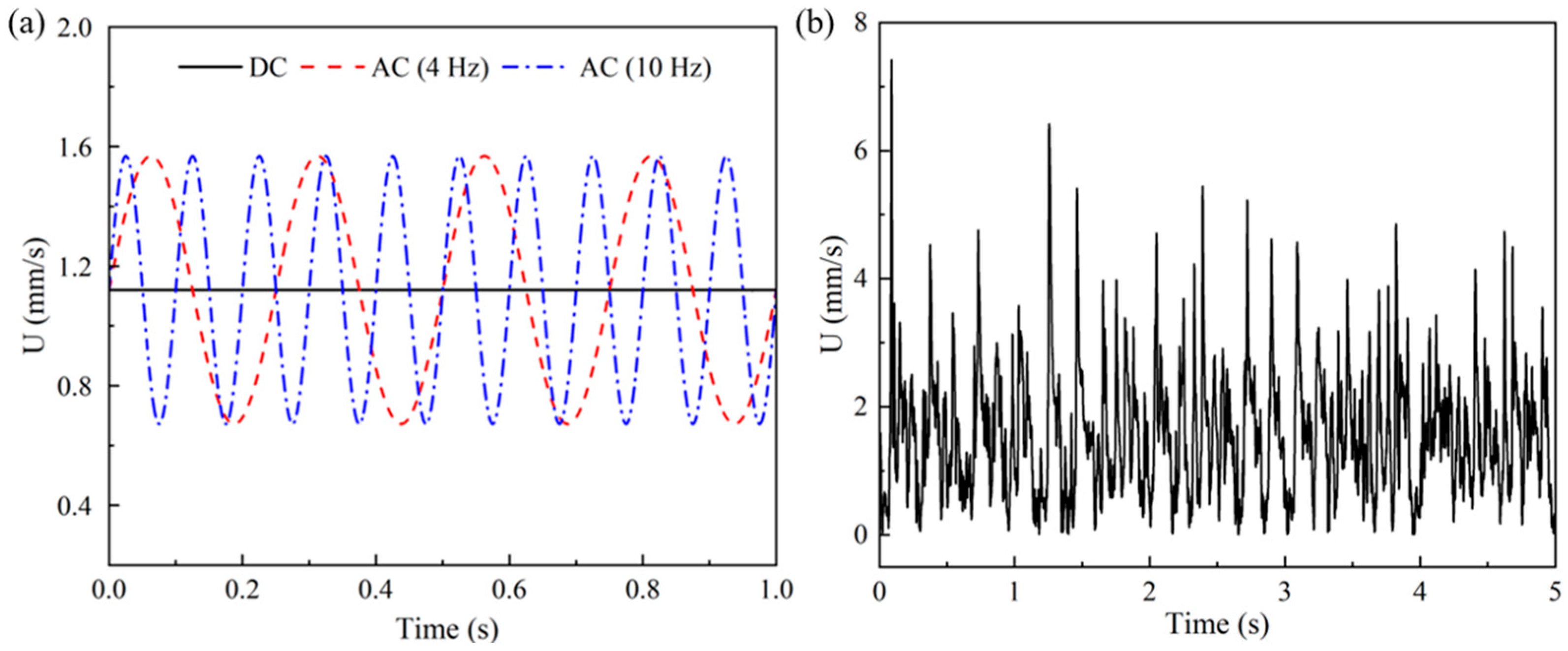
- Under the DC electric field, the Newtonian EOF is time-independent. Under the pulsating electric field with the same amplitude, the amplitude of the velocity and the average velocity in the Newtonian EOF is independent of the frequency of the pulsating electric field. However, the viscoelastic EOF shows significant fluctuations under the DC electric field and strong dependence on the frequency of the pulsating electric field;
- (2)
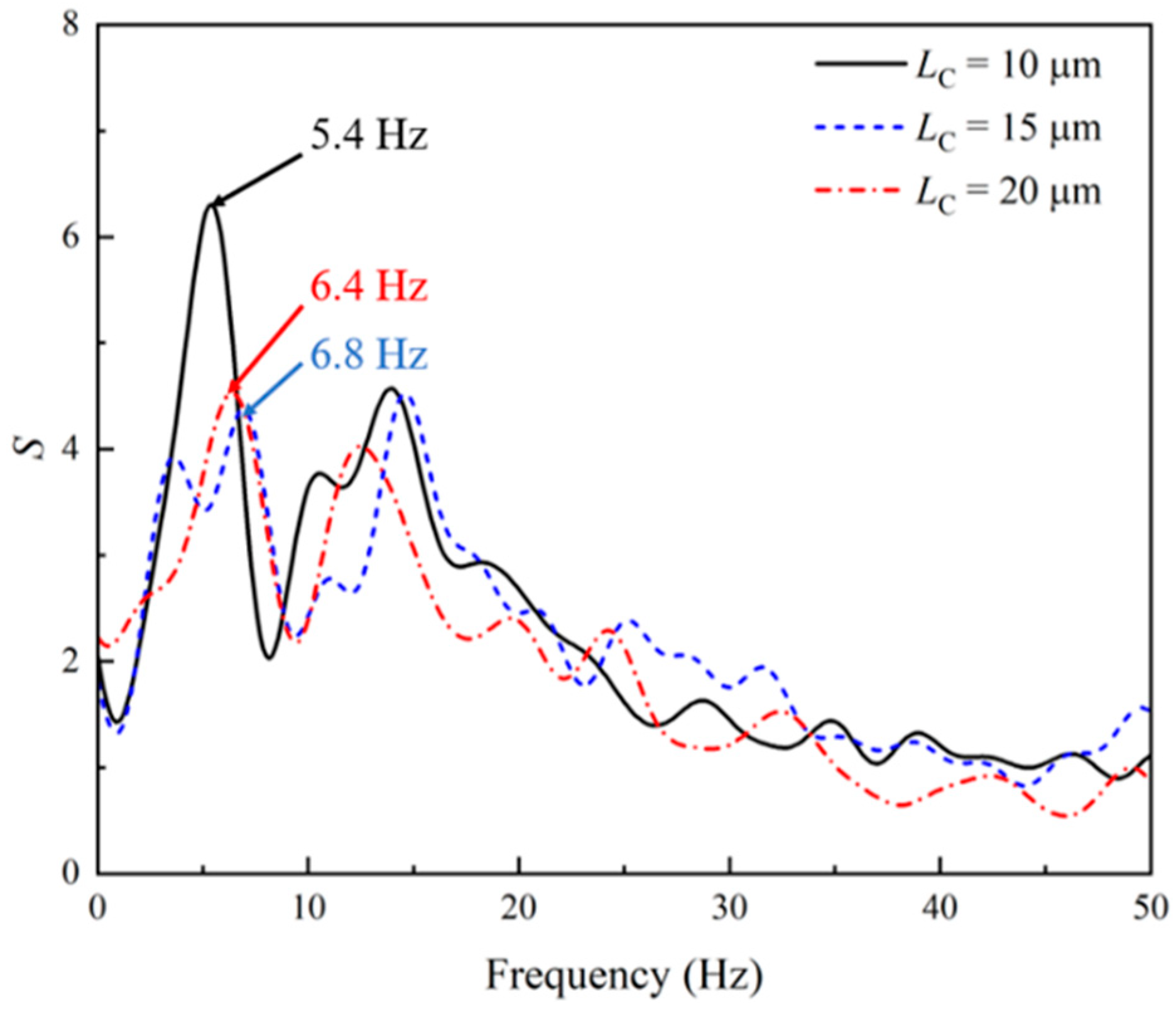
- For the viscoelastic EOF under the DC electric field, the dynamic energy spectra of the velocity fluctuation at the center of the microchannel viscoelastic EOF shows a dominant frequency, which indicates the existence of the characteristic frequency of the viscoelastic fluid;
- (3)
- Under pulsating electric fields with various frequencies, strong instabilities are triggered in the viscoelastic EOF, with random upstream and downstream vortices observed. The energy-spectra curves of the velocity fluctuations share similar general features with a peak at the dominant frequency and a power-law decay over a wide range of frequencies, which is a typical characteristic of elastic turbulence;
- (4)
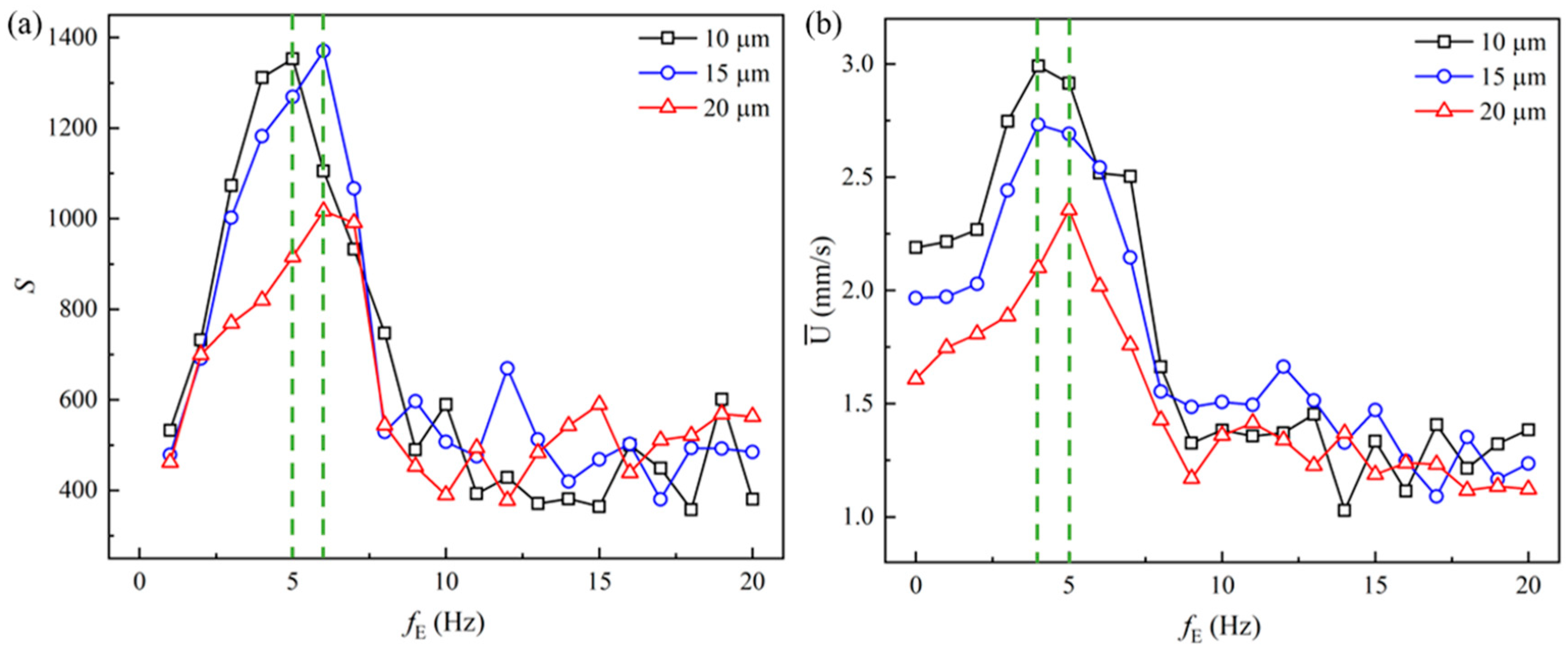
- The highest magnitude of the energy spectra is observed at the frequency of the pulsating electric field. However, the highest magnitude varies with the exciting frequency, and resonance occurs in the EOF when the frequency of the pulsating electric field is near the characteristic frequency of the viscoelastic fluid observed under the DC electric field;
- (5)
- The average velocity in the microchannel is highly dependent on the frequency of the pulsating electric field. When the frequency is relatively low, the average velocity increases with the increasing frequency, and the highest average velocity is observed near the characteristic frequency of the viscoelastic fluid. However, at relatively high frequencies, the average velocity decreases to a level even smaller than under the DC electric field.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Mesh-Independence Study
| Number of Cells | 10 µm | 15 µm | 20 µm |
|---|---|---|---|
| Mesh 1 | 526,560 | 530,780 | 535,000 |
| Mesh 2 | 547,580 | 552,100 | 556,620 |
| Mesh 3 | 632,400 | 636,620 | 640,840 |
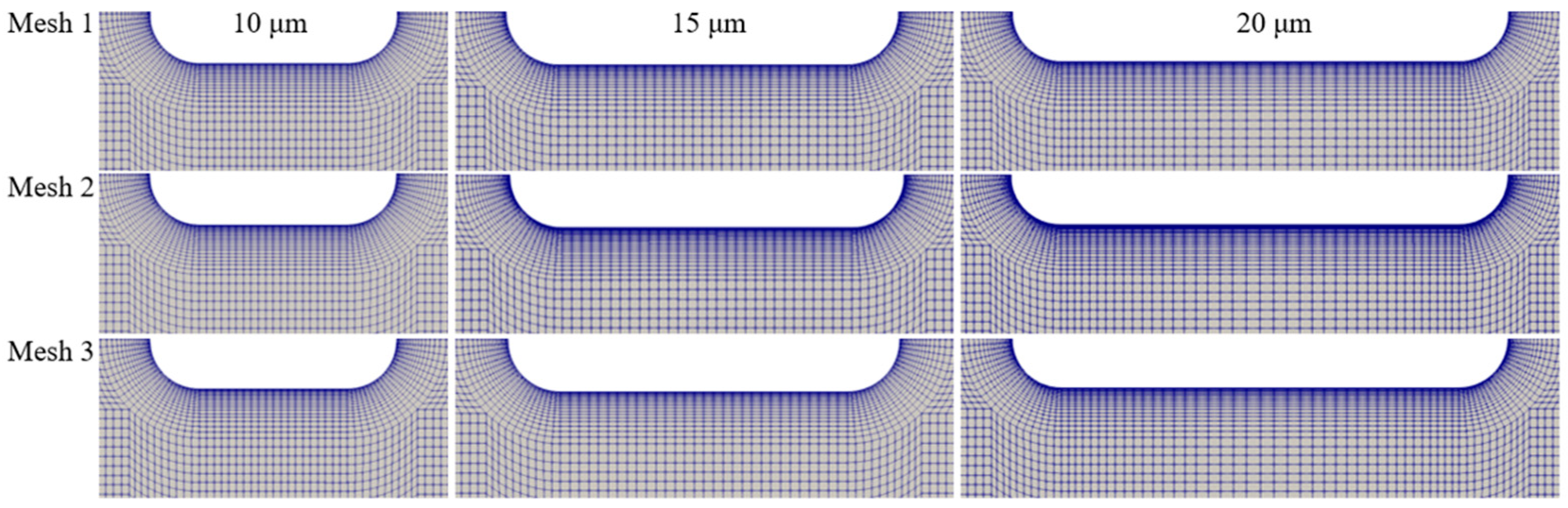
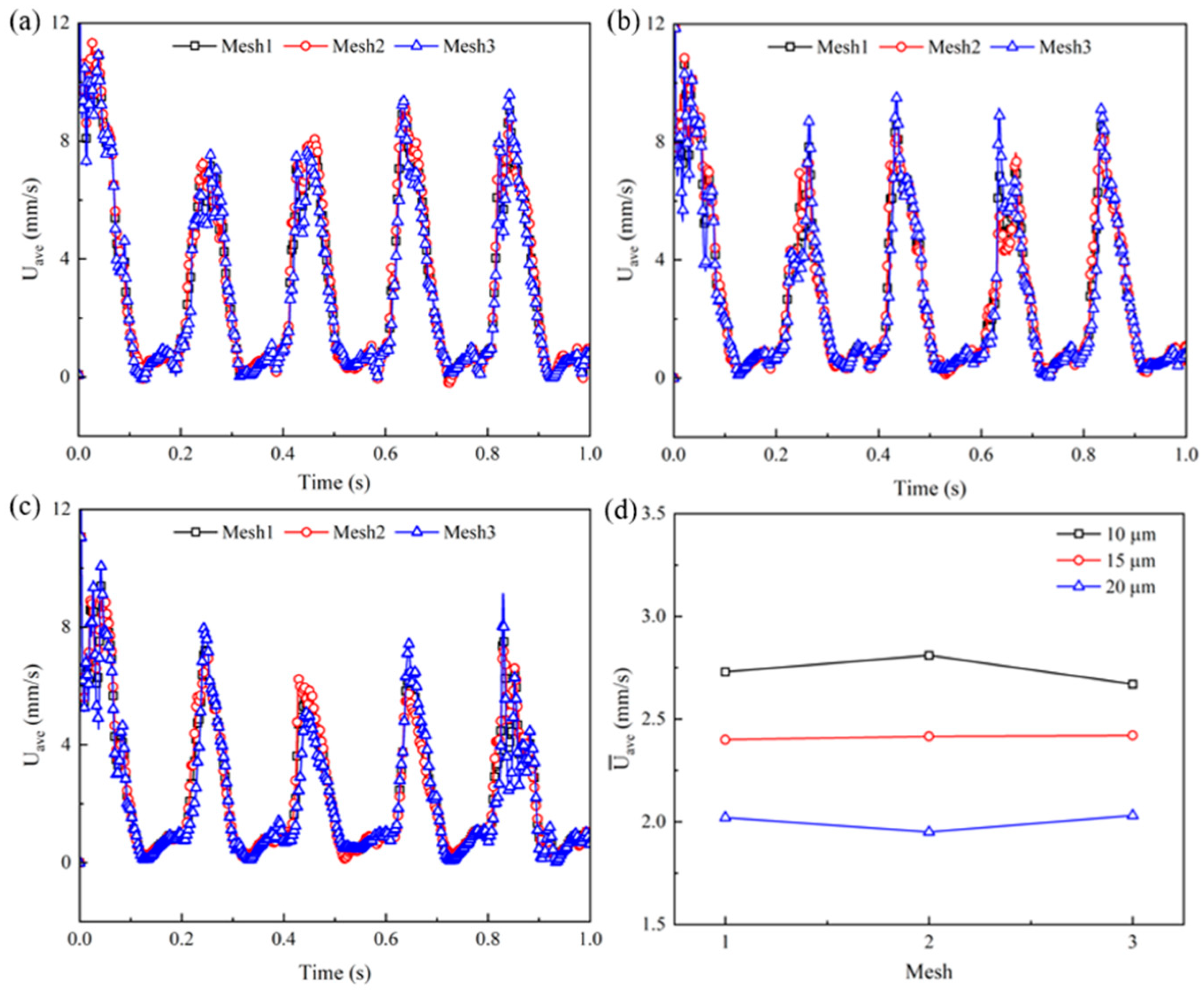
| Relative Error | 10 µm | 15 µm | 20 µm |
|---|---|---|---|
| Mesh 2 | 2.93% | 0.63% | 3.47% |
| Mesh 3 | 1.47% | 0.83% | 0.49% |
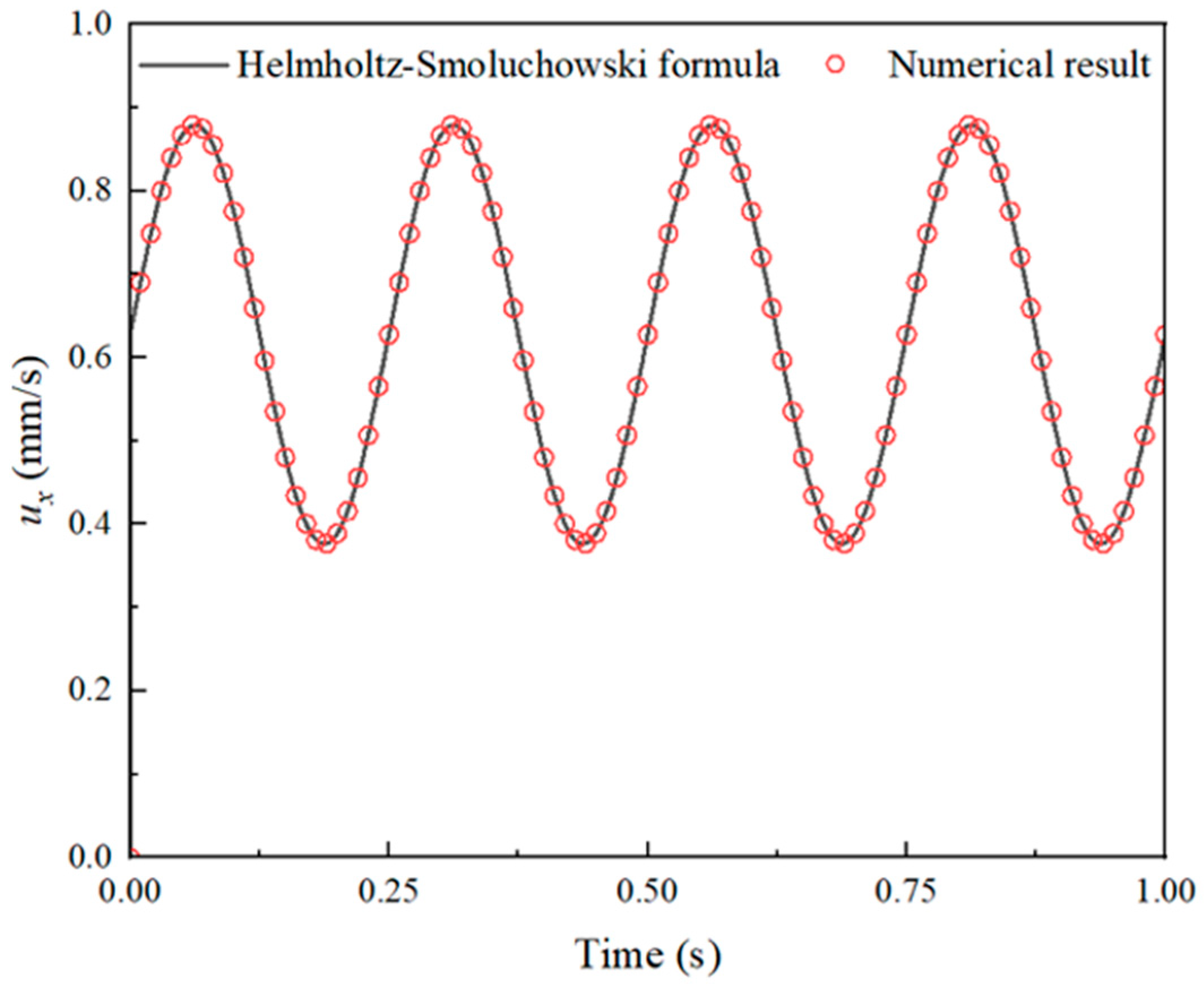
Appendix B. Code Validation



References
- Glasgow, I.; Batton, J.; Aubry, N. Electroosmotic mixing in microchannels. Lab. A Chip. 2004, 4, 558–562. [Google Scholar] [CrossRef]
- Wang, X.; Cheng, C.; Wang, S.; Liu, S. Electroosmotic pumps and their applications in microfluidic systems. Microfluid. Nanofluid. 2009, 6, 145–162. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Wang, S.; Gendhar, B.; Cheng, C.; Byun, C.K.; Li, G.; Zhao, M.; Liu, S. Electroosmotic pumps for microflow analysis. Trac Trends Anal. Chem. 2009, 28, 64–74. [Google Scholar] [CrossRef] [PubMed]
- Jiang, H.; Weng, X.; Chon, C.H.; Wu, X.; Li, D. A microfluidic chip for blood plasma separation using electro-osmotic flow control. J. Micromech. Microeng. 2011, 21, 085019. [Google Scholar] [CrossRef]
- Wu, C.-C.; Huang, W.-C.; Hu, C.-C. An ultrasensitive label-free electrochemical impedimetric DNA biosensing chip integrated with a DC-biased AC electroosmotic vortex. Sens. Actuators B Chem. 2015, 209, 61–68. [Google Scholar] [CrossRef]
- Reuss, F.F. Sur un nouvel effet de l’électricité galvanique. Mem. Soc. Imp. Natur. Moscou 1809, 2, 327–337. [Google Scholar]
- Burgreen, D.; Nakache, F. Electrokinetic flow in ultrafine capillary slits1. J. Phys. Chem. 1964, 68, 1084–1091. [Google Scholar] [CrossRef]
- Levine, S.; Marriott, J.R.; Robinson, K. Theory of electrokinetic flow in a narrow parallel-plate channel. J. Chem. Soc. Faraday Trans. 2 Mol. Chem. Phys. 1975, 71, 1–11. [Google Scholar] [CrossRef]
- Rice, C.L.; Whitehead, R. Electrokinetic flow in a narrow cylindrical capillary. J. Phys. Chem. 1965, 69, 4017–4024. [Google Scholar] [CrossRef]
- Levine, S.; Marriott, J.; Neale, G.; Epstein, N. Theory of electrokinetic flow in fine cylindrical capillaries at high zeta-potentials. J. Colloid Interface Sci. 1975, 52, 136–149. [Google Scholar] [CrossRef]
- Bianchi, F.; Ferrigno, R.; Girault, H. Finite element simulation of an electroosmotic-driven flow division at a T-junction of microscale dimensions. Anal. Chem. 2000, 72, 1987–1993. [Google Scholar] [CrossRef] [PubMed]
- Sadr, R.; Yoda, M.; Zheng, Z.; Conlisk, A. An experimental study of electro-osmotic flow in rectangular microchannels. J. Fluid Mech. 2004, 506, 357–367. [Google Scholar] [CrossRef]
- Yang, C.; Li, D. Analysis of electrokinetic effects on the liquid flow in rectangular microchannels. Colloids Surf. A Physicochem. Eng. Asp. 1998, 143, 339–353. [Google Scholar] [CrossRef]
- Tsao, H.-K. Electroosmotic flow through an annulus. J. Colloid Interface Sci. 2000, 225, 247–250. [Google Scholar] [CrossRef]
- Kang, Y.; Yang, C.; Huang, X. Electroosmotic flow in a capillary annulus with high zeta potentials. J. Colloid Interface Sci. 2002, 253, 285–294. [Google Scholar] [CrossRef]
- Wang, C.-Y.; Liu, Y.-H.; Chang, C.C. Analytical solution of electro-osmotic flow in a semicircular microchannel. Phys. Fluids 2008, 20, 063105. [Google Scholar] [CrossRef]
- Chang, C.C.; Wang, C.-Y. Electro-osmotic flow in a sector microchannel. Phys. Fluids 2009, 21, 042002. [Google Scholar] [CrossRef]
- Bello, M.S.; De Besi, P.; Rezzonico, R.; Righetti, P.G.; Casiraghi, E. Electroosmosis of polymer solutions in fused silica capillaries. Electrophoresis 1994, 15, 623–626. [Google Scholar] [CrossRef]
- Kamişli, F. Flow analysis of a power-law fluid confined in an extrusion die. Int. J. Eng. Sci. 2003, 41, 1059–1083. [Google Scholar] [CrossRef]
- Hakim, A. Mathematical analysis of viscoelastic fluids of White-Metzner type. J. Math. Anal. Appl. 1994, 185, 675–705. [Google Scholar] [CrossRef]
- Arcos, J.; Méndez, F.; Bautista, E.; Bautista, O. Dispersion coefficient in an electro-osmotic flow of a viscoelastic fluid through a microchannel with a slowly varying wall zeta potential. J. Fluid Mech. 2018, 839, 348–386. [Google Scholar] [CrossRef]
- Hernández, A.; Mora, A.; Arcos, J.; Bautista, O. Joule heating and Soret effects on an electro-osmotic viscoelastic fluid flow considering the generalized Phan-Thien–Tanner model. Phys. Fluids 2023, 35, 042010. [Google Scholar] [CrossRef]
- Hernández, A.; Arcos, J.; Martínez-Trinidad, J.; Bautista, O.; Sánchez, S.; Méndez, F. Thermodiffusive effect on the local Debye-length in an electroosmotic flow of a viscoelastic fluid in a slit microchannel. Int. J. Heat Mass Transf. 2022, 187, 122522. [Google Scholar] [CrossRef]
- Bryce, R.; Freeman, M. Abatement of mixing in shear-free elongationally unstable viscoelastic microflows. Lab. A Chip. 2010, 10, 1436–1441. [Google Scholar] [CrossRef] [PubMed]
- Afonso, A.; Pinho, F.; Alves, M. Electro-osmosis of viscoelastic fluids and prediction of electro-elastic flow instabilities in a cross slot using a finite-volume method. J. Non-Newton. Fluid Mech. 2012, 179, 55–68. [Google Scholar] [CrossRef]
- Pimenta, F.; Alves, M. Stabilization of an open-source finite-volume solver for viscoelastic fluid flows. J. Non-Newton. Fluid Mech. 2017, 239, 85–104. [Google Scholar] [CrossRef]
- Pimenta, F.; Alves, M. Electro-elastic instabilities in cross-shaped microchannels. J. Non-Newton. Fluid Mech. 2018, 259, 61–77. [Google Scholar] [CrossRef]
- Song, L.; Yu, L.; Li, D.; Jagdale, P.P.; Xuan, X. Elastic instabilities in the electroosmotic flow of non-Newtonian fluids through T-shaped microchannels. Electrophoresis 2020, 41, 588–597. [Google Scholar] [CrossRef]
- Sadek, S.H.; Pinho, F.T.; Alves, M.A. Electro-elastic flow instabilities of viscoelastic fluids in contraction/expansion micro-geometries. J. Non-Newton. Fluid Mech. 2020, 283, 104293. [Google Scholar] [CrossRef]
- Ji, J.; Qian, S.; Liu, Z. Electroosmotic flow of viscoelastic fluid through a constriction microchannel. Micromachines 2021, 12, 417. [Google Scholar] [CrossRef]
- Datta, S.S.; Ardekani, A.M.; Arratia, P.E.; Beris, A.N.; Bischofberger, I.; McKinley, G.H.; Eggers, J.G.; López-Aguilar, J.E.; Fielding, S.M.; Frishman, A. Perspectives on viscoelastic flow instabilities and elastic turbulence. Phys. Rev. Fluids 2022, 7, 080701. [Google Scholar] [CrossRef]
- Khan, M.B.; Sasmal, C. Electro-elastic instability in electroosmotic flows of viscoelastic fluids through a model porous system. Eur. J. Mech.-B/Fluids 2023, 97, 173–186. [Google Scholar] [CrossRef]
- Li, S.K.; Ghanem, A.H.; Higuchi, W.I. Pore charge distribution considerations in human epidermal membrane electroosmosis. J. Pharm. Sci. 1999, 88, 1044–1049. [Google Scholar] [PubMed]
- Lim, C.Y.; Lam, Y.C. Analysis on micro-mixing enhancement through a constriction under time periodic electroosmotic flow. Microfluid. Nanofluid. 2012, 12, 127–141. [Google Scholar] [CrossRef]
- Chakraborty, S.; Ray, S. Mass flow-rate control through time periodic electro-osmotic flows in circular microchannels. Phys. Fluids 2008, 20, 083602. [Google Scholar] [CrossRef]
- Dutta, P.; Beskok, A. Analytical solution of time periodic electroosmotic flows: Analogies to Stokes’ second problem. Anal. Chem. 2001, 73, 5097–5102. [Google Scholar] [CrossRef]
- Ramos, A.; Morgan, H.; Green, N.G.; Castellanos, A. AC electric-field-induced fluid flow in microelectrodes. J. Colloid Interface Sci. 1999, 217, 420–422. [Google Scholar] [CrossRef]
- Minor, M.; Van der Linde, A.; Van Leeuwen, H.; Lyklema, J. Dynamic aspects of electrophoresis and electroosmosis: A new fast method for measuring particle mobilities. J. Colloid Interface Sci. 1997, 189, 370–375. [Google Scholar] [CrossRef]
- Studer, V.; Pepin, A.; Chen, Y.; Ajdari, A. Fabrication of microfluidic devices for AC electrokinetic fluid pumping. Microelectron. Eng. 2002, 61, 915–920. [Google Scholar] [CrossRef]
- Olesen, L.H.; Bruus, H.; Ajdari, A. Ac electrokinetic micropumps: The effect of geometrical confinement, Faradaic current injection, and nonlinear surface capacitance. Phys. Rev. E 2006, 73, 056313. [Google Scholar] [CrossRef]
- Olesen, L.H.; Ajdari, A.; Bruus, H. AC electrokinetic micropumps: The effect of geometrical confinement. In Proceedings of the 9th International Conference on Miniaturized Systems for Chemistry and Life Sciences, Boston, MA, USA, 9 October 2005; pp. 560–562. [Google Scholar]
- Liu, Q.-s.; Jian, Y.-j.; Yang, L.-g. Time periodic electroosmotic flow of the generalized Maxwell fluids between two micro-parallel plates. J. Non-Newton. Fluid Mech. 2011, 166, 478–486. [Google Scholar] [CrossRef]
- Jian, Y.; Liu, Q.; Yang, L. AC electroosmotic flow of generalized Maxwell fluids in a rectangular microchannel. J. Non-Newton. Fluid Mech. 2011, 166, 1304–1314. [Google Scholar] [CrossRef]
- Jabari Moghadam, A. Time-periodic electroosmotic flow of non-Newtonian fluids in microchannels. Int. J. Eng. 2016, 29, 706–714. [Google Scholar]
- Moghadam, A.J.; Akbarzadeh, P. Non-Newtonian fluid flow induced by pressure gradient and time-periodic electroosmosis in a microtube. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 5015–5025. [Google Scholar] [CrossRef]
- Alipanah, M.; Ramiar, A. High efficiency micromixing technique using periodic induced charge electroosmotic flow: A numerical study. Colloids Surf. A Physicochem. Eng. Asp. 2017, 524, 53–65. [Google Scholar] [CrossRef]
- Dawn, S.; Sarkar, S. Control of mass flow-rate of viscoelastic fluids through time-periodic electro-osmotic flows in a microchannel. J. Fluids Eng. 2021, 143, 111209. [Google Scholar] [CrossRef]
- Li, D.; Li, K. Time periodic pulse electroosmotic flow of Jeffrey fluids in a circular microchannel under the depletion effect. J. Mech. Sci. Technol. 2022, 36, 1847–1856. [Google Scholar] [CrossRef]
- Kumar, V.; Mukherjee, J.; Sinha, S.K.; Ghosh, U. Combined electromechanically driven pulsating flow of nonlinear viscoelastic fluids in narrow confinements. J. R. Soc. Interface 2022, 19, 20210876. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Chen, J.; Wong, T.; Liow, J.-L. Experimental and theoretical investigations of non-Newtonian electro-osmotic driven flow in rectangular microchannels. Soft Matter 2016, 12, 6206–6213. [Google Scholar] [CrossRef]
- Oldroyd, J.G. On the formulation of rheological equations of state. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1950, 200, 523–541. [Google Scholar]
- Öztekin, A.; Brown, R.A.; McKinley, G.H. Quantitative prediction of the viscoelastic instability in cone-and-plate flow of a Boger fluid using a multi-mode Giesekus model. J. Non-Newton. Fluid Mech. 1994, 54, 351–377. [Google Scholar] [CrossRef]
- Thien, N.P.; Tanner, R.I. A new constitutive equation derived from network theory. J. Non-Newton. Fluid Mech. 1977, 2, 353–365. [Google Scholar] [CrossRef]
- Varagnolo, S.; Filippi, D.; Mistura, G.; Pierno, M.; Sbragaglia, M. Stretching of viscoelastic drops in steady sliding. Soft Matter 2017, 13, 3116–3124. [Google Scholar] [CrossRef] [PubMed]
- Fattal, R.; Kupferman, R. Constitutive laws for the matrix-logarithm of the conformation tensor. J. Non-Newton. Fluid Mech. 2004, 123, 281–285. [Google Scholar] [CrossRef]
- Fattal, R.; Kupferman, R. Time-dependent simulation of viscoelastic flows at high Weissenberg number using the log-conformation representation. J. Non-Newton. Fluid Mech. 2005, 126, 23–37. [Google Scholar] [CrossRef]
- Fogolari, F.; Brigo, A.; Molinari, H. The Poisson–Boltzmann equation for biomolecular electrostatics: A tool for structural biology. J. Mol. Recognit. 2002, 15, 377–392. [Google Scholar] [CrossRef] [PubMed]
- Pimenta, F.; Alves, M.A. Numerical simulation of electrically-driven flows using OpenFOAM. arXiv 2018, arXiv:1802.02843. [Google Scholar]
- Jasak, H.; Jemcov, A.; Tukovic, Z. OpenFOAM: A C++ library for complex physics simulations. In Proceedings of the International Workshop on Coupled Methods in Numerical Dynamics, Dubrovnik, Croatia, 19–21 September 2007; pp. 1–20. [Google Scholar]
- Alves, M.; Oliveira, P.; Pinho, F. A convergent and universally bounded interpolation scheme for the treatment of advection. Int. J. Numer. Methods Fluids 2003, 41, 47–75. [Google Scholar] [CrossRef]
- Duarte, A.; Miranda, A.I.; Oliveira, P.J. Numerical and analytical modeling of unsteady viscoelastic flows: The start-up and pulsating test case problems. J. Non-Newton. Fluid Mech. 2008, 154, 153–169. [Google Scholar] [CrossRef]
- Patankar, S.V.J.W. Numerical Heat Transfer and Fluid Flow; Hemisphere Publishing Corp.: Washington, DC, USA, 1980; 210p. [Google Scholar]
- Van Doormaal, J.P.; Raithby, G.D. Enhancements of the SIMPLE method for predicting incompressible fluid flows. Numer. Heat Transf. 1984, 7, 147–163. [Google Scholar] [CrossRef]
- Patankar, N.A.; Hu, H.H. Numerical simulation of electroosmotic flow. Anal. Chem. 1998, 70, 1870–1881. [Google Scholar] [CrossRef]
- Sousa, P.C.; Vega, E.J.; Sousa, R.G.; Montanero, J.M.; Alves, M.A. Measurement of relaxation times in extensional flow of weakly viscoelastic polymer solutions. Rheol. Acta 2017, 56, 11–20. [Google Scholar] [CrossRef]
- Ortiz, M.; De Kee, D.; Carreau, P. Rheology of concentrated poly (ethylene oxide) solutions. J. Rheol. 1994, 38, 519–539. [Google Scholar] [CrossRef]
- Mohyuddin, M.R.; Götz, T. Resonance behaviour of viscoelastic fluid in Poiseuille flow in the presence of a transversal magnetic field. Int. J. Numer. Methods Fluids 2005, 49, 837–847. [Google Scholar] [CrossRef]
- Collepardo-Guevara, R.; Poiré, E.C. Controlling viscoelastic flow by tuning frequency during occlusions. Phys. Rev. E 2007, 76, 026301. [Google Scholar] [CrossRef] [PubMed]
- Vazquez-Vergara, P.; Torres-Herrera, U.; Caballero-Robledo, G.A.; Olguin, L.F.; Corvera Poiré, E. Experimental resonances in viscoelastic microfluidics. Front. Phys. 2021, 9, 636070. [Google Scholar] [CrossRef]
- Andrienko, Y.A.; Siginer, D.; Yanovsky, Y.G. Resonance behavior of viscoelastic fluids in Poiseuille flow and application to flow enhancement. Int. J. Non-Linear Mech. 2000, 35, 95–102. [Google Scholar] [CrossRef]
- Groisman, A.; Steinberg, V. Elastic turbulence in curvilinear flows of polymer solutions. New J. Phys. 2004, 6, 29. [Google Scholar] [CrossRef]
- Sheng, P.; Zhou, M.-Y. Dynamic permeability in porous media. Phys. Rev. Lett. 1988, 61, 1591. [Google Scholar] [CrossRef] [PubMed]
- Castro, M.; Bravo-Gutiérrez, M.; Hernández-Machado, A.; Poiré, E.C. Dynamic characterization of permeabilities and flows in microchannels. Phys. Rev. Lett. 2008, 101, 224501. [Google Scholar] [CrossRef]
- Siginer, A. On some nearly viscometric flows of viscoelastic liquids. Rheol. Acta 1991, 30, 447–473. [Google Scholar] [CrossRef]
- Bandopadhyay, A.; Chakraborty, S. Electrokinetically induced alterations in dynamic response of viscoelastic fluids in narrow confinements. Phys. Rev. E 2012, 85, 056302. [Google Scholar] [CrossRef] [PubMed]
- Martins, F.; Oishi, C.M.; Afonso, A.M.; Alves, M.A. A numerical study of the kernel-conformation transformation for transient viscoelastic fluid flows. J. Comput. Phys. 2015, 302, 653–673. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, J.; Qian, S.; Parker, A.M.; Zhang, X. Numerical Study of the Time–Periodic Electroosmotic Flow of Viscoelastic Fluid through a Short Constriction Microchannel. Micromachines 2023, 14, 2077. https://doi.org/10.3390/mi14112077
Ji J, Qian S, Parker AM, Zhang X. Numerical Study of the Time–Periodic Electroosmotic Flow of Viscoelastic Fluid through a Short Constriction Microchannel. Micromachines. 2023; 14(11):2077. https://doi.org/10.3390/mi14112077
Chicago/Turabian StyleJi, Jianyu, Shizhi Qian, Armani Marie Parker, and Xiaoyu Zhang. 2023. "Numerical Study of the Time–Periodic Electroosmotic Flow of Viscoelastic Fluid through a Short Constriction Microchannel" Micromachines 14, no. 11: 2077. https://doi.org/10.3390/mi14112077
APA StyleJi, J., Qian, S., Parker, A. M., & Zhang, X. (2023). Numerical Study of the Time–Periodic Electroosmotic Flow of Viscoelastic Fluid through a Short Constriction Microchannel. Micromachines, 14(11), 2077. https://doi.org/10.3390/mi14112077







