Tackling Multi-Physics Nano-Scale Phenomena in Capillary Force Lithography with Small Data by Hybrid Intelligence
Abstract
1. Introduction
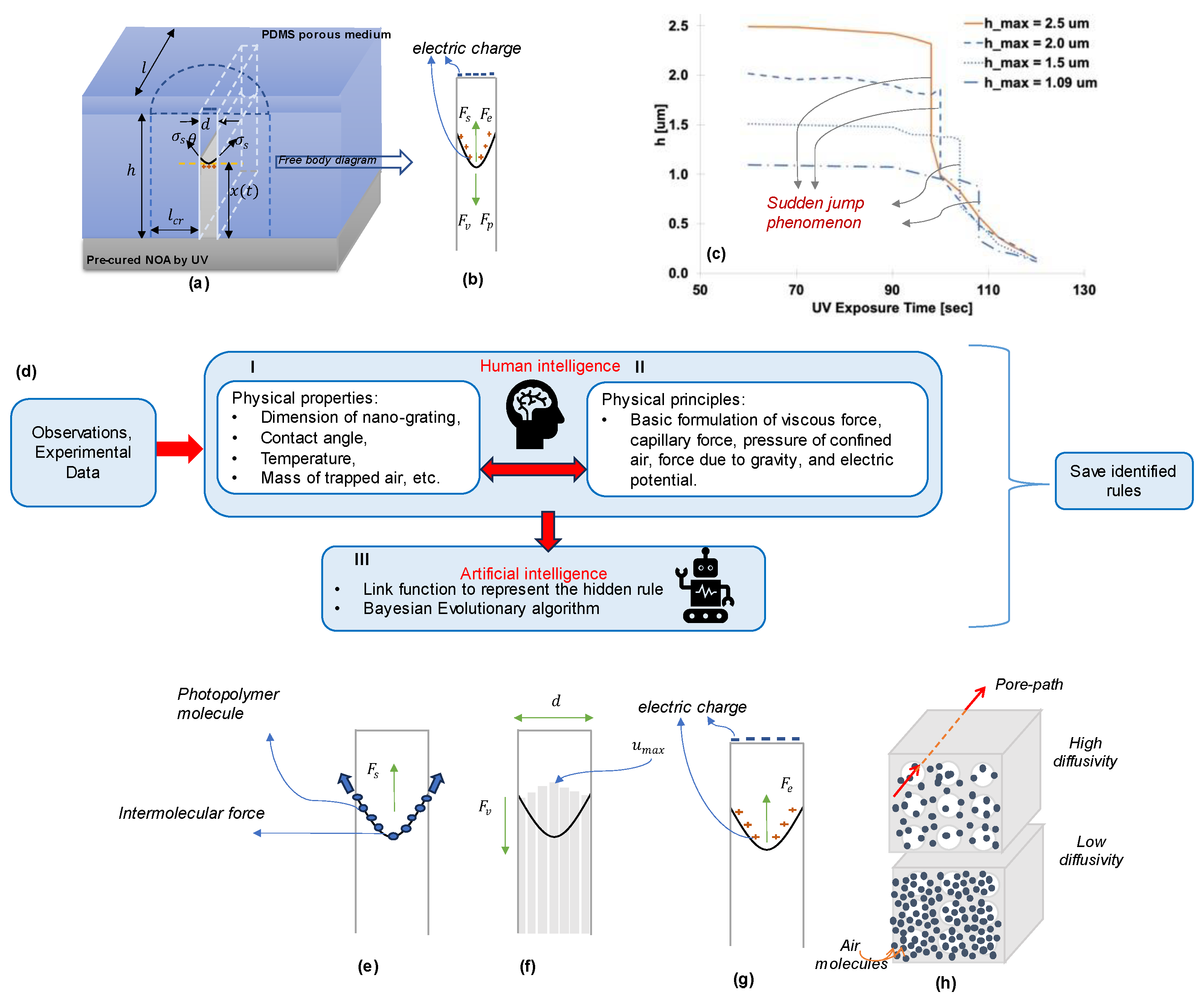
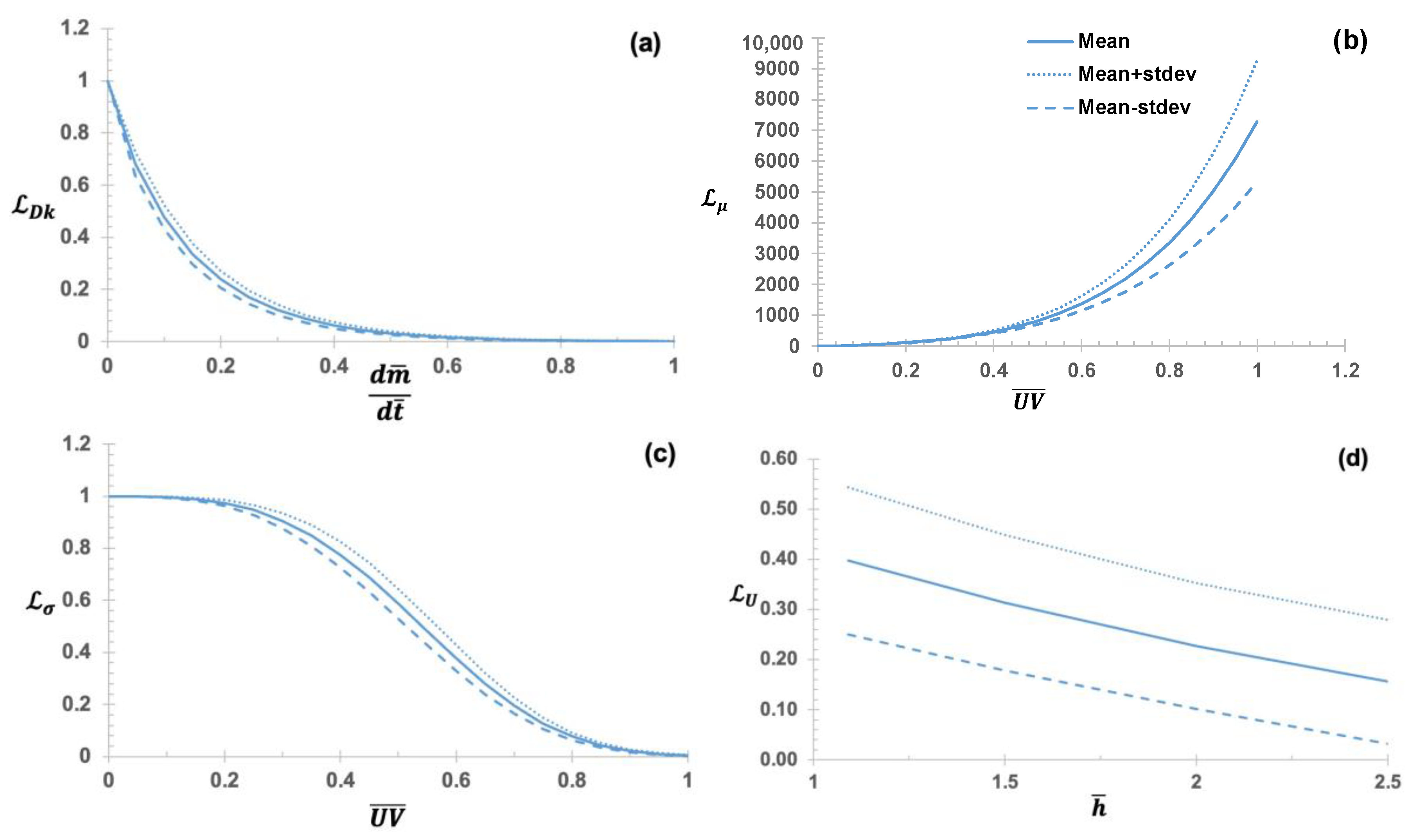
- Air diffusivity decreases as the rate of trapped air-mass transfer increases;
- The dynamic viscosity of the liquid increases upon exposure to UV radiation;
- Our results demonstrate that UV exposure leads to a reduction in the surface tension of the liquid;
- The electric potential between the liquid and the PDMS mold decreases as the distance between the liquid’s top surface and the bottom surface of the PDMS mold increases.
2. Materials and Methods
2.1. Data Preparation
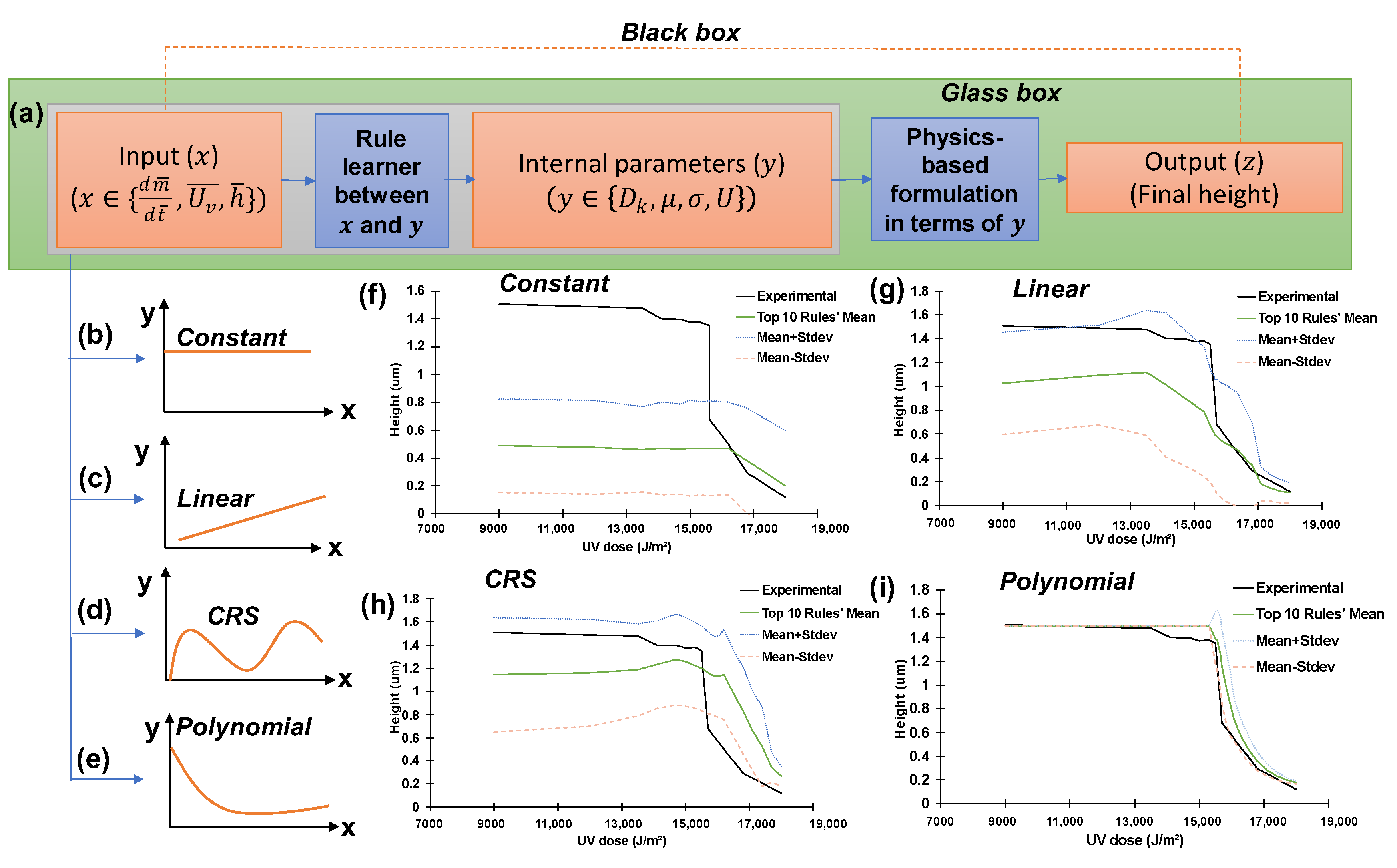
2.2. Two Pillars of the Hybrid Intelligence—Human and Artificial Intelligences
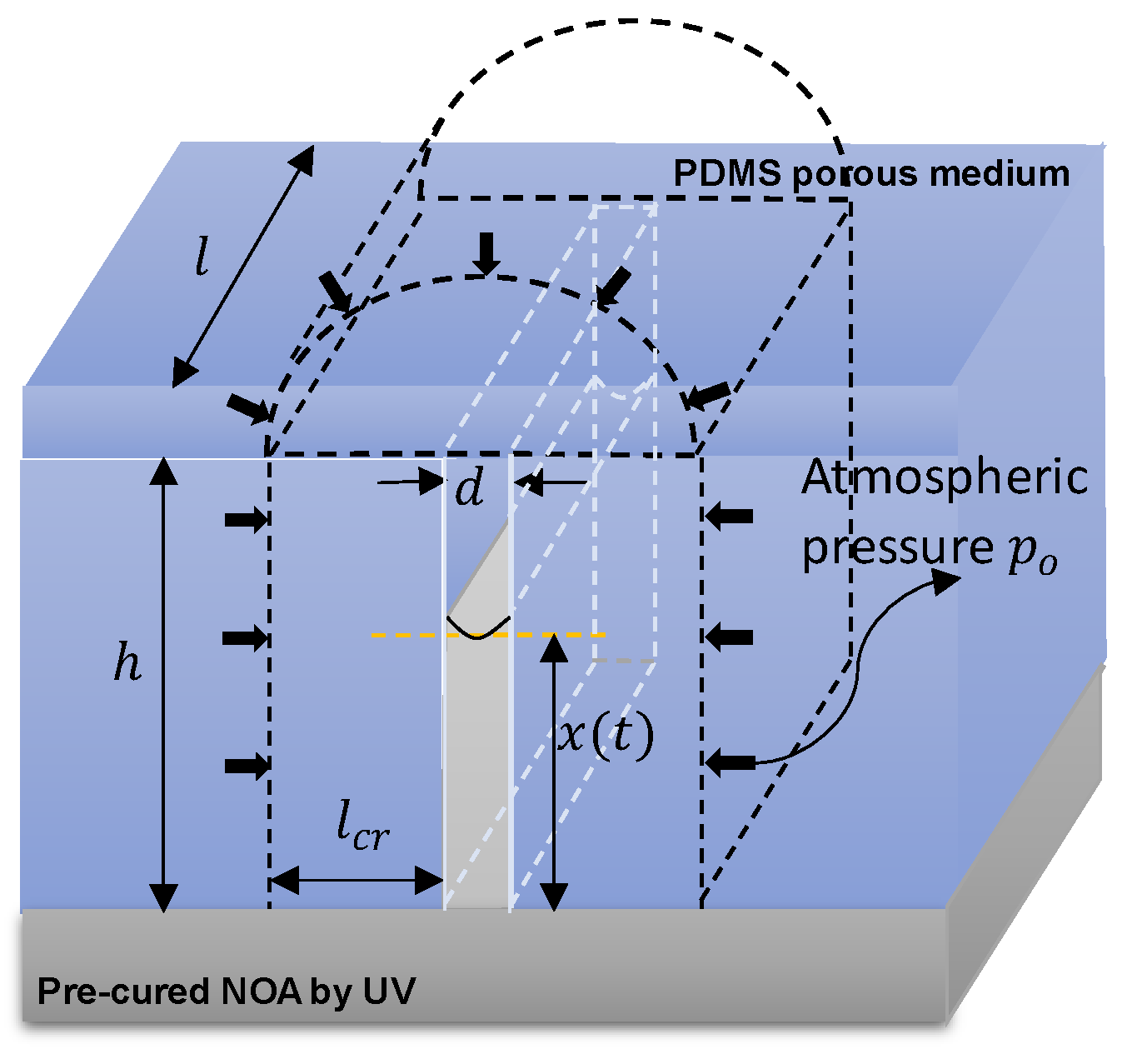
2.2.1. Human Intelligence for Providing Basic Formulations with Basic Physics Quantities
- Force equilibrium formulation
- 2.
- Mass balance formulation
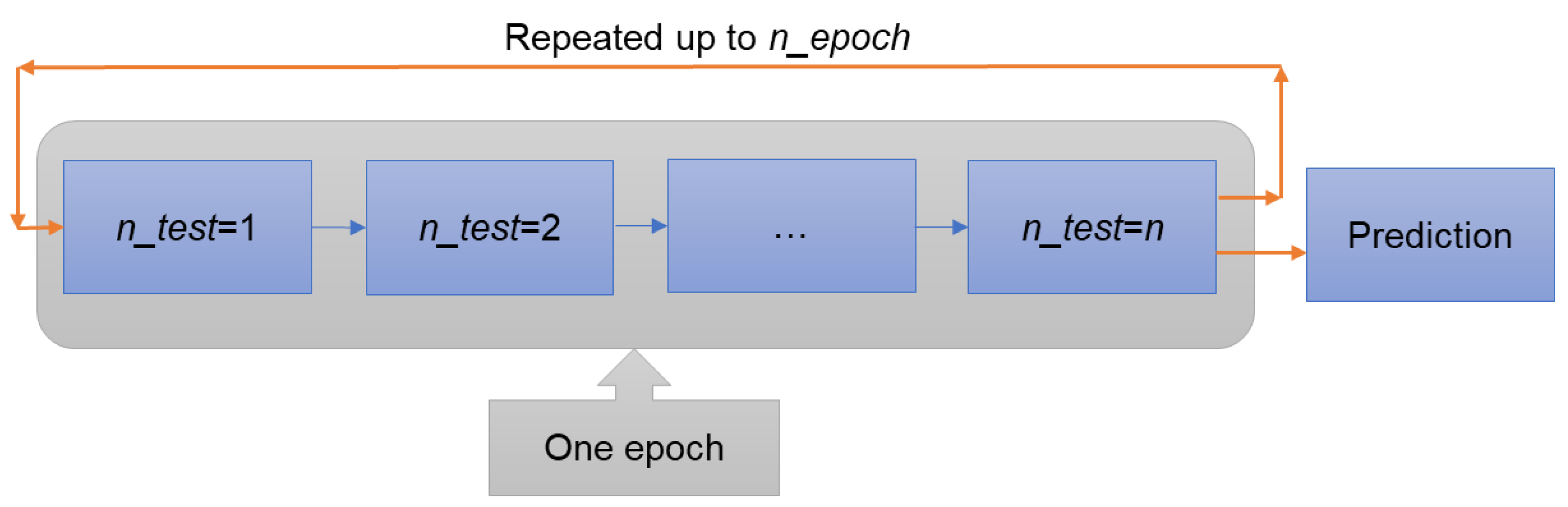
2.2.2. Artificial Intelligence for Exploring and Searching Hidden Rules
- Flexible link functions
- 2.
- Bayesian evolutionary algorithm
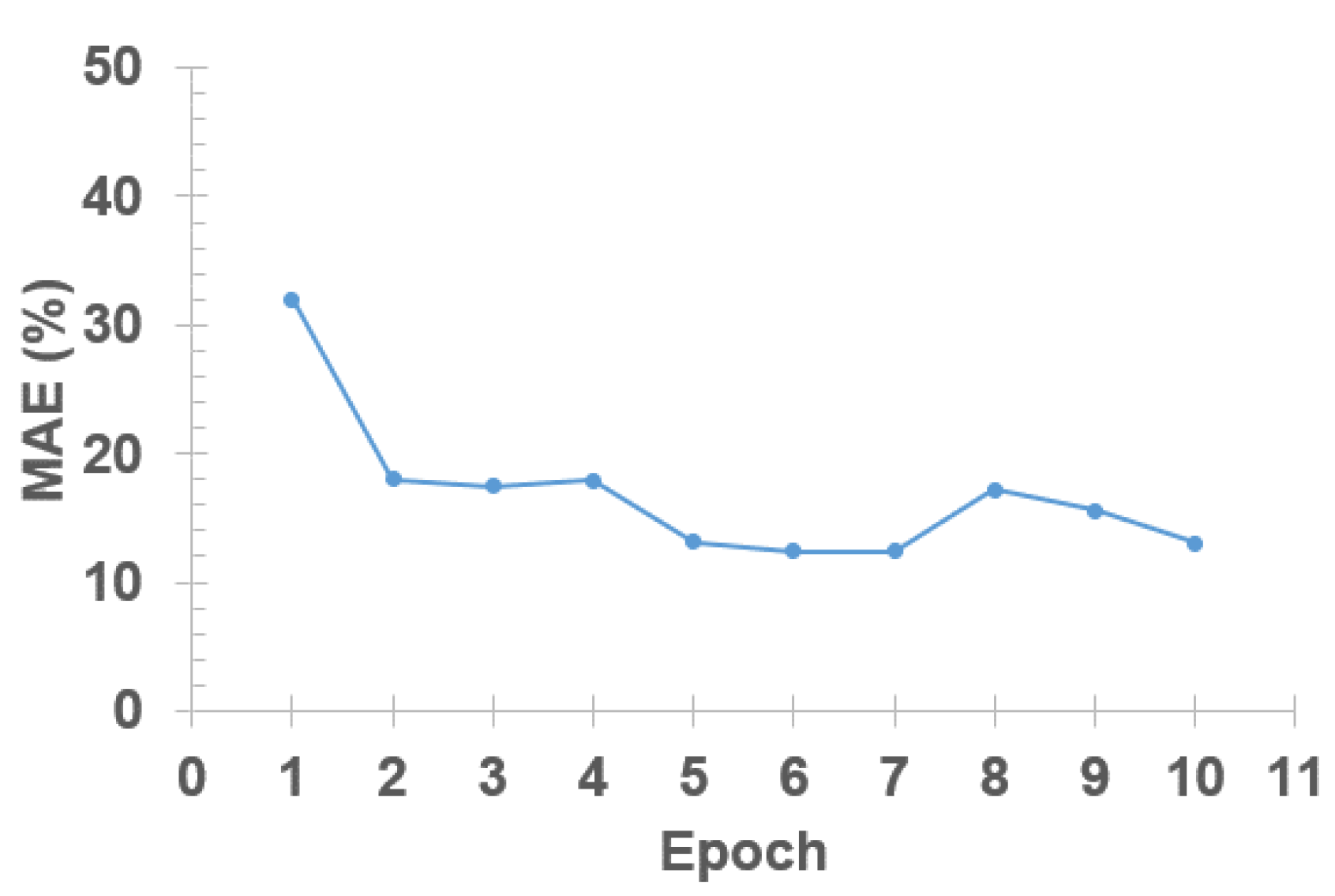
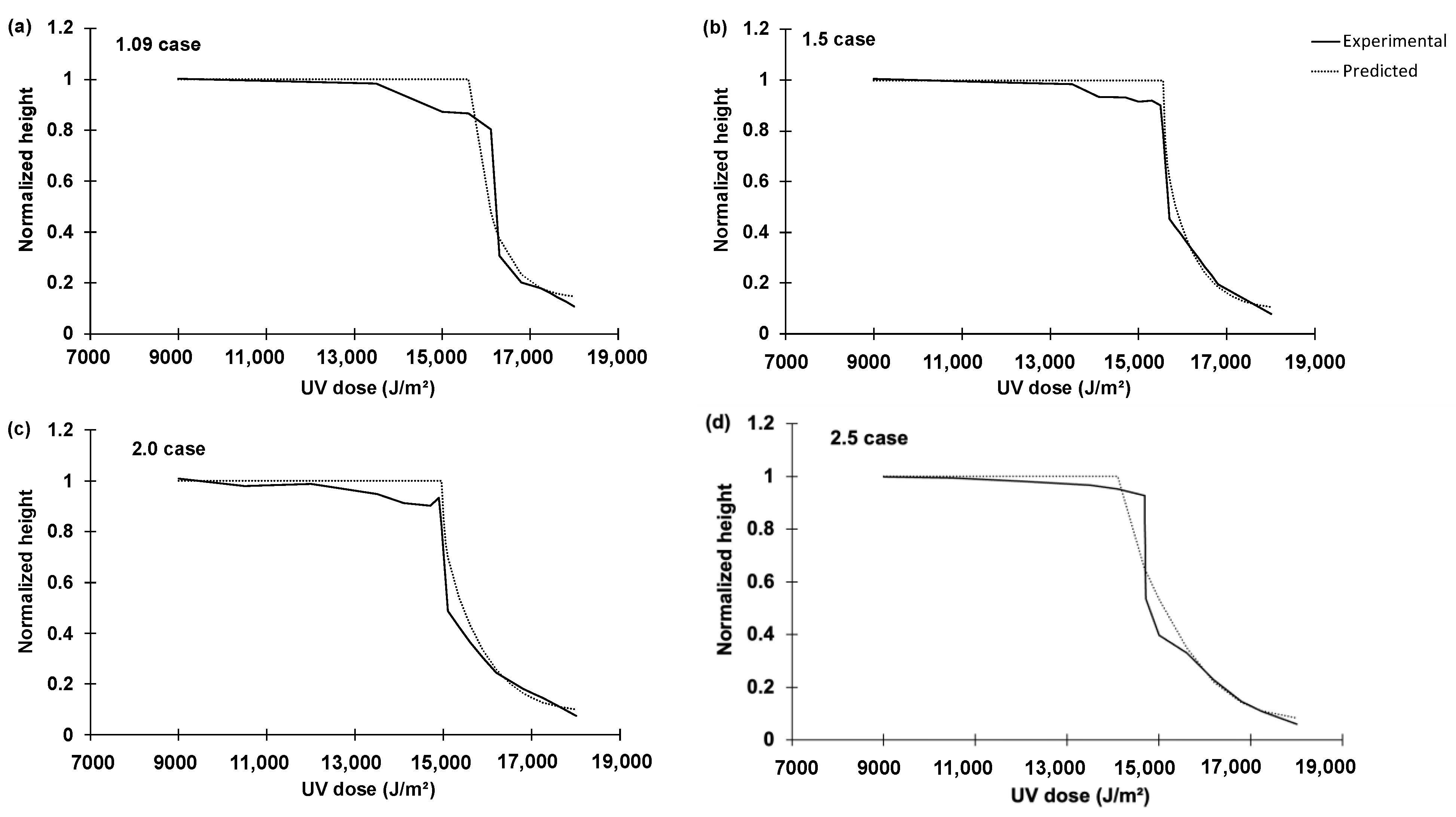
2.3. Feasibility Test Result
3. Discussion
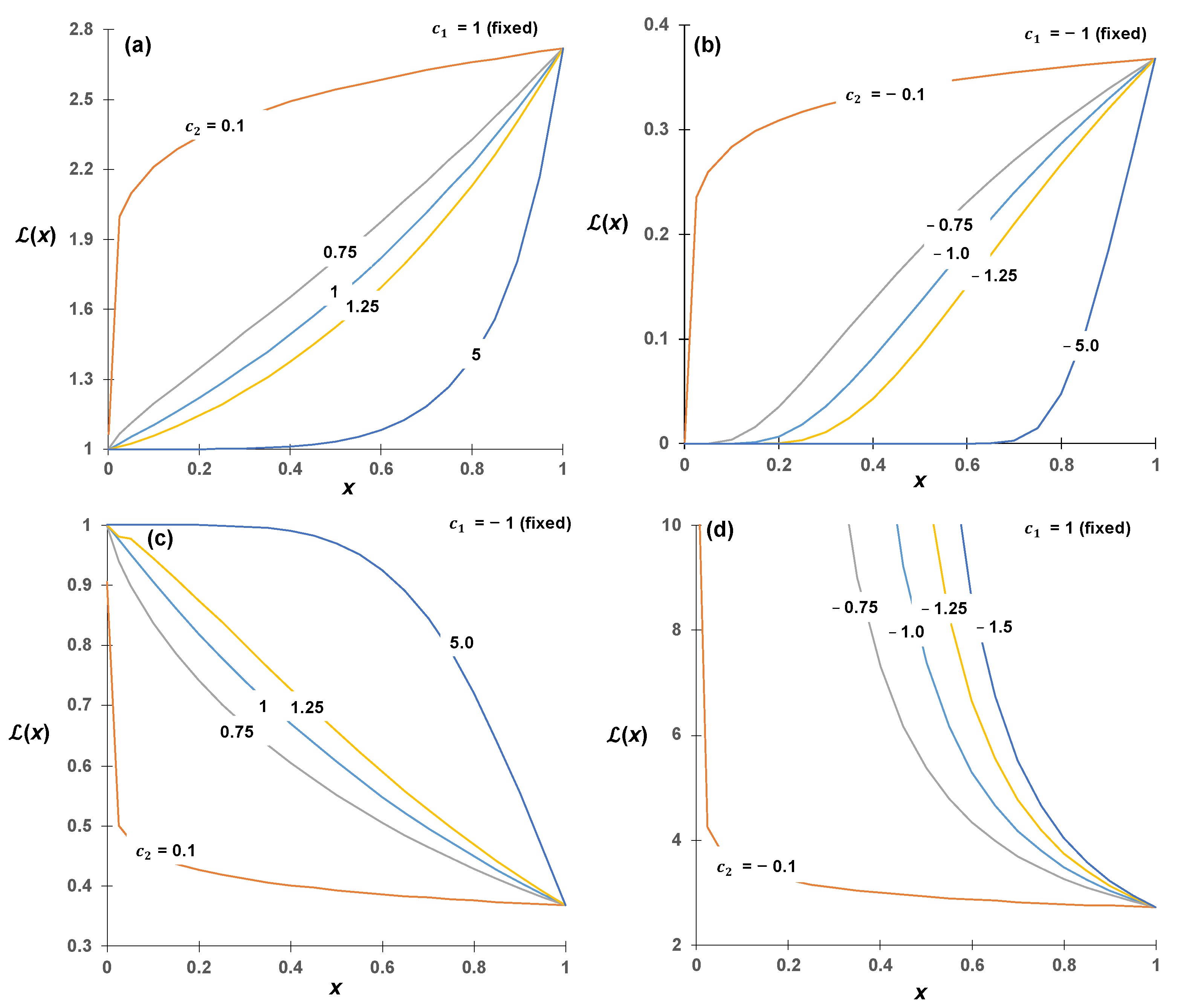
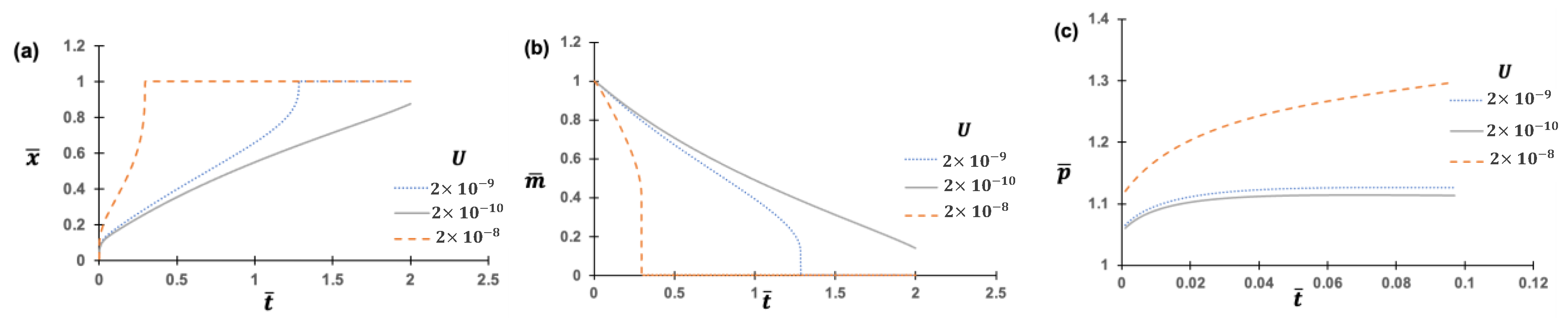
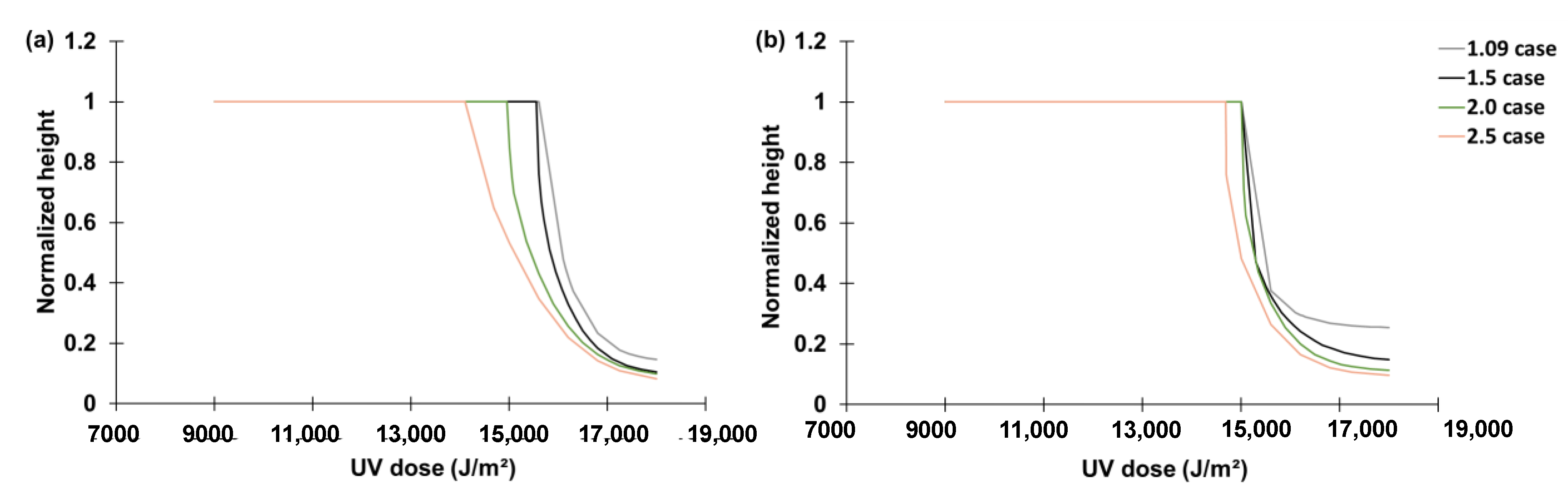
3.1. Parametric Study
3.2. Comparisons among Different LFs for Electric Potential-Dependent LF
3.3. Remarks on the Difference from Statistical Learning
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bandara, C.D.; Singh, S.; Afara, I.O.; Wolff, A.; Tesfamichael, T.; Ostrikov, K.; Oloyede, A. Bactericidal Effects of Natural Nanotopography of Dragonfly Wing on Escherichia Coli. ACS Appl. Mater. Interfaces 2017, 9, 6746–6760. [Google Scholar] [CrossRef]
- Siddique, R.H.; Gomard, G.; Hölscher, H. The Role of Random Nanostructures for the Omnidirectional Anti-Reflection Properties of the Glasswing Butterfly. Nat. Commun. 2015, 6, 6909. [Google Scholar] [CrossRef]
- Tadepalli, S.; Slocik, J.M.; Gupta, M.K.; Naik, R.R.; Singamaneni, S. Bio-Optics and Bio-Inspired Optical Materials. Chem. Rev. 2017, 117, 12705–12763. [Google Scholar] [CrossRef]
- Zhou, H.; Xu, J.; Liu, X.; Zhang, H.; Wang, D.; Chen, Z.; Zhang, D.; Fan, T. Bio-Inspired Photonic Materials: Prototypes and Structural Effect Designs for Applications in Solar Energy Manipulation. Adv. Funct. Mater. 2018, 28, 1705309. [Google Scholar] [CrossRef]
- Lee, Y.; Bae, S.-I.; Eom, J.; Suh, H.-C.; Jeong, K.H. Antireflective Glass Nanoholes on Optical Lenses. Opt. Express 2018, 26, 14786. [Google Scholar] [CrossRef]
- Li, Q.; Ji, M.G.; Kim, J. Grayscale nanopixel printing at sub-10-nanometer vertical resolution via light-controlled nanocapillarity. ACS Nano 2020, 14, 6058–6066. [Google Scholar] [CrossRef]
- Phan, V.N.; Nguyen, N.T.; Yang, C.; Joseph, P.; Djeghlaf, L.; Bourrier, D.; Gue, A.M. Capillary Filling in Closed End Nanochannels. Langmuir 2010, 26, 13251–13255. [Google Scholar] [CrossRef][Green Version]
- Kolliopoulos, P.K.; Jochem, K.S.; Lade, R.K., Jr.; Francis, L.F.; Kumar, S. Capillary Flow with Evaporation in Open Rectangular Microchannels. Langmuir 2019, 35, 8131–8143. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Zhou, X. General Exotic Capillary Tubes. J. Fluid Mech. 2019, 885, A1. [Google Scholar] [CrossRef]
- Zhang, F.; Zhou, X. Capillary Surfaces in and around Exotic Cylinders with Application to Stability Analysis. J. Fluid Mech. 2020, 882, A28. [Google Scholar] [CrossRef]
- Klinkenberg, L.J. The Permeability of Porous Media to Liquids and Gases. In Drilling and Production Practice; API-41-200; American Petroleum Institute: New York, NY, USA, 1941; pp. 200–213. [Google Scholar]
- Wu, Y.S.; Pruess, K.; Persoff, P. Steady and Transient Analytical Solutions for Gas Flow in Porous Media with Klinkenberg Effects; LBNL-39499, UC-1240; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 1996. [Google Scholar]
- Markov, P.; Rodionov, S. Numerical Simulation Using Finite-Difference Schemes with Continuous Symmetries for Processes of Gas Flow in Porous Media. Computation 2019, 7, 45. [Google Scholar] [CrossRef]
- Pavan, V.; Oxarango, L. A New Momentum Equation for Gas Flow in Porous Media: The Klinkenberg Effect Seen through the Kinetic Theory. J. Stat. Phys. 2007, 126, 355–389. [Google Scholar] [CrossRef]
- Cho, I.; Ji, M.G.; Kim, J. Pursuit of hidden rules behind the irregularity of nano capillary lithography by hybrid intelligence. Sci Rep. 2023, 13, 13649. [Google Scholar] [CrossRef]
- Tanaka, G.; Yamane, T.; Héroux, J.; Nakane, R.; Kanazawa, N.; Takeda, S.; Numata, H.; Nakano, D.; Hirose, A. Recent advances in physical reservoir computing: A review. Neural Netw. 2019, 115, 100–123. [Google Scholar] [CrossRef] [PubMed]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to forget: Continual prediction with LSTM. Neural Comput. 2000, 12, 2451–2471. [Google Scholar] [CrossRef]
- Karpatne, A.; Atluri, G.; Faghmous, J.H.; Steinbach, M.; Banerjee, A.; Ganguly, A.; Shekhar, S.; Samatova, N.; Kumar, V. Theory-Guided Data Science: A New Paradigm for Scientific Discovery from Data. IEEE Trans. Knowl. Data Eng. 2017, 29, 2318–2331. [Google Scholar] [CrossRef]
- Raissi, M.; Yazdani, A.; Karniadakis, G.E. Hidden fluid mechanics: Learning velocity and pressure fields from flow visualizations. Science 2020, 367, 1026–1030. [Google Scholar] [CrossRef] [PubMed]
- Champion, K.; Lusch, B.; Kutz, J.N.; Brunton, S.L. Data-driven discovery of coordinates and governing equations. Proc. Natl. Acad. Sci. USA 2019, 116, 22445–22451. [Google Scholar] [CrossRef]
- Schaschke, C. Fluid Mechanics Worked Examples for Engineers; Institution of Chemical Engineers: Rugby, UK, 1998; pp. 84–87. [Google Scholar]
- Yang, Q.; Li, Q.; Tian, H.; Li, X.; Shao, J.; Chen, X.; Xu, F. Deformation Hysteresis of Electrohydrodynamic Patterning on a Thin Polymer Film. ACS Appl. Mater. Interfaces 2016, 8, 17668–17675. [Google Scholar] [CrossRef]
- Cho, I.; Li, Q.; Biswas, R.; Kim, J. A Framework for Glass-Box Physics Rule Learner and Its Application to Nanoscale Phenomena. Nat. Commun. Phys. 2020, 3, 78. [Google Scholar] [CrossRef]
- Cho, I.; Yeom, S.; Sarkar, T.; Oh, T. Unraveling Hidden Rules Behind the Wet-To-Dry Transition of Bubble Array by Glass-Box Physics Rule Learner. Nat. Sci. Rep. 2022, 12, 3191. [Google Scholar] [CrossRef] [PubMed]
- Cho, I. A Framework for Self-Evolving Computational Material Models Inspired by Deep Learning. Int. J. Numer. Methods Eng. 2019, 120, 1202–1226. [Google Scholar] [CrossRef]
- Bazroun, M.; Yang, Y.; Cho, I. Flexible and Interpretable Generalization of Self-Evolving Computational Materials Framework. Comput. Struct. 2021, 260, 106706. [Google Scholar] [CrossRef]
- Cho, I. Gauss Curvature-Based Unique Signatures of Individual Large Earthquakes and Its Implications for Customized Data-Driven Prediction. Nat. Sci. Rep. 2022, 12, 8669. [Google Scholar] [CrossRef] [PubMed]




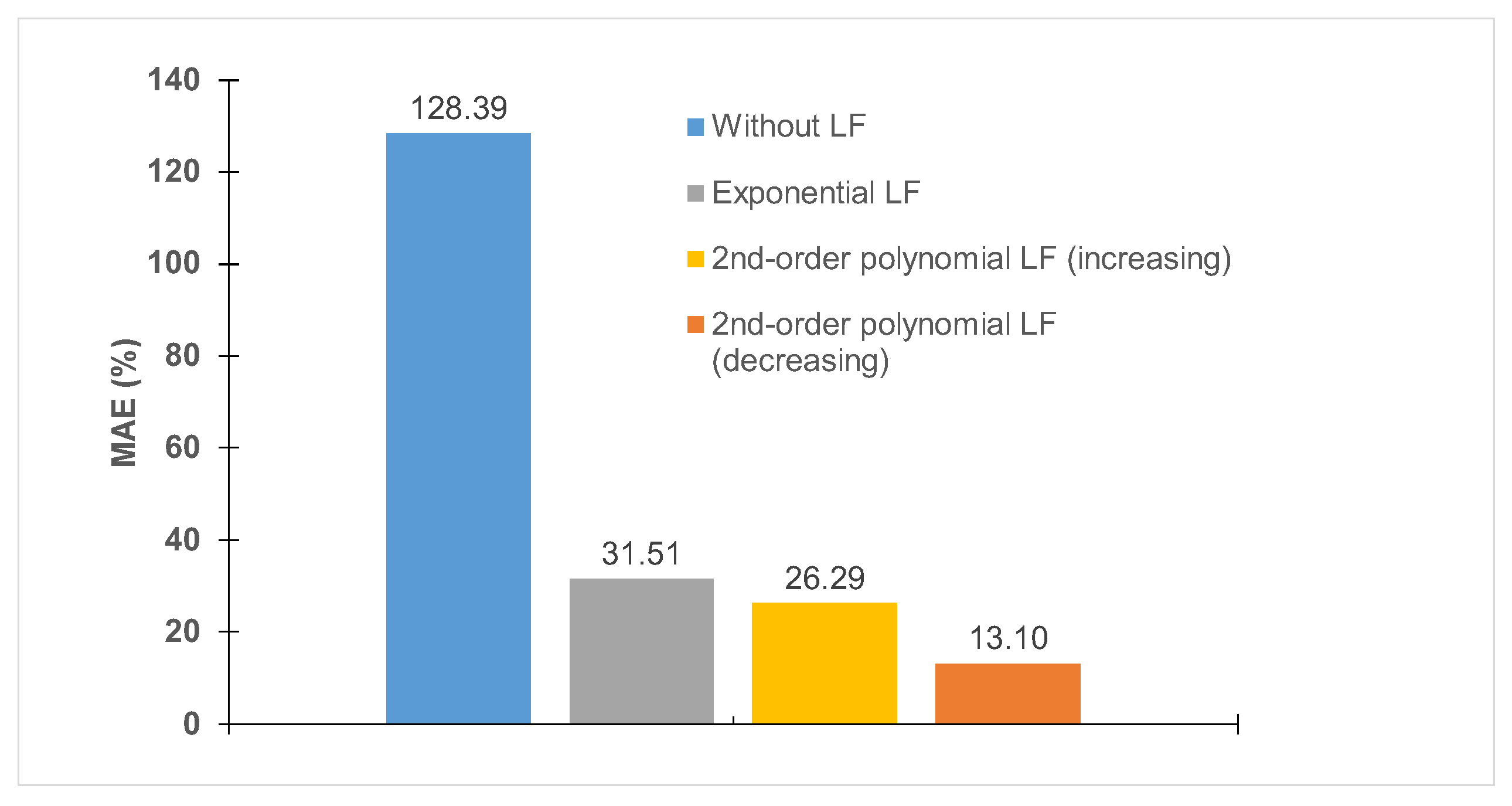
| Unknown Physics Term | Function Argument | Physical Meaning | Best Identified LF |
|---|---|---|---|
| Diffusivity of trapped air into PDMS pores | 2-parameter exponential function | ||
| Dynamic viscosity of the liquid | 2-parameter exponential function | ||
| Surface tension of the liquid | 2-parameter exponential function | ||
| Potential (voltage) difference between the lower surface of PDMS and the upper surface of the liquid and dielectric constants of the materials | 3-parameter 2nd-order polynomial function |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chapagain, A.; Cho, I.H. Tackling Multi-Physics Nano-Scale Phenomena in Capillary Force Lithography with Small Data by Hybrid Intelligence. Micromachines 2023, 14, 1984. https://doi.org/10.3390/mi14111984
Chapagain A, Cho IH. Tackling Multi-Physics Nano-Scale Phenomena in Capillary Force Lithography with Small Data by Hybrid Intelligence. Micromachines. 2023; 14(11):1984. https://doi.org/10.3390/mi14111984
Chicago/Turabian StyleChapagain, Ashish, and In Ho Cho. 2023. "Tackling Multi-Physics Nano-Scale Phenomena in Capillary Force Lithography with Small Data by Hybrid Intelligence" Micromachines 14, no. 11: 1984. https://doi.org/10.3390/mi14111984
APA StyleChapagain, A., & Cho, I. H. (2023). Tackling Multi-Physics Nano-Scale Phenomena in Capillary Force Lithography with Small Data by Hybrid Intelligence. Micromachines, 14(11), 1984. https://doi.org/10.3390/mi14111984






