Reflection and Transmission Analysis of Surface Acoustic Wave Devices
Abstract
:1. Introduction
2. Basic Theorem
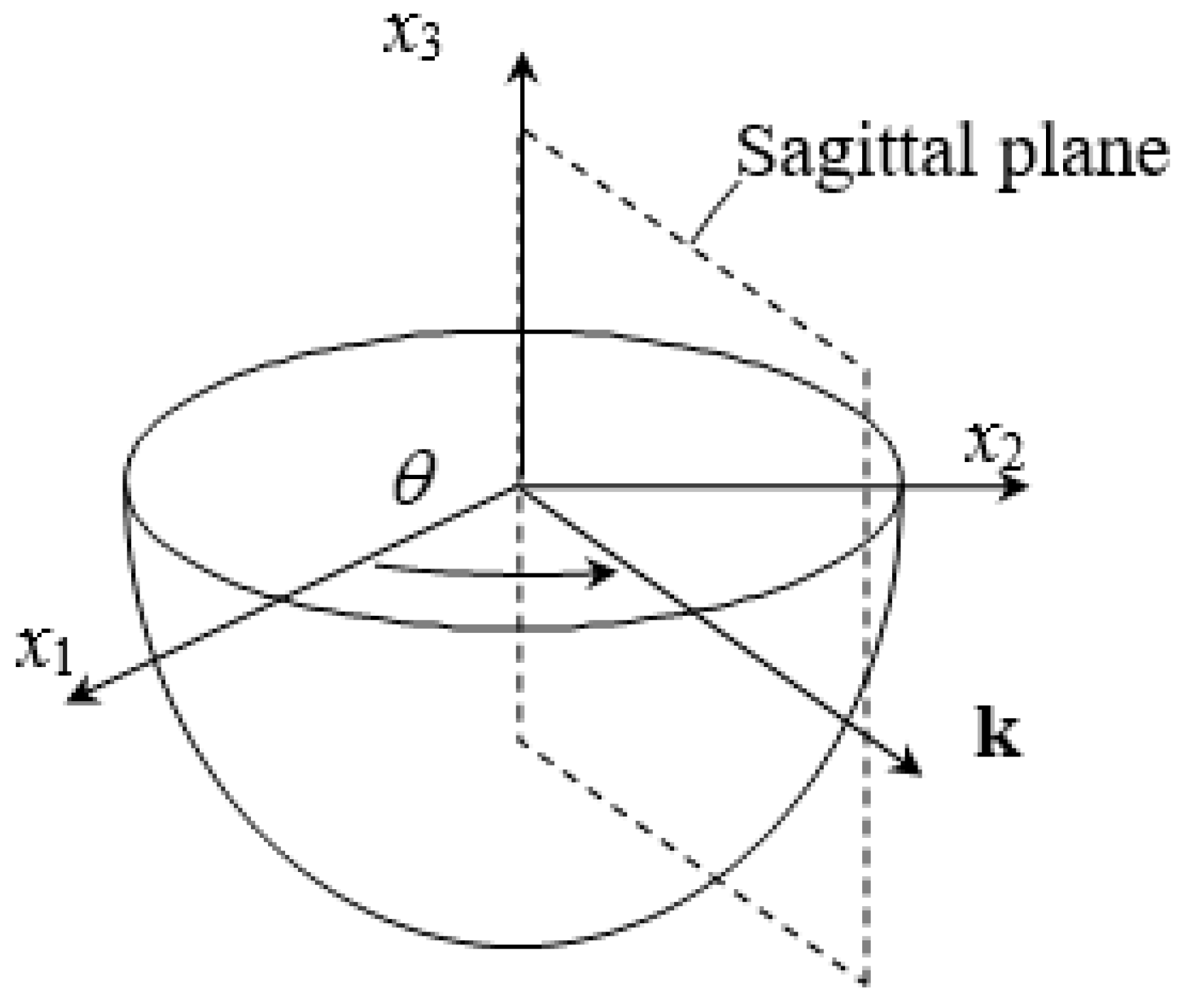
2.1. Dispersion Equation of SAWs
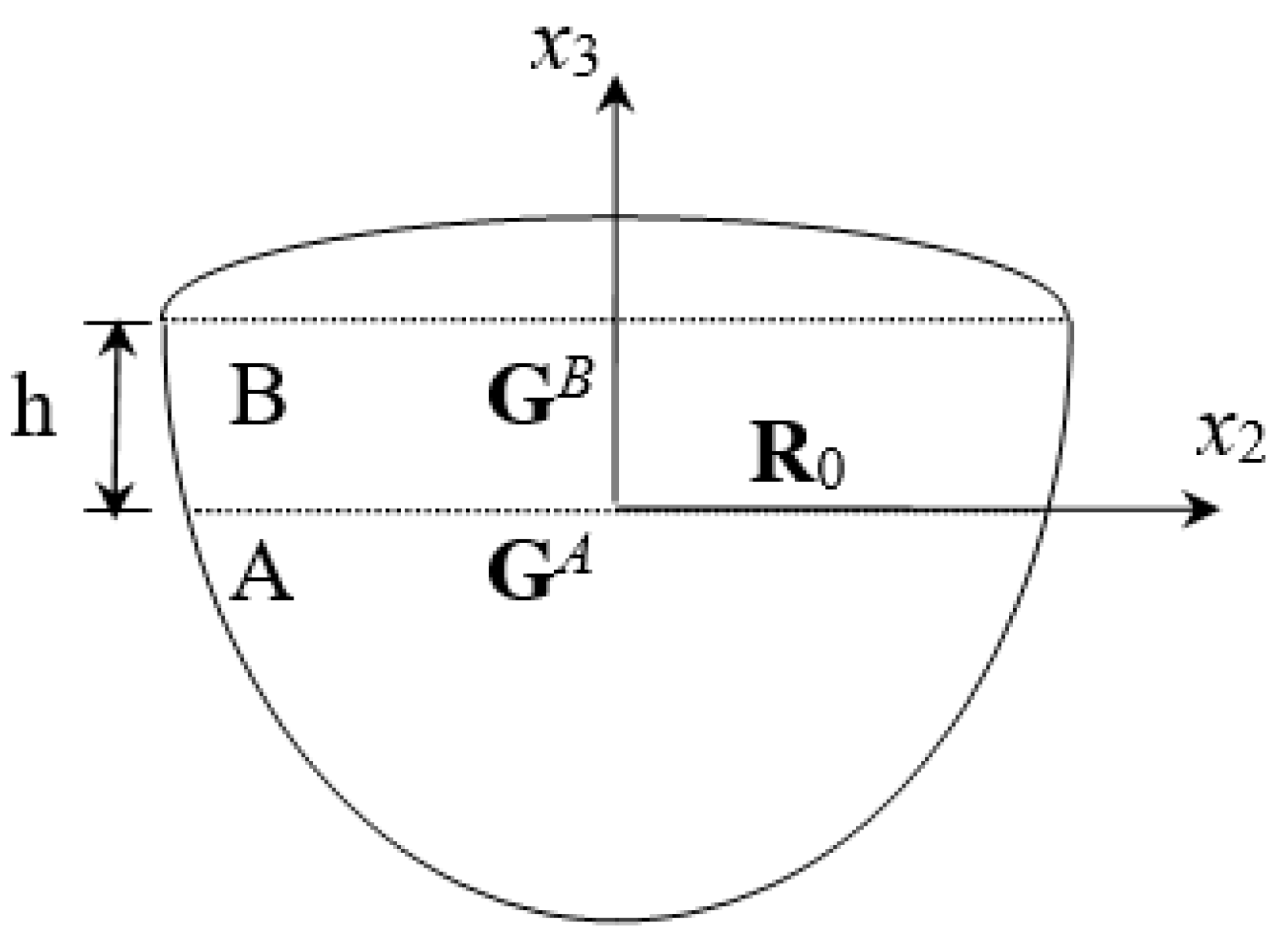
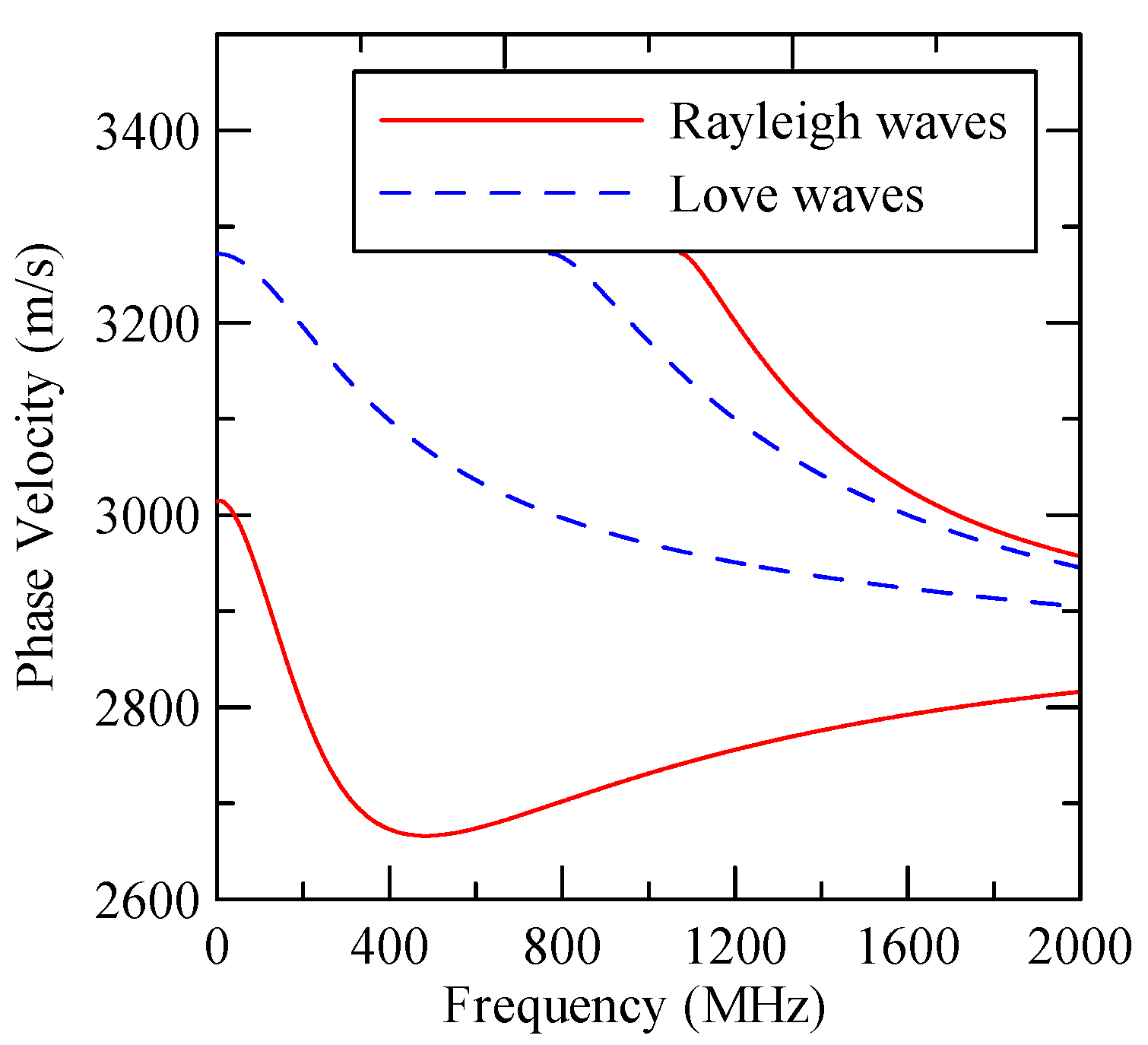
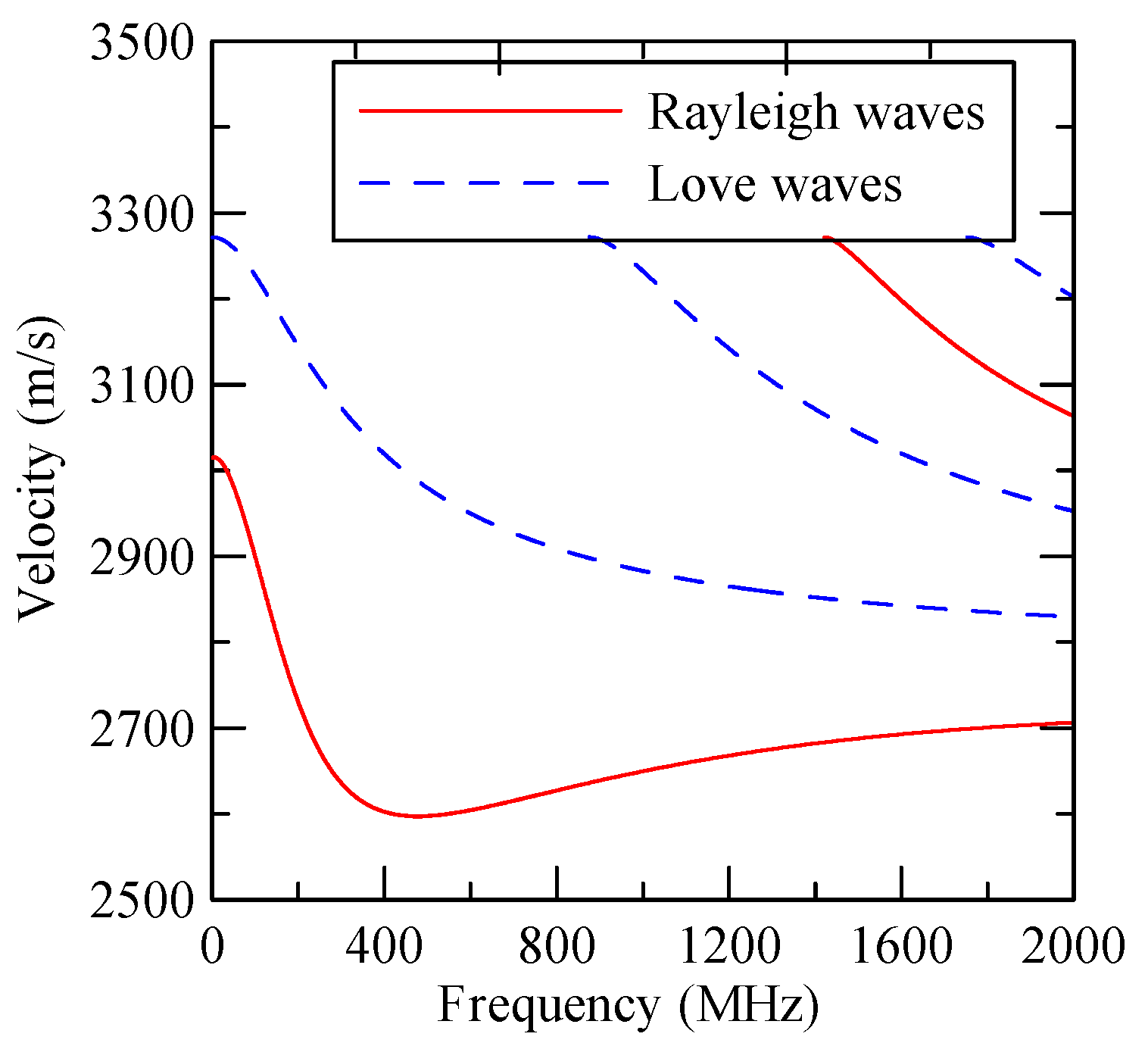
2.2. Rayleigh and Love Waves
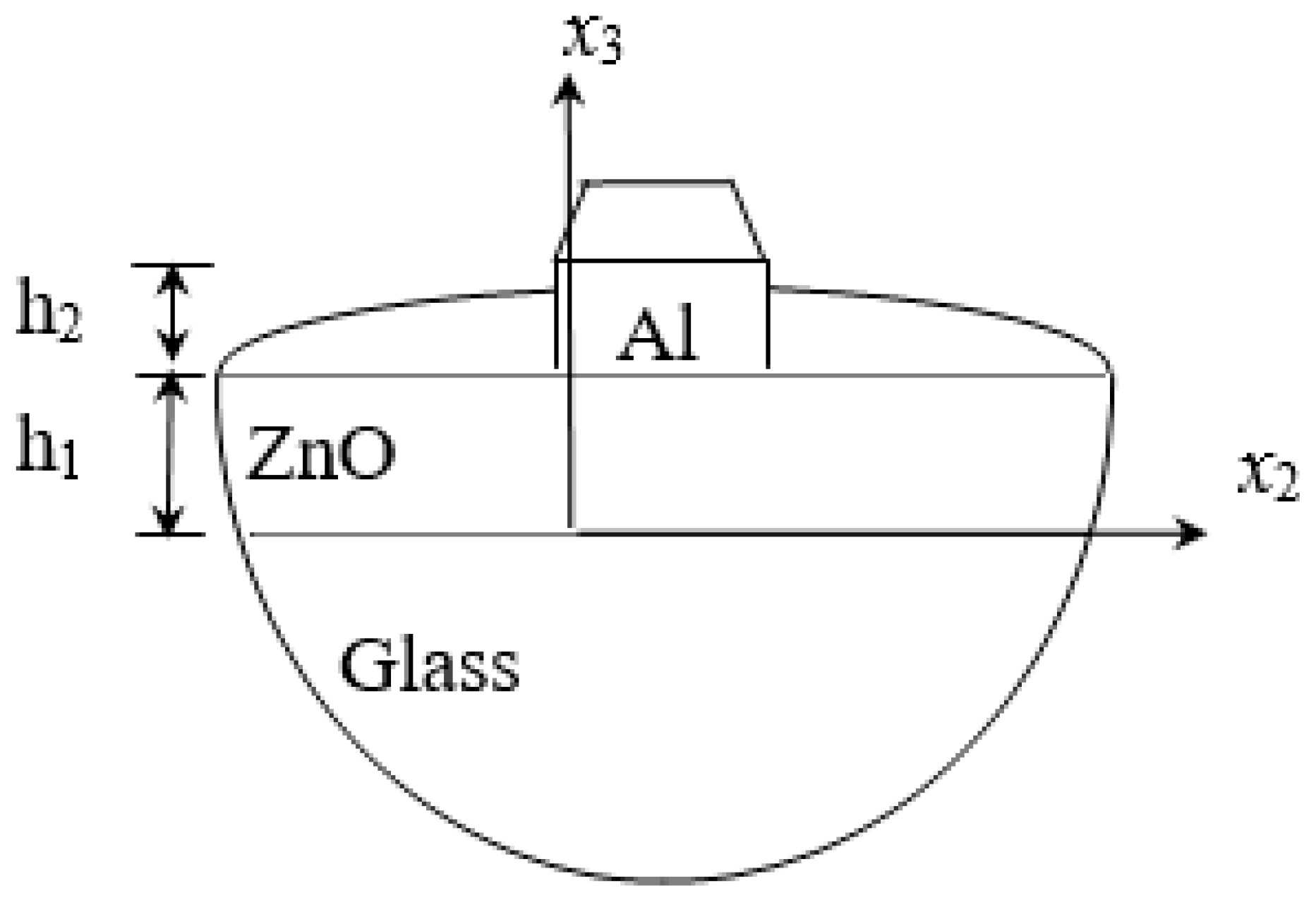
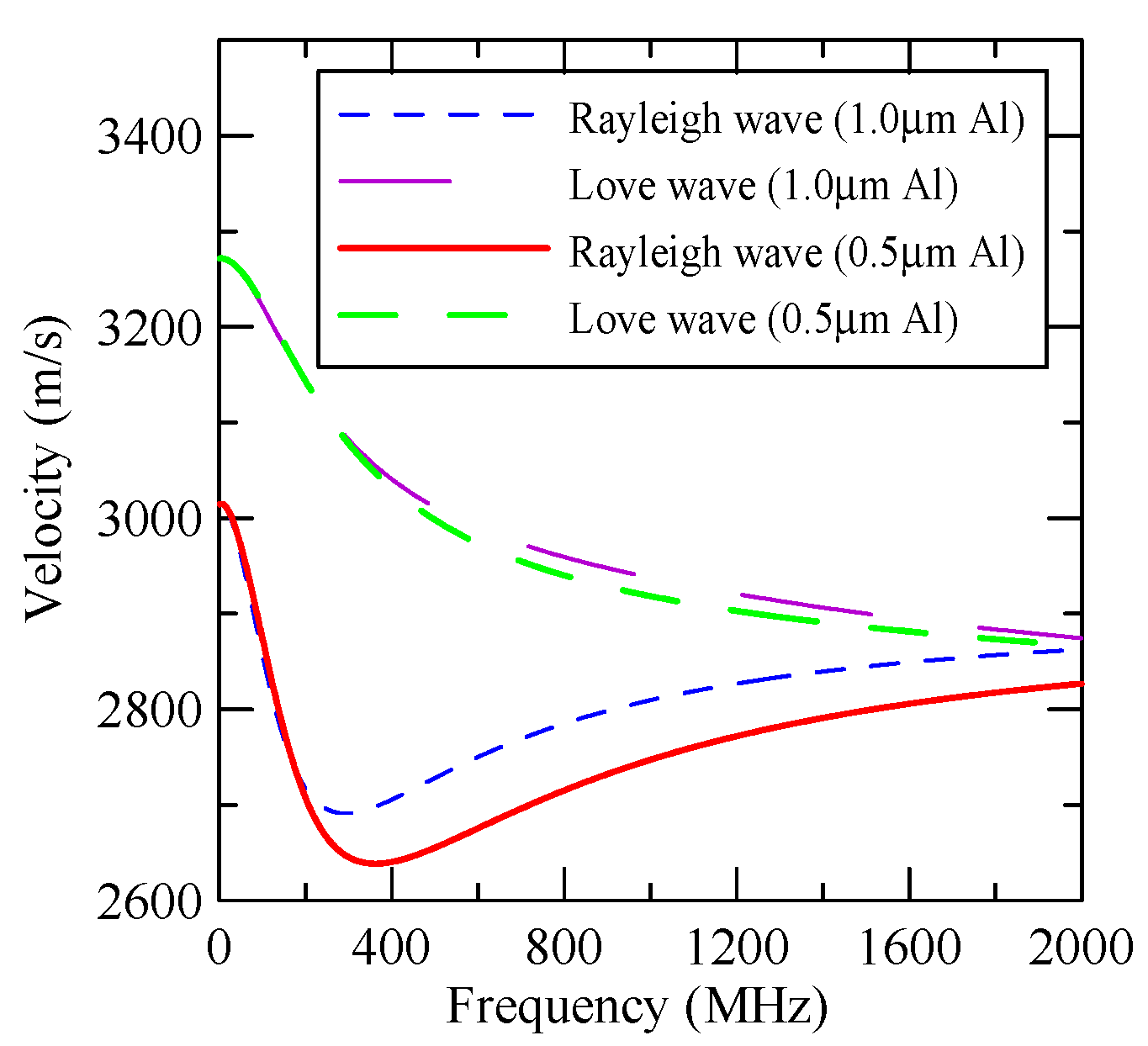
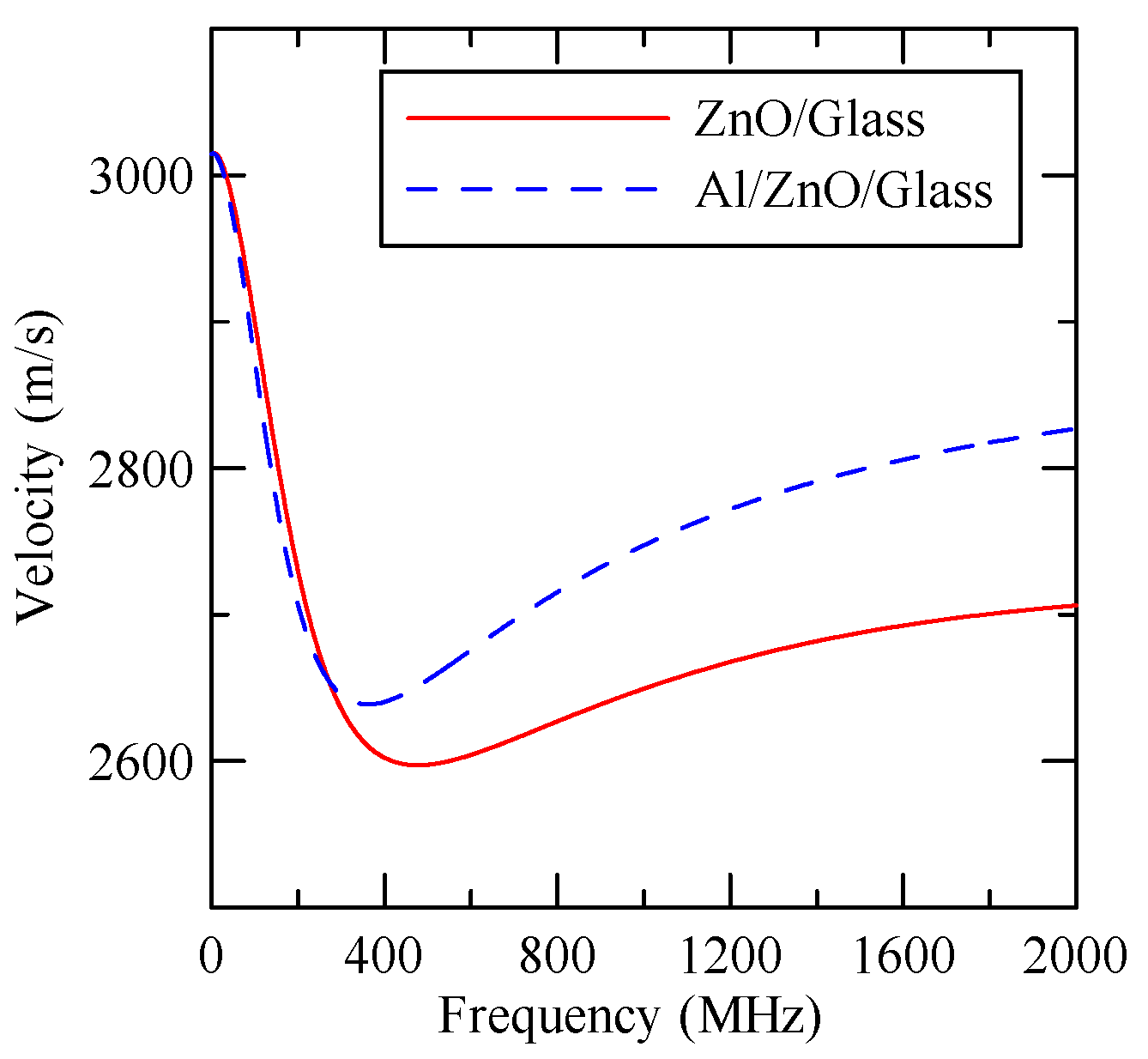
2.3. ZnO/Glass and Al/ZnO/Glass SAWs
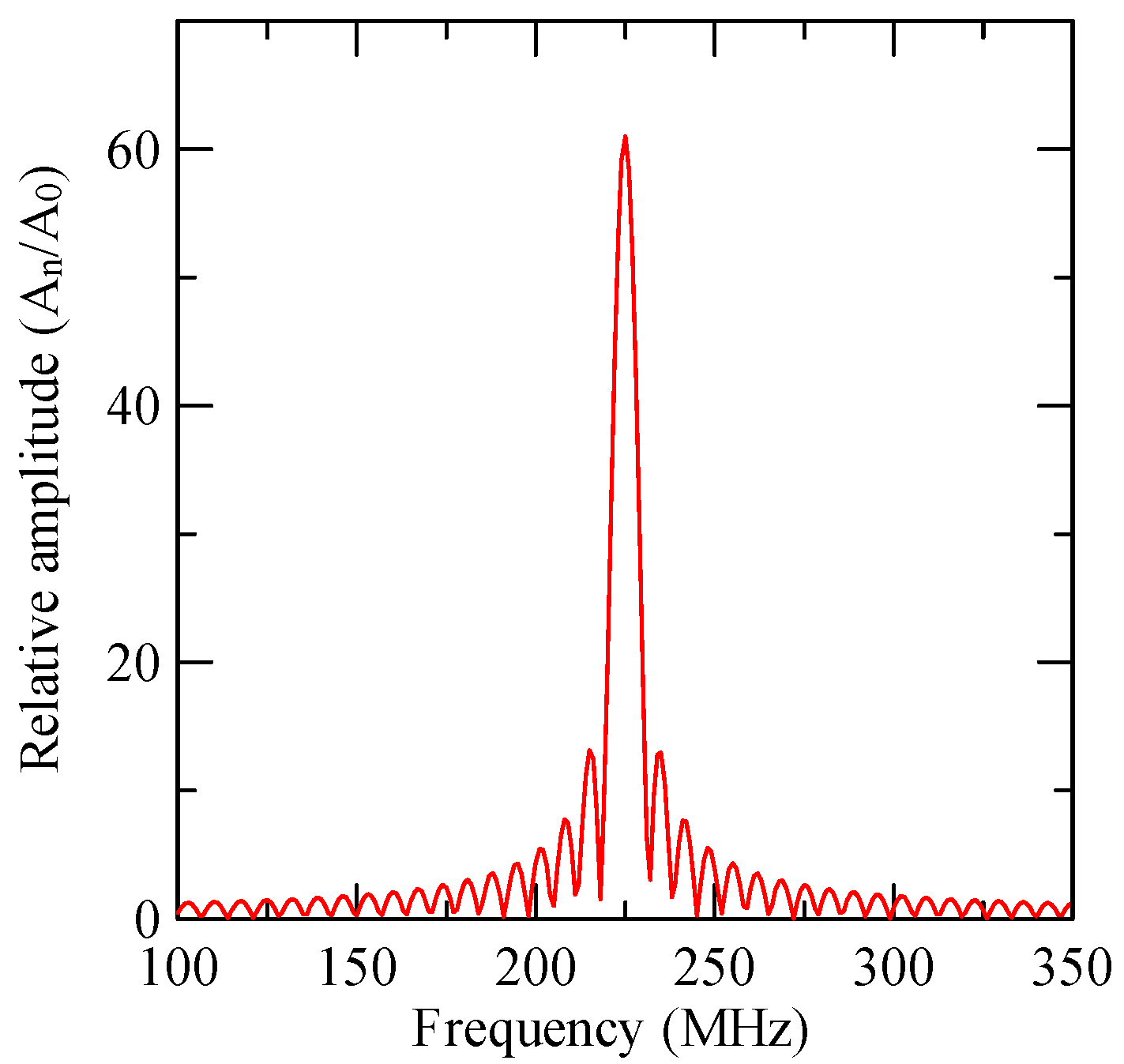
2.4. Delta Function Model
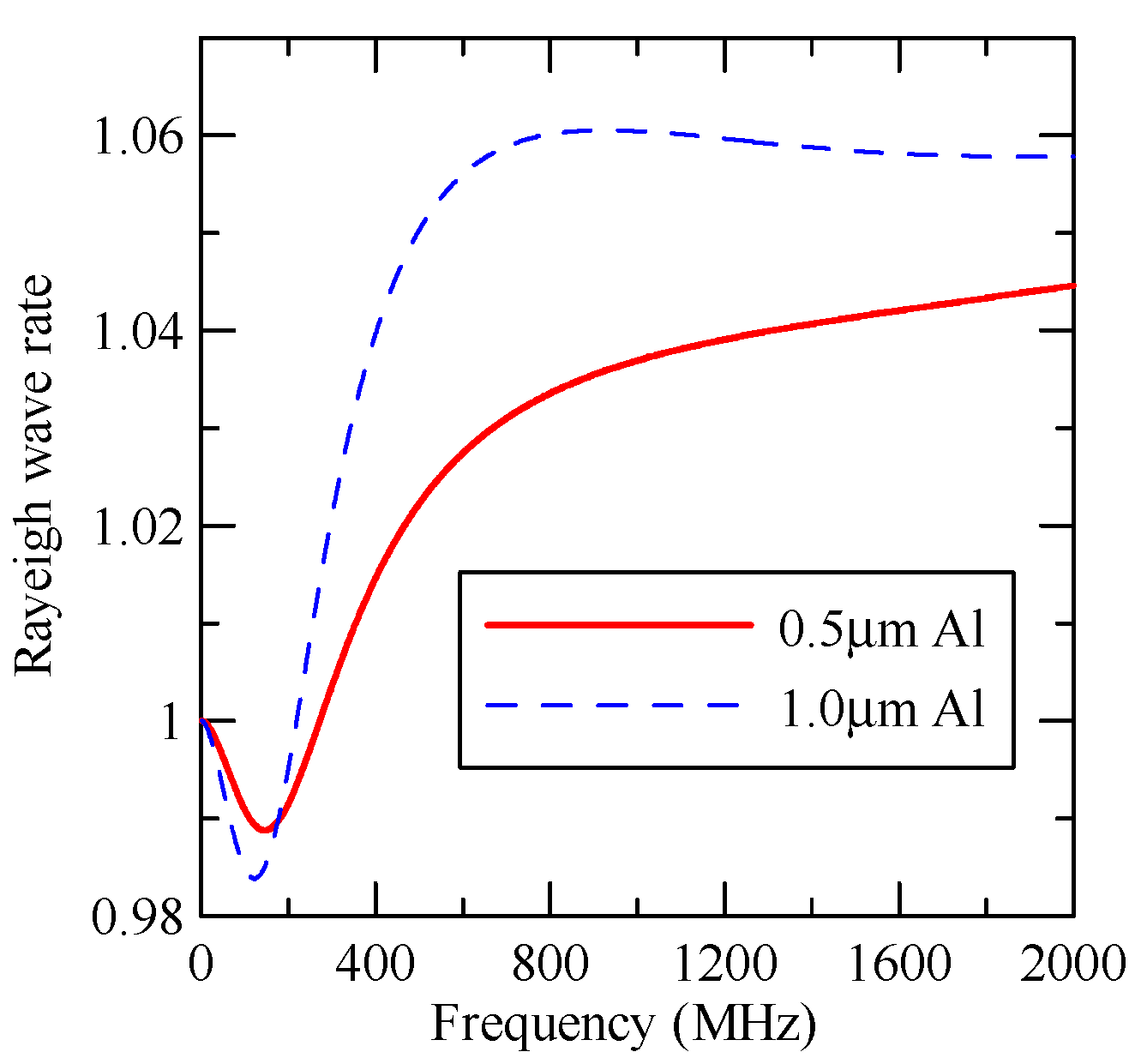
2.5. Al/ZnO/Glass Frequency Response
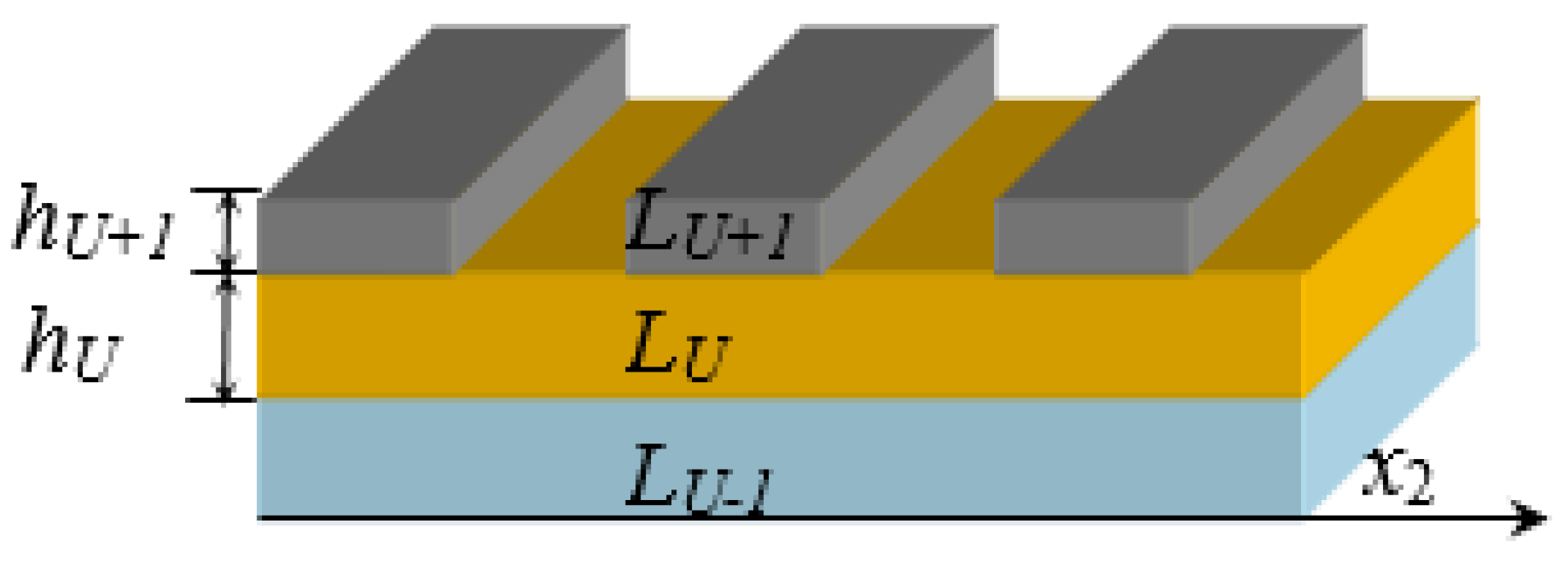
3. Wave Propagation Analysis of Grating Arrays
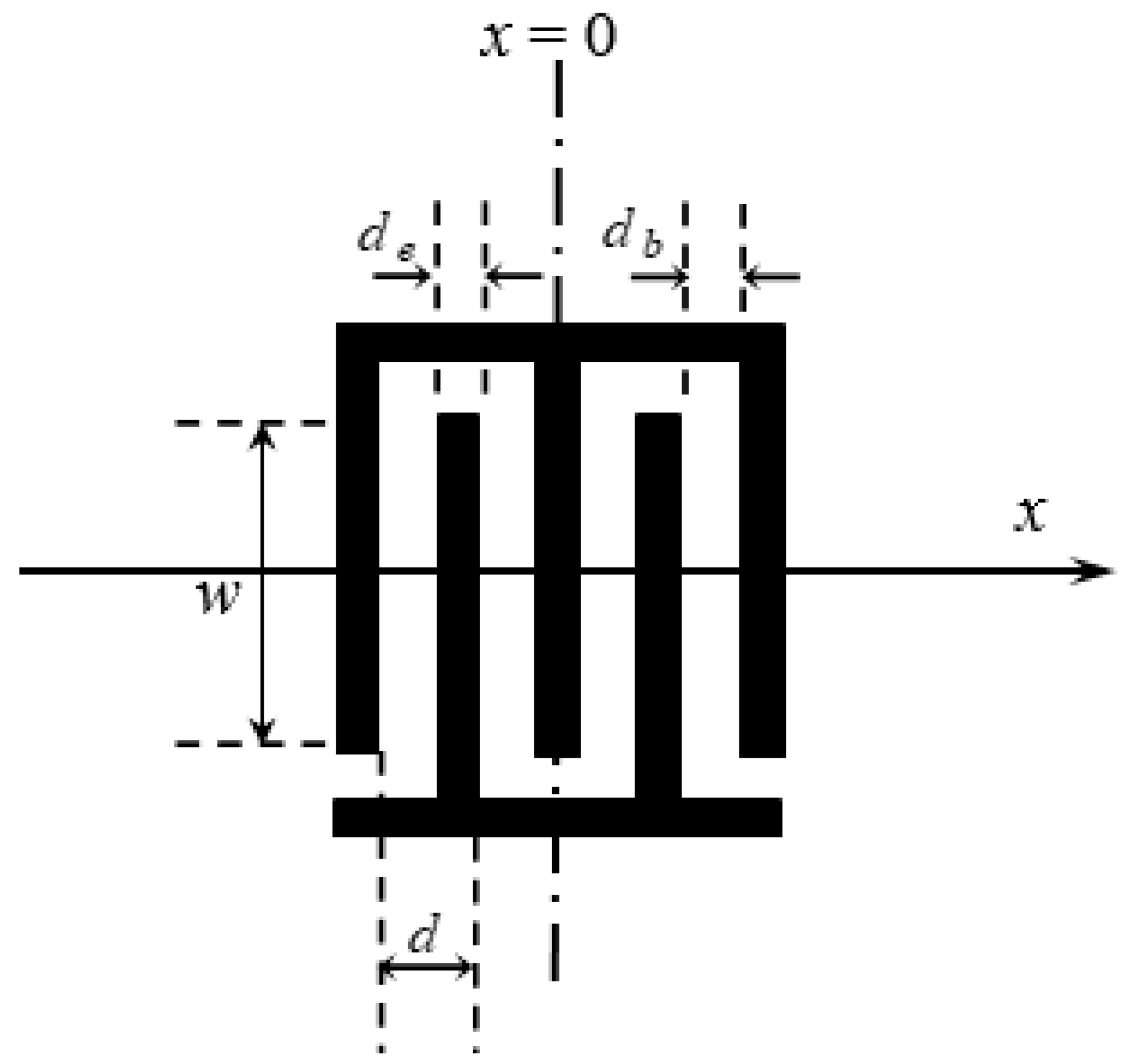
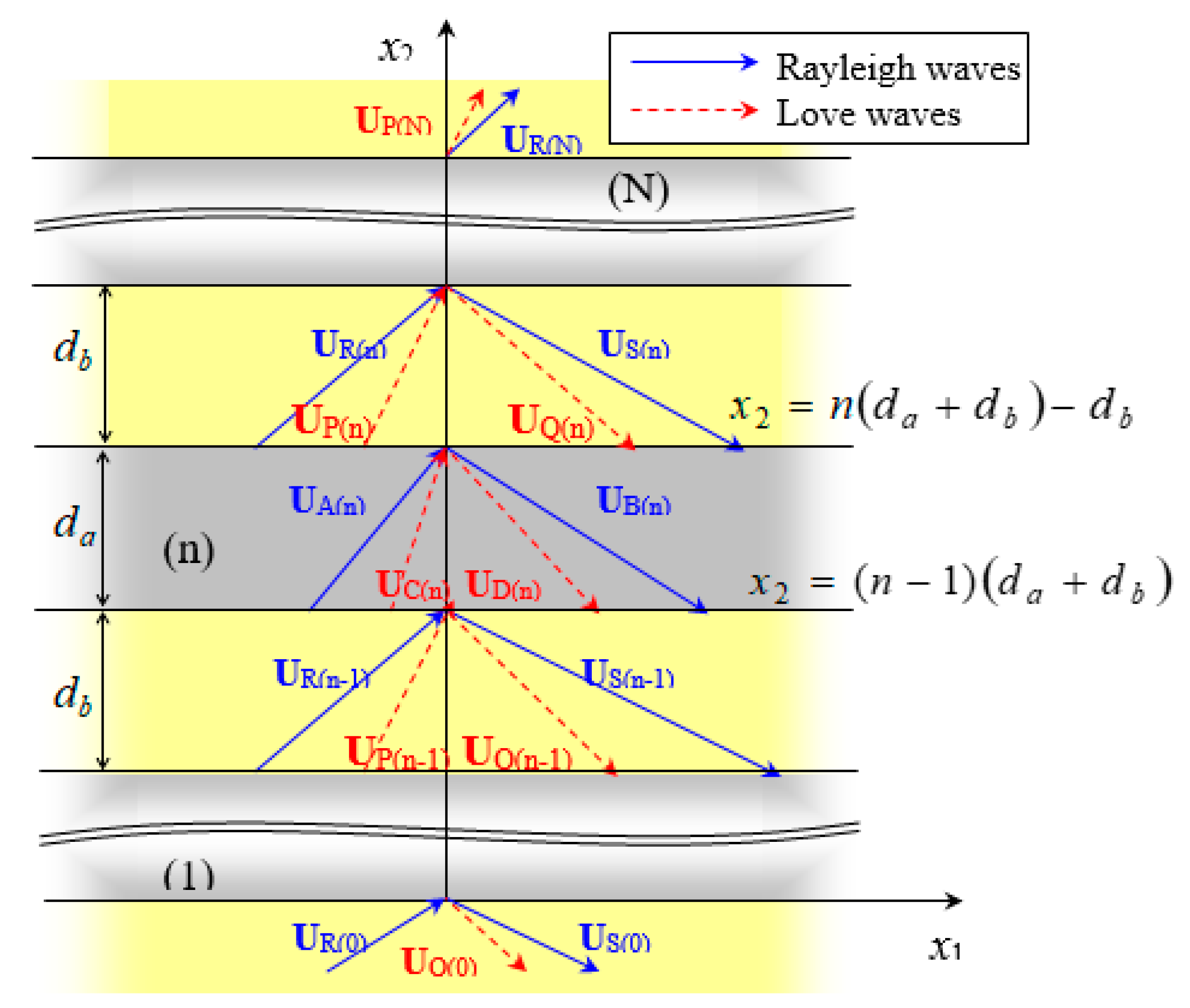
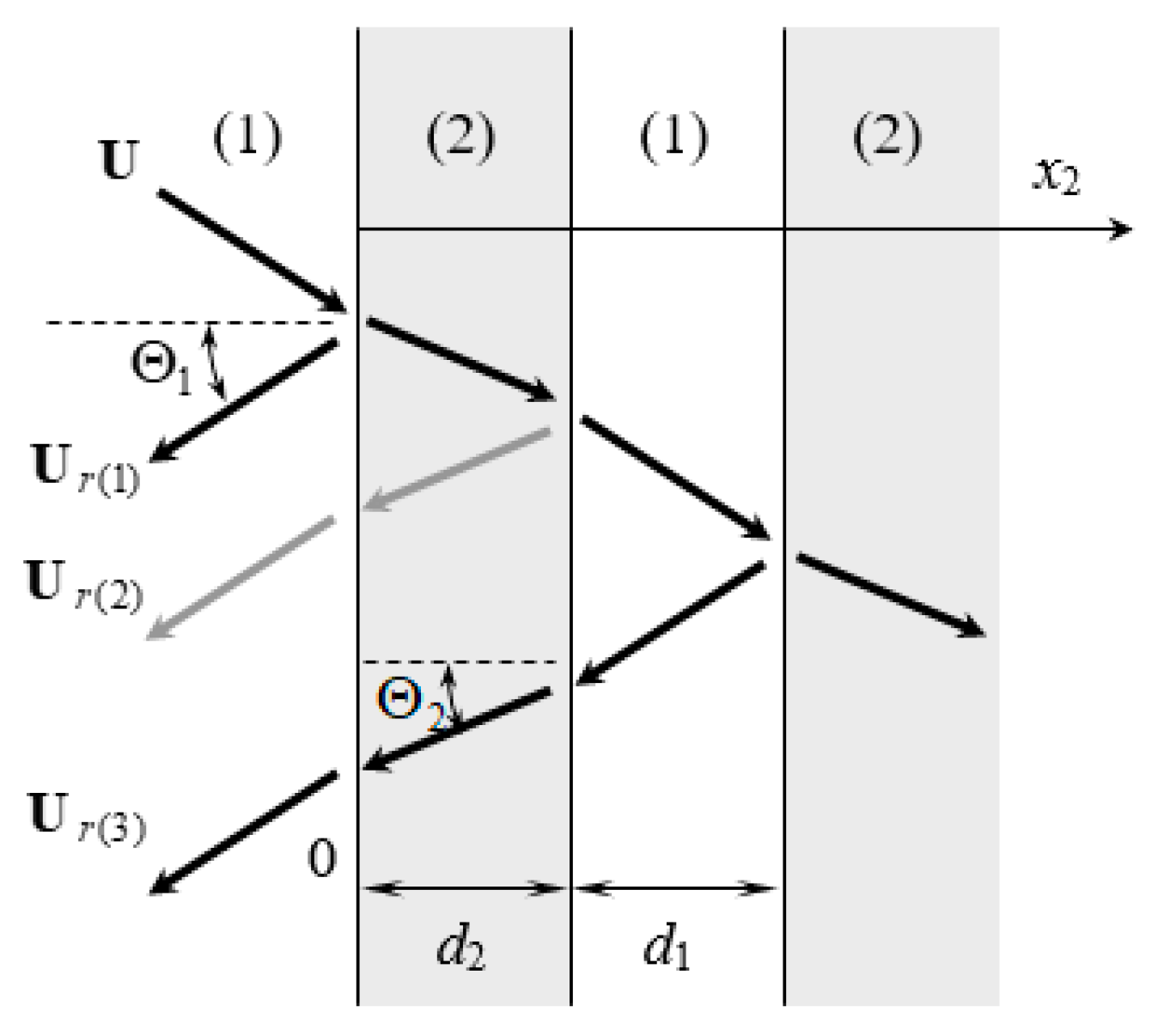
3.1. Horizontal Wave Propagation of SAWs
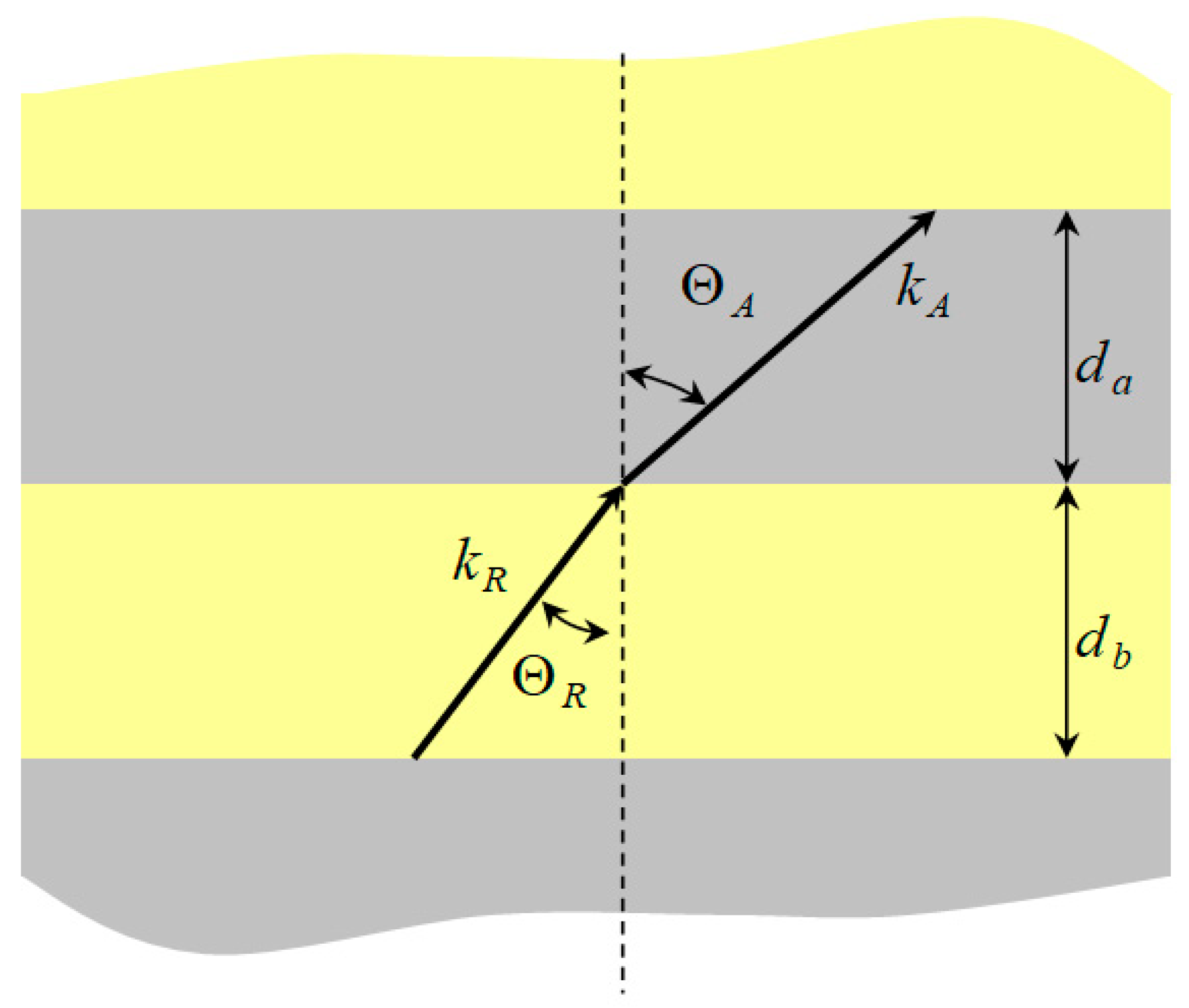
3.2. Reflection and Transmission on Grating Arrays
4. Simulation Results and Discussion
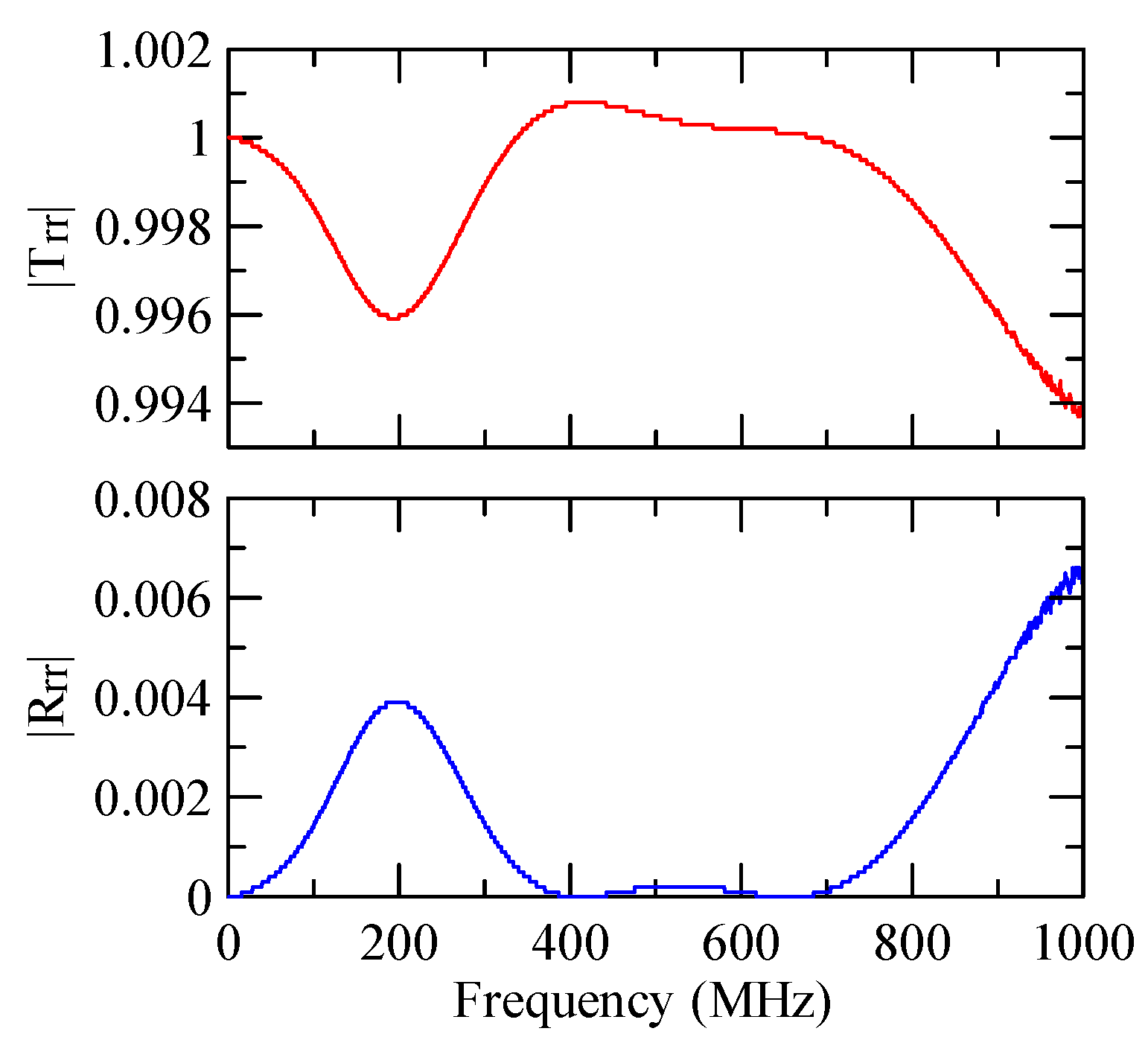
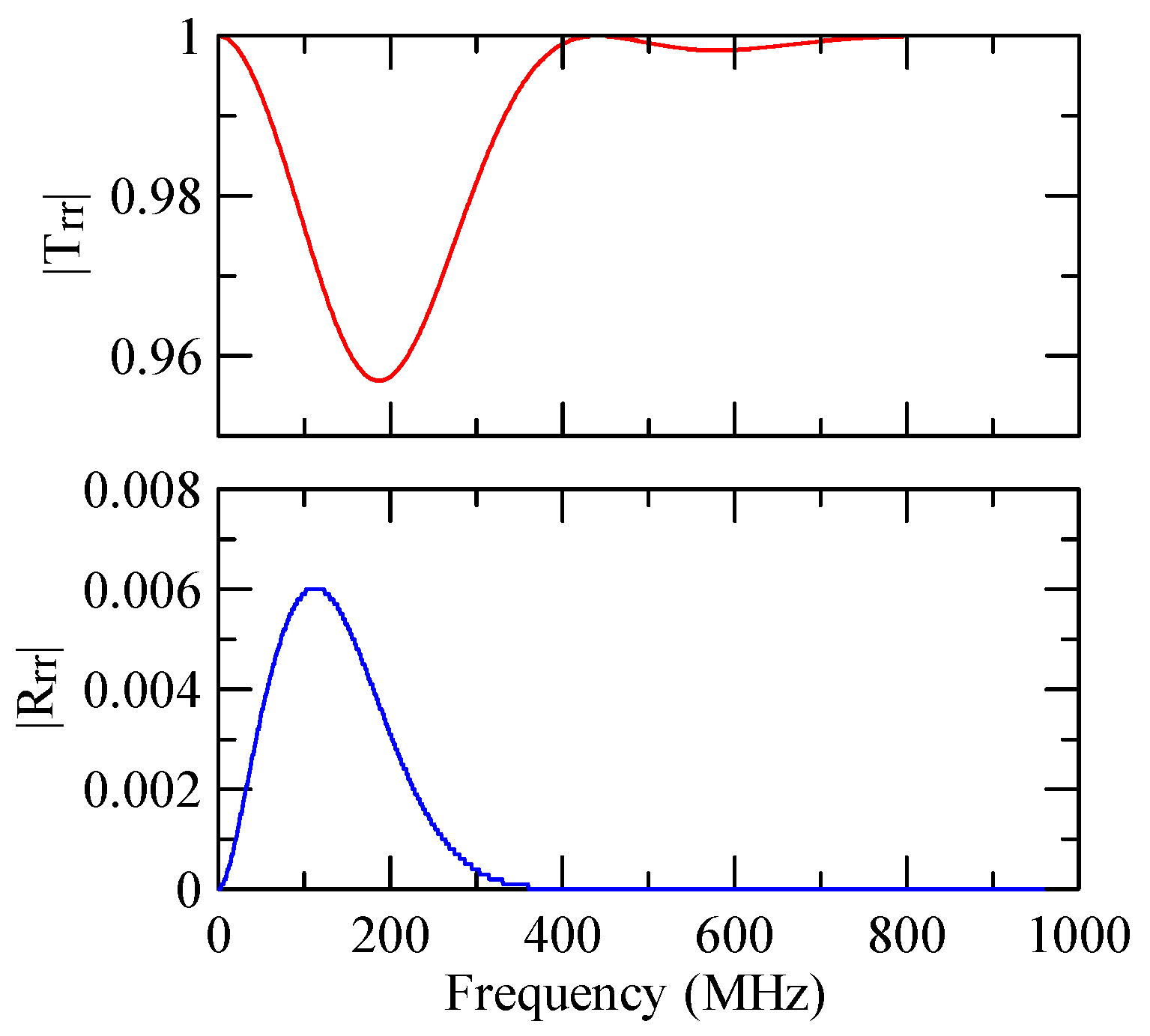
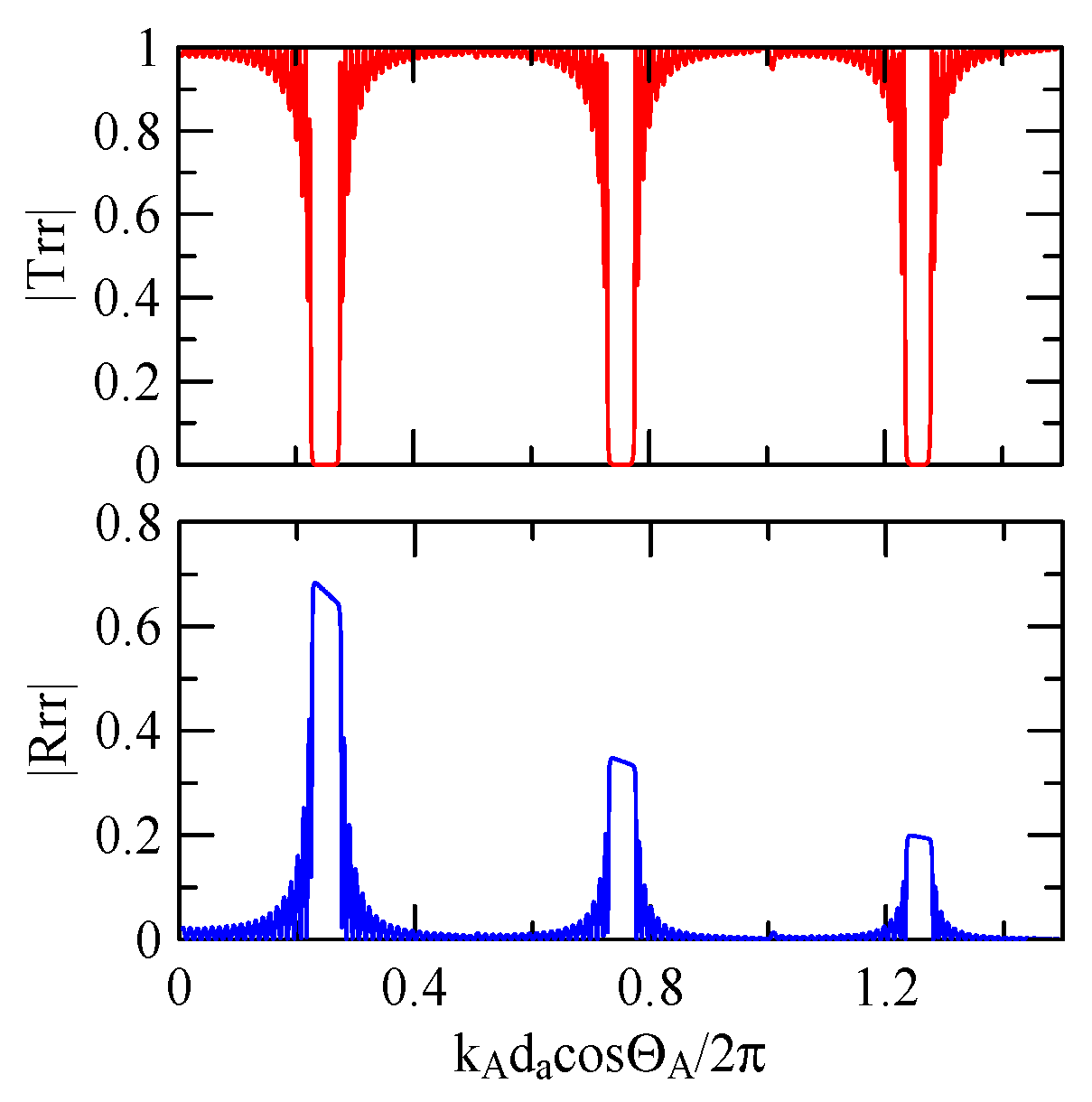
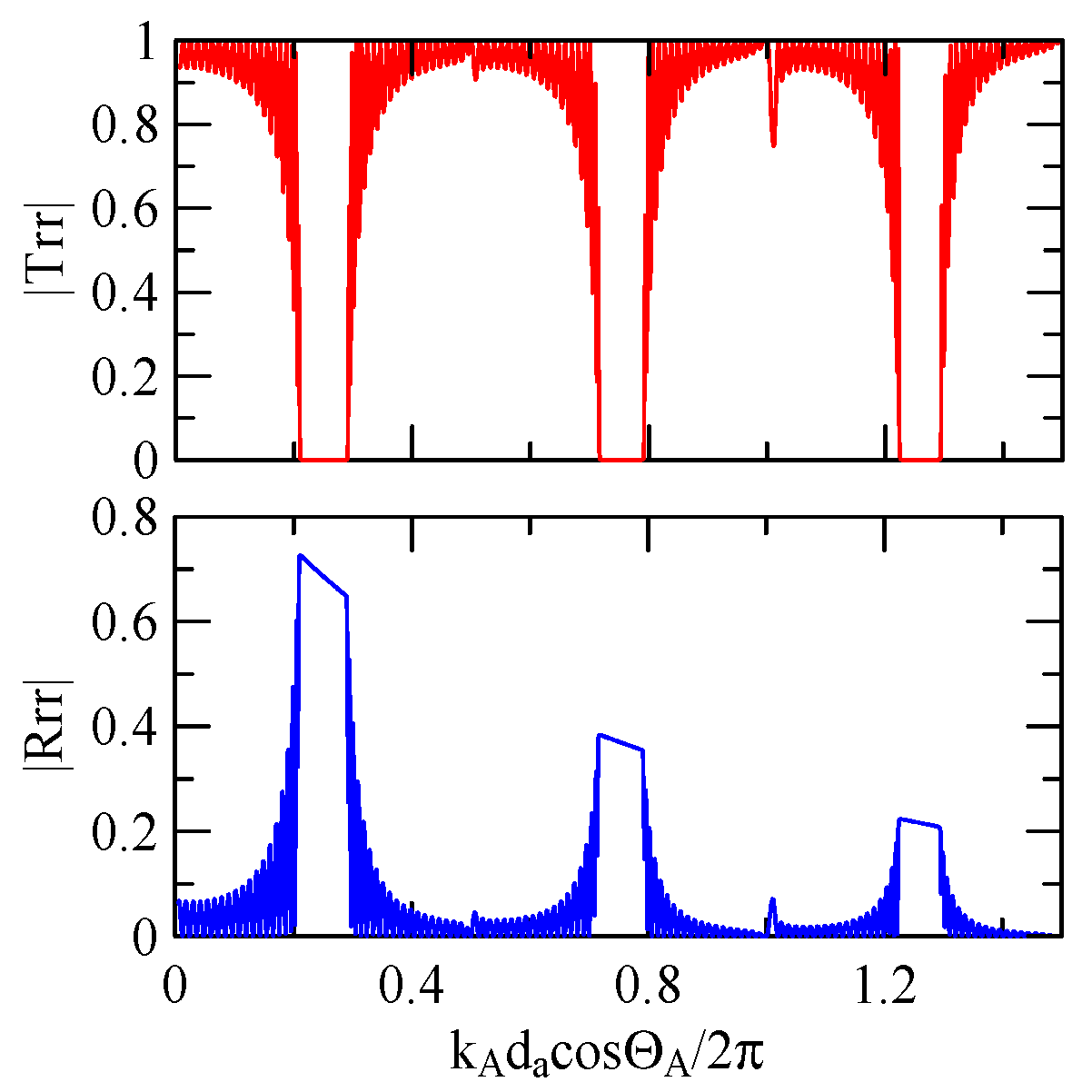
4.1. Frequency Analysis of Grating Arrays
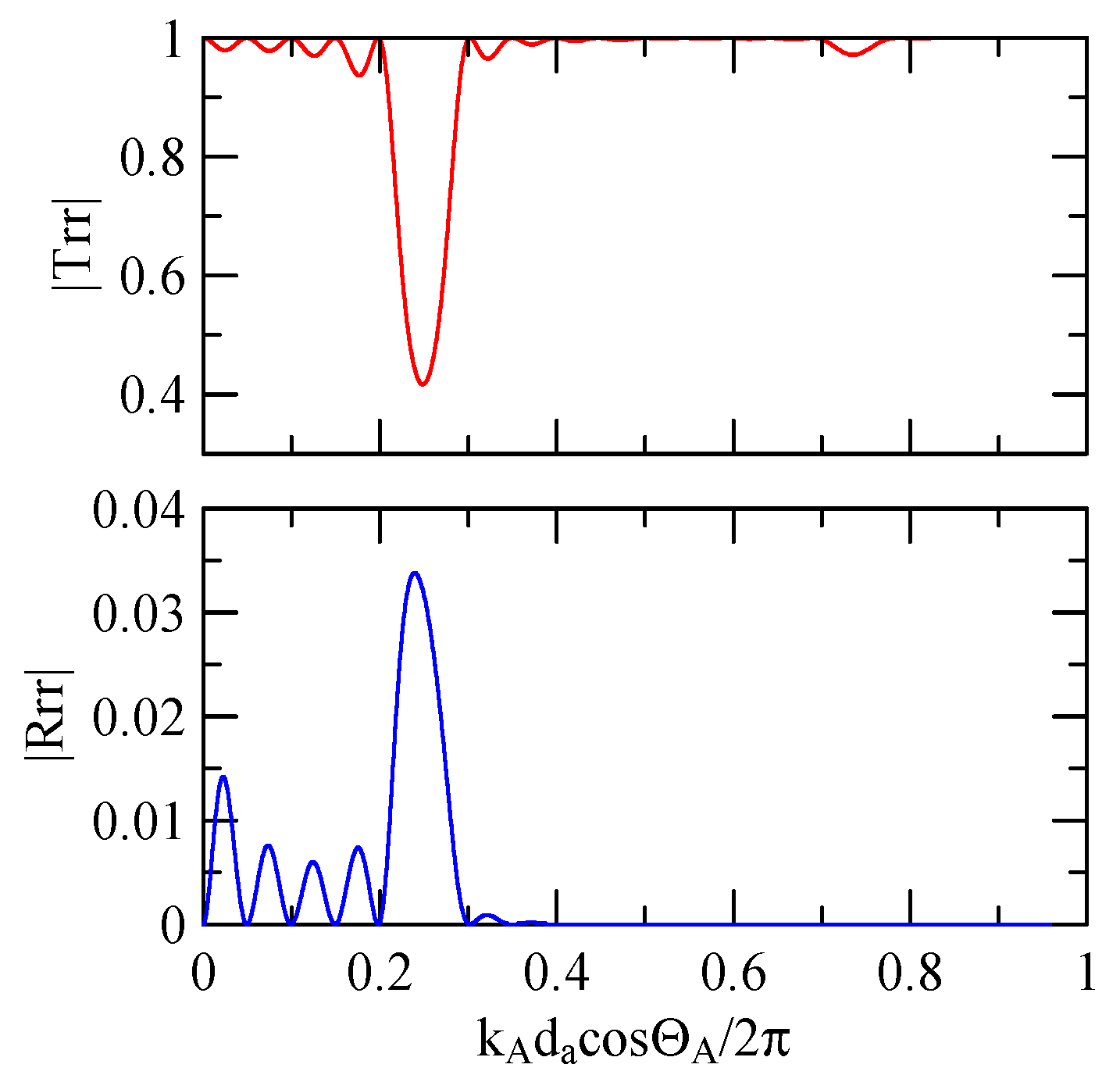
4.1.1. Effects of Strip Width and Incident Angle
4.1.2. Effects of the Strip Number
4.1.3. Effects of Strip Height
4.1.4. Unequal Gap and Strip Widths
4.2. Effect of Initial Conditions on Frequency Response
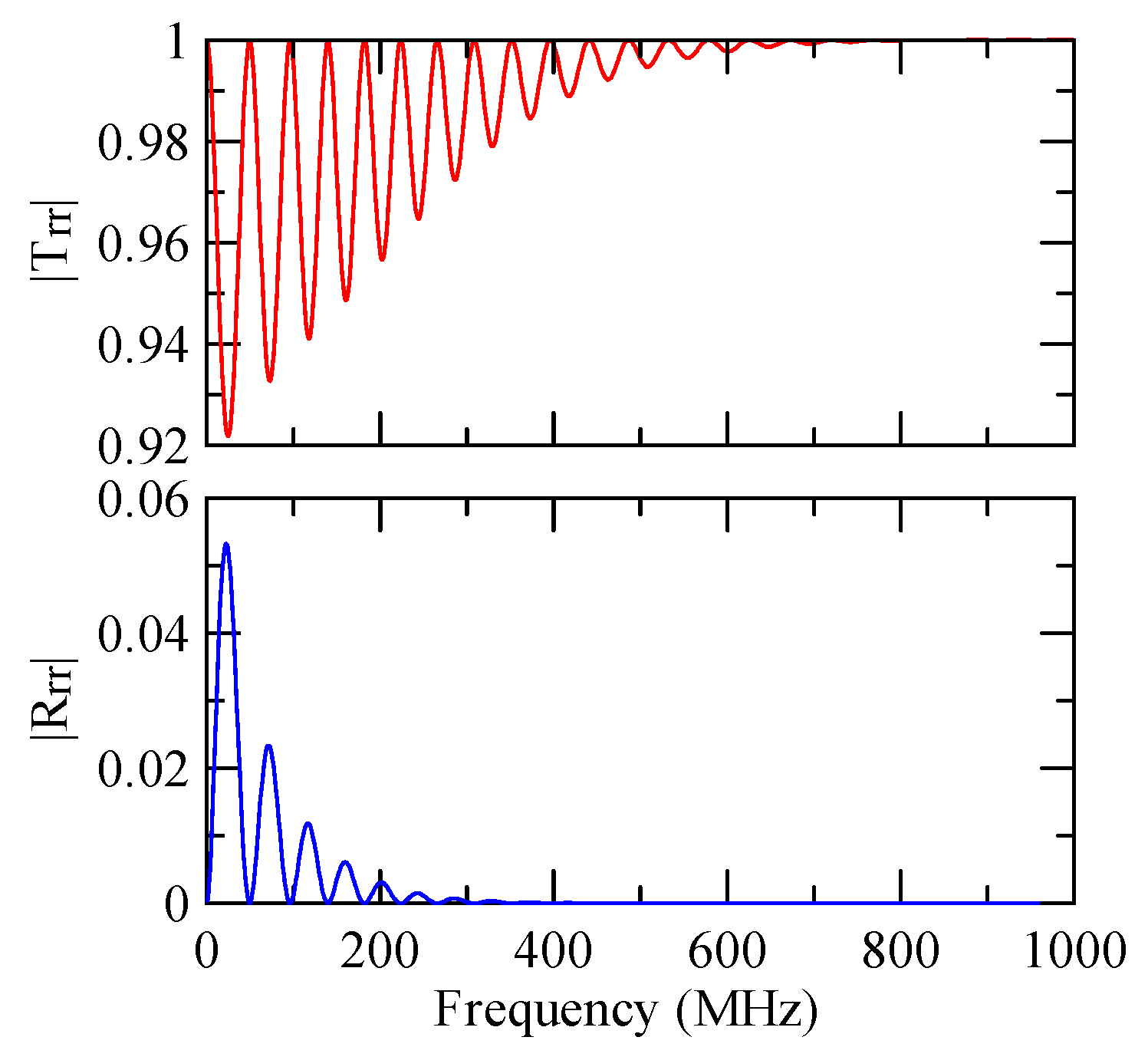
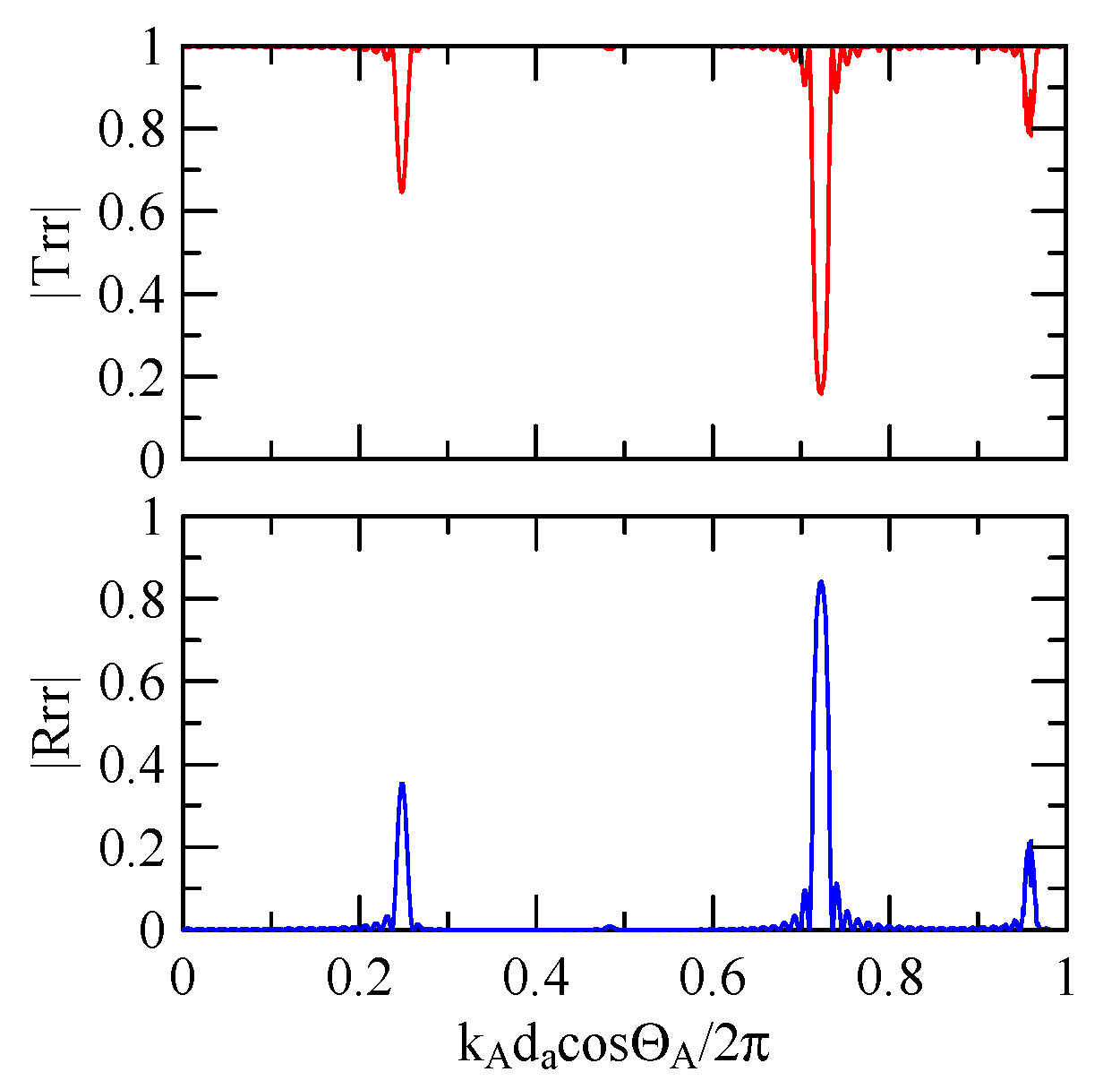
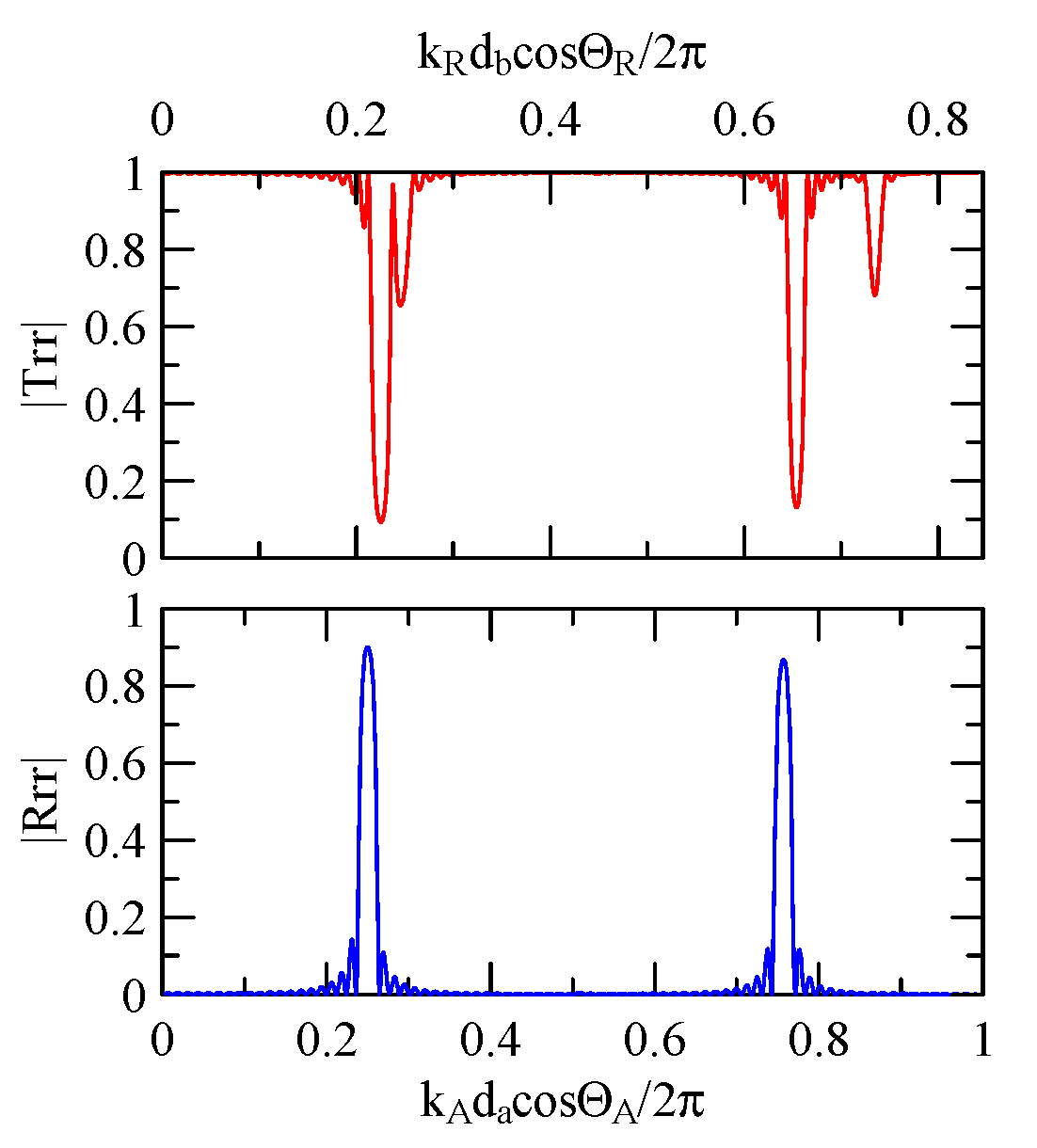
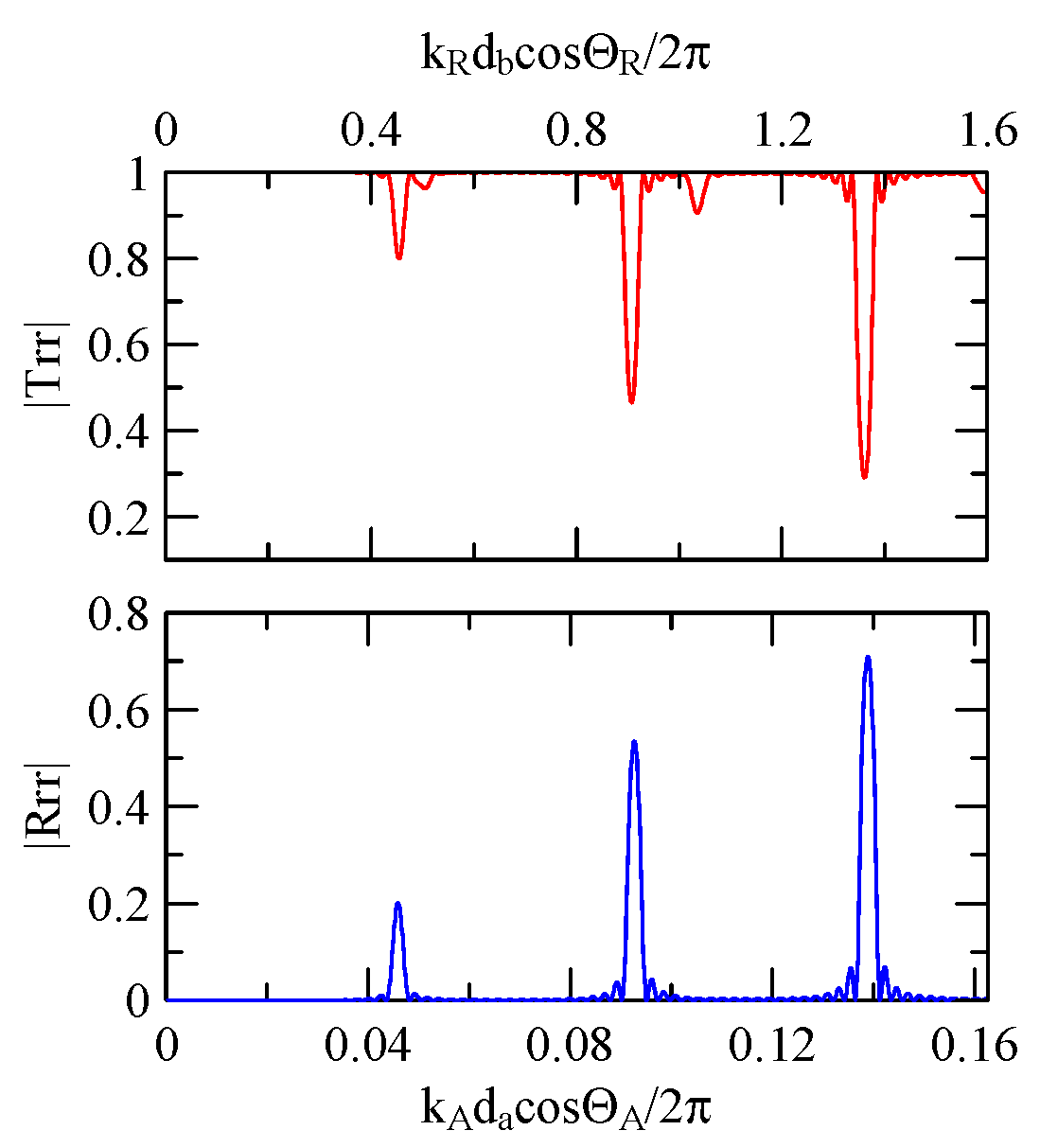
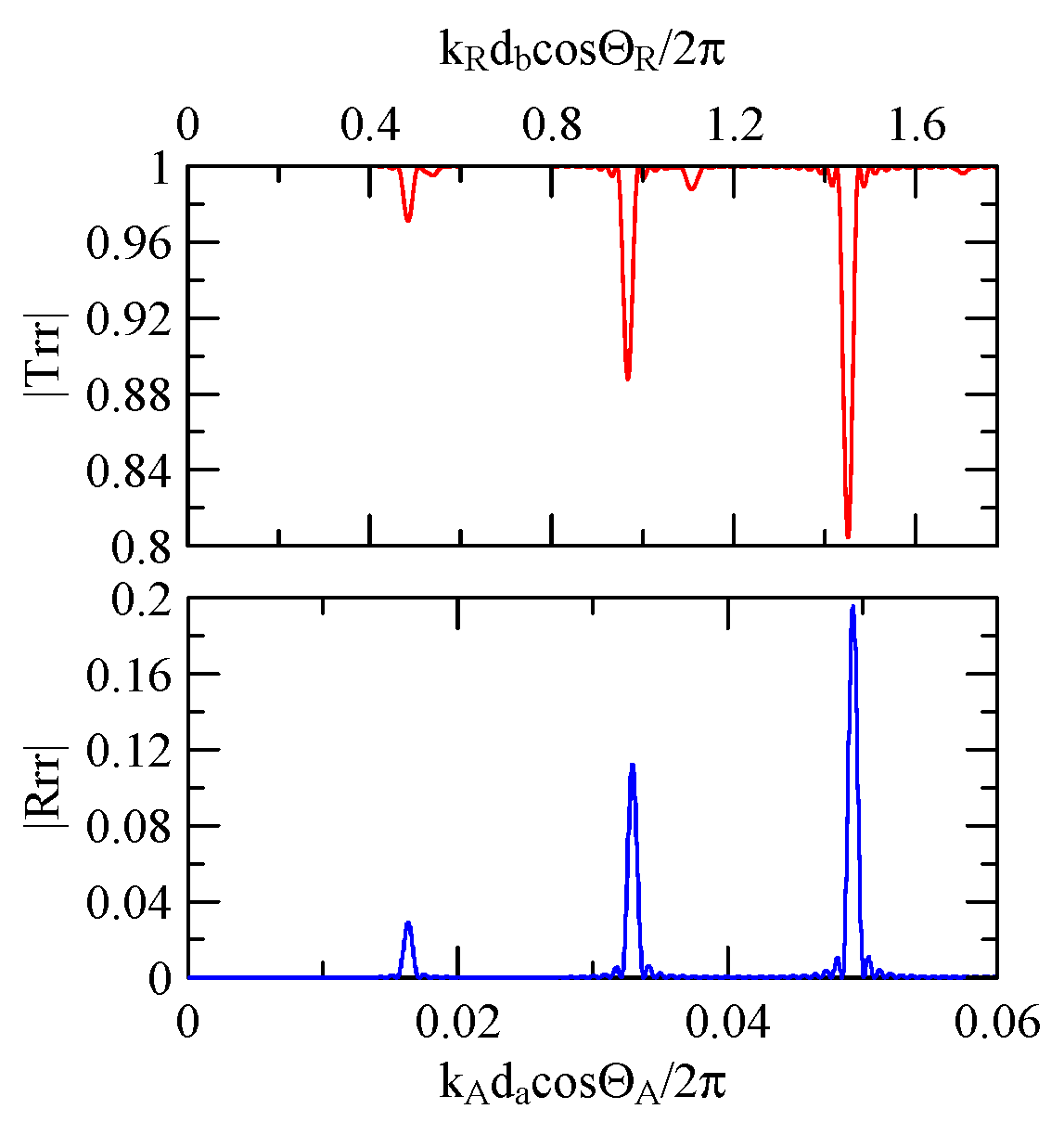
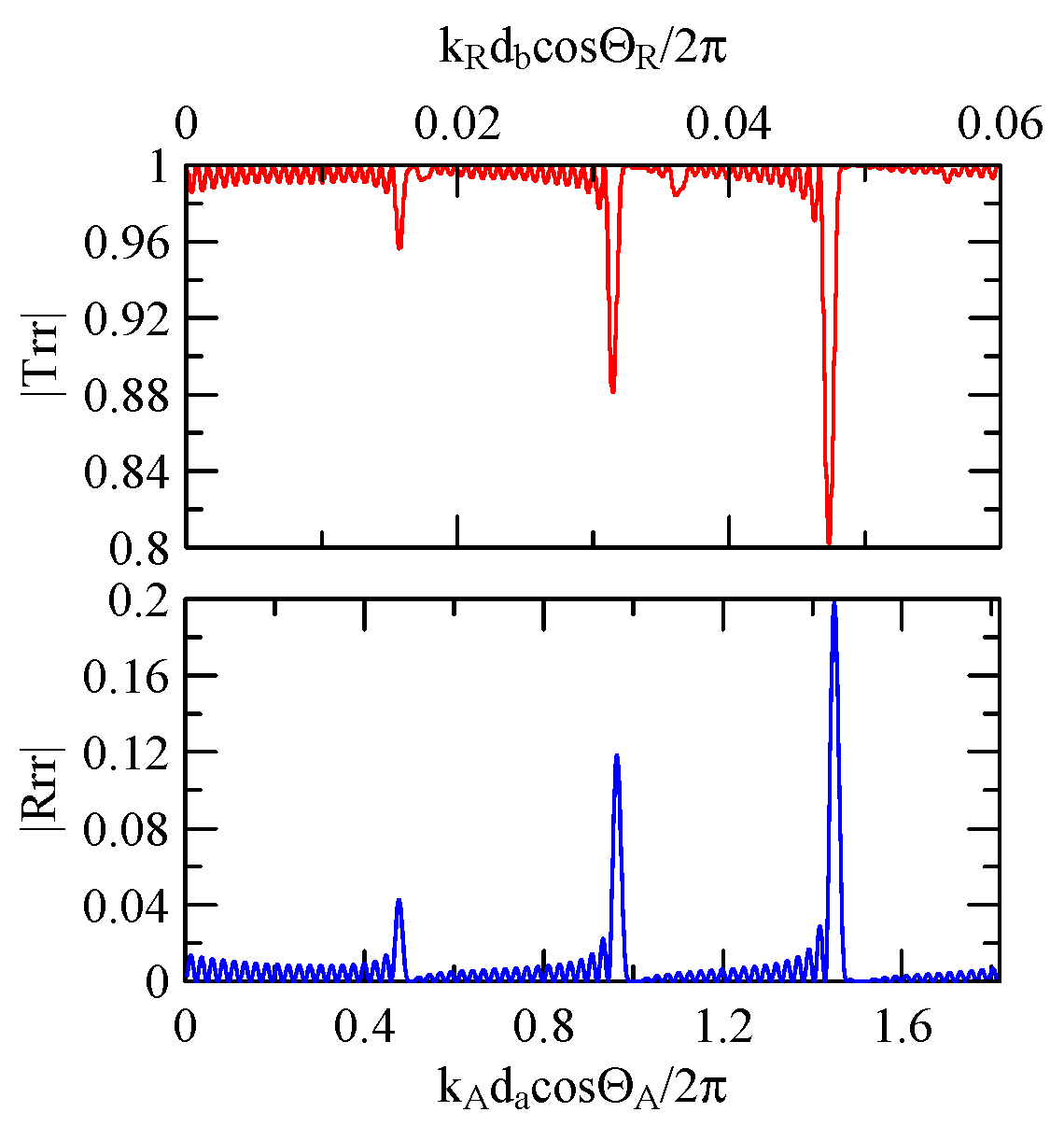
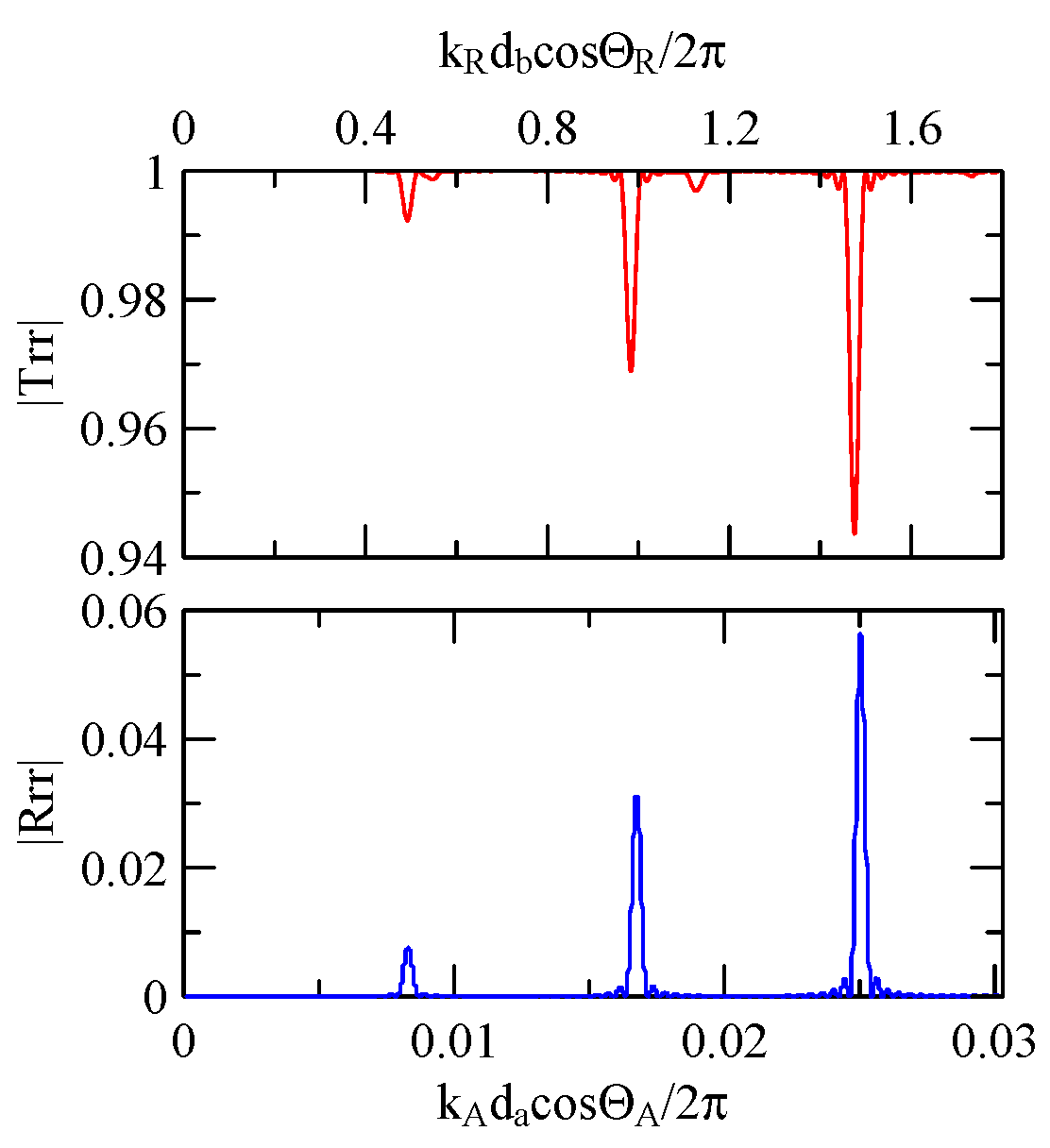
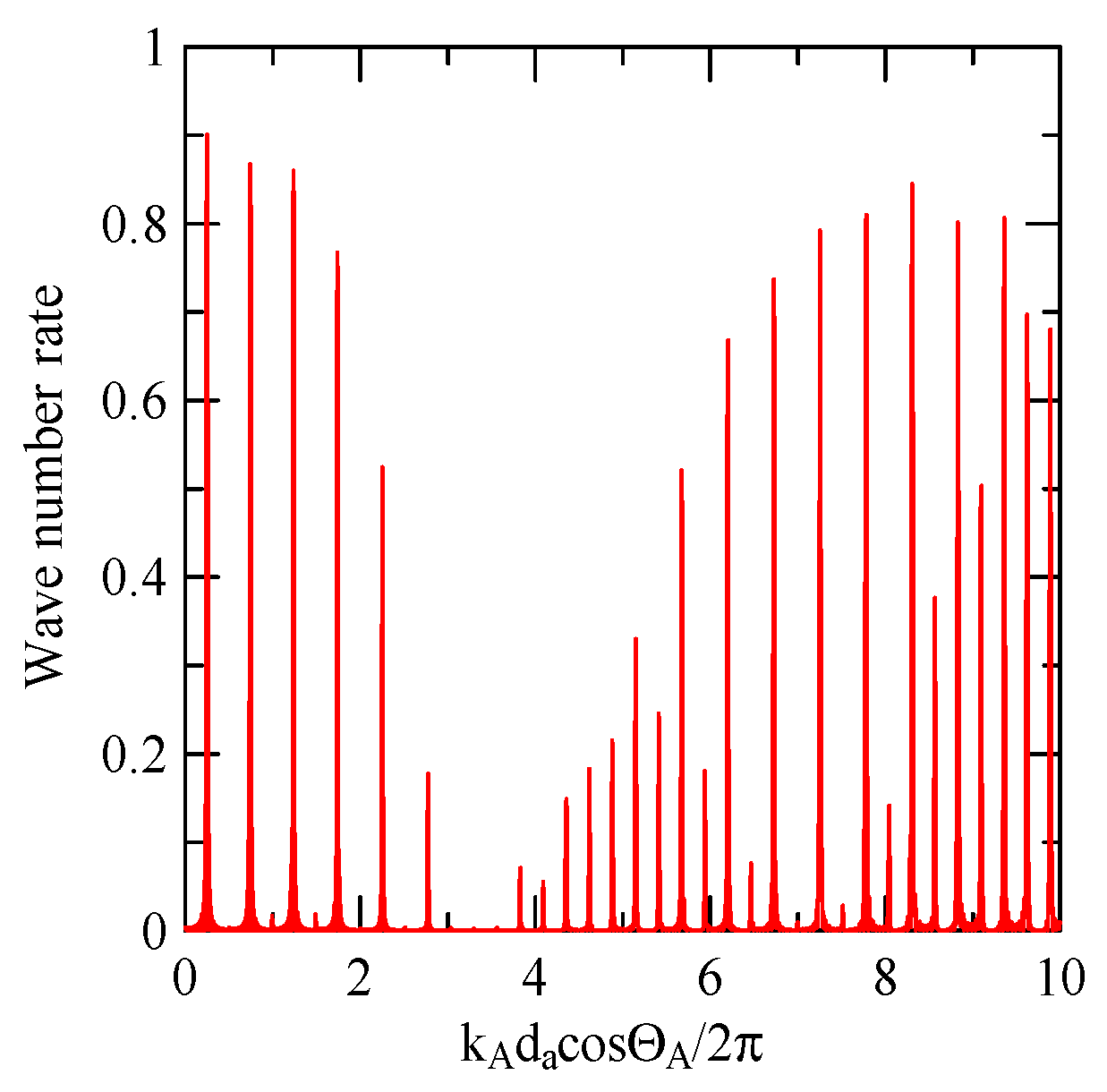
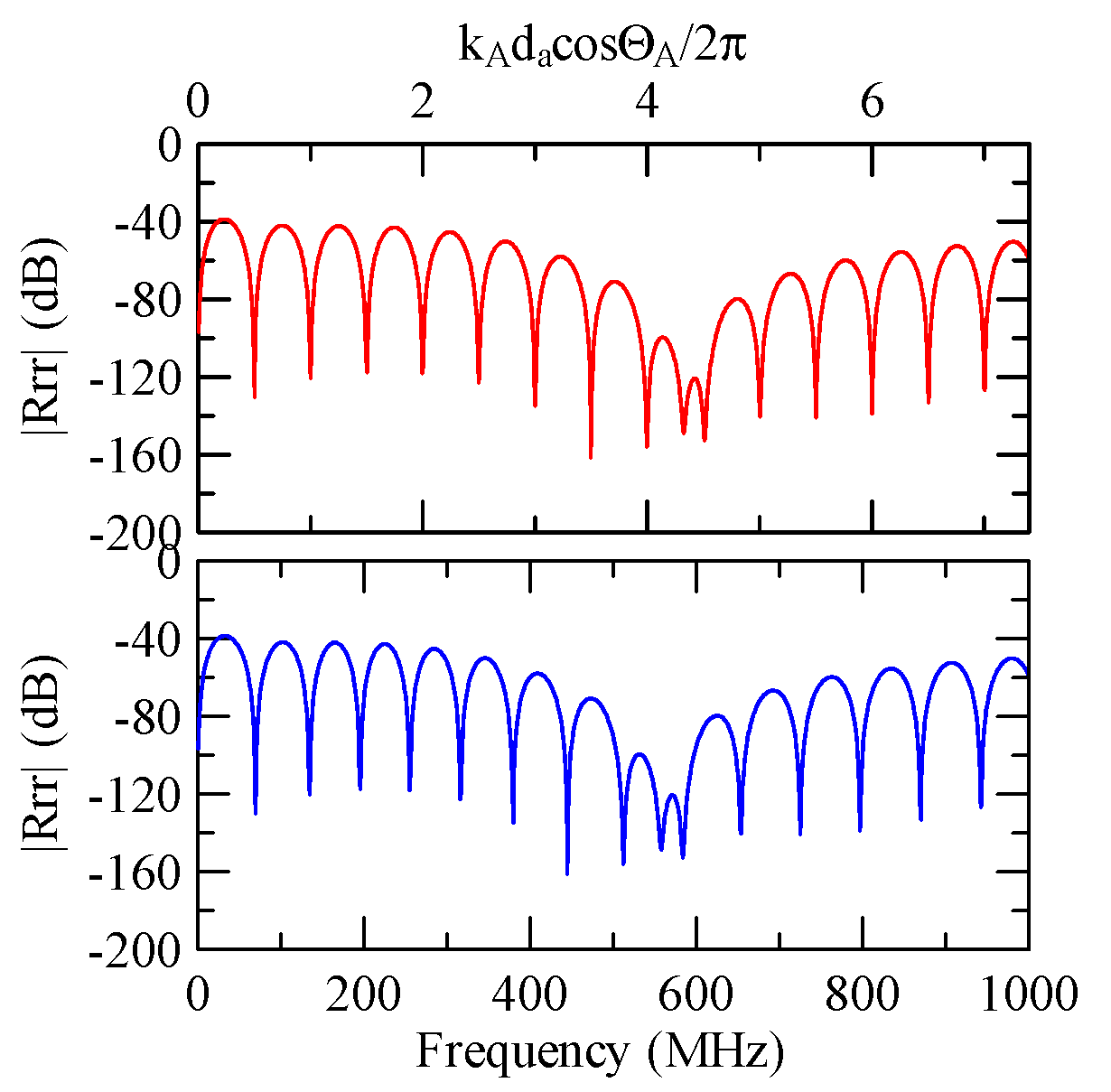
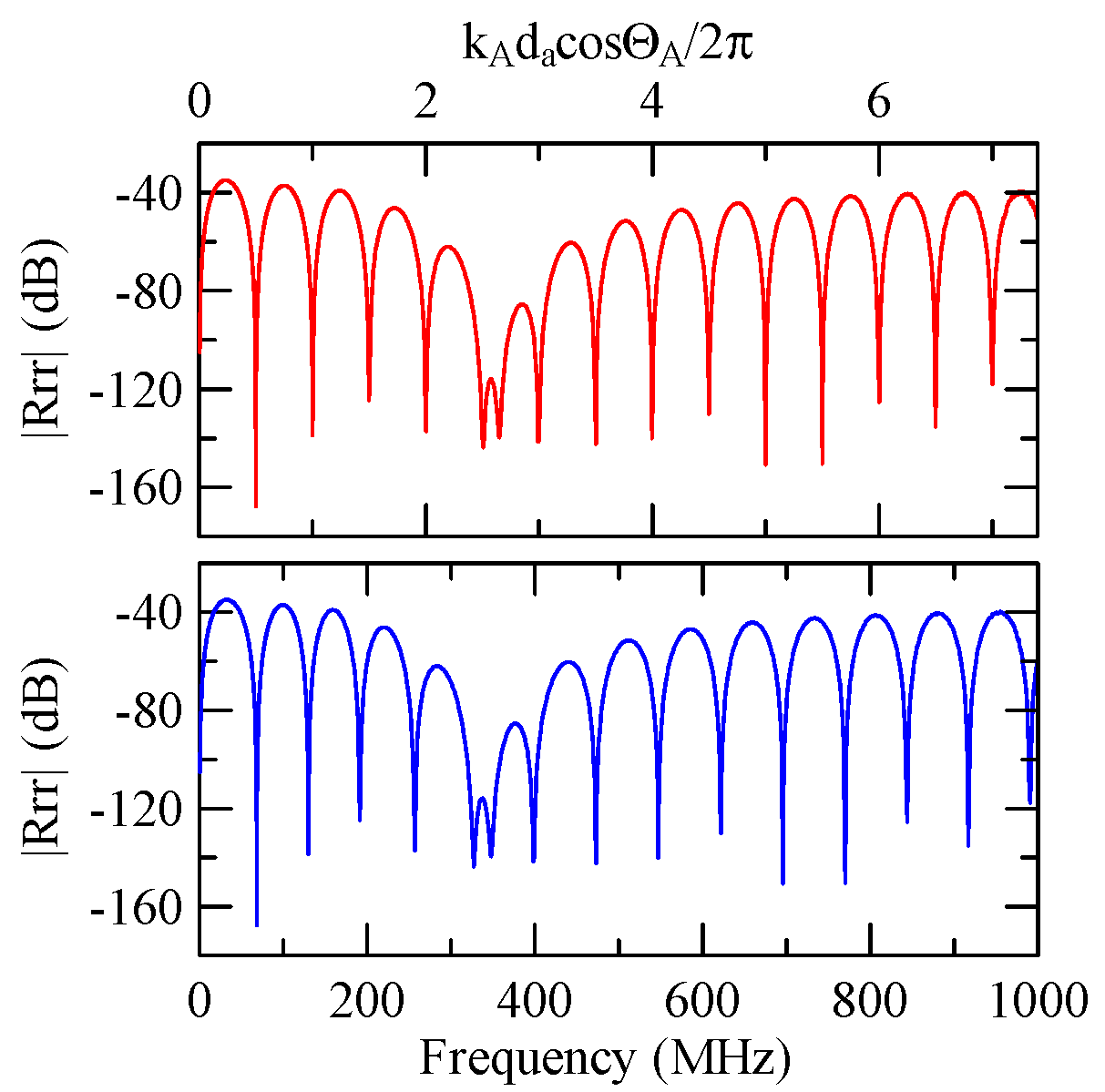
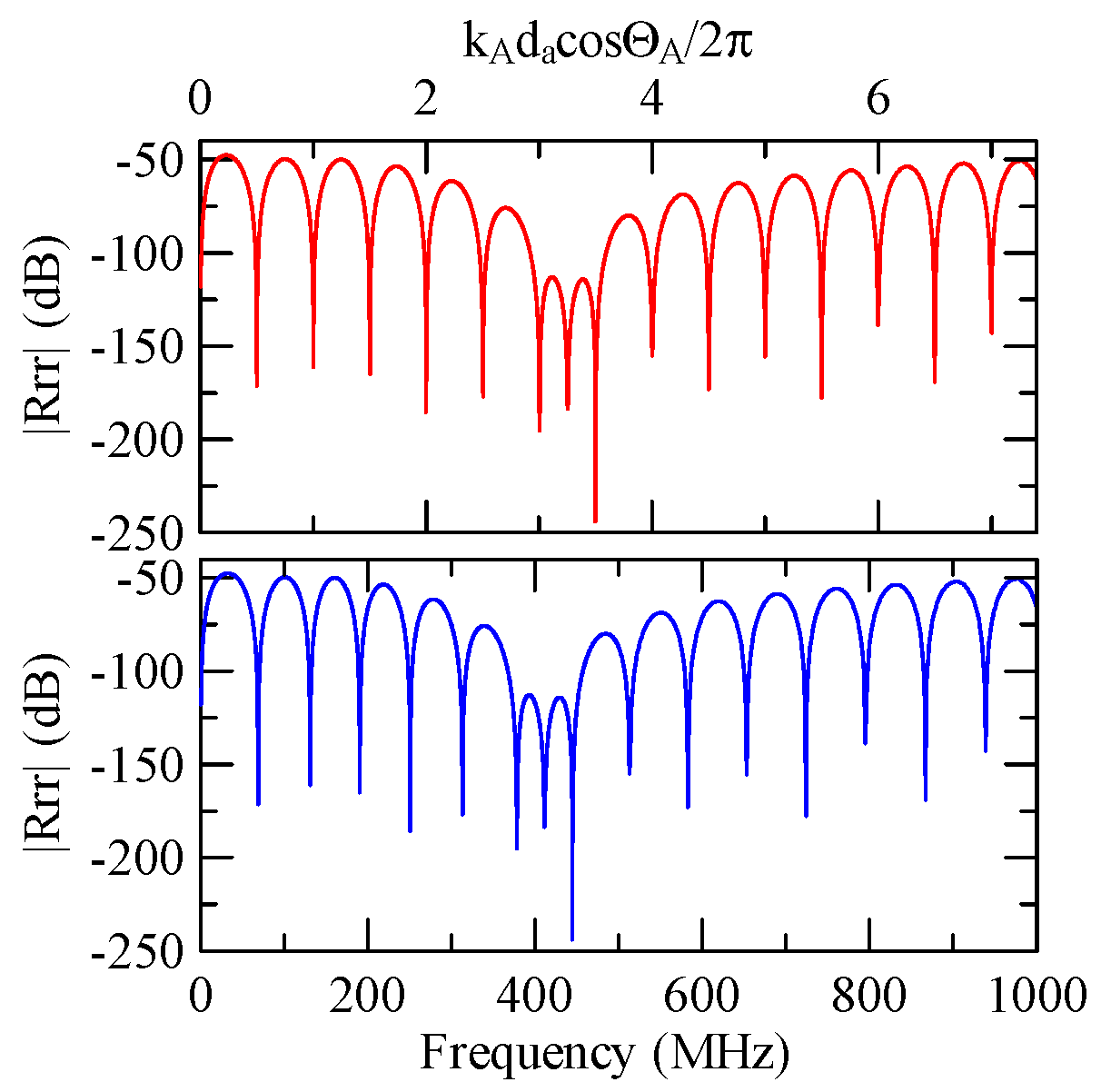
4.2.1. Dispersion Effects and Reflectivity
4.2.2. Oblique and Vertical Incidence
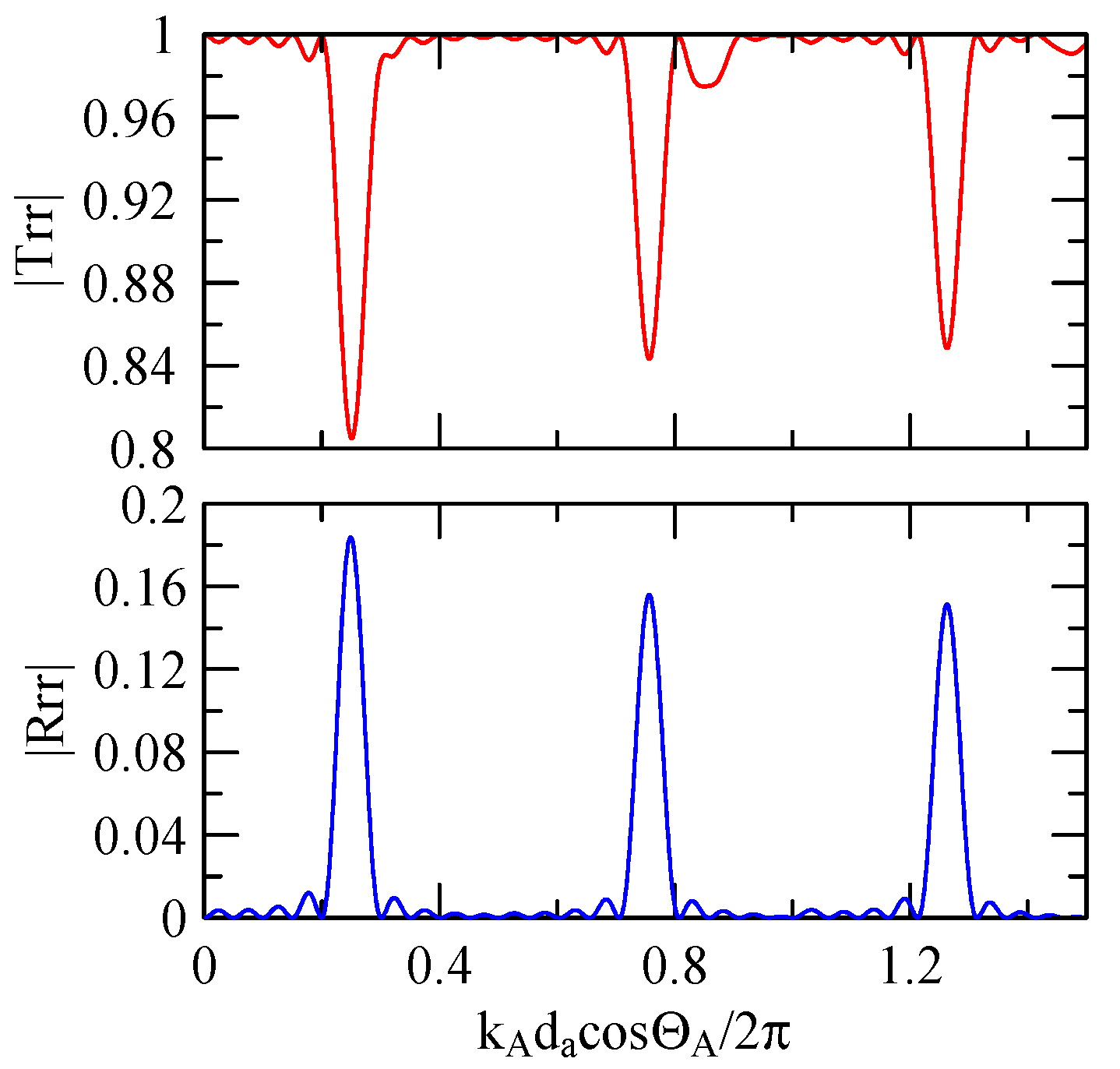
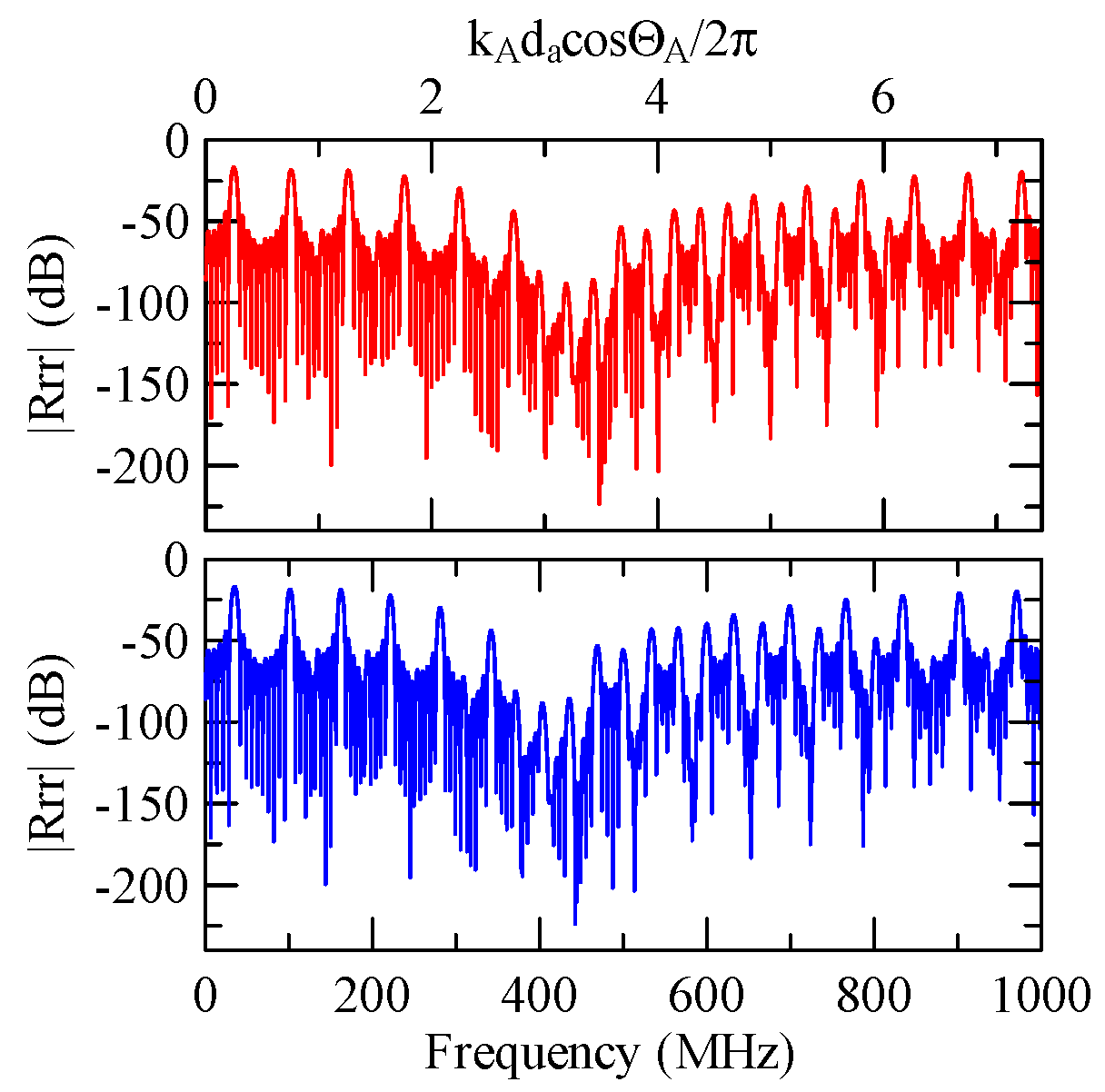
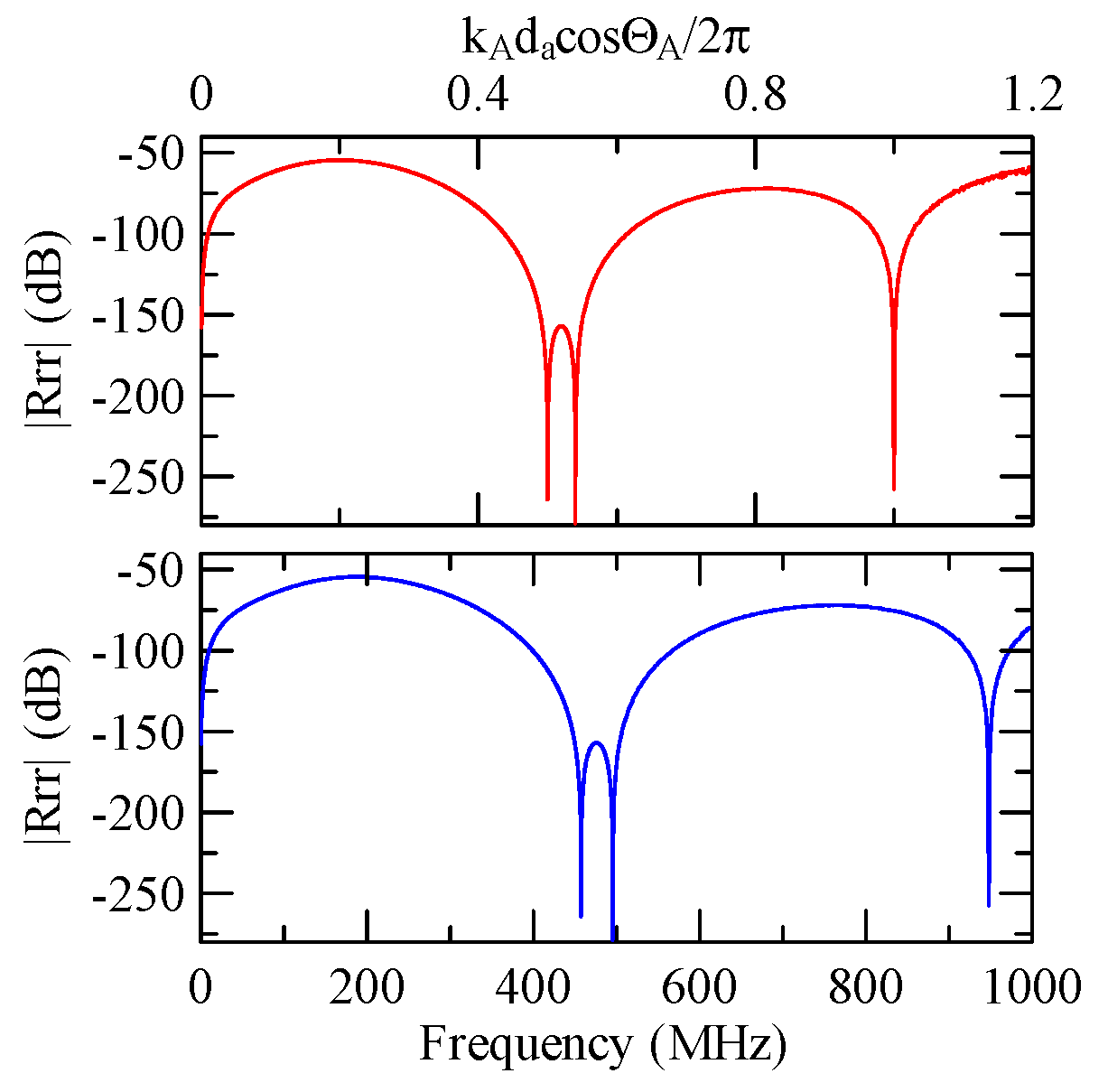
4.2.3. Global Notch of Reflectivity
4.3. Discussion
- 1.
- Analytical method:
- 2.
- Finite Element Method (FEM):
- 3.
- Boundary Element Method (BEM):
- 4.
- Semi-analytical method:
5. Conclusions
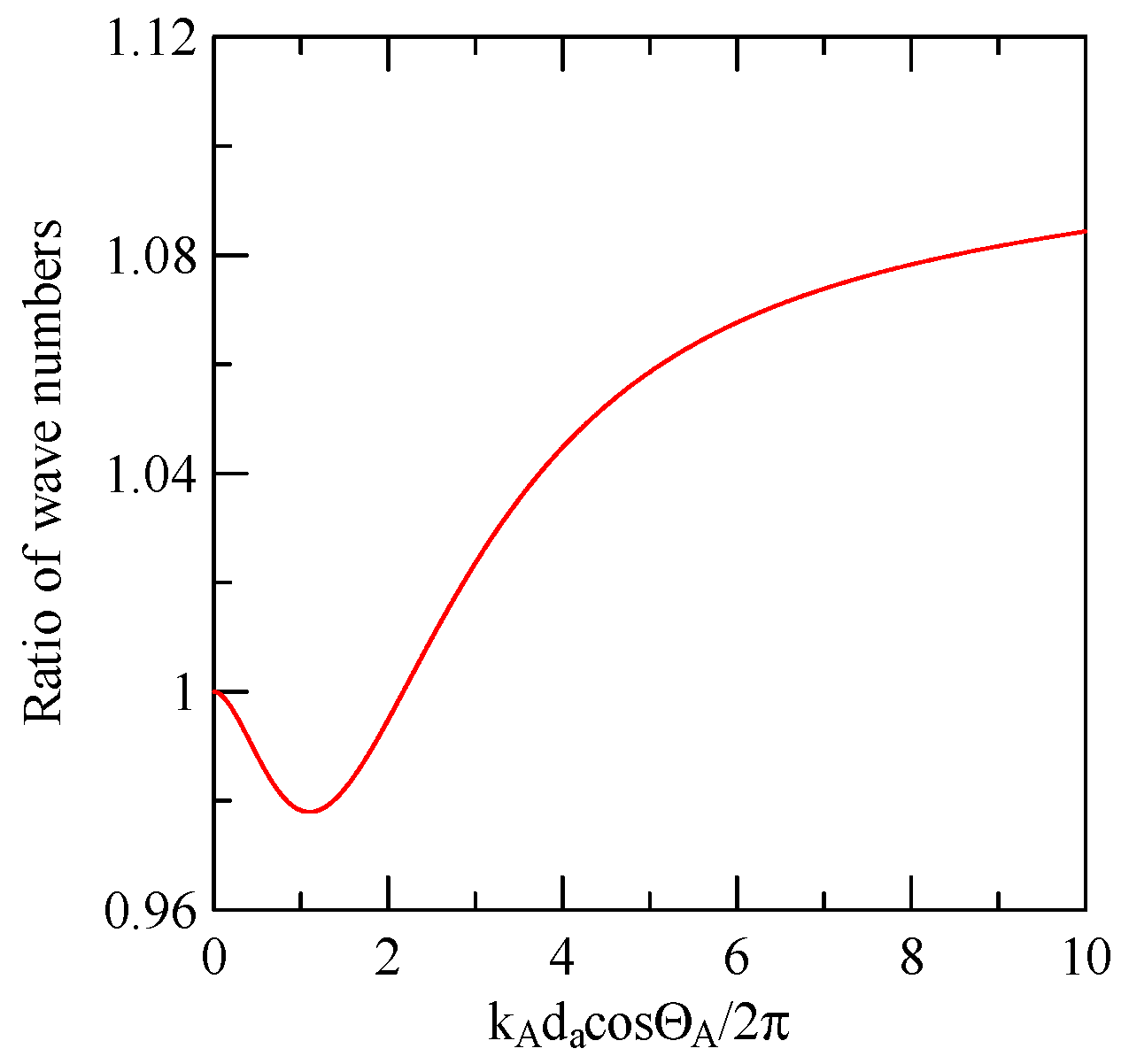
- When the width and gap of metal array strips are the same, the phase velocity difference in SAW in the strip and non-strip areas is insignificant when the reflectivity peak occurs at the dimensionless coordinate .
- With an increase in the number of array strips, the reflectivity of SAWs will increase, which will narrow the bandwidth of the extreme frequency.
- When the array strip height increases, alongside enhancing reflectivity, the difference between the SAW phase velocity in the strip area and the non-strip area becomes larger. As a result, the bandwidth of the extreme frequency increases.
- When the difference between and increases due to differences in the gap and width of the strips or difference in wave velocity between the strip and non-strip area, the extreme frequency of the reflectivity will move. In general, this tends to occur near where the dimensionless coordinate of the one with the larger ratio of is .
- The reflectivity spectrum of the metal array strips exhibits a global notch phenomenon influenced by the shape factor. It is a function of material, phase velocity of the SAW, and wave propagation direction that determines the frequency of the notch. It is not a function of strip array size, gap, and number.
- When a Rayleigh wave is obliquely incident, a mode conversion will occur at the interface between strips and non-strips and a Love wave will be generated. The notch frequency will change when the incident angle changes. When the incident angle is smaller, the frequency of the global notch tends to be higher.
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- Rayleigh, L. On waves propagated along the plane surface of an elastic solid. Proc. Lond. Math. Soc. 1885, 17, 4. [Google Scholar] [CrossRef]
- White, R.M.; Voltmer, F.W. Direct piezoelectric coupling to surface elastic waves. Appl. Phys. Lett. 1965, 7, 314–316. [Google Scholar] [CrossRef]
- Bleustein, J.L. A new surface wave in piezoelectric materials. Appl. Phys. Lett. 1968, 13, 412. [Google Scholar] [CrossRef]
- Gulyaer, Y.V. Electro acoustic surface waves in solids. JETP Lett. 1969, 9, 37–38. [Google Scholar]
- Schmidt, R.V.; Voltmer, F.W. Piezoelectric elastic surface waves in anisotropic layered media. Microw. Theory Tech. IEEE Trans. 1969, 17, 920–926. [Google Scholar] [CrossRef]
- Kino, G.S.; Wagers, R.S. Theory of interdigital couplers on nonpiezoelectric substrates. J. Appl. Phys. 1973, 44, 1480–1488. [Google Scholar] [CrossRef]
- Shimizu, Y.; Terazaki, A. Unidirectional surface acoustic wave transducers of ZnO on glass. Electronics Letters 1977, 13, 384. [Google Scholar] [CrossRef]
- Braga, A.M.B.; Herrmann, G. Plane waves in anisotropic layered composites. In Symposium on Wave Propagation in Structural Composites; Mal, A.K., Ting, T.C.T., Eds.; ASME-AMD: New York, NY, USA, 1988; Volume 90, pp. 89–98. [Google Scholar]
- Stroh, A.N. Steady state problem in anisotropic elasticity. J. Math. Phys. 1962, 41, 77–102. [Google Scholar] [CrossRef]
- Honein, G.; Braga, A.M.B.; Barbone, P.; Herrmann, G. Wave propagation in piezoelectric layered media with some applications. J. Intell. Mater. Syst. Struct. 1991, 2, 542–557. [Google Scholar] [CrossRef]
- Barnett, D.M.; Lothe, J. Free surface (Rayleigh) waves in anisotropic elastic halfs-paces: The surface impedance method. Proc. Rayal Soc. Londan A 1985, 402, 135–152. [Google Scholar]
- Tancrell, R.H.; Holland, M.G. Acoustic surface wave filters. IEEE Proc. 1971, 59, 393–409. [Google Scholar] [CrossRef]
- Hachigo, A.; Malocha, D.C. SAW device modeling including velocity disperion based on ZnO/diamond/Si layered structures. IEEE Trans. Ultrason. Ferroelect. Freq. Contr. 1998, 45, 660–665. [Google Scholar] [CrossRef] [PubMed]
- Pierce, J.R. Coupling of modes of propagation. J. Appl. Phys. 1954, 25, 179–183. [Google Scholar] [CrossRef]
- Cross, P.S.; Schmidt, R.V. Coupled surface-acoustic- wave resonators. Bell Syst. Tech. J. 1977, 56, 1447–1482. [Google Scholar] [CrossRef]
- Abbott, B.P. A Coupling-of-Modes Model for SAW Transducers with Arbitrary Reflectivity Weighting. Ph.D. Thesis, Department of Electrical Engineering, University of Central Florida, Orlando, FL, USA, 1989. [Google Scholar]
- Abbott, B.P.; Hartmann, C.S.; Malocha, D.C. A coupling- of-modes analysis of chirped transducers containing reflective electrode geometries. In Proceedings of the IEEE Ultrasonics Symposium, Montreal, QC, Canada, 3–6 October 1989; pp. 129–134. [Google Scholar]
- Royer, D.; Dieulesaint, E. Elastic Waves in Solids; Springer-Verlag: Berlin, Germany, 1999; Volume I, pp. 119–166. [Google Scholar]
- Royer, D.; Dieulesaint, E. Elastic Waves in Solids; Springer-Verlag: Berlin, Germany, 1999; Volume II, pp. 70–72. [Google Scholar]
- Finger, N.; Kovacs, G.; Schoberl, J.; Langer, U. AccurateFEM/BEM-Simulation of Surface Acoustic Wave Filters. In Proceedings of the 2003 IEEE Ultrasonics Symposium, Honolulu, HI, USA, 5–8 October 2003; pp. 1680–1685. [Google Scholar]
- Kuyper, L.H.; Eisele, D.A.; Reindl, L.M. The K-model-Green’s Function based Analysis of Surface Acoustic Wave Devices. In Proceedings of the 2005 IEEE Ultrasonics Symposium, Rotterdam, The Netherlands, 18–21 September 2005; pp. 1550–1555. [Google Scholar]
- Tagawa, K. Simulation Modeling and Optimization Technique for Balanced Surface Acoustic Wave Filters. In Proceedings of the 7th WSEAS International Conference on Simulation, Modeling and Optimization, Beijing, China, 15–17 September 2007; pp. 295–300. [Google Scholar]
- Tigli, O.; Zaghloul, M.E. Finite Element Modeling and Analysis of Surface Acoustic Devices in CMOS Technology. IEEE Trans. Compon. Packag. Manuf. Technol. 2012, 2, 1021–1029. [Google Scholar] [CrossRef]
- Elkordy, M.F.; Elsherbini, M.M.; Gomaa, A.M. Modeling and Simulation of Unapodized Surface Acoustic wave Filter. Afr. J. Eng. Res. 2013, 1, 1–5. [Google Scholar]
- Venkatesan, T.; Pandya, H.M. Surface Acoustic wWave Devices and Sensors—A Short Review on Design and Modeling by Impulse Response. J. Environ. Nanotechnol. 2013, 2, 81–90. [Google Scholar]
- Panneerselvam, G.; Thirumal, V.; Pandya, H.M. Review of Surface Acoustic Wave Sensors for the Detection and Identification of Toxic Environmental Gases/Vapours. Arch. Acoust. 2018, 43, 357–367. [Google Scholar]
- Wang, T.; Green, R.; Guldiken, R.; Wang, J.; Mohapatra, S.; Mohapatra, S.S. Finite Element Analysis for Surface Acoustic Wave Device Characteristic Properties and Sensitivity. Sensors 2019, 19, 1749. [Google Scholar] [CrossRef]
- Shen, J.; Fu, S.; Su, R.; Xu, H.; Lu, Z.; Zhang, Q.; Zeng, F.; Song, C.; Wang, W.; Pan, F. Ultra-Wideband Surface Acoustic Wave Filters Based on the Cu/LiNbO3/SiO2/SiC Structure. In Proceeding of the 2021 IEEE International Ultrasonics Symposium (IUS2021), Xi’an, China, 11–16 September 2021. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, Q.; Fu, S.; Wang, X.; Qiu, X.; Wu, H. Hybrid Full-Wave Analysis of Surface Acoustic Wave Devices for Accuracy and Fast Performance Prediction. Micromachines 2021, 12, 5. [Google Scholar] [CrossRef]
- Koigerov, A.S.; Balysheva, O.L. Numerical Approach for Extraction COM Surface Acoustic Wave Parameters from Periodic Structures. In Proceedings of the IEEE Wave Electronics and its Application in information and Telecommunication System (WECONF2021), St. Petersburg, Russia, 31 May–4 June 2021. [Google Scholar] [CrossRef]
- Su, R.; Shen, J.; Lu, Z.; Xu, H.; Niu, Q.; Xu, Z.; Zeng, F.; Song, C.; Wang, W.; Fu, S.; et al. Wideband and Low-Loss Surface Acoustic Wave Filter based on 15° YX-LiNbO3/SiO2/Si Structure. IEEE Electron Device Lett. 2021, 42, 438–441. [Google Scholar] [CrossRef]
- Su, R.; Fu, S.; Shen, J.; Lu, Z.; Xu, H.; Wang, R.; Song, C.; Zeng, F.; Wang, W.; Pan, F. Wideband Surface Acoustic Wave Filter at 3.7 GHz with Spurious Mode Mitigation. IEEE Trans. Microw. Theory Tech. 2023, 71, 480–487. [Google Scholar] [CrossRef]












| Density (g/cm3) | Lame Constants (GPa) | Poisson Ratio | Dielectric Constant (10−12 F/m) | |
|---|---|---|---|---|
| 2.484 | 23.953 | 29.228 | 0.229 | 64.634 |
| Density (g/cm3) | Stiffness Coefficients (GPa) | ||||
|---|---|---|---|---|---|
| 5.676 | 209.7 | 121.1 | 105.1 | 210.9 | 42.5 |
| Piezoelectric Constants (C/m2) | Dielectric Constants (10−12 F/m) | ||||
| −0.59 | −0.61 | 1.14 | 73.8 | 78.3 | |
| Density (g/cm3) | Young’s Modulus (GPa) | Poisson Ratio | Dielectric Constants (10−12 F/m) |
|---|---|---|---|
| E | |||
| 2.7 | 70 | 0.33 | 15.045 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, T.-H. Reflection and Transmission Analysis of Surface Acoustic Wave Devices. Micromachines 2023, 14, 1898. https://doi.org/10.3390/mi14101898
Yu T-H. Reflection and Transmission Analysis of Surface Acoustic Wave Devices. Micromachines. 2023; 14(10):1898. https://doi.org/10.3390/mi14101898
Chicago/Turabian StyleYu, Tai-Ho. 2023. "Reflection and Transmission Analysis of Surface Acoustic Wave Devices" Micromachines 14, no. 10: 1898. https://doi.org/10.3390/mi14101898
APA StyleYu, T.-H. (2023). Reflection and Transmission Analysis of Surface Acoustic Wave Devices. Micromachines, 14(10), 1898. https://doi.org/10.3390/mi14101898







