Active Adjustment of the Subreflector Shape for the Large Dual-Reflector Antenna
Abstract
:1. Introduction
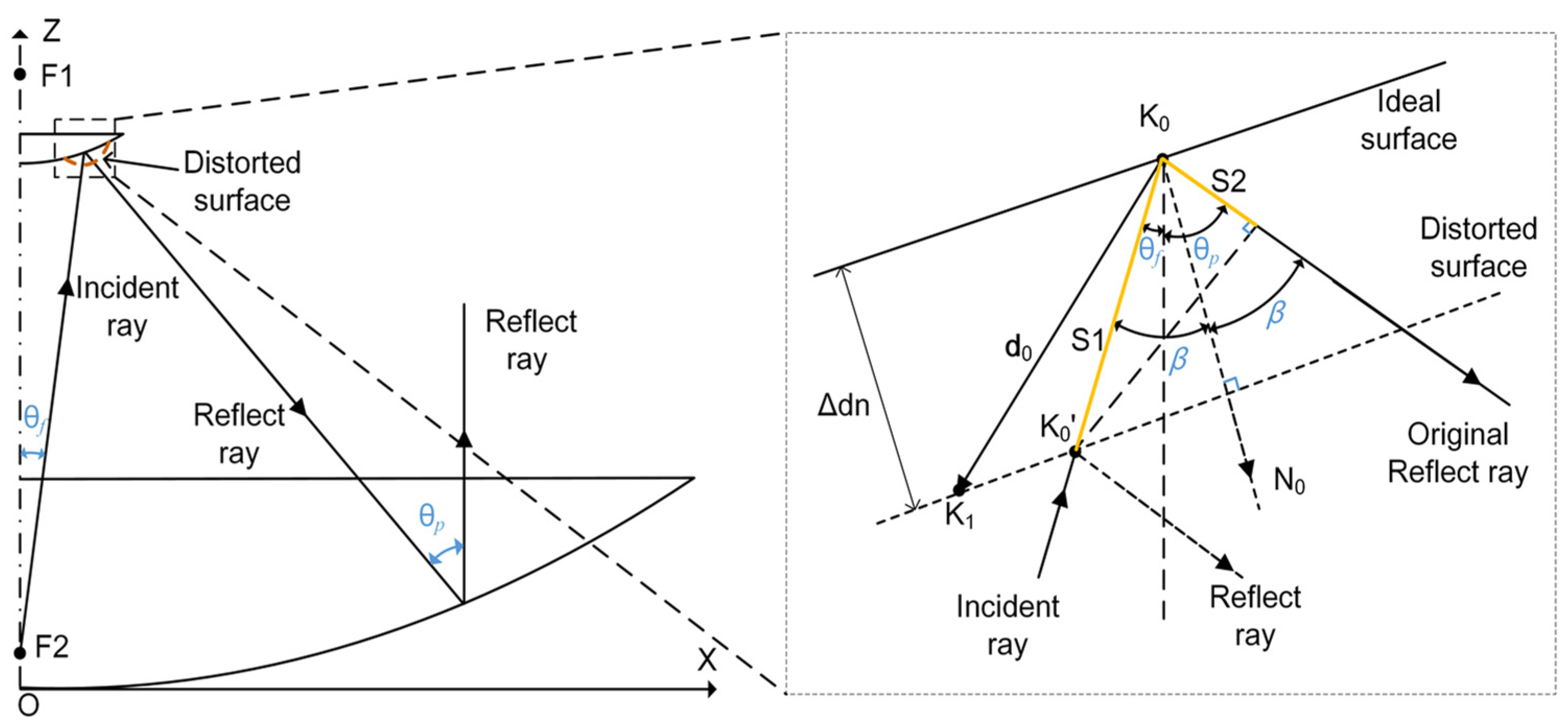
2. Influence of the Subreflector Surface Error
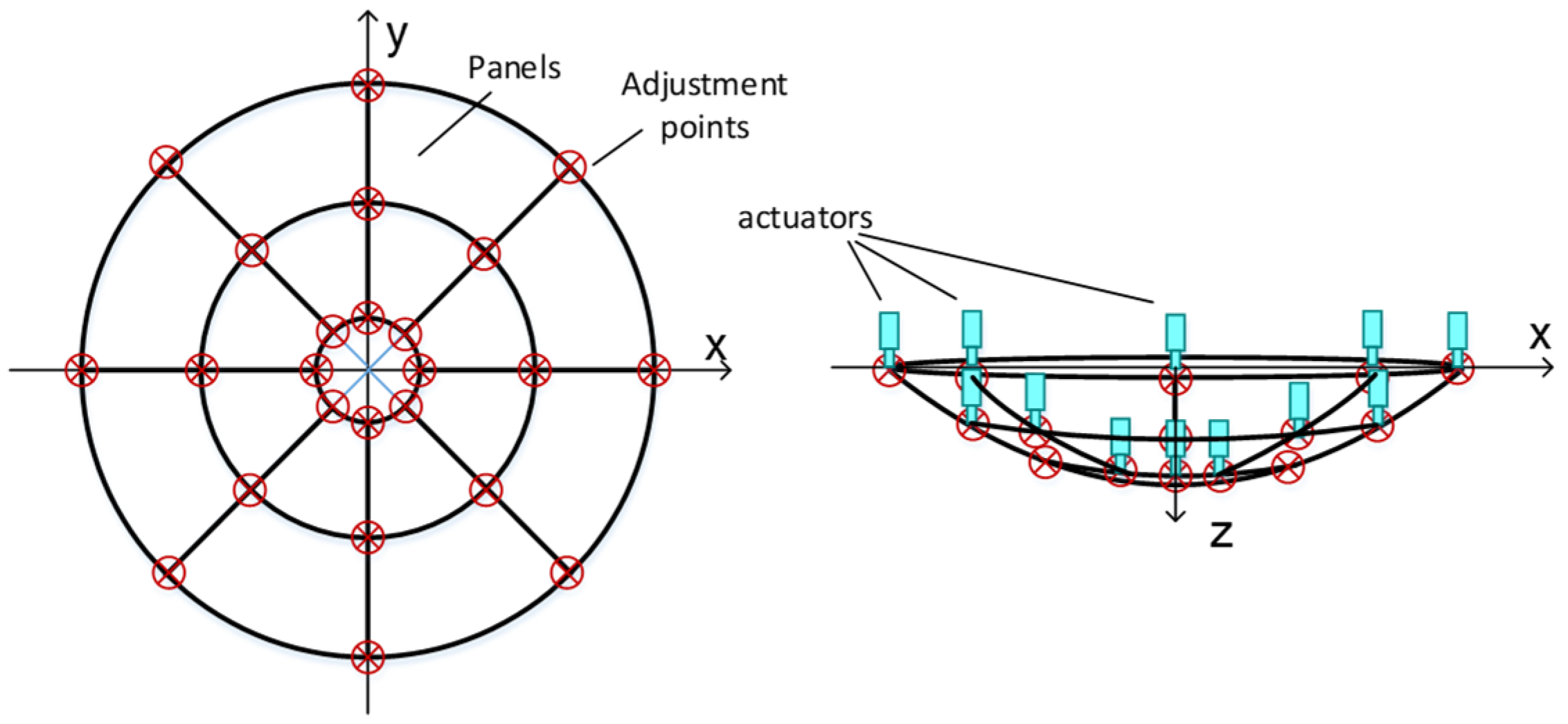
3. Shape Adjustment of the Subreflector
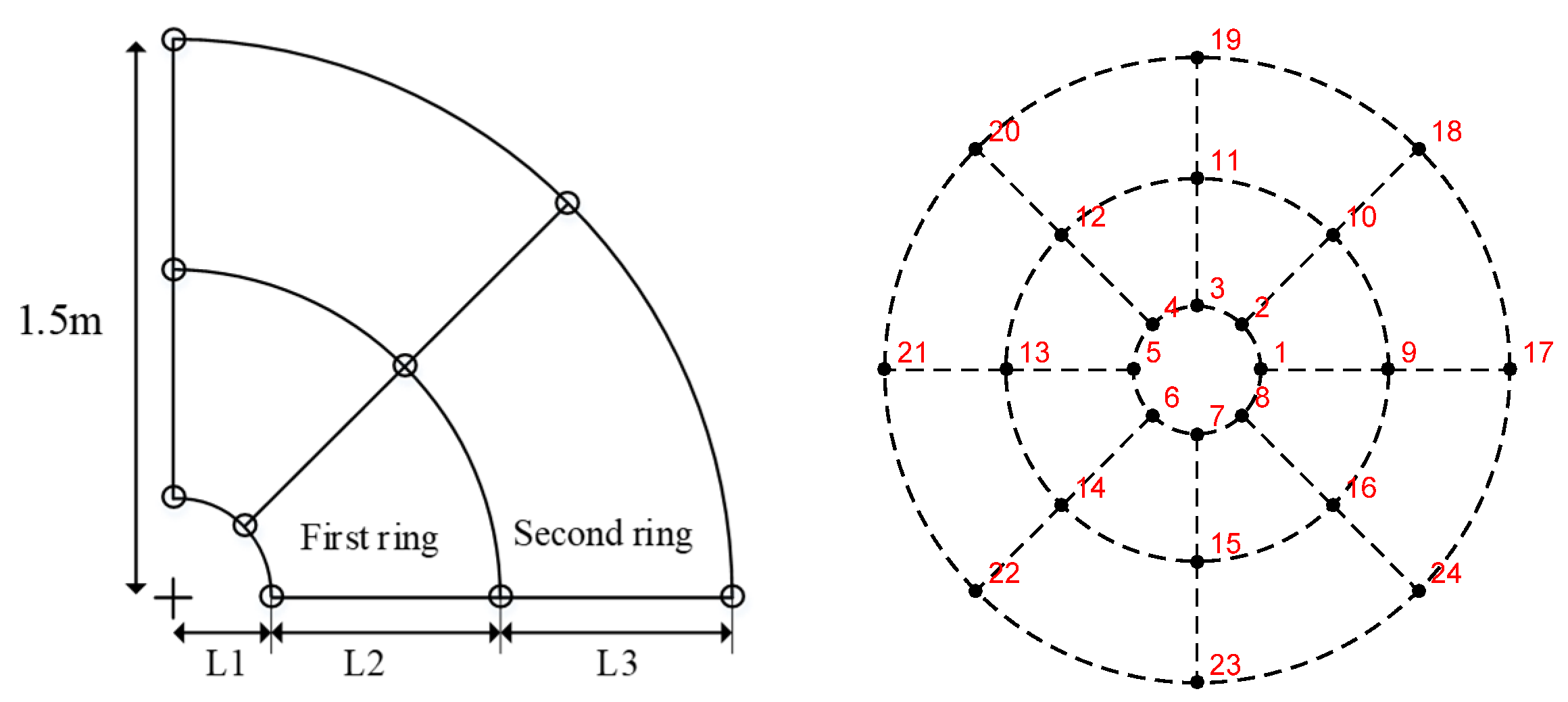
3.1. Actuators Influence Matrix
3.2. Least Squares Matrix Transformation
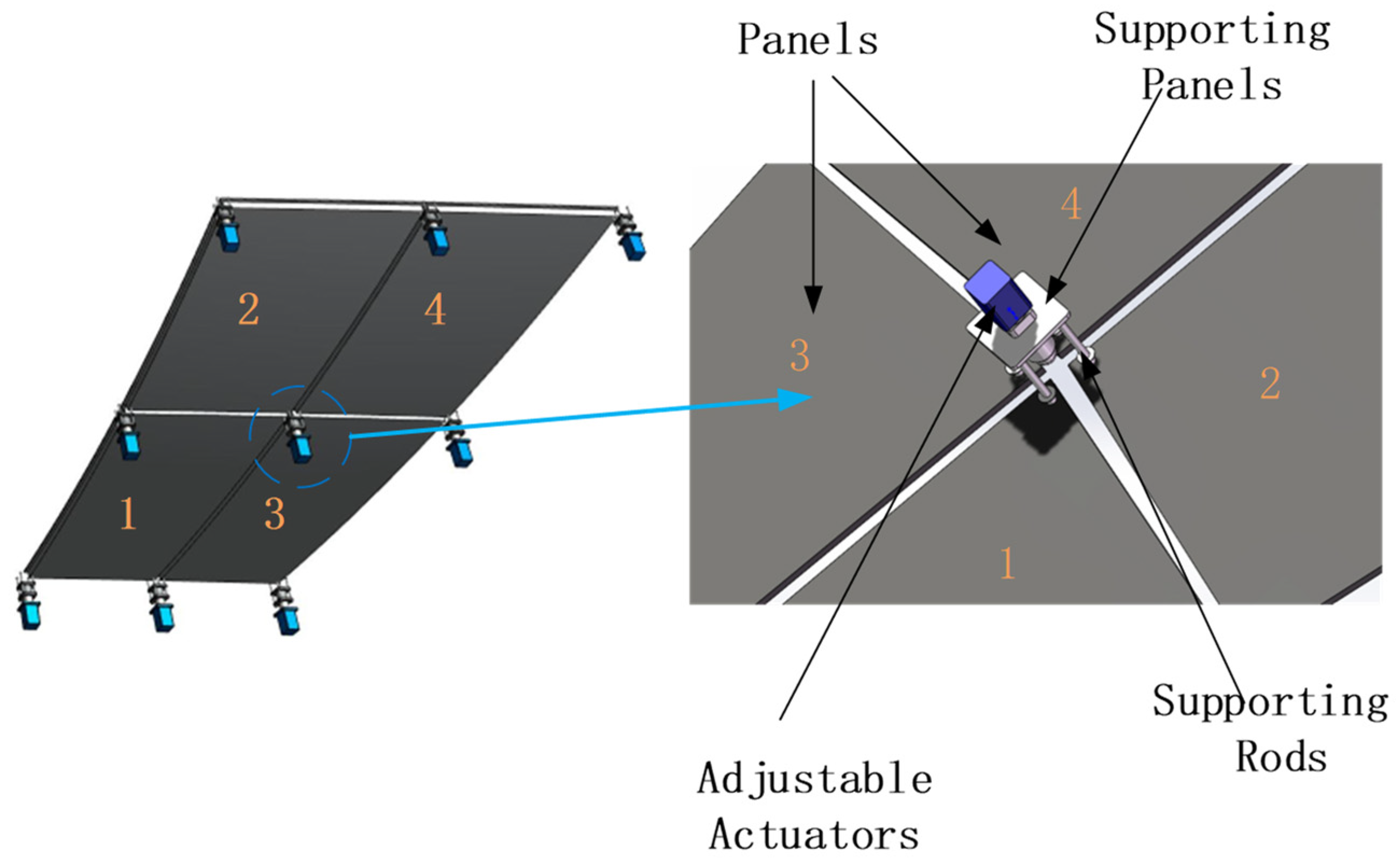
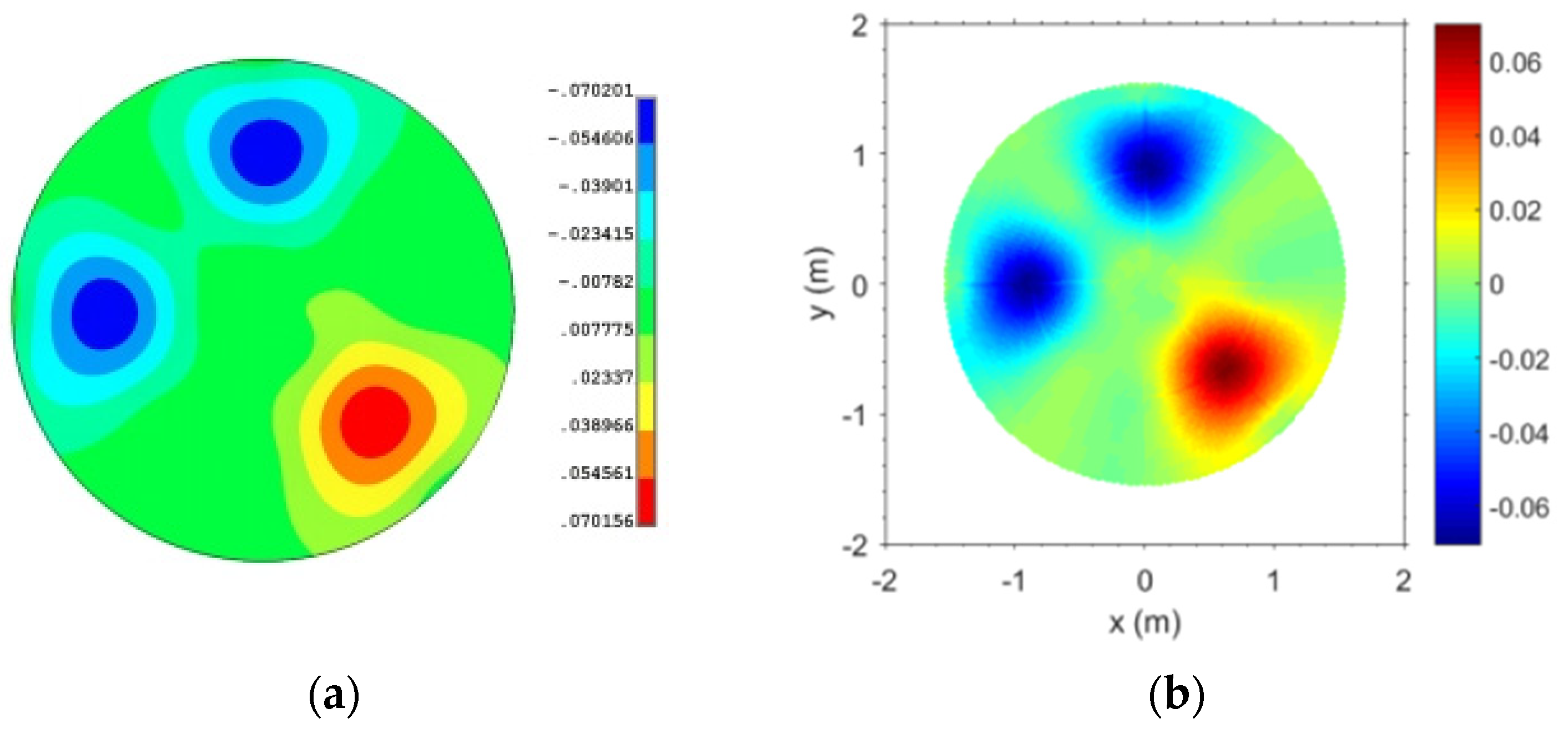
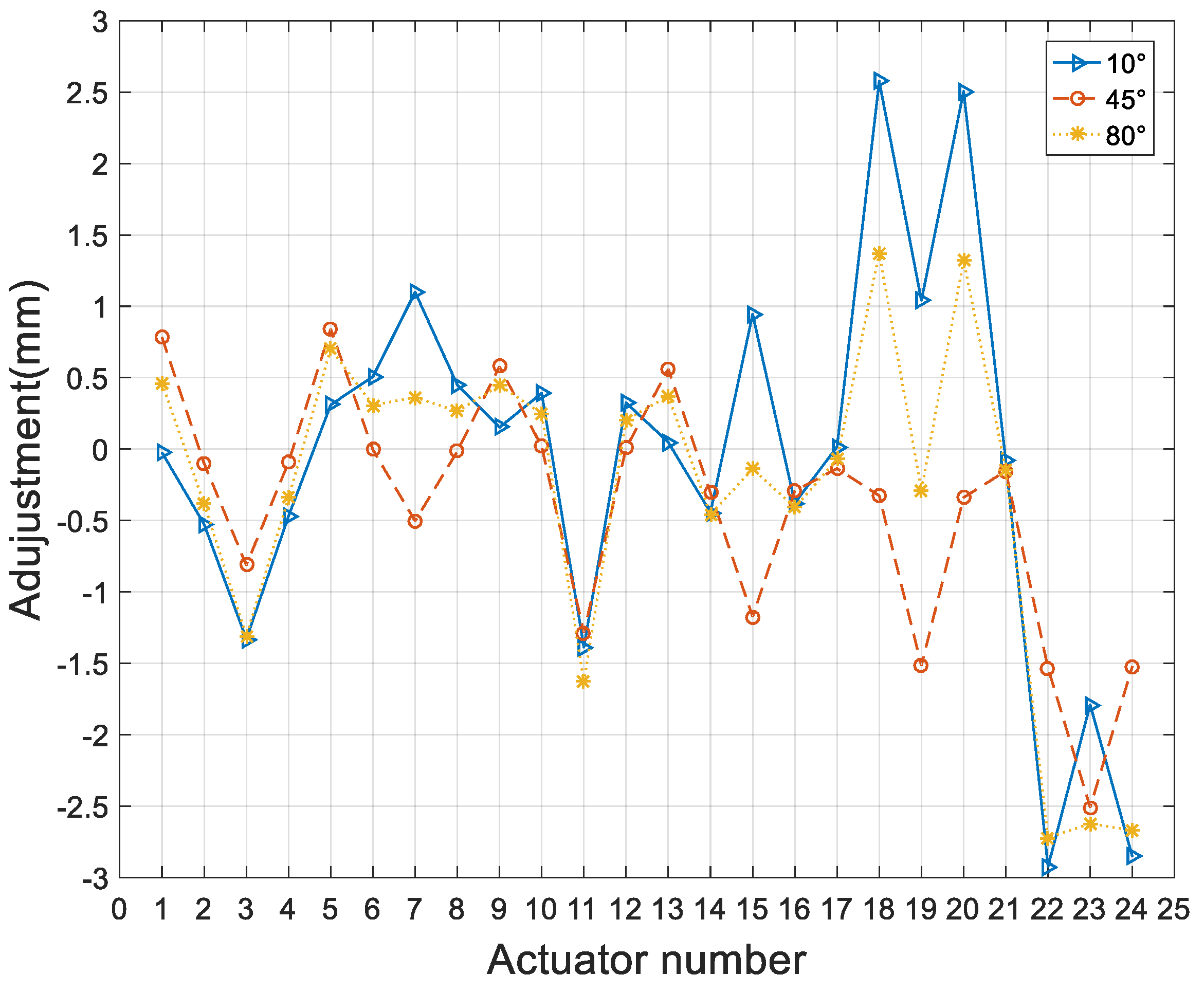
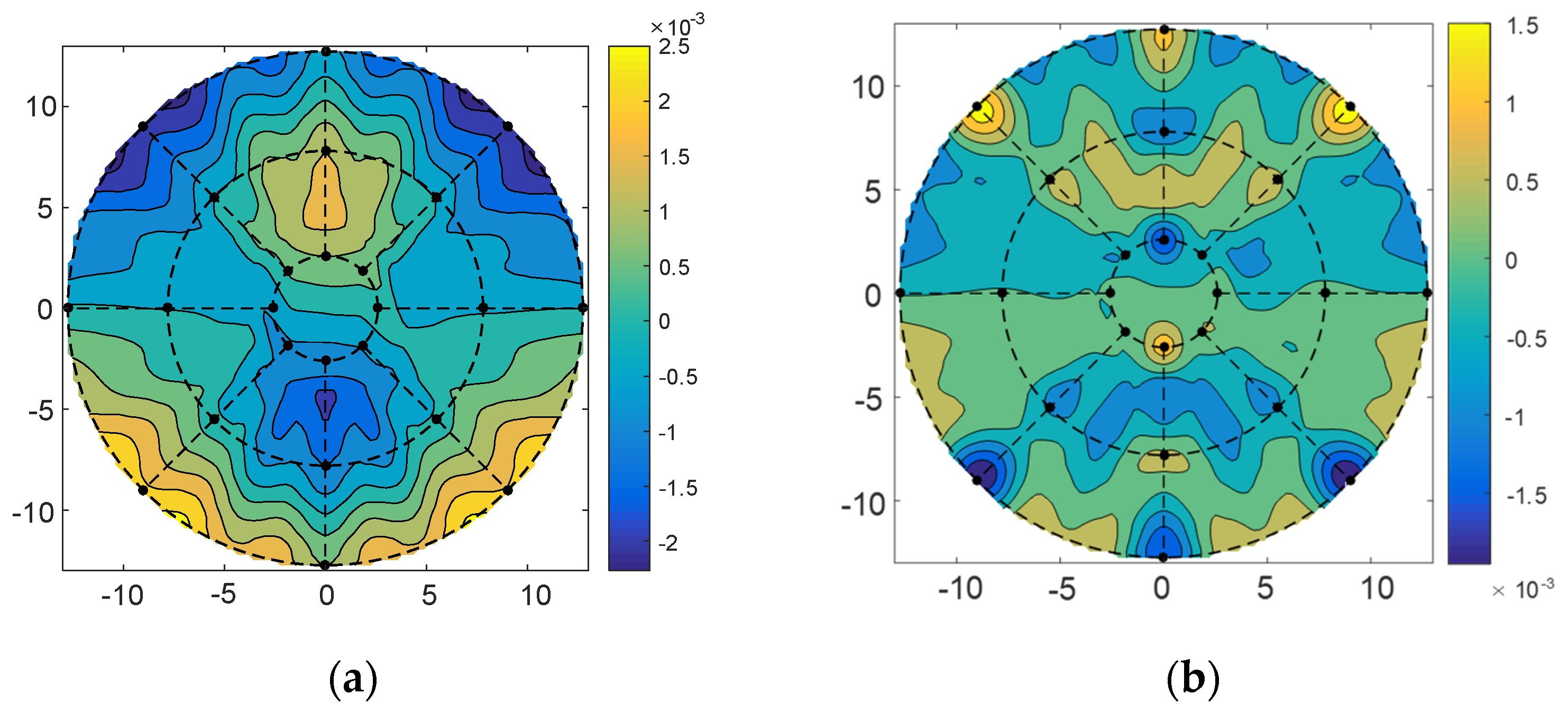
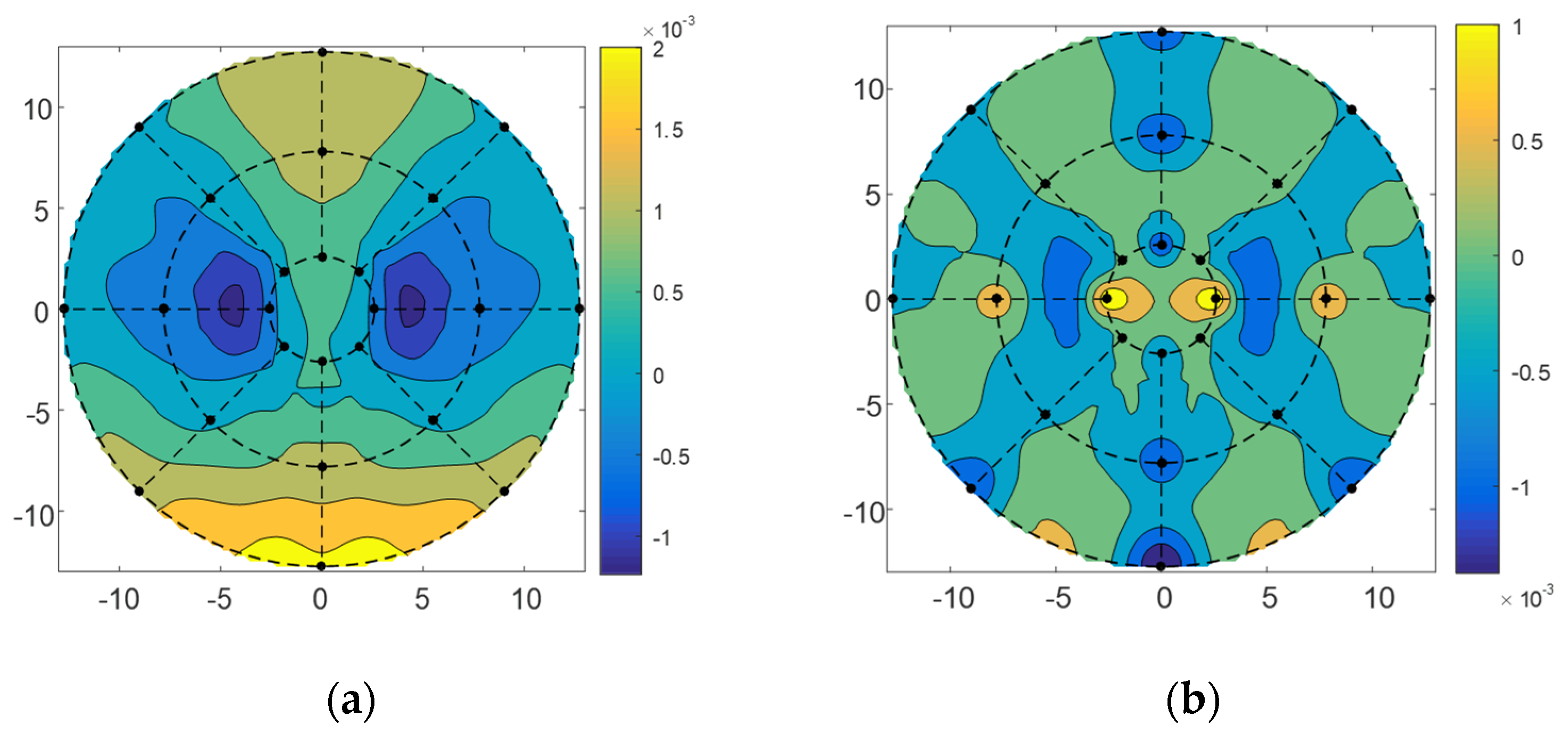
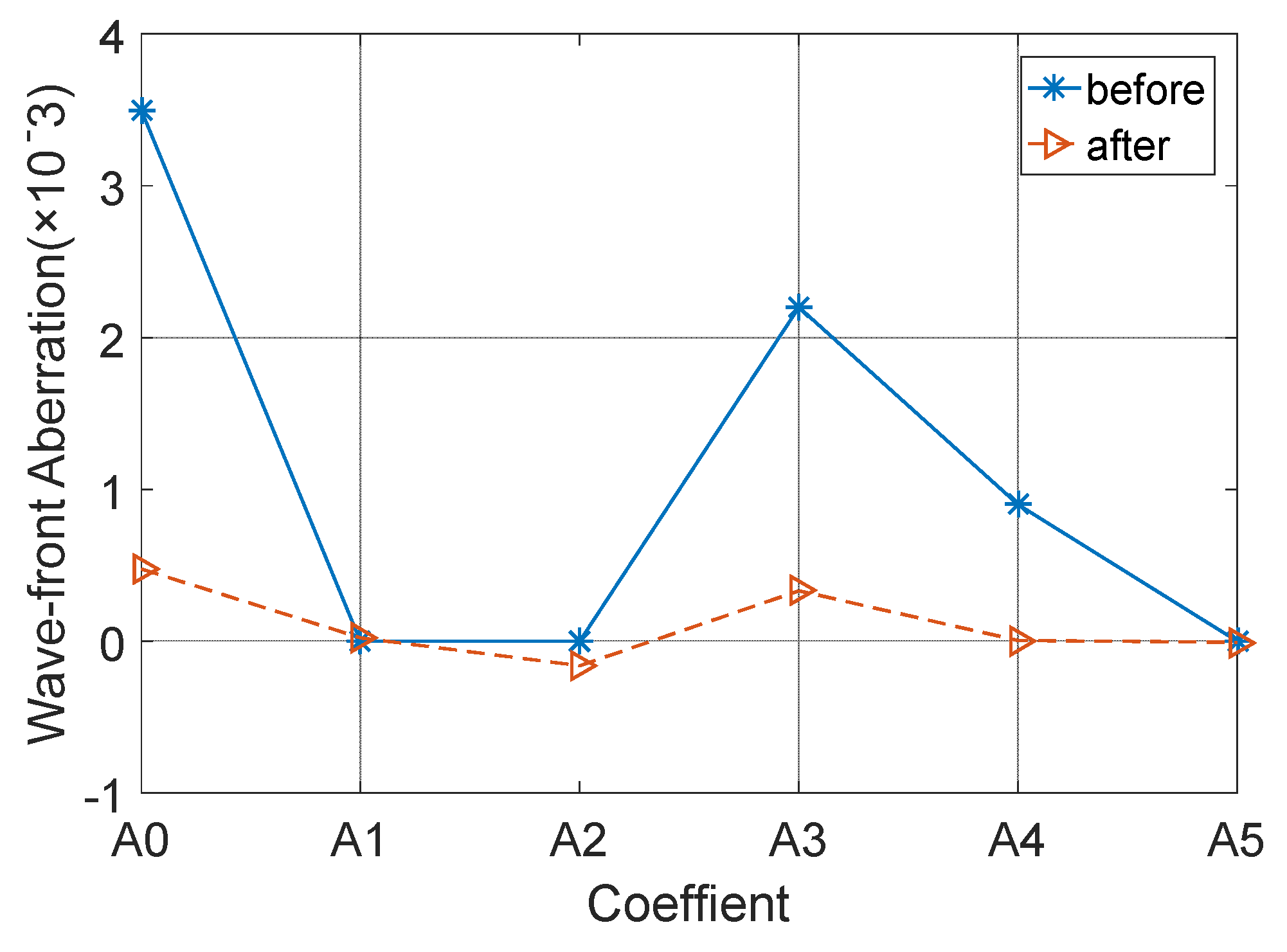
4. The Analysis and Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Xiang, B.B.; Wang, W.; Ban, Y.; Lin, S.M.; Wen, Z.G.; He, D.L.; Cai, M.H. Influence and Correction of Wavefront Primary Aberrations for Radio Telescopes using Aberration Theory. Res. Astron. Astrophys. 2023, 23, 189–198. [Google Scholar] [CrossRef]
- Theunissen, W.; Yoon, H.; Burnside, W.; Washington, G. Reconfigurable contour beam-reflector antenna synthesis using a mechanical finite-element description of the adjustable surface. IEEE Trans. Antennas Propag. 2001, 49, 272–279. [Google Scholar] [CrossRef]
- Zocchi, F.; Binda, P.; Viskum, H.H.; Klooster, K.v. A reconformable reflector for a sub-mm wave reflector antenna. In Proceedings of the IEEE Antennas and Propagation Society International Symposium, Columbus, OH, USA, 22–27 June 2003; Volume 2, pp. 377–380. [Google Scholar]
- Chen, X.D. Testing of a 9-points deformable mirror and its application in space camera system. Acta Opt. Sin. 2013, 33, 1519–1521. [Google Scholar]
- Wang, W.; Lian, P.; Zhang, S.; Xiang, B.B.; Xu, Q. Effect of Facet Displacement on Radiation Field and Its Application for Panel Adjustment of Large Reflector Antenna. Chin. J. Mech. Eng. 2017, 30, 578–586. [Google Scholar] [CrossRef]
- Li, W.; Tang, J.; Guo, Y.; Rao, C. Constrained least-squares algorithm for active optics correction of a primary mirror. Appl. Opt. 2022, 61, 108–114. [Google Scholar] [CrossRef] [PubMed]
- Li, H.Z.; Lin, X.D.; Liu, X.Y. Experiment system of 400 mm thin mirror active optics. Opt. Precis. Eng. 2009, 17, 2076–2083. [Google Scholar]
- Yu, Y.; Cao, G.R. A study on the corrective capability and optimization of active mirrors. Trans. Beijing Inst. Technol. 2003, 23, 229–233. [Google Scholar]
- Lin, X.D.; Chen, T.; Wang, J.L.; Wang, F.G. Active optics figure control of segmented mirror. Opt. Precis. Eng. 2009, 17, 98–103. [Google Scholar]
- Zhang, H.; Li, G.; Zhang, Y. Research on active surface based on angle feedback between adjacent reflector panels. Sci. Sin. Phys. Mech. Astron. 2019, 49, 099507. [Google Scholar] [CrossRef]
- Wang, W.; Duan, B.Y.; Li, P.; Song, L.W. Optimal Surface Adjustment by the Error-Transformation Matrix for a Segmented-Reflector Antenna. IEEE Antennas Propag. Mag. 2010, 52, 80–87. [Google Scholar] [CrossRef]
- Imbriale, W.A.; Rahmat-Samii, Y.; Rajagopalan, H.; Xu, S.H.; Jamnejad, V. Microelectromechanical Systems (MEMS) actuated wavefront correcting subreflector: Distortion compensation for large reflector antennas. In Proceedings of the 8th Annual NASA Earth Science Technology Conference (ESTC2008), College Park, MD, USA, 24–26 June 2008; Volume 127, pp. 277–281. [Google Scholar]
- Ahn, K.; Kihm, H. Moment actuator for correcting low-order aberrations of deformable mirrors. Opt. Lasers Eng. 2020, 126, 105864. [Google Scholar] [CrossRef]
- Peng, T.; Dai, C.; Lou, J.; Cui, Y.; Tao, B.; Ma, J. A low-cost deformable lens for correction of low-order aberrations. Opt. Commun. 2020, 460, 125209. [Google Scholar] [CrossRef]
- Hai, Z.; Clarricoats, P.; Monk, A. Experimental verification of an electronically controlled reconfigurable reflector antenna. Electron. Lett. 1991, 27, 64–65. [Google Scholar] [CrossRef]
- Wang, W.; Wang, C.S.; Li, P.; Song, L.W. Panel adjustment error of large reflector antennas considering electromechanical coupling. In Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Xi’an, China, 2–5 July 2008; Volume 2008, pp. 775–779. [Google Scholar]
- Wang, C.; Li, H.; Ying, K.; Xu, Q.; Wang, N.; Duan, B.; Gao, W.; Xiao, L.; Duan, Y. Active Surface Compensation for Large Radio Telescope Antennas. Int. J. Antennas Propag. 2018, 2018, 3903412. [Google Scholar] [CrossRef]
- Dell’accio, F.; Di Tommaso, F.; Hormann, K. On the approximation order of triangular Shepard interpolation. IMA J. Numer. Anal. 2016, 36, 359–379. [Google Scholar] [CrossRef]
- Yu, X.D.; Wu, Y.; He, L.M. Improvement and comparison of inverse distance weighted mesh interpolation algorithm. Chin. J. Eng. Geophys. 2013, 10, 900–904. [Google Scholar]

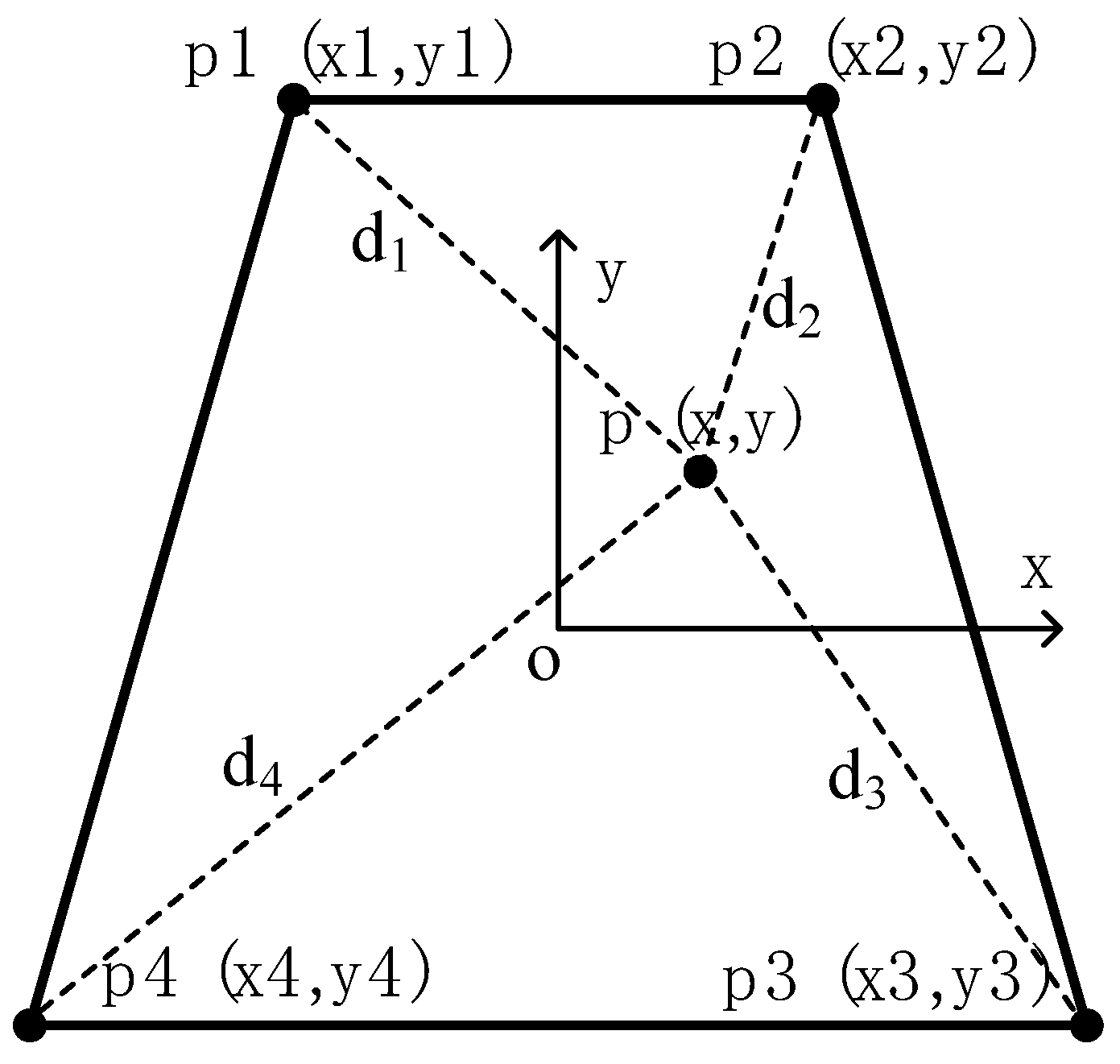



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiang, B.; Zheng, T.; Wang, W.; Lian, P.; Kazezkhan, G.; Zhou, J.; Li, K. Active Adjustment of the Subreflector Shape for the Large Dual-Reflector Antenna. Micromachines 2023, 14, 1893. https://doi.org/10.3390/mi14101893
Xiang B, Zheng T, Wang W, Lian P, Kazezkhan G, Zhou J, Li K. Active Adjustment of the Subreflector Shape for the Large Dual-Reflector Antenna. Micromachines. 2023; 14(10):1893. https://doi.org/10.3390/mi14101893
Chicago/Turabian StyleXiang, Binbin, Tianxiang Zheng, Wei Wang, Peiyuan Lian, Guljaina Kazezkhan, Jianping Zhou, and Kai Li. 2023. "Active Adjustment of the Subreflector Shape for the Large Dual-Reflector Antenna" Micromachines 14, no. 10: 1893. https://doi.org/10.3390/mi14101893
APA StyleXiang, B., Zheng, T., Wang, W., Lian, P., Kazezkhan, G., Zhou, J., & Li, K. (2023). Active Adjustment of the Subreflector Shape for the Large Dual-Reflector Antenna. Micromachines, 14(10), 1893. https://doi.org/10.3390/mi14101893






