Numerical Study of Gas Flow in Super Nanoporous Materials Using the Direct Simulation Monte-Carlo Method
Abstract
1. Introduction
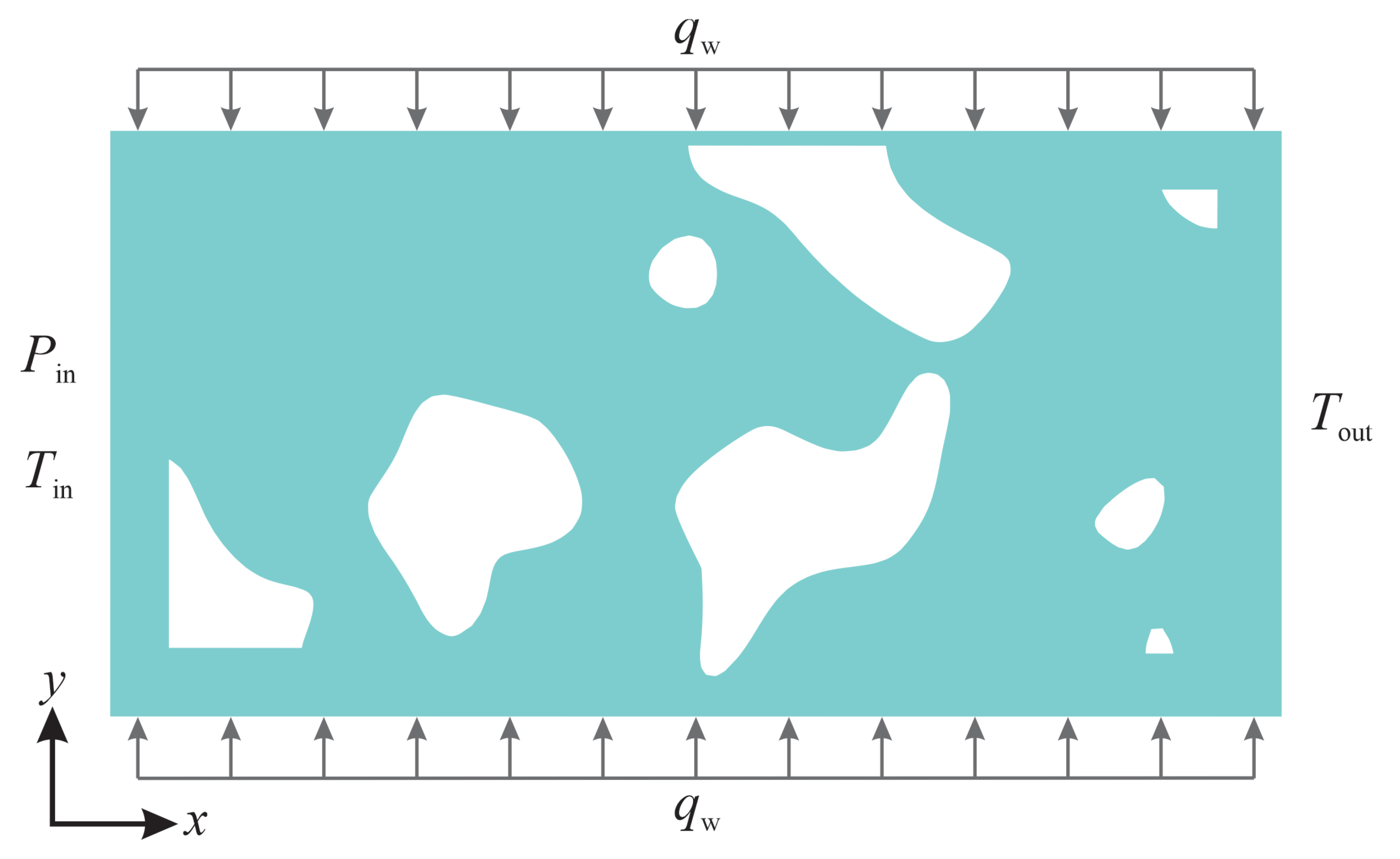
2. Methods
3. Results and Discussion
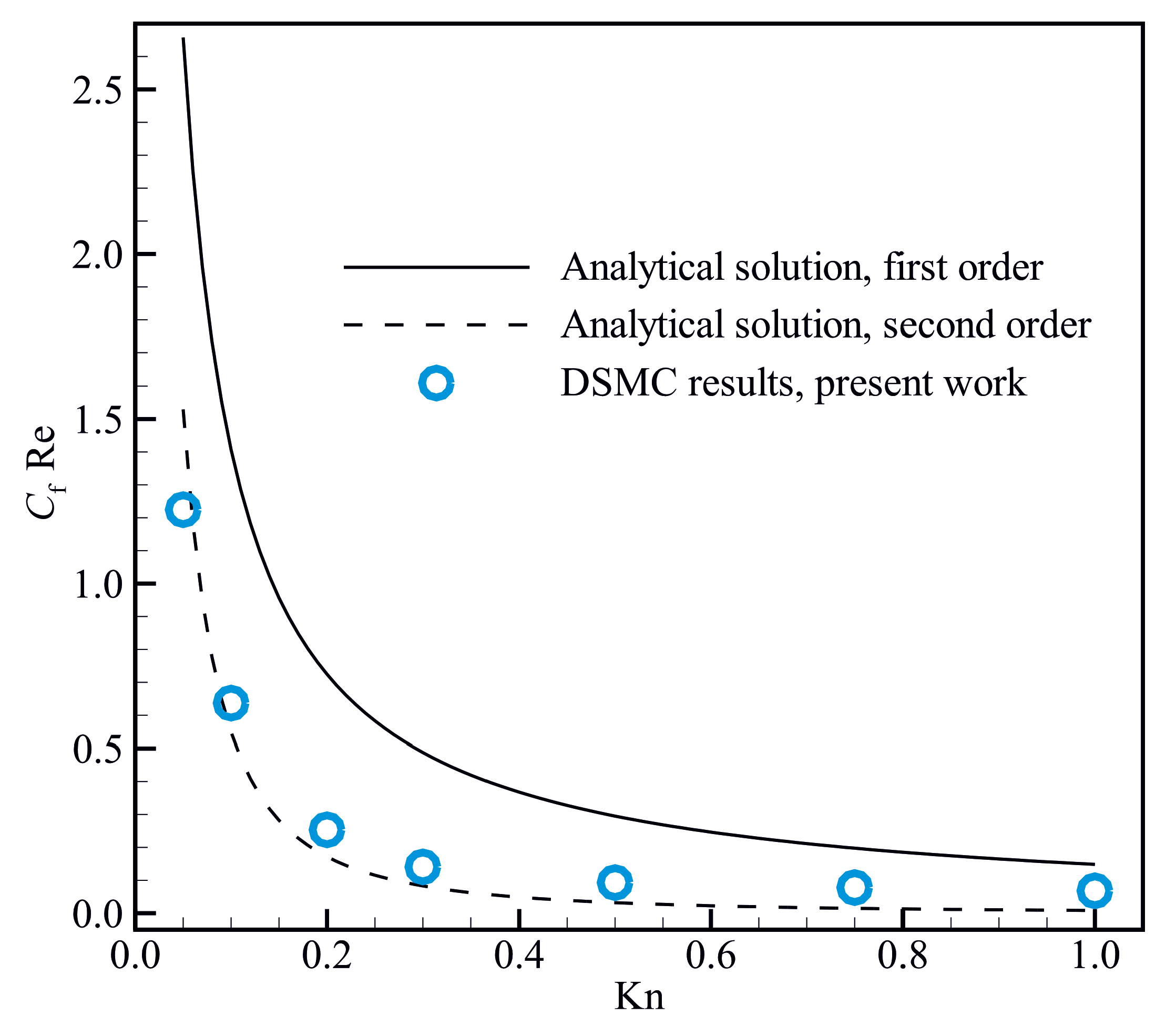
3.1. Model Validation
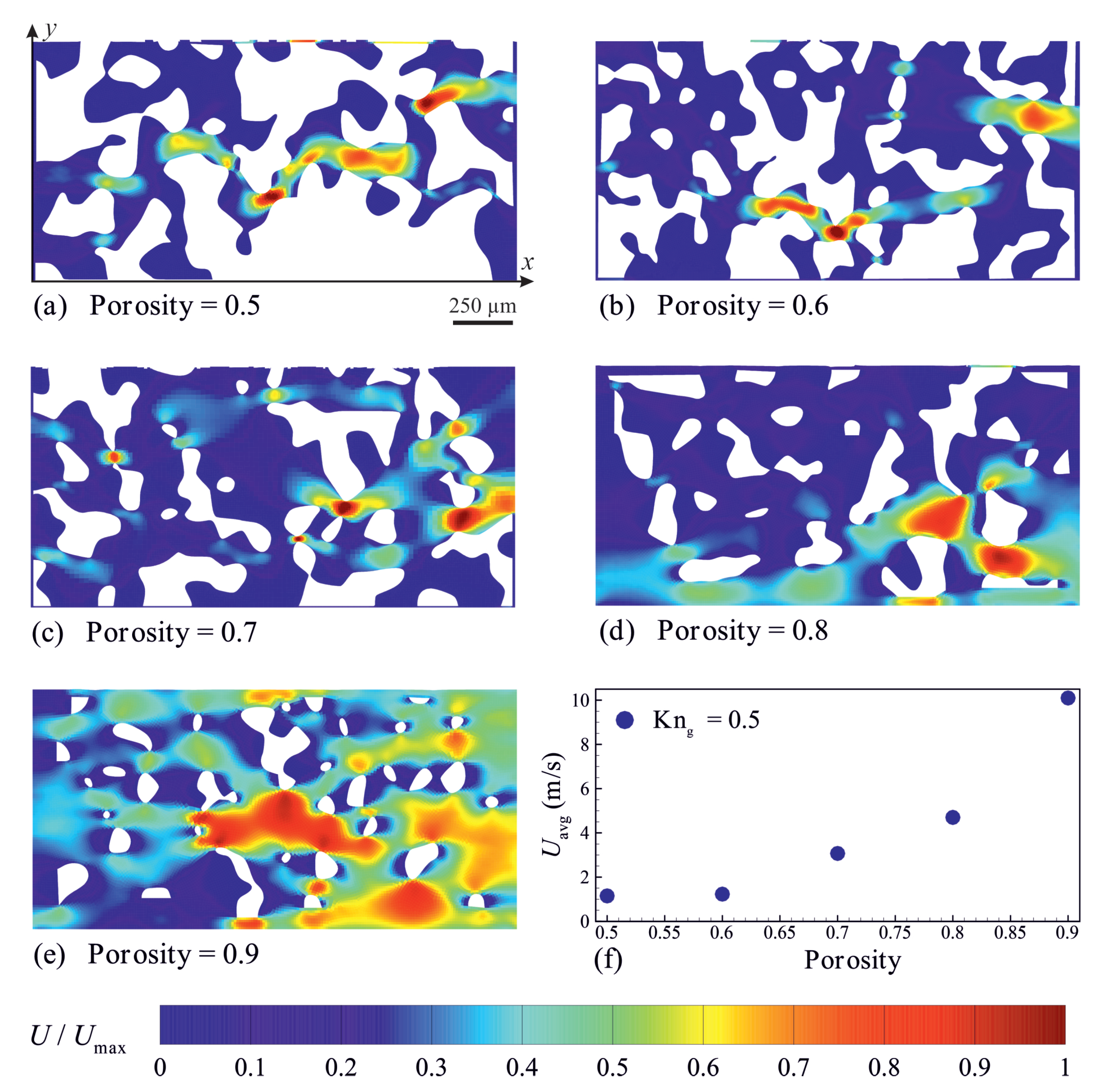
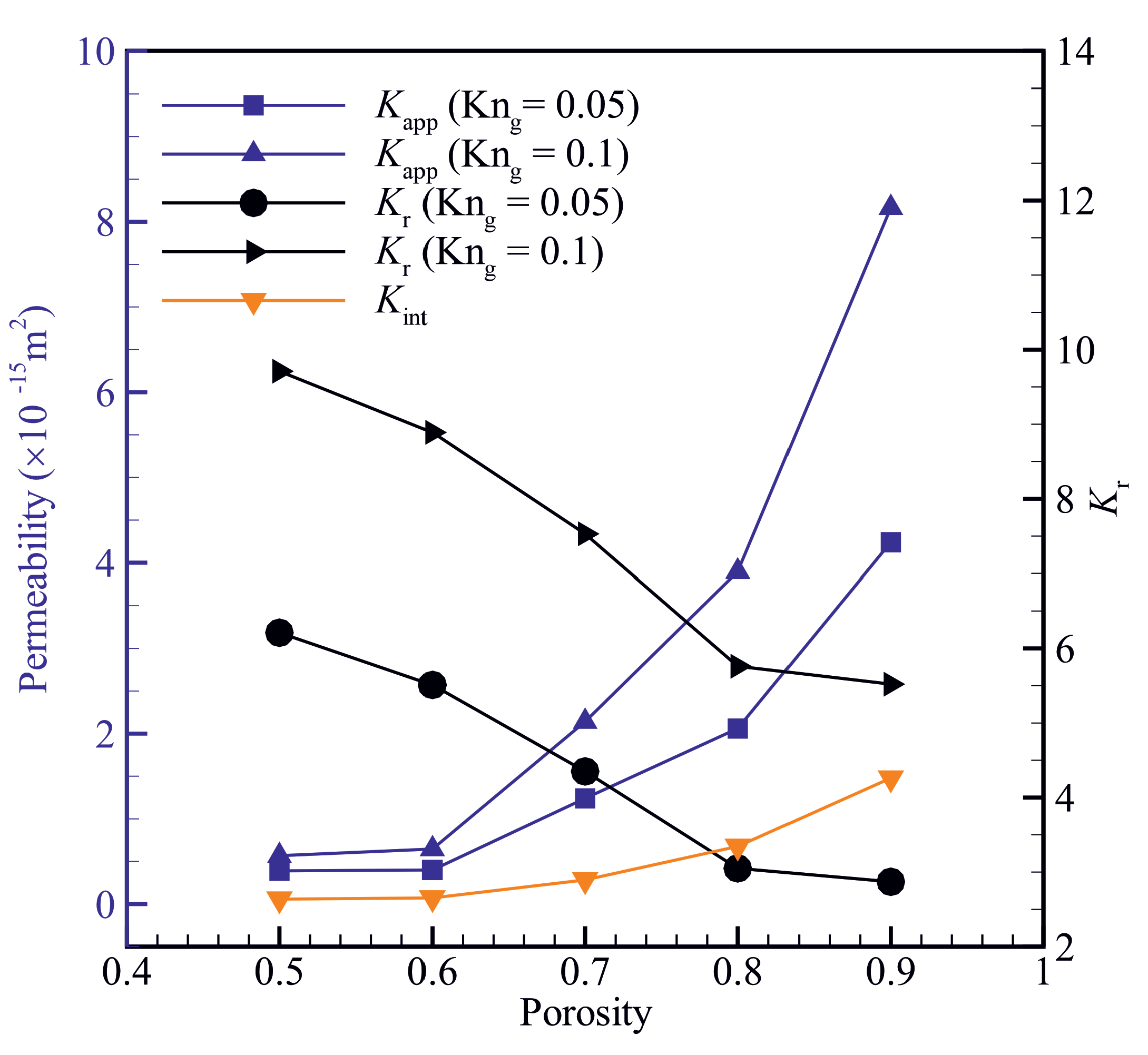
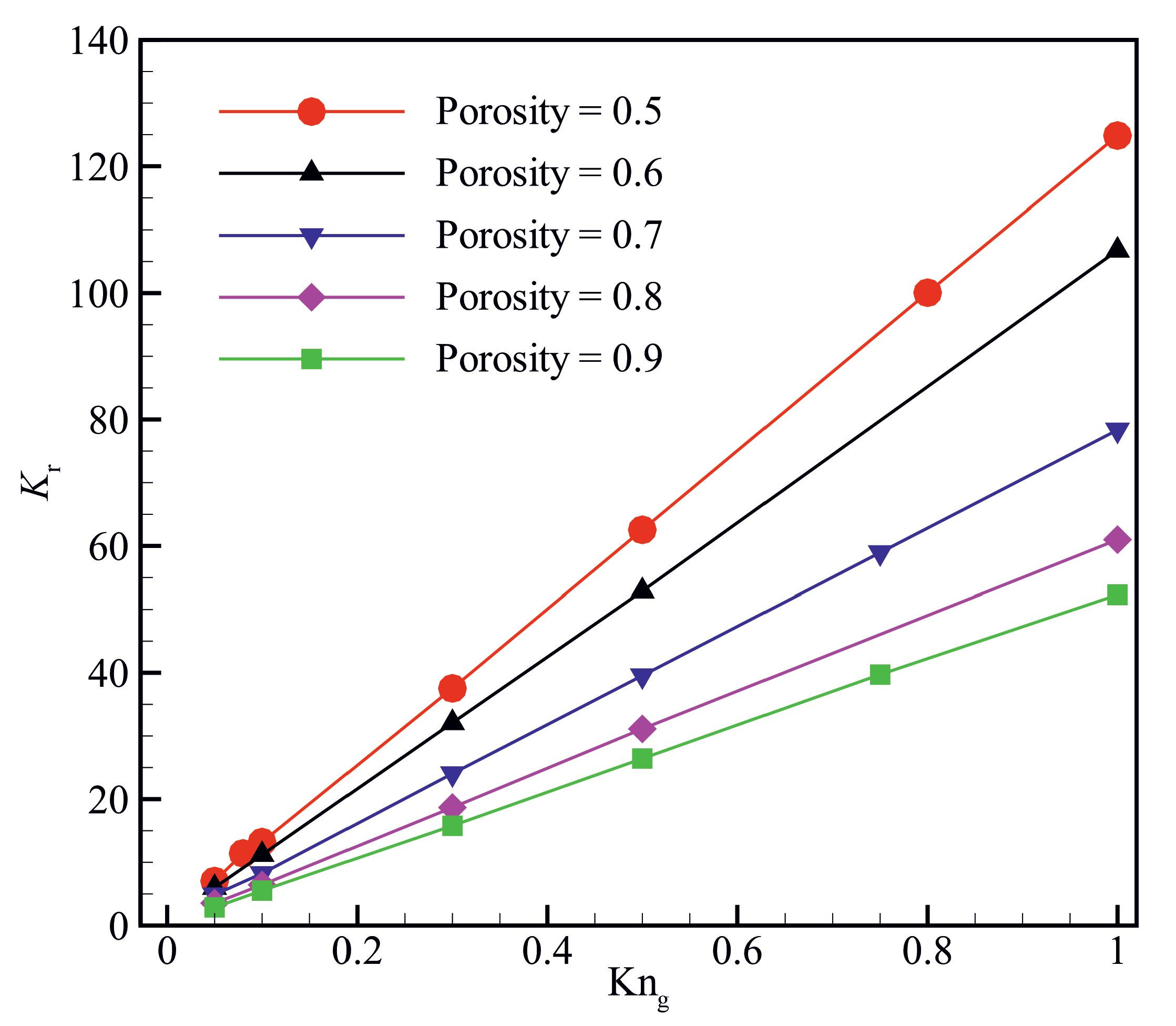
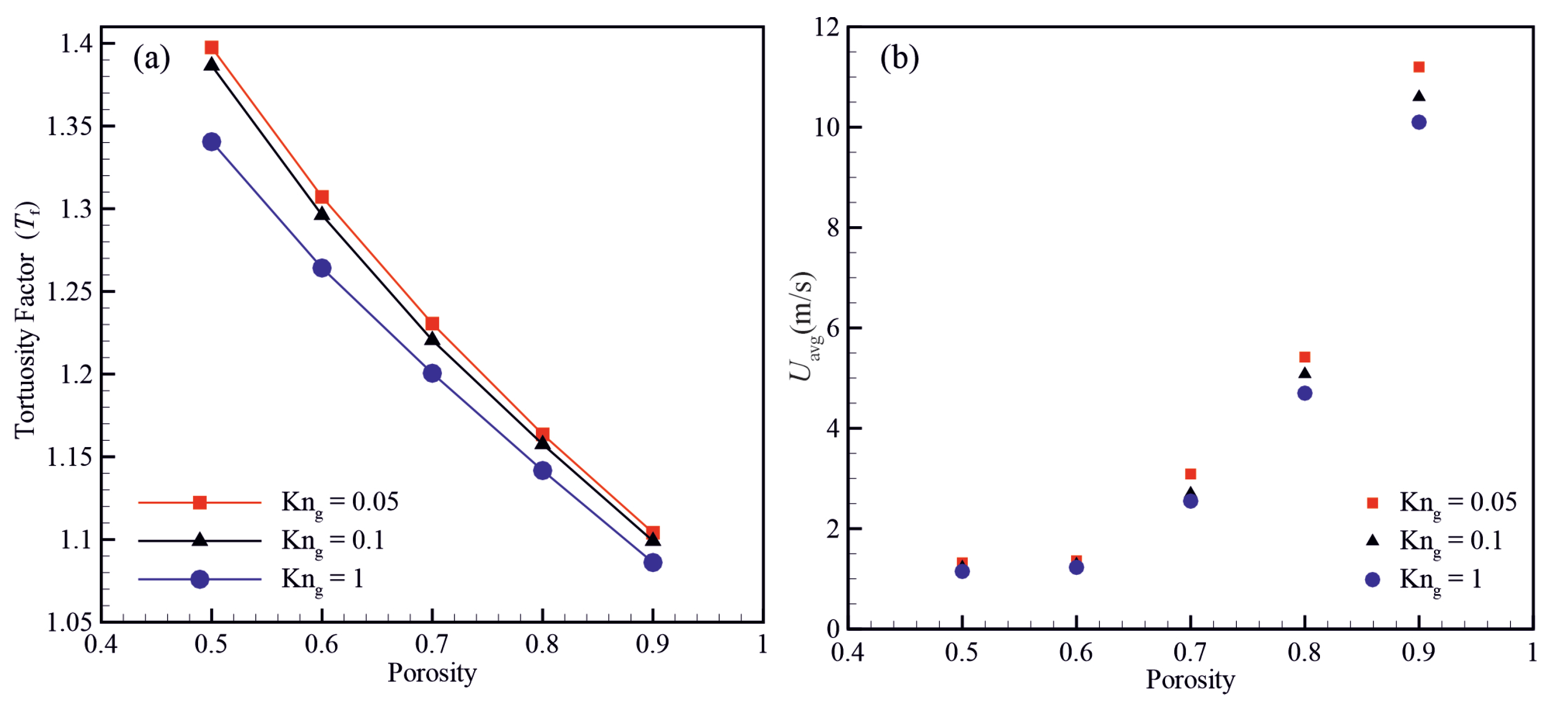
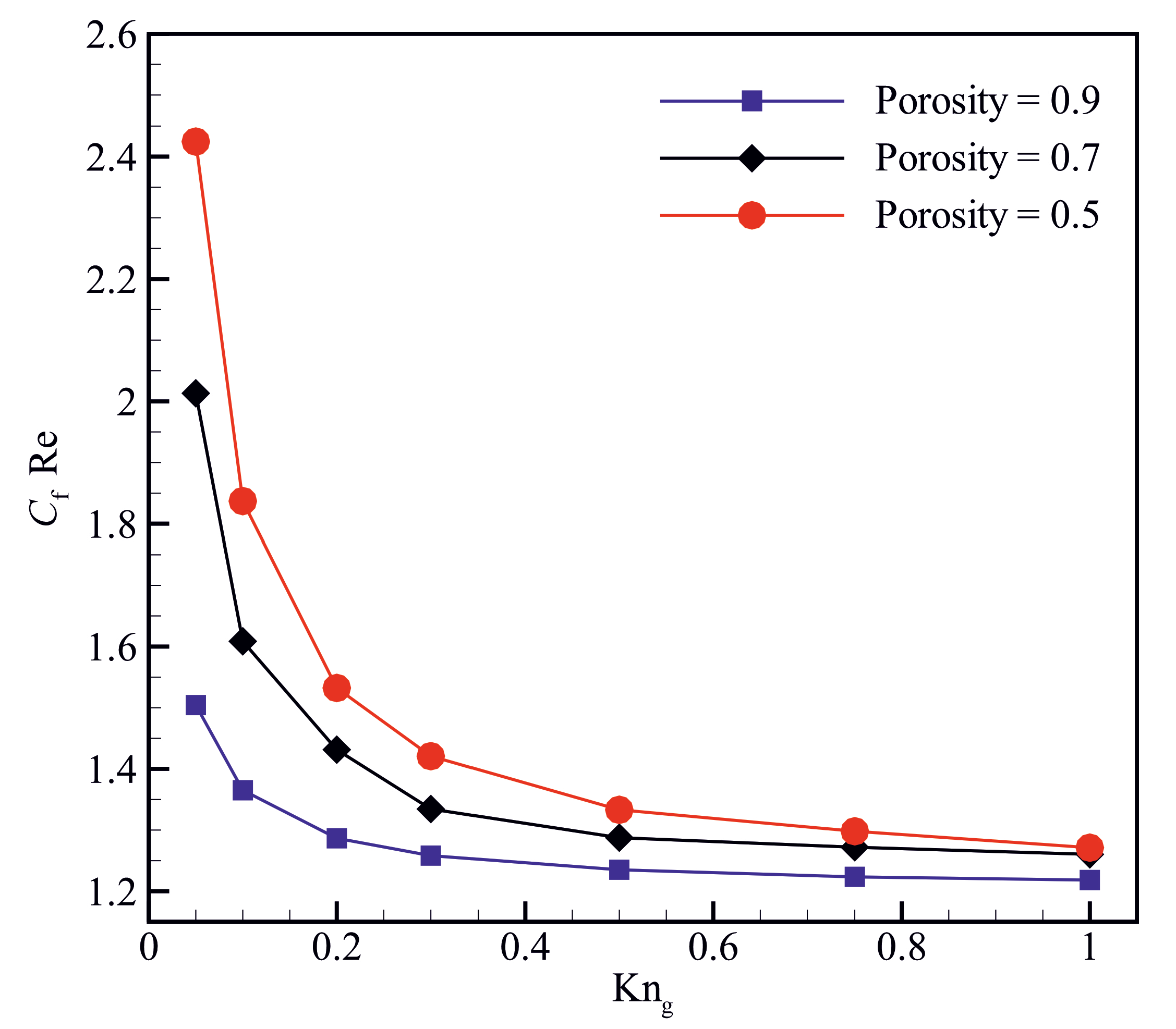
3.2. The Effects of Material Porosity on the Gas Flow Behaviour
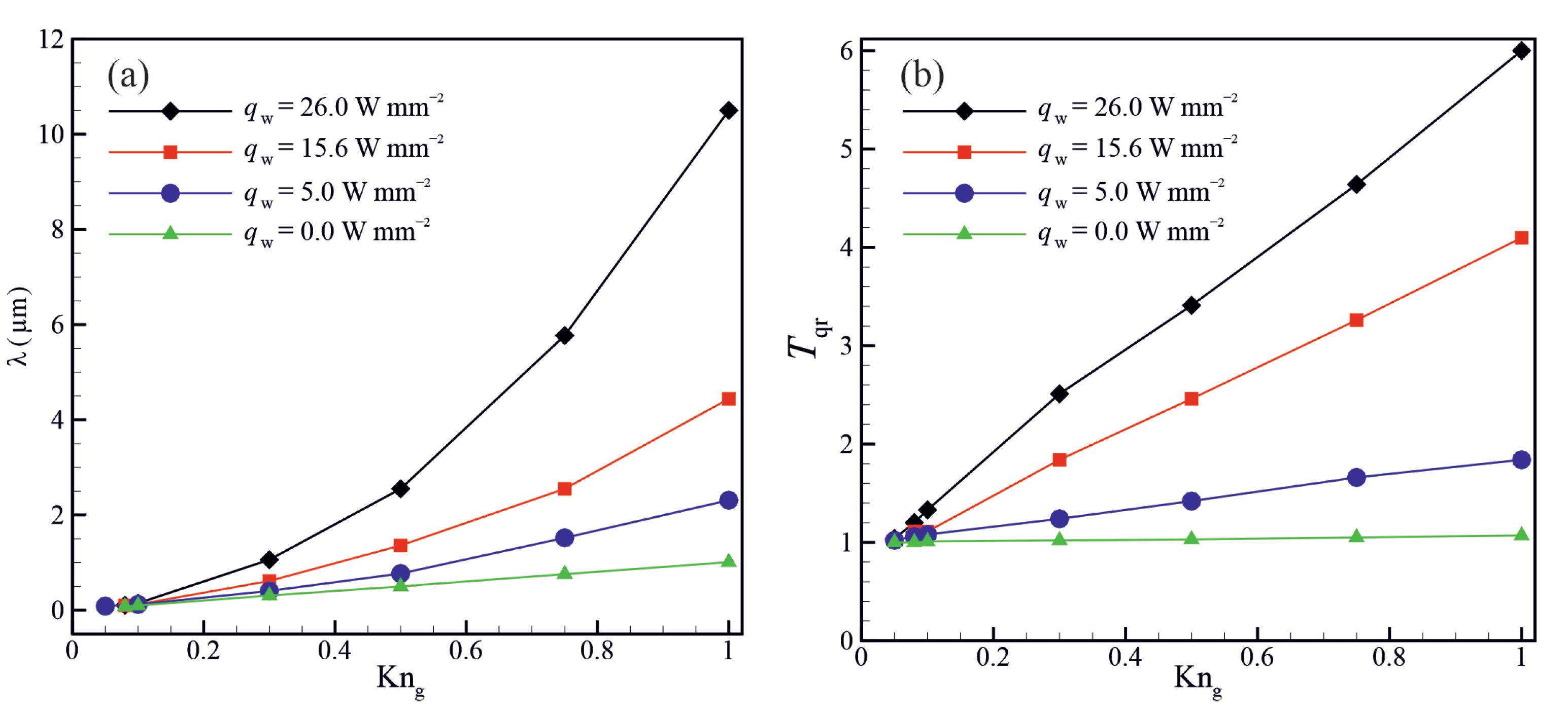
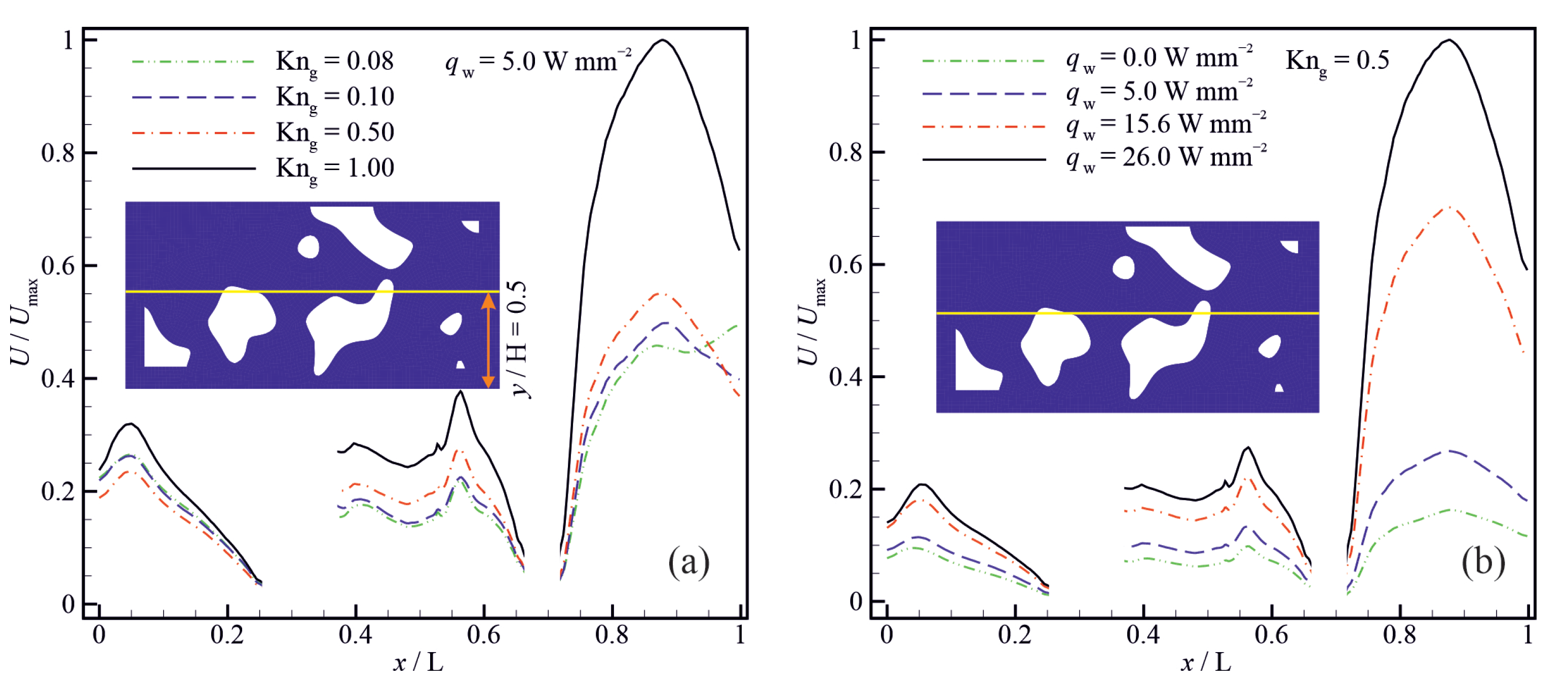
3.3. The Effects of Wall Heat-Flux on the Flow Behaviour
4. Conclusions
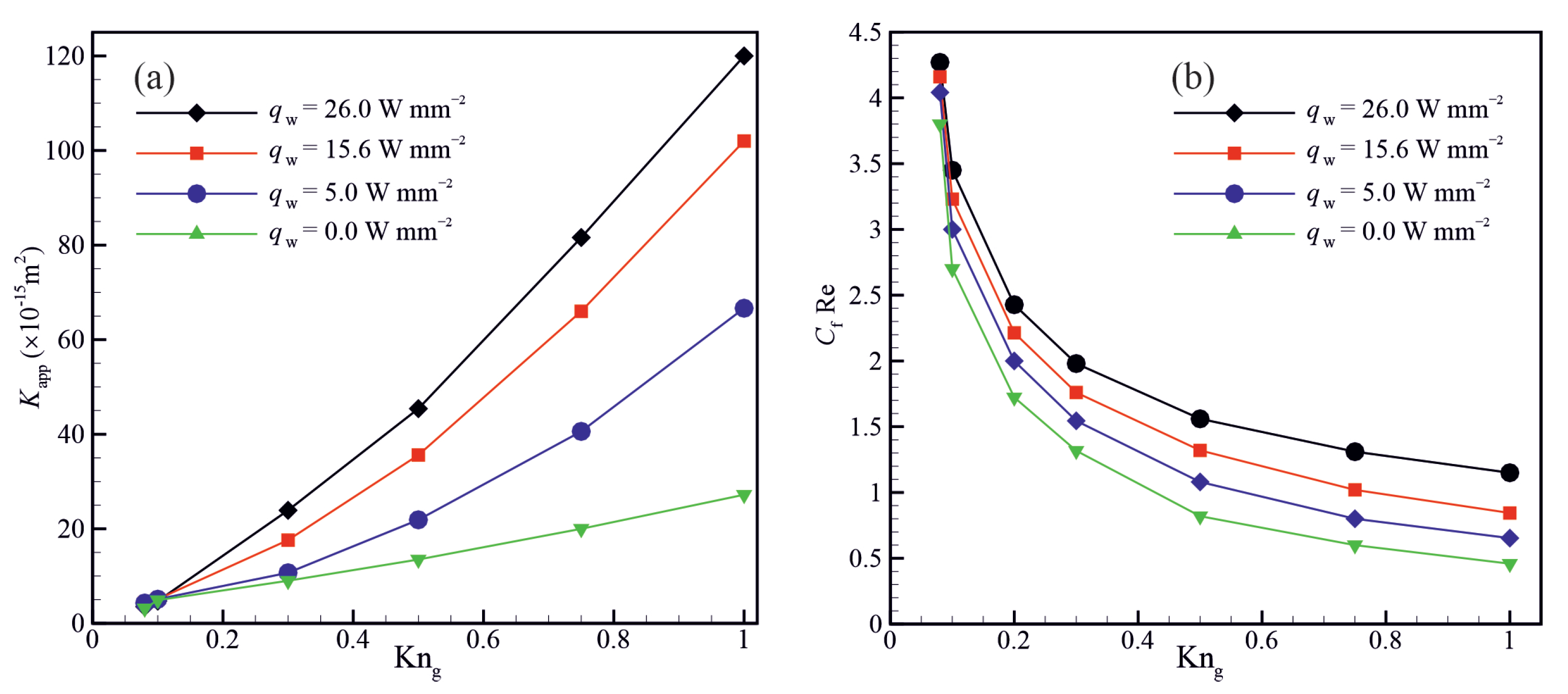
- The ratio of apparent to intrinsic permeability, hydraulic tortuosity, and skin friction factor increase with decreasing the material porosity.
- The hydraulic tortuosity and skin friction factor decrease with increasing the Knudsen number, leading to an increase in the apparent permeability.
- The skin friction factor and apparent permeability increase with increasing the wall heat flux at a specific Knudsen number.
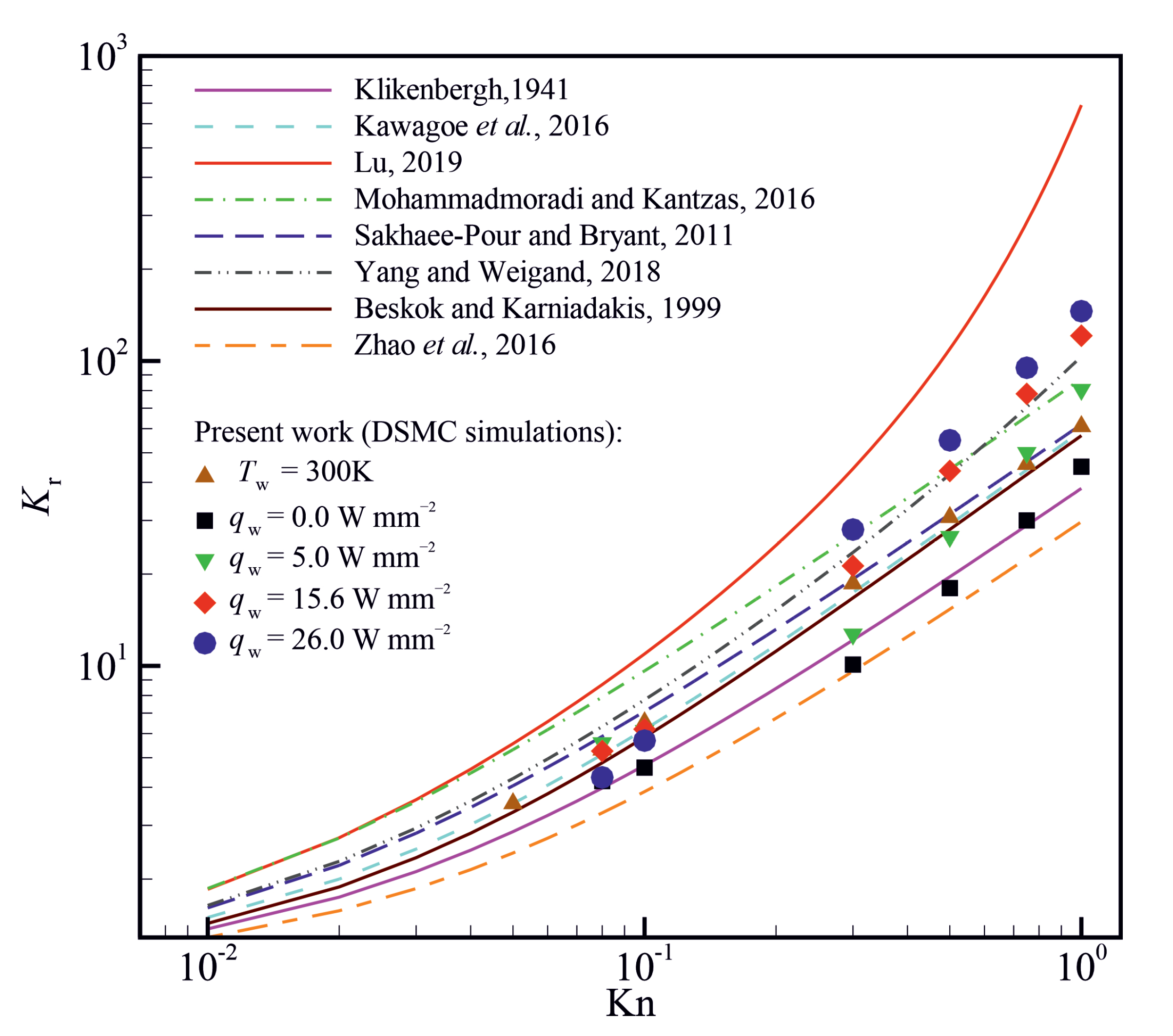
- When the outer boundaries of the porous material are subjected to a constant wall temperature boundary condition, the permeability values approximated using the model proposed by Kawagoe et al. [51] agree with DSMC results for a wide range of Knudsen numbers varying between and 1. However, the model of Kawagoe et al. [51] fails to approximate the value of the permeability ratio when a constant heat flux is applied on the outer boundaries of the porous material.
- Further investigations are required to improve the accuracy of models in approximating permeability in porous materials subject to a wall heat flux boundary condition.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mays, T.J. A new classification of pore sizes. In Studies in Surface Science and Catalysis; Elsevier: Amsterdam, The Netherlands, 2007; pp. 57–62. [Google Scholar] [CrossRef]
- Kärger, J. Transport Phenomena in Nanoporous Materials. ChemPhysChem 2014, 16, 24–51. [Google Scholar] [CrossRef]
- Shariati, V.; Ahmadian, M.H.; Roohi, E. Direct Simulation Monte Carlo investigation of fluid characteristics and gas transport in porous microchannels. Sci. Rep. 2019, 9, 17183. [Google Scholar] [CrossRef]
- Strizhenov, E.M.; Chugaev, S.S.; Men’shchikov, I.E.; Shkolin, A.V.; Zherdev, A.A. Heat and Mass Transfer in an Adsorbed Natural Gas Storage System Filled with Monolithic Carbon Adsorbent during Circulating Gas Charging. Nanomaterials 2021, 11, 3274. [Google Scholar] [CrossRef]
- Kalarakis, A.N.; Michalis, V.K.; Skouras, E.D.; Burganos, V.N. Mesoscopic Simulation of Rarefied Flow in Narrow Channels and Porous Media. Transp. Porous Media 2012, 94, 385–398. [Google Scholar] [CrossRef]
- Mohammadmoradi, P.; Kantzas, A. Pore-scale permeability calculation using CFD and DSMC techniques. J. Pet. Sci. Eng. 2016, 146, 515–525. [Google Scholar] [CrossRef]
- Zhao, J.; Yao, J.; Zhang, M.; Zhang, L.; Yang, Y.; Sun, H.; An, S.; Li, A. Study of Gas Flow Characteristics in Tight Porous Media with a Microscale Lattice Boltzmann Model. Sci. Rep. 2016, 6, 32393. [Google Scholar] [CrossRef]
- Borner, A.; Panerai, F.; Mansour, N.N. High temperature permeability of fibrous materials using direct simulation Monte Carlo. Int. J. Heat Mass Transf. 2017, 106, 1318–1326. [Google Scholar] [CrossRef]
- Gu, Q.; Ho, M.T.; Zhang, Y. Computational methods for pore-scale simulation of rarefied gas flow. Comput. Fluids 2021, 222, 104932. [Google Scholar] [CrossRef]
- Lai, B.; Wang, Z.; Wang, H.; Bai, J.; Li, W.; Ming, P. Prediction of the permeability of fibrous porous structures under the full flow regimes. Phys. Fluids 2022, 34, 082117. [Google Scholar] [CrossRef]
- Monteiro, P.J.M.; Rycroft, C.H.; Barenblatt, G.I. A mathematical model of fluid and gas flow in nanoporous media. Proc. Natl. Acad. Sci. USA 2012, 109, 20309–20313. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Roohi, E. Flow and thermal fields investigation in divergent micro/Nano channels. J. Therm. Eng. 2016, 2, 709–714. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Roohi, E. DSMC investigation of rarefied gas flow through diverging micro- and nanochannels. Microfluid. Nanofluid. 2017, 21, 18. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Shahabi, V.; Roohi, E. Pressure-Driven Nitrogen Flow in Divergent Microchannels with Isothermal Walls. Appl. Sci. 2021, 11, 3602. [Google Scholar] [CrossRef]
- Sone, Y. (Ed.) Molecular Gas Dynamics; Birkhäuser: Boston, MA, USA, 2007. [Google Scholar] [CrossRef]
- Song, W.; Liu, H.; Wang, W.; Zhao, J.; Sun, H.; Wang, D.; Li, Y.; Yao, J. Gas flow regimes judgement in nanoporous media by digital core analysis. Open Phys. 2018, 16, 448–462. [Google Scholar] [CrossRef]
- Kazmouz, S.J.; Giusti, A.; Mastorakos, E. Numerical simulation of shale gas flow in three-dimensional fractured porous media. J. Unconv. Oil Gas Resour. 2016, 16, 90–112. [Google Scholar] [CrossRef]
- Javadpour, F.; Singh, H.; Rabbani, A.; Babaei, M.; Enayati, S. Gas Flow Models of Shale: A Review. Energy Fuels 2021, 35, 2999–3010. [Google Scholar] [CrossRef]
- Ahmadian, M.H.; Roohi, E.; Teymourtash, A.; Stefanov, S. A dusty gas model-direct simulation Monte Carlo algorithm to simulate flow in micro-porous media. Phys. Fluids 2019, 31, 062007. [Google Scholar] [CrossRef]
- Bird, G.A. Molecular Gas Dynamics and the Direct Simulation of Gas Flows; Clarendon Press: Oxford, UK, 1994. [Google Scholar]
- Klinkenberg, L.J. The permeability of porous media to liquids and gases. Am. Petrol. Inst. Drill. Prod. Pract. 1941, 2, 200–213. [Google Scholar] [CrossRef]
- Ghassemi, A.; Pak, A. Pore scale study of permeability and tortuosity for flow through particulate media using Lattice Boltzmann method. Int. J. Numer. Anal. Methods Geomech. 2011, 35, 886–901. [Google Scholar] [CrossRef]
- Wang, J.; Chen, L.; Kang, Q.; Rahman, S.S. Apparent permeability prediction of organic shale with generalized lattice Boltzmann model considering surface diffusion effect. Fuel 2016, 181, 478–490. [Google Scholar] [CrossRef]
- Ziarani, A.S.; Aguilera, R. Knudsen’s Permeability Correction for Tight Porous Media. Transp. Porous Media 2011, 91, 239–260. [Google Scholar] [CrossRef]
- Ma, J.; Sanchez, J.P.; Wu, K.; Couples, G.D.; Jiang, Z. A pore network model for simulating non-ideal gas flow in micro- and nano-porous materials. Fuel 2014, 116, 498–508. [Google Scholar] [CrossRef]
- Hooman, K.; Tamayol, A.; Dahari, M.; Safaei, M.R.; Togun, H.; Sadri, R. A theoretical model to predict gas permeability for slip flow through a porous medium. Appl. Therm. Eng. 2014, 70, 71–76. [Google Scholar] [CrossRef]
- Lv, Q.; Wang, E.; Liu, X.; Wang, S. Determining the intrinsic permeability of tight porous media based on bivelocity hydrodynetics. Microfluid. Nanofluid. 2014, 16, 841–848. [Google Scholar] [CrossRef]
- Yuan, Y.; Doonechaly, N.G.; Rahman, S. An Analytical Model of Apparent Gas Permeability for Tight Porous Media. Transp. Porous Media 2015, 111, 193–214. [Google Scholar] [CrossRef]
- Wu, L.; Ho, M.T.; Germanou, L.; Gu, X.J.; Liu, C.; Xu, K.; Zhang, Y. On the apparent permeability of porous media in rarefied gas flows. J. Fluid Mech. 2017, 822, 398–417. [Google Scholar] [CrossRef]
- Wang, S.; Shi, J.; Wang, K.; Sun, Z.; Miao, Y.; Hou, C. Apparent permeability model for gas transport in shale reservoirs with nano-scale porous media. J. Nat. Gas Sci. Eng. 2018, 55, 508–519. [Google Scholar] [CrossRef]
- Wang, F.; Jiao, L.; Lian, P.; Zeng, J. Apparent gas permeability, intrinsic permeability and liquid permeability of fractal porous media: Carbonate rock study with experiments and mathematical modelling. J. Pet. Sci. Eng. 2019, 173, 1304–1315. [Google Scholar] [CrossRef]
- Sabet, S.; Barisik, M.; Mobedi, M.; Beskok, A. An extended Kozeny-Carman-Klinkenberg model for gas permeability in micro/nano-porous media. Phys. Fluids 2019, 31, 112001. [Google Scholar] [CrossRef]
- Wang, M.; Pan, N. Numerical analyses of effective dielectric constant of multiphase microporous media. J. Appl. Phys. 2007, 101, 114102. [Google Scholar] [CrossRef]
- Pant, L.M.; Huang, H.; Secanell, M.; Larter, S.; Mitra, S.K. Multi scale characterization of coal structure for mass transport. Fuel 2015, 159, 315–323. [Google Scholar] [CrossRef]
- Yu, H.; Chen, J.; Zhu, Y.; Wang, F.; Wu, H. Multiscale transport mechanism of shale gas in micro/nano-pores. Int. J. Heat Mass Transf. 2017, 111, 1172–1180. [Google Scholar] [CrossRef]
- Tian, J.; Qi, C.; Sun, Y.; Yaseen, Z.M.; Pham, B.T. Permeability prediction of porous media using a combination of computational fluid dynamics and hybrid machine learning methods. Eng. Comput. 2020, 37, 3455–3471. [Google Scholar] [CrossRef]
- Gostick, J.; Khan, Z.; Tranter, T.; Kok, M.; Agnaou, M.; Sadeghi, M.; Jervis, R. PoreSpy: A Python Toolkit for Quantitative Analysis of Porous Media Images. J. Open Source Softw. 2019, 4, 1296. [Google Scholar] [CrossRef]
- Qin, C.Z.; van Brummelen, H.; Hefny, M.; Zhao, J. Image-based modeling of spontaneous imbibition in porous media by a dynamic pore network model. Adv. Water Resour. 2021, 152, 103932. [Google Scholar] [CrossRef]
- Wieland, R.; Ukawa, C.; Joschko, M.; Krolczyk, A.; Fritsch, G.; Hildebrandt, T.B.; Schmidt, O.; Filser, J.; Jimenez, J.J. Use of deep learning for structural analysis of computer tomography images of soil samples. R. Soc. Open Sci. 2021, 8, 201275. [Google Scholar] [CrossRef]
- Zhao, J.; Yao, J.; Li, A.; Zhang, M.; Zhang, L.; Yang, Y.; Sun, H. Simulation of microscale gas flow in heterogeneous porous media based on the lattice Boltzmann method. J. Appl. Phys. 2016, 120, 084306. [Google Scholar] [CrossRef]
- Wang, J.; Kang, Q.; Wang, Y.; Pawar, R.; Rahman, S.S. Simulation of gas flow in micro-porous media with the regularized lattice Boltzmann method. Fuel 2017, 205, 232–246. [Google Scholar] [CrossRef]
- Li, J.; Ho, M.T.; Borg, M.K.; Cai, C.; Li, Z.H.; Zhang, Y. Pore-scale gas flow simulations by the DSBGK and DVM methods. Comput. Fluids 2021, 226, 105017. [Google Scholar] [CrossRef]
- Oran, E.S.; Oh, C.K.; Cybyk, B.Z. Direct Simulation Monte Carlo: Recent Advances and Applications. Annu. Rev. Fluid Mech. 1998, 30, 403–441. [Google Scholar] [CrossRef]
- Sun, Z.X.; Tang, Z.; He, Y.L.; Tao, W.Q. Proper cell dimension and number of particles per cell for DSMC. Comput. Fluids 2011, 50, 1–9. [Google Scholar] [CrossRef]
- Alexander, F.J.; Garcia, A.L.; Alder, B.J. Cell size dependence of transport coefficients in stochastic particle algorithms. Phys. Fluids 1998, 10, 1540–1542. [Google Scholar] [CrossRef]
- White, C.; Borg, M.; Scanlon, T.; Longshaw, S.; John, B.; Emerson, D.; Reese, J. dsmcFoam+: An OpenFOAM based direct simulation Monte Carlo solver. Comput. Phys. Commun. 2018, 224, 22–43. [Google Scholar] [CrossRef]
- Bhatia, S.K.; Bonilla, M.R.; Nicholson, D. Molecular transport in nanopores: A theoretical perspective. Phys. Chem. Chem. Phys. 2011, 13, 15350. [Google Scholar] [CrossRef]
- Huang, N.; Chen, X.; Krishna, R.; Jiang, D. Two-Dimensional Covalent Organic Frameworks for Carbon Dioxide Capture through Channel-Wall Functionalization. Angew. Chem. 2015, 127, 3029–3033. [Google Scholar] [CrossRef]
- Liu, L.; Nicholson, D.; Bhatia, S.K. Exceptionally high performance of charged carbon nanotube arrays for CO2 separation from flue gas. Carbon 2017, 125, 245–257. [Google Scholar] [CrossRef]
- Li, W.; Wang, D.; Wang, J.G. Improved mathematical model of apparent permeability: A focused study on free and multilayer adsorptive phase flow. J. Nat. Gas Sci. Eng. 2022, 101, 104508. [Google Scholar] [CrossRef]
- Kawagoe, Y.; Oshima, T.; Tomarikawa, K.; Tokumasu, T.; Koido, T.; Yonemura, S. A study on pressure-driven gas transport in porous media: From nanoscale to microscale. Microfluid. Nanofluid. 2016, 20. [Google Scholar] [CrossRef]
- Yang, G.; Weigand, B. Investigation of the Klinkenberg effect in a micro/nanoporous medium by direct simulation Monte Carlo method. Phys. Rev. Fluids 2018, 3, 044201. [Google Scholar] [CrossRef]
- Balaj, M.; Roohi, E.; Akhlaghi, H.; Myong, R.S. Investigation of convective heat transfer through constant wall heat flux micro/nano channels using DSMC. Int. J. Heat Mass Transf. 2014, 71, 633–638. [Google Scholar] [CrossRef]
- Varade, V.; Duryodhan, V.S.; Agrawal, A.; Pradeep, A.M.; Ebrahimi, A.; Roohi, E. Low Mach number slip flow through diverging microchannel. Comput. Fluids 2015, 111, 46–61. [Google Scholar] [CrossRef]
- Germanou, L.; Ho, M.T.; Zhang, Y.; Wu, L. Intrinsic and apparent gas permeability of heterogeneous and anisotropic ultra-tight porous media. J. Nat. Gas Sci. Eng. 2018, 60, 271–283. [Google Scholar] [CrossRef]
- Jambunathan, R.; Levin, D.A.; Borner, A.; Ferguson, J.C.; Panerai, F. Prediction of gas transport properties through fibrous carbon preform microstructures using Direct Simulation Monte Carlo. Int. J. Heat Mass Transf. 2019, 130, 923–937. [Google Scholar] [CrossRef]
- Lohman, S.W. Definitions of Selected Ground-Water Terms, Revisions and Conceptual Refinements; Technical Report; U.S. Government Printing Office: Washington, DC, USA, 1972. [Google Scholar] [CrossRef]
- Hadjiconstantinou, N.G. Comment on Cercignani’s second-order slip coefficient. Phys. Fluids 2003, 15, 2352–2354. [Google Scholar] [CrossRef]
- White, W.B. Hydrogeology of Karst Aquifers. In Encyclopedia of Caves; Elsevier: Amsterdam, The Netherlands, 2012; pp. 383–391. [Google Scholar] [CrossRef]
- Bird, G.A. Definition of mean free path for real gases. Phys. Fluids 1983, 26, 3222. [Google Scholar] [CrossRef]
- Sakhaee-Pour, A.; Bryant, S.L. Gas Permeability of Shale. SPE Reserv. Eval. Eng. 2012, 15, 401–409. [Google Scholar] [CrossRef]
- Beskok, A.; Karniadakis, G.E. Report: A Model for Flows in Channels, Pipes, and Ducts at Micro and Nano Scales. Microscale Thermophys. Eng. 1999, 3, 43–77. [Google Scholar] [CrossRef]
- Lu, Y. Higher-order Knudsen’s permeability correction model for rarefied gas in micro-scale channels. Nat. Gas Ind. B 2019, 6, 502–508. [Google Scholar] [CrossRef]

| Reference | Remark | |
|---|---|---|
| Zhao et al. [7] | ||
| Klinkenberg [21] | ||
| Mohammadmoradi and Kantzas [6] | ||
| Sakhaee-Pour and Bryant [61] | - | |
| Beskok and Karniadakis [62] | ||
| Kawagoe et al. [51] | and | |
| Yang and Weigand [52] | and | |
| Lu [63] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shariati, V.; Roohi, E.; Ebrahimi, A. Numerical Study of Gas Flow in Super Nanoporous Materials Using the Direct Simulation Monte-Carlo Method. Micromachines 2023, 14, 139. https://doi.org/10.3390/mi14010139
Shariati V, Roohi E, Ebrahimi A. Numerical Study of Gas Flow in Super Nanoporous Materials Using the Direct Simulation Monte-Carlo Method. Micromachines. 2023; 14(1):139. https://doi.org/10.3390/mi14010139
Chicago/Turabian StyleShariati, Vahid, Ehsan Roohi, and Amin Ebrahimi. 2023. "Numerical Study of Gas Flow in Super Nanoporous Materials Using the Direct Simulation Monte-Carlo Method" Micromachines 14, no. 1: 139. https://doi.org/10.3390/mi14010139
APA StyleShariati, V., Roohi, E., & Ebrahimi, A. (2023). Numerical Study of Gas Flow in Super Nanoporous Materials Using the Direct Simulation Monte-Carlo Method. Micromachines, 14(1), 139. https://doi.org/10.3390/mi14010139








