RLC Circuit Forecast in Analog IC Packaging and Testing by Machine Learning Techniques
Abstract
:1. Introduction
| Literature | Years | Application | Method(s) |
|---|---|---|---|
| Ren et al. [4] | 2021 | Predict net parasitics and device parameters | GNN |
| Shook et al. [5] | 2020 | Parasitic estimation | Random forest |
| Wu and Chu [6] | 2021 | The structural design optimization of chip package integration | Random forest |
| Hsiao and Chiang [7] | 2020 | Packaging reliability analysis and prediction | Random forest |
| Lee et al. [8] | 2021 | Interactive risk assessment of chip packaging | FEA, MOGA |
| Acharya et al. [9] | 2021 | Predict the thermal behavior of a power electronics package | Random forest, SVR, ANN |
| Durgam et al. [10] | 2022 | The optimization of temperature on printed circuit board | XG Boost, ANN, SVR, RFR |
| Jing et al. [11] | 2021 | Predicting the temperature curve of SMT reflow soldering | Genetic Algorithm |
| Cecchetti et al. [12] | 2020 | Power delivery network (PDN) | ANN, Genetic Algorithm |
| Sourav et al. [13] | 2020 | Power delivery network (PDN) | Regressor trees, LSTM |
| Mao et al. [14] | 2022 | Predicting three-dimensional board-level drop responses for ball grid array (BGA) encapsulation structures | BPNN |
| Jin et al. [15] | 2022 | Predicting the radiated electric field of a wire-bonded ball grid array package | DNN, SVR, K-nearest neighbors, LR |
| Wang et al. [16] | 2021 | Full wave radiation simulation of package design process | CNN |
| Schierholz et al. [2] | 2021 | Signal integrity (SI) and power integrity (PI) database based on PCB interconnection | ANN, Genetic Algorithm |
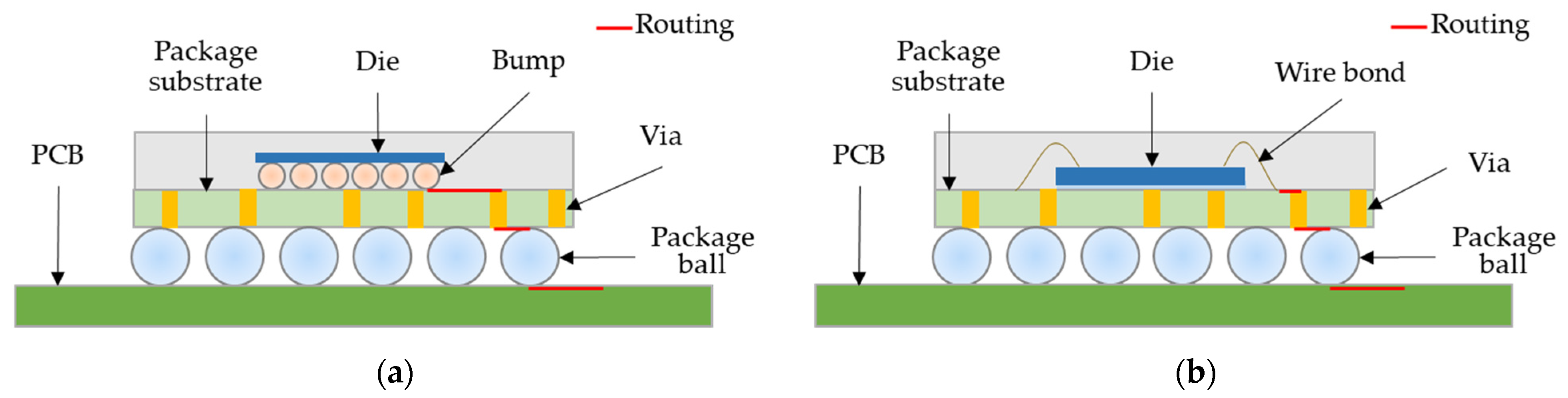
2. The Substrate and Interface of the IC Package Transmit Electrical Properties
3. Forecasting RLC Values of Integrated Circuits by LSSVR-GA Models
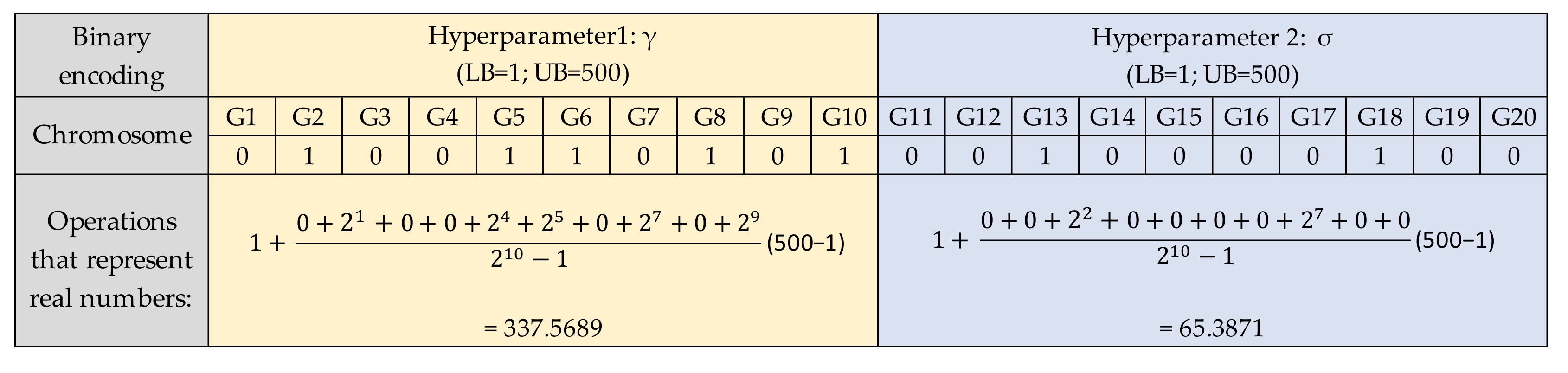
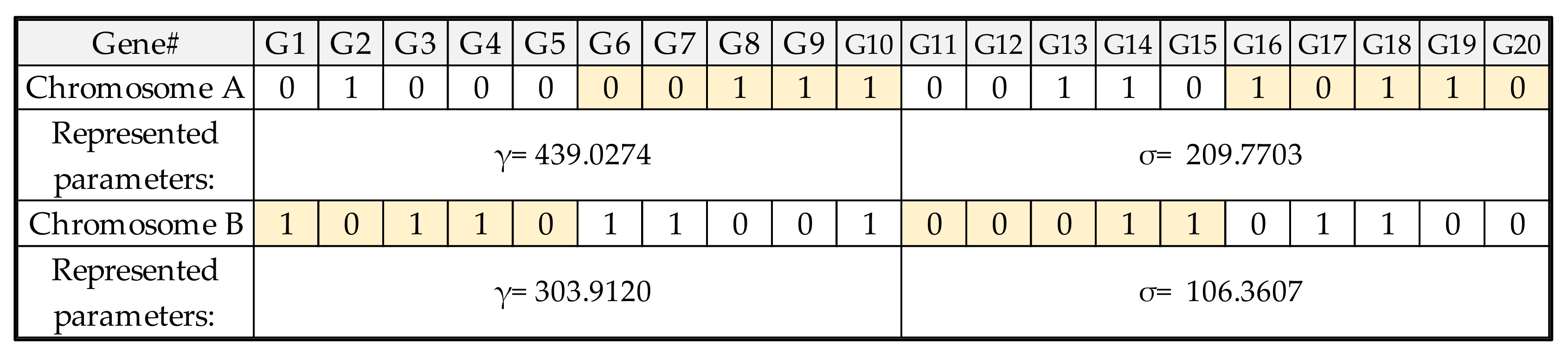
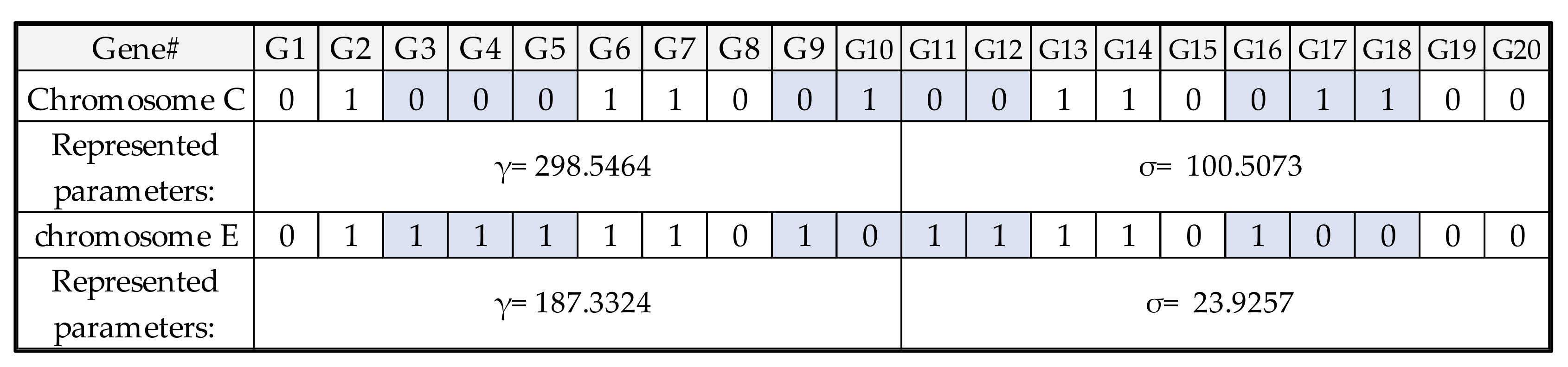
3.1. LSSVR Models with Genetic Algorithms
3.2. LSSVR-GA Architecture for RLC Prediction
4. Numerical Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Swaminathan, M.; Torun, H.M.; Yu, H.; Hejase, J.A.; Becker, W.D. Demystifying machine learning for signal and power integrity problems in packaging. IEEE Trans. Compon. Packag. Technol. 2020, 10, 1276–1295. [Google Scholar] [CrossRef]
- Schierholz, M.; Sánchez-Masís, A.; Carmona-Cruz, A.; Duan, X.; Roy, K.; Yang, C.; Rimolo-Donadio, R.; Schuster, C. Si/pi-database of pcb-based interconnects for machine learning applications. IEEE Access 2021, 9, 34423–34432. [Google Scholar] [CrossRef]
- Abdolrasol, M.G.; Hussain, S.S.; Ustun, T.S.; Sarker, M.R.; Hannan, M.A.; Mohamed, R.; Ali, J.A.; Mekhilef, S.; Milad, A. Artificial neural networks based optimization techniques: A review. Electronics 2021, 10, 2689. [Google Scholar] [CrossRef]
- Ren, H.; Kokai, G.F.; Turner, W.J.; Ku, T.-S. Paragraph: Layout parasitics and device parameter prediction using graph neural networks. In Proceedings of the 2020 57th ACM/IEEE Design Automation Conference (DAC), San Francisco, CA, USA, 20–24 July 2020; pp. 1–6. [Google Scholar]
- Shook, B.; Bhansali, P.; Kashyap, C.; Amin, C.; Joshi, S. Mlparest: Machine learning based parasitic estimation for custom circuit design. In Proceedings of the 2020 57th ACM/IEEE Design Automation Conference (DAC), San Francisco, CA, USA, 20–24 July 2020; pp. 1–6. [Google Scholar]
- Wu, H.; Chu, W. Machine learning assisted structural design optimization for flip chip packages. In Proceedings of the 2021 6th International Conference on Integrated Circuits and Microsystems (ICICM), Nanjing, China, 22–24 October 2021; pp. 132–136. [Google Scholar]
- Hsiao, H.; Chiang, K. Ai-assisted reliability life prediction model for wafer-level packaging using the random forest method. J. Mech. 2021, 37, 28–36. [Google Scholar] [CrossRef]
- Lee, M.S.; Baick, I.; Kim, M.; Kwon, S.H.; Yeo, M.S.; Rhee, H.; Lee, E. Chip to package interaction risk assessment of fcbga devices using fea simulation, meta-modeling and multi-objective genetic algorithm optimization technique. In Proceedings of the 2021 IEEE International Reliability Physics Symposium (IRPS), Monterey, CA, USA, 21–25 March 2021; pp. 1–6. [Google Scholar]
- Acharya, P.V.; Lokanathan, M.; Ouroua, A.; Hebner, R.; Strank, S.; Bahadur, V. Machine learning-based predictions of benefits of high thermal conductivity encapsulation materials for power electronics packaging. J. Electron. Packag. 2021, 143, 041109. [Google Scholar] [CrossRef]
- Durgam, S.; Bhosale, A.; Bhosale, V.; Deshpande, R.; Sutar, P.; Kamble, S. Effective computational approach for optimization of temperature on printed circuit board. J. Inst. Eng. Ser. C 2022, 103, 763–776. [Google Scholar] [CrossRef]
- Jing, S.; Li, M.; Li, X.; Yin, P. Optimization of reflow soldering temperature curve based on genetic algorithm. Energy Rep. 2021, 7, 772–782. [Google Scholar] [CrossRef]
- Cecchetti, R.; de Paulis, F.; Olivieri, C.; Orlandi, A.; Buecker, M. Effective pcb decoupling optimization by combining an iterative genetic algorithm and machine learning. Electronics 2020, 9, 1243. [Google Scholar] [CrossRef]
- Sourav, S.; Roy, A.; Cao, Y.; Pandey, S. Machine learning framework for power delivery network modelling. In Proceedings of the 2020 IEEE International Symposium on Electromagnetic Compatibility & Signal/Power Integrity (EMCSI), Reno, NV, USA, 28 July–28 August 2020; pp. 10–15. [Google Scholar]
- Mao, M.; Wang, W.; Lu, C.; Jia, F.; Long, X. Machine learning for board-level drop response of bga packaging structure. Microelectron. Reliab. 2022, 134, 114553. [Google Scholar] [CrossRef]
- Jin, H.; Gu, Z.-M.; Tao, T.-M.; Li, E. Hierarchical attention-based machine learning model for radiation prediction of wb-bga package. IEEE Trans. Electromagn. Compat. 2021, 63, 1972–1980. [Google Scholar] [CrossRef]
- Wang, D.; Deng, L.; Zhang, L.; Zhang, F.; Qi, X.; Jin, H. Inverse design for wb-bga package structure by deep learning. In Proceedings of the 2021 13th Global Symposium on Millimeter-Waves & Terahertz (GSMM), Nanjing, China, 23–25 May 2021; pp. 1–3. [Google Scholar]
- Kuo, C.-H.; Hu, A.H.; Hung, L.H.; Yang, K.-T.; Wu, C.-H. Life cycle impact assessment of semiconductor packaging technologies with emphasis on ball grid array. J. Clean. Prod. 2020, 276, 124301. [Google Scholar] [CrossRef]
- Su, D.; Zhao, D.; Zhang, L.; Yang, H.; Wang, C.; Jiang, W. Reliability assessment of flip chip interconnect electronic packaging under thermal shocks. In Proceedings of the 2020 21st International Conference on Electronic Packaging Technology (ICEPT), Guangzhou, China, 12–15 August 2020; pp. 1–4. [Google Scholar]
- Wang, D.; Zhao, Y.; Yao, Q.; Cao, Y.; Lian, B.; Zhang, H. Study on electrical performance of fc and wb in ic ceramic package. In Proceedings of the 2016 3rd International Conference on Materials Engineering, Manufacturing Technology and Control, Taiyuan, China, 27–28 February 2016; pp. 1670–1675. [Google Scholar]
- Venkataiah, C.; Prasad, K.S.; Prasad, T.J.C. Effect of interconnect parasitic variations on circuit performance parameters. In Proceedings of the 2016 International Conference on Communication and Electronics Systems (ICCES), Coimbatore, India, 21–22 October 2016; pp. 1–4. [Google Scholar]
- Khan, R.A.; Muhaisin, M.M.; Roberts, G.W. Extracting rlc parasitics from a flexible electronic hybrid assembly using on-chip esd protection circuits. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 4025–4037. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Suykens, J.A.; Vandewalle, J. Least squares support vector machine classifiers. Neural Processing Lett. 1999, 9, 293–300. [Google Scholar] [CrossRef]
- Suykens, J.A.; De Brabanter, J.; Lukas, L.; Vandewalle, J. Weighted least squares support vector machines: Robustness and sparse approximation. Neurocomputing 2002, 48, 85–105. [Google Scholar] [CrossRef]
- Lodhi, H.; Saunders, C.; Shawe-Taylor, J.; Cristianini, N.; Watkins, C. Text classification using string kernels. J. Mach. Learn. Res. 2002, 2, 419–444. [Google Scholar]
- Vert, J.-P.; Tsuda, K.; Schölkopf, B. A primer on kernel methods. Kernel Methods Comput. Biol. 2004, 47, 35–70. [Google Scholar]
- Goldberg, Y.; Elhadad, M. Splitsvm: Fast, space-efficient, non-heuristic, polynomial kernel computation for nlp applications. In Proceedings of the 46th Annual Meeting of the Association for Computational Linguistics on Human Language Technologies: Short Papers, Columbus, OH, USA, 15–20 June 2008; pp. 237–240. [Google Scholar]
- Holland, J.H. Adaptation in Natural and Artificial Systems; The University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools 2021, 80, 8091–8126. [Google Scholar] [CrossRef] [PubMed]
- Lewis, C.D. Industrial and Business forecasting METHODS: A Practical Guide to Exponential Smoothing and Curve Fitting; Butterworth-Heinemann: Oxford, UK, 1982. [Google Scholar]




| Data Sets | Features (X Variables) | Samples | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ball | Bump | Base | L1 | L2 | L3 | L4 | L5 | Via | Wire | Total | ||
| FC_2L_T1 | 1 | 1 | 2 | 2 | 2 | 8 X | 2232 | |||||
| FC_4L_T1 | 1 | 1 | 2 | 2 | 2 | 2 | 6 | 16 X | 999 | |||
| FC_6L_T1 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 10 | 24 X | 742 | |
| WB_2L_T1 | 1 | 2 | 2 | 2 | 1 | 8 X | 1400 | |||||
| WB_4L_T1 | 1 | 2 | 2 | 2 | 2 | 6 | 1 | 16 X | 2704 | |||
| WB_6L_T1 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 10 | 1 | 24 X | 450 | |
| Method | Parameters | Ls (nH) | Cs (pF) | R (mΩ) | Ls (nH) | Cs (pF) | R (mΩ) | Ls (nH) | Cs (pF) | R (mΩ) |
|---|---|---|---|---|---|---|---|---|---|---|
| Products | FC_2L_T1 | FC_4L_T1 | FC_6L_T1 | |||||||
| GA-LSSVR | gamma | 3.5241 | 220.2197 | 266.8764 | 386.9266 | 388.4704 | 336.2926 | 237.4034 | 386.9266 | 199.8153 |
| sigma | 490.8269 | 2.3006 | 1.7176 | 1.4692 | 3.2476 | 4.0466 | 2.1650 | 1.4692 | 1.0638 | |
| GA-BPNN | learning rate | 0.278163 | 0.725969 | 0.380188 | 0.316992 | 0.77501 | 0.668117 | 0.609052 | 0.168028 | 0.1674687 |
| momentum | 0.790603 | 0.415267 | 0.424905 | 0.803841 | 0.748888 | 0.770531 | 0.864727 | 0.890341 | 0.186707 | |
| GA-RF | NTG * | 162 | 122 | 313 | 281 | 268 | 423 | 491 | 316 | 159 |
| MTRY * | 7 | 7 | 7 | 16 | 14 | 15 | 22 | 24 | 23 | |
| NS * | 32 | 25 | 13 | 9 | 11 | 9 | 10 | 5 | 11 | |
| SSD * | 3 | 5 | 6 | 7 | 15 | 12 | 23 | 16 | 23 | |
| MN * | 99 | 99 | 99 | 99 | 90 | 94 | 100 | 95 | 90 | |
| GA-XGBoost | CB * | 0.9652 | 0.95019 | 0.94883 | 0.88056 | 0.85548 | 0.97795 | 0.83369 | 0.83964 | 0.95994 |
| SS * | 0.73781 | 0.95313 | 0.9539 | 0.93509 | 0.93643 | 0.9374 | 0.9856 | 0.93392 | 0.9727 | |
| MD * | 9 | 10 | 9 | 9 | 9 | 9 | 10 | 9 | 7 | |
| learning rate | 0.0792 | 0.0981 | 0.08608 | 0.08813 | 0.08183 | 0.09519 | 0.04556 | 0.07721 | 0.07101 | |
| gamma | 0.03703 | 0.44082 | 0.9867 | 0.26736 | 0.00473 | 0.99912 | 0.0118 | 0.00621 | 0.19647 | |
| MW * | 4.67495 | 3.0224 | 3.60389 | 3.51156 | 3.60387 | 3.88513 | 3.15073 | 5.40802 | 3.43816 | |
| Lambda * | 0.84143 | 1.0274 | 0.73609 | 0.62597 | 1.06227 | 0.66675 | 0.58733 | 1.23425 | 0.66977 | |
| Products | WB_2L_T1 | WB_4L_T1 | WB_6L_T1 | |||||||
| GA-LSSVR | gamma | 487.8397 | 461.7180 | 253.7229 | 260.8126 | 138.0979 | 291.6471 | 264.8891 | 386.9266 | 261.5888 |
| sigma | 2.1064 | 1.6639 | 3.5726 | 2.1926 | 1.6762 | 2.3001 | 2.0693 | 1.4692 | 4.8404 | |
| GA-BPNN | learning rate | 0.195829 | 0.558181 | 0.897148 | 0.270761 | 0.652679 | 0.405238 | 0.301158 | 0.86155 | 0.105814 |
| momentum | 0.864213 | 0.65859 | 0.694771 | 0.894708 | 0.765861 | 0.88196 | 0.318845 | 0.639695 | 0.634643 | |
| GA-RF | NTG * | 338 | 179 | 356 | 275 | 435 | 193 | 492 | 381 | 255 |
| MTRY * | 7 | 7 | 7 | 14 | 11 | 13 | 22 | 24 | 21 | |
| NS * | 21 | 16 | 20 | 33 | 29 | 32 | 8 | 4 | 8 | |
| SSD * | 7 | 5 | 4 | 5 | 11 | 6 | 5 | 7 | 18 | |
| MN * | 97 | 100 | 99 | 99 | 100 | 98 | 99 | 96 | 85 | |
| GA-XGBoost | CB * | 0.91655 | 0.88732 | 0.87073 | 0.98352 | 0.94273 | 0.82735 | 0.90711 | 0.81666 | 0.94269 |
| SS * | 0.52606 | 0.70242 | 0.92529 | 0.66074 | 0.89115 | 0.91367 | 0.74513 | 0.90611 | 0.9466 | |
| MD * | 10 | 8 | 10 | 9 | 9 | 10 | 10 | 8 | 9 | |
| learning rate | 0.09689 | 0.06631 | 0.08815 | 0.09564 | 0.08211 | 0.08766 | 0.09008 | 0.09676 | 0.08981 | |
| gamma | 0.00929 | 0.02931 | 0.11065 | 0.01612 | 0.00016 | 0.1768 | 0.01459 | 0.01058 | 0.48457 | |
| MW * | 3.52074 | 5.63888 | 3.38181 | 4.18612 | 4.3746 | 3.62682 | 3.1284 | 3.44193 | 4.72415 | |
| Lambda * | 0.56806 | 1.17406 | 0.87922 | 0.78879 | 0.77885 | 0.52211 | 0.7232 | 1.13934 | 0.79814 | |
| MAPE Values (%) | Accuracy |
|---|---|
| <10 | Highly accurate prediction |
| 10–20 | Good prediction |
| 20–50 | Reasonable prediction |
| >50 | Inaccurate prediction |
| Product Type | Method | Ls (nH) | Cs (pF) | R (mΩ) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MAPE (%) | WAPE (%) | NMAE | MAPE (%) | WAPE (%) | NMAE | MAPE (%) | WAPE (%) | NMAE | ||
| FC_2L_T1 | GA-LSSVR | 16.88 | 15.63 | 0.04818 | 13.25 | 13.47 | 0.05634 | 6.20 | 6.48 | 0.02528 |
| GA-BPNN | 18.03 | 17.55 | 0.05410 | 13.93 | 13.49 | 0.05642 | 7.48 | 6.72 | 0.02623 | |
| GA-RF | 18.64 | 18.79 | 0.05792 | 13.43 | 13.44 | 0.05619 | 7.25 | 6.96 | 0.02712 | |
| GA-XGBoost | 19.01 | 19.49 | 0.06008 | 14.12 | 14.02 | 0.05862 | 8.74 | 7.77 | 0.03029 | |
| FC_4L_T1 | GA-LSSVR | 12.18 | 8.92 | 0.01625 | 6.75 | 5.11 | 0.01527 | 12.15 | 5.99 | 0.00845 |
| GA-BPNN | 35.86 | 22.67 | 0.04130 | 9.81 | 8.12 | 0.02423 | 25.05 | 14.35 | 0.02024 | |
| GA-RF | 12.30 | 9.61 | 0.01751 | 8.60 | 6.95 | 0.02074 | 16.68 | 7.80 | 0.01100 | |
| GA-XGBoost | 15.16 | 11.06 | 0.02015 | 7.54 | 6.01 | 0.01796 | 17.85 | 7.87 | 0.01110 | |
| FC_6L_T1 | GA-LSSVR | 10.35 | 7.81 | 0.05383 | 9.09 | 7.42 | 0.04804 | 11.99 | 8.33 | 0.04320 |
| GA-BPNN | 10.37 | 8.74 | 0.06019 | 9.26 | 8.63 | 0.05588 | 15.77 | 12.87 | 0.06674 | |
| GA-RF | 10.40 | 8.56 | 0.05897 | 9.46 | 8.35 | 0.05402 | 12.10 | 9.74 | 0.05053 | |
| GA-XGBoost | 10.87 | 9.15 | 0.06302 | 9.32 | 8.27 | 0.05352 | 12.23 | 10.45 | 0.05420 | |
| WB_2L_T1 | GA-LSSVR | 13.28 | 12.63 | 0.05518 | 5.61 | 5.25 | 0.02018 | 7.21 | 6.79 | 0.02781 |
| GA-BPNN | 15.23 | 13.39 | 0.05852 | 6.64 | 6.00 | 0.02307 | 11.40 | 9.71 | 0.03980 | |
| GA-RF | 13.86 | 12.40 | 0.05417 | 6.10 | 5.86 | 0.02255 | 9.70 | 8.98 | 0.03680 | |
| GA-XGBoost | 13.42 | 11.48 | 0.05015 | 6.62 | 6.07 | 0.02337 | 9.05 | 8.05 | 0.03298 | |
| WB_4L_T1 | GA-LSSVR | 14.54 | 11.65 | 0.03301 | 6.71 | 5.84 | 0.02074 | 10.00 | 7.10 | 0.02697 |
| GA-BPNN | 16.00 | 12.19 | 0.03453 | 9.19 | 7.53 | 0.02676 | 13.19 | 9.20 | 0.03497 | |
| GA-RF | 14.96 | 12.28 | 0.03480 | 9.16 | 7.79 | 0.02767 | 10.59 | 8.08 | 0.03071 | |
| GA-XGBoost | 15.81 | 11.74 | 0.03325 | 7.33 | 6.35 | 0.02255 | 10.10 | 7.47 | 0.02840 | |
| WB_6L_T1 | GA-LSSVR | 8.68 | 9.28 | 0.05880 | 6.48 | 7.31 | 0.03904 | 4.08 | 4.89 | 0.03481 |
| GA-BPNN | 9.95 | 9.21 | 0.05838 | 6.56 | 6.63 | 0.03541 | 4.36 | 4.63 | 0.03299 | |
| GA-RF | 10.13 | 9.92 | 0.06289 | 6.61 | 6.79 | 0.03624 | 7.39 | 8.18 | 0.05819 | |
| GA-XGBoost | 9.60 | 8.75 | 0.05546 | 6.60 | 6.73 | 0.03593 | 6.71 | 7.43 | 0.05285 | |
| Average | GA-LSSVR | 12.65 | 10.99 | 0.04421 | 7.98 | 7.40 | 0.03327 | 8.60 | 6.60 | 0.02775 |
| GA-BPNN | 17.57 | 13.96 | 0.05117 | 9.23 | 8.40 | 0.03696 | 12.87 | 9.58 | 0.03683 | |
| GA-RF | 13.38 | 11.93 | 0.04771 | 8.89 | 8.19 | 0.03624 | 10.62 | 8.29 | 0.03573 | |
| GA-XGBoost | 13.98 | 11.94 | 0.04702 | 8.59 | 7.91 | 0.03533 | 10.78 | 8.17 | 0.03497 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lai, J.-P.; Lin, Y.-L.; Lin, H.-C.; Shih, C.-Y.; Wang, Y.-P.; Pai, P.-F. RLC Circuit Forecast in Analog IC Packaging and Testing by Machine Learning Techniques. Micromachines 2022, 13, 1305. https://doi.org/10.3390/mi13081305
Lai J-P, Lin Y-L, Lin H-C, Shih C-Y, Wang Y-P, Pai P-F. RLC Circuit Forecast in Analog IC Packaging and Testing by Machine Learning Techniques. Micromachines. 2022; 13(8):1305. https://doi.org/10.3390/mi13081305
Chicago/Turabian StyleLai, Jung-Pin, Ying-Lei Lin, Ho-Chuan Lin, Chih-Yuan Shih, Yu-Po Wang, and Ping-Feng Pai. 2022. "RLC Circuit Forecast in Analog IC Packaging and Testing by Machine Learning Techniques" Micromachines 13, no. 8: 1305. https://doi.org/10.3390/mi13081305
APA StyleLai, J.-P., Lin, Y.-L., Lin, H.-C., Shih, C.-Y., Wang, Y.-P., & Pai, P.-F. (2022). RLC Circuit Forecast in Analog IC Packaging and Testing by Machine Learning Techniques. Micromachines, 13(8), 1305. https://doi.org/10.3390/mi13081305








