An RBF Meshless Approach to Evaluate Strain Due to Large Displacements in Flexible Printed Circuit Boards
Abstract
1. Introduction
2. Mathematical Background
2.1. Radial Basis Functions
2.2. Kinematics of Large Displacements for a Bi-Dimensional Plate
2.3. Analytical Test Cases
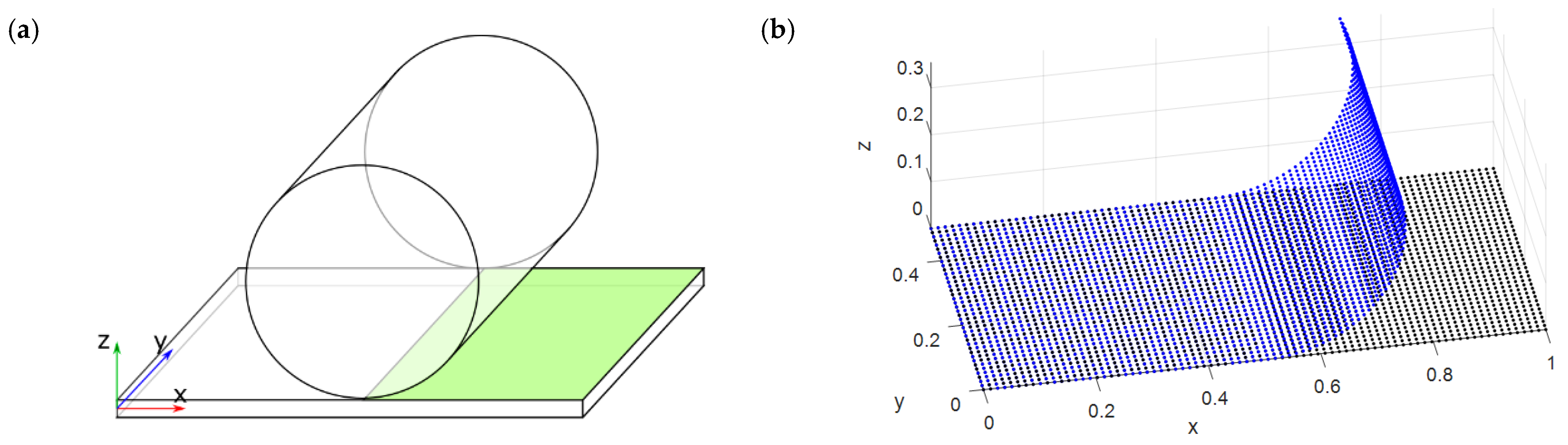
2.3.1. Test Case 1
2.3.2. Test Case 2
3. Results
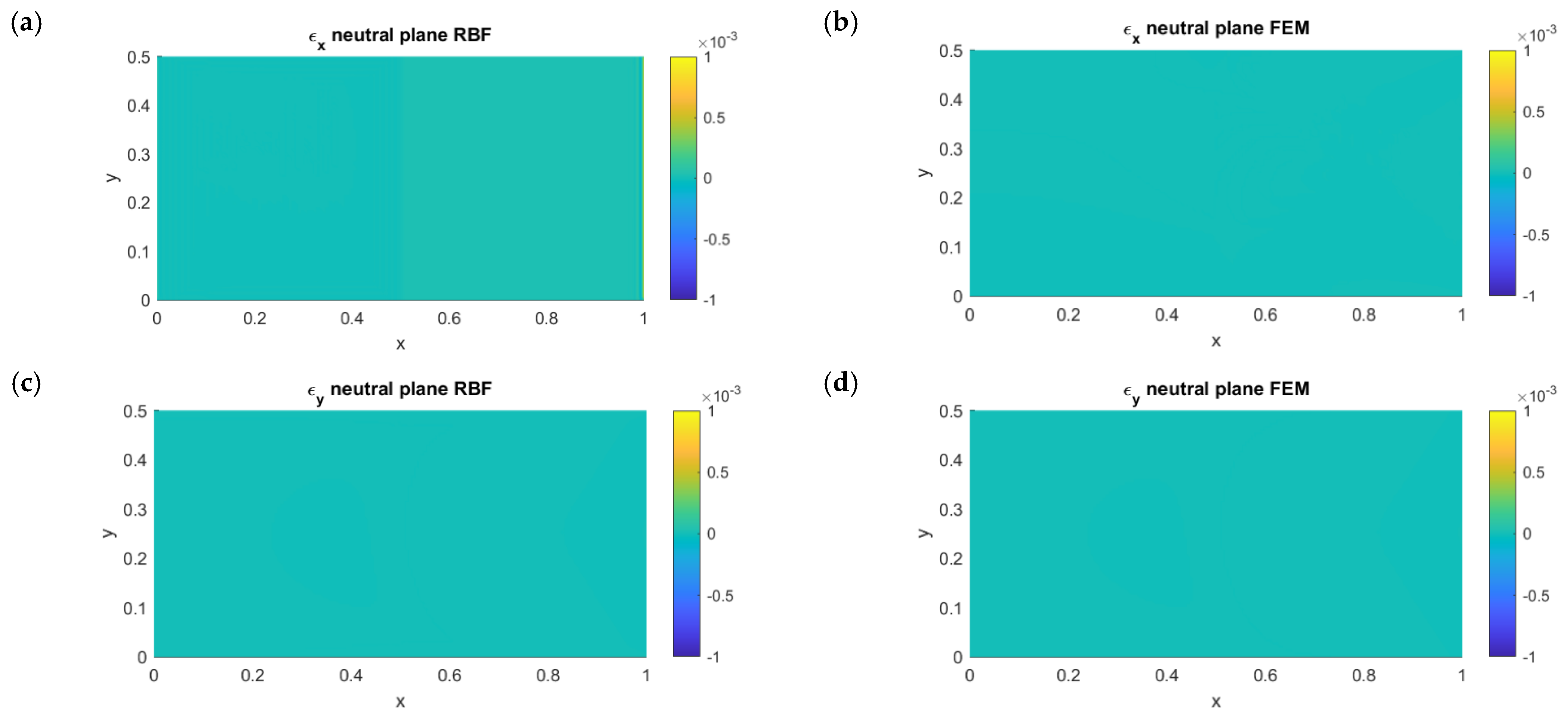
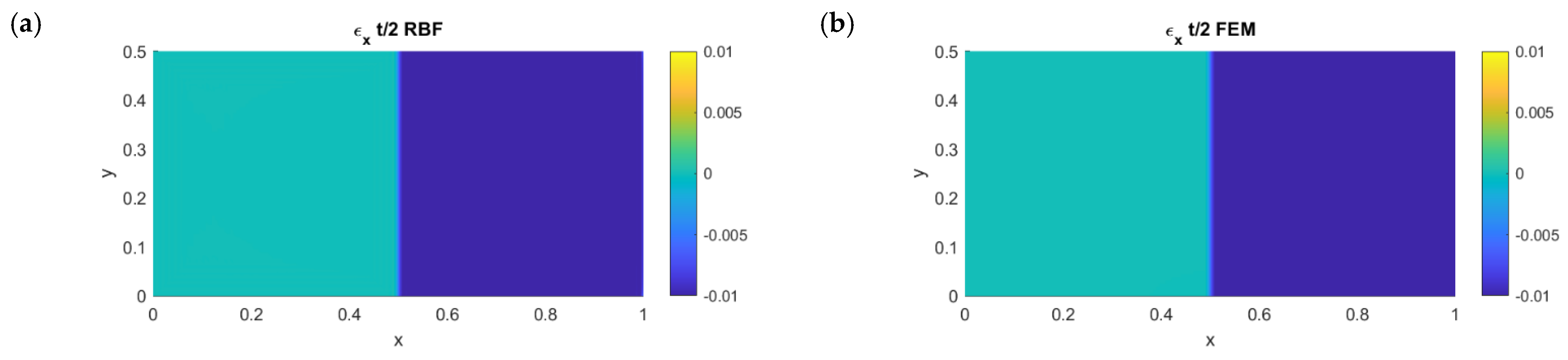
3.1. Test Case 1
3.2. Test Case 2
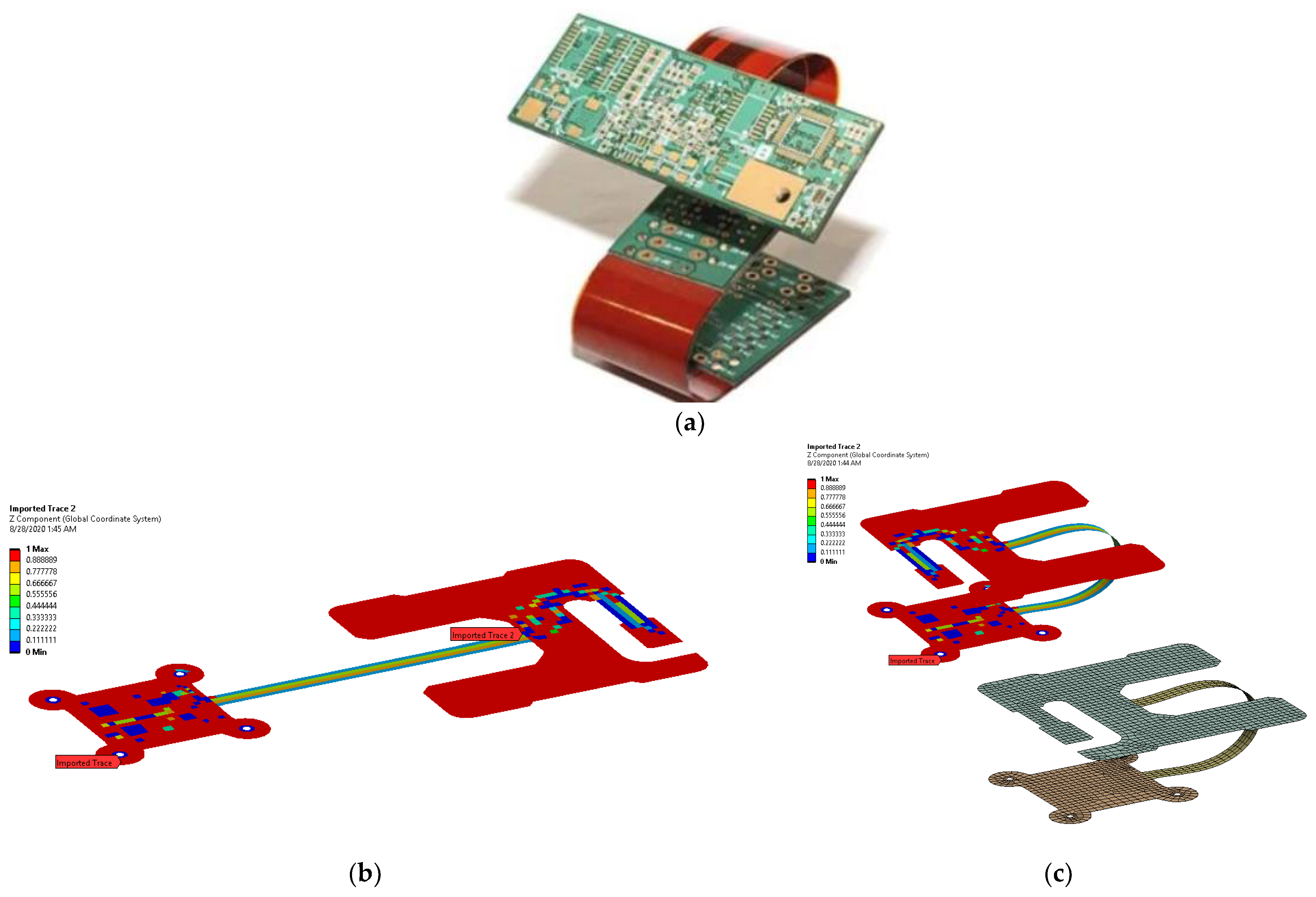
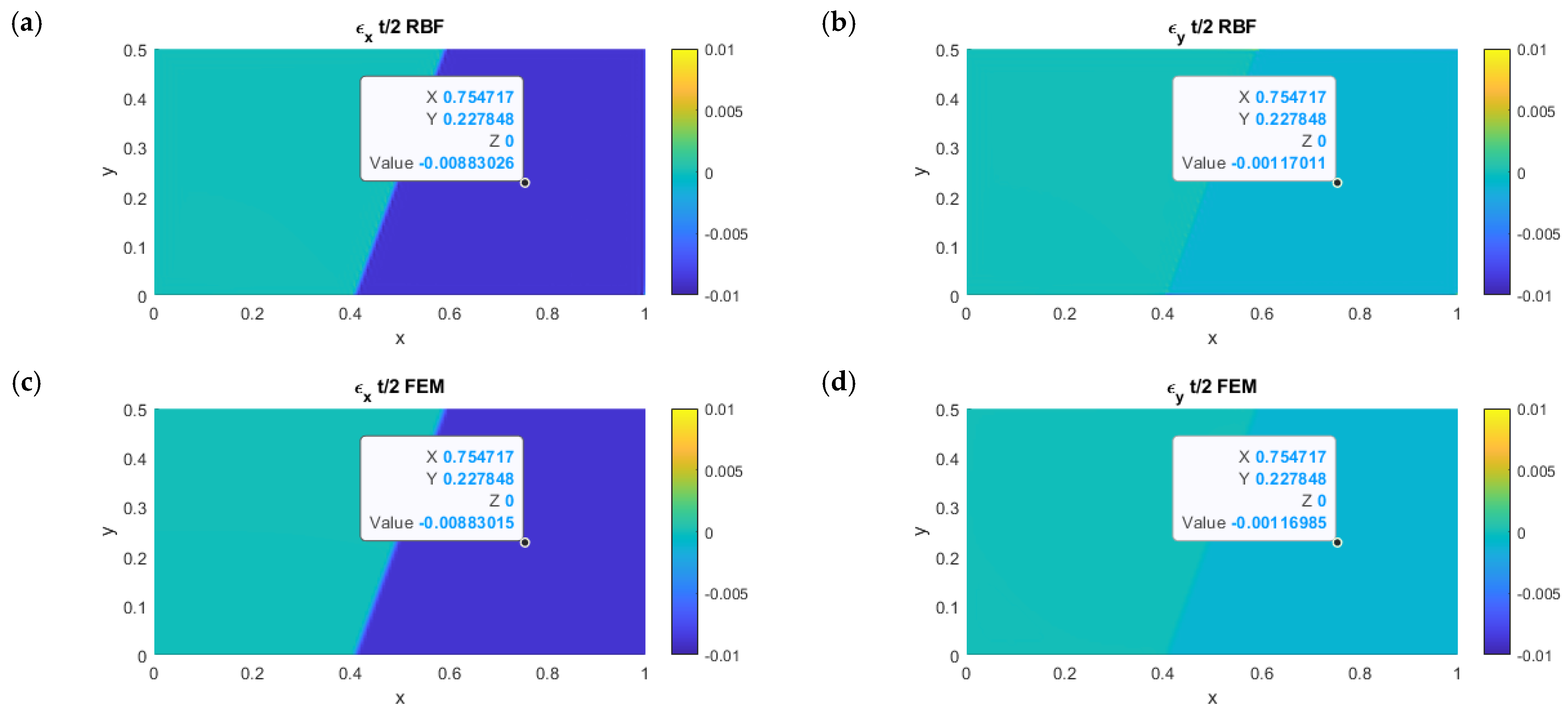
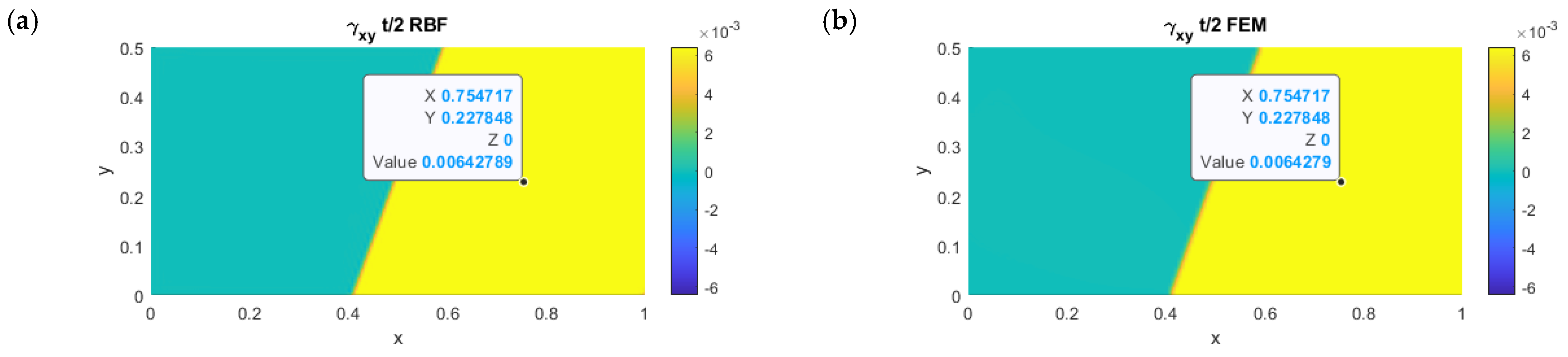
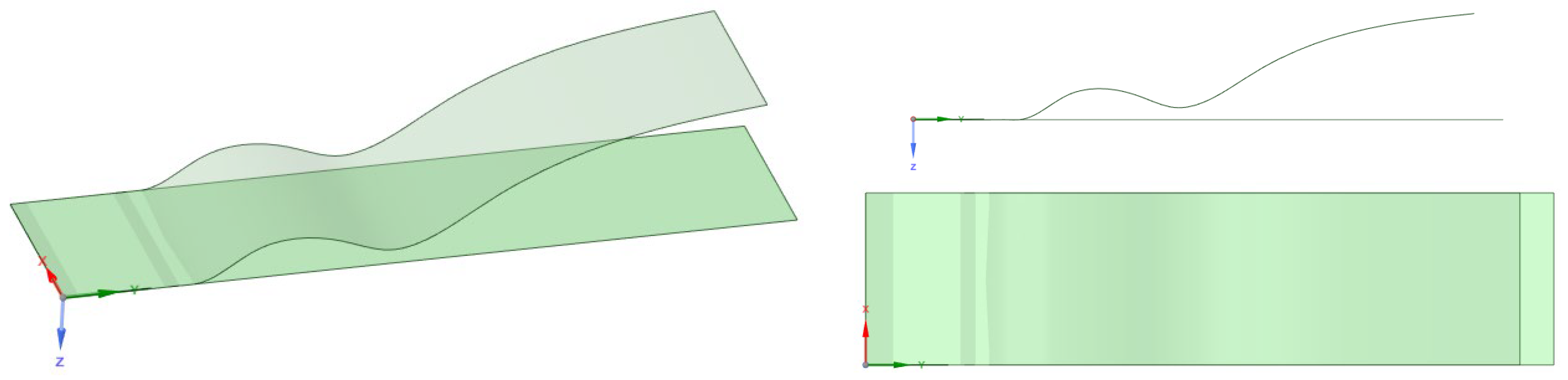
3.3. CAD-Based Test Case
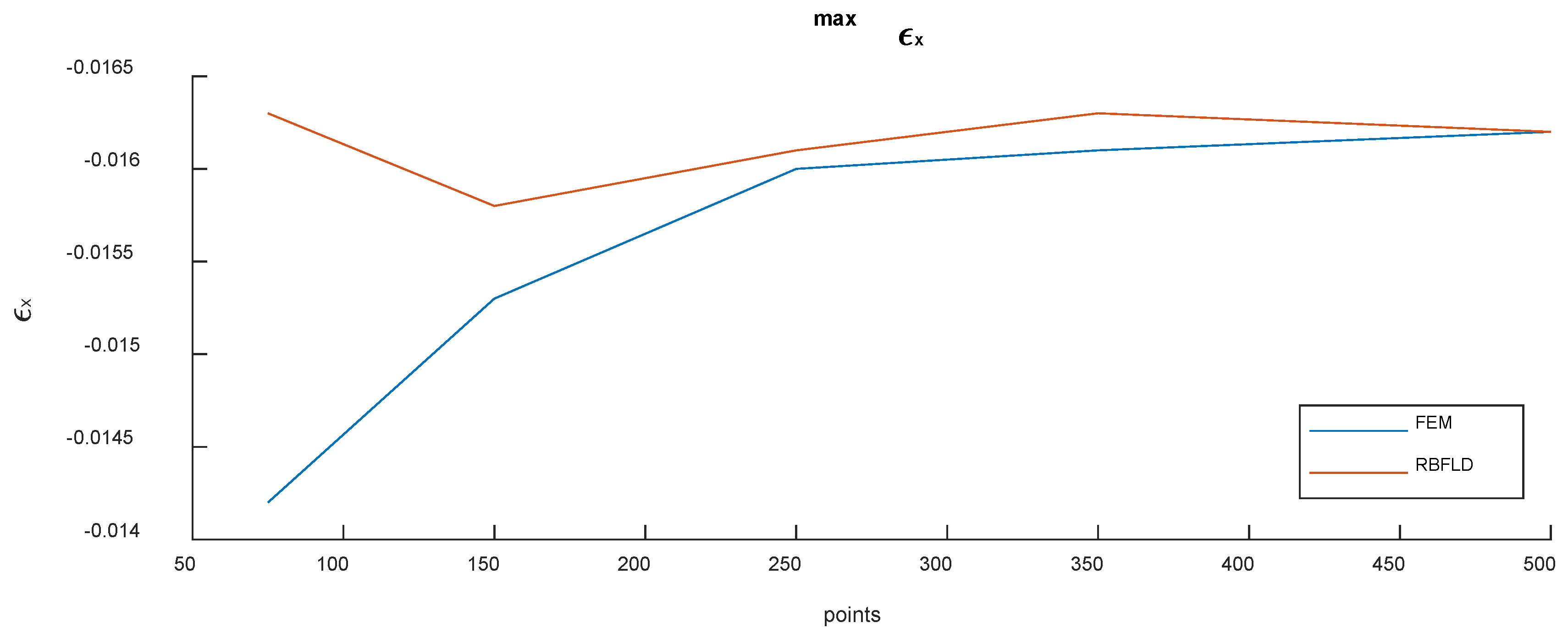
3.4. Result
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Fries, T.-P.; Belytschko, T. The extended/generalized finite element method: An overview of the method and its applications. Int. J. Numer. Methods Eng. 2010, 84, 253–304. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Taylor, R.L.; Zhu, J.Z. The Finite Element Method: Its Basis and Fundamentals, 6th ed.; Butterworth-Heinemann: Oxford, UK, 2005. [Google Scholar]
- Griebel, M.; Schweitzer, M.A. A particle-partition of unity method for the solution of elliptic, parabolic and hyperbolic PDEs. SIAM J. Sci. Comput. 2000, 22, 853–890. [Google Scholar] [CrossRef]
- Kwon, K.-C.; Youn, S.-K. The least-squares meshfree method for rigid-plasticity with frictional contact. Int. J. Solids Struct. 2006, 43, 7450–7841. [Google Scholar] [CrossRef][Green Version]
- Rao, B.N.; Rahman, S. An efficient meshless method for fracture analysis of cracks. Comput. Mech. 2000, 26, 398–408. [Google Scholar] [CrossRef]
- Belytschko, T.; Krongauz, Y.; Organ, D.; Fleming, M.; Krysl, P. Meshless methods: An overview and recent developments. Comput. Methods Appl. Mech. Eng. 1996, 139, 3–47. [Google Scholar] [CrossRef]
- Lucy, L.B. A numerical approach to the testing of the fission hypothesis. Astron. J. 1977, 82, 1013–1024. [Google Scholar] [CrossRef]
- Libersky, L.D.; Petscheck, A.G.; Carney, T.C.; Hipp, J.R.; Allahdadi, F.A. High strain Lagrangian hydrodynamics. J. Comput. Phys. 1993, 109, 67–75. [Google Scholar] [CrossRef]
- Nayroles, B.; Touzor, G.; Villon, P. Generalizing the finite element method: Diffuse approximation and diffuse elements. Comput. Mech. 1992, 10, 307–318. [Google Scholar] [CrossRef]
- Babuška, I.; Melenk, J.M. The partition of unity method. Int. J. Numer. Methods Eng. 1997, 40, 727–758. [Google Scholar] [CrossRef]
- Belytschko, T.; Lu, Y.Y.; Gu, L. Element-free Galerkin methods. Int. J. Numer. Methods Eng. 1994, 37, 229–256. [Google Scholar] [CrossRef]
- Atluri, S.N.; Zhu, T. A new meshless local Petrov–Galerkin (MLPG) approach in computational mechanics. Comput. Mech. 1998, 22, 117–127. [Google Scholar] [CrossRef]
- Amy, R.A.; Aglietti, G.S.; Richardson, G. Microelectronics Reliability; Elsevier: Amsterdam, The Netherlands, 2010; Volume 50, pp. 86–97. ISSN 00262714. [Google Scholar]
- Dogruoz, M.B.; Nagulapally, M.K. Journal of Thermal Science and Engineering Applications; American Society of Mechanical Engineers: New York, NY, USA, 2009; Volume 1, pp. 1–10. ISSN 19485093. [Google Scholar]
- Biancolini, M.E.; Medikonda, S.; Morgan, K.; Porziani, S. Modeling flexible/curved PCBs using RBF mesh morphing. Procedia Struct. Integr. 2020; in press. [Google Scholar] [CrossRef]
- Davis, P.J. Interpolation and Approximation; Blaisdell: London, UK, 1963. [Google Scholar]
- Haykin, S. Neural Network: A Comprehensive Foundation, 2nd ed.; Prentice-Hall: Englewood Cliffs, NJ, USA, 1999. [Google Scholar]
- Casciola, G.; Lazzaro, D.; Montefusco, L.B.; Morigi, S. Shape preserving surface reconstruction using locally anisotropic radial basis function interpolants. Comput. Math. Appl. 2006, 51, 1185–1198. [Google Scholar] [CrossRef]
- Biancolini, M.E. Mesh morphing and smoothing by means of radial basis functions (RBF): A practical example using fluent and RBF morph. In Handbook of Research on Computational Science and Engineering: Theory and Practice; IGI Global: Hershey, PA, USA, 2011; pp. 347–380. [Google Scholar]
- de Boer, A.; van der Schoot, M.S.; Bijl, H. Mesh deformation based on radial basis function interpolation. Comput. Struct. 2007, 85, 784–795. [Google Scholar] [CrossRef]
- Biancolini, M.E.; Salvini, P. Radial basis functions for the image analysis of deformations. In Computational Modelling of Objects Represented in Images: Fundamentals, Methods and Applications III Proceedings of the International Symposium; CRC Press: Boca Raton, FL, USA, 2012; pp. 361–365. [Google Scholar]
- Biancolini, M.E.; Cella, U.; Groth, C.; Genta, M. Static aeroelastic analysis of an aircraft wind-tunnel model by means of modal RBF mesh updating. J. Aerosp. Eng. 2016, 29, 04016061. [Google Scholar] [CrossRef]
- Biancolini, M.E.; Costa, E.; Cella, U.; Groth, C.; Veble, G.; Andrejasic, M. Glider fuselage-wing junction optimization using CFD and RBF mesh morphing. Aircr. Eng. Aerosp. Technol. 2016, 88, 740–752. [Google Scholar] [CrossRef]
- Groth, C.; Chiappa, A.; Biancolini, M.E. Shape optimization using structural adjoint and RBF mesh morphing. Procedia Struct. Integr. 2018, 8, 379–389. [Google Scholar] [CrossRef]
- Valentini, P.P.; Biancolini, M.E. Interactive sculpting using augmented-reality, mesh morphing, and force feedback: Force-feedback capabilities in an augmented reality environment. IEEE Consum. Electron. Mag. 2018, 7, 83–90. [Google Scholar] [CrossRef]
- Chiappa, A.; Salvini, P.; Brutti, C.; Biancolini, M.E. Upscaling 2D finite element analysis stress results using radial basis functions. Comput. Struct. 2019, 220, 131–143. [Google Scholar] [CrossRef]
- Biancolini, M.E.; Chiappa, A.; Giorgetti, F.; Groth, C.; Cella, U.; Salvini, P. A balanced load mapping method based on radial basis functions and fuzzy sets. Int. J. Numer. Methods Eng. 2018, 115, 1411–1429. [Google Scholar] [CrossRef]
- Chiappa, A.; Groth, C.; Brutti, C.; Salvini, P.; Biancolini, M.E. Post-processing of 2D FEM Q1 models for fracture mechanics by radial basis functions and balance equations. Int. J. Mech. 2019, 13, 104–113. [Google Scholar]
- Kansa, E.J. Multiquadrics—A scattered data approximation scheme with applications to computational fluid-dynamics—I surface approximations and partial derivative estimates. Comput. Math. Appl. 1990, 19, 127–145. [Google Scholar] [CrossRef]
- Kansa, E.J. Multiquadrics—A scattered data approximation scheme with applications to computational fluid-dynamics—II solutions to parabolic, hyperbolic and elliptic partial differential equations. Comput. Math. Appl. 1990, 19, 147–161. [Google Scholar] [CrossRef]
- Chiappa, A.; Groth, C.; Reali, A.; Biancolini, M.E. A stress recovery procedure for laminated composite plates based on strong-form equilibrium enforced via the RBF Kansa method. Compos. Struct. 2020, 244, 112292. [Google Scholar] [CrossRef]
- Buhmann, M.D. Radial Basis Functions: Theory and Implementations; Cambridge University Press: Cambridge, UK, 2003; Volume 12. [Google Scholar]
- Biancolini, M.E. Fast Radial Basis Functions for Engineering Applications; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Holzapfel, A.G. Nonlinear Solid Mechanics II; John Wiley & Sons: Hoboken, NJ, USA, 2000. [Google Scholar]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Groth, C.; Chiappa, A.; Porziani, S.; Salvini, P.; Biancolini, M.E. An RBF Meshless Approach to Evaluate Strain Due to Large Displacements in Flexible Printed Circuit Boards. Micromachines 2022, 13, 1163. https://doi.org/10.3390/mi13081163
Groth C, Chiappa A, Porziani S, Salvini P, Biancolini ME. An RBF Meshless Approach to Evaluate Strain Due to Large Displacements in Flexible Printed Circuit Boards. Micromachines. 2022; 13(8):1163. https://doi.org/10.3390/mi13081163
Chicago/Turabian StyleGroth, Corrado, Andrea Chiappa, Stefano Porziani, Pietro Salvini, and Marco Evangelos Biancolini. 2022. "An RBF Meshless Approach to Evaluate Strain Due to Large Displacements in Flexible Printed Circuit Boards" Micromachines 13, no. 8: 1163. https://doi.org/10.3390/mi13081163
APA StyleGroth, C., Chiappa, A., Porziani, S., Salvini, P., & Biancolini, M. E. (2022). An RBF Meshless Approach to Evaluate Strain Due to Large Displacements in Flexible Printed Circuit Boards. Micromachines, 13(8), 1163. https://doi.org/10.3390/mi13081163





