Topological and Mechanical Properties of Different Lattice Structures Based on Additive Manufacturing
Abstract
:1. Introduction
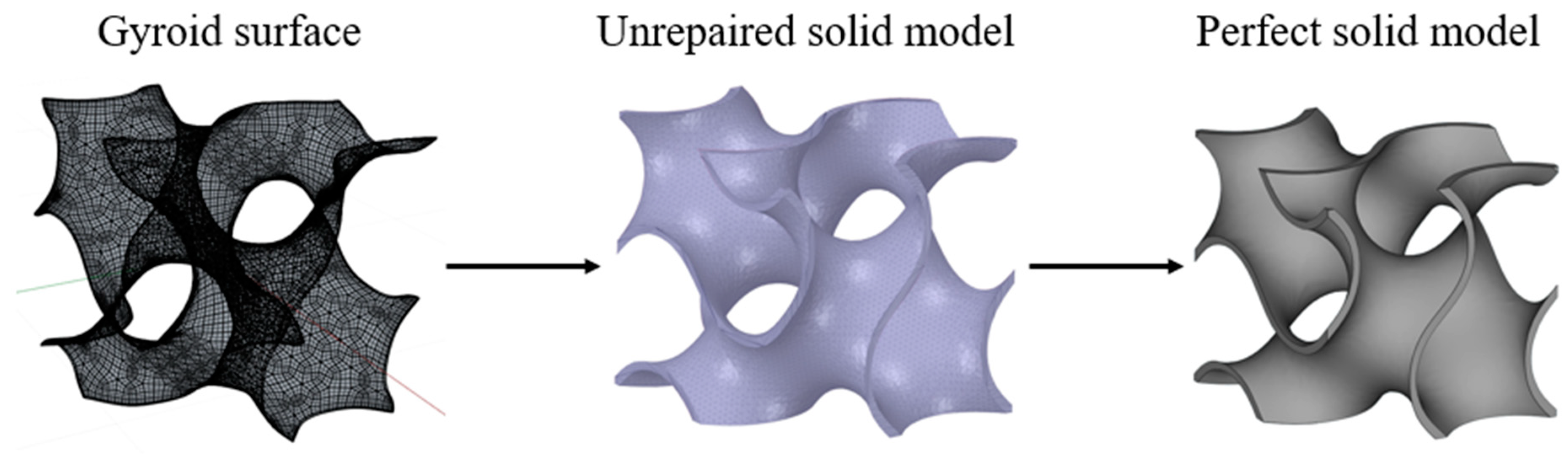
2. Design and Modeling
3. Printing and Morphological Characteristics
3.1. Manufacture
3.2. Morphology Characterization
4. Finite Element Modeling and Compression Testing
4.1. Finite Element Modeling
4.2. Compression Testing
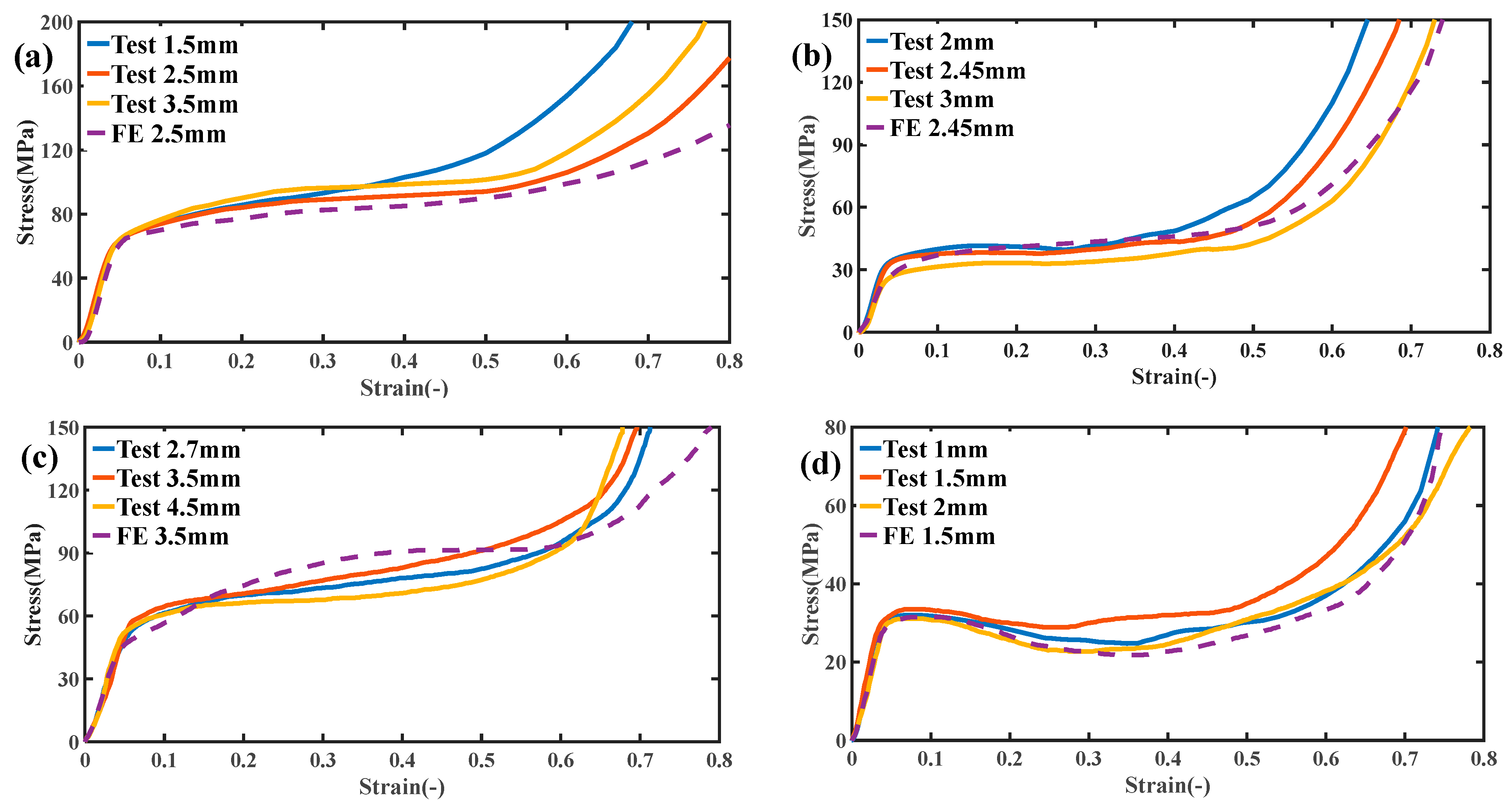
4.3. Simulation and Experimental Results
5. Conclusions
- The precision camera and naked eye observation show that all test blocks printed by SLM technology are in good shape without obvious macro defects, such as deformation, bubbles, or large cracks. The printed test blocks have a high degree of reduction;
- Under unidirectional compression test and numerical simulation, a continuous hardening of the Gyroid curved and truss lattice structures on the stress–strain curves is observed, and the stress softening and fluctuation are negligible;
- Due to shear stress, the surface structure of Primitive showed obvious softening and stress fluctuation on the stress–strain curve. The Bcc lattice structure also shows slight stress fluctuations on the curve due to the yield failure of its rigid rods;
- The result of numerical simulation has a high coincidence with the structure of the compression experiment. The difference between the two mainly lies in the fact that the printing process cannot achieve the perfect reduction of the structure, and that the external conditions of the compression experiment are changeable, therefore all conditions cannot be taken into account in the simulation;
- The Gyroid TPMS significantly outperforms the other three in stiffness (Young’s modulus), strength (yield stress, plateau stress), and energy absorption (toughness). The second is the truss lattice structure, which still has excellent mechanical properties;
- Through the exploration of the mechanical properties of the four structures, the superiority of the TPMS structure can be concluded, which can be used as a reference for future topological structure research.
Author Contributions
Funding
Conflicts of Interest
References
- Tofail, S.A.; Koumoulos, E.P.; Bandyopadhyay, A.; Bose, S.; O’Donoghue, L.; Charitidis, C. Additive manufacturing: Scientific and technological challenges, market uptake and opportunities. Mater. Today 2018, 21, 22–37. [Google Scholar] [CrossRef]
- Lim, Y.-E.; Kim, N.-H.; Choi, H.-J.; Park, K. Design for additive manufacturing of customized cast with porous shell structures. J. Mech. Sci. Technol. 2017, 31, 5477–5483. [Google Scholar] [CrossRef]
- Goh, G.D.; Agarwala, S.; Goh, G.L.; Dikshit, V.; Sing, S.L.; Yeong, W.Y. Additive manufacturing in unmanned aerial vehicles (UAVs): Challenges and potential. Aerosp. Sci. Technol. 2017, 63, 140–151. [Google Scholar] [CrossRef]
- Liu, J.; Ren, Y.; Chen, R.; Wu, Y.; Lei, W. The Effect of Pore Structure on Impact Behavior of Concrete Hollow Brick, Autoclaved Aerated Concrete and Foamed Concrete. Materials 2022, 15, 4075. [Google Scholar] [CrossRef] [PubMed]
- Abdi, M.; Ashcroft, I.; Wildman, R.D. Design optimisation for an additively manufactured automotive component. Int. J. Powertrains 2018, 7, 142–161. [Google Scholar] [CrossRef]
- Melchels, F.P.W.; Feijen, J.; Grijpma, D.W. A review on stereolithography and its applications in biomedical engineering. Biomaterials 2010, 31, 6121–6130. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alomar, O.R.; Miguel, A.A.; Mendes, T.D.; Ray, S. Numerical simulation of complete liquidevapour phase change process inside porous media: A comparison between local thermal equilibrium and non-equilibrium models. Int. J. Therm. Sci. 2017, 112, 222–241. [Google Scholar] [CrossRef]
- Topkaya, T.; Solmaz, M.Y. Investigation of low velocity impact behaviors of honeycomb sandwich composites. J. Mech. Sci. Technol. 2018, 32, 3161–3167. [Google Scholar] [CrossRef]
- Yue, S.; Bai, Y.; Du, Z.; Zou, H.; Shi, W.; Zheng, G. Dynamic Behavior of Kinetic Projectile Impact on Honeycomb Sandwich Panels and Multi-Layer Plates. Crystals 2022, 12, 572. [Google Scholar] [CrossRef]
- Pham, M.-S.; Liu, C.; Todd, I.; Lertthanasarn, J. Damage-tolerant architected materials inspired by crystal microstructure. Nature 2019, 565, 305–311. [Google Scholar] [CrossRef]
- Lee, K.-W.; Lee, S.-H.; Noh, K.-H.; Park, J.-Y.; Cho, Y.-J.; Kim, S.-H. Theoretical and numerical analysis of the mechanical responses of BCC and FCC lattice structures. J. Mech. Sci. Technol. 2019, 33, 2259–2266. [Google Scholar] [CrossRef]
- Szatkiewicz, T.; Laskowska, D.; Bałasz, B.; Mitura, K. The Influence of the Structure Parameters on the Mechanical Properties of Cylindrically Mapped Gyroid TPMS Fabricated by Selective Laser Melting with 316L Stainless Steel Powder. Materials 2022, 15, 4352. [Google Scholar] [CrossRef] [PubMed]
- Kapfer, S.C.; Hyde, S.T.; Mecke, K.; Arns, C.H.; Schröder-Turk, G.E. Minimal surface scaffold designs for tissue engineering. Biomaterials 2011, 32, 6875–6882. [Google Scholar] [CrossRef] [PubMed]
- Rajagopalan, S.; Robb, R. Schwarz meets Schwann: Design and fabrication of biomorphic and durataxic tissue engineering scaffolds. Med. Image Anal. 2006, 10, 693–712. [Google Scholar] [CrossRef] [PubMed]
- Abueidda, D.W.; Bakir, M.; Abu Al-Rub, R.K.; Bergström, J.S.; Sobh, N.A.; Jasiuk, I. Mechanical properties of 3D printed poly-meric cellular materials with triply periodic minimal surface architectures. Mater. Des. 2017, 122, 255–267. [Google Scholar] [CrossRef]
- Al-Ketan, O.; Abu Al-Rub, R.K.; Rowshan, R. Mechanical Properties of a New Type of Architected Interpenetrating Phase Composite Materials. Adv. Mater. Technol. 2016, 2, 1600235. [Google Scholar] [CrossRef]
- Zhong, M.; Zhou, W.; Xi, H.; Liang, Y.; Wu, Z. Double-Level Energy Absorption of 3D Printed TPMS Cellular Structures via Wall Thickness Gradient Design. Materials 2021, 14, 6262. [Google Scholar] [CrossRef]
- Torquato, S.; Donev, A. Minimal surfaces and multifunctionality, Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences. R. Soc. 2004, 460, 1849–1856. [Google Scholar] [CrossRef]
- Jung, Y.; Torquato, S. Fluid permeabilities of triply periodic minimal surfaces. Phys. Rev. E 2005, 72, 056319. [Google Scholar] [CrossRef] [Green Version]
- Babaee, S.; Viard, N.; Wang, P.; Fang, N.X.; Bertoldi, K. Harnessing Deformation to Switch On and Off the Propagation of Sound. Adv. Mater. 2015, 28, 1631–1635. [Google Scholar] [CrossRef]
- Ha, Y.-H.; Vaia, R.A.; Lynn, W.F.; Costantino, J.P.; Shin, J.; Smith, A.B.; Matsudaira, P.T.; Thomas, E.L. Three-Dimensional Network Photonic Crystals via Cyclic Size Reduction/ Infiltration of Sea Urchin Exoskeleton. Adv. Mater. 2004, 16, 1091–1094. [Google Scholar] [CrossRef]
- Dong, L.; Deshpande, V.; Wadley, H. Mechanical response of Ti–6Al–4V octet-truss lattice structures. Int. J. Solids Struct. 2015, 60–61, 107–124. [Google Scholar] [CrossRef]
- Singh, S.; Bhatnagar, N. A survey of fabrication and application of metallic foams (1925–2017). J. Porous Mater. 2017, 25, 537–554. [Google Scholar] [CrossRef]
- Banhart, J.; Baumeister, J.; Weber, M. Damping properties of aluminium foams, Materials Science & Engineering A (Structural Ma-terials: Properties. Microstruct. Processing 1996, 205, 221–228. [Google Scholar]
- Rogkas, N.; Vakouftsis, C.; Spitas, V.; Lagaros, N.D.; Georgantzinos, S.K. Design Aspects of Additive Manufacturing at Microscale: A Review. Micromachines 2022, 13, 775. [Google Scholar] [CrossRef]
- Cheng, A.; Humayun, A.; Cohen, D.J.; Boyan, B.D.; Schwartz, Z. Additively manufactured 3D porous Ti-6Al-4V constructs mimic trabecular bone structure and regulate osteoblast proliferation, differentiation and local factor production in a porosity and surface roughness dependent manner. Biofabrication 2014, 6, 045007. [Google Scholar] [CrossRef]
- Wang, D.; Yang, Y.; Liu, R.; Xiao, D.; Sun, J. Study on the designing rules and processability of porous structure based on selective laser melting (SLM). J. Mater. Processing Technol. 2013, 213, 1734–1742. [Google Scholar] [CrossRef]
- Allaire, G.; Dapogny, C.; Estevez, R.; Faure, A.; Michailidis, G. Structural optimization under overhang constraints imposed by additive manufacturing technologies. J. Comput. Phys. 2017, 351, 295–328. [Google Scholar] [CrossRef] [Green Version]
- Sharma, F.; Dixit, U.S. Fuzzy set based cost model of additive manufacturing with specific example of selective laser sintering. J. Mech. Sci. Technol. 2019, 33, 4439–4449. [Google Scholar] [CrossRef]
- Li, R.; Kim, Y.S.; Van Tho, H.; Yum, Y.J.; Kim, W.J.; Yang, S.Y. Additive manufacturing (AM) of piercing punches by the PBF method of metal 3D printing using mold steel powder materials. J. Mech. Sci. Technol. 2019, 33, 809–817. [Google Scholar] [CrossRef]
- Singh, S.; Ramakrishna, S.; Singh, R. Material issues in additive manufacturing: A review. J. Manuf. Process. 2017, 25, 185–200. [Google Scholar] [CrossRef]
- Bikas, H.; Stavropoulos, P.; Chryssolouris, G. Additive manufacturing methods and modelling approaches: A critical review. Int. J. Adv. Manuf. Technol. 2015, 83, 389–405. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Feih, S.; Daynes, S.; Chang, S.; Wang, M.Y.; Wei, J.; Lu, W.F. Energy absorption characteristics of metallic triply periodic minimal surface sheet structures under compressive loading. Addit. Manuf. 2018, 23, 505–515. [Google Scholar] [CrossRef]
- Al-Ketan, O.; Rowshan, R.; Abu Al-Rub, R.K. Topology-mechanical property relationship of 3D printed strut, skeletal, and sheet based periodic metallic cellular materials. Addit. Manuf. 2018, 19, 167–183. [Google Scholar] [CrossRef]
- Lu, Y.; Wu, S.; Gan, Y.; Huang, T.; Yang, C.; Junjie, L.; Lin, J. Study on the microstructure, mechanical property and residual stress of SLM Inconel-718 alloy manufactured by differing island scanning strategy. Opt. Laser Technol. 2015, 75, 197–206. [Google Scholar] [CrossRef]
- Riemer, A.; Leuders, S.; Thöne, M.; Richard, H.; Tröster, T.; Niendorf, T. On the fatigue crack growth behavior in 316L stainless steel manufactured by selective laser melting. Eng. Fract. Mech. 2014, 120, 15–25. [Google Scholar] [CrossRef]
- Abueidda, D.W.; Abu Al-Rub, R.; Dalaq, A.S.; Lee, D.-W.; Khan, K.A.; Jasiuk, I. Effective conductivities and elastic moduli of novel foams with triply periodic minimal surfaces. Mech. Mater. 2016, 95, 102–115. [Google Scholar] [CrossRef]
- Lee, M.G.; Lee, J.W.; Han, S.C.; Kang, K. Mechanical analyses of “Shellular”, an ultralow-density material. Acta Mater. 2016, 103, 595–607. [Google Scholar] [CrossRef]
- ISO 13314:2011; Mechanical testing of metals—ductility testing—compression test for porous and cellular metals. International Organization for Standardization: Geneva, Switzerland, 2011.






| Name | TPMS Function | Unit Interval |
|---|---|---|
| Primitive | (0, 2π) | |
| Gyroid | (0, 2π) | |
| Diamond | (−π, π) | |
| I-WP | (0, 2π) | |
| Neovius | (0, 2π) |
| Structure | Nominal Shell Thickness (mm) | Measured Shell Thickness (mm) | Nominal Cell Size (mm) | Nominal Relative Density [-] | Measured Relative Density [-] |
|---|---|---|---|---|---|
| Bcc lattice | 2 | 1.94 ± 0.01 | 10.2 | 0.3 | 0.295 ± 0.000 |
| 2.45 | 2.35 ± 0.01 | 12.5 | 0.3 | 0.293 ± 0.001 | |
| 3 | 2.95 ± 0.01 | 15.3 | 0.3 | 0.288 ± 0.001 | |
| Primitive | 1 | 0.89 ± 0.01 | 15.2 | 0.3 | 0.289 ± 0.001 |
| 1.5 | 1.38 ± 0.01 | 17.5 | 0.3 | 0.290 ± 0.003 | |
| 2 | 1.91 ± 0.01 | 19.2 | 0.3 | 0.288 ± 0.001 | |
| Gyroid | 1.5 | 1.40 ± 0.01 | 15.4 | 0.3 | 0.283 ± 0.000 |
| 2.5 | 2.39 ± 0.01 | 25.7 | 0.3 | 0.279 ± 0.001 | |
| 3.5 | 3.38 ± 0.01 | 36.1 | 0.3 | 0.291 ± 0.001 | |
| Truss lattice | 2.7 | 2.66 ± 0.01 | 7.6 | 0.3 | 0.298 ± 0.003 |
| 3.5 | 3.42 ± 0.01 | 9.8 | 0.3 | 0.295 ± 0.001 | |
| 4.5 | 4.47 ± 0.01 | 12.6 | 0.3 | 0.295 ± 0.001 |
| Parameter | Value |
|---|---|
| Laser power | 500 W |
| Laser type | Fiber Laser (IPG) |
| Powder spreading method | Scraper powder spreading |
| Layer thickness | 0.03 mm |
| Scan speed | 2000 mm/s |
| Spot size | 0.05~0.15 mm |
| Ambient temperature | 20~26 °C |
| Hatch spacing | 0.1 mm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Teng, F.; Sun, Y.; Guo, S.; Gao, B.; Yu, G. Topological and Mechanical Properties of Different Lattice Structures Based on Additive Manufacturing. Micromachines 2022, 13, 1017. https://doi.org/10.3390/mi13071017
Teng F, Sun Y, Guo S, Gao B, Yu G. Topological and Mechanical Properties of Different Lattice Structures Based on Additive Manufacturing. Micromachines. 2022; 13(7):1017. https://doi.org/10.3390/mi13071017
Chicago/Turabian StyleTeng, Fei, Yongguo Sun, Shuai Guo, Bingwei Gao, and Guangbin Yu. 2022. "Topological and Mechanical Properties of Different Lattice Structures Based on Additive Manufacturing" Micromachines 13, no. 7: 1017. https://doi.org/10.3390/mi13071017
APA StyleTeng, F., Sun, Y., Guo, S., Gao, B., & Yu, G. (2022). Topological and Mechanical Properties of Different Lattice Structures Based on Additive Manufacturing. Micromachines, 13(7), 1017. https://doi.org/10.3390/mi13071017





