Rational Design of Microfluidic Glaucoma Stent
Abstract
:1. Introduction
2. Numerical Methods
3. Mathematical Models
3.1. Circuit Model of Stent Flow
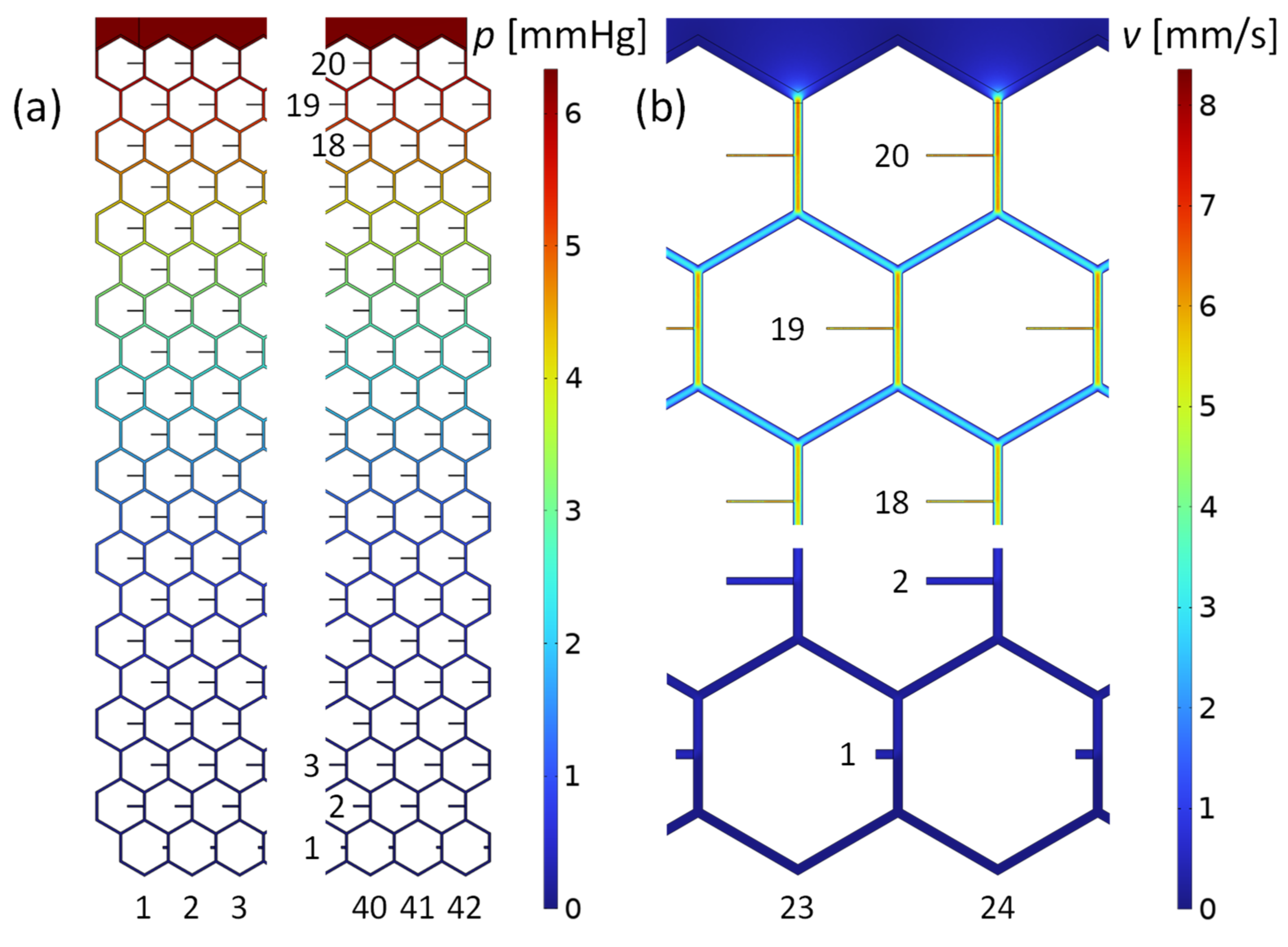
3.2. Numerical Model of Stent Flow
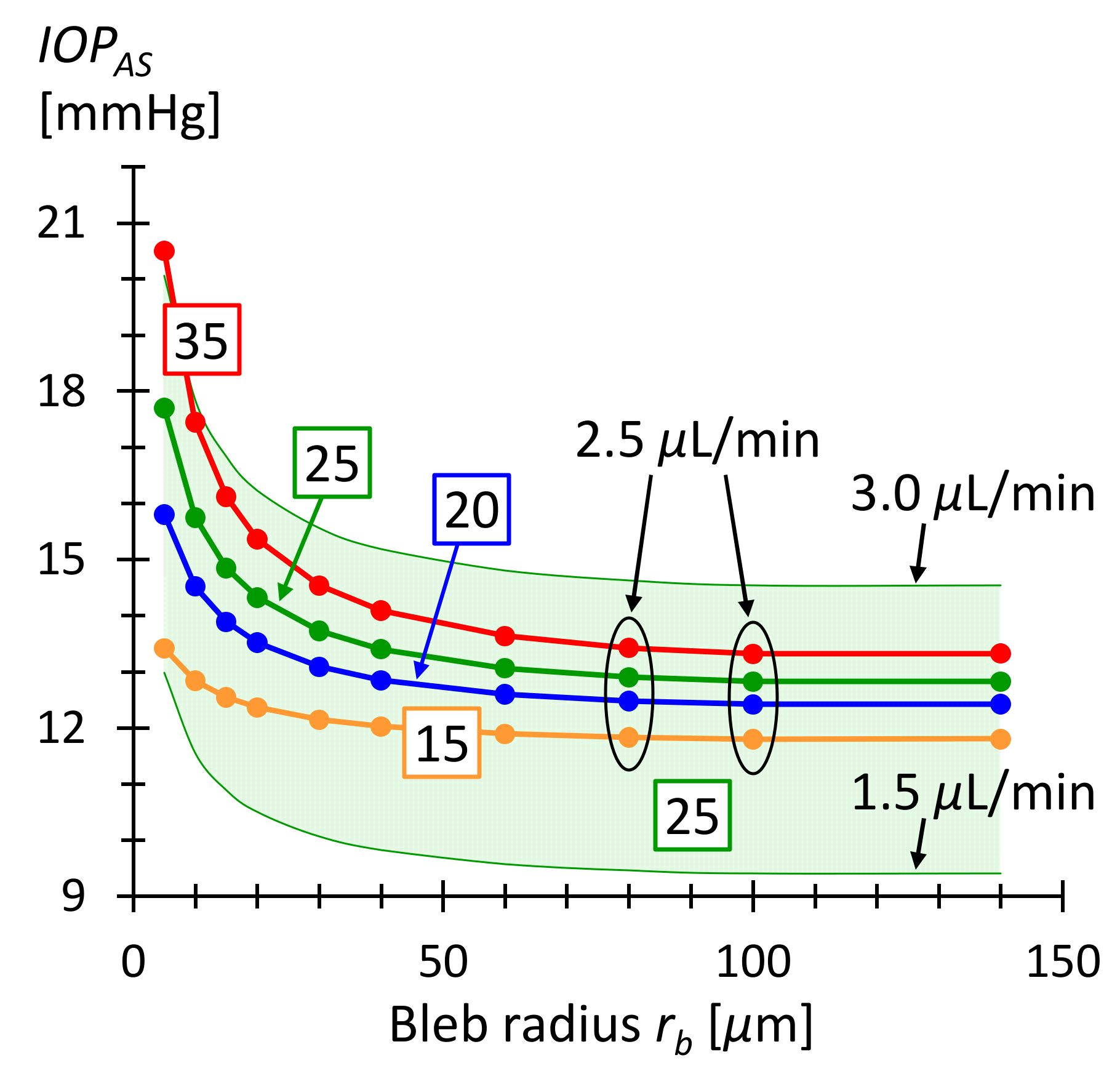
3.3. Model of Drainage to Subconjunctival Tissue
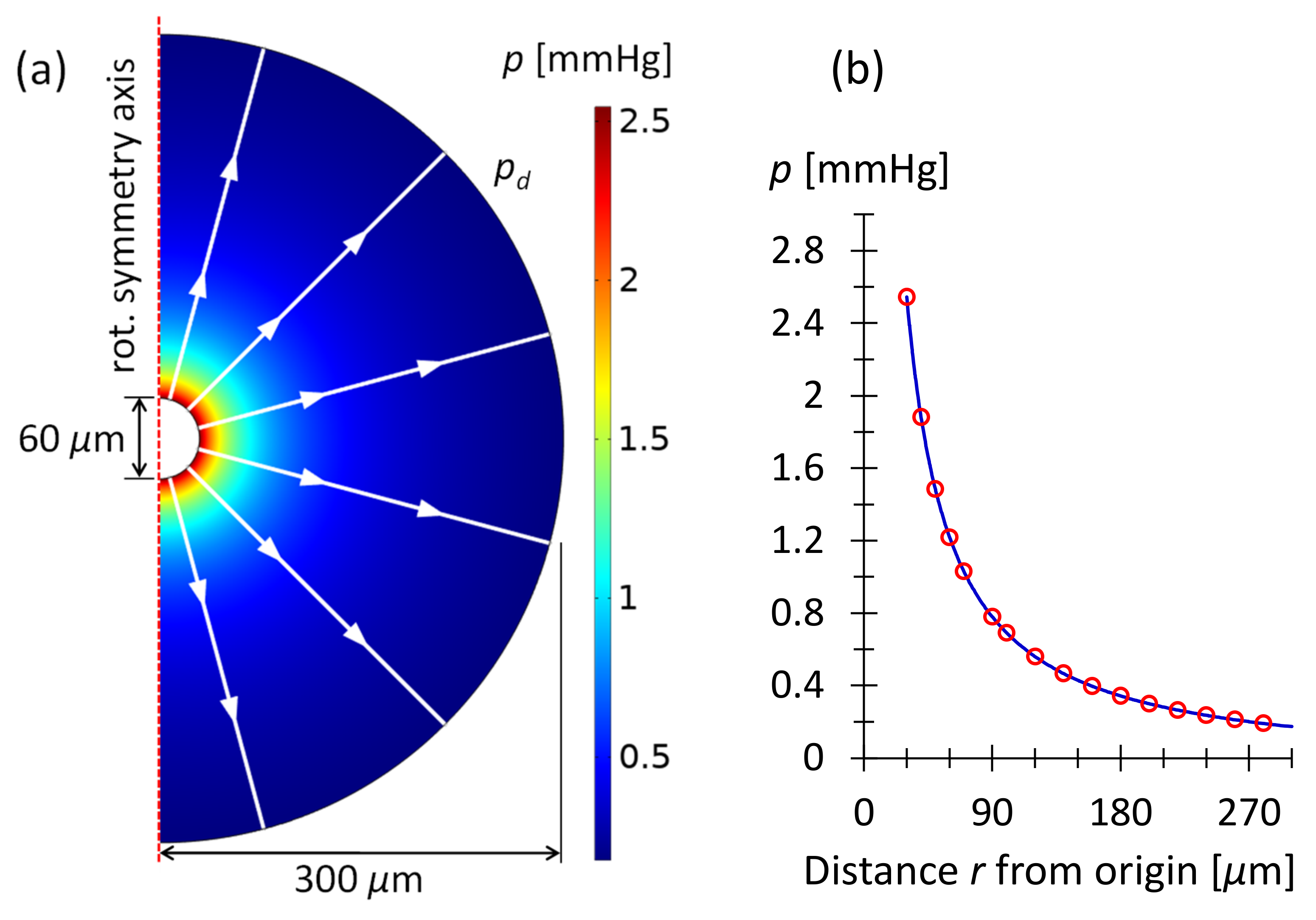
3.3.1. Drainage from Hemispherical Microbleb
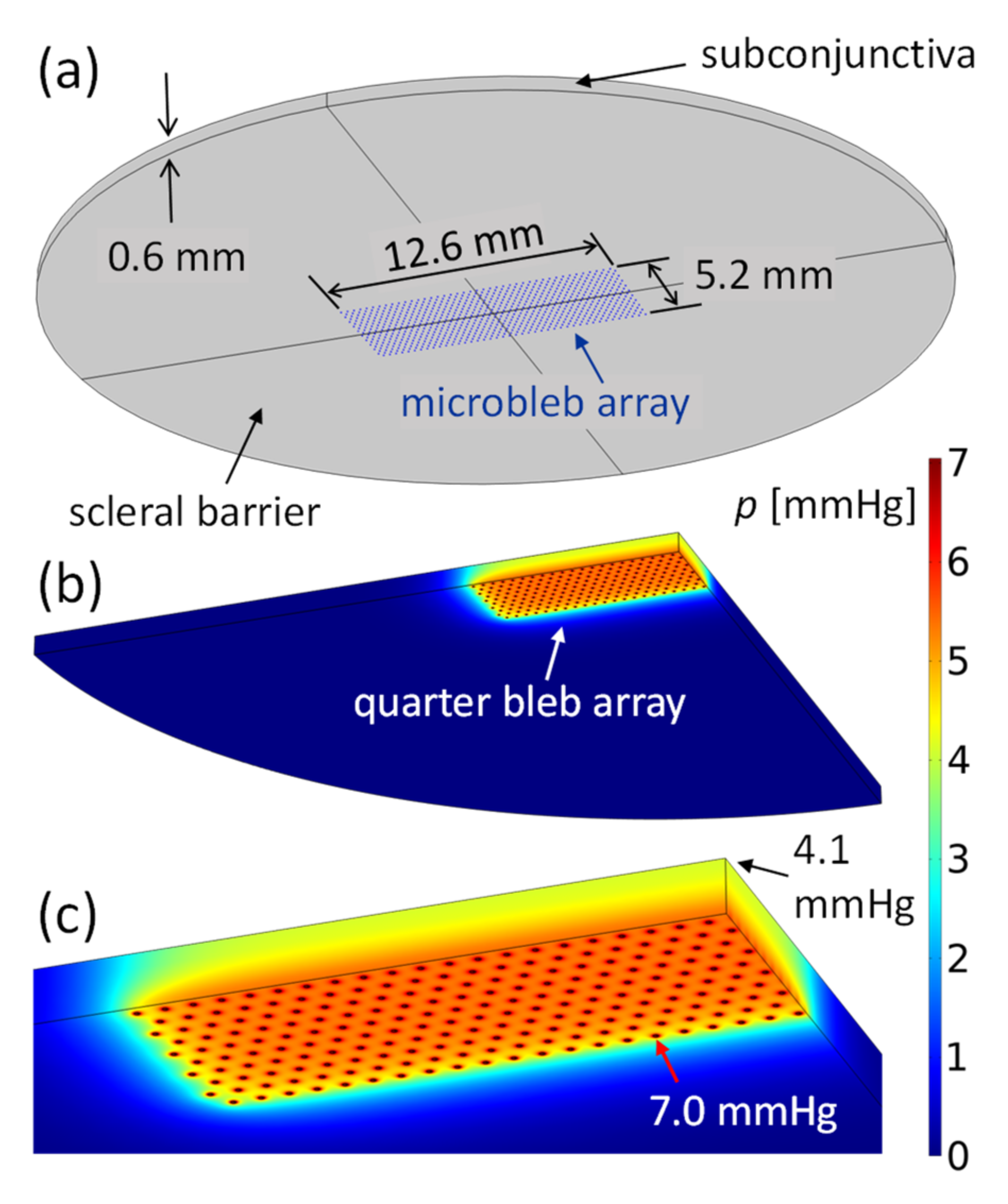
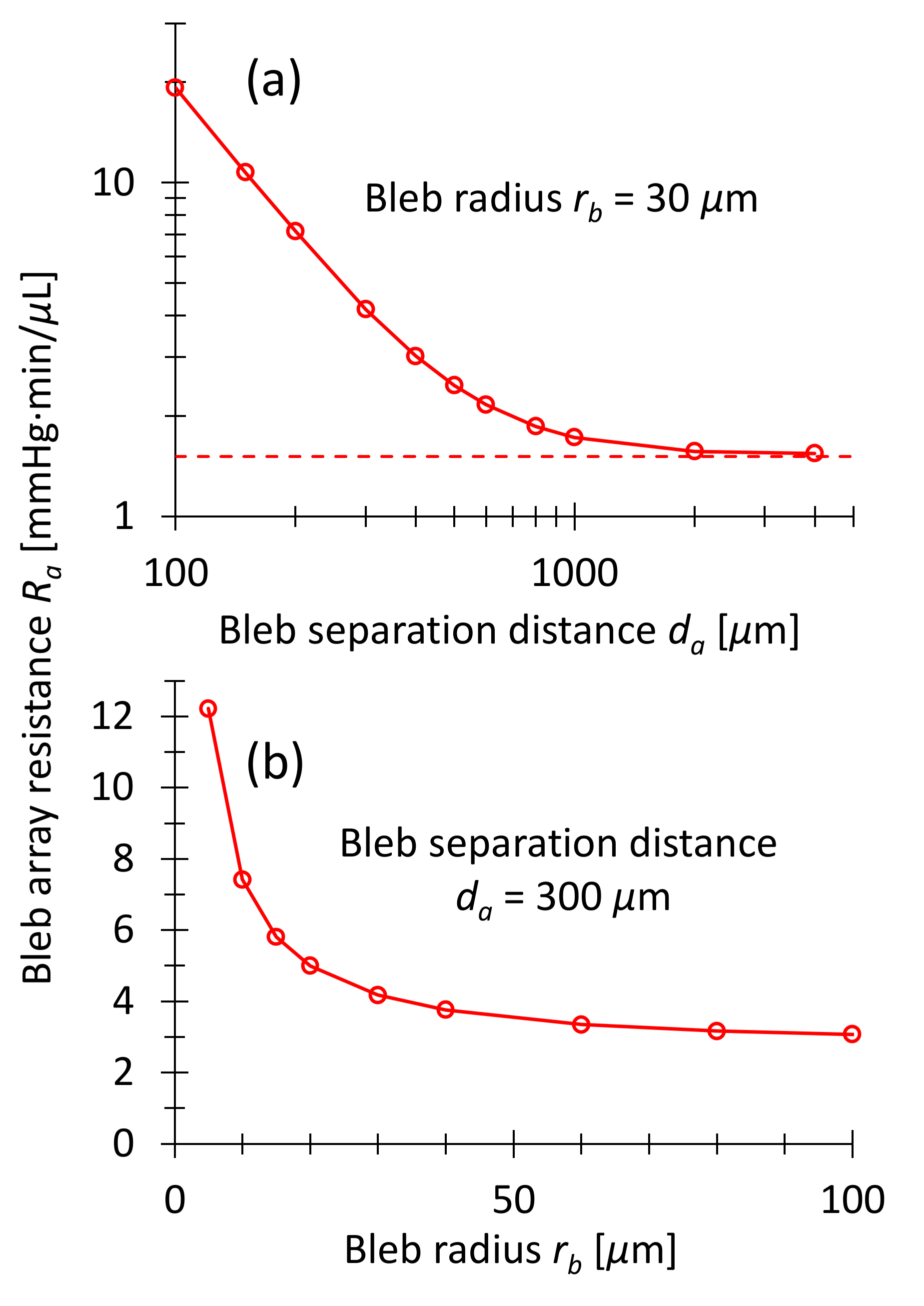
3.3.2. Drainage from Bleb Array
3.4. IOP after Surgery
3.5. Study Limitations
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
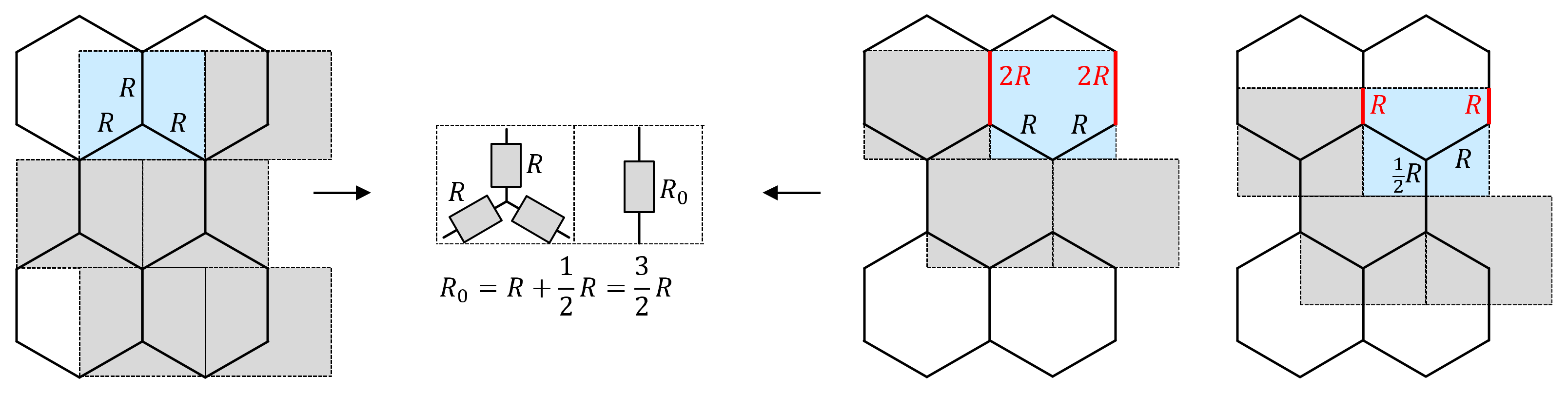
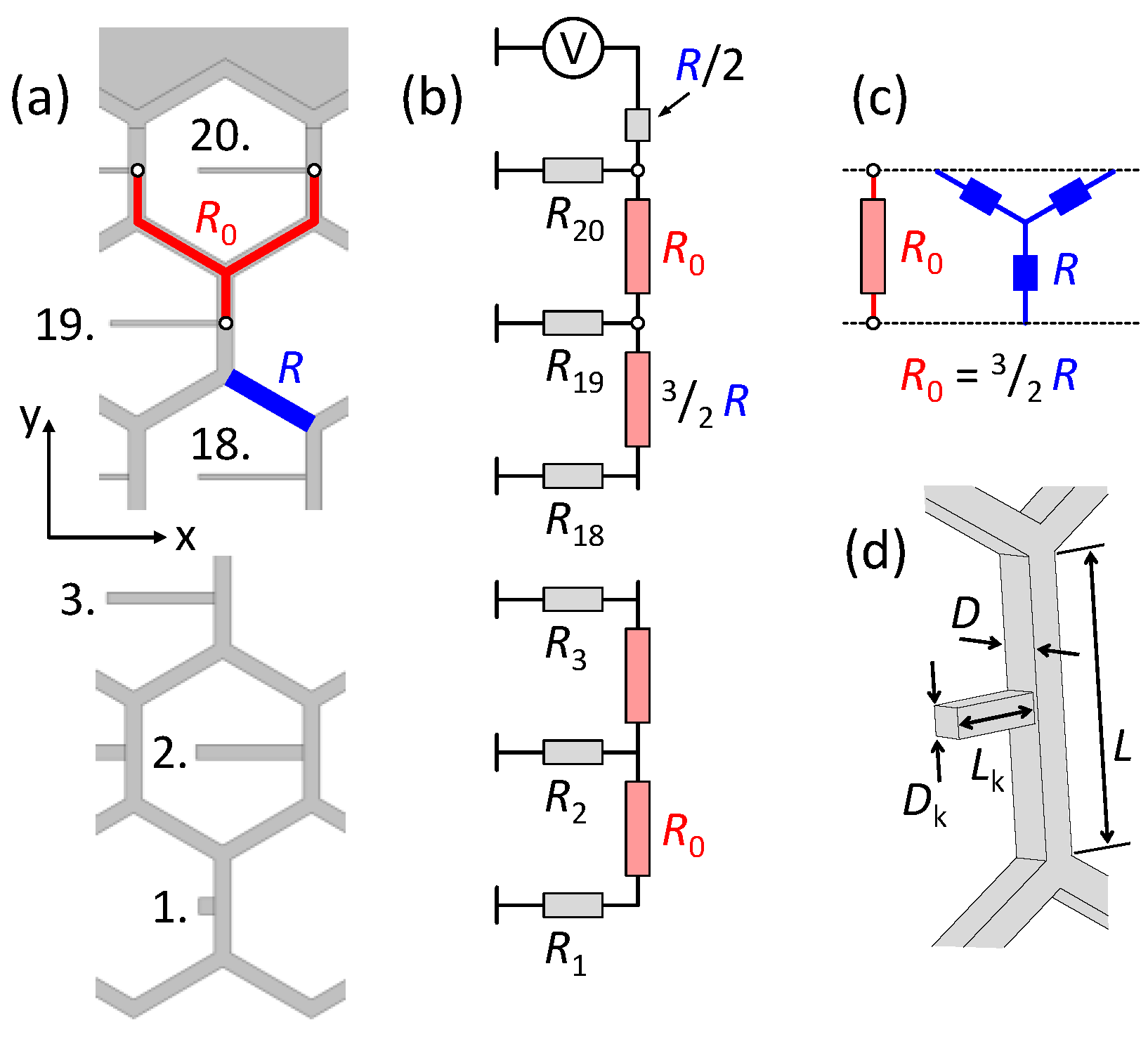
Appendix A. Calculation of Resistance
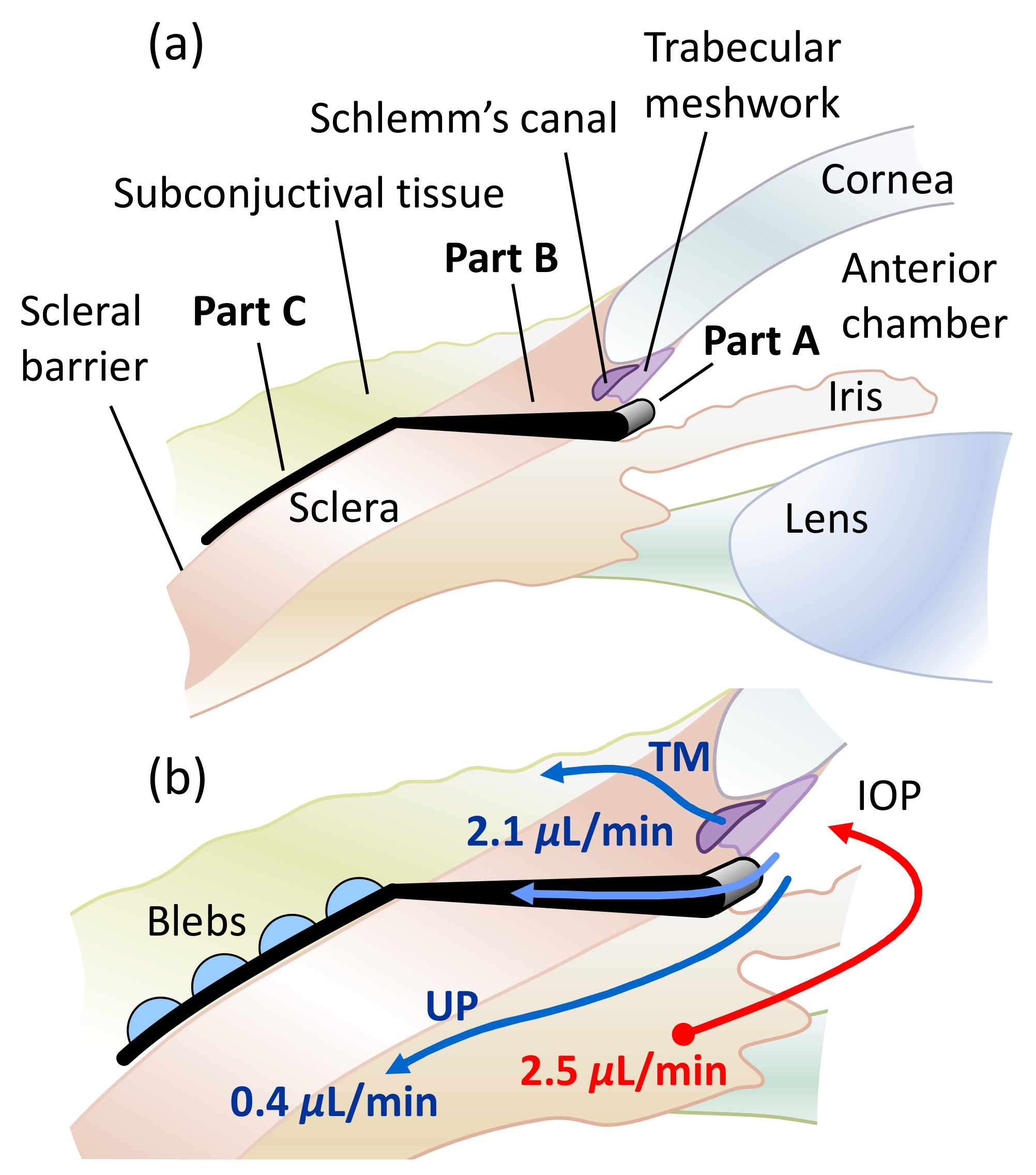
Appendix B. Aqueous Humor Production Rate and Uveoscleral Outflow
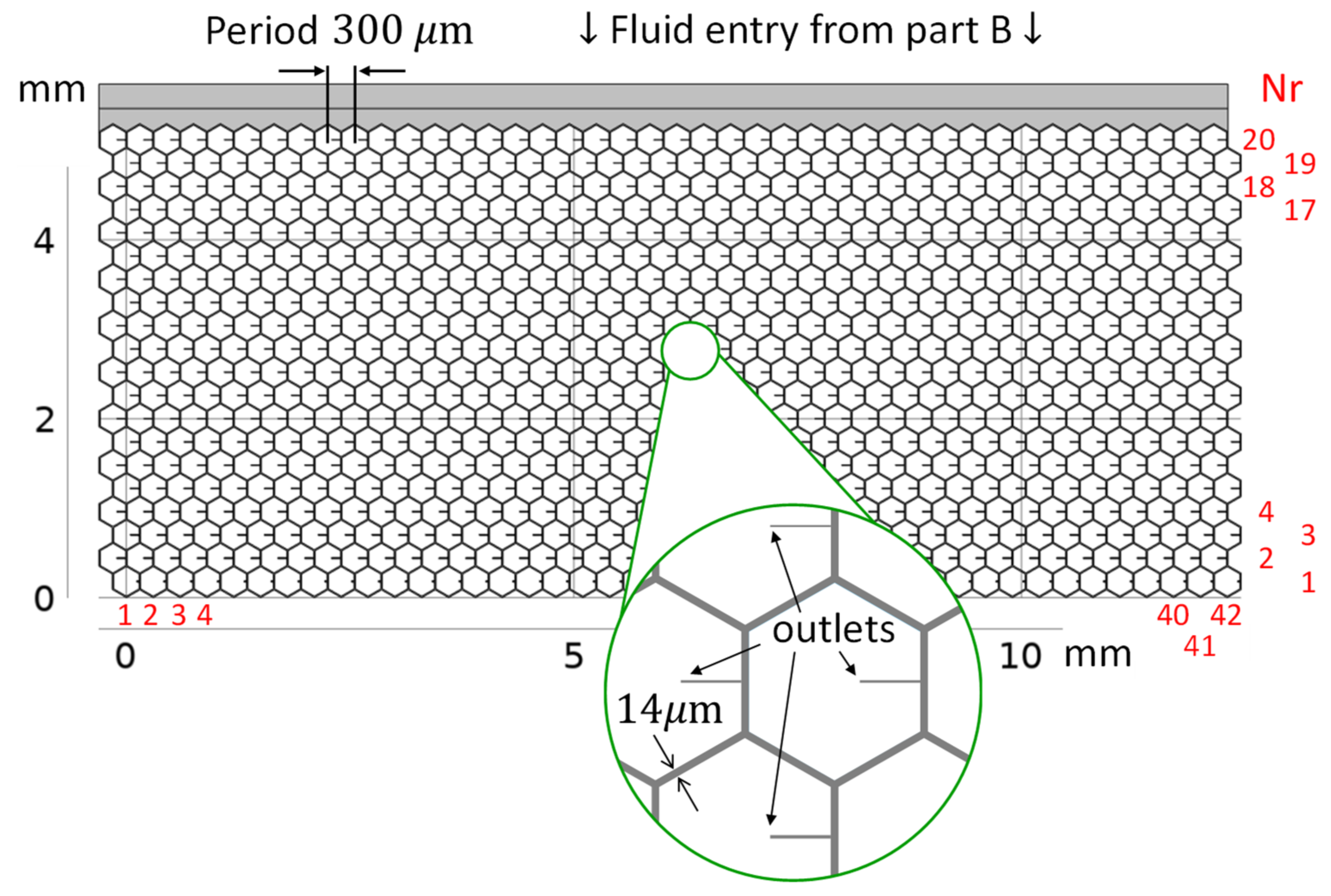
Appendix C. Step-by-Step Procedure for a Hexagonal Glaucoma Stent Design
| Steps | Input | Input | Output | Equation |
|---|---|---|---|---|
| 1 | measured before surgery, e.g., | targeted after surgery, e.g., | Serial outflow resistance of stent and bleb array | Equation (16), e.g., |
| 2 | Hemispherical bleb radius for COMSOL simulation, e.g., | Bleb spacing in array for COMSOL simulation, e.g., | Bleb array drainage resistance | where is the pressure in the blebs from COMSOL simulation and is the flow rate through the stent, e.g., Equation (13), where is the number of outlets |
| 3 | (from step 1) | (from step 2) | Stent flow resistance | |
| 4 | Number of stent columns, e.g., | Number of stent rows, e.g., | Number of stent outlets and micro blebs | |
| 5 | Stent column resistance | Fix lowest stent outlet resistance, e.g., | Stent flow resistance connecting two outlet tubes | Equation (5) |
| 6 | Hexagonal segment flow resistance | Bleb spacing | Channel length and cross section width of hex. segment | (geometry of hexagon) Equations (1) and (2) |
| 7 | (from step 5) | Lowest stent outlet resistance (from step 5) | Flow resistance of outlet tube in row number | Equation (4) |
| 8 | Length of straight outlet tube, e.g., | Row number | Cross section width of outlet tube | Equation (3) |
Appendix D. List of Parameters Used for Calculations
| Parameter | Value | SI Units | Description |
|---|---|---|---|
| Density of fluid, of AH | |||
| Dynamic viscosity of liquid | |||
| Hydraulic conductivity in subconjunctival tissue [6] | |||
| Fluid permeability in subconjunctival tissue, used in Equation (6) | |||
| Used in Equation (6) | |||
| Hydraulic permeability of blood vessel wall [6] | |||
| Vessel wall area per tissue volume [6] | |||
| Characteristic drainage length, used in Equation (8) | |||
| Typical AH production rate | |||
| Constant outflow rate through uveoscleral pathway | |||
| Episcleral venous pressure, ranging from to [6] |
References
- Allison, K.; Patel, D.; Alabi, O. Epidemiology of Glaucoma: The Past, Present, and Predictions for the Future. Cureus 2020, 12, e11686. [Google Scholar] [CrossRef] [PubMed]
- Zhang, N.; Wang, J.; Li, Y.; Jiang, B. Prevalence of primary open angle glaucoma in the last 20 years: A meta-analysis and systematic review. Sci. Rep. 2021, 11, 13762. [Google Scholar] [CrossRef] [PubMed]
- Tham, Y.C.; Li, X.; Wong, T.Y.; Quigley, H.A.; Aung, T.; Cheng, C.Y. Global prevalence of glaucoma and projections of glaucoma burden through 2040: A systematic review and meta-analysis. Ophthalmology 2014, 121, 2081–2090. [Google Scholar] [CrossRef] [PubMed]
- Lee, R.M.H.; Bouremel, Y.; Eames, I.; Brocchini, S.; Khaw, P.T. Translating Minimally Invasive Glaucoma Surgery Devices. Clin. Transl. Sci. 2020, 13, 14–25. [Google Scholar] [CrossRef] [Green Version]
- Do, A.T.; Parikh, H.; Panarelli, J.F. Subconjunctival microinvasive glaucoma surgeries: An update on the Xen gel stent and the PreserFlo MicroShunt. Curr. Opin. Ophthalmol. 2020, 31, 132–138. [Google Scholar] [CrossRef]
- Gardiner, B.S.; Smith, D.W.; Coote, M.; Crowston, J.G. Computational modeling of fluid flow and intra-ocular pressure following glaucoma surgery. PLoS ONE 2010, 5, e13178. [Google Scholar] [CrossRef] [Green Version]
- Zada, M.; Pattamatta, U.; White, A. Modulation of Fibroblasts in Conjunctival Wound Healing. Ophthalmology 2018, 125, 179–192. [Google Scholar] [CrossRef]
- Yamanaka, O.; Kitano-Izutani, A.; Tomoyose, K.; Reinach, P.S. Pathobiology of wound healing after glaucoma filtration surgery. BMC Ophthalmol. 2015, 15, 19–27. [Google Scholar] [CrossRef] [Green Version]
- Andrew, N.H.; Akkach, S.; Casson, R.J. A review of aqueous outflow resistance and its relevance to microinvasive glaucoma surgery. Surv. Ophthalmol. 2019, 65, 18–31. [Google Scholar] [CrossRef] [Green Version]
- Fea, A.M.; Durr, G.M.; Marolo, P.; Malinverni, L.; Economou, M.A.; Ahmed, I. Xen® gel stent: A comprehensive review on its use as a treatment option for refractory glaucoma. Clin. Ophthalmol. 2020, 14, 1805–1832. [Google Scholar] [CrossRef]
- Wang, J.; Barton, K. Overview of MIGS. In Minimally Invasive Glaucoma Surgery; Springer: Singapore, 2021; pp. 1–10. [Google Scholar] [CrossRef]
- Lenzhofer, M.; Hohensinn, M.; Strohmaier, C.; Reitsamer, H.A. Subconjunctival minimally invasive glaucoma surgery: Methods and clinical results. Ophthalmologe 2018, 115, 381–387. [Google Scholar] [CrossRef] [Green Version]
- Green, W.; Lind, J.T.; Sheybani, A. Review of the Xen Gel Stent and InnFocus MicroShunt. Curr. Opin. Ophthalmol. 2018, 29, 162–170. [Google Scholar] [CrossRef]
- Ishida, K.; Nakano, Y.; Ojino, K.; Shimazawa, M.; Otsuka, T.; Inagaki, S.; Kawase, K.; Hara, H.; Yamamoto, T. Evaluation of Bleb Characteristics after Trabeculectomy and Glaucoma Implant Surgery in the Rabbit. Ophthalmic Res. 2020, 64, 68–76. [Google Scholar] [CrossRef]
- Fea, A.M.; Spinetta, R.; Cannizzo, P.M.L.; Consolandi, G.; Lavia, C.; Aragno, V.; Germinetti, F.; Rolle, T. Evaluation of Bleb Morphology and Reduction in IOP and Glaucoma Medication following Implantation of a Novel Gel Stent. J. Ophthalmol. 2017, 2017, 9364910. [Google Scholar] [CrossRef]
- Shobayashi, K.; Inoue, T.; Kawai, M.; Iwao, K.; Ohira, S.; Kojima, S.; Kuroda, U.; Nakashima, K.; Tanihara, H. Postoperative changes in aqueous monocyte chemotactic protein-1 levels and bleb morphology after trabeculectomy vs. Ex-PRESS shunt surgery. PLoS ONE 2015, 10, e0139751. [Google Scholar] [CrossRef]
- Kokubun, T.; Yamamoto, K.; Sato, K.; Akaishi, T.; Shimazaki, A.; Nakamura, M.; Shiga, Y.; Tsuda, S.; Omodaka, K.; Nakazawa, T. The effectiveness of colchicine combined with mitomycin C to prolong bleb function in trabeculectomy in rabbits. PLoS ONE 2019, 14, e0213811. [Google Scholar] [CrossRef] [Green Version]
- Amoozgar, B.; Wei, X.; Lee, J.H.; Bloomer, M.; Zhao, Z.; Coh, P.; He, F.; Luan, L.; Xie, C.; Han, Y. A novel flexible microfluidic meshwork to reduce fibrosis in glaucoma surgery. PLoS ONE 2017, 12, e0172556. [Google Scholar] [CrossRef]
- Hinkle, D.M.; Zurakowski, D.; Ayyala, R.S. A comparison of the polypropylene plate AhmedTM glaucoma valve to the silicone plate AhmedTM glaucoma flexible valve. Eur. J. Ophthalmol. 2007, 17, 696–701. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties, 2nd ed.; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar] [CrossRef]
- COMSOL Multiphysics 5.6. 2020. Available online: https://www.comsol.com/comsol-multiphysics (accessed on 16 June 2022).
- Kudsieh, B.; Fernández-Vigo, J.I.; Agujetas, R.; Montanero, J.M.; Ruiz-Moreno, J.M.; Fernández-Vigo, J.Á.; García-Feijóo, J. Numerical model to predict and compare the hypotensive efficacy and safety of minimally invasive glaucoma surgery devices. PLoS ONE 2020, 15, e0239324. [Google Scholar] [CrossRef]
- Sheybani, A.; Reitsamer, H.; Ahmed, I.I.K. Fluid dynamics of a novel micro-fistula implant for the surgical treatment of glaucoma. Investig. Ophthalmol. Vis. Sci. 2015, 56, 4789–4795. [Google Scholar] [CrossRef]
- Bruus, H. Theoretical Microfluidics; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Ethier, C.R.; Johnson, M.; Ruberti, J. Ocular biomechanics and biotransport. Annu. Rev. Biomed. Eng. 2004, 6, 249–273. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Villamarin, A.; Roy, S.; Hasballa, R.; Vardoulis, O.; Reymond, P.; Stergiopulos, N. 3D simulation of the aqueous flow in the human eye. Med. Eng. Phys. 2012, 34, 1462–1470. [Google Scholar] [CrossRef] [PubMed]
- Alm, A.; Nilsson, S.F.E. Uveoscleral outflow—A review. Exp. Eye Res. 2009, 88, 760–768. [Google Scholar] [CrossRef] [PubMed]
- Szopos, M.; Cassani, S.; Guidoboni, G.; Prud’homme, C.; Sacco, R.; Siesky, B.; Harris, A. Mathematical modeling of aqueous humor flow and intraocular pressure under uncertainty: Towards individualized glaucoma management. Model Artif. Intell. Ophthalmol. 2016, 1, 29–39. [Google Scholar] [CrossRef]
- Jain, R.K.; Tong, R.T.; Munn, L.L. Effect of vascular normalization by antiangiogenic therapy on interstitial hypertension, peritumor edema, and lymphatic metastasis: Insights from a mathematical model. Cancer Res. 2007, 67, 2729–2735. [Google Scholar] [CrossRef] [Green Version]
- Jonušauskas, L.; Baravykas, T.; Andrijec, D.; Gadišauskas, T.; Purlys, V. Stitchless support-free 3D printing of free-form micromechanical structures with feature size on-demand. Sci. Rep. 2019, 9, 17533. [Google Scholar] [CrossRef] [Green Version]
- Merkininkaitė, G.; Gailevičius, D.; Šakirzanovas, S.; Jonušauskas, L. Polymers for Regenerative Medicine Structures Made via Multiphoton 3D Lithography. Int. J. Polym. Sci. 2019, 2019, 3403548. [Google Scholar] [CrossRef]
- Mačiulaitis, J.; Deveikyte, M.; Rekštyte, S.; Bratchikov, M.; Darinskas, A.; Šimbelyte, A.; Daunoras, G.; Laurinavičiene, A.; Laurinavičius, A.; Gudas, R.; et al. Preclinical study of SZ2080 material 3D microstructured scaffolds for cartilage tissue engineering made by femtosecond direct laser writing lithography. Biofabrication 2015, 7, 015015. [Google Scholar] [CrossRef]
- Maus, T.L.; Brubaker, R.F. Measurement of aqueous humor flow by fluorophotometry in the presence of a dilated pupil. IOVS 1999, 40, 542–546. [Google Scholar]
- Gabelt, B.T.; Kaufman, P.L. Changes in aqueous humor dynamics with age and glaucoma. Prog. Retin. Eye Res. 2005, 24, 612–637. [Google Scholar] [CrossRef]
- Beltran-Agullo, L.; Alaghband, P.; Rashid, S.; Gosselin, J.; Obi, A.; Husain, R.; Lim, K.S. Comparative human aqueous dynamics study between black and white subjects with glaucoma. Investig. Ophthalmol. Vis. Sci. 2011, 52, 9425–9430. [Google Scholar] [CrossRef] [Green Version]
- Nilsson, S.F.E. The uveoscleral outflow routes. Eye 1997, 11, 149–154. [Google Scholar] [CrossRef]
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 |
| Equation (1) | ||||
| Equation (2) | ||||
| Equation (3) | ||||
| Equation (5) | Resistance of a whole column composed of 20 rows | |||
| Resistance of a whole stent meshwork composed of 20 rows and 42 columns | ||||
| 1.7 | specified | typical stent flow rate | ||
| Flow rate of a whole column of 20 outlet tubes | ||||
| Flow rate of a single outlet tube | ||||
| COMSOL simulations | Section 3.2. and Figure 4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Graf, T.; Kancerevycius, G.; Jonušauskas, L.; Eberle, P. Rational Design of Microfluidic Glaucoma Stent. Micromachines 2022, 13, 978. https://doi.org/10.3390/mi13060978
Graf T, Kancerevycius G, Jonušauskas L, Eberle P. Rational Design of Microfluidic Glaucoma Stent. Micromachines. 2022; 13(6):978. https://doi.org/10.3390/mi13060978
Chicago/Turabian StyleGraf, Thomas, Gitanas Kancerevycius, Linas Jonušauskas, and Patric Eberle. 2022. "Rational Design of Microfluidic Glaucoma Stent" Micromachines 13, no. 6: 978. https://doi.org/10.3390/mi13060978
APA StyleGraf, T., Kancerevycius, G., Jonušauskas, L., & Eberle, P. (2022). Rational Design of Microfluidic Glaucoma Stent. Micromachines, 13(6), 978. https://doi.org/10.3390/mi13060978






