A Parametric Analysis of Capillary Height in Single-Layer, Small-Scale Microfluidic Artificial Lungs
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
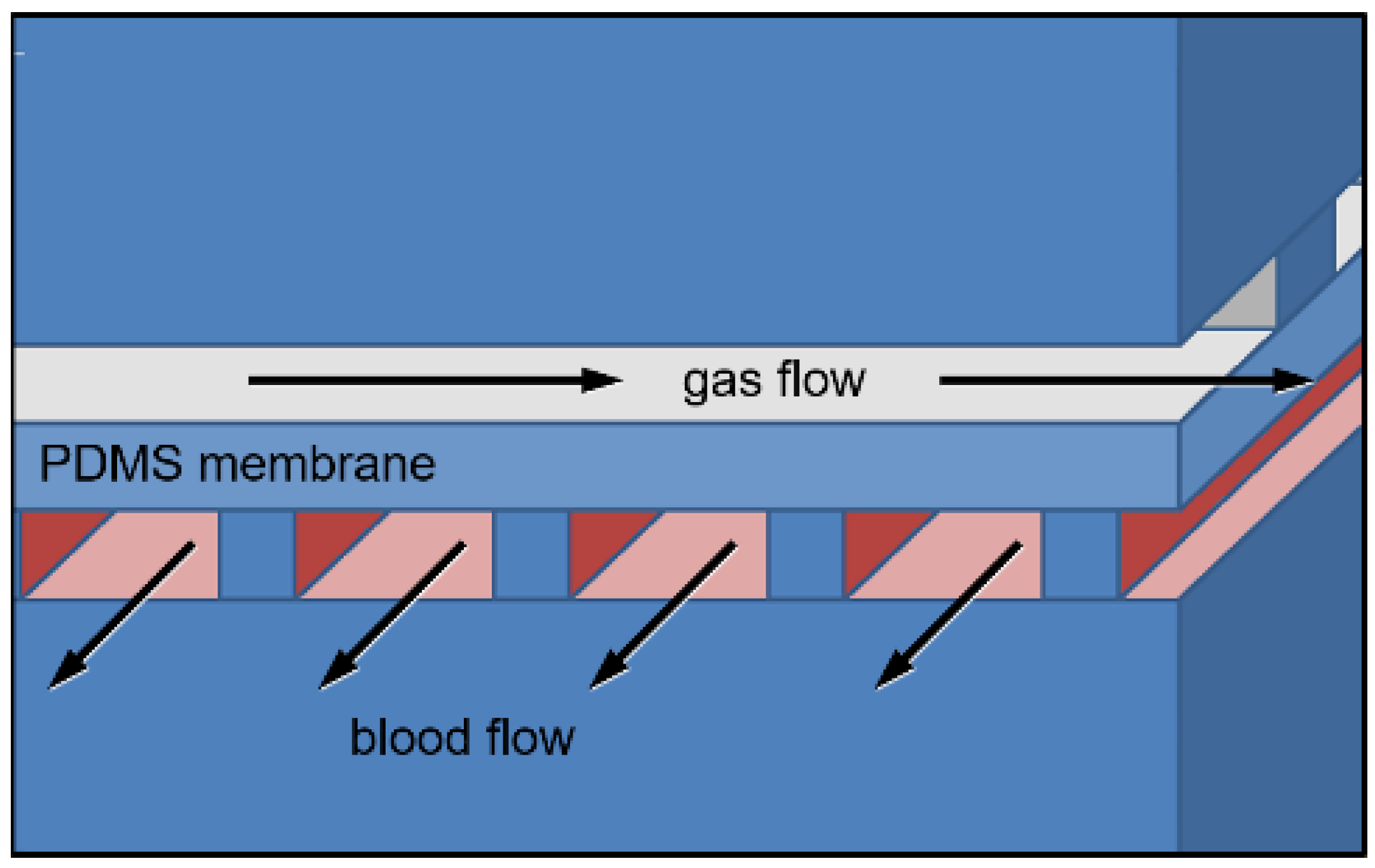
2.2. Mathematical Models of μALs with 10–100 μm Tall Capillaries
2.3. Computer Aided Drawing and 3D Modeling
2.4. Blood and Gas Mold Construction
2.5. Device Construction
2.6. In Vitro Flow Experiments
2.7. Statistics
3. Results
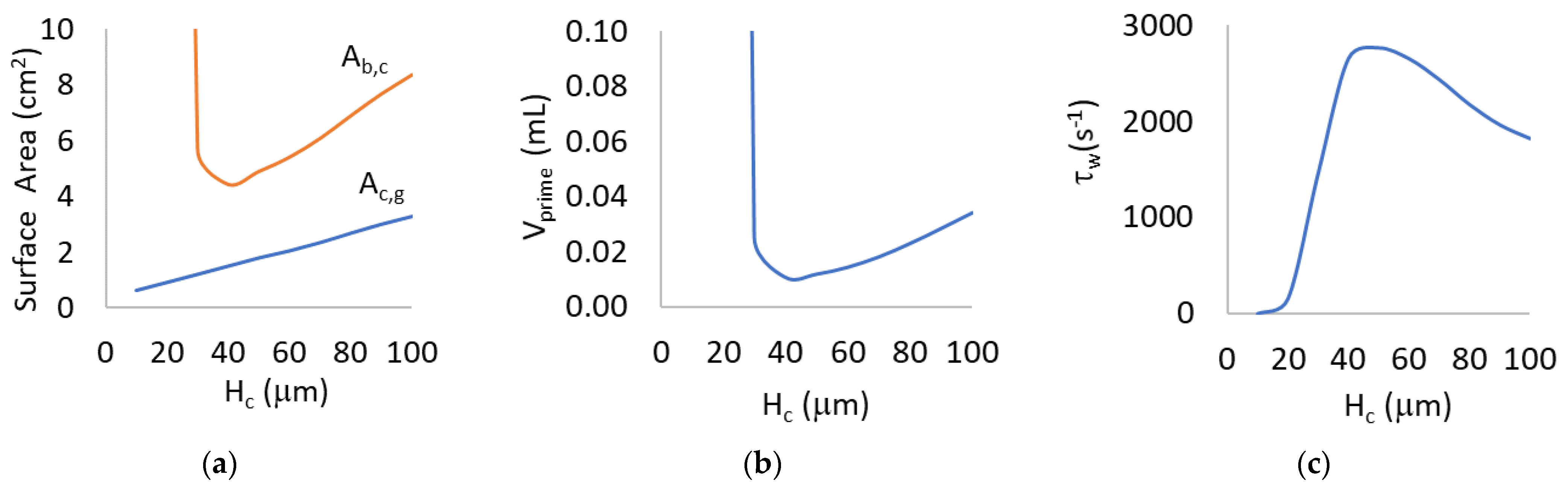
3.1. Mathematical Modeling for Hc = 10 to 100 μm
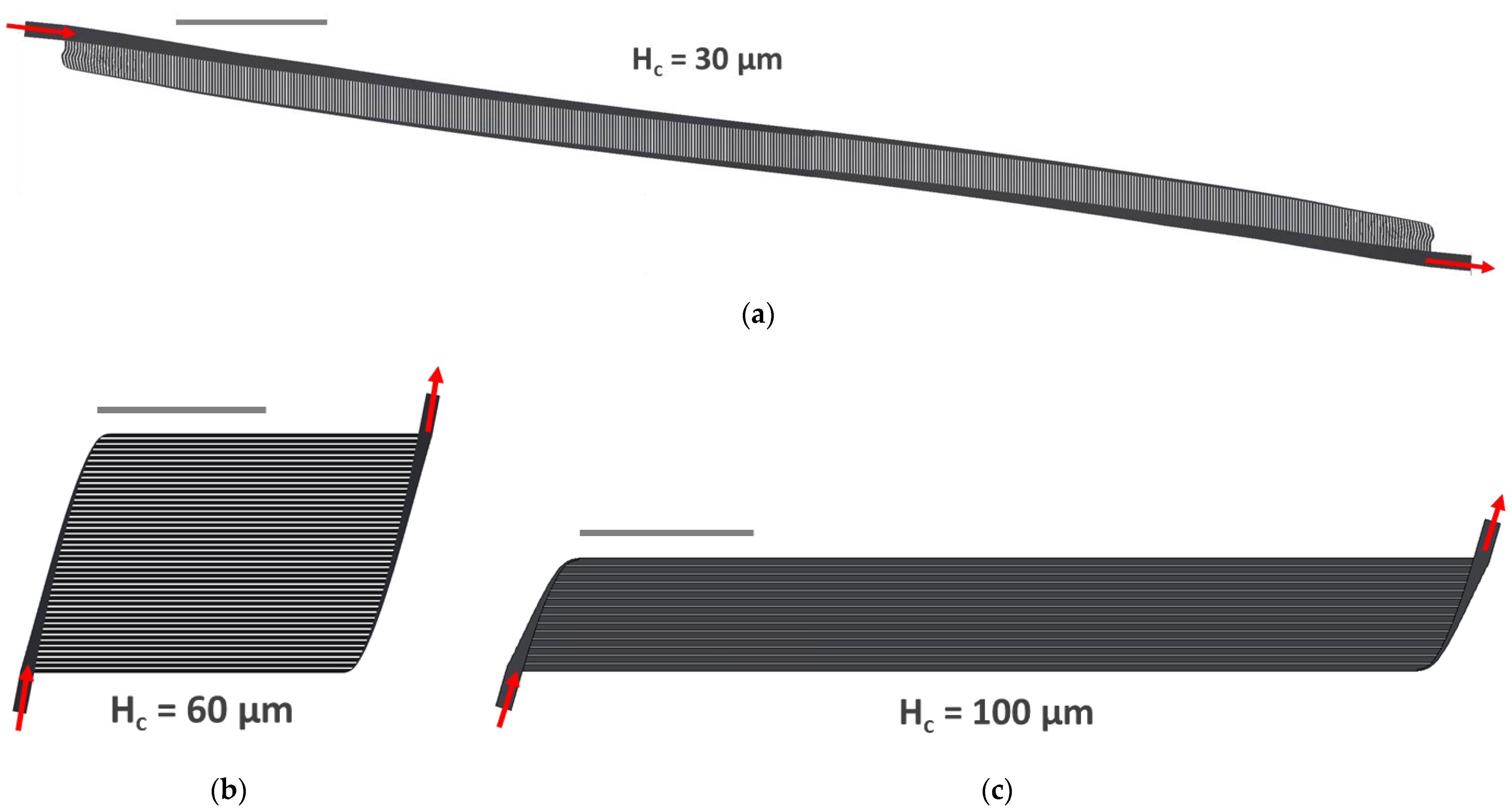
3.2. Implementation of 3 Specific Designs (Hc = 30, 60, 100 μm)
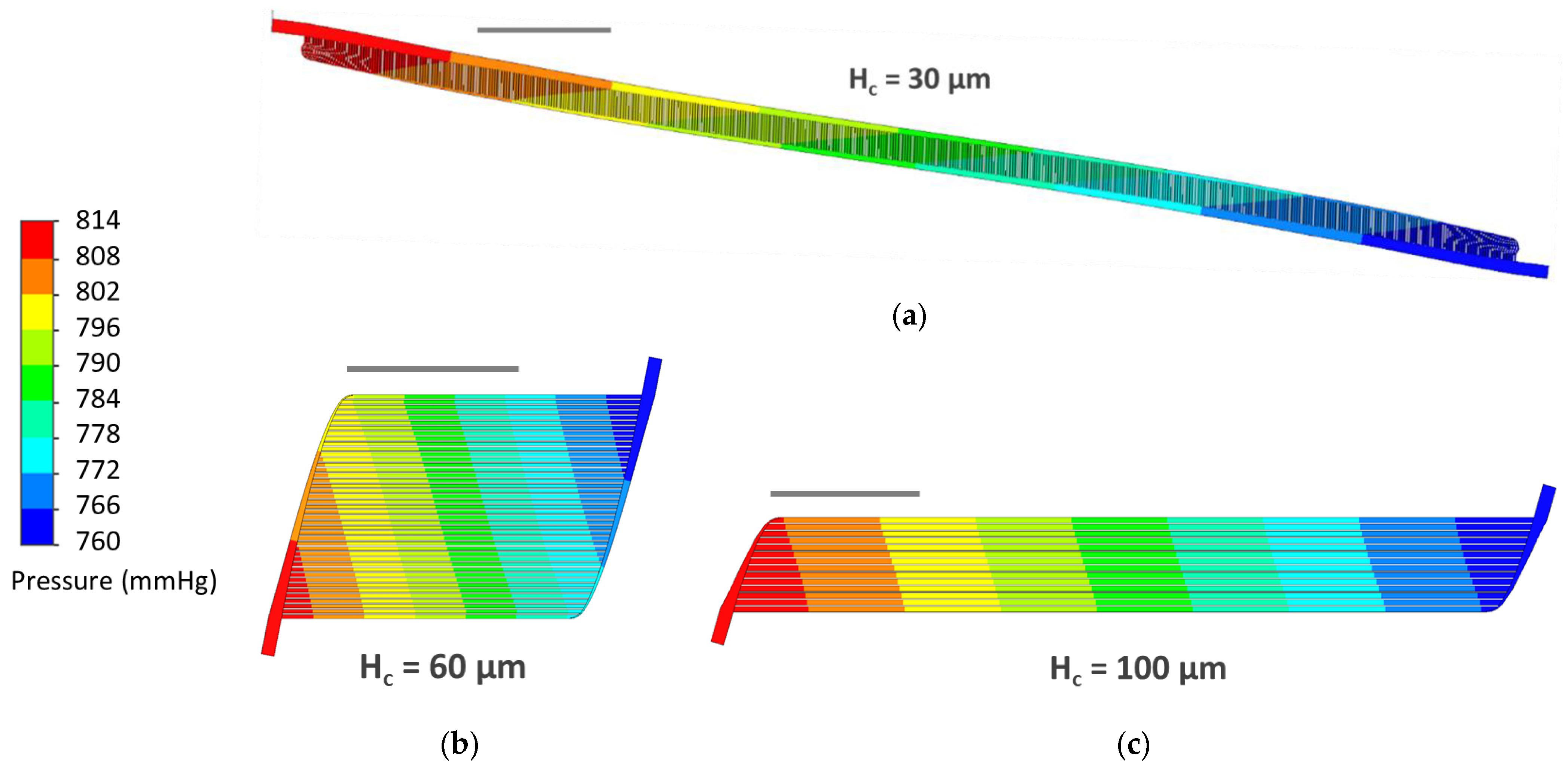
3.3. CFD Simulations
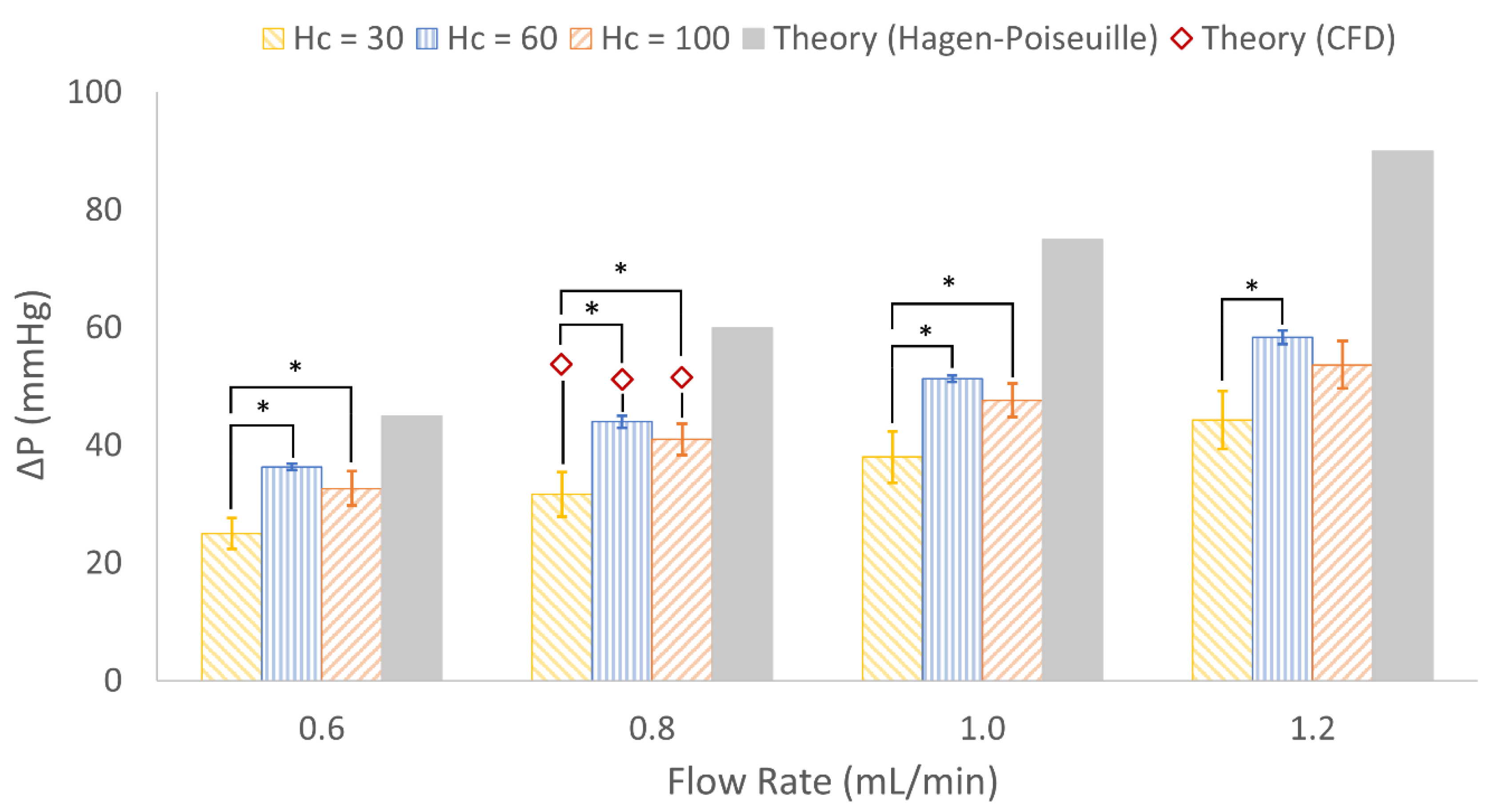
3.4. In Vitro Experimental Results
4. Discussion
4.1. Mathematical Modeling for Hc = 10 to 100 µm
4.2. CFD Simulations
4.3. In Vitro Results
4.4. Limitations
4.5. Continuing Efforts
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Intended Channel Height (μm) | Actual Channel Height (μm) | Spin Speed (rpm) | Soft Bake (65 °C) (min) | Soft Bake (90 °C) (min) | UV Exposure (s) | PEB (65 °C) (min) | PEB (90 °C) (min) | |
|---|---|---|---|---|---|---|---|---|
| Capillary | 30 | 30.8 ± 1.8 | 2800 | 2 | 5 | 25 | 2 | 3 |
| 60 | 60.2 ± 3.7 | 1480 | 3.5 | 7 | 70 | 2 | 3 | |
| 100 | 101.7 ± 5.9 | 730 | 5 | 13 | 80 | 2.5 | 3.5 | |
| Distribution | 239 | 238.8 ± 10.4 | 1450, 1450 | 4, 12 | 5, 30 | 450 | 6 | 15 |
| 210 | 215.4 ± 5.6 | 1600, 2000 | 4, 5 | 5, 15 | 300 | 5 | 12 | |
| 241 | 237.1 ± 15.8 | 900, 2100 | 4, 5 | 5, 20 | 300 | 5 | 12 | |
References
- Hoopes, C.W.; Kukreja, J.; Golden, J.; Davenport, D.L.; Diaz-Guzman, E.; Zwischenberger, J.B. Extracorporeal membrane oxygenation as a bridge to pulmonary transplantation. J. Thorac. Cardiovasc. Surg. 2013, 145, 862–868. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Toyoda, Y.; Bhama, J.K.; Shigemura, N.; Zaldonis, D.; Pilewski, J.; Crespo, M.; Bermudez, C. Efficacy of extracorporeal membrane oxygenation as a bridge to lung transplantation. J. Thorac. Cardiovasc. Surg. 2013, 145, 1065–1071. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lehr, C.J.; Zaas, D.W.; Cheifetz, I.M.; Turner, D.A. Ambulatory extracorporeal membrane oxygenation as a bridge to lung transplantation: Walking while waiting. Chest 2015, 147, 1213–1218. [Google Scholar] [CrossRef] [PubMed]
- Badulak, J.H.; Shinar, Z. Extracorporeal membrane oxygenation in the emergency department. Emerg. Med. Clin. 2020, 38, 945–959. [Google Scholar] [CrossRef]
- Potkay, J.A. The promise of microfluidic artificial lungs. Lab Chip 2014, 14, 4122–4138. [Google Scholar] [CrossRef]
- Ikeda, Y.; Handa, M.; Kawano, K.; Kamata, T.; Murata, M.; Araki, Y.; Anbo, H.; Kawai, Y.; Watanabe, K.; Itagaki, I. The role of von Willebrand factor and fibrinogen in platelet aggregation under varying shear stress. J. Clin. Investig. 1991, 87, 1234–1240. [Google Scholar] [CrossRef] [Green Version]
- Malek, A.M.; Alper, S.L.; Izumo, S. Hemodynamic shear stress and its role in atherosclerosis. JAMA 1999, 282, 2035–2042. [Google Scholar] [CrossRef]
- Chlebowski, M.M.; Baltagi, S.; Carlson, M.; Levy, J.H.; Spinella, P.C. Clinical controversies in anticoagulation monitoring and antithrombin supplementation for ECMO. Crit. Care 2020, 24, 19. [Google Scholar] [CrossRef] [Green Version]
- Federspiel, W.; Henchir, K. Lung, artificial: Basic principles and current applications. In Encyclopedia of Biomaterials and Biomedical Engineering; Marcel Dekker AG: New York, NY, USA, 2004. [Google Scholar]
- Potkay, J.A.; Magnetta, M.; Vinson, A.; Cmolik, B. Bio-inspired, efficient, artificial lung employing air as the ventilating gas. Lab Chip 2011, 11, 2901. [Google Scholar] [CrossRef]
- Santos, J.; Vedula, E.M.; Lai, W.; Isenberg, B.C.; Lewis, D.J.; Lang, D.; Sutherland, D.; Roberts, T.R.; Harea, G.T.; Wells, C.; et al. Toward development of a higher flow rate hemocompatible biomimetic microfluidic blood oxygenator. Micromachines 2021, 12, 888. [Google Scholar] [CrossRef]
- Hoganson, D.M.; Ii, H.I.P.; Bassett, E.K.; Spool, I.D.; Vacanti, J.P. Lung assist device technology with physiologic blood flow developed on a tissue engineered scaffold platform. Lab Chip 2011, 11, 700–707. [Google Scholar] [CrossRef] [PubMed]
- Kniazeva, T.; Hsiao, J.C.; Charest, J.L.; Borenstein, J.T. A microfluidic respiratory assist device with high gas permeance for artificial lung applications. Biomed. Microdevices 2011, 13, 315–323. [Google Scholar] [CrossRef] [PubMed]
- Kniazeva, T.; Epshteyn, A.A.; Hsiao, J.C.; Kim, E.S.; Kolachalama, V.B.; Charest, J.L.; Borenstein, J.T. Performance and scaling effects in a multilayer microfluidic extracorporeal lung oxygenation device. Lab Chip 2012, 12, 1686–1695. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kovach, K.M.M.; LaBarbera, M.A.A.; Moyer, M.C.C.; Cmolik, B.L.L.; van Lunteren, E.; Gupta, A.S.; Capadona, J.R.R.; Potkay, J.A.A. In Vitro evaluation and in vivo demonstration of a biomimetic, hemocompatible, microfluidic artificial lung. Lab Chip 2015, 15, 1366–1375. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gimbel, A.A.; Flores, E.; Koo, A.; García-Cardeña, G.; Borenstein, J.T. Development of a biomimetic microfluidic oxygen transfer device. Lab Chip 2016, 16, 3227–3234. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Santos, J.A.; Gimbel, A.A.; Peppas, A.; Truslow, J.G.; Lang, D.A.; Sukavaneshvar, S.; Solt, D.; Mulhern, T.J.; Markoski, A.; Kim, E.S.; et al. Design and construction of three-dimensional physiologically-based vascular branching networks for respiratory assist devices. Lab Chip 2021, 21, 4637–4651. [Google Scholar] [CrossRef]
- Malankowska, M.; Julian, I.; Pellejero, I.; Rho, H.S.; Schlautmann, S.; Tiggelaar, R.M.; Pina, M.P.; Gardeniers, H.J.G.E.; Mallada, R. Understanding blood oxygenation in a microfluidic meander double side membrane contactor. Sens. Actuators B Chem. 2019, 288, 414–424. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Borenstein, J.; Guiney, L.; Miller, R.; Sukavaneshvar, S.; Loose, C. Polybetaine modification of PDMS microfluidic devices to resist thrombus formation in whole blood. Lab Chip 2013, 13, 1963–1968. [Google Scholar] [CrossRef]
- Kovach, K.M.; Capadona, J.R.; Gupta, A.S.; Potkay, J.A. The effects of PEG-based surface modification of PDMS microchannels on long-term hemocompatibility. J. Biomed. Mater. Res. Part A 2014, 102, 4195–4205. [Google Scholar] [CrossRef] [Green Version]
- Plegue, T.; Kovach, K.; Thompson, A.; Potkay, J. Stability of PEG and zwitterionic surface modifications on PDMS. In Proceedings of the 63rd Annual Conference, Chicago, IL, USA, 21–24 June 2017; p. 38. [Google Scholar]
- Plegue, T.J.; Kovach, K.M.; Thompson, A.J.; Potkay, J.A. Stability of polyethylene glycol and zwitterionic surface modifications in PDMS microfluidic flow chambers. Langmuir 2017, 34, 492–502. [Google Scholar] [CrossRef]
- Burgess, K.A.; Hu, H.-H.; Wagner, W.R.; Federspiel, W.J. Towards microfabricated biohybrid artificial lung modules for chronic respiratory support. Biomed. Microdevices 2009, 11, 117–127. [Google Scholar] [CrossRef] [PubMed]
- Dabaghi, M.; Tiessen, N.; Cao, Q.; Chandiramohan, A.; Saraei, N.; Kim, Y.; Gupta, T.; Selvaganapathy, P.R.; Hirota, J.A. Adhesive-based fabrication technique for culture of lung airway epithelial cells with applications in cell patterning and microfluidics. ACS Biomater. Sci. Eng. 2021, 7, 5301–5314. [Google Scholar] [CrossRef]
- Lachaux, J.; Hwang, G.; Arouche, N.; Naserian, S.; Harouri, A.; Lotito, V.; Casari, C.; Lok, T.; Menager, J.B.; Issard, J.; et al. A compact integrated microfluidic oxygenator with high gas exchange efficiency and compatibility for long-lasting endothelialization. Lab Chip 2021, 21, 4791–4804. [Google Scholar] [CrossRef] [PubMed]
- Rochow, N.; Manan, A.; Wu, W.-I.; Fusch, G.; Monkman, S.; Leung, J.; Chan, E.; Nagpal, D.; Predescu, D.; Brash, J.; et al. An integrated array of microfluidic oxygenators as a neonatal lung assist device: In vitro characterization and in vivo demonstration. Artif. Organs 2014, 38, 856–866. [Google Scholar] [CrossRef] [PubMed]
- Rieper, T.; Müller, C.; Reinecke, H. Novel scalable and monolithically integrated extracorporeal gas exchange device. Biomed. Microdevices 2015, 17, 86. [Google Scholar] [CrossRef]
- Thompson, A.J.; Marks, L.H.; Goudie, M.J.; Rojas-Pena, A.; Handa, H.; Potkay, J.A. A small-scale, rolled-membrane microfluidic artificial lung designed towards future large area manufacturing. Biomicrofluidics 2017, 11, 024113. [Google Scholar] [CrossRef] [Green Version]
- Gimbel, A.A.; Hsiao, J.C.; Kim, E.S.; Lewis, D.J.; Risoleo, T.F.; Urban, J.N.; Borenstein, J.T. A high gas transfer efficiency microfluidic oxygenator for extracorporeal respiratory assist applications in critical care medicine. Artif. Organs 2021, 45, E247–E264. [Google Scholar] [CrossRef]
- Dabaghi, M.; Fusch, G.; Saraei, N.; Rochow, N.; Brash, J.L.; Fusch, C.; Selvaganapathy, P.R. An artificial placenta type microfluidic blood oxygenator with double-sided gas transfer microchannels and its integration as a neonatal lung assist device. Biomicrofluidics 2018, 12, 044101. [Google Scholar] [CrossRef]
- Matharoo, H.; Dabaghi, M.; Rochow, N.; Fusch, G.; Saraei, N.; Tauhiduzzaman, M.; Veldhuis, S.; Brash, J.; Fusch, C.; Selvaganapathy, P.R. Steel reinforced composite silicone membranes and its integration to microfluidic oxygenators for high performance gas exchange. Biomicrofluidics 2018, 12, 014107. [Google Scholar] [CrossRef]
- Vedula, E.M.; Isenberg, B.C.; Santos, J.; Lai, W.; Lewis, D.J.; Sutherland, D.; Roberts, T.R.; Harea, G.T.; Wells, C.; Teece, B.; et al. Multilayer scaling of a biomimetic microfluidic oxygenator. ASAIO J. 2022. [Google Scholar] [CrossRef]
- Ma, L.J.; Akor, E.; Thompson, A.J.; Potkay, J.A. Microfluidic Artificial Lungs: A Parametric Analysis of Capillary Height. In Proceedings of the 66th Annual Conference, Washington, DC, USA, 9–12 June 2021; pp. 25–26. [Google Scholar]
- Potkay, J.A. A simple, closed-form, mathematical model for gas exchange in microchannel artificial lungs. Biomed. Microdevices 2013, 15, 397–406. [Google Scholar] [CrossRef] [PubMed]
- Murray, C.D. The physiological principle of minimum work: I. The vascular system and the cost of blood volume. Proc. Natl. Acad. Sci. USA 1926, 12, 207–214. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Murray, C.D. The physiological principle of minimum work applied to the angle of branching of arteries. J. Gen. Physiol. 1926, 9, 835–841. [Google Scholar] [CrossRef]
- Sherman, T.F. On connecting large vessels to small. The meaning of Murray’s law. J. Gen. Physiol. 1981, 78, 431–453. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Thompson, A.J.; Ma, L.J.; Plegue, T.J.; Potkay, J.A. Design analysis and optimization of a single-layer PDMS microfluidic artificial lung. IEEE Trans. Biomed. Eng. 2019, 66, 1082–1093. [Google Scholar] [CrossRef] [PubMed]
- Hall, J.E.; Hall, M.E. Guyton and Hall Textbook of Medical Physiology, 14th ed.; Elsevier: Amsterdam, The Netherlands, 2021. [Google Scholar]
- U.S. Department of Health and Human Services; Food and Drug Administration Center for Devices and Radiological Health. Guidance for Cardiopulmonary Bypass Oxygenators 510(k) Submissions—Final Guidance for Industry and FDA Staff; Food and Drug Administration: Washington, DC, USA, 2000.
- Bruus, H. Chapter 1. Governing equations in microfluidics. In Microscale Acoustofluidics; Royal Society of Chemistry: London, UK, 2014; pp. 1–28. [Google Scholar] [CrossRef]
- Zaman, A.; Ali, N.; Sajid, M.; Hayat, T. Effects of unsteadiness and non-Newtonian rheology on blood flow through a tapered time-variant stenotic artery. AIP Adv. 2015, 5, 037129. [Google Scholar] [CrossRef] [Green Version]
- Wu, W.-I.; Rochow, N.; Chan, E.; Fusch, G.; Manan, A.; Nagpal, D.; Selvaganapathy, P.R.; Fusch, C. Lung assist device: Development of microfluidic oxygenators for preterm infants with respiratory failure. Lab Chip 2013, 13, 2641–2650. [Google Scholar] [CrossRef]
- Shibeshi, S.S.; Collins, W.E. The rheology of blood flow in a branched arterial system. Appl. Rheol. 2005, 15, 398–405. [Google Scholar] [CrossRef]
- Janela, J.; Moura, A.; Sequeira, A. A 3D non-Newtonian fluid–structure interaction model for blood flow in arteries. J. Comput. Appl. Math. 2010, 234, 2783–2791. [Google Scholar] [CrossRef] [Green Version]
- Sequeira, A. Hemorheology: Non-Newtonian constitutive models for blood flow simulations. In Non-Newtonian Fluid Mechanics and Complex Flows; Springer: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Microchem. SU-8 2000 Permanent Epoxy Negative Photoresist Processing Guidelines for: SU-8 2025, SU-8 2035, SU-8 2050 and SU-8 2075; Microchem: Newton, MA, USA.
- Tyona, M.D. A theoritical study on spin coating technique. Adv. Mater. Res. 2013, 2, 195–208. [Google Scholar] [CrossRef] [Green Version]
- Aziz, F.; Penupolu, S.; Xu, X.; He, J. Lung transplant in end-staged chronic obstructive pulmonary disease (COPD) patients: A concise review. J. Thorac. Dis. 2010, 2, 111. [Google Scholar] [PubMed]
- Todd, E.M.; Roy, S.B.; Hashimi, A.S.; Serrone, R.; Panchanathan, R.; Kang, P.; Varsch, K.E.; Steinbock, B.E.; Huang, J.; Omar, A.; et al. Extracorporeal membrane oxygenation as a bridge to lung transplantation: A single-center experience in the present era. J. Thorac. Cardiovasc. Surg. 2017, 154, 1798–1809. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Langer, T.; Santini, A.; Bottino, N.; Crotti, S.; Batchinsky, A.I.; Pesenti, A.; Gattinoni, L. “Awake” extracorporeal membrane oxygenation (ECMO): Pathophysiology, technical considerations, and clinical pioneering. Crit. Care 2016, 20, 150. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Adili, R.; Tourdot, B.E.; Mast, K.; Yeung, J.; Freedman, J.C.; Green, A.; Luci, D.K.; Jadhav, A.; Simeonov, A.; Maloney, D.J.; et al. First selective 12-LOX inhibitor, ML355, impairs thrombus formation and vessel occlusion in vivo with minimal effects on hemostasis. Arter. Thromb. Vasc. Biol. 2017, 37, 1828–1839. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Colace, T.V.; Tormoen, G.W.; McCarty, O.J.; Diamond, S.L. Microfluidics and coagulation biology. Annu. Rev. Biomed. Eng. 2013, 15, 283–303. [Google Scholar] [CrossRef] [Green Version]
- Colace, T.V.; Muthard, R.W.; Diamond, S.L. Thrombus growth and embolism on tissue factor-bearing collagen surfaces under flow: Role of thrombin with and without fibrin. Arter. Thromb. Vasc. Biol. 2012, 32, 1466–1476. [Google Scholar] [CrossRef] [Green Version]
- White, F.M. Fluid Mechanics, 8th ed.; McGraw-Hill Education: New York, NY, USA, 2016. [Google Scholar]
- Hardy, B.S.; Uechi, K.; Zhen, J.; Kavehpour, H.P. The deformation of flexible PDMS microchannels under a pressure driven flow. Lab Chip 2009, 9, 935–938. [Google Scholar] [CrossRef]






| Blood Density (kg∙m−3) | Maximum Dynamic Viscosity (Pa∙s) | Minimum Dynamic Viscosity (Pa∙s) | Power-Law Index | Time Constant (s) |
|---|---|---|---|---|
| 1060 | 0.056 | 0.00345 | 0.3568 | 3.313 |
| Mathematical Theory | CFD | |||||||
|---|---|---|---|---|---|---|---|---|
| Designs | QR (mL/min) | Ac,g (cm2) | Ab,g (cm2) | Vprime (µL) | ΔP (mmHg) | τw (s−1) | ΔP (mmHg) | τw (s−1) |
| Hc = 30 | 0.8 | 1.2 | 5.4 | 25 | 60 | 1458 | 53.8 | 1500 |
| Hc = 60 | 0.8 | 2.1 | 5.0 | 15 | 60 | 2546 | 51.2 | 2588 |
| Hc = 100 | 0.8 | 3.1 | 7.3 | 33 | 60 | 1818 | 51.5 | 1729 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, L.J.; Akor, E.A.; Thompson, A.J.; Potkay, J.A. A Parametric Analysis of Capillary Height in Single-Layer, Small-Scale Microfluidic Artificial Lungs. Micromachines 2022, 13, 822. https://doi.org/10.3390/mi13060822
Ma LJ, Akor EA, Thompson AJ, Potkay JA. A Parametric Analysis of Capillary Height in Single-Layer, Small-Scale Microfluidic Artificial Lungs. Micromachines. 2022; 13(6):822. https://doi.org/10.3390/mi13060822
Chicago/Turabian StyleMa, Lindsay J., Emmanuel A. Akor, Alex J. Thompson, and Joseph A. Potkay. 2022. "A Parametric Analysis of Capillary Height in Single-Layer, Small-Scale Microfluidic Artificial Lungs" Micromachines 13, no. 6: 822. https://doi.org/10.3390/mi13060822
APA StyleMa, L. J., Akor, E. A., Thompson, A. J., & Potkay, J. A. (2022). A Parametric Analysis of Capillary Height in Single-Layer, Small-Scale Microfluidic Artificial Lungs. Micromachines, 13(6), 822. https://doi.org/10.3390/mi13060822







