Enhanced Phonon Antibunching in a Circuit Quantum Acoustodynamical System Containing Two Surface Acoustic Wave Resonators
Abstract
1. Introduction
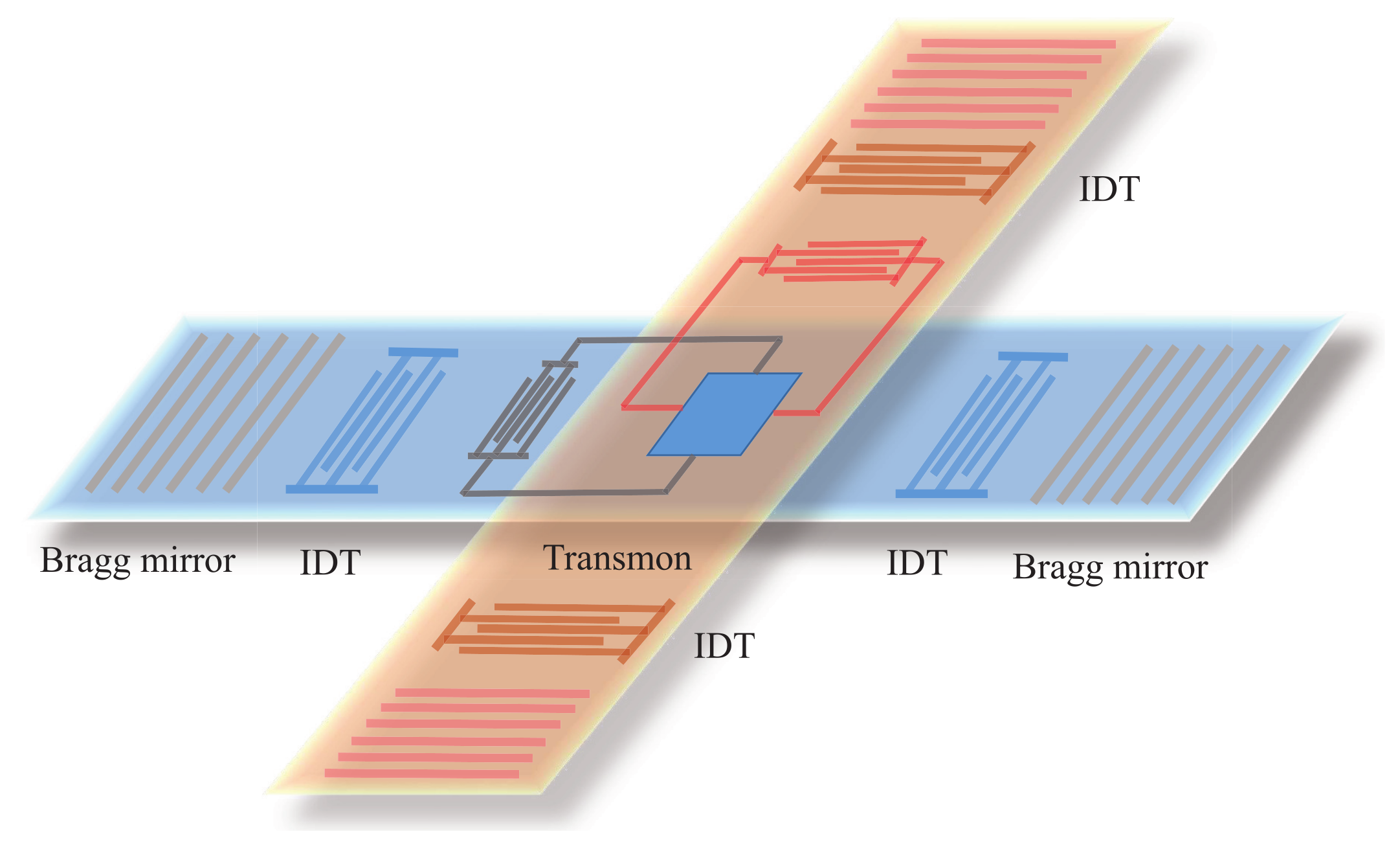
2. Theoretical Model
3. Results
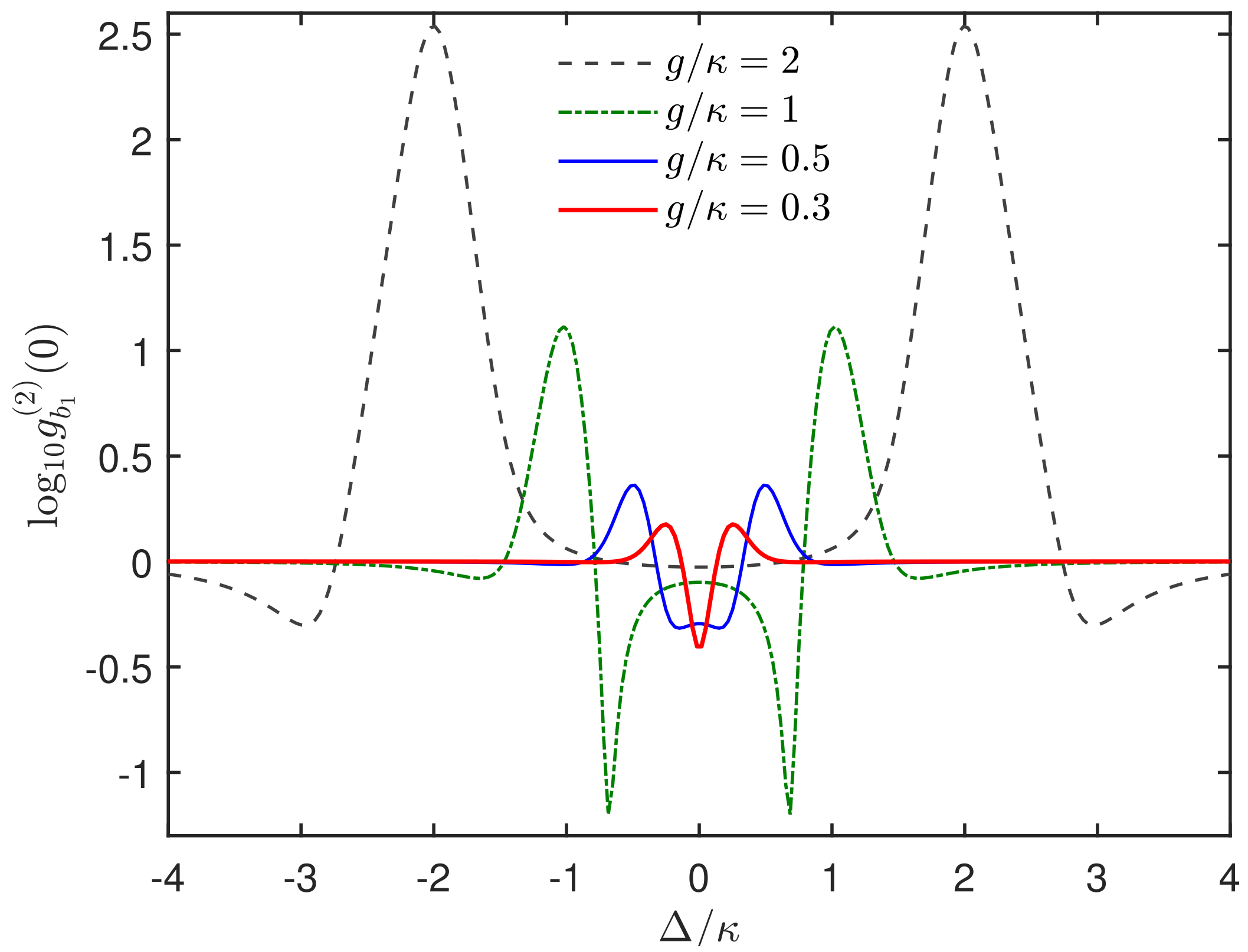
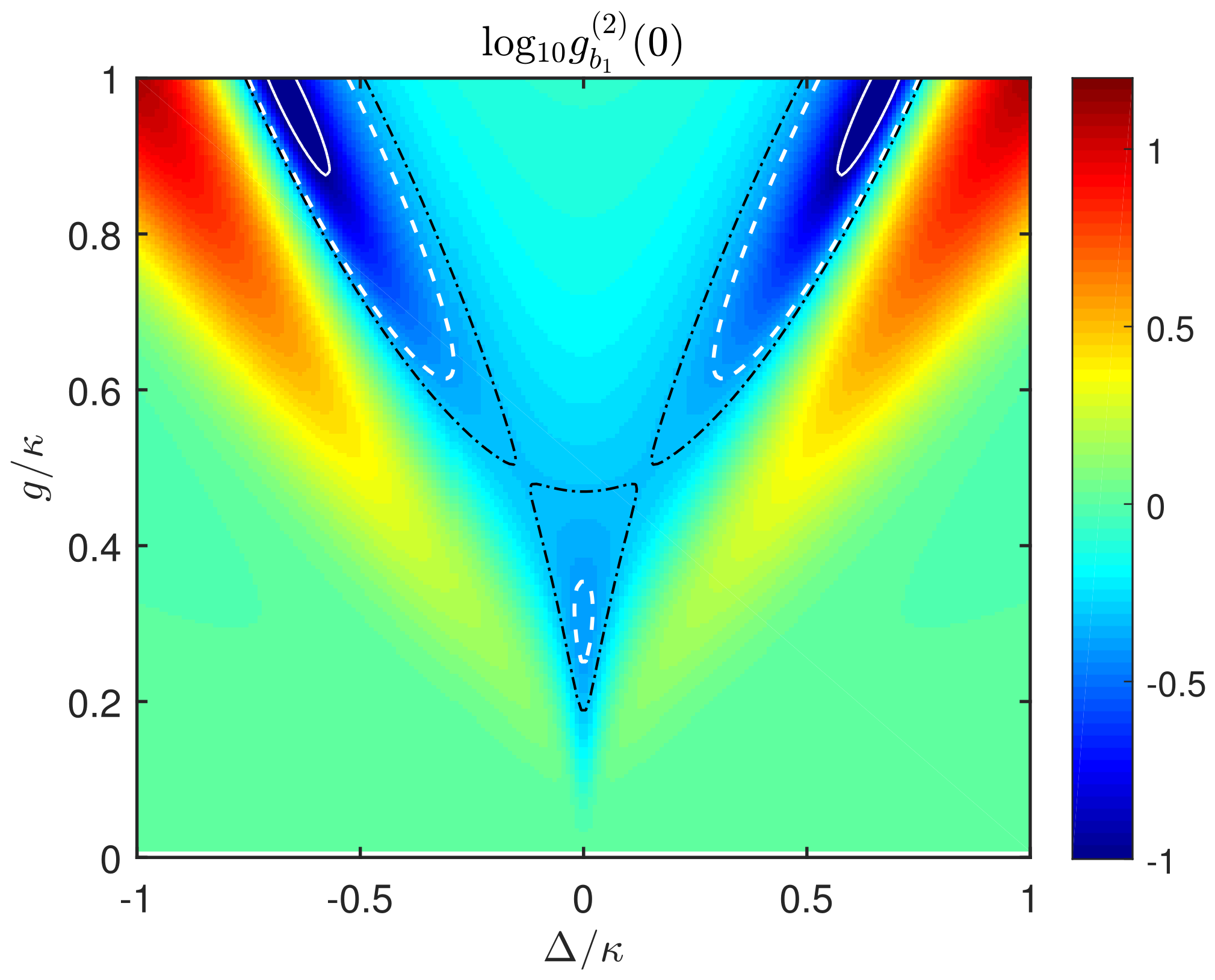
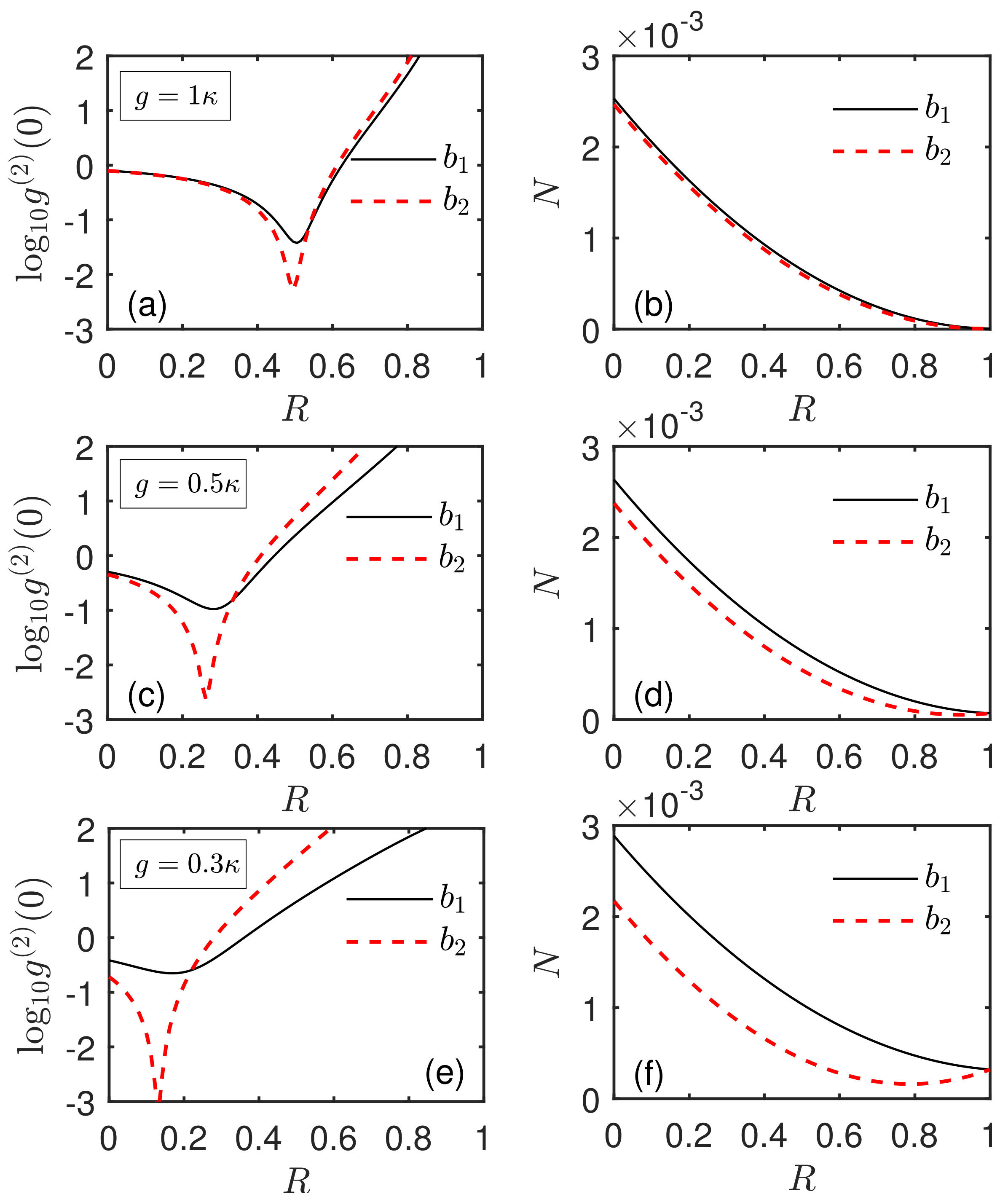
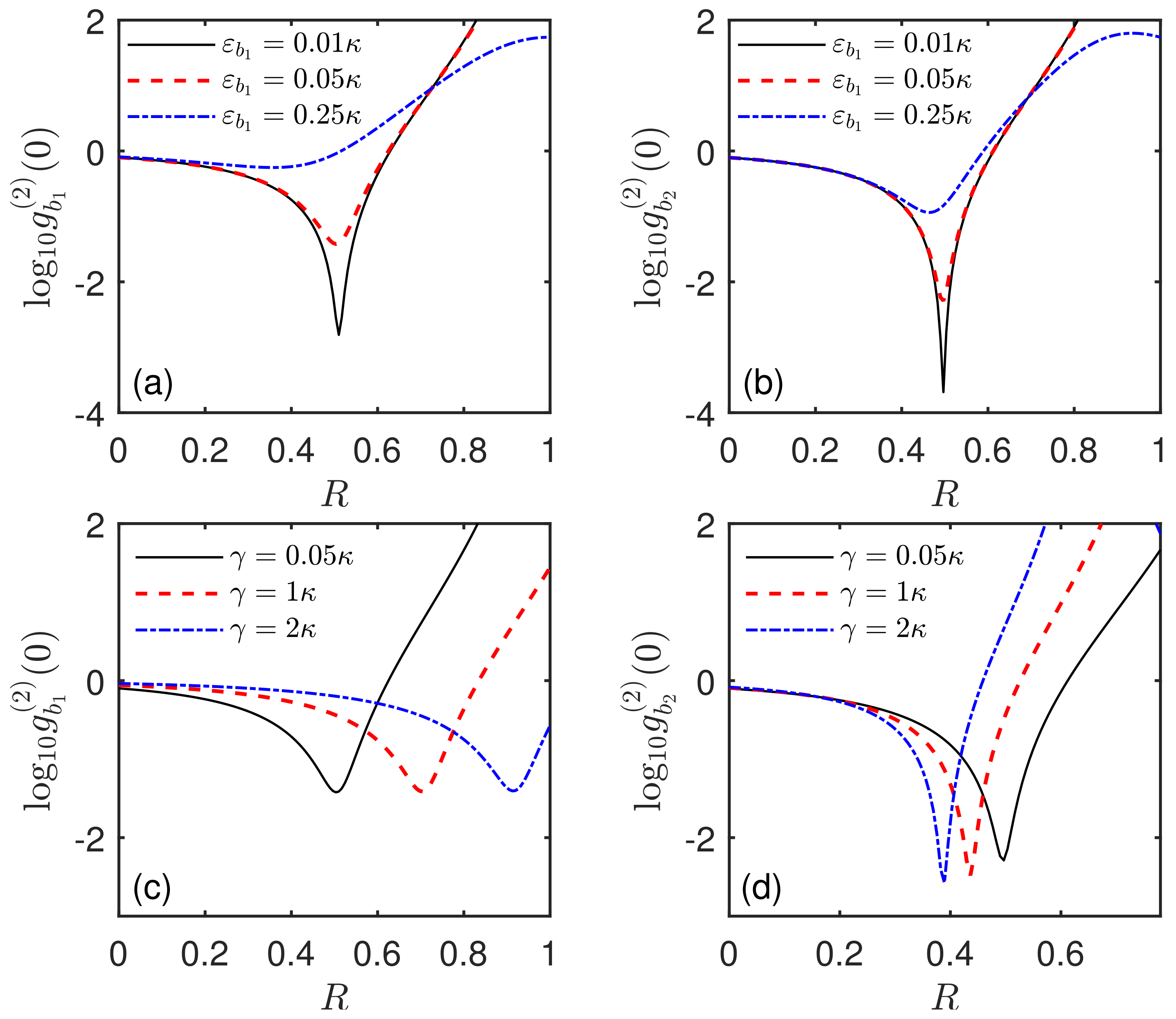
3.1. The Phonon Antibunching When Only One SAW Resonator Is Driven
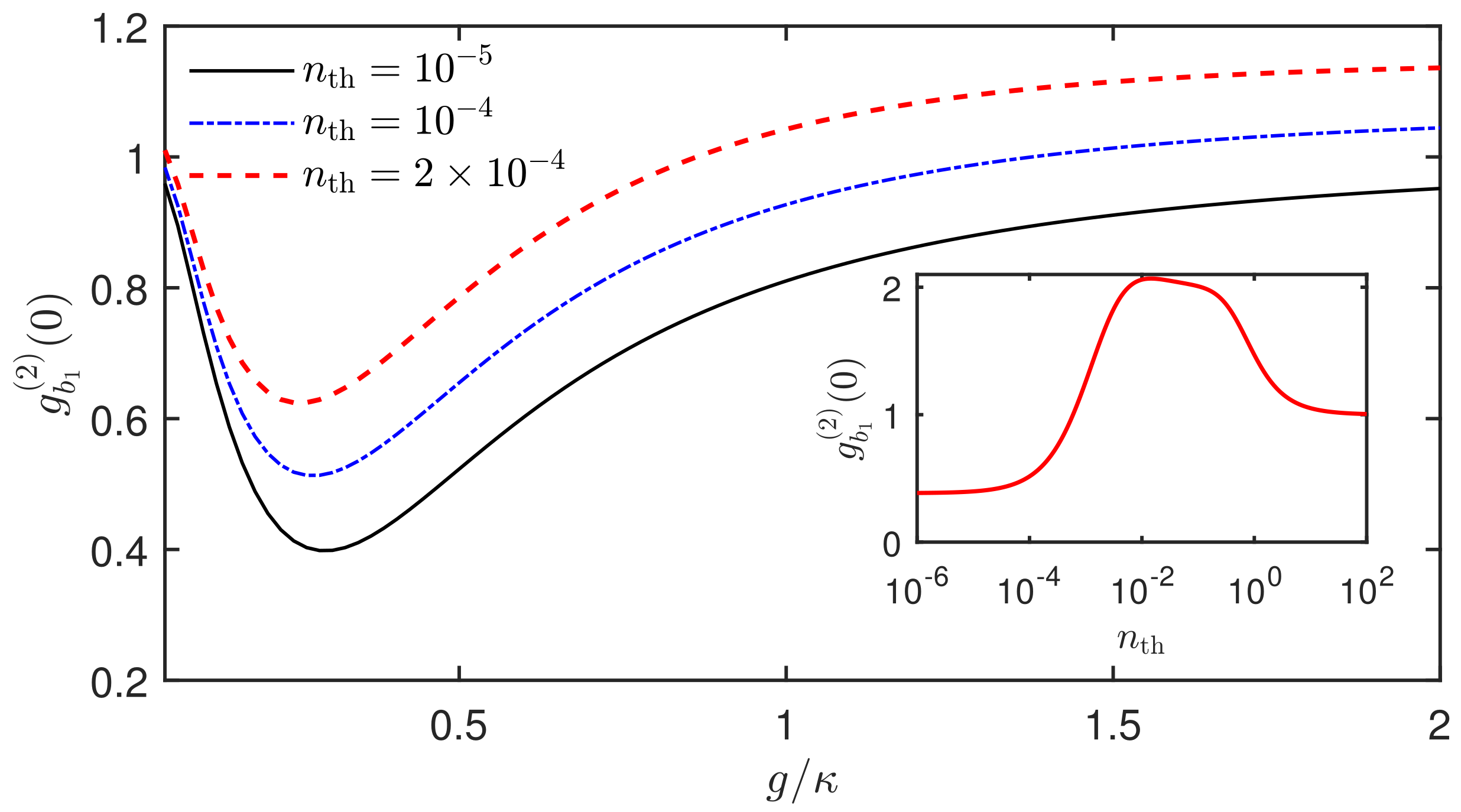
3.2. Enhanced Phonon Antibunching When the Two SAW Resonators Are Both Driven
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zurek, W.H. Decoherence and the Transition from Quantum to Classical. Phys. Today 1991, 44, 36. [Google Scholar] [CrossRef]
- Mancini, S.; Man’ko, V.I.; Tombesi, P. Ponderomotive control of quantum macroscopic coherence. Phys. Rev. A 1997, 55, 3042. [Google Scholar] [CrossRef]
- Bose, S.; Jacobs, K.; Knight, P.L. Preparation of nonclassical states in cavities with a moving mirror. Phys. Rev. A 1997, 56, 4175. [Google Scholar] [CrossRef]
- Marshall, W.; Simon, C.; Penrose, R.; Bouwmeester, D. Towards Quantum Superpositions of a Mirror. Phys. Rev. Lett. 2003, 91, 130401. [Google Scholar] [CrossRef]
- Schwab, K.C.; Roukes, M.L. Putting mechanics into quantum mechanics. Phys. Today 2005, 58, 36. [Google Scholar] [CrossRef]
- Braginsky, V.B.; Khalili, F.Y.; Thorne, K.S. Quantum Measurement; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- LaHaye, M.D.; Buu, O.; Camarota, B.; Schwab, K.C. Approaching the quantum limit of a nanomechanical resonator. Science 2004, 304, 74. [Google Scholar] [CrossRef]
- Stannigel, K.; Komar, P.; Habraken, S.J.M.; Bennett, S.D.; Lukin, M.D.; Zoller, P.; Rabl, P. Optomechanical Quantum Information Processing with Photons and Phonons. Phys. Rev. Lett. 2012, 109, 013603. [Google Scholar] [CrossRef]
- O’Connell, A.D.; Hofheinz, M.; Ansmann, M.; Bialczak, R.C.; Lenander, M.; Lucero, E.; Neeley, M.; Sank, D.; Wang, H.; Weides, M.; et al. Quantum ground state and single-phonon control of a mechanical resonator. Nature 2010, 464, 697. [Google Scholar] [CrossRef]
- Teufel, J.D.; Donner, T.; Li, D.; Harlow, J.W.; Allman, M.S.; Cicak, K.; Sirois, A.J.; Whittaker, J.D.; Lehnert, K.W.; Simmonds, R.W. Sideband cooling of micromechanical motion to the quantum ground state. Nature 2011, 475, 359. [Google Scholar] [CrossRef]
- Chan, J.; Alegre, T.P.M.; Safavi-Naeini, A.H.; Hill, J.T.; Krause, A.; Gröblacher, S.; Aspelmeyer, M.; Painter, O. Laser cooling of a nanomechanical oscillator into its quantum ground state. Nature 2011, 478, 89. [Google Scholar] [CrossRef]
- Clark, J.B.; Lecocq, F.; Simmonds, R.W.; Aumentado, J.; Teufel, J.D. Sideband cooling beyond the quantum backaction limit with squeezed light. Nature 2017, 541, 191. [Google Scholar] [CrossRef]
- Xiang, Z.-L.; Ashhab, S.; You, J.Q.; Nori, F. Hybrid quantum circuits: Superconducting circuits interacting with other quantum systems. Rev. Mod. Phys. 2013, 85, 623. [Google Scholar] [CrossRef]
- Kurizki, G.; Bertet, P.; Kubo, Y.; Mølmer, K.; Petrosyan, D.; Rabl, P.; Schmiedmayer, J. Quantum technologies with hybrid systems. Proc. Natl. Acad. Sci. USA 2015, 112, 3866. [Google Scholar] [CrossRef] [PubMed]
- Habraken, S.J.M.; Stannigel, K.; Lukin, M.D.; Zoller, P.; Rabl, P. Continuous mode cooling and phonon routers for phononic quantum networks. New J. Phys. 2012, 14, 115004. [Google Scholar] [CrossRef]
- Poot, M.; van der Zant, H.S.J. Mechanical systems in the quantum regime. Phys. Rep. 2012, 511, 273. [Google Scholar] [CrossRef]
- Treutlein, P.; Genes, C.; Hammerer, K.; Poggio, M.; Rabl, P. Hybrid Mechanical Systems; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Aspelmeyer, M.; Kippenberg, T.J.; Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 2014, 86, 1391. [Google Scholar] [CrossRef]
- Xiong, H.; Si, L.-G.; Lü, X.-Y.; Yang, X.-X.; Wu, Y. Review of cavity optomechanics in the weak-coupling regime: From linearization to intrinsic nonlinear interactions. Sci. China Phys. Mech. Astron. 2015, 58, 1–13. [Google Scholar] [CrossRef]
- Lü, X.-Y.; Wu, Y.; Johansson, J.R.; Jing, H.; Zhang, J.; Nori, F. Squeezed Optomechanics with Phase-Matched Amplification and Dissipation. Phys. Rev. Lett. 2015, 114, 093602. [Google Scholar] [CrossRef]
- Bin, Q.; Lü, X.-Y.; Laussy, F.P.; Nori, F.; Wu, Y. N-Phonon Bundle Emission via the Stokes Process. Phys. Rev. Lett. 2020, 124, 053601. [Google Scholar] [CrossRef]
- LaHaye, M.D.; Suh, J.; Echternach, P.M.; Schwab, K.C.; Roukes, M.L. Nanomechanical measurements of a superconducting qubit. Nature 2009, 459, 960. [Google Scholar] [CrossRef]
- Pirkkalainen, J.-M.; Cho, S.U.; Li, J.; Paraoanu, G.S.; Hakonen, P.J.; Sillanpäxax, M.A. Hybrid circuit cavity quantum electrodynamics with a micromechanical resonator. Nature 2013, 494, 211. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.X.; Miranowicz, A.; Gao, Y.B.; Bajer, J.; Sun, C.P.; Nori, F. Qubit-induced phonon blockade as a signature of quantum behavior in nanomechanical resonators. Phys. Rev. A 2010, 82, 032101. [Google Scholar] [CrossRef]
- Wang, X.; Miranowicz, A.; Li, H.R.; Nori, F. Method for observing robust and tunable phonon blockade in a nanomechanical resonator coupled to a charge qubit. Phys. Rev. A 2016, 93, 063861. [Google Scholar] [CrossRef]
- Xu, X.-W.; Chen, A.-X.; Liu, Y.-X. Phonon blockade in a nanomechanical resonator resonantly coupled to a qubit. Phys. Rev. A 2016, 94, 063853. [Google Scholar] [CrossRef]
- Ramos, T.; Sudhir, V.; Stannigel, K.; Zoller, P.; Kippenberg, T.J. Nonlinear Quantum Optomechanics via Individual Intrinsic Two-Level Defects. Phys. Rev. Lett. 2013, 110, 193602. [Google Scholar] [CrossRef]
- Bennett, S.D.; Yao, N.Y.; Otterbach, J.; Zoller, P.; Rabl, P.; Lukin, M.D. Phonon-Induced Spin-Spin Interactions in Diamond Nanostructures: Application to Spin Squeezing. Phys. Rev. Lett. 2013, 110, 156402. [Google Scholar] [CrossRef]
- MacQuarrie, E.R.; Gosavi, T.A.; Jungwirth, N.R.; Bhave, S.A.; Fuchs, G.D. Mechanical Spin Control of Nitrogen-Vacancy Centers in Diamond. Phys. Rev. Lett. 2013, 111, 227602. [Google Scholar] [CrossRef]
- Kepesidis, K.V.; Bennett, S.D.; Portolan, S.; Lukin, M.D.; Rabl, P. Phonon cooling and lasing with nitrogen-vacancy centers in diamond. Phys. Rev. B 2013, 88, 064105. [Google Scholar] [CrossRef]
- Ovartchaiyapong, P.; Lee, K.W.; Myers, B.A.; Jayich, A.C.B. Dynamic strain-mediated coupling of a single diamond spin to a mechanical resonator. Nat. Commun. 2014, 5, 4429. [Google Scholar] [CrossRef]
- Teissier, J.; Barfuss, A.; Appel, P.; Neu, E.; Maletinsky, P. Strain Coupling of a Nitrogen-Vacancy Center Spin to a Diamond Mechanical Oscillator. Phys. Rev. Lett. 2014, 113, 020503. [Google Scholar] [CrossRef]
- Arcizet, O.; Jacques, V.; Siria, A.; Poncharal, P.; Vincent, P.; Seidelin, S. A single nitrogen-vacancy defect coupled to a nanomechanical oscillator. Nat. Phys. 2011, 7, 879. [Google Scholar] [CrossRef]
- Kolkowitz, S.; Jayich, A.C.B.; Unterreithmeier, Q.P.; Bennett, S.D.; Rabl, P.; Harris, J.G.E.; Lukin, M.D. Coherent Sensing of a Mechanical Resonator with a Single-Spin Qubit. Science 2012, 335, 1603. [Google Scholar] [CrossRef] [PubMed]
- Pigeau, B.; Rohr, S.; Lépinay, L.M.D.; Gloppe, A.; Jacques, V.; Arcizet, O. Observation of a phononic Mollow triplet in a multimode hybrid spin-nanomechanical system. Nat. Commun. 2015, 6, 8603. [Google Scholar] [CrossRef]
- Ma, Y.; Yin, Z.Q.; Huang, P.; Yang, W.L.; Du, J. Cooling a mechanical resonator to the quantum regime by heating it. Phys. Rev. A 2016, 94, 053836. [Google Scholar] [CrossRef]
- Cai, K.; Wang, R.X.; Yin, Z.Q.; Long, G.L. Second-order magnetic field gradient-induced strong coupling between nitrogen-vacancy centers and a mechanical oscillator. Sci. China Phys. Mech. Astron. 2017, 60, 070311. [Google Scholar] [CrossRef][Green Version]
- Mu noz, C.S.; Lara, A.; Puebla, J.; Nori, F. Hybrid Systems for the Generation of Nonclassical Mechanical States via Quadratic Interactions. Phys. Rev. Lett. 2018, 121, 123604. [Google Scholar]
- Hoff, U.B.; Kollath-Bönig, J.; Neergaard-Nielsen, J.S.; Andersen, U.L. Measurement-Induced Macroscopic Superposition States in Cavity Optomechanics. Phys. Rev. Lett. 2016, 117, 143601. [Google Scholar] [CrossRef]
- Milburn, T.J.; Kim, M.S.; Vanner, M.R. Nonclassical-state generation in macroscopic systems via hybrid discrete-continuous quantum measurements. Phys. Rev. A 2016, 93, 053818. [Google Scholar] [CrossRef]
- Lecocq, F.; Clark, J.B.; Simmonds, R.W.; Aumentado, J.; Teufel, J.D. Quantum Nondemolition Measurement of a Nonclassical State of a Massive Object. Phys. Rev. X 2015, 5, 041037. [Google Scholar] [CrossRef]
- Hong, S.; Riedinger, R.; Marinković, I.; Wallucks, A.; Hofer, S.G.; Norte, R.A.; Aspelmeyer, M.; Gröblacher, S. Hanbury Brown and Twiss interferometry of single phonons from an optomechanical resonator. Science 2017, 358, 203. [Google Scholar] [CrossRef]
- Riedinger, R.; Wallucks, A.; Marinković, I.; Löschnauer, C.; Aspelmeyer, M.; Hong, S.; Grxoxblacher, S. Remote quantum entanglement between two micromechanical oscillators. Nature 2018, 556, 473. [Google Scholar] [CrossRef] [PubMed]
- Ockeloen-Korppi, C.F.; Damskägg, E.; Pirkkalainen, J.-M.; Asjad, M.; Clerk, A.A.; Massel, F.; Woolley, M.J.; Sillanpää, M.A. Stabilized entanglement of massive mechanical oscillators. Nature 2018, 556, 478. [Google Scholar] [CrossRef] [PubMed]
- Marinković, I.; Wallucks, A.; Riedinger, R.; Hong, S.; Aspelmeyer, M.; Gröblacher, S. Optomechanical Bell Test. Phys. Rev. Lett. 2018, 121, 220404. [Google Scholar] [CrossRef]
- Nunnenkamp, A.; Børkje, K.; Harris, J.G.E.; Girvin, S.M. Cooling and squeezing via quadratic optomechanical coupling. Phys. Rev. A 2010, 82, 021806. [Google Scholar] [CrossRef]
- Lü, X.-Y.; Liao, J.-Q.; Tian, L.; Nori, F. Steady-state mechanical squeezing in an optomechanical system via Duffing nonlinearity. Phys. Rev. A 2015, 91, 013834. [Google Scholar] [CrossRef]
- Wang, M.; Lü, X.-Y.; Wang, Y.-D.; You, J.Q.; Wu, Y. Macroscopic quantum entanglement in modulated optomechanics. Phys. Rev. A 2016, 94, 053807. [Google Scholar] [CrossRef]
- Seok, H.; Wright, E.M. Antibunching in an optomechanical oscillator. Phys. Rev. A 2017, 95, 053844. [Google Scholar] [CrossRef]
- Xie, H.; Liao, C.G.; Shang, X.; Ye, M.Y.; Lin, X.M. Phonon blockade in a quadratically coupled optomechanical system. Phys. Rev. A 2017, 96, 013861. [Google Scholar] [CrossRef]
- Xie, H.; Liao, C.G.; Shang, X.; Chen, Z.H.; Lin, X.M. Optically induced phonon blockade in an optomechanical system with second-order nonlinearity. Phys. Rev. A 2018, 98, 023819. [Google Scholar] [CrossRef]
- Shi, H.Q.; Zhou, X.T.; Xun, X.W.; Liu, N.H. Tunable phonon blockade in quadratically coupled optomechanical systems. Sci. Rep. 2018, 8, 2212. [Google Scholar] [CrossRef]
- Zheng, L.-L.; Yin, T.-S.; Bin, Q.; Lü, X.-Y.; Wu, Y. Single-photon-induced phonon blockade in a hybrid spin-optomechanical system. Phys. Rev. A 2019, 99, 013804. [Google Scholar] [CrossRef]
- Yin, T.-S.; Bin, Q.; Zhu, G.-L.; Gin, G.-R.; Chen, A.-X. Phonon blockade in a hybrid system via the second-order magnetic gradient. Phys. Rev. A 2019, 100, 063840. [Google Scholar] [CrossRef]
- Aref, T.; Delsing, P.; Ekström, M.K.; Kockum, A.F.; Gustafsson, M.V.; Johansson, G.; Leek, P.J.; Magnusson, E.; Manenti, R. Chapter 9 in Superconducting Devices in Quantum Optics; Springer: New York, NY, USA, 2016; pp. 217–244. [Google Scholar]
- Morgan, D. Surface Acoustic Wave Filters: With Applications to Electronic Communications and Signal Processing; Academic Press: New York, NY, USA, 2007. [Google Scholar]
- Ekström, M.K.; Aref, T.; Ask, A.; Andersson, G.; Suri, B.; Sanada, H.; Johansson, G.; Delsing, P. Towards phonon routing: Controlling propagating acoustic waves in the quantum regime. New J. Phys. 2019, 21, 123013. [Google Scholar] [CrossRef]
- Chu, Y.; Kharel, P.; Renninger, W.H.; Burkhart, L.D.; Frunzio, L.; Rakich, P.T.; Schoelkopf, R.J. Quantum acoustics with superconducting qubits. Science 2017, 358, 199. [Google Scholar] [CrossRef] [PubMed]
- Delsing, P.; Cleland, A.N.; Schuetz, M.J.; Knörzer, J.; Giedke, G.; Cirac, J.I.; Srinivasan, K.; Wu, M.; Balram, K.C.; Bäuerle, C.; et al. The 2019 surface acoustic waves roadmap. J. Phys. D Appl. Phys. 2019, 52, 353001. [Google Scholar] [CrossRef]
- Sasaki, R.; Nii, Y.; Iguchi, Y.; Onose, Y. Nonreciprocal propagation of surface acoustic wave in Ni/LiNbO3. Phys. Rev. B 2017, 95, 020407. [Google Scholar] [CrossRef]
- Verba, R.; Lisenkov, I.; Krivorotov, I.; Tiberkevich, V.; Slavin, A. Nonreciprocal Surface Acoustic Waves in Multilayers with Magnetoelastic and Interfacial Dzyaloshinskii-Moriya Interactions. Phys. Rev. Appl. 2018, 9, 064014. [Google Scholar] [CrossRef]
- Shao, L.; Mao, W.; Maity, S.; Sinclair, N.; Hu, Y.; Yang, L.; Lončar, M. Non-reciprocal transmission of microwave acoustic waves in nonlinear parity–time symmetric resonators. Nat. Electron. 2020, 3, 267. [Google Scholar] [CrossRef]
- Gustafsson, M.V.; Santos, P.V.; Johansson, G.; Delsing, P. Local probing of propagating acoustic waves in a gigahertz echo chamber. Nat. Phys. 2012, 8, 338. [Google Scholar] [CrossRef]
- Gustafsson, M.V.; Aref, T.; Kockum, A.F.; Ekstrom, M.K.; Johansson, G.; Delsing, P. Propagating phonons coupled to an artificial atom. Science 2014, 346, 207. [Google Scholar] [CrossRef]
- Andersson, G.; Ekström, M.K.; Delsing, P. Electromagnetically Induced Acoustic Transparency with a Superconducting Circuit. Phys. Rev. Lett. 2020, 124, 240402. [Google Scholar] [CrossRef]
- Magnusson, E.B.; Williams, B.H.; Manenti, R.; Nam, M.-S.; Nersisyan, A.; Peterer, M.J.; Ardavan, A.; Leek, P.J. Surface acoustic wave devices on bulk ZnO crystals at low temperature. Appl. Phys. Lett. 2015, 106, 063509. [Google Scholar] [CrossRef]
- Manenti, R.; Peterer, M.J.; Nersisyan, A.; Magnusson, E.B.; Patterson, A.; Leek, P.J. Surface acoustic wave resonators in the quantum regime. Phys. Rev. B 2016, 93, 041411. [Google Scholar] [CrossRef]
- Xu, Y.; Fu, W.; Zou, C.-l.; Shen, Z.; Tang, H.X. High quality factor surface Fabry-Perot cavity of acoustic waves. Appl. Phys. Lett. 2018, 112, 073505. [Google Scholar] [CrossRef]
- Shao, L.; Maity, S.; Zheng, L.; Wu, L.; Shams-Ansari, A.; Sohn, Y.-I.; Puma, E.; Gadalla, M.N.; Zhang, M.; Wang, C.; et al. Phononic Band Structure Engineering for High-Q Gigahertz Surface Acoustic Wave Resonators on Lithium Niobate. Phys. Rev. Appl. 2019, 12, 014022. [Google Scholar] [CrossRef]
- Noguchi, A.; Yamazaki, R.; Tabuchi, Y.; Nakamura, Y. Qubit-Assisted Transduction for a Detection of Surface Acoustic Waves near the Quantum Limit. Phys. Rev. Lett. 2017, 119, 180505. [Google Scholar] [CrossRef] [PubMed]
- Manenti, R.; Kockum, A.F.; Patterson, A.; Behrle, T.; Rahamim, J.; Tancredi, G.; Nori, F.; Leek, P.J. Circuit quantum acoustodynamics with surface acoustic waves. Nat. Commun. 2017, 8, 975. [Google Scholar] [CrossRef]
- Moores, B.A.; Sletten, L.R.; Viennot, J.J.; Lehnert, K.W. Cavity Quantum Acoustic Device in the Multimode Strong Coupling Regime. Phys. Rev. Lett. 2018, 120, 227701. [Google Scholar] [CrossRef]
- Bolgar, A.N.; Zotova, J.I.; Kirichenko, D.D.; Besedin, I.S.; Semenov, A.V.; Shaikhaidarov, R.S.; Astafiev, O.V. Quantum Regime of a Two-Dimensional Phonon Cavity. Phys. Rev. Lett. 2018, 120, 223603. [Google Scholar] [CrossRef]
- Satzinger, K.J.; Zhong, Y.P.; Chang, H.-S.; Peairs, G.A.; Bienfait, A.; Chou, M.; Cleland, A.Y.; Conner, C.R.; Dumur, É.; Grebel, J.; et al. Quantum control of surface acoustic-wave phonons. Nature 2018, 563, 661. [Google Scholar] [CrossRef]
- Ask, A.; Ekström, M.; Delsing, P.; Johansson, G. Cavity-free vacuum-Rabi splitting in circuit quantum acoustodynamics. Phys. Rev. A 2019, 99, 013840. [Google Scholar] [CrossRef]
- Chu, Y.; Kharel, P.; Yoon, T.; Frunzio, L.; Rakich, P.T.; Schoelkopf, R.J. Creation and control of multi-phonon Fock states in a bulk acoustic-wave resonator. Nature 2018, 563, 666. [Google Scholar] [CrossRef] [PubMed]
- Zeng, G.-H.; Zhang, Y.; Bolgar, A.N.; He, D.; Li, B.; Ruan, X.-H.; Zhou, L.; Kuang, L.-M.; Astafiev, O.V.; Liu, Y.-X.; et al. Quantum versus classical regime in circuit quantum acoustodynamics. New J. Phys. 2021, 23, 123001. [Google Scholar] [CrossRef]
- Raimond, J.M.; Brune, M.; Haroche, S. Manipulating quantum entanglement with atoms and photons in a cavity. Rev. Mod. Phys. 2001, 73, 565. [Google Scholar] [CrossRef]
- Walther, H.; Varcoe, B.T.H.; Englert, B.-G.; Becker, T. Cavity quantum electrodynamics. Rep. Prog. Phys. 2006, 69, 1325. [Google Scholar] [CrossRef]
- Wallraff, A.; Schuster, D.I.; Blais, A.; Frunzio, L.; Huang, R.-S.; Majer, J.; Kumar, S.; Girvin, S.M.; Schoelkopf, R.J. Strong coupling of a single photon to a superconducting qubit using circuit quantum electrodynamics. Nature 2004, 431, 162. [Google Scholar] [CrossRef]
- Bienfait, A.; Satzinger, K.J.; Zhong, Y.P.; Chang, H.-S.; Chou, M.-H.; Conner, C.R.; Dumur, É.; Grebel, J.; Peairs, G.A.; Povey, R.G.; et al. Phonon-mediated quantum state transfer and remote qubit entanglement. Science 2019, 364, 368. [Google Scholar] [CrossRef]
- Sletten, L.R.; Moores, B.A.; Viennot, J.J.; Lehnert, K.W. Resolving Phonon Fock States in a Multimode Cavity with a Double-Slit Qubit. Phys. Rev. X 2019, 9, 021056. [Google Scholar] [CrossRef]
- Shumeiko, V.S. Quantum acousto-optic transducer for superconducting qubits. Phys. Rev. A 2016, 93, 023838. [Google Scholar] [CrossRef]
- Metcalfe, M.; Carr, S.M.; Muller, A.; Solomon, G.S.; Lawall, J. Resolved Sideband Emission of InAs/GaAs Quantum Dots Strained by Surface AcousticWaves. Phys. Rev. Lett. 2010, 105, 037401. [Google Scholar] [CrossRef]
- Schuetz, M.J.A.; Knörzer, J.; Giedke, G.; Vandersypen, L.M.K.; Lukin, M.D.; Cirac, J.I. Acoustic Traps and Lattices for Electrons in Semiconductors. Phys. Rev. X 2017, 7, 041019. [Google Scholar] [CrossRef]
- Golter, D.A.; Oo, T.; Amezcua, M.; Lekavicius, I.; Stewart, K.A.; Wang, H. Coupling a Surface Acoustic Wave to an Electron Spin in Diamond via a Dark State. Phys. Rev. X 2016, 6, 041060. [Google Scholar] [CrossRef]
- Golter, D.A.; Oo, T.; Amezcua, M.; Stewart, K.A.; Wang, H. Optomechanical Quantum Control of a Nitrogen-Vacancy Center in Diamond. Phys. Rev. Lett. 2016, 116, 143602. [Google Scholar] [CrossRef] [PubMed]
- Schuetz, M.J.A.; Kessler, E.M.; Giedke, G.; Vandersypen, L.M.K.; Lukin, M.D.; Cirac, J.I. Universal Quantum Transducers Based on Surface Acoustic Waves. Phys. Rev. X 2015, 5, 031031. [Google Scholar] [CrossRef]
- Okada, A.; Oguro, F.; Noguchi, A.; Tabuchi, Y.; Yamazaki, R.; Usami, K.; Nakamura, Y. Cavity Enhancement of Anti-Stokes Scattering via Optomechanical Coupling with Surface Acoustic Waves. Phys. Rev. Appl. 2018, 10, 024002. [Google Scholar] [CrossRef]
- Noguchi, A.; Yamazaki, R.; Tabuchi, Y.; Nakamura, Y. Single-photon quantum regime of artificial radiation pressure on a surface acoustic wave resonator. Nat. Commun. 2020, 11, 1183. [Google Scholar] [CrossRef]
- Wu, S.-C.; Zhang, L.; Lu, J.; Qin, L.-G.; Wang, Z.-Y. Surface-acoustic-wave-controlled optomechanically induced transparency in a hybrid piezo-optomechanical planar distributed Bragg-reflector-cavity system. Phys. Rev. A 2021, 103, 013719. [Google Scholar] [CrossRef]
- Majumdar, A.; Bajcsy, M.; Vučković, J. Probing the ladder of dressed states and nonclassical light generation in quantum-dot–cavity QED. Phys. Rev. A 2012, 85, 041801. [Google Scholar] [CrossRef]
- Majumdar, A.; Bajcsy, M.; Rundquist, A.; Vučković, J. Loss-Enabled Sub-Poissonian Light Generation in a Bimodal Nanocavity. Phys. Rev. Lett. 2012, 108, 183601. [Google Scholar] [CrossRef]
- Zhang, W.; Yu, Z.; Liu, Y.; Peng, Y. Optimal photon antibunching in a quantum-dot–bimodal-cavity system. Phys. Rev. A 2014, 89, 043832. [Google Scholar] [CrossRef]
- Tang, J.; Wu, Y.; Wang, Z.; Sun, H.; Tang, L.; Zhang, H.; Li, T.; Lu, Y.; Xiao, M.; Xia, K. Vacuum-induced surface-acoustic-wave phonon blockade. Phys. Rev. A 2020, 101, 053802. [Google Scholar] [CrossRef]
- Xue, J.-J.; Zhu, W.-Q.; He, Y.-N.; Wang, X.; Li, H.-R. Two-acoustic-cavity interaction mediated by superconducting artificial atoms. Quantum Inf. Process. 2020, 19, 333. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, T.-S.; Jin, G.-R.; Chen, A. Enhanced Phonon Antibunching in a Circuit Quantum Acoustodynamical System Containing Two Surface Acoustic Wave Resonators. Micromachines 2022, 13, 591. https://doi.org/10.3390/mi13040591
Yin T-S, Jin G-R, Chen A. Enhanced Phonon Antibunching in a Circuit Quantum Acoustodynamical System Containing Two Surface Acoustic Wave Resonators. Micromachines. 2022; 13(4):591. https://doi.org/10.3390/mi13040591
Chicago/Turabian StyleYin, Tai-Shuang, Guang-Ri Jin, and Aixi Chen. 2022. "Enhanced Phonon Antibunching in a Circuit Quantum Acoustodynamical System Containing Two Surface Acoustic Wave Resonators" Micromachines 13, no. 4: 591. https://doi.org/10.3390/mi13040591
APA StyleYin, T.-S., Jin, G.-R., & Chen, A. (2022). Enhanced Phonon Antibunching in a Circuit Quantum Acoustodynamical System Containing Two Surface Acoustic Wave Resonators. Micromachines, 13(4), 591. https://doi.org/10.3390/mi13040591





