Design and Manufacturing of Equipment for Investigation of Low Frequency Bioimpedance
Abstract
1. Introduction
- The first range, α dispersion, for the frequency range of between 10 Hz to 10 kHz, is related to the phenomena of ionic diffusion of the cell membrane and the counterion effects;
- The second range, β dispersion, for the frequency range between 10 kHz and 100 MHz, is produced by the polarization phenomenon of cell membranes, the behavior of which is similar to that of capacitance. The polarization phenomena of proteins and other organic macromolecules contribute to the dispersion;
2. Materials and Methods
2.1. Bioimpedance Measurement Sensors and Body Injection Current Electrodes
- -
- Ag (silver) foil, Code AG000470/37, having 99.99% purity, 0.5 mm thickness, purchased from ALDRICH;
- -
- Au (gold) foil, Code PREMION, having 99.99% purity, 0.127 mm thickness, purchased from ALFA AESAR.
2.2. General Cole Model for Skin, Organs, and Electrodes
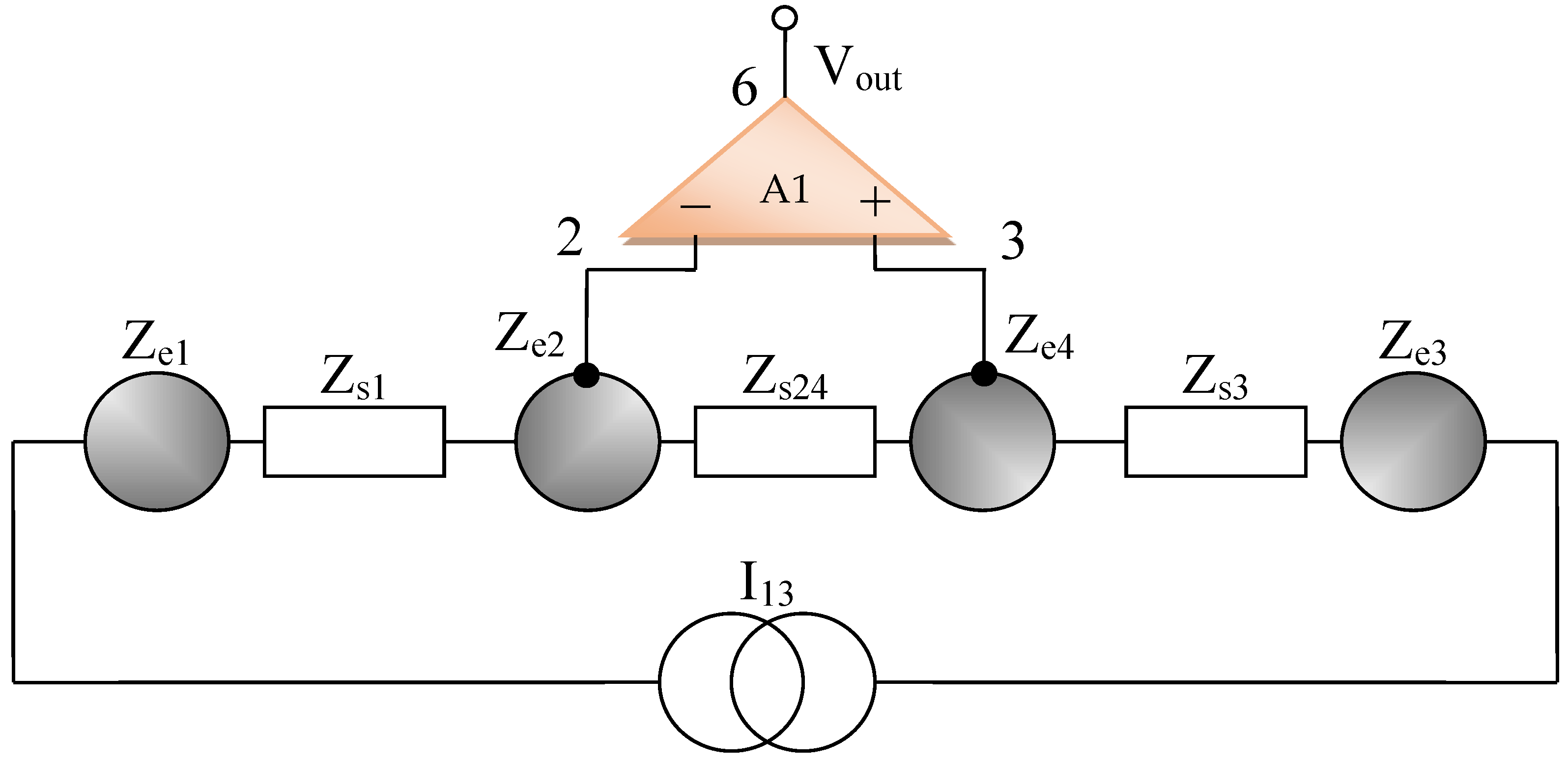
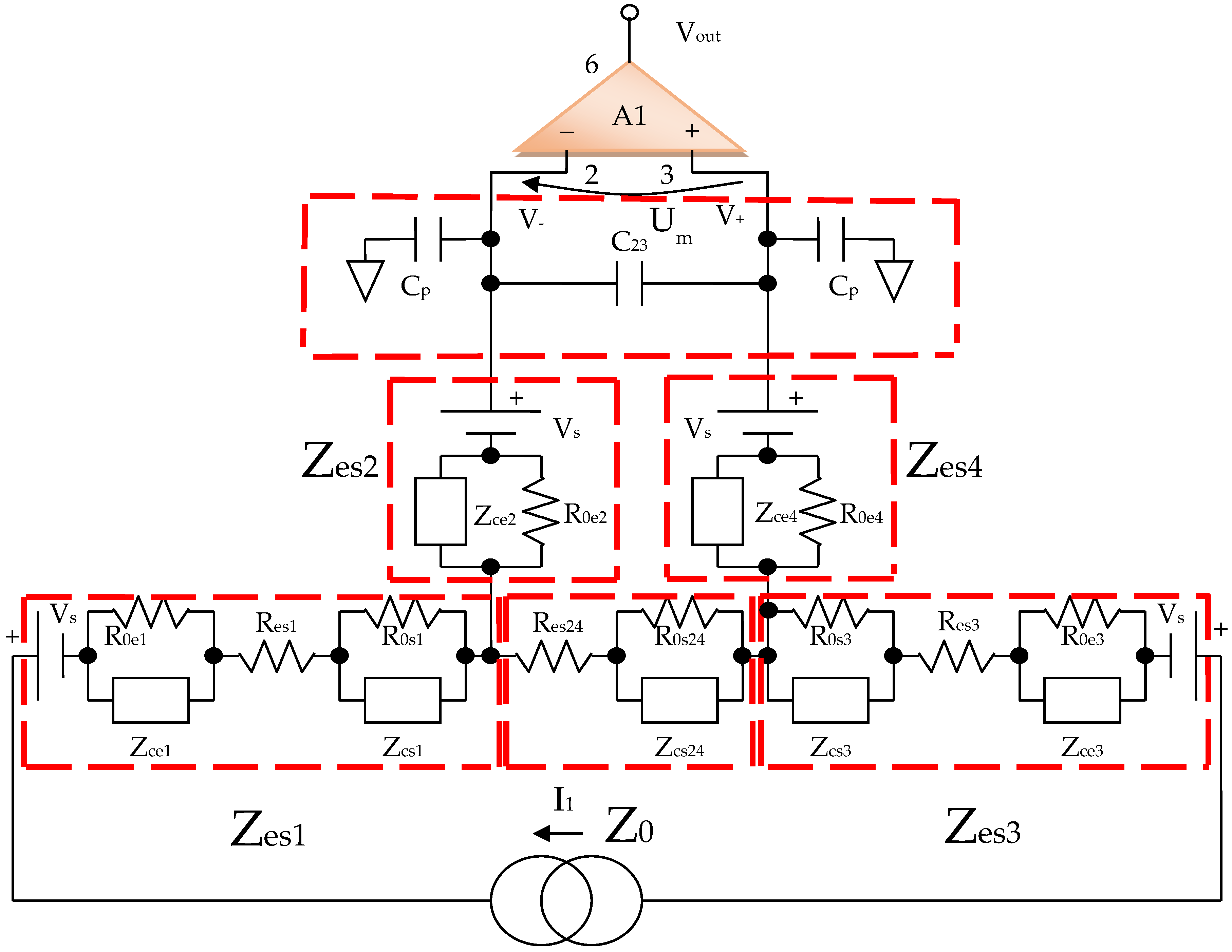
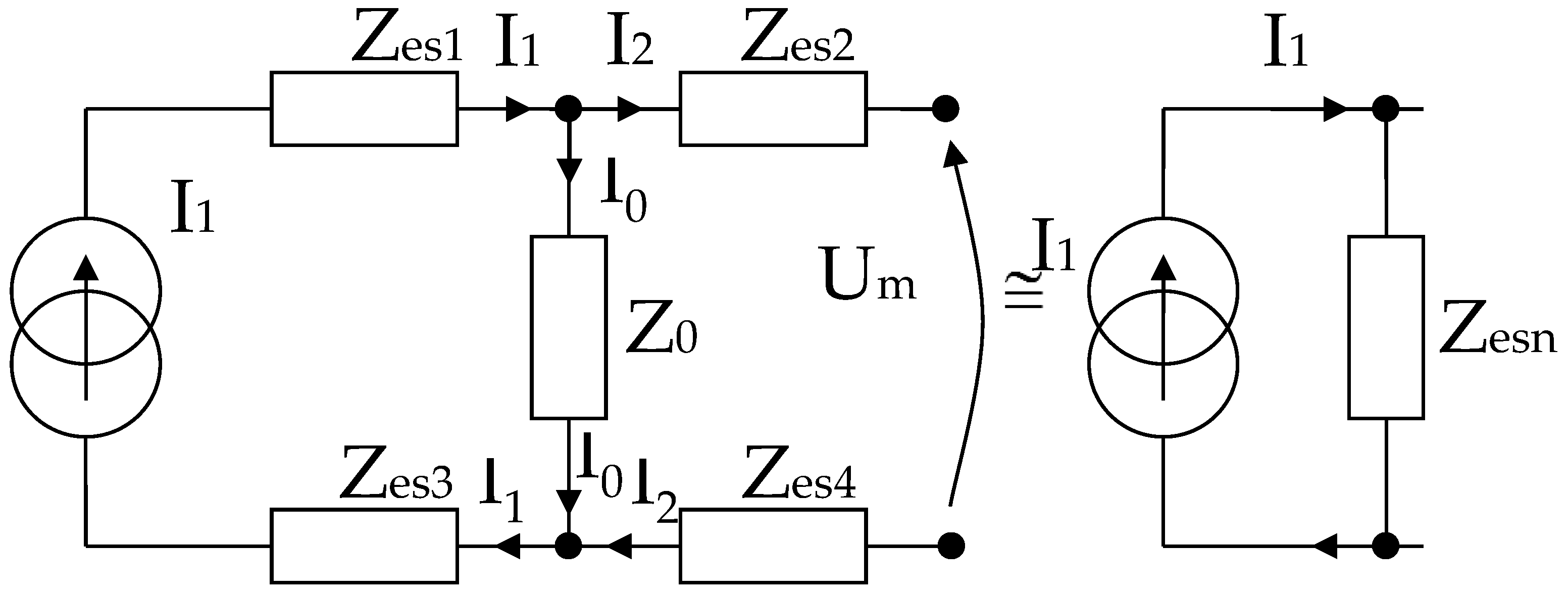
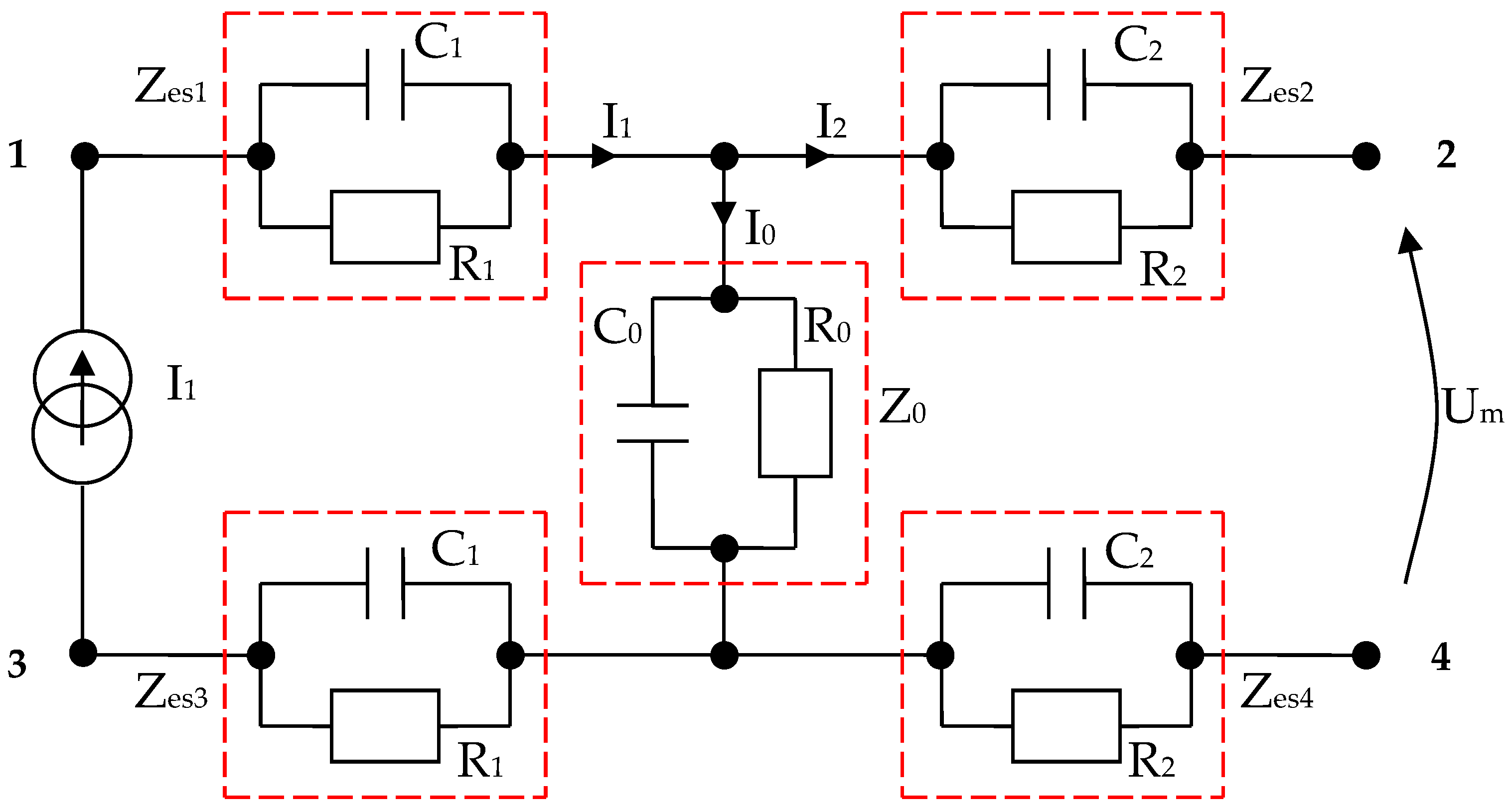
2.3. Modeling a System of Electrodes in Contact with the Skin and a Target Organ
3. Design of Equipment for the Investigation of Low Frequency Bioimpedance
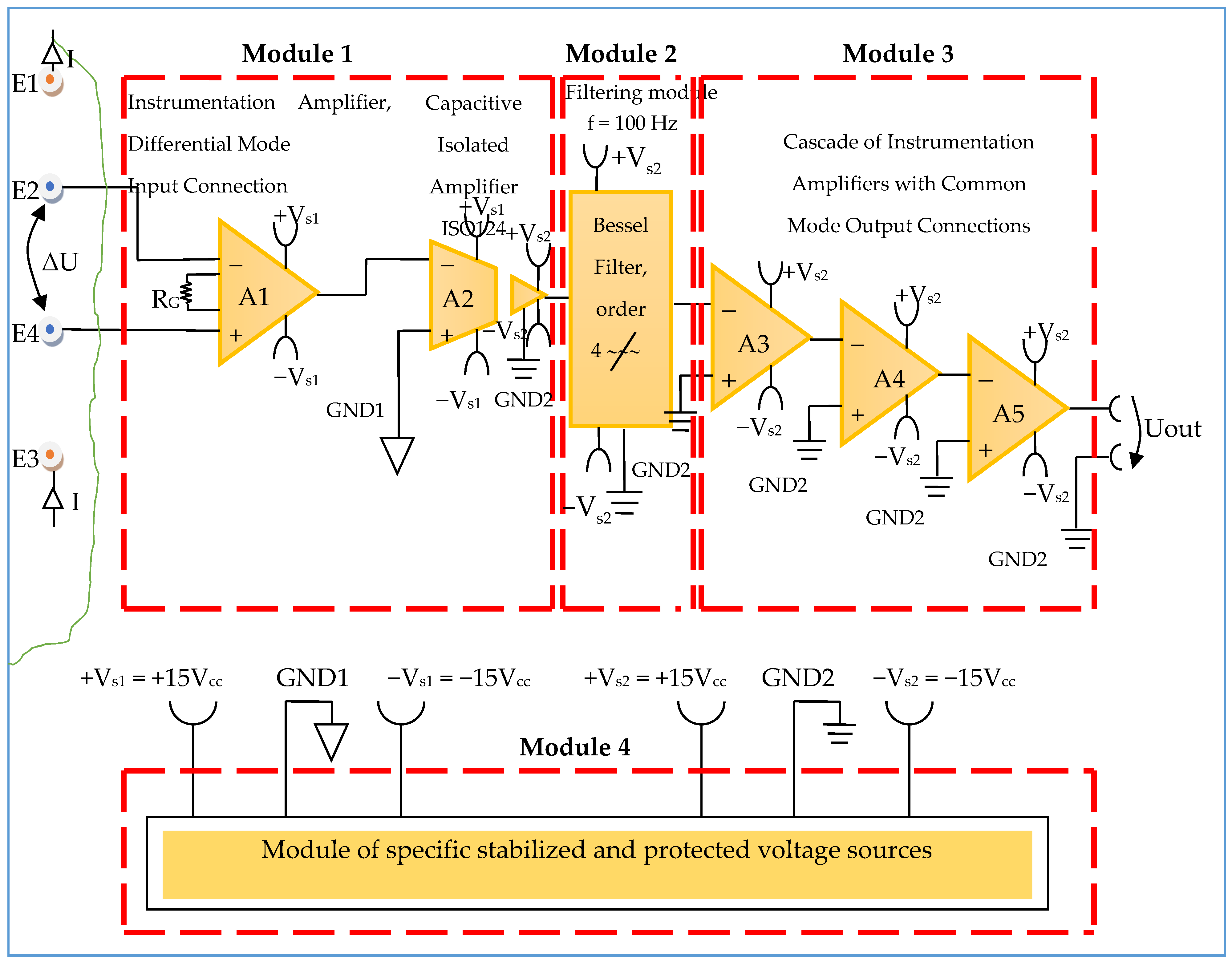
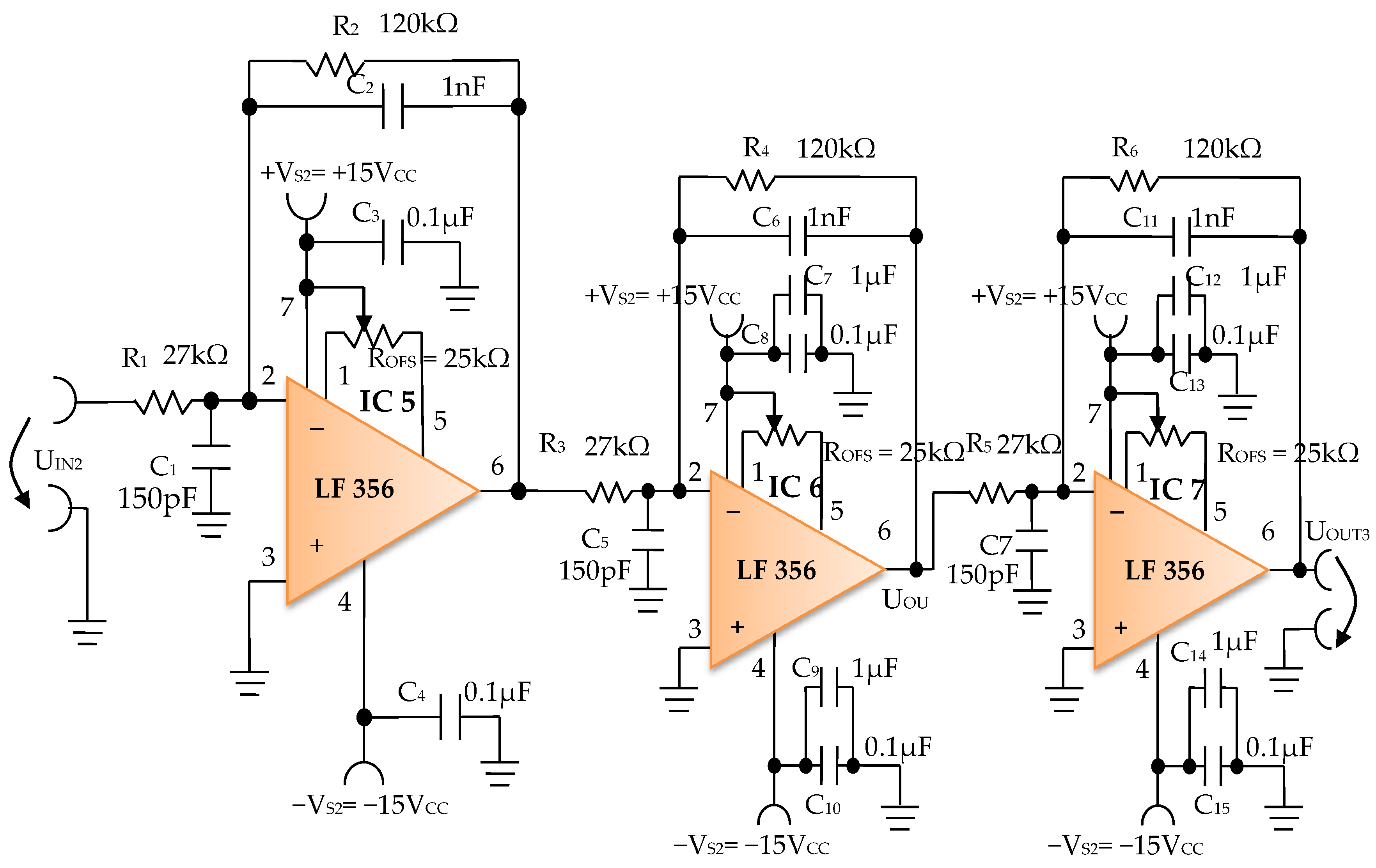
3.1. Electronic Conditioning System Used in Biological Signals Acquisition
- -
- Module 1—electronic module for acquiring biological signals;
- -
- Module 2—filtering electronic module;
- -
- Module 3—common mode amplifier module for electronic signal output.
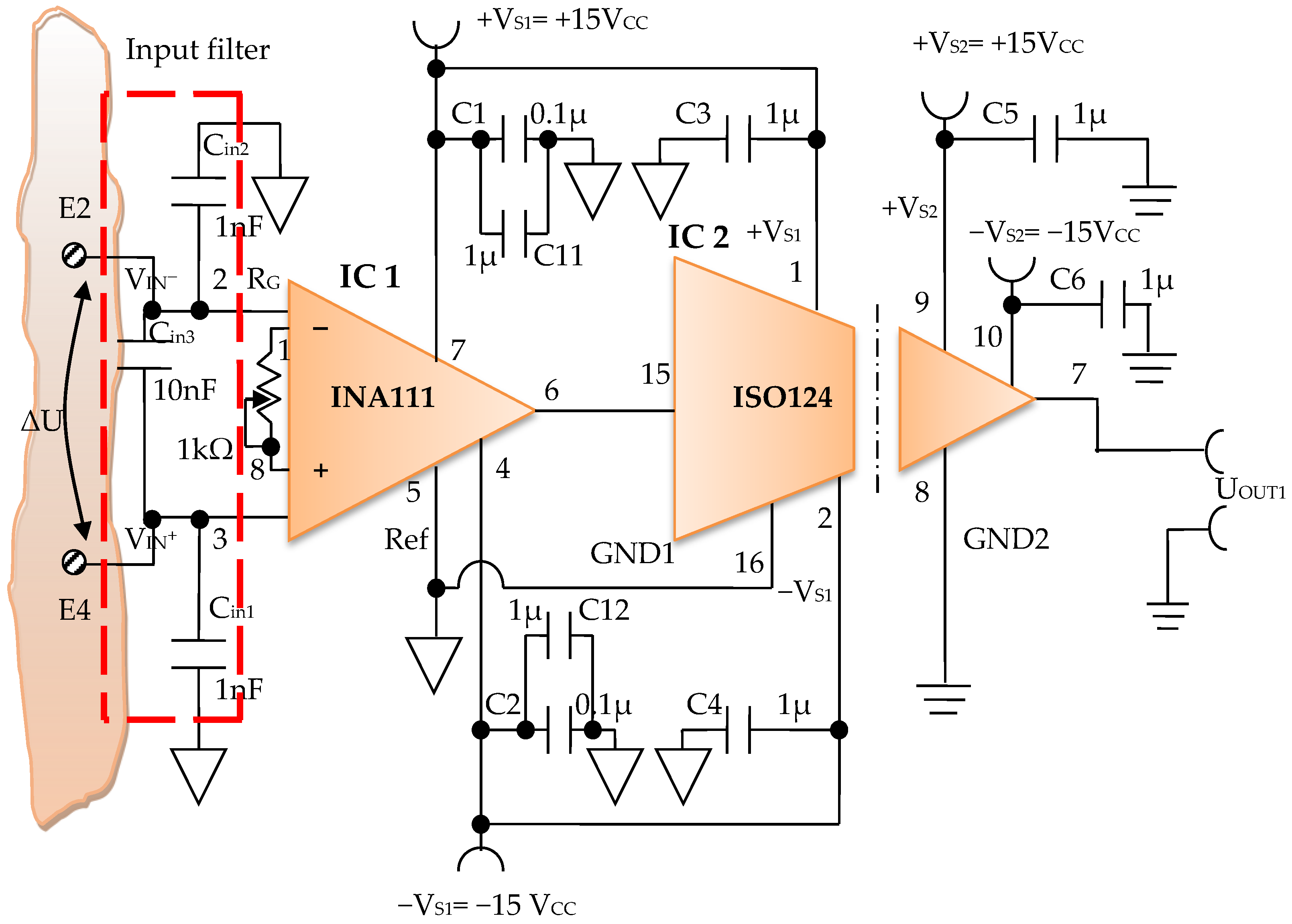
3.1.1. Electronic Module for Acquiring Biological Signals
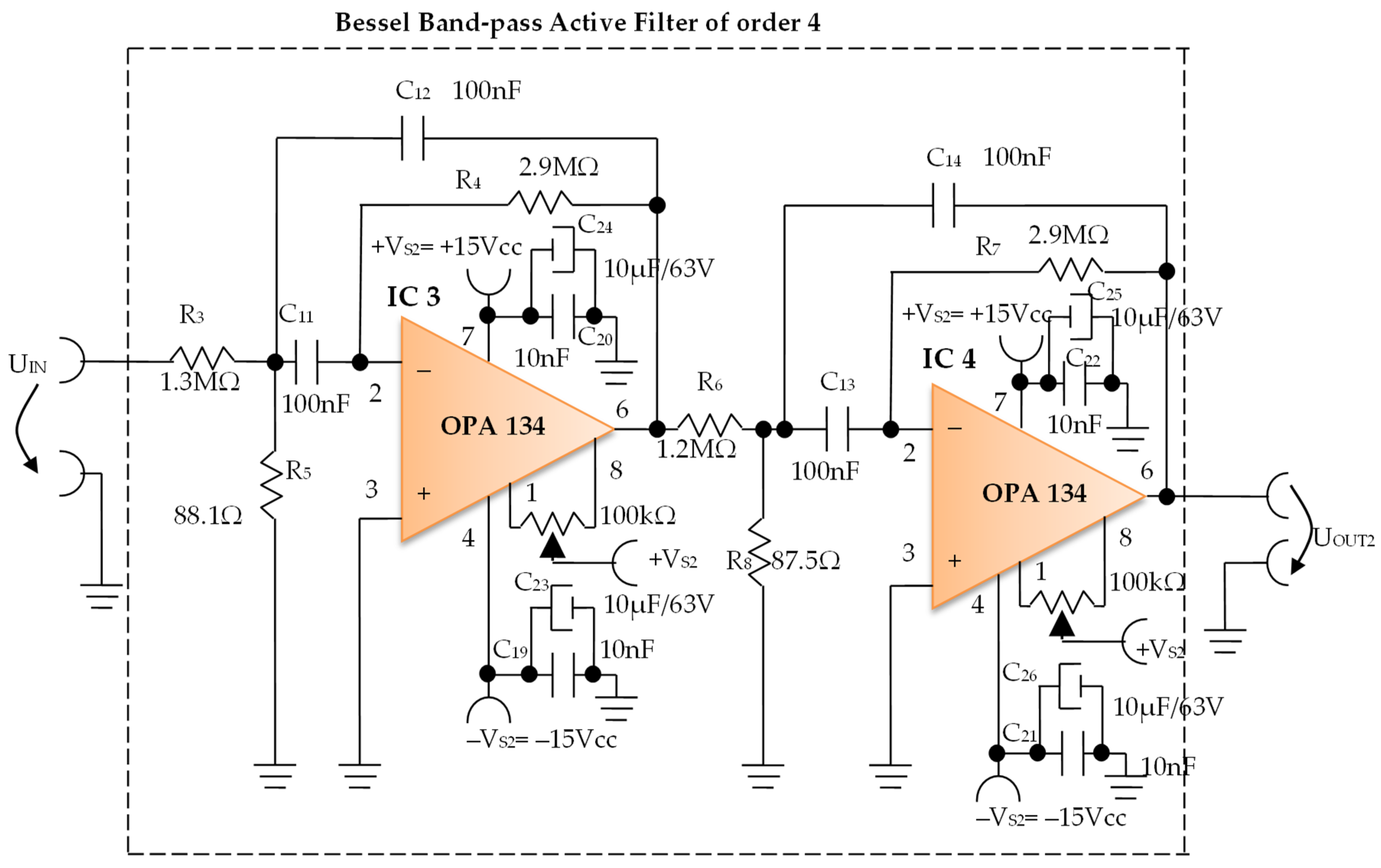
3.1.2. Electronic Filtering Module
3.1.3. Electronic Common Mode Output Amplifier Module
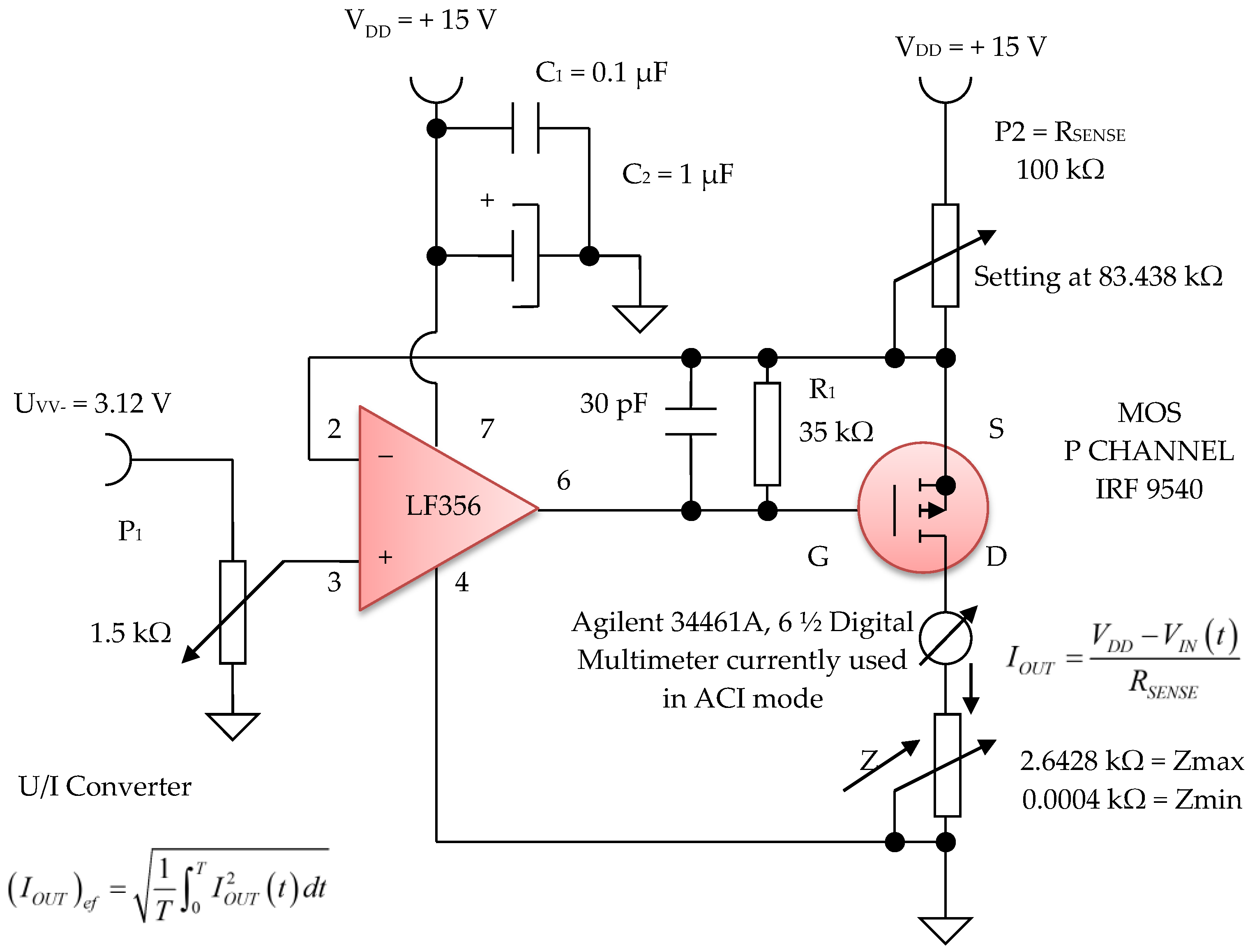
3.2. Electronic Module of the Constant Current Generator, I1 = 100 μA Average Value
- Electronic sinusoidal oscillator block;
- Buffer electronic block;
- Electronic block of voltage/constant current converter, average values of 100 µA (Figure 16).
- -
- k is a constant;
- -
- ∆U is the biological signal charged with the biopotentials generated by the human body that is taken from the electrodes E2 and E4 (Figure 8);
- -
- I is a constant current in the average value, with a peak value of I = 100 µA that is injected into the human body by means of the current injection electrodes E1 and E3 (Figure 8). If we consider the four-electrode configuration (tetrapolar), where the external electrodes inject a constant current, Gómez-Cortés, J.C. et al. as well as Yu, Y. et al. [56,57] and the resulting voltage is picked up by internal electrodes and applied to an amplifier, it can be considered that the two physical quantities, bioimpedance and bioelectrical resistivity, differ only by a constant.
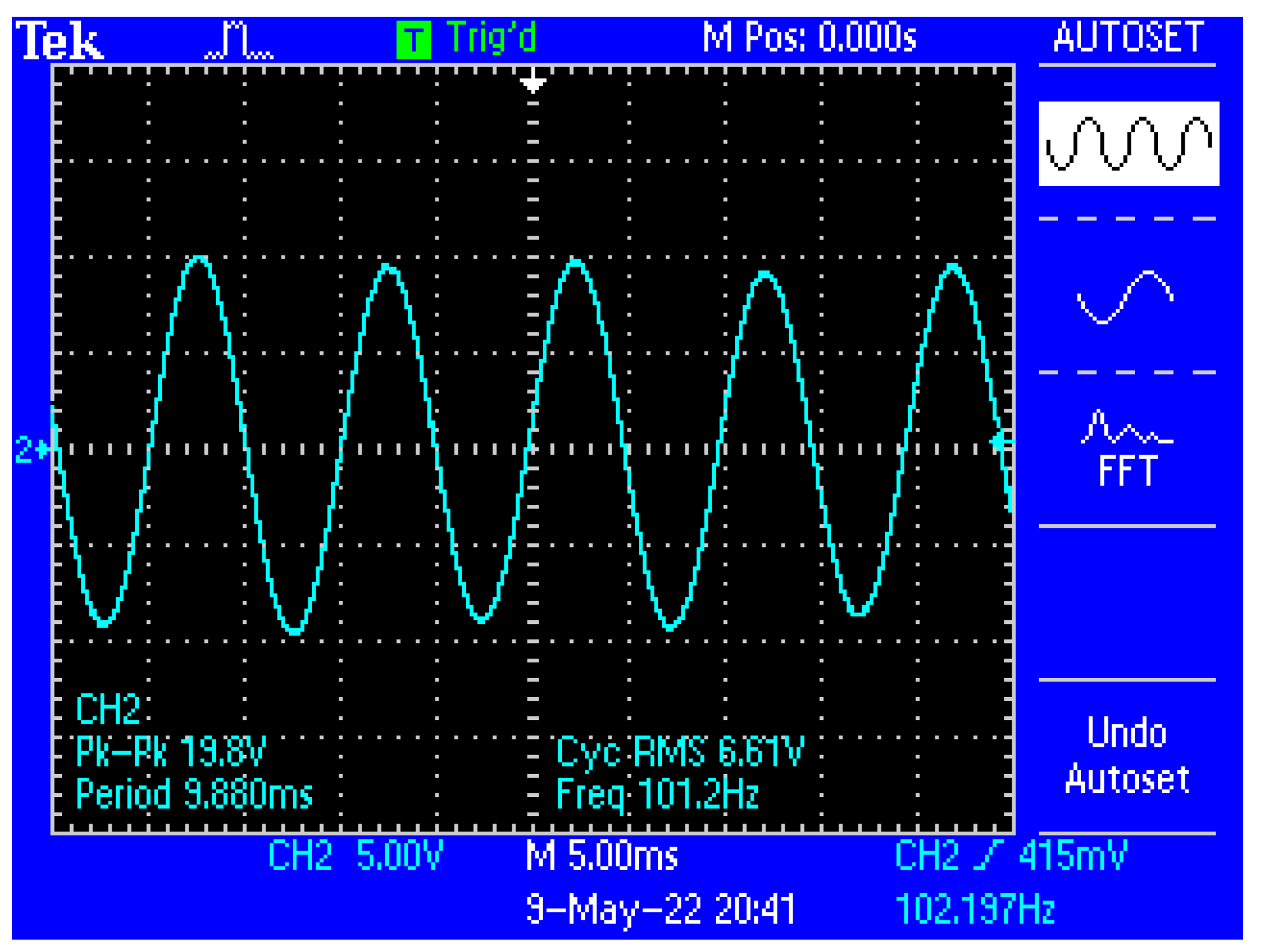
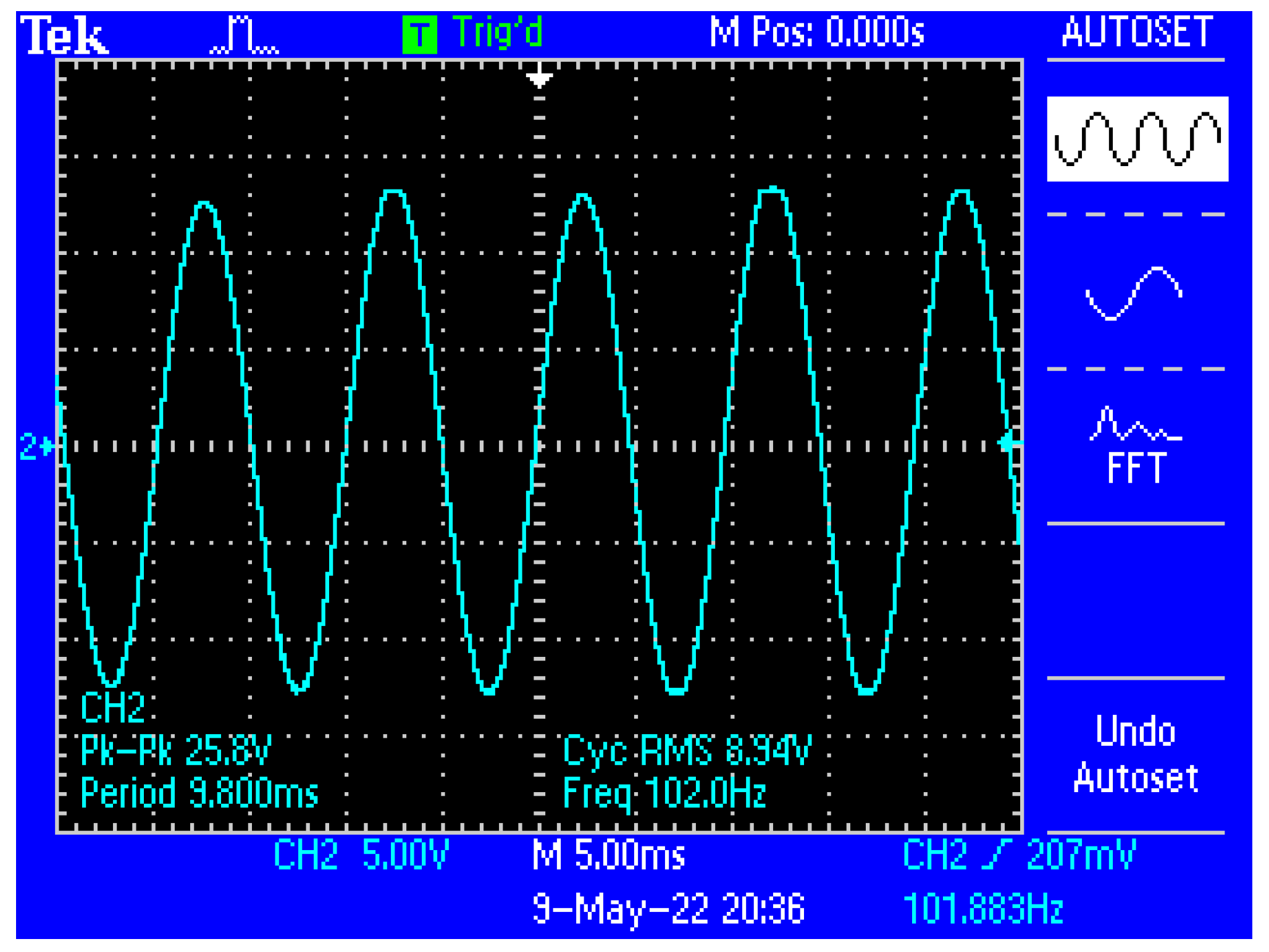
4. Experimental Data Obtained with Equipment for the Investigation of Low Frequency Bioimpedance and Evaluation of the Accuracy of the Measurements
5. Discussion
- (a)
- (b)
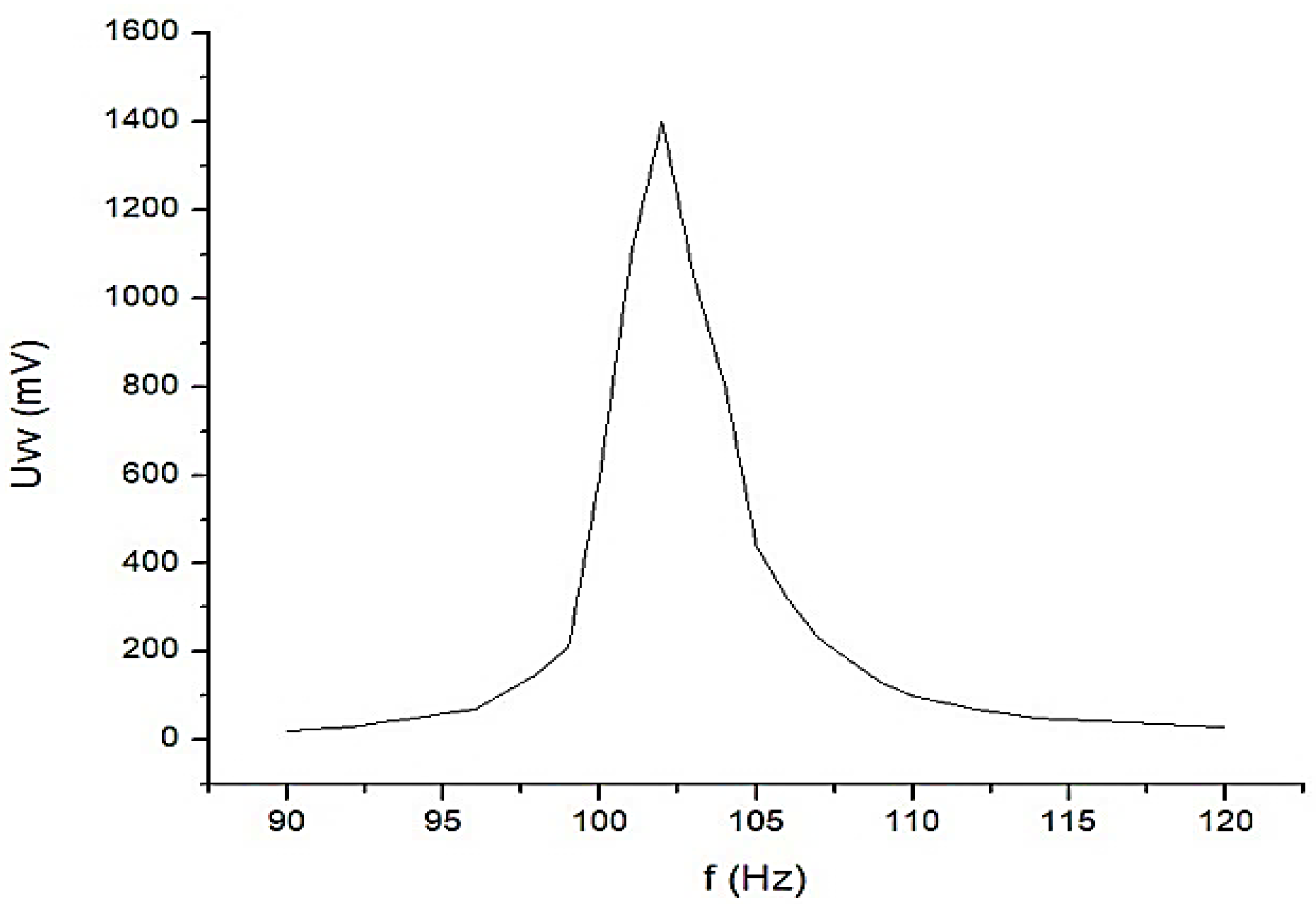
- The possibility of picking up some biological signals from the target organs having extremely small amplitudes, up to 5 mV, precisely as a consequence of using the very narrow bandwidth filter;
- (c)
- Increasing the measurement precision by placing an additional filter in the cascade, a Bessel fourth-order band-pass filter, also having a very narrow bandwidth of 1 Hz.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kadir, M.A.; Wilson, A.J.; Siddique-Rabbani, K. A multi-frequency focused impedance measurement system based on analogue synchronous peak detection. Front. Electron. 2021, 2, 791016. [Google Scholar] [CrossRef]
- Lukaski, H.C.; Diaz, V.N.; Talluri, A.; Nescolarde, L. Classification of Hydration in Clinical Conditions: Indirect and Direct Approaches Using Bioimpedance. Nutrients 2019, 11, 809. [Google Scholar] [CrossRef] [PubMed]
- Vermeiren, E.; Ysebaert, M.; Van Hoorenbeeck, K.; Bruyndonckx, L.; Van Dessel, K.; Van Helvoirt, M. Comparison of Bioimpedance Spectroscopy and Dual Energy X-ray Absorptiometry for Assessing Body Composition Changes in Obese Children during Weight Loss. Eur. J. Clin. Nutr. 2021, 75, 73–84. [Google Scholar] [CrossRef] [PubMed]
- Naranjo-Hernández, D.; Reina-Tosina, J.; Roa, L.M.; Barbarov-Rostán, G.; Aresté-Fosalba, N.; Lara-Ruiz, A.; Cejudo-Ramos, P.; Ortega-Ruiz, F. Smart Bioimpedance Spectroscopy Device for Body Composition Estimation. Sensors 2020, 20, 70. [Google Scholar] [CrossRef] [PubMed]
- Khalil, S.F.; Mohktar, M.S.; Ibrahim, F. The Theory and Fundamentals of Bioimpedance Analysis in Clinical Status Monitoring and Diagnosis of Diseases. Sensors 2014, 14, 10895–10928. [Google Scholar] [CrossRef]
- Anand, G.; Yu, Y.; Lowe, A.; Kalra, A. Bioimpedance Analysis as a Tool for Hemodynamic Monitoring: Overview, Methods and Challenges. Physiol. Meas. 2021, 42, 03TR01. [Google Scholar] [CrossRef]
- Cheng, Z.; Carobbio, A.L.; Soggiu, L.; Migliorini, M.; Guastini, L.; Mora, F.; Fragale, M.; Ascoli, A.; Africano, S.; Caldwell, D.G.; et al. SmartProbe: A Bioimpedance Sensing System for Head and Neck Cancer Tissue Detection. Physiol. Meas. 2020, 41, 054003. [Google Scholar] [CrossRef]
- Ugwah, J.; Savage, N.Y.; Whelton, E.; O′Donovan, A.M.; O′Sullivan, M.J.; Donnell, B.D.O.; Moore, E.J. Ex-vivo detection of breast cancer with a bio-impedance sensor. J. Cancer Treatment Diagn. 2021, 5, 18–22. [Google Scholar] [CrossRef]
- Kusche, R.; Hauschild, S.; Ryschka, M. A bioimpedance based cardiovascular measurement system. In World Congress on Medical Physics and Biomedical Engineering; Springer: Singapore, 2018; pp. 839–842. [Google Scholar] [CrossRef]
- Ferrari, L.M.; Sudha, S.; Tarantino, S.; Esposti, R.; Bolzoni, F.; Cavallari, P.; Cipriani, C.; Mattoli, V.; Greco, F. Ultraconformable Temporary Tattoo Electrodes for Electrophysiology. Adv. Sci. 2018, 5, 1700771. [Google Scholar] [CrossRef]
- Takamatsu, S.; Lonjaret, T.; Badier, J.M.; Malliaras, G.G.; Isamailova, E. Direct patterning of organic conductors on knitted textiles for long-term electrocardiography. Sci. Rep. 2015, 5, 15003. [Google Scholar] [CrossRef]
- Takeshita, T.; Yoshida, M.; Takei, Y.; Ouchi, A.; Hinoki, A.; Uchida, H.; Kobayashi, T. Relationship between Contact Pressure and Motion Artifacts in ECG Measurement with Electrostatic Flocked Electrodes Fabricated on Textile. Sci. Rep. 2019, 9, 5897–5907. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.-H.; De Beeck, M.O.; Vanderheyden, L.; Carrette, E.; Mihajlović, V.; Vanstreels, K.; Grundlehner, B.; Gadeyne, S.; Boon, P.; Van Hoof, C. Soft, Comfortable Polymer Dry Electrodes for High Quality ECG and EEG Recording. Sensors 2014, 14, 23758–23780. [Google Scholar] [CrossRef]
- Naranjo-Hernández, D.; Reina-Tosina, J.; Min, M. Fundamentals, Recent Advances, and Future Challenges in Bioimpedance Devices for Healthcare Applications. J. Sens. 2019, 2019, 9210258. [Google Scholar] [CrossRef]
- Harvey, J.R.; Mendelson, Y. A Portable Sensor for Skin Bioimpedance Measurements. Int. J. Sens. Sens. Netw. 2019, 7, 1–8. [Google Scholar] [CrossRef]
- Roy, A.; Bhattacharjee, S.; Podder, S.; Ghosh, A. Measurement of bioimpedance and application of Cole model to study the effect of moisturizing cream on human skin. AIMS Biophys. 2020, 7, 362–379. [Google Scholar] [CrossRef]
- Buchholz, A.C.; Bartok, C.; Schoeller, D.A. The validity of bioelectrical impedance models in clinical populations. Nutritionin Clin. Pract. 2004, 19, 433–446. [Google Scholar] [CrossRef]
- Lin, M.C.; Hu, D.; Marmor, M.; Herfat, S.T.; Bahney, C.S.; Maharbiz, M.M. Smart bone plates can monitor fracture healing. Sci. Rep. 2019, 9, 2122. [Google Scholar] [CrossRef] [PubMed]
- Bhardwaj, P.; Rai, D.V.; Garg, M.L.; Mohanty, B.P. Potential of electrical impedance spectroscopy to differentiate between healthy and osteopenic bone. Clin. Biomech. 2018, 57, 81–88. [Google Scholar] [CrossRef] [PubMed]
- Amini, M.; Hisdal, J.; Kalvøy, H. Applications of bioimpedance measurement techniques in tissue engineering. J. Electr. Bioimpedance 2018, 9, 142–158. [Google Scholar] [CrossRef]
- Telipan, G.; Pîslaru-Dănescu, L.; Lungulescu, E.-M.; Ion, I.; Marinescu, V.A. Comparative Study of Polypyrrole and Ag/Polypyrrole Hybrid Nanocomposites as Sensitive Material Used for New Dry Polarizable Bioimpedance Sensors. Appl. Sci. 2021, 11, 4168. [Google Scholar] [CrossRef]
- Taji, B.; Shirmohammadi, S.; Groza, V.; Batkin, I. Impact of Skin-Electrode Interface on Electrocardiogram Measurements Using Conductive Textile Electrodes. IEEE Trans. Instrum. Meas. 2014, 63, 1412–1422. [Google Scholar] [CrossRef]
- Karplus, K. S2014, BME 101L: Applied Circuits Lab 4 Polarising and Non-polarising Electrodes. Available online: https://users.soe.ucsc.edu/~karplus/bme101/s14/04-electrodes.pdf (accessed on 15 May 2022).
- Kumar, R.; Singh, R.; Hui, D.; Feo, L.; Fraternali, F. Graphene as biomedical sensing element: State of art review and potential engineering applications. Compos. Part B Eng. 2018, 134, 193–206. [Google Scholar] [CrossRef]
- Kusche, R.; Kaufmann, S.; Ryschka, M. Dry electrodes for bioimpedance measurements-design, characterization and comparison. IOP Biomed. Phys. Eng. Express 2018, 5, 015001. [Google Scholar] [CrossRef]
- Chlaihawi, A.A.; Narakathu, B.B.; Emamian, S.; Bazuin, B.J.; Atashbar, M.Z. Development of printed and flexible dry ECG electrodes. Sens. Bio. Sens. Res. 2018, 20, 9–15. [Google Scholar] [CrossRef]
- Jung, H.C.; Moon, J.H.; Baek, D.H.; Lee, J.H.; Choi, Y.Y.; Hong, J.S.; Lee, S.H. CNT/PDMS Composite Flexible Dry Electrodes for Long-Term ECG Monitoring. IEEE Trans. Bio. Med. Eng. 2012, 59, 1472–1479. [Google Scholar] [CrossRef]
- Baek, J.Y.; An, J.H.; Choi, J.M.; Park, K.S.; Lee, S.H. Flexible polymeric dry electrodes for the long-term monitoring of ECG. Sens. Actuat. A Phys. 2008, 143, 423–429. [Google Scholar] [CrossRef]
- Karimullah, A.S.; Cumming, D.R.S.; Riehle, M.; Gadegaard, N. Development of a conducting polymer cell impedance sensor. Sens. Actuators B Chem. 2013, 176, 667–674. [Google Scholar] [CrossRef]
- Yussuf, A.; Al-Saleh, M.; Al-Enezi, S.; Abraham, G. Synthesis and Characterization of Conductive Polypyrrole: The Influence of the Oxidants and Monomer on the Electrical, Thermal, and Morphological Properties. Int. J. Polym. Sci. 2018, 2018, 4191747. [Google Scholar] [CrossRef]
- Farghaly, A.A.; Collinson, M.M. Mesoporous Hybrid Polypyrrole-Silica Nanocomposite Films with a Strata-Like Structure. Langmuir 2016, 32, 5925–5936. [Google Scholar] [CrossRef]
- Sowmiya, G.; Anbarasan, P.M.; Velraj, G. Synthesis, Characterisation and Electrical Conductivity Study of Conductive Polypyrrole doped with Nano Tin Composite for Antibacterial Application. Int. Res. J. Eng. Technol. 2017, 4, 127–131. [Google Scholar]
- Shrestha, B.K.; Ahmad, R.; Shrestha, S.; Park, C.H.; Kim, C.S. Globular Shaped Polypyrrole Doped Well-Dispersed Functionalized Multiwall Carbon Nanotubes/Nafion Composite for Enzymatic Glucose Biosensor Application. Sci. Rep. 2017, 7, 16191. [Google Scholar] [CrossRef] [PubMed]
- Borthakur, L.J.; Sharma, S.; Dolui, S.K. Studies on Ag/Polypyrrole composite deposited on the surface of styrene-methyl acrylate copolymer microparticles and their electrical and electrochemical properties. J. Mater. Sci. Mater. Electron. 2011, 22, 949–958. [Google Scholar] [CrossRef]
- Critcher, S.; Freeborn, T.J. Localized Bioimpedance Measurements with the MAX3000x Integrated Circuit: Characterization and Demonstration. Sensors 2021, 21, 3013. [Google Scholar] [CrossRef] [PubMed]
- Nescolarde, L.; Yanguas, J.; Lukaski, H.; Alomar, X.; Rosell-Ferrer, J.; Rodas, G. Localized bioimpedance to assess muscle injury. Physiol. Meas. 2013, 34, 237–245. [Google Scholar] [CrossRef]
- Nescolarde, L.; Yanguas, J.; Lukaski, H.; Alomar, X.; Rosell-Ferrer, J.; Rodas, G. Effects of muscle injury severity on localized bioimpedance measurements. Physiol. Meas. 2014, 36, 27. [Google Scholar] [CrossRef]
- Fu, B.; Freeborn, T.J. Biceps tissue bioimpedance changes from isotonic exercise-induced fatigue at different intensities. Biomed. Phys. Eng. Express 2018, 4, 025037. [Google Scholar] [CrossRef]
- Freeborn, T.J.; Regard, G.; Fu, B. Localized Bicep Tissue Bioimpedance Alterations Following Eccentric Exercise in Healthy Young Adults. IEEE Access 2020, 8, 23100–23109. [Google Scholar] [CrossRef]
- Sanchez, B.; Rutkove, S. Present uses, future applications, and technical underpinnings of electrical impedance myography. Curr. Neurol. Neurosci. Rep. 2017, 17, 86. [Google Scholar] [CrossRef]
- Zhu, F.; Kotanko, P.; Handelman, G.; Raimann, J.; Liu, L.; Carter, M.; Kuhlmann, M.; Seibert, E.; Leonard, E.; Levin, N. Estimation of normal hydration in dialysis patients using whole body and calf bioimpedance analysis. Physiol. Meas. 2011, 32, 887–902. [Google Scholar] [CrossRef]
- Hersek, S.; Toreyin, H.; Teague, C.; Millard-Stafford, M.; Jeong, H.; Bavare, M.; Wolkoff, P.; Sawka, M.; Inan, O. Wearable vector electrical bioimpedance system to assess knee joint health. IEEE Trans. Biomed. Eng. 2017, 64, 2353–2360. [Google Scholar] [CrossRef]
- Mabrouk, S.; Whittingslow, D.; Inan, O. Robust method for mid-activity tracking and evaluation of ankle health post-injury. IEEE Trans. Biomed. Eng. 2020, 68, 1341–1350. [Google Scholar] [CrossRef]
- Huynh, T.H.; Jafari, R.; Chung, W.-Y. An Accurate Bioimpedance Measurement System for Blood Pressure Monitoring. Sensors 2018, 18, 2095. [Google Scholar] [CrossRef] [PubMed]
- Blanco-Almazan, D.; Groenedaal, W.; Catthoor, F.; Jane, R. Wearable bioimpedance measurement for respiratory monitoring during inspiratory loading. IEEE Access 2019, 7, 89487–89496. [Google Scholar] [CrossRef]
- Grimnes, S.; Martinsen, O.G. Bioimpedance and Bioelectricity Basics Book, 2nd ed; Elsevier: Amsterdam, The Netherlands; Academic Press: Cambridge, MA, USA, 2008. [Google Scholar] [CrossRef]
- Alimisis, V.; Dimas, C.; Pappas, G.; Sotiriadis, P.P. Analog Realization of Fractional-Order Skin-Electrode Model for Tetrapolar Bio-Impedance Measurements. Technologies 2020, 8, 61. [Google Scholar] [CrossRef]
- Faes, T.J.C.; van der Meij, H.A.; de Munck, J.C.; Heethaar, R.M. The electric resistivity of human tissues (100 Hz-10 MHz): A meta-analysis of review studies. Physiol. Meas. 1999, 20, R1–R10. [Google Scholar] [CrossRef] [PubMed]
- Freeborn, T.J.; Critcher, S. Cole-Impedance Model Representations of Right-Side Segmental Arm, Leg, and Full-Body Bioimpedances of Healthy Adults: Comparison of Fractional-Order. Fractal Fract. 2021, 5, 13. [Google Scholar] [CrossRef]
- Birgersson, U. Electrical Impedance of Human Skin and Tissue Alterations: Mathematical Modeling and Measurements; Karolinska Institutet: Stockholm, Sweden, 2012. [Google Scholar]
- Gun, L.; Ning, D.; Liang, Z. Effective Permittivity of Biological Tissue: Comparison of Theoretical Model and Experiment. Math. Probl. Eng. 2017, 2017, 7249672. [Google Scholar] [CrossRef]
- Sverre, G.; Ørjan, G.M. Alpha-dispersion in human tissue. J. Phys. Conf. Ser. 2010, 224, 012073. [Google Scholar] [CrossRef]
- Bishay, S.T. Numerical Methods for the Calculation of the Cole-Cole Parameters. Egypt. J. Sol. 2000, 3, 179–188. [Google Scholar]
- Kaufmann, S.; Ardelt, G.; Ryschka, M. Measurements of electrode skin impedance using carbon rubber electrodes-first results. J. Phys. Conf. Ser. 2013, 434, 012020. [Google Scholar] [CrossRef]
- Mills, A.C.; Huang, H.; Zhu, Y. Wearable silver nanowire dry electrode for electrophys Iological sensing. RCS Adv. 2015, 5, 11627–11632. [Google Scholar] [CrossRef]
- Gómez-Cortés, J.C.; Díaz-Carmona, J.J.; Padilla-Medina, J.A.; Calderon, A.E.; Gutiérrez, A.I.B.; Gutiérrez-López, M.; Prado-Olivarez, J. Electrical Impedance Tomography Technical Contributions for Detection and 3D Geometric Localization of Breast Tumors: A Systematic Review. Micromachines 2022, 13, 496. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y.; Anand, G.; Lowe, A.; Zhang, H.; Kalra, A. Towards Estimating Arterial Diameter Using Bioimpedance Spectroscopy: A Computational Simulation and Tissue Phantom Analysis. Sensors 2022, 22, 4736. [Google Scholar] [CrossRef] [PubMed]
- Grossi, M.; Parolin, C.; Vitali, B.; Riccò, B. Electrical Impedance Spectroscopy (EIS) characterization of saline solutions with a low-cost portable measurement system. Eng. Sci. Technol. Int. J. 2019, 22, 102–108. [Google Scholar] [CrossRef]
- Pîslaru-Dănescu, L.; Zărnescu, G.-C.; Stoica, V. Human Subjects Protection by Monitoring the Stabilized Supply Voltages of the Medical Equipment. Electroteh. Electron. Autom. 2022, 70, 1–11. [Google Scholar] [CrossRef]



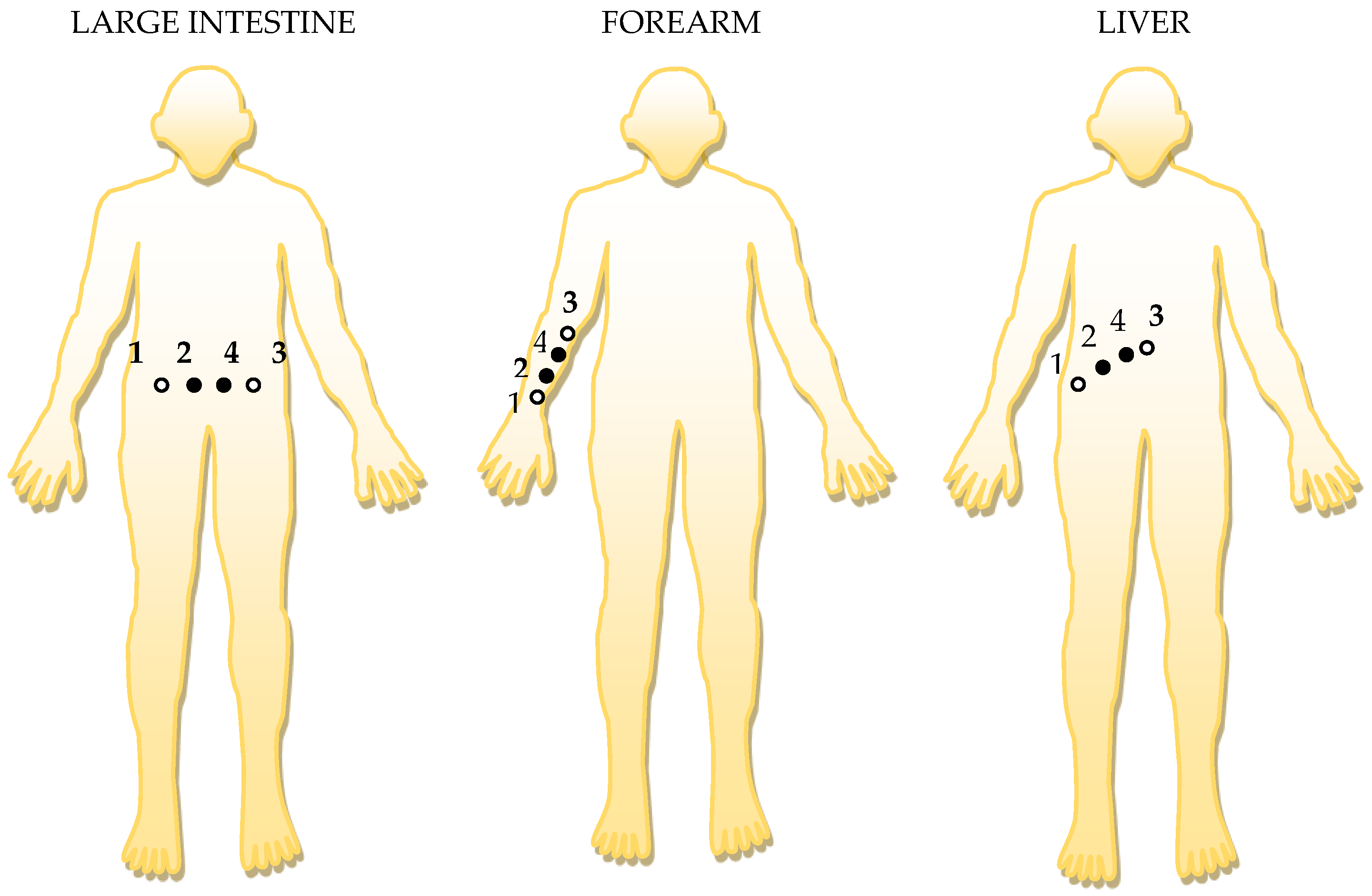


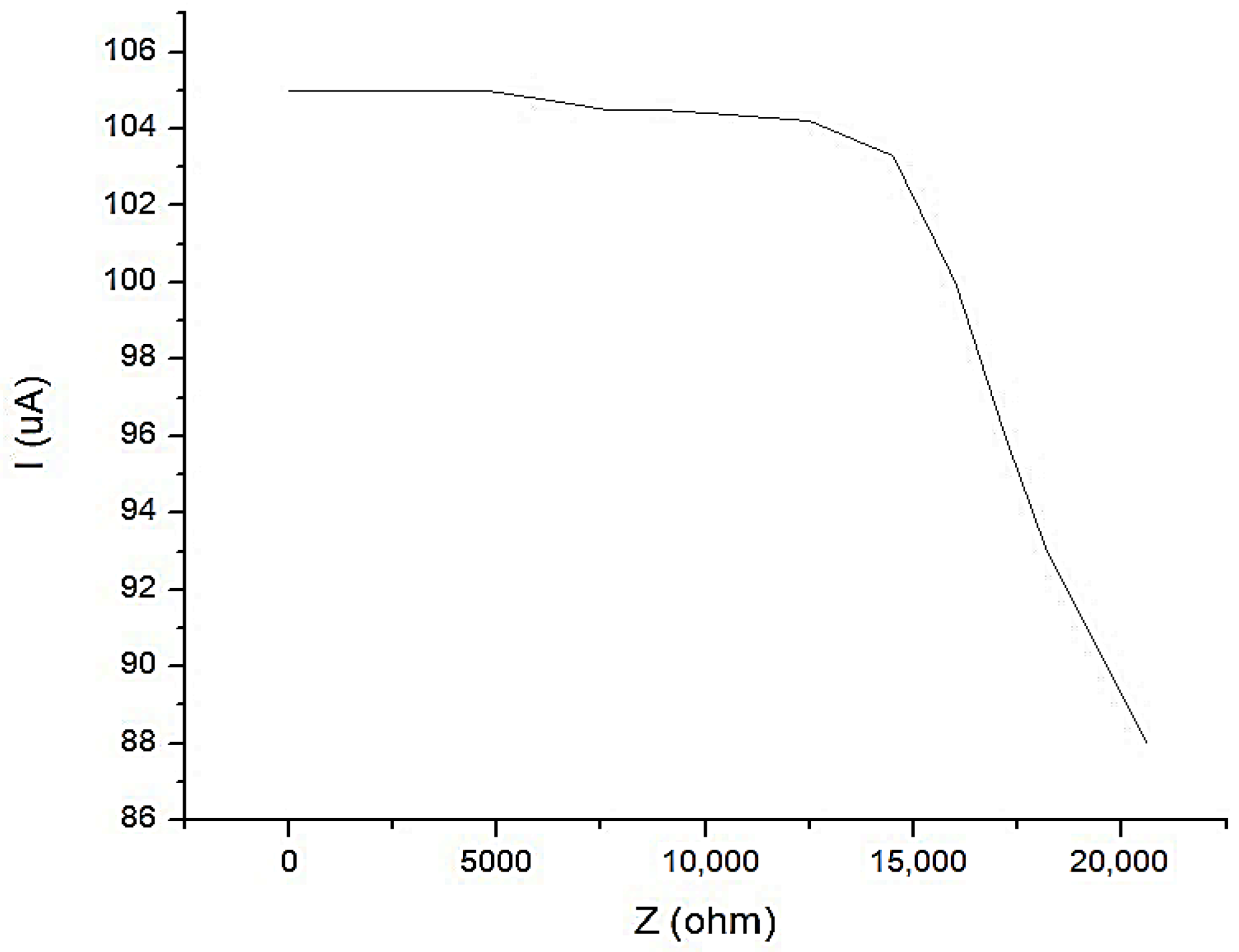
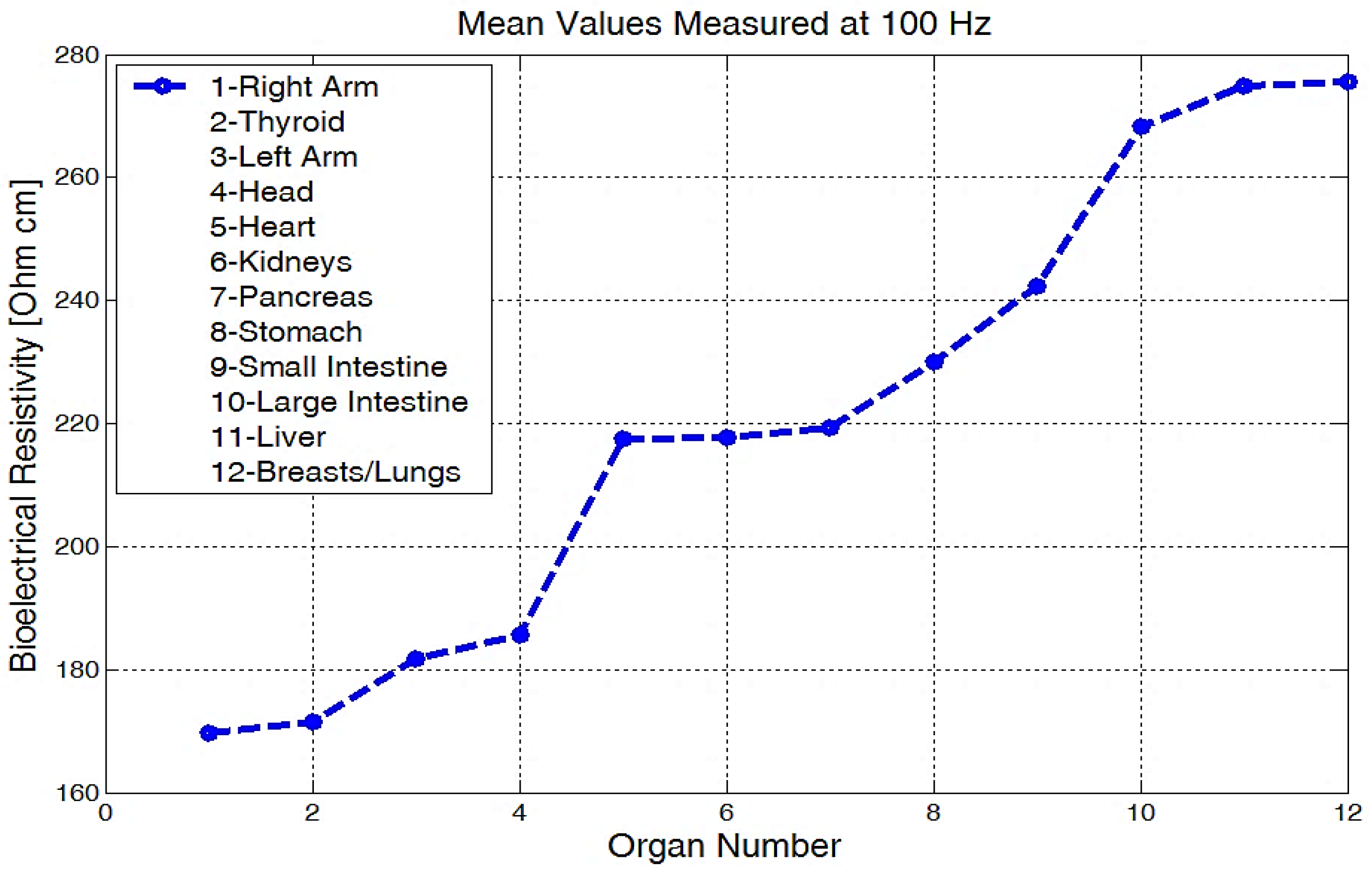
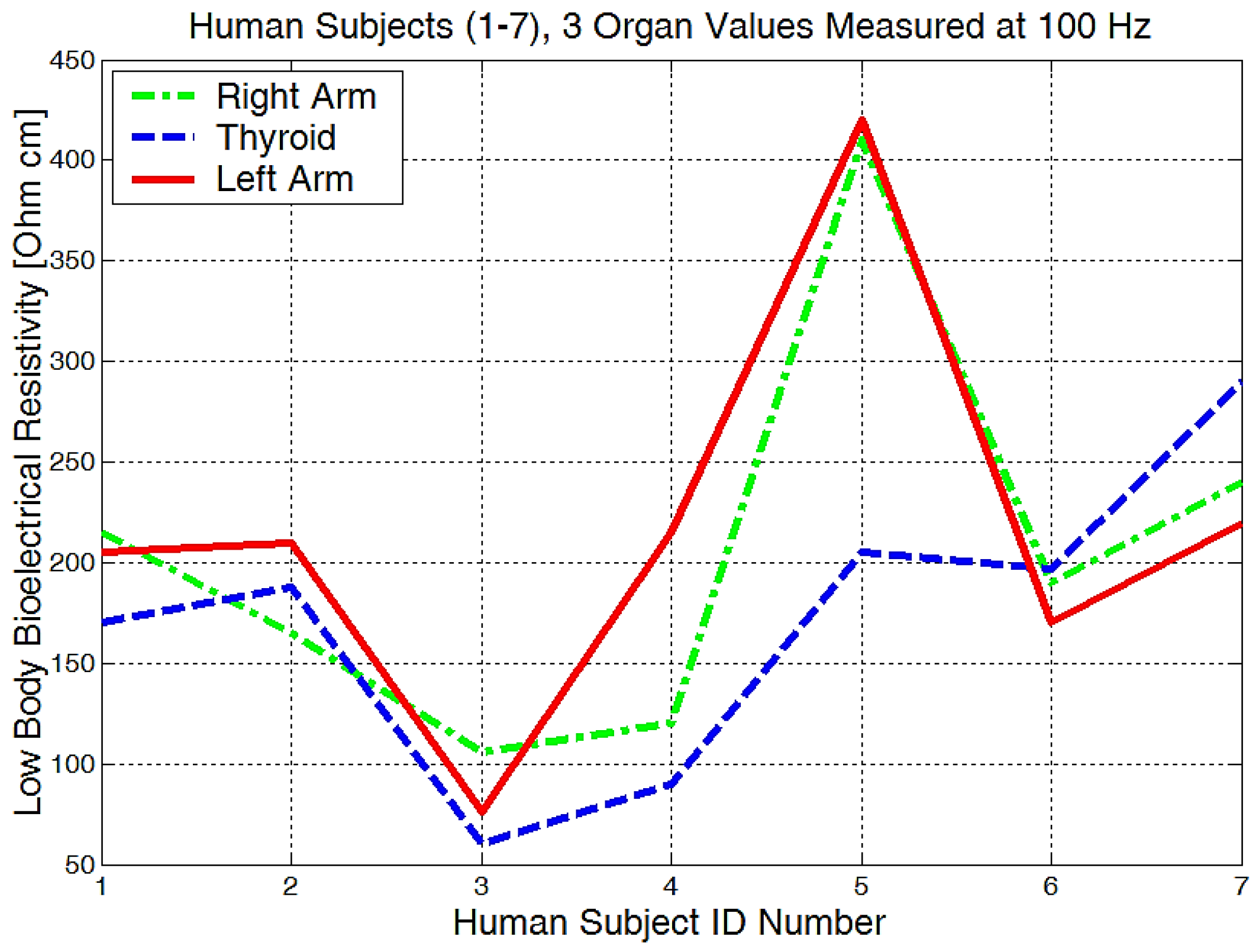

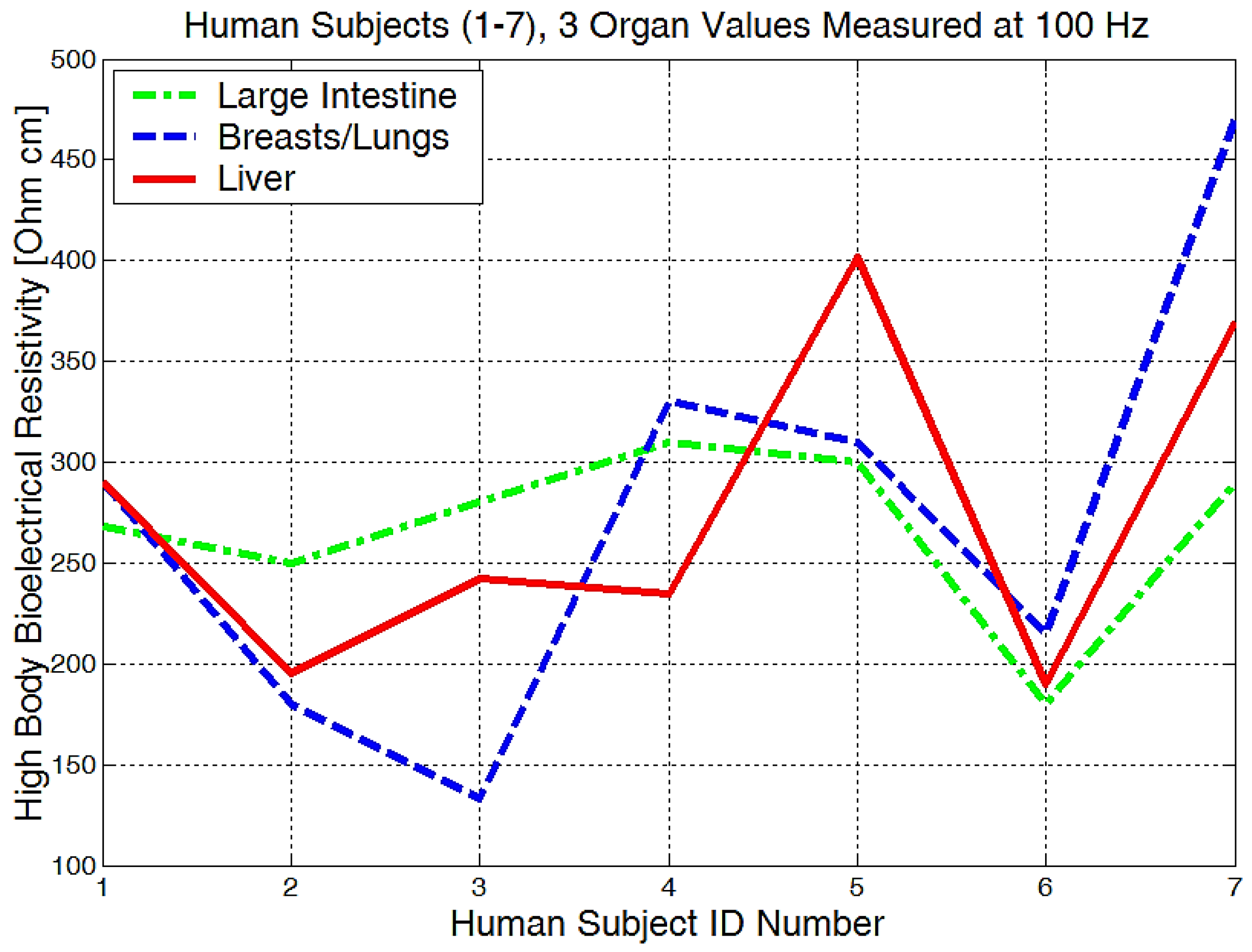

| Skin–Electrode Parameters, Ag-Au (1-2) | Rs [kΩ] | Cs [pF] | Zseq [kΩ] | R0p [kΩ] | Cp [pF] | Zpeq [kΩ] | tanδ |
|---|---|---|---|---|---|---|---|
| Forearm | 1120 | 2200 | 1333 | 2240 | 830 | 1377 | 0.57 |
| Large Intestine | 882 | 3380 | 999.4 | 2910 | 710 | 1395 | 0.67 |
| Liver | 665 | 3770 | 787.5 | 3650 | 690 | 1916 | 0.66 |
| Skin–Electrode Parameters, Ag-Au (3-4) | Rs [kΩ] | Cs [pF] | R0p [kΩ] | Cp [pF] | tanδ |
|---|---|---|---|---|---|
| Forearm | 1100 | 2250 | 2320 | 780 | 0.57 |
| Large Intestine | 920 | 3410 | 1660 | 1050 | 0.67 |
| Liver | 700 | 3880 | 1830 | 750 | 0.66 |
| Skin-Sensors Parameters Au-Au (2-4) | Rs [kΩ] | Cs [pF] | R0p [kΩ] | Cp [pF] | tanδ |
|---|---|---|---|---|---|
| Forearm | 1590 | 980 | 2210 | 800 | 0.57 |
| Large Intestine | 1670 | 2830 | 2780 | 710 | 0.60 |
| Liver | 928 | 3280 | 3630 | 690 | 0.60 |
| Skin-Sensors Parameters Res24 [Ω] Au-Au (2-4) | f = 40 kHz | f = 100 kHz | f = 300 kHz |
|---|---|---|---|
| Forearm | 1520 | 523 | 426 |
| Large Intestine | 1830 | 880 | 570 |
| Liver | 2610 | 930 | 620 |
| Calibration and Accuracy of the Measurements | R1 [kΩ] | C1 [pF] | R2 [kΩ] | C2 [pF] | R0 [kΩ] | C0 [nF] | Z0 [kΩ] | Zesn [kΩ] | ρ [Ωcm] |
|---|---|---|---|---|---|---|---|---|---|
| Forearm | 6.172 | 981 | 6.179 | 985 | 11.95 | 221.24 | 6.164 | 16.456 | 180 |
| Kidney | 6.172 | 981 | 6.179 | 985 | 11.95 | 221.06 | 6.168 | 16.459 | 220 |
| Large Intestine | 6.172 | 981 | 6.179 | 985 | 11.95 | 220.74 | 6.174 | 16.461 | 265 |
| Liver | 6.172 | 981 | 6.179 | 985 | 11.95 | 220.65 | 6.176 | 16.463 | 277 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pîslaru-Dănescu, L.; Zărnescu, G.-C.; Telipan, G.; Stoica, V. Design and Manufacturing of Equipment for Investigation of Low Frequency Bioimpedance. Micromachines 2022, 13, 1858. https://doi.org/10.3390/mi13111858
Pîslaru-Dănescu L, Zărnescu G-C, Telipan G, Stoica V. Design and Manufacturing of Equipment for Investigation of Low Frequency Bioimpedance. Micromachines. 2022; 13(11):1858. https://doi.org/10.3390/mi13111858
Chicago/Turabian StylePîslaru-Dănescu, Lucian, George-Claudiu Zărnescu, Gabriela Telipan, and Victor Stoica. 2022. "Design and Manufacturing of Equipment for Investigation of Low Frequency Bioimpedance" Micromachines 13, no. 11: 1858. https://doi.org/10.3390/mi13111858
APA StylePîslaru-Dănescu, L., Zărnescu, G.-C., Telipan, G., & Stoica, V. (2022). Design and Manufacturing of Equipment for Investigation of Low Frequency Bioimpedance. Micromachines, 13(11), 1858. https://doi.org/10.3390/mi13111858








