Numerical Investigation on the Heat and Mass Transfer in Microchannel with Discrete Heat Sources Considering the Soret and Dufour Effects
Abstract
1. Introduction
2. Mathematical Model
2.1. Control Equations
2.2. Physical Properties
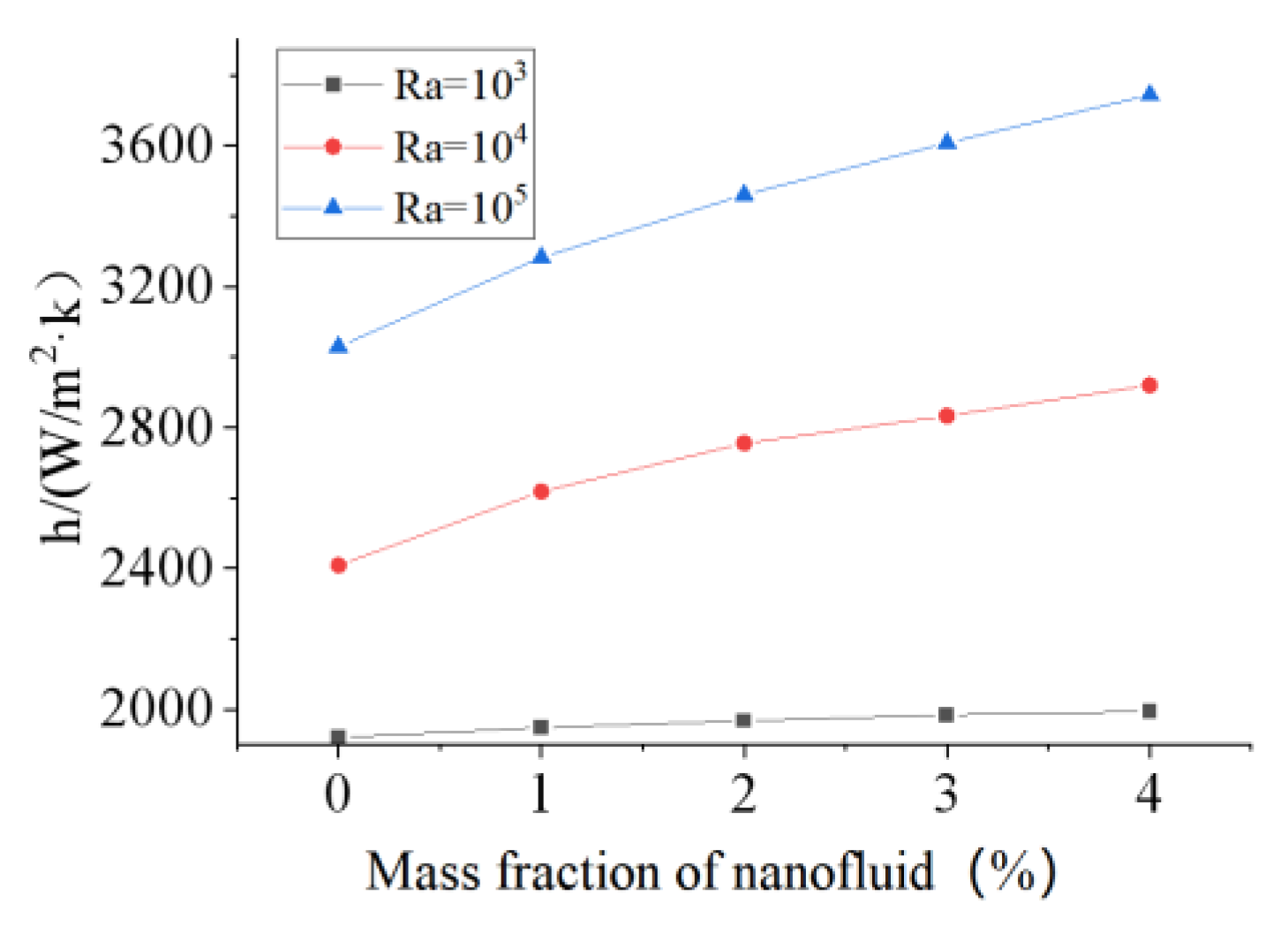
2.3. Validation of Numerical Model
3. Results and Discussions
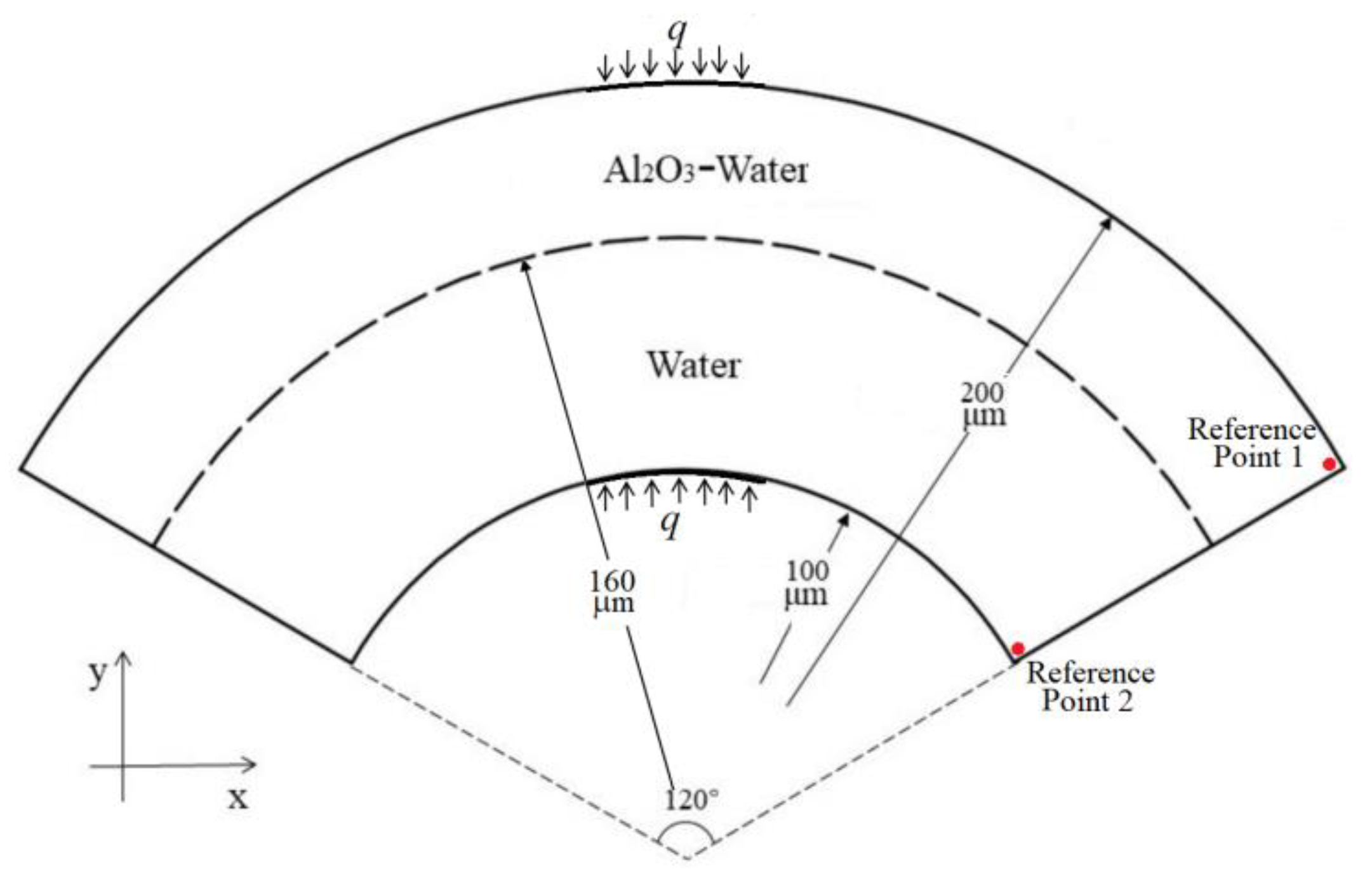
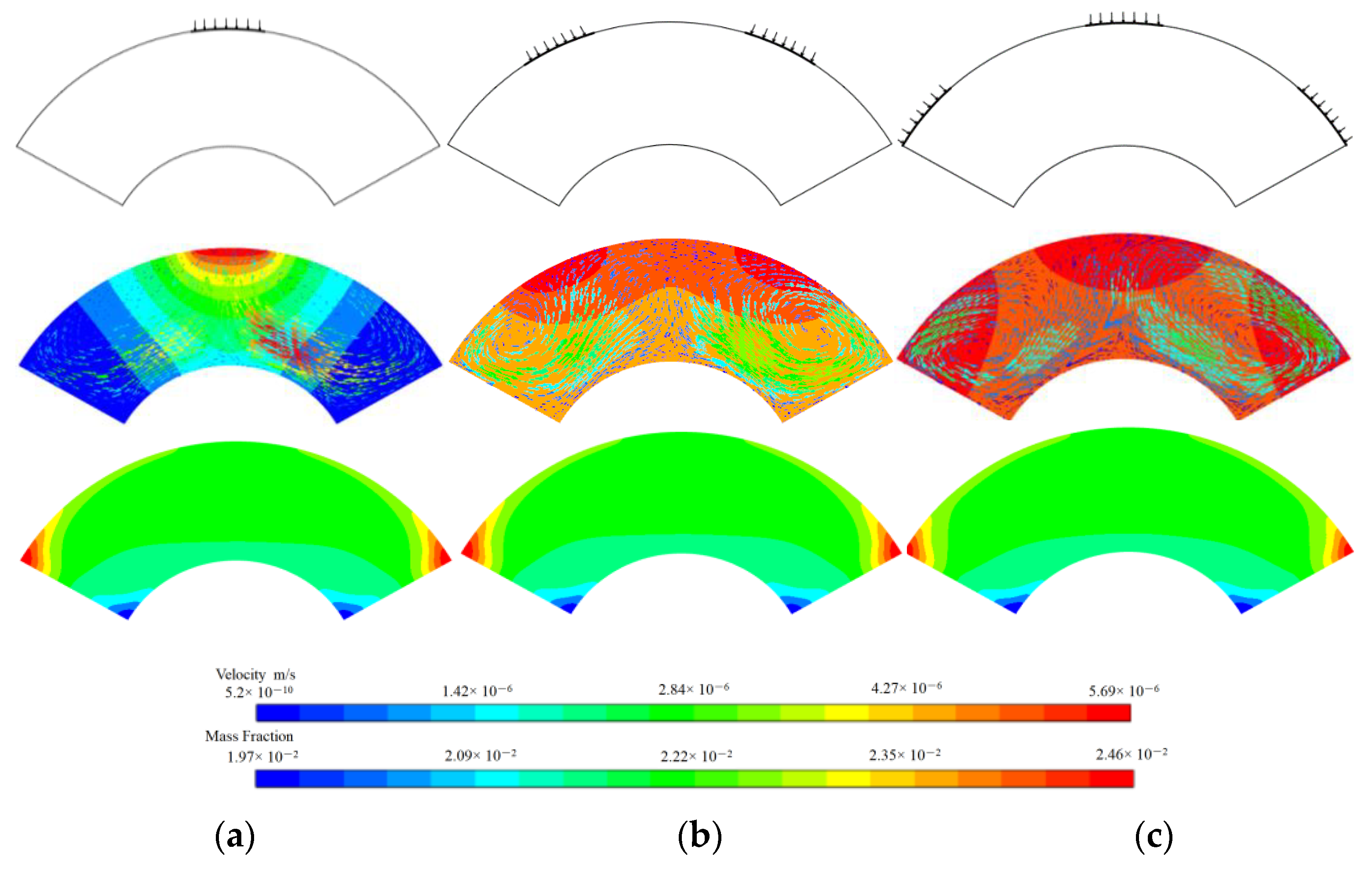
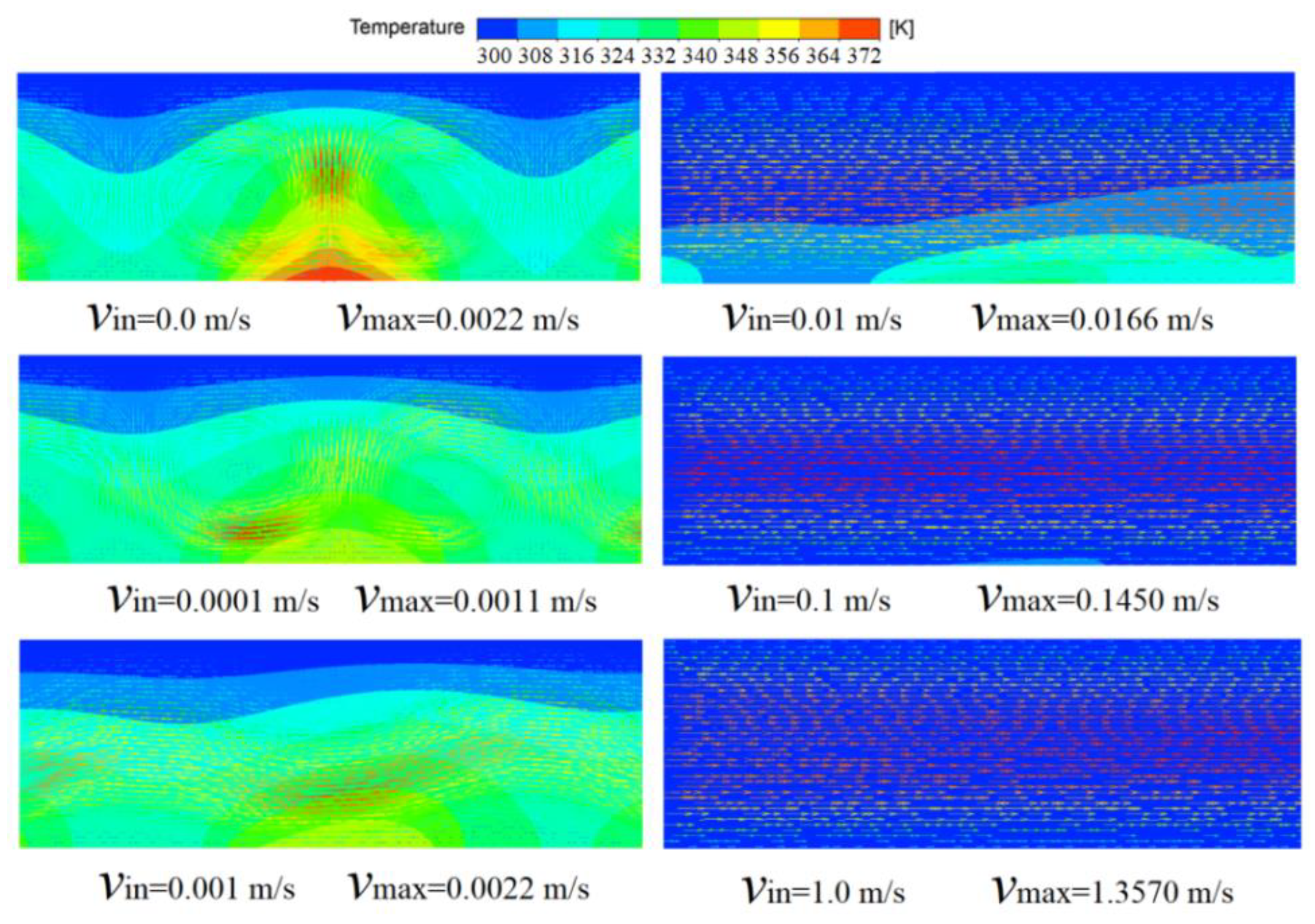
3.1. The Flows in a Fan-Shaped Ring
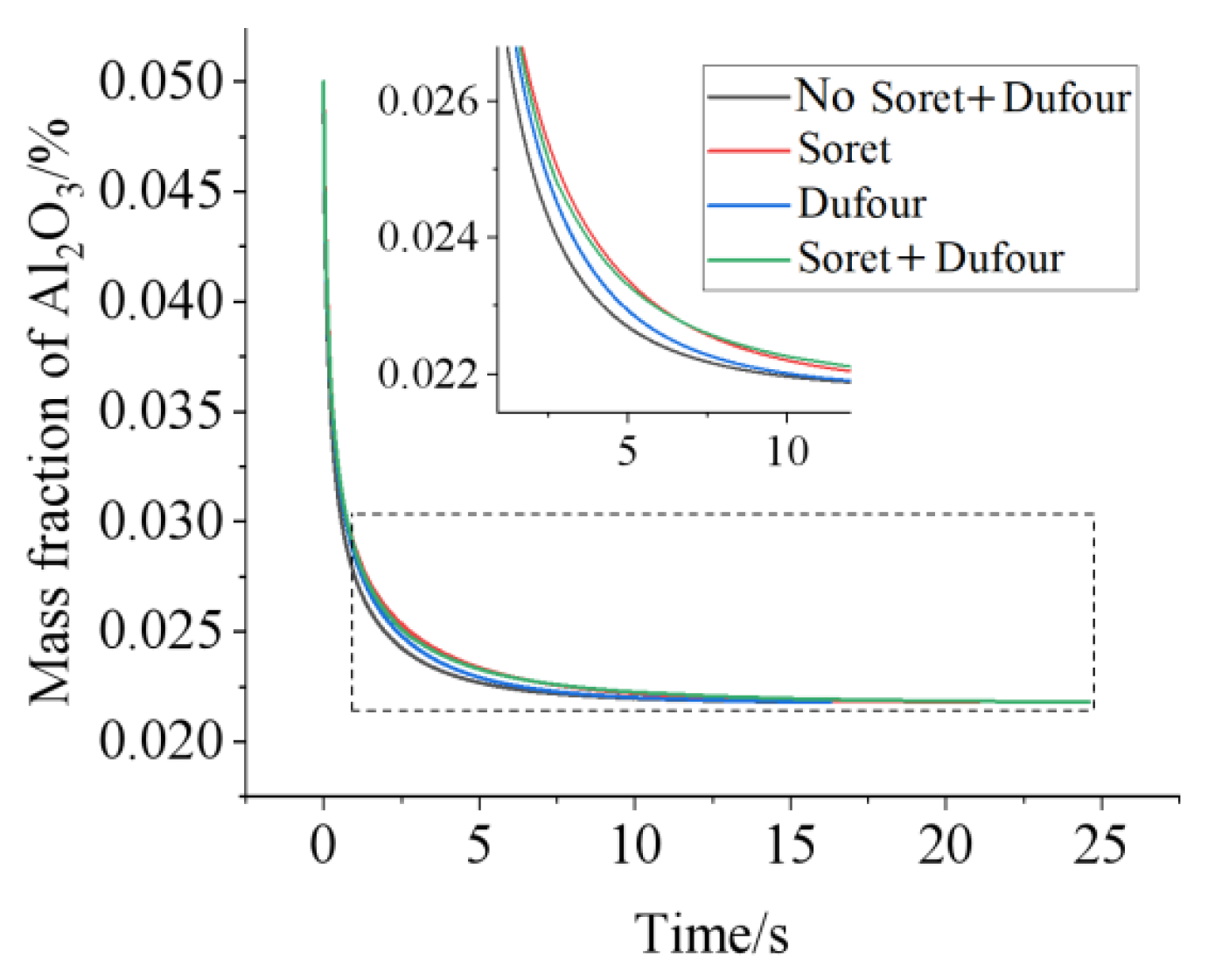
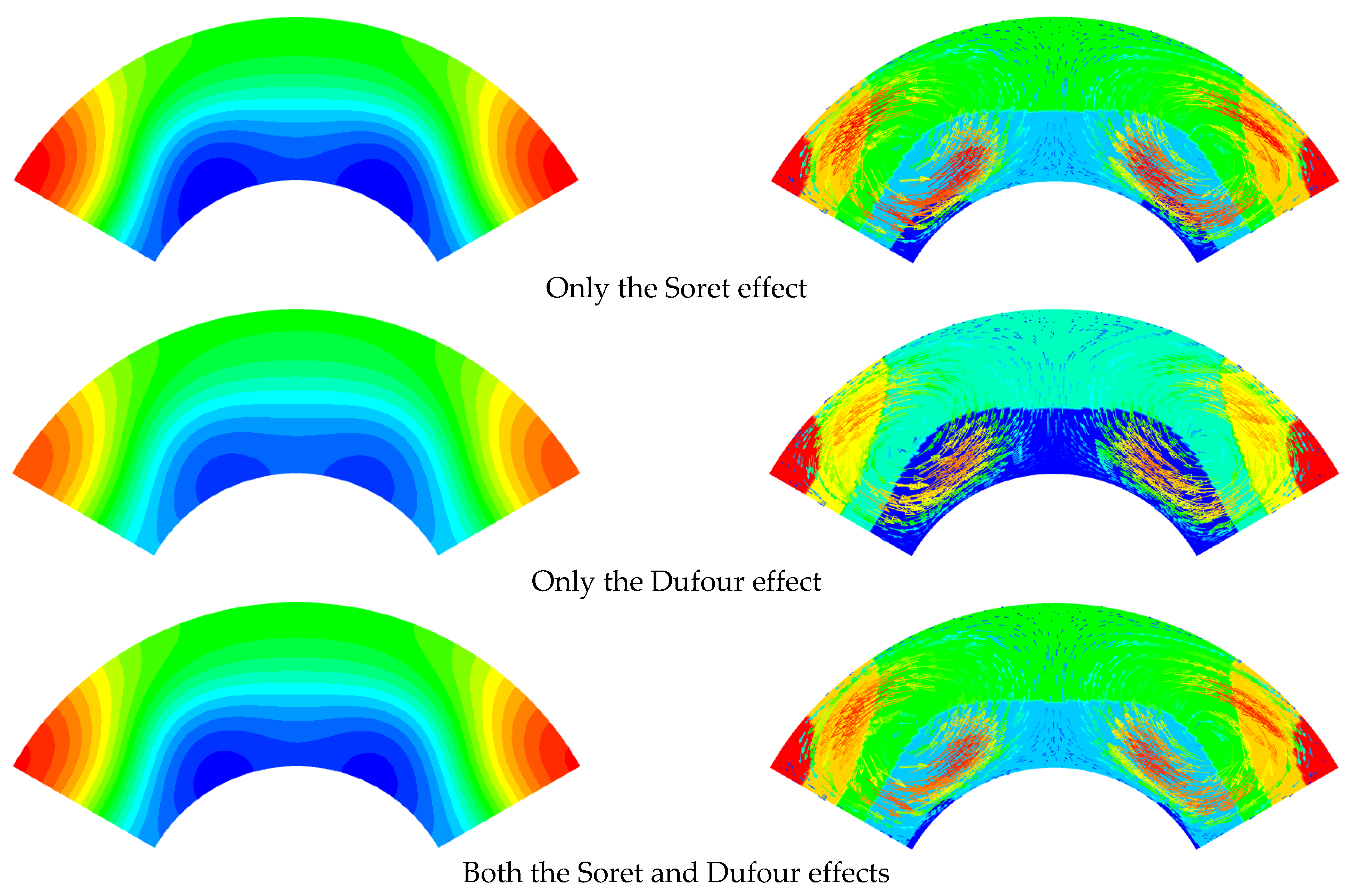
3.2. Influence of the Dufour and Soret Effects
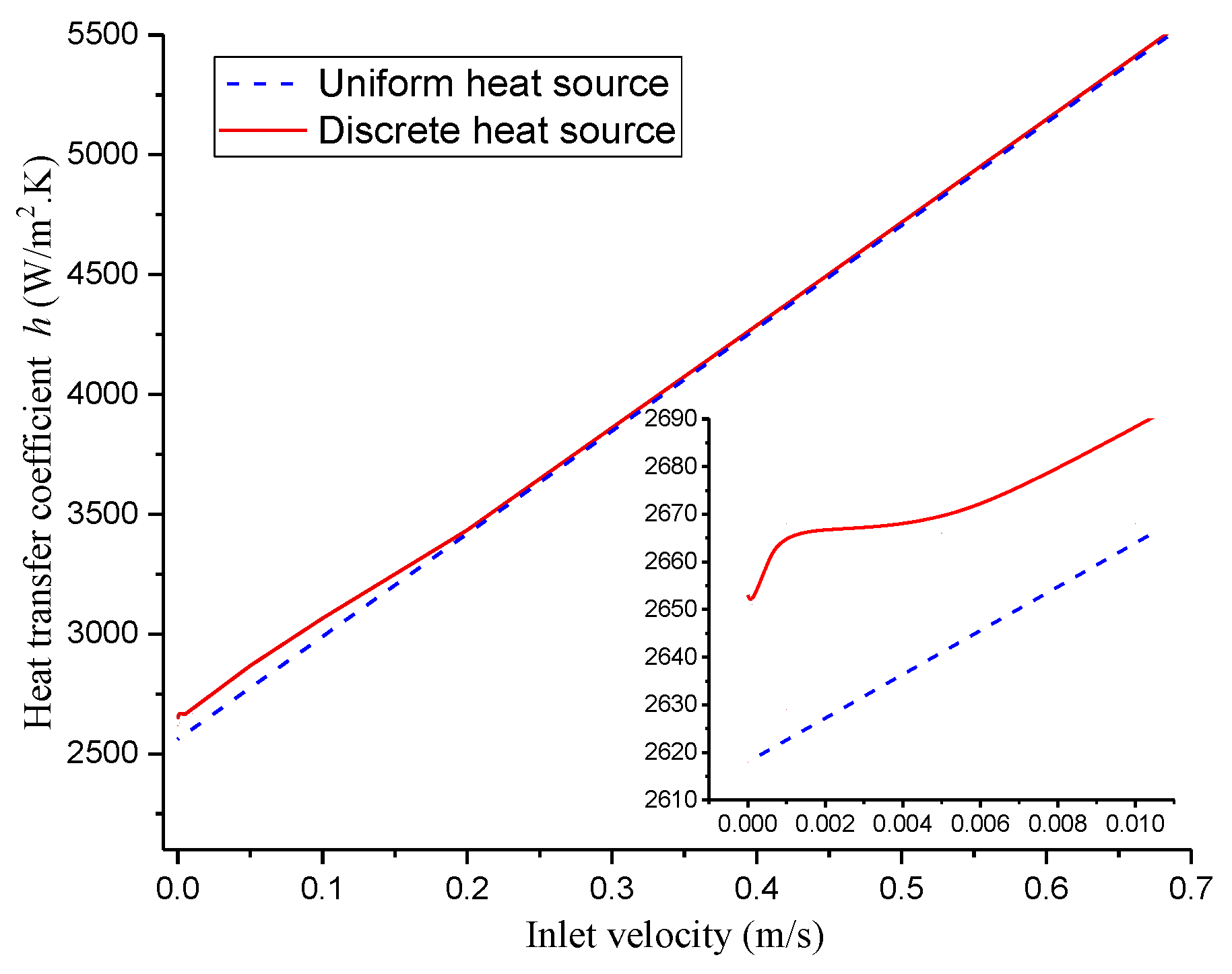
3.3. Heat Transfer in Microchannel with Discrete Heat Sources
4. Conclusions
- (1)
- Based on the Buongiorno model, a modified model was proposed by adding a term for the Soret effect in the momentum equation and another term for the Dufour effect in the energy equation. Such models are suitable for modeling HMT in MCHS or heat exchangers with two species or discrete heat sources.
- (2)
- The Soret effect influences HMT more greatly than the Dufour effect. The result, due to the combined the Dufour and Soret effects, is better than the result due to the individual Soret or Dufour effects, but it is not simply due to the superposition of two individual factors, as they will interact with each other.
- (3)
- The heat-transfer coefficient for the discrete heat source is substantially greater than that for the uniform heat source when the inlet velocity <0.01 m/s. It first rises and then falls for inlet velocities ranging from zero to 0.004 m/s, and continues to rise for inlet velocities larger than 0.004 m/s due to the presence of visible flow perturbations.
- (4)
- The underlying mechanism is that severer convection can be provoked when the Dufour effect and Soret effect are considered, because a pair vortex can be generated near each DHS. This can provide beneficial guidance for the design of MCHS with DHS in the future.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| c | specific heat |
| concentration sensitivity | |
| diffusion coefficient | |
| gravitational acceleration | |
| heat transfer coefficient | |
| thermal conductivity | |
| thermal diffusion ratio | |
| Boltzman constant | |
| characteristic length | |
| Nu | Nusselt number |
| pressure | |
| Pr | Prandtl number |
| heat flux | |
| Ra | Rayleigh number |
| Re | Reynolds number |
| time | |
| temperature | |
| velocity | |
| inlet velocity | |
| Greek letters | |
| thermal diffusivity | |
| expansion coefficient | |
| volume fraction | |
| density | |
| viscosity | |
| Superscripts and subscripts | |
| B | Brownian |
| f | fluid |
| mass | |
| nf | nanofluid |
| p | particle |
| T | thermophoresis |
| wall | |
| Abbreviations | |
| DHS | discrete heat sources |
| MCHS | microchannel heat sink |
| MHD | magnetohydrodynamics |
| HMT | heat and mass transfer |
References
- Muhammad, I.A.; Ashraf, M.U.; Muhammad, Q.; Wakif, A. Numerical simulation of entropy transport in the oscillating fluid flow with transpiration and internal fluid heating by GGDQM. Waves Random Complex Media 2022, 32. [Google Scholar] [CrossRef]
- Hou, E.R.; Wang, F.Z.; El-Zahar, E.R.; Nazir, U.; Sohail, M. Computational Assessment of Thermal and Solute Mechanisms in Carreau–Yasuda Hybrid Nanoparticles Involving Soret and Dufour Effects over Porous Surface. Micromachines 2021, 12, 1302. [Google Scholar] [CrossRef] [PubMed]
- Muhammad, I.A.; Muhammad, Q.; Lu, D.C. Transpiration and Viscous Dissipation Effects on Entropy Generation in Hybrid Nanofluid Flow over a Nonlinear Radially Stretching Disk. Entropy 2018, 20, 668. [Google Scholar]
- Akhter, R.; Ali, M.M.; Alim, M.A. Hydromagnetic Natural Convection Heat Transfer in a Partially Heated Enclosure Filled with Porous Medium Saturated by Nanofluid. Int. J. App. Comp. Math. 2019, 5, 1–27. [Google Scholar] [CrossRef]
- Du, J.Y.; Wang, R.J.; Zhuo, Q.Y.; Yuan, W.J. Heat transfer enhancement of Fe3O4-water nanofluid by the thermo-magnetic convection and thermophorestic effect. Int. J. Energy Res. 2022, 47, 1345–1359. [Google Scholar]
- Wang, R.J.; Chen, T.C.; Qi, J.L.; Du, J.Y.; Pan, G.S.; Huang, L.Z. Investigation on the heat transfer enhancement by nanofluid under electric field considering electrophorestic and thermophoretic effect. Case Stud. Therm. Eng. 2021, 28, 101498. [Google Scholar] [CrossRef]
- Kumar, R.N.; Gamaoun, F.; Abdulrahman, A.; Chohan, J.S.; Gowda, R.J.P. Heat transfer analysis in three-dimensional unsteady magnetic fluid flow of water-based ternary hybrid nanofluid conveying three various shaped nanoparticles: A comparative study. Int. J. Mod. Phys. B 2022, 36, 2250170. [Google Scholar] [CrossRef]
- Alizadeh, M.R.; Dehghan, A.A. Conjugate Natural Convection of Nanofluids in an Enclosure with a Volumetric Heat Source. Arab. J. Sci. Eng. 2014, 39, 1195–1207. [Google Scholar]
- Rostamzadeh, A.; Razavi, S.E.; Mirsajedi, S.M. Towards Multidimensional Artificially Characteristic-Based Scheme for Incompressible Thermo-Fluid Problems. Mechanika 2017, 23, 826–834. [Google Scholar] [CrossRef][Green Version]
- Rahbarshahlan, S.; Esmaeilzadeh, E.; Rostamzadeh, A.; Ghaffarzadeh, A. Numerical simulation of fluid flow and heat transfer in microchannels with patterns of hydrophobic/hydrophilic walls. Eur. Phys. J. Plus 2020, 135, 157. [Google Scholar]
- Hayat, T.; Nasir, T.; Khan, M.I.A. Numerical investigation of MHD flow with Soret and Dufour effect. Results Phys. 2018, 8, 1017–1022. [Google Scholar] [CrossRef]
- Hou, E.R.; Wang, F.Z.; Nazir, U.; Sohail, M.; Jabbar, N.; Thounthong, P. Dynamics of Tri-Hybrid Nanoparticles in the Rheology of Pseudo-Plastic Liquid with Dufour and Soret Effects. Micromachines 2022, 13, 201. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Yang, M.; He, Y.L.; Zhang, Y.W. The onset of transient Soret-driven MHD convection confined within a Hele-Shaw cell with nanoparticles suspension. Int. J. Therm. Sci. 2016, 106, 57–69. [Google Scholar] [CrossRef]
- Kumar, R.N.; Saleh, B.; Abdelrhman, Y.; Afzal, A.; Gowda, R.J.P. Soret and Dufour effects on Oldroyd-B fluid flow under the influences of convective boundary condition with Stefan blowing effect. Indian J. Phys. 2022, 96, 3881–3888. [Google Scholar] [CrossRef]
- Yadav, D.; Nam, D.; Lee, J.J. The onset of transient Soret-driven MHD convection confined within a Hele-Shaw cell with nanoparticles suspension. Taiwan Inst. Chem. Eng. 2016, 58, 235–244. [Google Scholar] [CrossRef]
- Rghif, Y.; Zeghmati, B.; Bahraoui, F. Soret and Dufour effects on thermosolutal convection developed in a salt gradient solar pond. Int. J. Therm. Sci. 2021, 161, 106760. [Google Scholar] [CrossRef]
- Srinivasacharya, D.; Ramana, K.S. Thermal radiation and double diffusive effects on bioconvection flow of a nanofluid past an inclined wavy surface. Therm. Sci. Eng. Prog. 2021, 22, 100830. [Google Scholar] [CrossRef]
- Salleh, S.N.A.; Bachok, N.; Arifin, N.M.; Ali, F.M. Influence of Soret and Dufour on forced convection flow towards a moving thin needle considering Buongiorno’s nanofluid model. Alex. Eng. J. 2020, 59, 3897–3906. [Google Scholar] [CrossRef]
- Jawad, M.; Saeed, A.; Kumam, P.; Shah, Z.; Khan, A. Analysis of boundary layer MHD Darcy-Forch heimer radiative nanofluid flow with soret and dufour effects by means of marangoni convection. Case Stud. Therm. Eng. 2021, 23, 100792. [Google Scholar] [CrossRef]
- Mondal, H.; Pal, D.; Chatterjee, S.; Sibanda, P. Thermophoresis and Soret-Dufour on MHD mixed convection mass transfer over an inclined plate with non-uniform heat source/sink and chemical reaction. Ain. Shams Eng. J. 2018, 9, 2111–2121. [Google Scholar] [CrossRef]
- Sardar, H.; Ahmad, L.; Khan, M.; Alshomrani, A.S. Investigation of mixed convection flow of Carreau nanofluid over a wedge in the presence of Soret and Dufour effects. Int. J. Heat Mass Transf. 2019, 137, 809–822. [Google Scholar] [CrossRef]
- Mahajan, A.; Sharma, M.K. Double-diffusive convection in a magnetic nanofluid layer with cross diffusion effects. J. Eng. Math. 2019, 115, 67–87. [Google Scholar] [CrossRef]
- Akram, S.; Afzal, Q.; Aly, E.H. Half-breed effects of thermal and concentration convection of peristaltic pseudoplastic nanofluid in a tapered channel with induced magnetic field. Case Stud. Therm. Eng. 2020, 22, 100775. [Google Scholar] [CrossRef]
- Mosayebidorcheh, S.; Hatami, M. Analytical investigation of peristaltic nanofluid flow and heat transfer in an asymmetric wavy wall channel (Part II: Divergent channel). Int. J. Heat Mass Transf. 2018, 126, 800–808. [Google Scholar] [CrossRef]
- Tripathi, D.P.J.; Reddy, M.G.; Misra, J.C. Numerical simulation of double diffusive convection and electroosmosis during peristaltic transport of a micropolar nanofluid on an asymmetric microchannel. J. Therm. Aanl. Calorim. 2021, 143, 2499–2514. [Google Scholar] [CrossRef]
- Bahiraei, M.; Mashaei, P.R.J. J. Using nanofluid as a smart suspension in cooling channels with discrete heat sources. Therm. Anal. Calorim. 2015, 119, 2079–2091. [Google Scholar] [CrossRef]
- Mebarek-Oudina, F.; Mahanthesh, A.B.; Oztop, H.F. Heat transport of magnetized Newtonian nanoliquids in an annular space between porous vertical cylinders with discrete heat source. Int. Comm. Heat Mass Transf. 2020, 117, 104737. [Google Scholar] [CrossRef]
- Hussain, S.; Ahmad, S.; Mehmood, K.; Sagheer, M. Effects of inclination angle on mixed convective nanofluid flow in a double lid-driven cavity with discrete heat sources. Int. J. Heat Mass Transf. 2017, 106, 847–860. [Google Scholar] [CrossRef]
- Mebarek-Oudina, F.; Bessaïh, R. Numerical simulation of natural convection heat transfer of copper-water nanofluid in a vertical cylindrical annulus with heat sources. Thermophy. Aeromech. 2019, 26, 325–334. [Google Scholar] [CrossRef]
- Parveen, R.; Mahapatra, T.R. Heat and mass source effect on MHD double-diffusive mixed convection and entropy generation in a curved enclosure filled with nanofluid, Nonlinear Anal. Modelling Control. Nonlinear Anal. Mod. Contr. 2022, 27, 25338. [Google Scholar]
- Mondal, P.; Mahapatra, T.R. MHD double-diffusive mixed convection and entropy generation of nanofluid in a trapezoidal cavity. Int. J. Mech. Sci. 2021, 208, 106665. [Google Scholar] [CrossRef]
- Qu, W.; Mudawar, I. Experimental and numerical study of pressure drop and heat transfer in a single-phase microchannel heat sink. Int. J. Heat Mass Transf. 2002, 45, 2549–2565. [Google Scholar] [CrossRef]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Brinkman, H.C. The Viscosity of Concentrated Suspensions and Solutions. J. Chem. Phys. 2004, 20, 571. [Google Scholar] [CrossRef]
- Einstein, A. An Investigation on the Theory of Brownian Movement. James Joyce Q. 1956, 35, 155–158. [Google Scholar]
- Chon, C.H.; Kihm, K.D.; Lee, S.P.; Choi, S.U. Empirical correlation finding the role of temperature and particle size for nanofluid, thermal conductivity enhancement. Appl. Phys. Let. 2005, 87, 2406–2409. [Google Scholar] [CrossRef]
- Wan, J.W.; Yang, K.L.; Zhang, W.J.; Zhang, J.L. A new method of determination of indoor temperature and relative humidity with consideration of human thermal comfort. Build. Environ. 2009, 44, 411–417. [Google Scholar] [CrossRef]
- Tiwari, P.K.; Das, M.K. Heat Transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. Int. J. Heat Mass Transf. 2007, 50, 2002–2018. [Google Scholar] [CrossRef]
- Bazylak, A.; Djilali, N.; Sinton, D. Natural Convection with Distributed Heat Sources Modulation. Int. J. Heat Mass Transf. 2007, 50, 1649–1655. [Google Scholar] [CrossRef]



| Parameters | |||||
|---|---|---|---|---|---|
| Water | 998.2 | 0.6 | 4182 | 1.47 | 210 |
| Al2O3 | 3970 | 45 | 880 | 131.7 | 8.5 |
| Ra | Present | Reference [38] | Error |
|---|---|---|---|
| 105 | 4.689 | 4.465 | 4.8% |
| 106 | 9.437 | 8.838 | 6.3% |
| Cases | 0.1 s | 1 s | 2 s | 4 s | 6 s |
|---|---|---|---|---|---|
| Neither Soret Nor Dufour | 5944.0 | 3784.8 | 3716.9 | 3718.0 | 3718.2 |
| Only the Soret | 5956.6 | 3785.6 | 3741.0 | 3739.2 | 3738.8 |
| Only the Dufour | 5947.9 | 3767.1 | 3721.7 | 3719.7 | 3719.5 |
| Both Soret and Dufour | 5966.3 | 3797.8 | 3752.1 | 3749.9 | 3749.5 |
| vin (m/s) | 0 | 0.0001 | 0.001 | 0.01 | 0.1 | 1 |
| Tmax for q = 106 W/m2 (K) | / | 368 | 359 | 350 | 336 | 312 |
| Tmax for q = 5 × 105 W/m2 (K) | 370 | 357 | 352 | 339 | 313 | 304 |
| Tmax for q = 2 × 105 W/m2 (K) | 364 | 352 | 338 | 316 | 304 | 302 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ou, X.; Wang, R.; Guo, T.; Shao, C.; Zhu, Z. Numerical Investigation on the Heat and Mass Transfer in Microchannel with Discrete Heat Sources Considering the Soret and Dufour Effects. Micromachines 2022, 13, 1848. https://doi.org/10.3390/mi13111848
Ou X, Wang R, Guo T, Shao C, Zhu Z. Numerical Investigation on the Heat and Mass Transfer in Microchannel with Discrete Heat Sources Considering the Soret and Dufour Effects. Micromachines. 2022; 13(11):1848. https://doi.org/10.3390/mi13111848
Chicago/Turabian StyleOu, Xueyu, Ruijin Wang, Tongwei Guo, Chun Shao, and Zefei Zhu. 2022. "Numerical Investigation on the Heat and Mass Transfer in Microchannel with Discrete Heat Sources Considering the Soret and Dufour Effects" Micromachines 13, no. 11: 1848. https://doi.org/10.3390/mi13111848
APA StyleOu, X., Wang, R., Guo, T., Shao, C., & Zhu, Z. (2022). Numerical Investigation on the Heat and Mass Transfer in Microchannel with Discrete Heat Sources Considering the Soret and Dufour Effects. Micromachines, 13(11), 1848. https://doi.org/10.3390/mi13111848







