Estimation of Surface Roughness on Milled Surface Using Capacitance Sensor Based Micro Gantry System through Single-Shot Approach
Abstract
1. Introduction
2. Materials and Methods
2.1. Study on Capacitance Response for Rough Surface
2.2. Proposed Methodology
2.3. Specimen Preparation
2.4. Stylus Measurement Setup
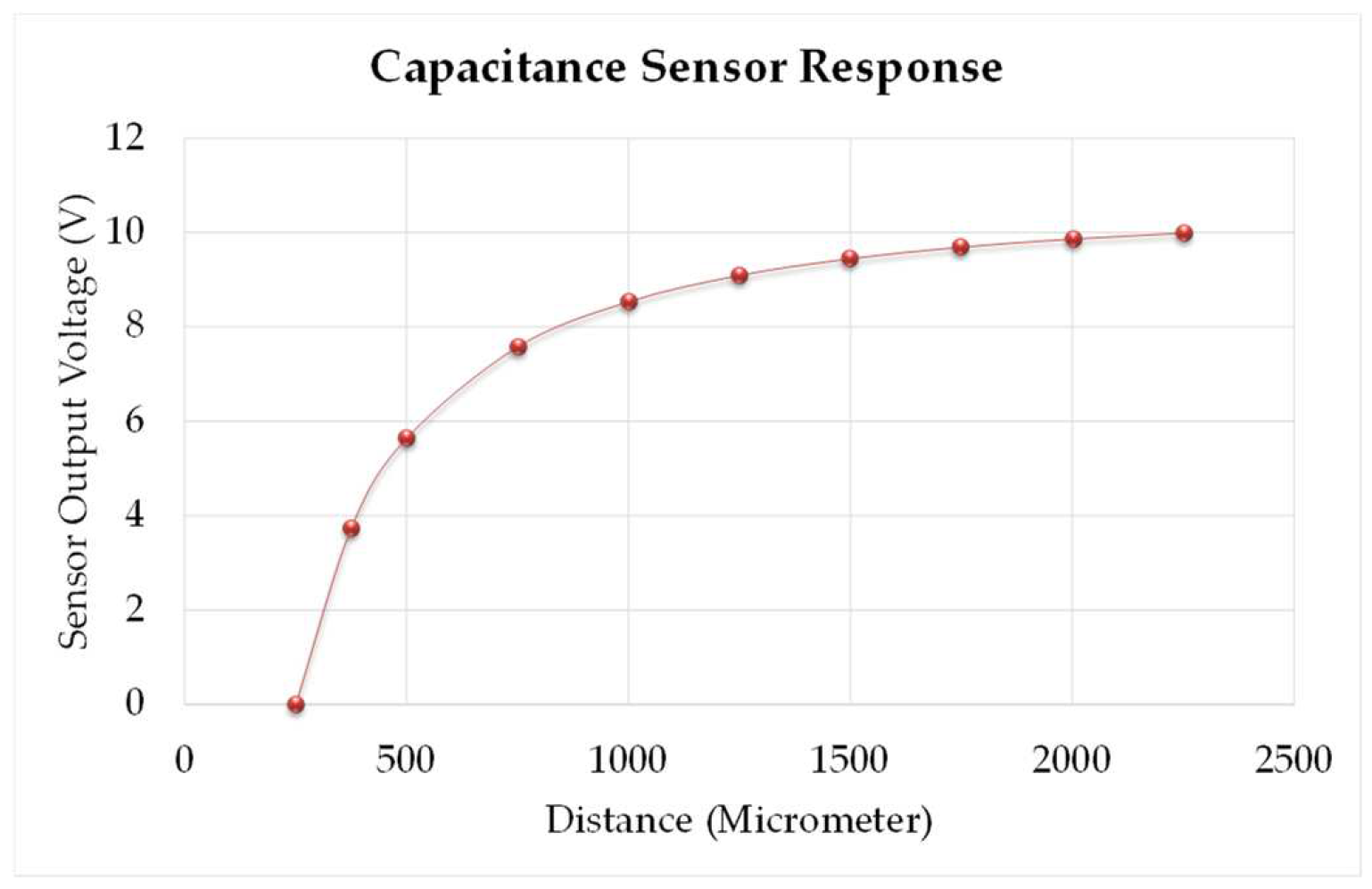
2.5. Calibration of Capacitance Sensor with Flat Surface
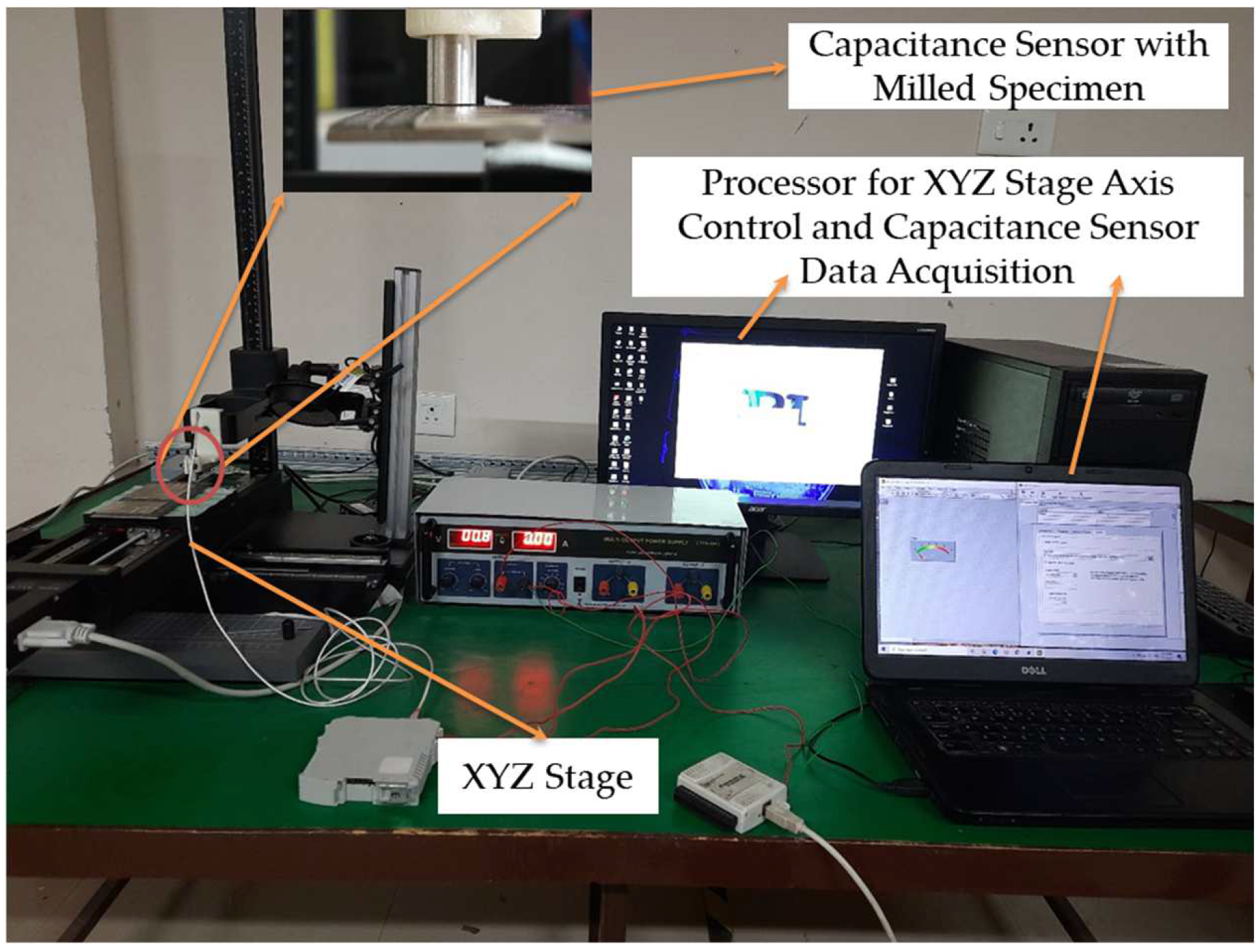
2.6. XYZ Micro Gantry System for Roughness Measurement and Experimental Procedure
- The specimen was prepared using a vertical milling process for varying roughness by varying speed, feed rate, and depth of cut.
- Laser marking was made the specimen with the dimensions of 6 mm × 6 mm for performing the measurement with both the stylus and capacitance sensor on the same spot.
- Measurement using a stylus profilometer was performed within the laser-marked spot.
- The sensor, which had been calibrated using a flat surface, was fixed in the XYZ stage.
- The laser-marked part of the specimen was exactly placed under the calibrated capacitance sensor for the selected stand-off distance (SOD) for measurement.
- The voltage data for the particular spot of the machined surface were recorded using LABVIEW software and the data acquisition card.
- Steps 1 to 6 were repeated for all 13 specimens used. Six of these specimens with a wide roughness range were selected for calibrating the sensor for a wide roughness range.
- For the voltage obtained for the selected 6 specimens, Ra was estimated in two ways.
- Firstly, the relation between roughness (Ra) and voltage (V) was obtained using a regression model. This relation was used to estimate roughness for the remaining specimen.
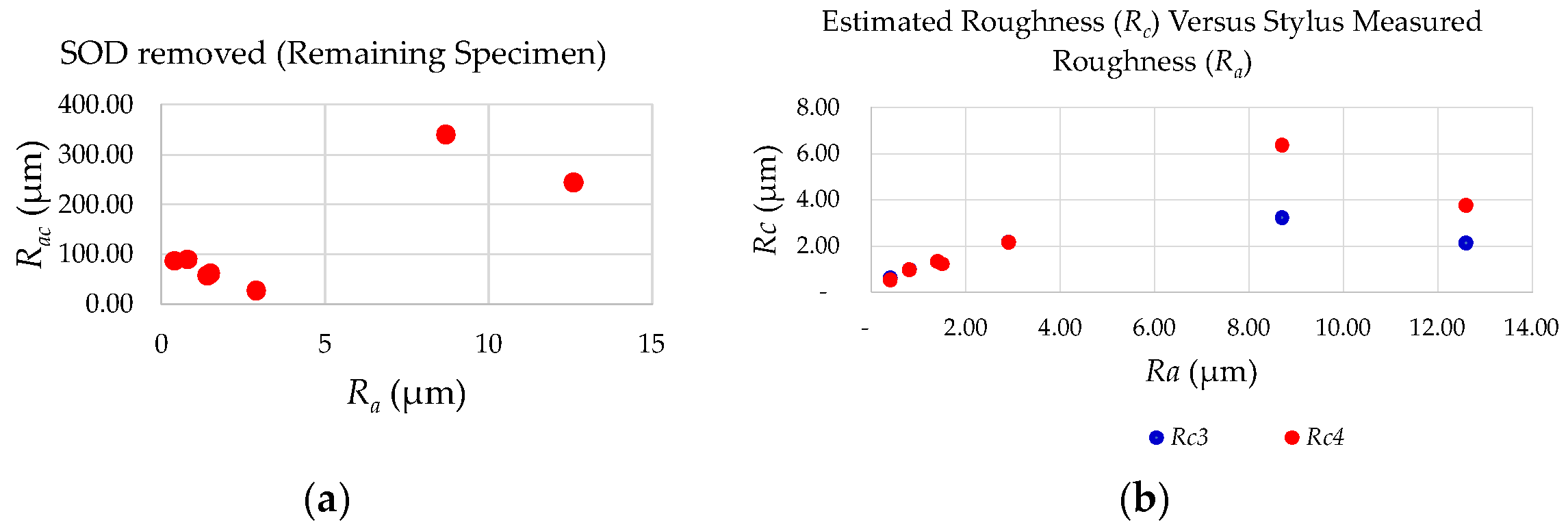
- Secondly, the obtained voltage was converted to distance by using Equation (6). The stand-off distance needed to be subtracted from the obtained distance (Zm) to determine Rac as shown in Equation (2). Then, the relation between Ra and Rac was determined using regression.
- The measurement performed using the capacitance sensor for the remaining 7 specimens was substituted in the regression model to estimate the roughness Ra.
3. Results and Discussions
3.1. Calibration of C1-A Capacitance Sensor using Flat Surface
3.2. Experiment to Estimate Roughness Using 5.6 mm Capacitance Sensor
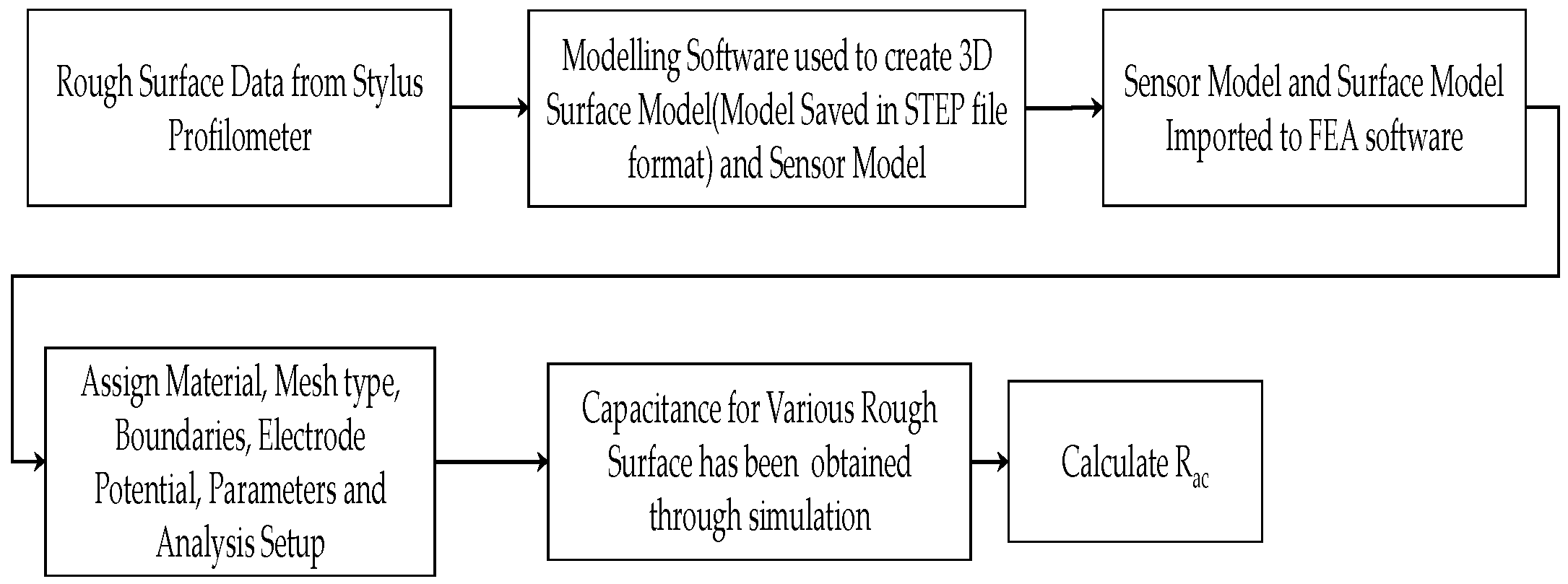
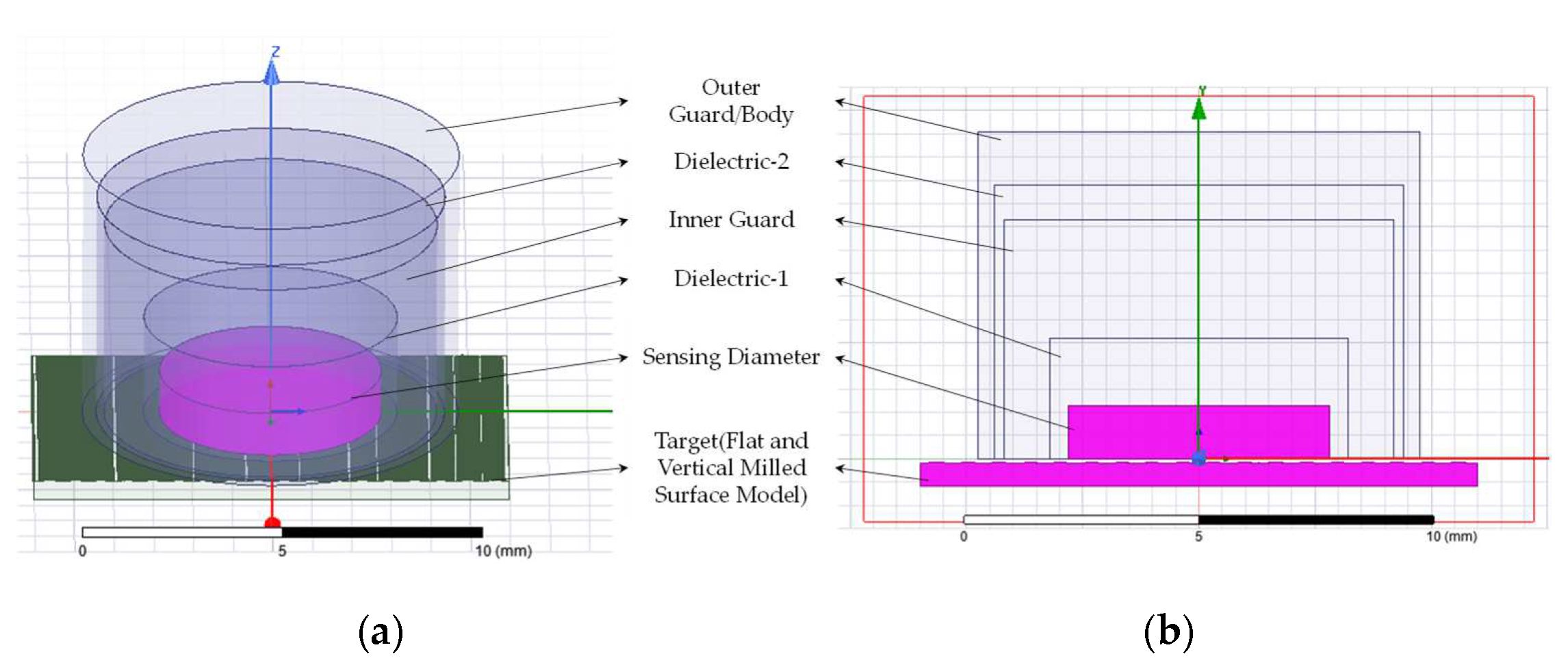
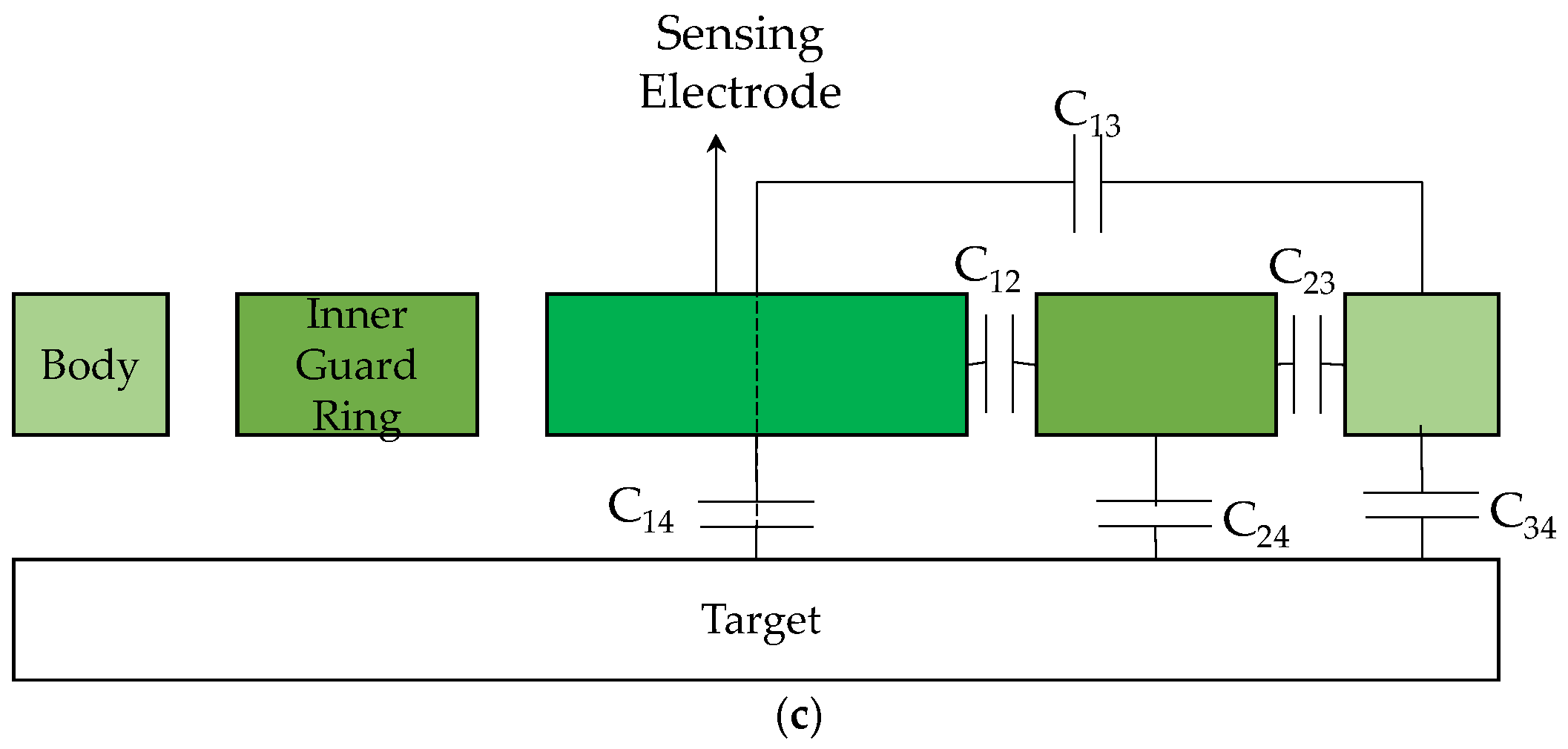
3.3. Model Development and Simulation Steps to Study Response of 5.6 mm Sensing Diameter Sensor for Flat and Rough Specimens using Finite Element Analysis
3.4. FEA Simulation Results for Vertically Milled Surface using 5.6 mm Capacitance Sensor Model
3.5. Sensor Sensing Diameter Selection for Roughness Estimation
3.6. Stand-Off Distance Selection for Roughness Estimation
4. Conclusions
- The developed gantry system approach can reduce error and setting time for achieving the required SOD before measurement.
- The capacitance sensor with a sensing diameter of 5.6 mm can perform well in the range of 0.3 µm to 2.9 µm roughness owing to the resolution constraints and area of measurement involved.
- FEA analysis results show that tilt and waviness are the error source in roughness measurement.
- Further, this method can be recommended for online measurement with the same machining conditions in mass production after considering suitable retrofitting arrangements for removing coolant during machining.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zeng, L.; Tao, Y.; Pan, Y.; Liu, J.; Yang, K.; Luo, H. Experimental Study on Variation of Surface Roughness and Q Factors of Fused Silica Cylindrical Resonators with Different Grinding Speeds. Micromachines 2021, 12, 1052. [Google Scholar] [CrossRef] [PubMed]
- Amirzada, M.R.; Khan, Y.; Ehsan, M.K.; Rehman, A.U.; Jamali, A.A.; Khatri, A.R. Prediction of Surface Roughness as a Function of Temperature for SiO2 Thin-Film in PECVD Process. Micromachines 2022, 13, 314. [Google Scholar] [CrossRef] [PubMed]
- Xu, D.; Yang, Q.; Wang, X.; He, H.; Sun, Y.; Li, W. An Experimental Investigation of Steel Surface Topography Transfer by Cold Rolling. Micromachines 2020, 11, 916. [Google Scholar] [CrossRef] [PubMed]
- Raina, A.; Anand, A. Influence of surface roughness and nanoparticles concentration on the friction and wear characteristics of PAO base oil. Mater. Res. Express 2018, 5, 095018. [Google Scholar] [CrossRef]
- Reinert, L.; Schütz, S.; Suárez, S.; Mücklich, F. Influence of Surface Roughness on the Lubrication Effect of Carbon Nanoparticle-Coated Steel Surfaces. Tribol. Lett. 2018, 66, 45. [Google Scholar] [CrossRef]
- Podgornik, B.; Hogmark, S.; Sandberg, O. Influence of surface roughness and coating type on the galling properties of coated forming tool steel. Surf. Coat. Technol. 2004, 184, 338–348. [Google Scholar] [CrossRef]
- Grzesik, W. Prediction of the Functional Performance of Machined Components Based on Surface Topography: State of the Art. J. Mater. Eng. Perform. 2016, 25, 4460–4468. [Google Scholar] [CrossRef]
- Grochalski, K.; Mendak, M.; Jakubowicz, M.; Gapiński, B.; Swojak, N.; Wieczorowski, M.; Krawczyk, A. Differences in Roughness Parameter Values from Skid and Skidless Contact Stylus Profilometers. Adv. Sci. Technol. Res. J. 2021, 15, 58–70. [Google Scholar] [CrossRef]
- Mathia, T.G.; Pawlus, P.; Wieczorowski, M. Recent trends in surface metrology. Wear 2011, 271, 494–508. [Google Scholar] [CrossRef]
- Thomas, T.R. Surface Roughness Measurement: Alternatives to the Stylus. In Proceedings of the Nineteenth International Machine Tool Design and Research Conference: Held in Manchester, 13–15 September 1978; Davies, B.J., Ed.; Macmillan Education UK: London, UK, 1979; pp. 383–390. [Google Scholar] [CrossRef]
- Tanner, L.H. An improved pneumatic Wheatstone bridge for roughness measurement. J. Phys. E Sci. Instrum. 1980, 13, 593–594. [Google Scholar] [CrossRef]
- Varghese, S.; Radharkrishnan, V. A multi sensor approach to in-process monitoring of surface roughness. J. Mater. Process. Technol. 1994, 44, 353–362. [Google Scholar] [CrossRef]
- Kruse, D.; Patzelt, S.; Dollinger, C.; Tausendfreund, A.; Goch, G. Laser Optical Characterization of Smooth Surfaces with Respect to Roughness and Defects in the Micrometer Range. Procedia Eng. 2011, 19, 235–240. [Google Scholar] [CrossRef]
- Sherrington, I.; Smith, E.H. Modern measurement techniques in surface metrology: Part II; optical instruments. Wear 1988, 125, 289–308. [Google Scholar] [CrossRef]
- Kayahan, E.; Oktem, H.; Hacizade, F.; Nasibov, H.; Gundogdu, O. Measurement of surface roughness of metals using binary speckle image analysis. Tribol. Int. 2010, 43, 307–311. [Google Scholar] [CrossRef]
- Guo, R.; Tao, Z. A study of neural network for surface characteristics in-process optical measurement. Opt. Int. J. Light Electron Opt. 2013, 124, 2821–2824. [Google Scholar] [CrossRef]
- Al-Kindi, G.A.; Shirinzadeh, B. An evaluation of surface roughness parameters measurement using vision-based data. Int. J. Mach. Tools Manuf. 2007, 47, 697–708. [Google Scholar] [CrossRef]
- Gadelmawla, E.S. A vision system for surface roughness characterization using the gray level co-occurrence matrix. NDT E Int. 2004, 37, 577–588. [Google Scholar] [CrossRef]
- Youssef, D.; El-Ghandoor, H.; Kandel, H.; El-Azab, J.; Hassab-Elnaby, S. Estimation of Articular Cartilage Surface Roughness Using Gray-Level Co-Occurrence Matrix of Laser Speckle Image. Materials 2017, 10, 714. [Google Scholar] [CrossRef]
- Liu, J.; Lu, E.; Yi, H.; Wang, M.; Ao, P. A new surface roughness measurement method based on a color distribution statistical matrix. Measurement 2017, 103, 165–178. [Google Scholar] [CrossRef]
- Elango, V.; Karunamoorthy, L. Effect of lighting conditions in the study of surface roughness by machine vision—An experimental design approach. Int. J. Adv. Manuf. Technol. 2008, 37, 92–103. [Google Scholar] [CrossRef]
- Murugarajan, A.; Samuel, G. Measurement, Modeling and Evaluation of Surface Parameter Using Capacitive-Sensor-Based Measurement System. Metrol. Meas. Syst. 2011, 18, 403. [Google Scholar] [CrossRef]
- Sherwood, K.F.; Crookall, J.R. Paper 31: Surface Finish Assessment by an Electrical Capacitance Technique. Proc. Inst. Mech. Eng. Conf. Proc. 1967, 182, 344–349. [Google Scholar] [CrossRef]
- Garbini, J.L.; Koh, S.-P.; Jorgensen, J.E.; Ramulu, M. Surface Profile Measurement During Turning Using Fringe-Field Capacitive Profilometry. J. Dyn. Syst. Meas. Control 1992, 114, 234–243. [Google Scholar] [CrossRef]
- Nowicki, B.; Jarkiewicz, A. The in-process surface roughness measurement using fringe field capacitive (FFC) method. Int. J. Mach. Tools Manuf. 1998, 38, 725–732. [Google Scholar] [CrossRef]
- Guadarrama-Santana, A.; Garcia-Valenzuela, A.; Bruce, N.C.; HernandezCordero, J. A New Approach for Measuring Surface Parameters by a Capacitive Sensor. Sensors 2003, 1, 553–558. [Google Scholar]
- Mathiyazhagan, R.; Sampathkumar, S.; Muthuramalingam, T. Prediction Modeling of Surface Roughness Using Capacitive Sensing Technique in Machining Process. IEEE Sens. J. 2019, 19, 9997–10002. [Google Scholar] [CrossRef]
- Reichold, T.V.; Ruiz, P.D.; Huntley, J.M. Nine-hundred-channel single-shot surface roughness measurement using hyperspectral interferometry. Meas. Sci. Technol. 2020, 31, 045014. [Google Scholar] [CrossRef]
- ISO4288:1996; Geometrical Product Specifications (GPS)—Surface Texture: Profile Method—Rules and Procedures for the Assessment of Surface Texture. ISO: London, UK, 1996.
- Harichandra, B.P.; Prashanth, M.; Mahapathi, M.; Prakash, S.V. Evaluation of MechanicalProperties of EN31 steel heat treated using Biodegradable oilsEvaluation of MechanicalProperties of EN31 steel heat treated using Biodegradable oils. Int. J. Appl. Eng. Res. 2015, 10, 1248–1252. [Google Scholar]
- Singh, I.; Garg, T.K.; Chhatwal, G.S. Methods to improve mechanical properties of EN31 (high carbon steel) and D3 (High- Carbon, High Chromium Steel) materials. Int. J. Res. Eng. Appl. Sci. 2014, 4, 67–92. [Google Scholar]
- Maxwell, J.C. Treatise on Electricity and Magnetism; Oxford University Press: Oxford, UK, 1873; Volume 1. [Google Scholar]
- Smith, P.T.; Vallance, R.R.; Marsh, E.R. Correcting capacitive displacement measurements in metrology applications with cylindrical artifacts. Precis. Eng. 2005, 29, 324–335. [Google Scholar] [CrossRef]
- Smith, J.R.; Philip, T. Analysis and Application of Capacitive Displacement Sensors to Curved Surfaces. Master’s Theses, University of Kentucky, Lexington, KY, USA, 2003. [Google Scholar]







| Capacitive Sensor (Lion Precision C1-A) | |
|---|---|
| Sensing Diameter | 5.6 mm |
| Sensor Resolution (RMS) | 478.92 nm |
| Near Gap | 250 µm |
| Range | 2000 µm |
| Output | 0–10 VDC |
| Bandwidth | 15,000 Hz |
| XYZ Stage (PI—Physik Instrumente) | |
| Travel Range | 300 mm |
| Velocity | 2.5 µm/s |
| Operating Voltage | 12 V |
| Minimum Incremental Movement | 0.2 µm |
| Resolution | 0.018 µm |
| Specimen No. | Distance to Target (D) (µm) | Capacitance Value (C14) (pF) | Real Sensor Output Voltage (V) |
|---|---|---|---|
| 1 | 250.004 | 0.980 | 0.0 |
| 2 | 375.001 | 0.663 | 3.729 |
| 3 | 499.99 | 0.500 | 5.644 |
| 4 | 750.007 | 0.329 | 7.578 |
| 5 | 999.996 | 0.245 | 8.536 |
| 6 | 1250.004 | 0.201 | 9.094 |
| 7 | 1499.996 | 0.180 | 9.451 |
| 8 | 1749.997 | 0.153 | 9.694 |
| 9 | 2000 | 0.133 | 9.865 |
| 10 | 2250 | 0.118 | 9.992 |
| Specimen No. | Stylus Roughness Ra (µm) | Measured Voltage (Volt) | Mean Distance (Zm) (µm) | Stand-Off Distance (SOD) Removed-(Rac) (µm) |
|---|---|---|---|---|
| 1 | 0.3 | 5.668 | 498.495 | 98.495 |
| 2 | 0.6 | 5.348 | 471.959 | 71.959 |
| 3 | 1.8 | 5.063 | 450.540 | 50.540 |
| 4 | 2.7 | 4.354 | 404.910 | 4.910 |
| 5 | 7.2 | 7.516 | 740.222 | 340.222 |
| 6 | 9.4 | 6.949 | 644.224 | 244.224 |
| Specimen No. | SS Roughness Ra (µm) | Measured Voltage (Volt) | Estimated Roughness (Rc3) (µm) | Mean Distance (Zm) (µm) | Stand-Off Distance Removed (Rac) (µm) | Estimated Roughness (Rc4) (µm) |
|---|---|---|---|---|---|---|
| 7 | 0.4 | 5.534 | 0.59 | 487.035 | 87.035 | 0.52 |
| 8 | 0.8 | 5.338 | 0.97 | 489.867 | 89.867 | 0.95 |
| 9 | 1.4 | 5.163 | 1.31 | 457.819 | 57.819 | 1.32 |
| 10 | 1.5 | 5.213 | 1.21 | 461.549 | 61.549 | 1.21 |
| 11 | 2.9 | 4.716 | 2.17 | 426.993 | 26.993 | 2.15 |
| 12 | 8.7 | 7.516 | 3.22 | 740.222 | 340.222 | 6.37 |
| 13 | 12.6 | 6.949 | 2.13 | 644.224 | 244.224 | 3.75 |
| Specimen No. | Stylus Roughness Ra (µm) | Capacitance Value (C14) (pF) | Mean Distance (Zm) (µm) | Stand-Off Distance Removed (Rac) (µm) |
|---|---|---|---|---|
| 1 | 0.3 | 0.4956 | 500.296 | 0.296 |
| 2 | 0.6 | 0.4965 | 499.371 | 0.629 |
| 3 | 1.8 | 0.4978 | 498.065 | 1.935 |
| 4 | 2.7 | 0.4983 | 497.480 | 2.520 |
| 5 | 7.2 | 0.5067 | 489.179 | 10.821 |
| 6 | 9.4 | 0.5140 | 482.179 | 17.821 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mathiyazhagan, R.; SampathKumar, S.; Karthikeyan, P. Estimation of Surface Roughness on Milled Surface Using Capacitance Sensor Based Micro Gantry System through Single-Shot Approach. Micromachines 2022, 13, 1746. https://doi.org/10.3390/mi13101746
Mathiyazhagan R, SampathKumar S, Karthikeyan P. Estimation of Surface Roughness on Milled Surface Using Capacitance Sensor Based Micro Gantry System through Single-Shot Approach. Micromachines. 2022; 13(10):1746. https://doi.org/10.3390/mi13101746
Chicago/Turabian StyleMathiyazhagan, Rajendran, SenthamaraiKannan SampathKumar, and Palanisamy Karthikeyan. 2022. "Estimation of Surface Roughness on Milled Surface Using Capacitance Sensor Based Micro Gantry System through Single-Shot Approach" Micromachines 13, no. 10: 1746. https://doi.org/10.3390/mi13101746
APA StyleMathiyazhagan, R., SampathKumar, S., & Karthikeyan, P. (2022). Estimation of Surface Roughness on Milled Surface Using Capacitance Sensor Based Micro Gantry System through Single-Shot Approach. Micromachines, 13(10), 1746. https://doi.org/10.3390/mi13101746






