Electrostatically Tuned Optical Filters Based on Hybrid Plasmonic-Dielectric Thin Films for Hyperspectral Imaging
Abstract
1. Introduction
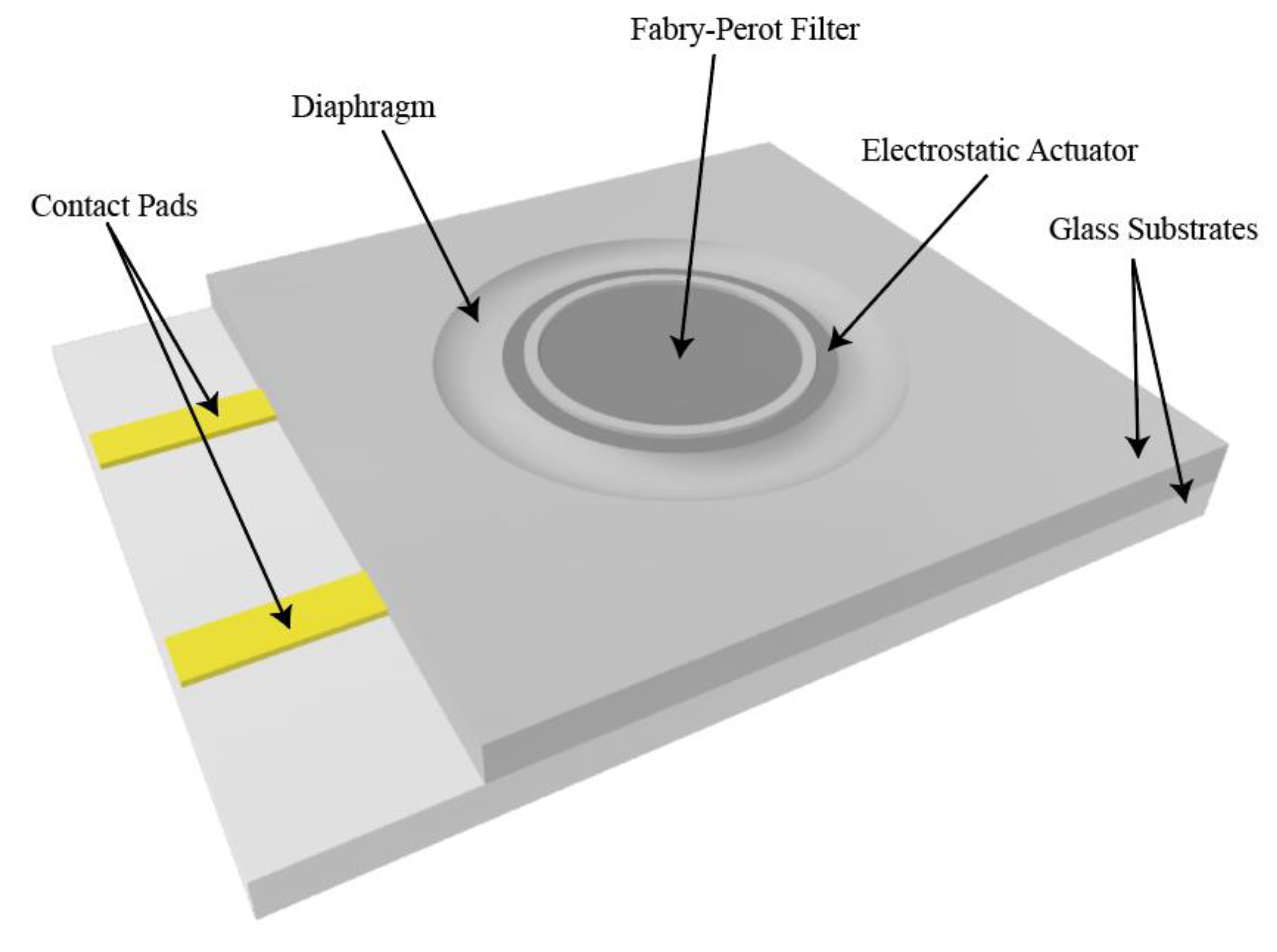
2. Device Design
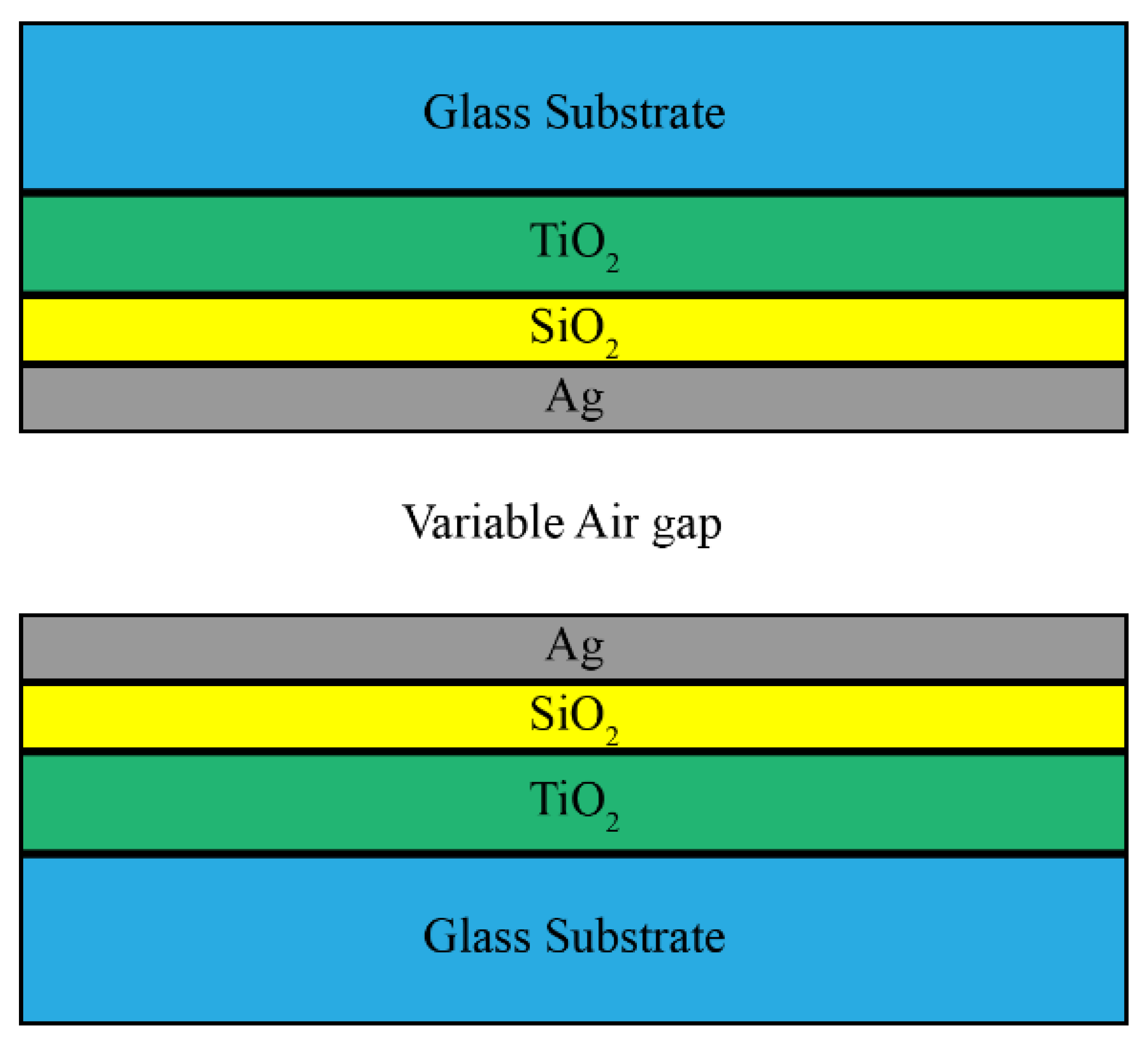
2.1. Filter Design
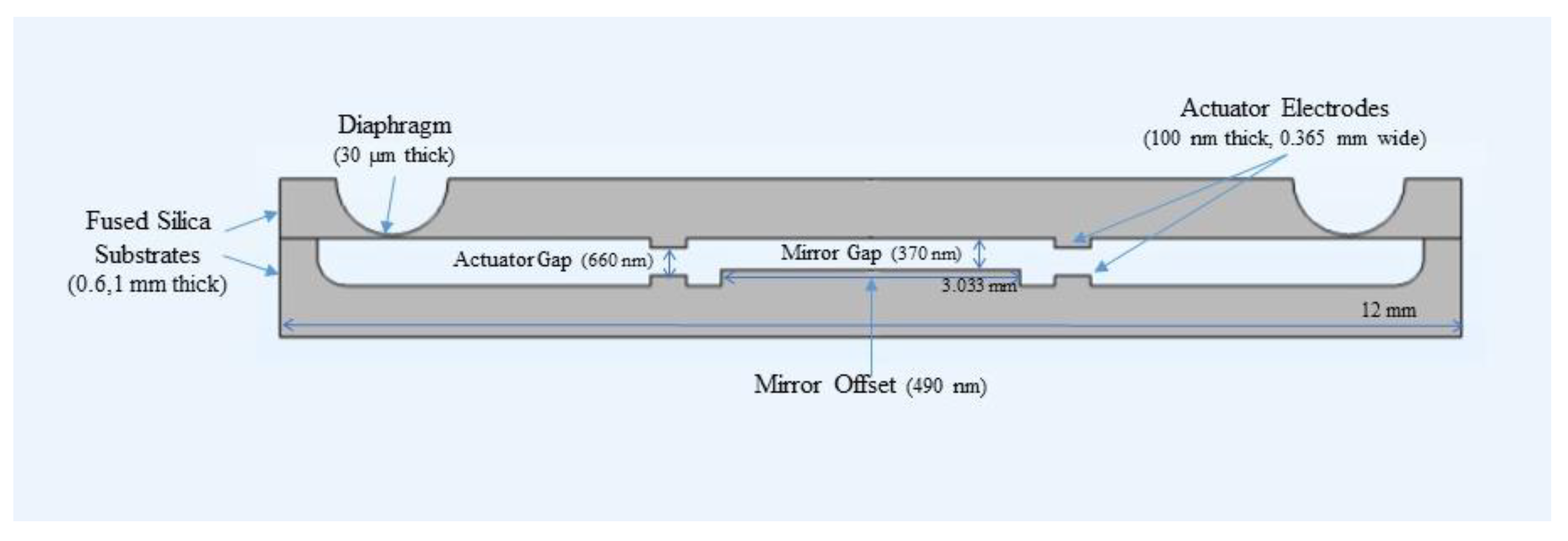
2.2. Actuator Design
3. Results and Discussion
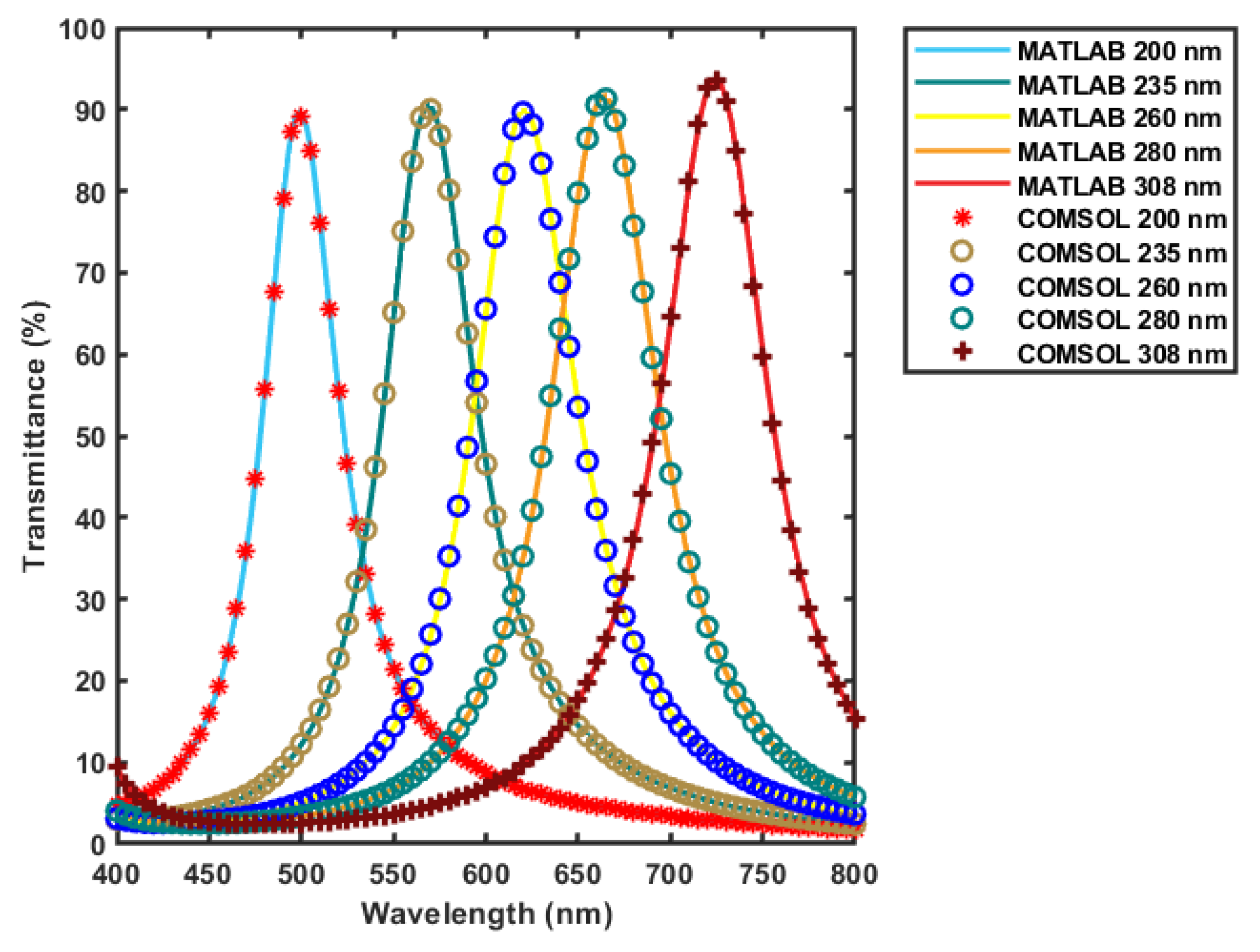
3.1. Filter Design Results
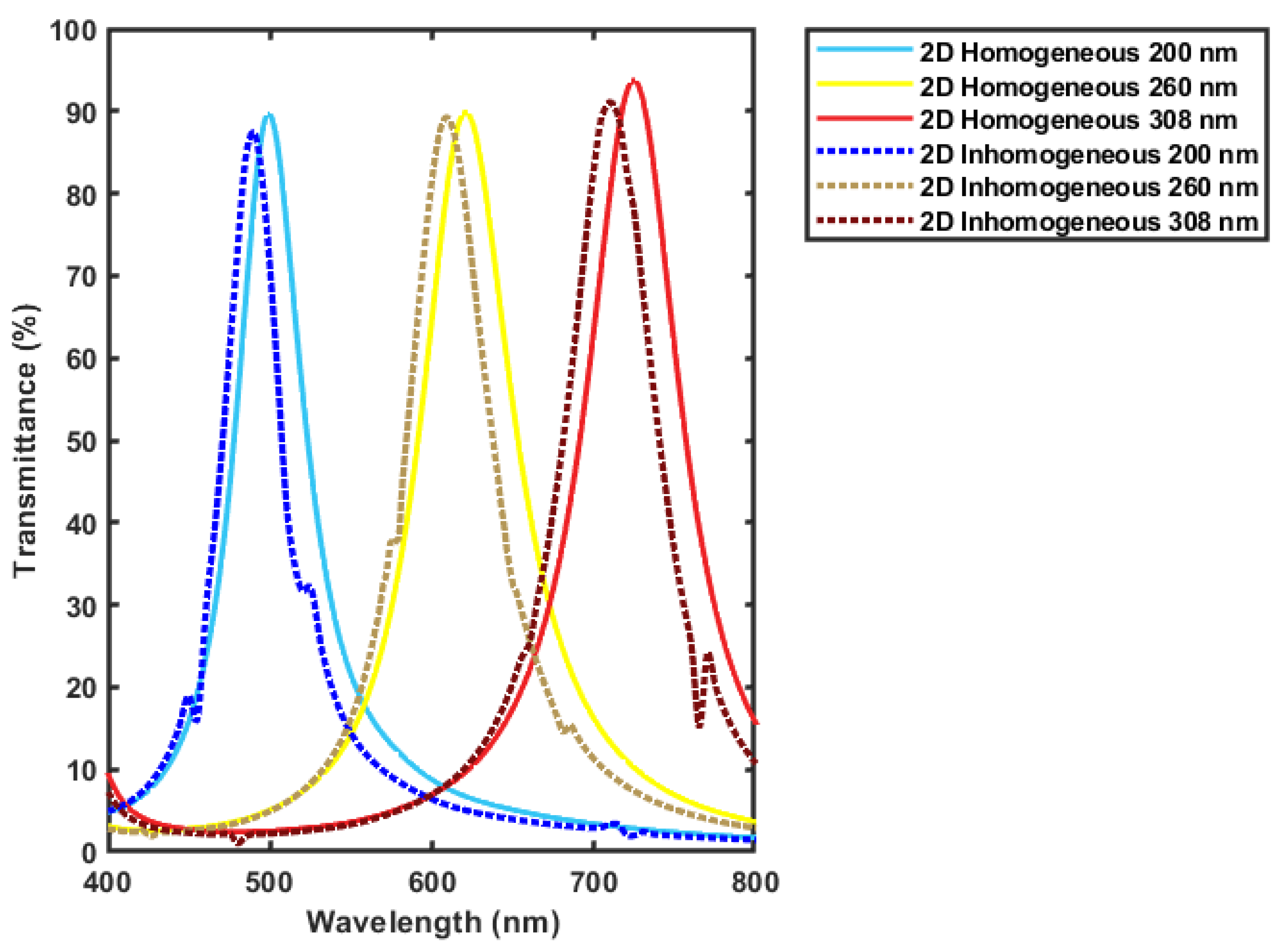
3.2. Filter Results Verification
3.3. Actuator Design Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lu, G.; Fei, B. Medical hyperspectral imaging: A review. J. Biomed. Opt. 2014, 19, 010901. [Google Scholar] [CrossRef]
- Monakhova, K.; Yanny, K.; Aggarwal, N.; Waller, L. Spectral DiffuserCam: Lensless snapshot hyperspectral imaging with a spectral filter array. Optica 2020, 7, 1298. [Google Scholar] [CrossRef]
- Gat, N. Imaging spectroscopy using tunable filters: A review. Proc. SPIE 2000, 4056, 50–65. [Google Scholar] [CrossRef]
- Dong, X.; Jakobi, M.; Wang, S.; Köhler, M.H.; Zhang, X.; Koch, A.W. A review of hyperspectral imaging for nanoscale materials research. Appl. Spectrosc. Rev. 2018, 54, 285–305. [Google Scholar] [CrossRef]
- Vo-Dihn, T. A hyperspectral imaging system for in vivo optical diagnostics. IEEE Eng. Med. Biol. Mag. 2004, 23, 40–49. [Google Scholar] [CrossRef] [PubMed]
- Gowen, A.; O’Donnell, C.; Cullen, P.; Downey, G.; Frias, J. Hyperspectral imaging–an emerging process analytical tool for food quality and safety control. Trends Food Sci. Technol. 2007, 18, 590–598. [Google Scholar] [CrossRef]
- Sun, D.-W. Hyperspectral Imaging for Food Quality Analysis and Control, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Govender, M.; Chetty, K.; Bulcock, H. A review of hyperspectral remote sensing and its application in vegetation and water resource studies. Water SA 2017, 33, 145–151. [Google Scholar] [CrossRef]
- Huang, W.; Li, J.; Wang, Q.; Chen, L. Development of a multispectral imaging system for online detection of bruises on apples. J. Food Eng. 2015, 146, 62–71. [Google Scholar] [CrossRef]
- Fischer, C.; Kakoulli, I. Multispectral and hyperspectral imaging technologies in conservation: Current research and potential applications. Stud. Conserv. 2006, 7, 3–16. [Google Scholar] [CrossRef]
- Liang, H. Advances in multispectral and hyperspectral imaging for archaeology and art conservation. Appl. Phys. A 2012, 6, 309–323. [Google Scholar] [CrossRef]
- Hege, E.K.; O’Connell, D.; Johnson, W.R.; Basty, S.; Dereniak, E.L. Hyperspectral imaging for astronomy and space surviellance. Proc. SPIE 2004, 5159, 380–391. [Google Scholar] [CrossRef]
- Bacon, C.P.; Mattley, Y.; DeFrece, R. Miniature spectroscopic instrumentation: Applications to biology and chemistry. Rev. Sci. Instrum. 2004, 75, 1–16. [Google Scholar] [CrossRef]
- Abdelghfar, A.; Anous, N.; Gaber, N. Tunable optical filters with hybrid plasmonic-dielectric thin-films for fluorescence sensing. Proc. SPIE 2021, 116970, 116970O. [Google Scholar] [CrossRef]
- Benavides, J.M.; Chang, S.; Park, S.Y.; Richards-Kortum, R.; Mackinnon, N.; MacAulay, C.; Milbourne, A.; Malpica, A.; Follen, M. Multispectral digital colposcopy for in vivo detection of cervical cancer. Opt. Express 2003, 11, 1223–1236. [Google Scholar] [CrossRef] [PubMed]
- Ferris, D.G.; Lawhead, R.A.; Dickman, E.D.; Holtzapple, N.; Miller, J.A.; Grogan, S.; Bambot, S.; Agrawal, A.; Faupel, M.L. Multimodal hyperspectral imaging for the noninvasive diagnosis of cervical neoplasia. J. Low. Genit. Tract Dis. 2001, 5, 65–72. [Google Scholar] [CrossRef][Green Version]
- Shah, S.A.; Bachrach, N.; Spear, S.J.; Letbetter, D.S.; Stone, R.A.; Dhir, R.; Prichard, J.W.; Brown, H.G.; LaFramboise, W.A. Cutaneous wound analysis using hyperspectral imaging. Biotechniques 2003, 34, 408–413. [Google Scholar] [CrossRef]
- Dicker, D.T.; Lerner, J.; Van Belle, P.; Barth, S.F.; Guerry, D.; Herlyn, M.; E Elder, D.; El-Deiry, W.S. Differentiation of normal skin and melanoma using high resolution hyperspectral imaging. Cancer Biol. Ther. 2006, 5, 1033–1038. [Google Scholar] [CrossRef]
- Larsen, E.L.P.; Randeberg, L.L.; Olstad, E.; Haugen, O.A.; Aksnes, A.; Svaasand, L.O. Hyperspectral imaging of atherosclerotic plaques in vitro. J. Biomed. Opt. 2011, 16, 026011. [Google Scholar] [CrossRef]
- Greenman, R.L.; Panasyuk, S.; Wang, X.; E Lyons, T.; Dinh, T.; Longoria, L.; Giurini, J.M.; Freeman, J.; Khaodhiar, L.; Veves, A. Early changes in the skin microcirculation and muscle metabolism of the diabetic foot. Lancet 2005, 366, 1711–1717. [Google Scholar] [CrossRef]
- Kong, S.G.; Martin, M.E.; Vo-Dinh, T. Hyperspectral fluorescence imaging for mouse skin tumor detection. Anglais 2006, 28, 770–776. [Google Scholar] [CrossRef]
- Yudovsky, D.; Nouvong, A.; Schomacker, K.; Pilon, L. Assessing diabetic foot ulcer development risk with hyperspectral tissue oximetry. J. Biomed. Opt. 2011, 16, 026009. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Wang, Y.; Liu, H.; Chen, Z. Nerve fibers identification based on molecular hyperspectral imaging technology. In Proceedings of the 2012 IEEE International Conference on Computer Science and Automation Engineering (CSAE), Zhangjiajie, China, 25–27 May 2012; pp. 15–17. [Google Scholar]
- Favreau, P.; Hernandez, C.; Lindsey, A.S.; Alvarez, D.F.; Rich, T.; Prabhat, P.; Leavesley, S.J. Thin-film tunable filters for hyperspectral fluorescence microscopy. J. Biomed. Opt. 2013, 19, 011017. [Google Scholar] [CrossRef] [PubMed]
- Thorlabs Inc. Liquid Crystal Tunable Bandpass Filters. Available online: https://www.thorlabs.us/newgrouppage9.cfm?objectgroup_id=3488 (accessed on 27 April 2021).
- Taylor and Francis Online. Molecular Crystals and Liquid Crystals Science and Technology. Section a. Molecular Crystals and Liquid Crystals. Available online: https://www.tandfonline.com/toc/gmcl19/346/1 (accessed on 27 April 2021).
- Blomberg, M.; Kattelus, H.; Miranto, A. Electrically tunable surface micromachined Fabry–Perot interferometer for visible light. Procedia Chem. 2010, 1, 184–188. [Google Scholar] [CrossRef]
- Hirokubo, N.; Komatsu, H.; Hashimoto, N.; Sonehara, M.; Sato, T. Wideband Visible Wavelength Range MEMS Fabry–Perot Tunable Filter With Highly Accurate Calibration System. IEEE Sens. J. 2013, 13, 2930–2936. [Google Scholar] [CrossRef]
- Benjamin, P.; Weaver, C. Adhesion of metal films to glass. Proc. R. Soc. Soc. A 1960, 254, 177–183. [Google Scholar] [CrossRef]
- Kikuchi, A.; Baba, S.; Kinbara, A. Measurement of the adhesion of silver films to glass substrates. Thin Solid Film. 1985, 124, 343–349. [Google Scholar] [CrossRef]
- Peng, J.I.; Park, S.C.; Gao, S.; Lee, S.S.; Choi, D.Y. Angle-tolerant linear variable color filter based on a tapered etalon. Opt. Express 2017, 25, 2153–2161. [Google Scholar]
- Tran, A.; Lo, Y.; Zhu, Z.; Haronian, D.; Mozdy, E. Surface micromachined Fabry-Perot tunable filter. IEEE Photon Technol. Lett. 1996, 8, 393–395. [Google Scholar] [CrossRef]
- Jen, Y.J.; Lee, C.C.; Lu, K.H.; Jheng, C.Y.; Chen, Y.J. Fabry-Perot based metal-dielectric multilayered filters and metamaterials. Opt. Express 2015, 23, 33008–33017. [Google Scholar] [CrossRef] [PubMed]
- Macleod, H.A. Thin-Film Optical Filters, 3rd ed.; IOP Publisher: Bristol, UK, 2001. [Google Scholar]
- Anous, N.; Abdallah, M.; Ramadan, T.; Qaraqe, K.; Khalil, D. Angle-tolerant hybrid plasmonic filters for visible light communi-cations. Appl. Opt. 2017, 56, C106–C116. [Google Scholar] [CrossRef]
- Sarkar, S.; Gupta, V.; Kumar, M.; Schubert, J.; Probst, P.T.; Joseph, J.; Koenig, T.A. Hybridized Guided-Mode Resonances via Colloidal Plasmonic Self-Assembled Grating. ACS Appl. Mater. Interfaces 2019, 11, 13752–13760. [Google Scholar] [CrossRef] [PubMed]
- Malitson, I.H. Interspecimen Comparison of the Refractive Index of Fused Silica. J. Opt. Soc. Am. 1965, 55, 1205–1209. [Google Scholar] [CrossRef]
- Shen, Y.; Yu, H.; Yao, J.; Shao, S.; Fan, Z.; He, H.; Shao, J. Investigation on properties of TiO2 thin films deposited at different oxygen pressures. Opt. Laser Technol. 2008, 40, 550–554. [Google Scholar] [CrossRef]
- Guo, C.; Kong, M. Fabrication of Ultralow Stress TiO2/SiO2 Optical Coatings by Plasma Ion-Assisted Deposition. Coatings 2020, 10, 720. [Google Scholar] [CrossRef]
- Kääriäinen, T.; Jaanson, P.; Vaigu, A.; Mannila, R.; Manninen, A. Active Hyperspectral Sensor Based on MEMS Fabry-Pérot Interferometer. Sensors 2019, 19, 2192. [Google Scholar] [CrossRef] [PubMed]
- Mannila, R.; Holmlund, C.; Ojanen, H.J.; Näsilä, A.; Saari, H. Short-wave infrared (SWIR) spectral imager based on Fabry-Perot interferometer for remote sensing. SPIE Remote Sens. 2014, 9241, 92411M. [Google Scholar] [CrossRef]
- Manual tunable fiber optical Filter 1NM—Etalon-Based. Available online: https://agiltron.com/product/manual-etalon-based-fiber-otf (accessed on 27 April 2021).
- Doc.comsol.com. Wave Optics Module User’s Guide. 2021. Available online: https://doc.comsol.com/5.4/doc/com.comsol.help.woptics/WaveOpticsModuleUsersGuide.pdf (accessed on 30 April 2021).


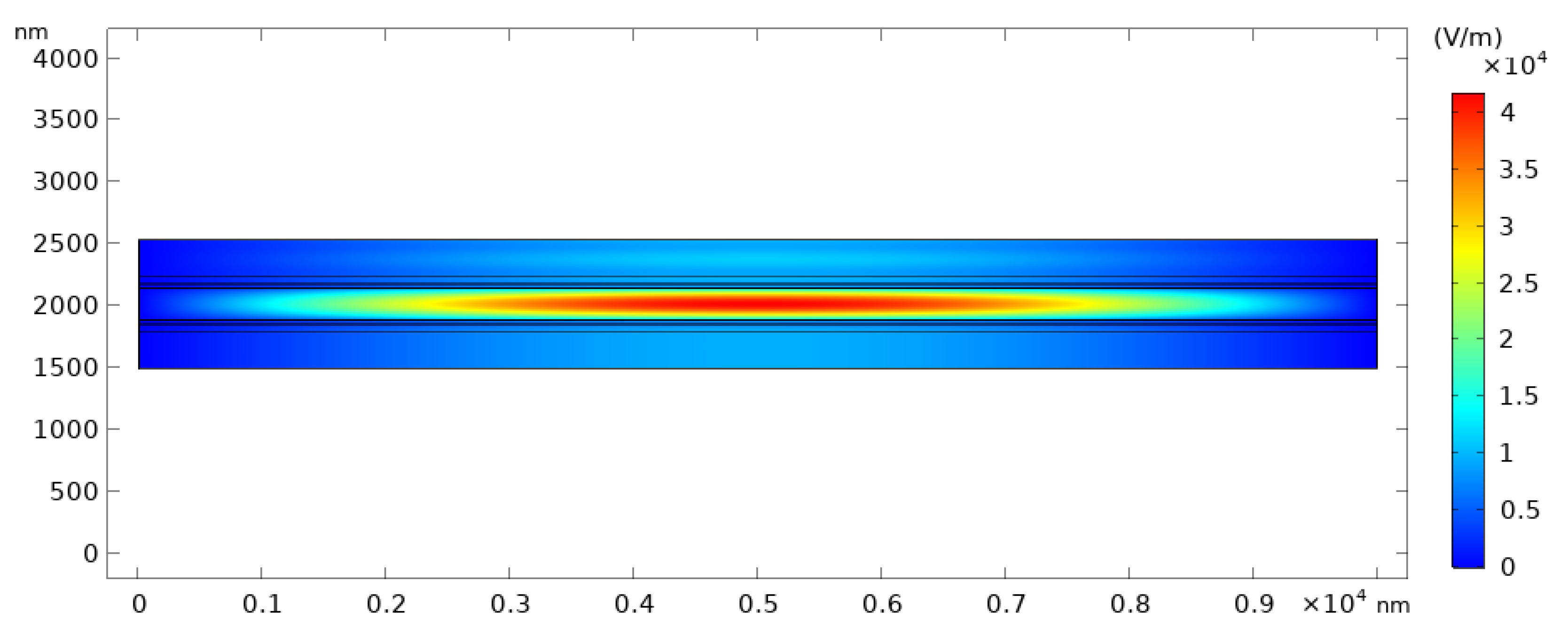


| Layer | Maximum Transmission Filter | Minimum FWHM Filter |
|---|---|---|
| TiO2 Layer | 43 nm | 63 nm |
| SiO2 Layer | 25 nm | 50 nm |
| Ag Layer | 20 nm | 40 nm |
| Variable Air Gap | (150 nm–320 nm) | (150 nm–320 nm) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdelghfar, A.; Mousa, M.A.; Fouad, B.M.; Saad, A.H.; Anous, N.; Gaber, N. Electrostatically Tuned Optical Filters Based on Hybrid Plasmonic-Dielectric Thin Films for Hyperspectral Imaging. Micromachines 2021, 12, 767. https://doi.org/10.3390/mi12070767
Abdelghfar A, Mousa MA, Fouad BM, Saad AH, Anous N, Gaber N. Electrostatically Tuned Optical Filters Based on Hybrid Plasmonic-Dielectric Thin Films for Hyperspectral Imaging. Micromachines. 2021; 12(7):767. https://doi.org/10.3390/mi12070767
Chicago/Turabian StyleAbdelghfar, Ahmed, Mohamed A. Mousa, Bassant M. Fouad, Ahmed H. Saad, Noha Anous, and Noha Gaber. 2021. "Electrostatically Tuned Optical Filters Based on Hybrid Plasmonic-Dielectric Thin Films for Hyperspectral Imaging" Micromachines 12, no. 7: 767. https://doi.org/10.3390/mi12070767
APA StyleAbdelghfar, A., Mousa, M. A., Fouad, B. M., Saad, A. H., Anous, N., & Gaber, N. (2021). Electrostatically Tuned Optical Filters Based on Hybrid Plasmonic-Dielectric Thin Films for Hyperspectral Imaging. Micromachines, 12(7), 767. https://doi.org/10.3390/mi12070767








