Dynamic Modeling and Frequency Characteristic Analysis of a Novel 3-PSS Flexible Parallel Micro-Manipulator
Abstract
1. Introduction
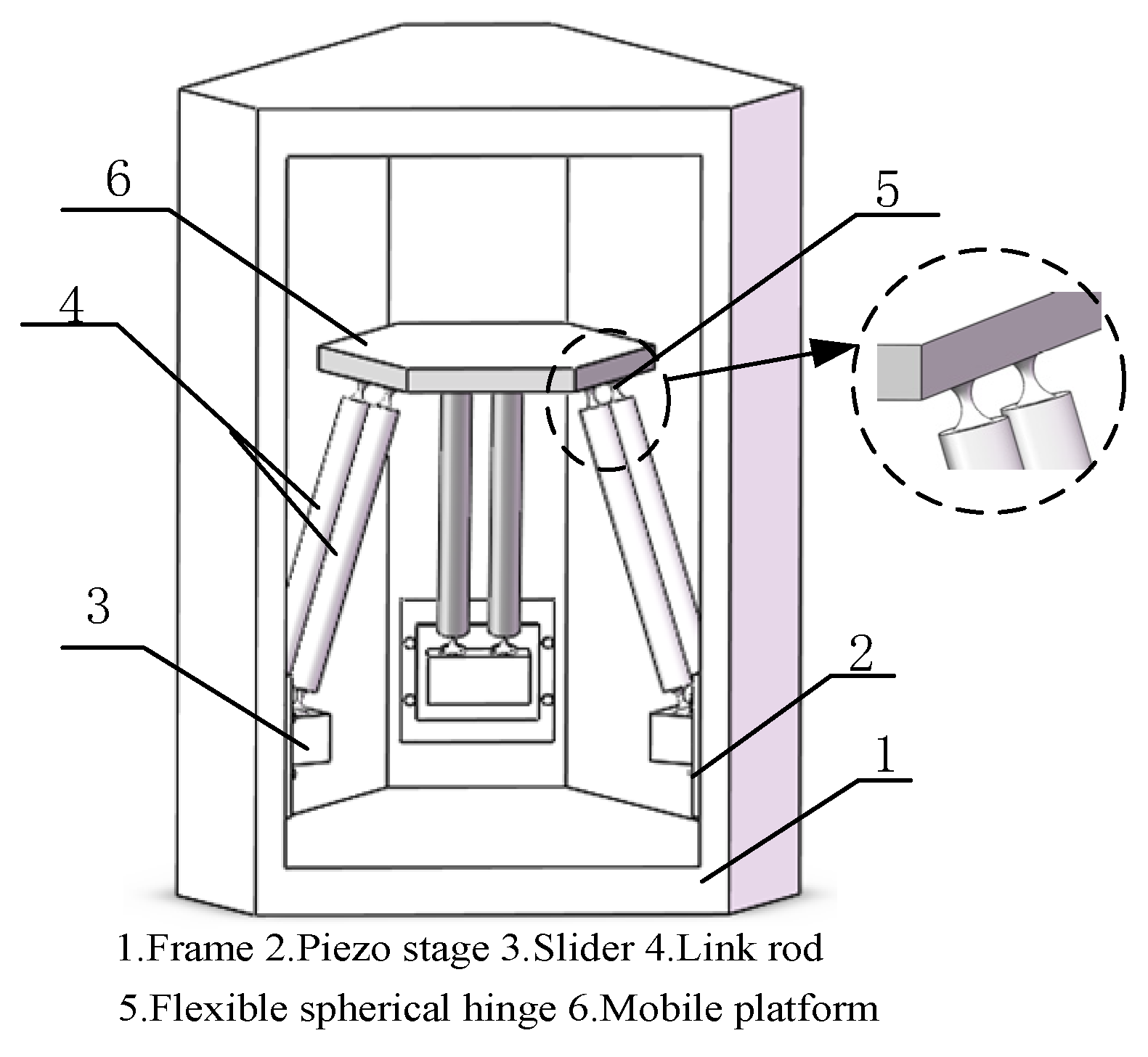
2. Structure of Micro-Manipulator
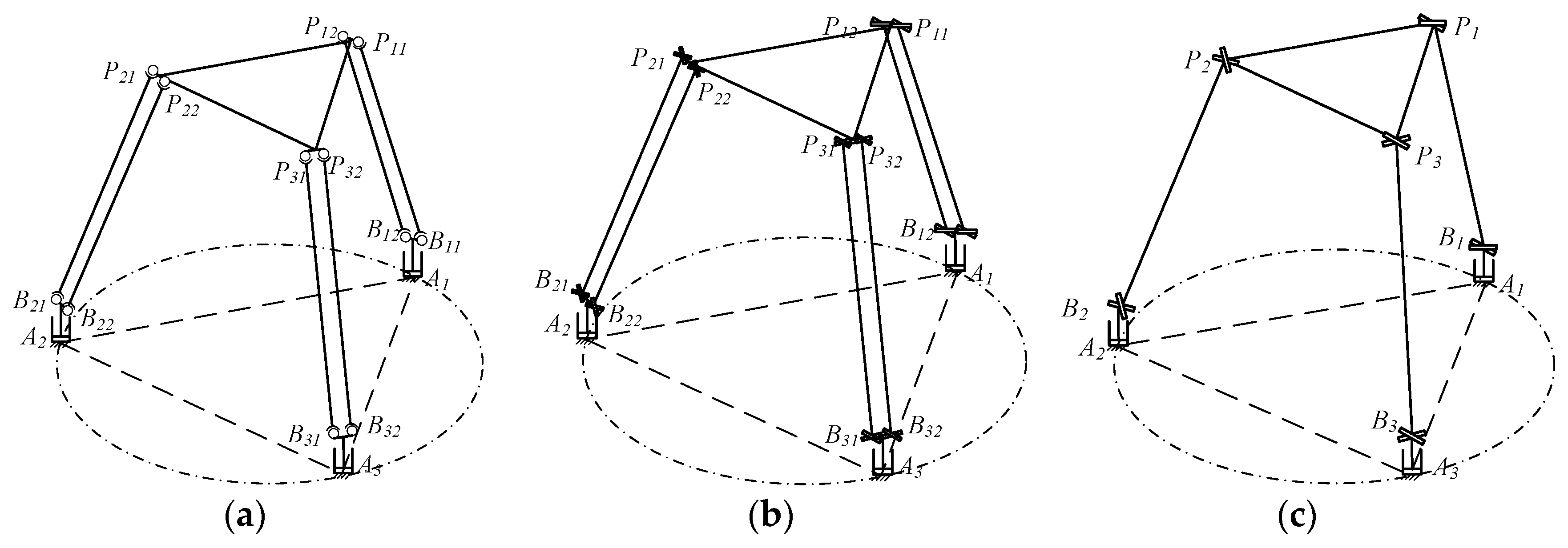
3. Inverse Kinematic Analysis
3.1. Jacobian Matrix
3.2. The Relationship between the Micro Angular Deformation of the Flexible Spherical Hinge and the End Pose of Mobile Platform
4. Dynamic Modeling
5. Examples and Simulation Analysis
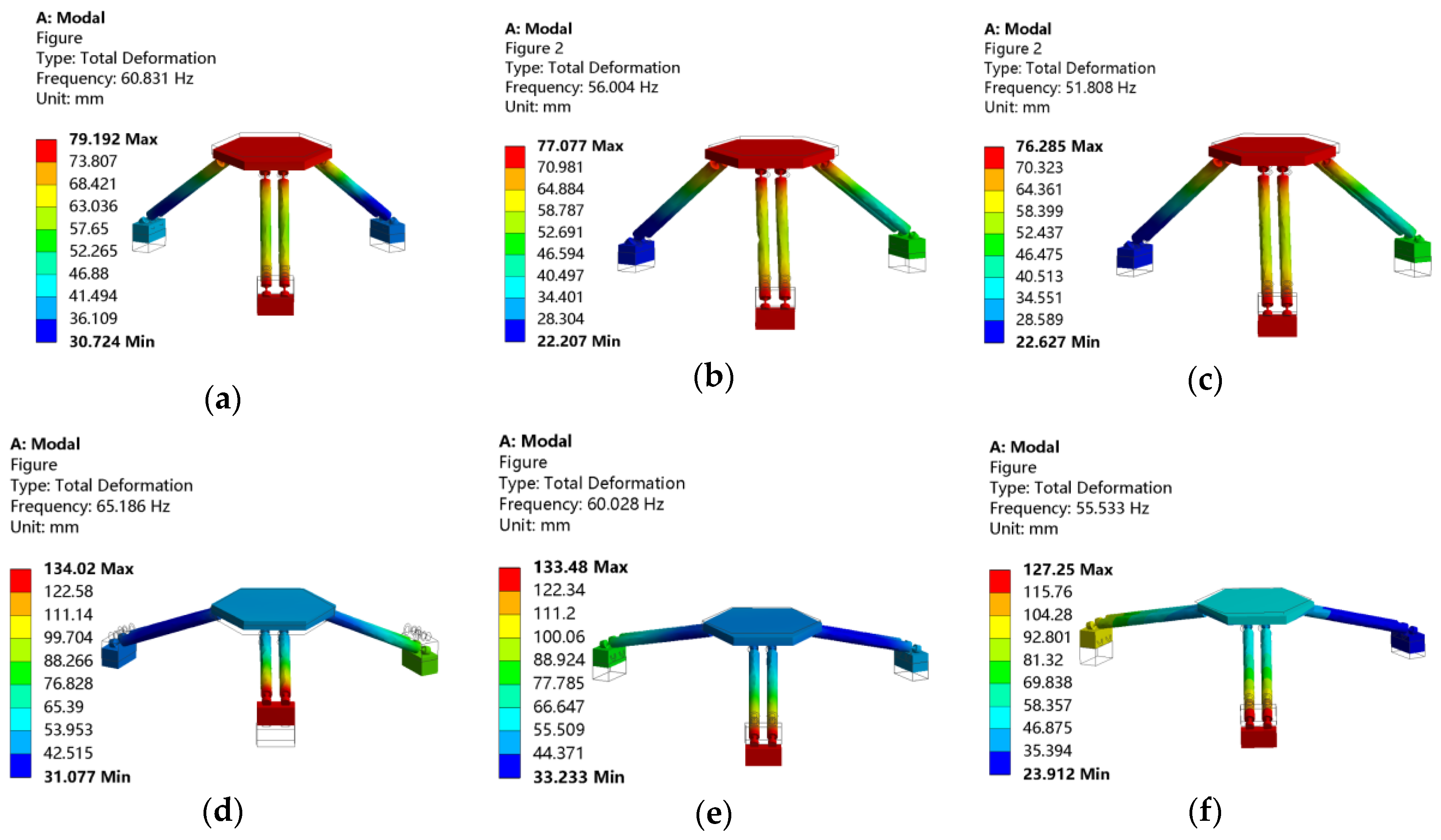
5.1. Numerical Examples and Modal Analysis
5.2. The Influence of Basic Structural Parameters Changes on Natural Frequencies
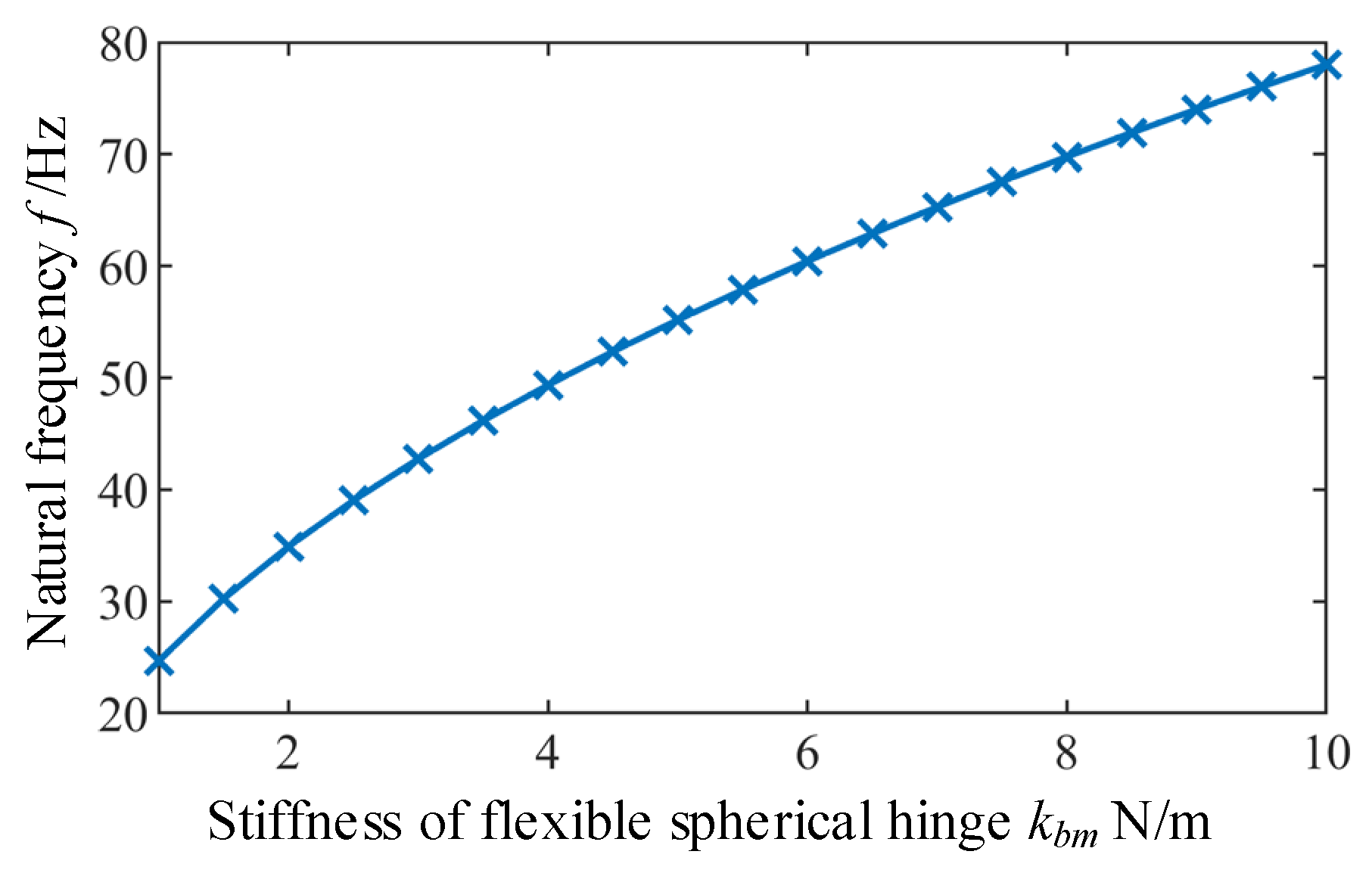
5.2.1. Influence of the Stiffness kbm of Flexible Spherical Hinge on the Natural Frequency
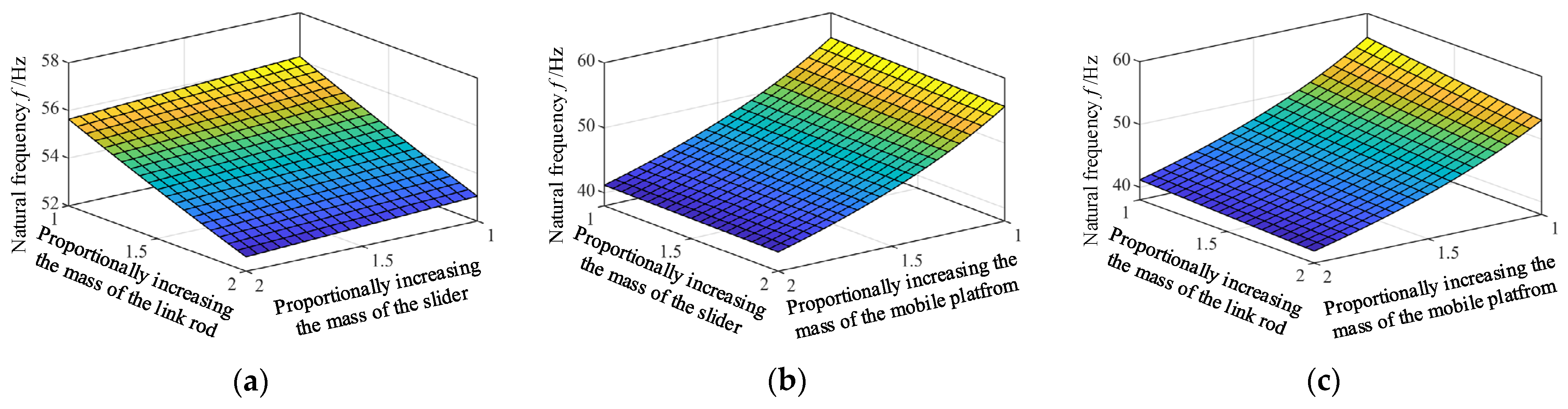
5.2.2. Influence of the Mass of Main Component on the Natural Frequency
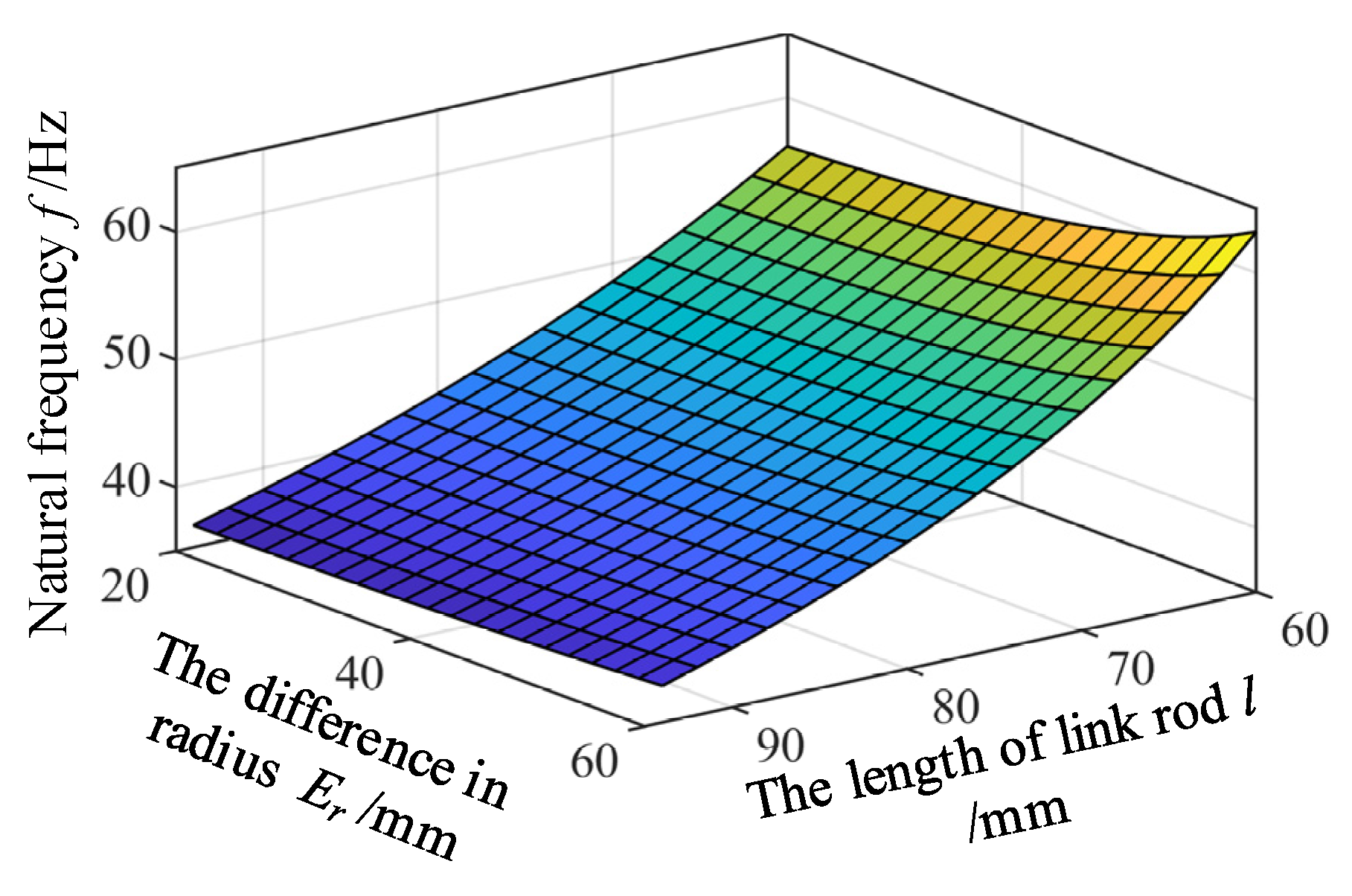
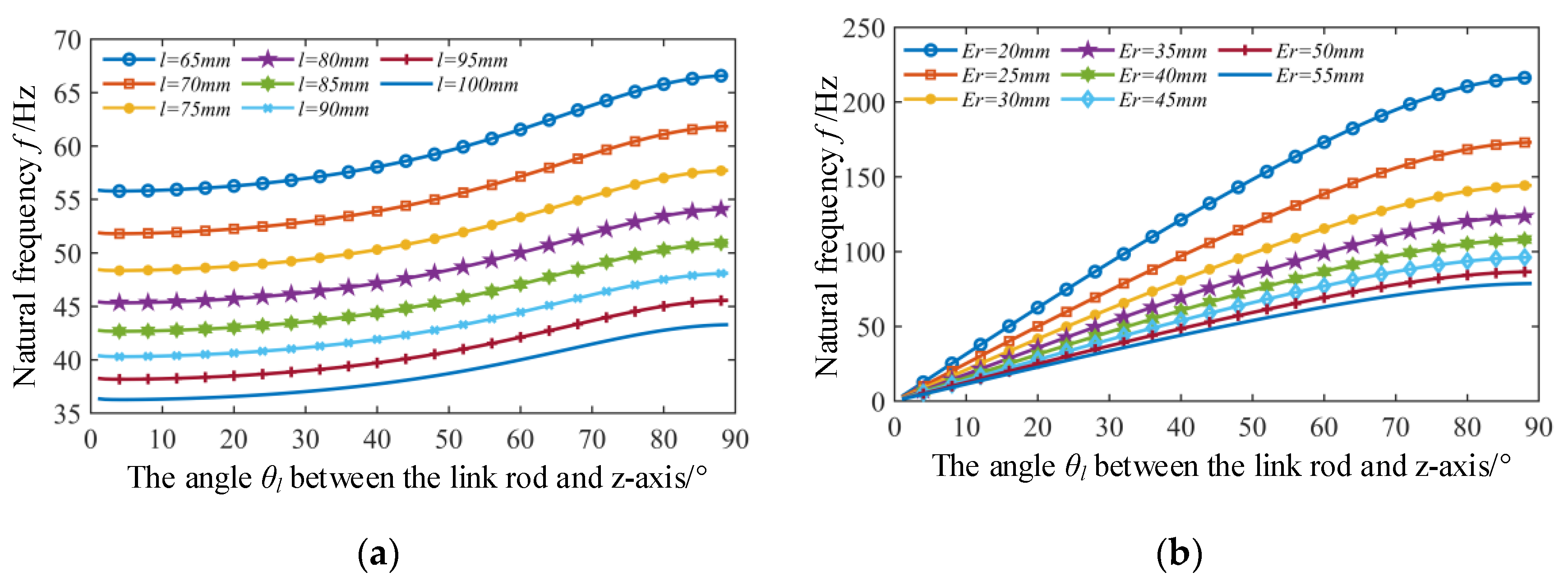
5.2.3. The Influence of the Variations of the Length l of Link Rod and the Difference in Radius Er on the Natural Frequency
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ghafarian, M.; Shirinzadeh, B.; Al-Jodah, A.; Das, T.K.; Wei, W.; Tian, Y.; Zhang, D. An XYZ micromanipulator for precise positioning applications. J. Micro Bio Robot. 2020, 16, 53–63. [Google Scholar] [CrossRef]
- Yun, Y.; Xu, Q.; Li, Y. Survey on parallel manipulators with micro/nano manipulation technology and applications. Chin. J. Mech. Eng. 2008, 44, 12–23. [Google Scholar] [CrossRef]
- Ling, M.; Howell, L.L.; Cao, J.; Chen, G. Kinetostatic and Dynamic Modeling of Flexure-Based Compliant Mechanisms: A Survey. Appl. Mech. Rev. 2020, 72, 030802. [Google Scholar] [CrossRef]
- Xu, Q.; Li, Y. A novel design of a 3-PRC translational compliant parallel micromanipulator for nanomanipulation. Robotica 2006, 24, 527–528. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Q. Design and testing of a new 3-DOF spatial flexure parallel micropositioning stage. Int. J. Precis. Eng. Manuf. 2018, 19, 109–118. [Google Scholar] [CrossRef]
- Chen, X.; Li, Y. Design and Analysis of a New High Precision Decoupled XY Compact Parallel Micromanipulator. Micromachines 2017, 8, 82. [Google Scholar] [CrossRef]
- Lai, L.; Gu, G.; Zhu, L. Design and control of a decoupled two degree of freedom translational parallel micro-positioning stage. Rev. Sci. Instrum. 2012, 83, 045105. [Google Scholar] [CrossRef] [PubMed]
- Tian, Y.; Shirinzadeh, B.; Zhang, D.; Zhong, Y. Modelling and analysis of a three-revolute parallel micro-positioning mechanism. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2011, 225, 1273–1286. [Google Scholar] [CrossRef]
- Zhang, J.; Gao, F.; Chen, Y.; Zhao, H. Study on statics and stiffness of parallel micro-manipulators with PZT actuators. Chin. J. Mech. Eng. 2004, 40, 82–87. [Google Scholar] [CrossRef]
- Xueyan, T.; Huy-Hoang, P.; Qing, L.; Ming, C. Dynamic analysis of a 3-DOF flexure parallel micromanipulator. In Proceedings of the IEEE Conference on Robotics, Automation and Mechatronics 2004, Singapore, 1–3 December 2004; pp. 95–100. [Google Scholar]
- Yun, Y.; Li, Y. Modeling and Control Analysis of a 3-PUPU Dual Compliant Parallel Manipulator for Micro Positioning and Active Vibration Isolation. J. Dyn. Syst. Meas. Control 2012, 134, 021001. [Google Scholar] [CrossRef]
- Wu, G.; Caro, S.; Bai, S.; Kepler, J. Dynamic modeling and design optimization of a 3-DOF spherical parallel manipulator. Robot. Auton. Syst. 2014, 62, 1377–1386. [Google Scholar] [CrossRef]
- Howell, L.L.; Midha, A. A Method for the Design of Compliant Mechanisms with Small-Length Flexural Pivots. J. Mech. Des. 1994, 116, 280–290. [Google Scholar] [CrossRef]
- Huang, J.; Li, Y. Analysis of a novel 2-DOF flexure hinge-based parallel micromanipulator in a polar coordinate system. In Proceedings of the 2010 IEEE International Conference on Automation and Logistics, ICAL 2010, Hong Kong, China, 16–20 August 2010; pp. 323–328. [Google Scholar]
- Xu, Q.; Li, Y. Kinematic analysis and optimization of a new compliant parallel micromanipulator. Int. J. Adv. Robot. Syst. 2006, 3, 351–358. [Google Scholar] [CrossRef]
- Xu, Q.; Li, Y.; Xi, N. Design, fabrication, and visual servo control of an xy parallel micromanipulator with piezo-actuation. IEEE Trans. Autom. Sci. Eng. 2009, 6, 710–719. [Google Scholar]
- Tian, Y.; Shirinzadeh, B.; Zhang, D. Design and dynamics of a 3-DOF flexure-based parallel mechanism for micro/nano manipulation. Microelectron. Eng. 2010, 87, 230–241. [Google Scholar] [CrossRef]
- Jia, X.; Liu, J.; Tian, Y. Dynamics analysis of spatial compliant parallel mechanism. Trans. Chin. Soc. Agric. Mach. 2012, 43, 210–214. [Google Scholar]
- Jia, X.; Tian, Y.; Zhang, D. Inverse dynamics of 3-RRPR compliant precision positioning stage based on the principle of virtue work. J. Mech. Eng. 2011, 47, 68–74. [Google Scholar] [CrossRef]
- Qi, K.; Ding, Y.; Xiang, Y.; Fang, C.; Zhang, Y. A novel 2-DOF compound compliant parallel guiding mechanism. Mech. Mach. Theory 2017, 117, 21–34. [Google Scholar] [CrossRef]
- Li, X.; Li, Y.; Ding, B.; Xu, H. An investigation on kinematics and dynamics performance of a novel 3-PRC-compliant parallel micromanipulator. Adv. Mech. Eng. 2018, 10, 168781401878980. [Google Scholar] [CrossRef]
- Hao, G.; Li, H. Conceptual designs of multi-degree of freedom compliant parallel manipulators composed of wire-beam based compliant mechanisms. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2015, 229, 538–555. [Google Scholar] [CrossRef]
- Murphy, M.D.; Midha, A.; Howell, L.L. The topological synthesis of compliant mechanisms. Mech. Mach. Theory 1996, 31, 185–199. [Google Scholar] [CrossRef]
- Pennock, J.D. Robots and Screw Theory: Applications of Kinematics and Statics to Robotics. J. Mech. Des. 2004, 126, 763–764. [Google Scholar]
- Howell, L.L. Compliant Mechanisms. In Encyclopedia of Nanotechnology; Bhushan, B., Ed.; Springer: Dordrecht, The Netherlands, 2012; pp. 457–463. [Google Scholar]
- Yang, C.-H. Design and calculation of compliance of arc flexure spherical hinge. Chin. J. Eng. Des. 2014, 21, 389–392. [Google Scholar]
- Chen, H. Analysis of the Rigidity of Arc Flexible Hinge with Different Geometrical Parameters. In Computer and Computing Technologies in Agriculture V; Li, D., Chen, Y., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 195–200. [Google Scholar]
- Wu, G.; Li, J.; Fei, R. Kinematics Analysis of 3-PU*U* Translational Parallel Manipulator. China Mech. Eng. 2004, 15, 64–67. [Google Scholar]
- Ren, J.; Zhang, Q. Structural Reanalysis Based on FRFs Using Sherman–Morrison–Woodbury Formula. Shock Vib. 2020, 2020, 1–12. [Google Scholar] [CrossRef]



| Parameter | rp/mm | ra/mm | l/mm | tb/mm | R/mm | θm/° |
|---|---|---|---|---|---|---|
| Numerical value | 45 | 25 | 65 | 1 | 2.5 | 60 |
| No | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Natural Frequencies f/Hz | 0 | 57.681 | 57.682 | 353.35 | 708.63 | 708.67 |
| No | Natural Frequencies f/Hz | Relative Error/% | |
|---|---|---|---|
| Theoretical Value | Simulation Value | ||
| 1 | 0 | 0 | 0 |
| 2 | 56.16 | 57.681 | 2.71 |
| 3 | 56.16 | 57.682 | 2.71 |
| Parameters | l = 65 mm | l = 70 mm | l = 75 mm | ||||
|---|---|---|---|---|---|---|---|
| f/Hz | θl = 45° | θl = 70° | θl = 45° | θl = 70° | θl = 45° | θl = 70° | |
| Numerical results/Hz | 58.74 | 63.81 z | 54.55 | 59.27 | 50.91 | 55.3 | |
| Simulation results/Hz | 60.88 | 65.186 | 56.004 | 60.028 | 51.808 | 55.533 | |
| Relative error/% | 3.64 | 2.15 | 2.66 | 1.27 | 1.76 | 0.42 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, J.; Cao, Q. Dynamic Modeling and Frequency Characteristic Analysis of a Novel 3-PSS Flexible Parallel Micro-Manipulator. Micromachines 2021, 12, 678. https://doi.org/10.3390/mi12060678
Ren J, Cao Q. Dynamic Modeling and Frequency Characteristic Analysis of a Novel 3-PSS Flexible Parallel Micro-Manipulator. Micromachines. 2021; 12(6):678. https://doi.org/10.3390/mi12060678
Chicago/Turabian StyleRen, Jun, and Qiuyu Cao. 2021. "Dynamic Modeling and Frequency Characteristic Analysis of a Novel 3-PSS Flexible Parallel Micro-Manipulator" Micromachines 12, no. 6: 678. https://doi.org/10.3390/mi12060678
APA StyleRen, J., & Cao, Q. (2021). Dynamic Modeling and Frequency Characteristic Analysis of a Novel 3-PSS Flexible Parallel Micro-Manipulator. Micromachines, 12(6), 678. https://doi.org/10.3390/mi12060678






