Spin-Mechanics with Nitrogen-Vacancy Centers and Trapped Particles
Abstract
1. Introduction
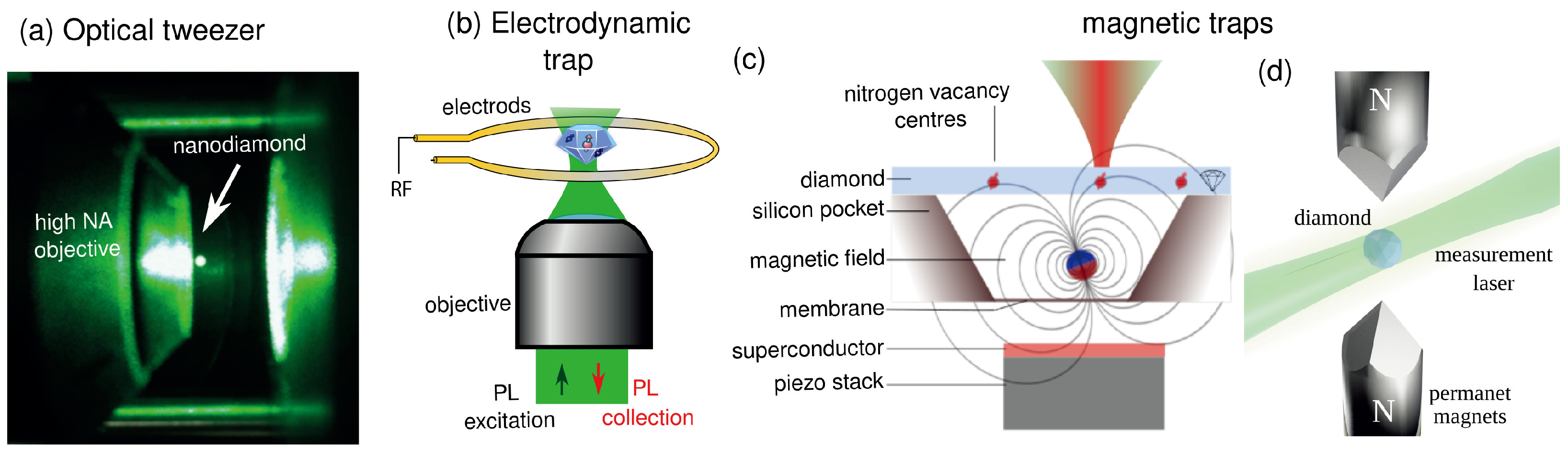
2. Trapping Crystals
2.1. Center of Mass Harmonic Motion
2.2. Angular Confinement: The Librational Mode
2.3. Trapping Platforms
3. Coupling to an Ancillary Quantum System: The Special Case of the NV− Center
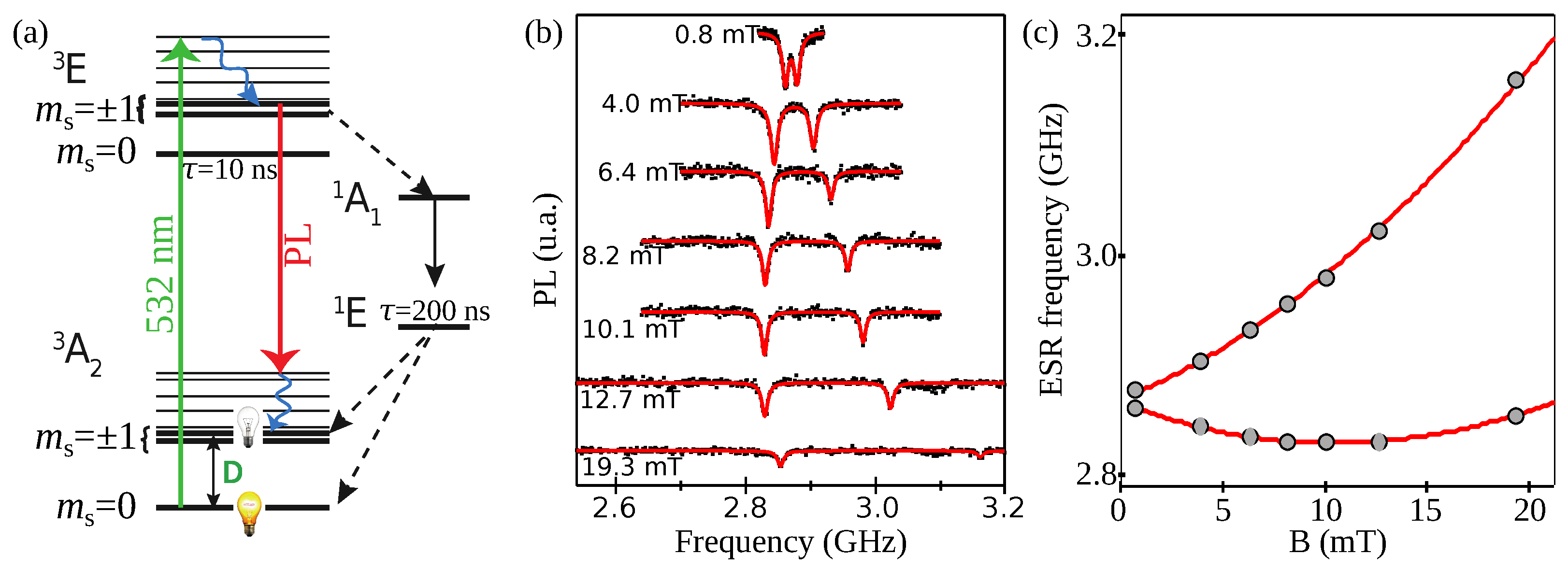
3.1. The NV− Center
3.2. The NV− Center Electronic Spin
4. Hamiltonian of the Spin–Mechanical System
4.1. Coupling to the Center of Mass
4.2. Coupling to the Libration
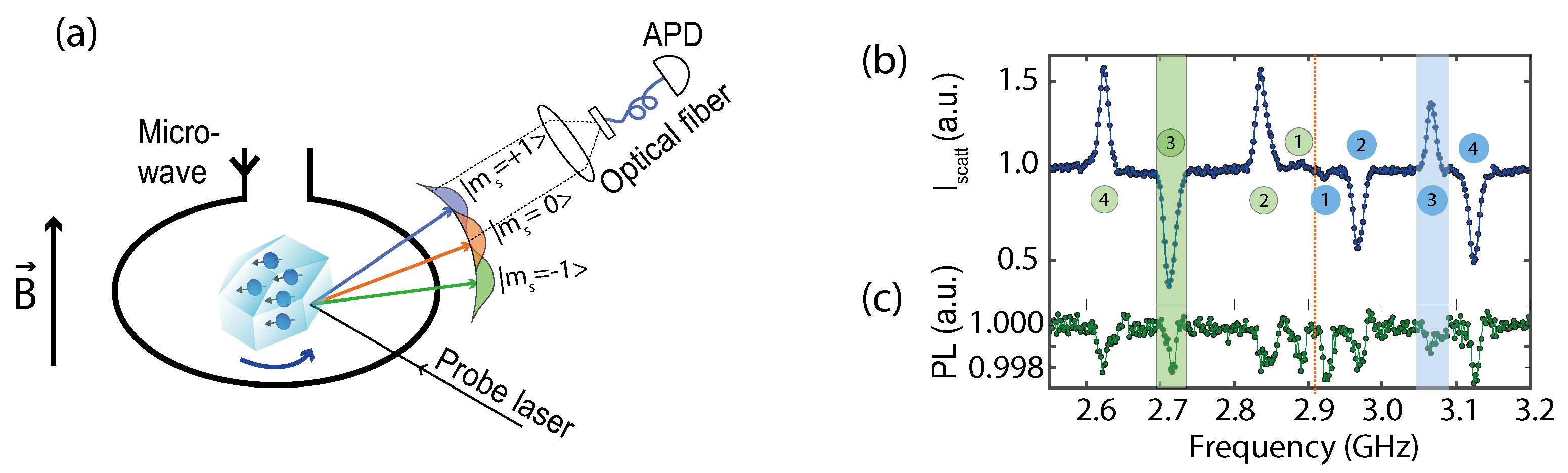
5. Sensing the Motion of a Trapped Particle Using NV− Centers
6. Magnetic Forces and Torques on a Trapped Particle from the Spin of NV− Centers
6.1. Force and Torque Sensitivity
6.2. Observing NV Static Spin-Dependent Torque and Force
6.2.1. Angular Displacement Using NV− Centers
6.2.2. Center of Mass Displacement Using NV− Centers
7. Dynamical Resonant Spin–Mechanical Interaction
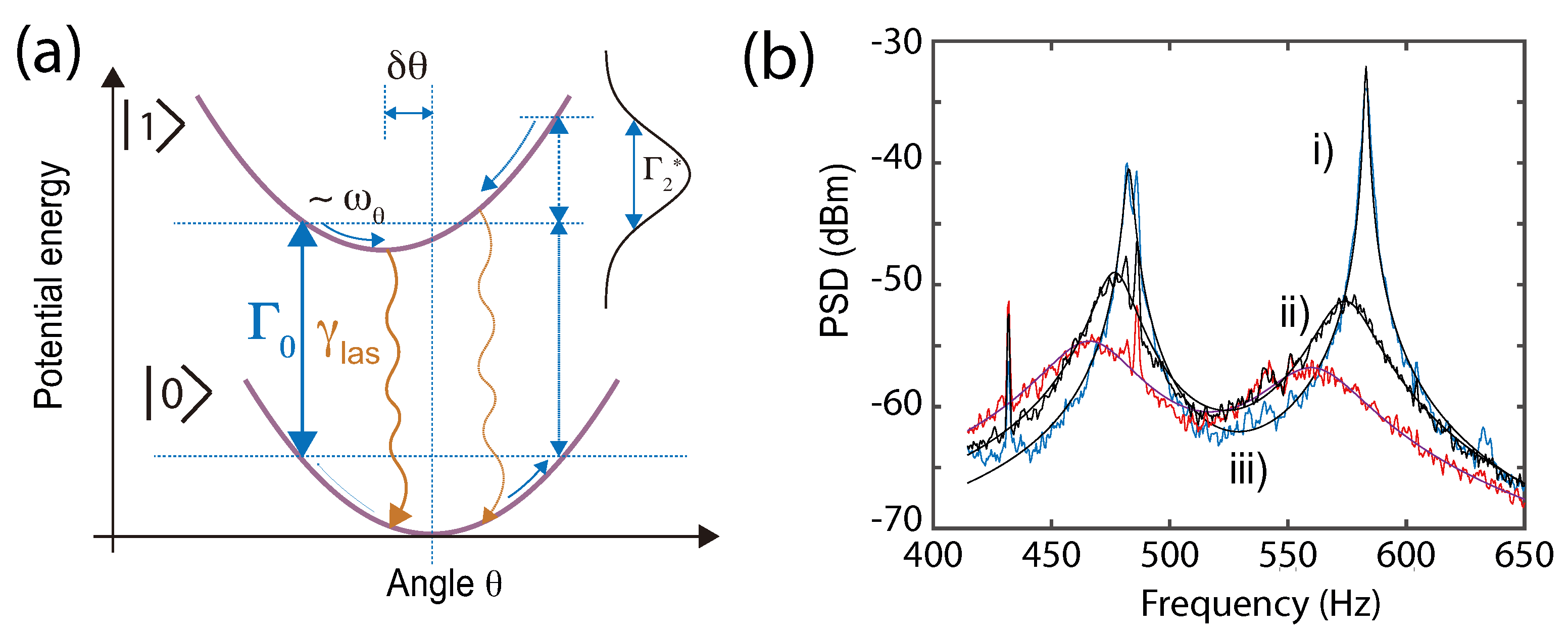
7.1. Bistability and Spin-Spring Effect
7.1.1. Spin-Bistability
7.1.2. Dynamical Backaction: Spin-Spring Effect
7.2. Spin-Cooling
7.2.1. Equations of Motion
7.2.2. Stationary Solutions
7.2.3. Effective Susceptibility
7.2.4. Dynamical Spin-Rigidity in the Adiabatic Limit
8. Challenges Ahead for Levitated Spin-Mechanics
8.1. Production of Diamond
8.2. Control of Diamond Shape and Properties
8.3. Increasing the NV− Concentration
8.4. Internal Temperature of Levitated Diamonds
8.5. Beyond NV− Centers and Diamond
9. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ESR | Electron spin resonance |
| ODMR | Optically detected magnetic resonance |
| CVD | Chemical Vapor Deposition |
| PSD | Power spectral density |
Appendix A. Derivation of a Simplified Hamiltonian
Appendix A.1. Moving to the Particle Frame
Appendix A.2. Diagonalization of the NV - Hamiltonian
Appendix A.3. Equilibrium Position of the Paul Trap
Appendix A.4. Rotating Frame of the Micro-Wave
Appendix B. Diamond Synthesis
- The HPHT process (high pressure, high temperature): A carbon precursor is brought under conditions of high pressure (typically > 5 GPa) and high temperature (T ≈ 2000 °C) in order to create diamond. While this approach has been known since the 1950s, the control of impurities in the diamond is not straigthforward. The diamonds produced are often rich in nitrogen impurities, typically around 200 ppm. Most recent works on diamond levitation used HPHT diamonds due to their ease of use and commercial availability.
- The CVD growth (chemical vapor deposition). A reactor is used to deposit carbon atoms from a methane gas, layer by layer on a diamond substrate. It is then possible to finely control the impurities present in the diamond. It is the method of choice to create diamonds with very high purity. The concentration of paramagnetic species such a nitrogen or silicon can indeed be reduced below the detection level, and the concentration of atoms below natural abundance. Importantly, CVD growth also enables NV center doping at any time during the growth [112].
- Detonation nanodiamonds are obtained by an explosive reaction from a carbon precursor. This approach provides very small nanodiamonds, typically <10 nm, which are often highly graphitized [113]. Such diamonds are thus not suited for the applications discussed in the present review.
References
- Aspelmeyer, M.; Kippenberg, T.J.; Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 2014, 86, 1391–1452. [Google Scholar] [CrossRef]
- Millen, J.; Monteiro, T.S.; Pettit, R.; Vamivakas, A.N. Optomechanics with levitated particles. Rep. Prog. Phys. 2020, 83, 026401. [Google Scholar] [CrossRef]
- Hebestreit, E.; Frimmer, M.; Reimann, R.; Novotny, L. Sensing Static Forces with Free-Falling Nanoparticles. Phys. Rev. Lett. 2018, 121, 063602. [Google Scholar] [CrossRef]
- Chang, D.E.; Regal, C.A.; Papp, S.B.; Wilson, D.J.; Ye, J.; Painter, O.; Kimble, H.J.; Zoller, P. Cavity Opto-Mechanics Using an Optically Levitated Nanosphere. Proc. Natl. Acad. Sci. USA 2010, 107, 1005–1010. [Google Scholar] [CrossRef]
- Romero-Isart, O.; Juan, M.L.; Quidant, R.; Cirac, J.I. Toward Quantum Superposition of Living Organisms. New J. Phys. 2010, 12, 033015. [Google Scholar] [CrossRef]
- Barker, P.F.; Shneider, M.N. Cavity cooling of an optically trapped nanoparticle. Phys. Rev. A 2010, 81, 023826. [Google Scholar] [CrossRef]
- Delić, U.; Reisenbauer, M.; Dare, K.; Grass, D.; Vuletić, V.; Kiesel, N.; Aspelmeyer, M. Motional Quantum Ground State of a Levitated Nanoparticle from Room Temperature. arXiv 2019, arXiv:191104406. [Google Scholar]
- Tebbenjohanns, F.; Frimmer, M.; Jain, V.; Windey, D.; Novotny, L. Motional Sideband Asymmetry of a Nanoparticle Optically Levitated in Free Space. Phys. Rev. Lett. 2020, 124, 013603. [Google Scholar] [CrossRef] [PubMed]
- Magrini, L.; Rosenzweig, P.; Bach, C.; Deutschmann-Olek, A.; Hofer, S.G.; Hong, S.; Kiesel, N.; Kugi, A.; Aspelmeyer, M. Optimal Quantum Control of Mechanical Motion at Room Temperature: Ground-State Cooling. arXiv 2020, arXiv:201215188. [Google Scholar]
- Tebbenjohanns, F.; Mattana, M.L.; Rossi, M.; Frimmer, M.; Novotny, L. Quantum control of a nanoparticle optically levitated in cryogenic free space. arXiv 2021, arXiv:2103.03853. [Google Scholar]
- Moore, D.C.; Geraci, A.A. Searching for New Physics Using Optically Levitated Sensors. arXiv 2020, arXiv:200813197. [Google Scholar]
- Xiong, F.; Wu, T.; Leng, Y.; Li, R.; Duan, C.; Kong, X.; Huang, P.; Li, Z.; Gao, Y.; Rong, X.; et al. Searching Spin-Mass Interaction Using a Diamagnetic Levitated Magnetic Resonance Force Sensor. arXiv 2020, arXiv:201014199. [Google Scholar]
- Vinante, A.; Carlesso, M.; Bassi, A.; Chiasera, A.; Varas, S.; Falferi, P.; Margesin, B.; Mezzena, R.; Ulbricht, H. Narrowing the Parameter Space of Collapse Models with Ultracold Layered Force Sensors. Phys. Rev. Lett. 2020, 125, 100404. [Google Scholar] [CrossRef] [PubMed]
- Rabl, P.; Cappellaro, P.; Dutt, M.V.G.; Jiang, L.; Maze, J.R.; Lukin, M.D. Strong magnetic coupling between an electronic spin qubit and a mechanical resonator. Phys. Rev. B 2009, 79, 041302. [Google Scholar] [CrossRef]
- Treutlein, P.; Genes, C.; Hammerer, K.; Poggio, M.; Rabl, P. Hybrid Mechanical Systems. In Cavity Optomechanics: Nano- and Micromechanical Resonators Interacting with Light; Aspelmeyer, M., Kippenberg, T.J., Marquardt, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 327–351. [Google Scholar] [CrossRef]
- Arcizet, O.; Jacques, V.; Siria, A.; Poncharal, P.; Vincent, P.; Seidelin, S. A single nitrogen-vacancy defect coupled to a nanomechanical oscillator. Nat. Phys. 2011, 7, 879–883. [Google Scholar] [CrossRef]
- Kolkowitz, S.; Bleszynski Jayich, A.C.; Unterreithmeier, Q.P.; Bennett, S.D.; Rabl, P.; Harris, J.G.E.; Lukin, M.D. Coherent Sensing of a Mechanical Resonator with a Single-Spin Qubit. Science 2012, 335, 1603–1606. [Google Scholar] [CrossRef] [PubMed]
- Yin, Z.; Zhao, N.; Li, T. Hybrid opto-mechanical systems with nitrogen-vacancy centers. Sci. China Phys. Mech. Astron. 2015, 58, 1–12. [Google Scholar] [CrossRef]
- Ma, Y.; Hoang, T.M.; Gong, M.; Li, T.; Yin, Z.Q. Proposal for quantum many-body simulation and torsional matter-wave interferometry with a levitated nanodiamond. Phys. Rev. A 2017, 96, 023827. [Google Scholar] [CrossRef]
- Wei, B.B.; Burk, C.; Wrachtrup, J.; Liu, R.B. Magnetic ordering of nitrogen-vacancy centers in diamond via resonator-mediated coupling. EPJ Quantum Technol. 2015, 2, 18. [Google Scholar] [CrossRef][Green Version]
- Scala, M.; Kim, M.S.; Morley, G.W.; Barker, P.F.; Bose, S. Matter-Wave Interferometry of a Levitated Thermal Nano-Oscillator Induced and Probed by a Spin. Phys. Rev. Lett. 2013, 111, 180403. [Google Scholar] [CrossRef]
- Pedernales, J.S.; Morley, G.W.; Plenio, M.B. Motional Dynamical Decoupling for Interferometry with Macroscopic Particles. Phys. Rev. Lett. 2020, 125, 023602. [Google Scholar] [CrossRef]
- Rabl, P.; Kolkowitz, S.J.; Koppens, F.H.L.; Harris, J.G.E.; Zoller, P.; Lukin, M.D. A quantum spin transducer based on nanoelectromechanical resonator arrays. Nat. Phys. 2010, 6, 602. [Google Scholar] [CrossRef]
- Martinetz, L.; Hornberger, K.; Stickler, B.A. Gas-Induced Friction and Diffusion of Rigid Rotors. Phys. Rev. E 2018, 97, 052112. [Google Scholar] [CrossRef] [PubMed]
- Gieseler, J.; Novotny, L.; Quidant, R. Thermal Nonlinearities in a Nanomechanical Oscillator. Nat. Phys. 2013, 9, 806–810. [Google Scholar] [CrossRef]
- Ashkin, A. Optical trapping and manipulation of neutral particles using lasers. Proc. Natl. Acad. Sci. USA 1997, 94, 4853–4860. [Google Scholar] [CrossRef] [PubMed]
- Jones, P.H.; Marag, O.M.; Volpe, G. Optical Tweezers: Principles and Applications, 1st ed.; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Gieseler, J.; Deutsch, B.; Quidant, R.; Novotny, L. Subkelvin Parametric Feedback Cooling of a Laser-Trapped Nanoparticle. Phys. Rev. Lett. 2012, 109, 103603. [Google Scholar] [CrossRef] [PubMed]
- Kiesel, N.; Blaser, F.; Delić, U.; Grass, D.; Kaltenbaek, R.; Aspelmeyer, M. Cavity Cooling of an Optically Levitated Submicron Particle. Proc. Natl. Acad. Sci. USA 2013, 110, 14180–14185. [Google Scholar] [CrossRef]
- Magrini, L.; Norte, R.A.; Riedinger, R.; Marinković, I.; Grass, D.; Delić, U.; Gröblacher, S.; Hong, S.; Aspelmeyer, M. Near-Field Coupling of a Levitated Nanoparticle to a Photonic Crystal Cavity. Optica 2018, 5, 1597–1602. [Google Scholar] [CrossRef]
- Paul, W. Electromagnetic traps for charged and neutral particles. Rev. Mod. Phys. 1990, 62, 531–540. [Google Scholar] [CrossRef]
- Dania, L.; Bykov, D.S.; Knoll, M.; Mestres, P.; Northup, T.E. Optical and electrical feedback cooling of a silica nanoparticle levitated in a Paul trap. Phys. Rev. Res. 2021, 3, 013018. [Google Scholar] [CrossRef]
- Nagornykh, P.; Coppock, J.E.; Kane, B.E. Cooling of levitated graphene nanoplatelets in high vacuum. Appl. Phys. Lett. 2015, 106, 244102. [Google Scholar] [CrossRef]
- Conangla, G.P.; Schell, A.W.; Rica, R.A.; Quidant, R. Motion Control and Optical Interrogation of a Levitating Single Nitrogen Vacancy in Vacuum. Nano Lett. 2018, 18, 3956–3961. [Google Scholar] [CrossRef]
- Gieseler, J.; Kabcenell, A.; Rosenfeld, E.; Schaefer, J.D.; Safira, A.; Schuetz, M.J.A.; Gonzalez-Ballestero, C.; Rusconi, C.C.; Romero-Isart, O.; Lukin, M.D. Single-Spin Magnetomechanics with Levitated Micromagnets. Phys. Rev. Lett. 2020, 124, 163604. [Google Scholar] [CrossRef] [PubMed]
- Hsu, J.F.; Ji, P.; Dutt, M.V.G.; D’Urso, B.R. Loading an Optical Trap with Diamond Nanocrystals Containing Nitrogen-Vacancy Centers from a Surface. arXiv 2015, arXiv:150608215. [Google Scholar]
- O’Brien, M.C.; Dunn, S.; Downes, J.E.; Twamley, J. Magneto-mechanical trapping of micro-diamonds at low pressures. Appl. Phys. Lett. 2019, 114, 053103. [Google Scholar] [CrossRef]
- Arita, Y.; Mazilu, M.; Dholakia, K. Laser-Induced Rotation and Cooling of a Trapped Microgyroscope in Vacuum. Nat. Commun. 2013, 4, 2374. [Google Scholar] [CrossRef] [PubMed]
- Reimann, R.; Doderer, M.; Hebestreit, E.; Diehl, R.; Frimmer, M.; Windey, D.; Tebbenjohanns, F.; Novotny, L. GHz Rotation of an Optically Trapped Nanoparticle in Vacuum. Phys. Rev. Lett. 2018, 121, 033602. [Google Scholar] [CrossRef] [PubMed]
- Monteiro, F.; Ghosh, S.; van Assendelft, E.C.; Moore, D.C. Optical Rotation of Levitated Spheres in High Vacuum. Phys. Rev. A 2018, 97, 051802. [Google Scholar] [CrossRef]
- Ahn, J.; Xu, Z.; Bang, J.; Deng, Y.H.; Hoang, T.M.; Han, Q.; Ma, R.M.; Li, T. Optically Levitated Nanodumbbell Torsion Balance and GHz Nanomechanical Rotor. Phys. Rev. Lett. 2018, 121, 033603. [Google Scholar] [CrossRef]
- Barnett, S.J. Gyromagnetic and Electron-Inertia Effects. Rev. Mod. Phys. 1935, 7, 129–166. [Google Scholar] [CrossRef]
- Hoang, T.M.; Ma, Y.; Ahn, J.; Bang, J.; Robicheaux, F.; Yin, Z.Q.; Li, T. Torsional Optomechanics of a Levitated Nonspherical Nanoparticle. Phys. Rev. Lett. 2016, 117, 123604. [Google Scholar] [CrossRef]
- Vinante, A.; Falferi, P.; Gasbarri, G.; Setter, A.; Timberlake, C.; Ulbricht, H. Ultralow Mechanical Damping with Meissner-Levitated Ferromagnetic Microparticles. Phys. Rev. Appl. 2020, 13, 064027. [Google Scholar] [CrossRef]
- Delord, T.; Huillery, P.; Nicolas, L.; Hétet, G. Spin-Cooling of the Motion of a Trapped Diamond. Nature 2020, 1–4. [Google Scholar] [CrossRef]
- Delord, T.; Nicolas, L.; Chassagneux, Y.; Hétet, G. Strong Coupling between a Single Nitrogen-Vacancy Spin and the Rotational Mode of Diamonds Levitating in an Ion Trap. Phys. Rev. A 2017, 96, 063810. [Google Scholar] [CrossRef]
- Ranjit, G.; Montoya, C.; Geraci, A.A. Cold Atoms as a Coolant for Levitated Optomechanical Systems. Phys. Rev. A 2015, 91, 013416. [Google Scholar] [CrossRef]
- Bykov, D.S.; Mestres, P.; Dania, L.; Schmöger, L.; Northup, T.E. Direct Loading of Nanoparticles under High Vacuum into a Paul Trap for Levitodynamical Experiments. Appl. Phys. Lett. 2019, 115, 034101. [Google Scholar] [CrossRef]
- Karg, T.M.; Gouraud, B.; Ngai, C.T.; Schmid, G.L.; Hammerer, K.; Treutlein, P. Light-Mediated Strong Coupling between a Mechanical Oscillator and Atomic Spins 1 Meter Apart. Science 2020, 369, 174–179. [Google Scholar] [CrossRef] [PubMed]
- Thomas, R.A.; Parniak, M.; Østfeldt, C.; Møller, C.B.; Bærentsen, C.; Tsaturyan, Y.; Schliesser, A.; Appel, J.; Zeuthen, E.; Polzik, E.S. Entanglement between Distant Macroscopic Mechanical and Spin Systems. Nat. Phys. 2020, 1–6. [Google Scholar] [CrossRef]
- Salakhutdinov, V.; Sondermann, M.; Carbone, L.; Giacobino, E.; Bramati, A.; Leuchs, G. Single Photons Emitted by Nanocrystals Optically Trapped in a Deep Parabolic Mirror. Phys. Rev. Lett. 2020, 124, 013607. [Google Scholar] [CrossRef] [PubMed]
- Rahman, A.T.M.A.; Barker, P.F. Laser Refrigeration, Alignment and Rotation of Levitated Yb3+:YLF Nanocrystals. Nat. Photonics 2017, 11, 634. [Google Scholar] [CrossRef]
- Pettit, R.M.; Neukirch, L.P.; Zhang, Y.; Vamivakas, A.N. Coherent Control of a Single Nitrogen-Vacancy Center Spin in Optically Levitated Nanodiamond. J. Opt. Soc. Am. B JOSAB 2017, 34, C31–C35. [Google Scholar] [CrossRef]
- Delord, T.; Nicolas, L.; Schwab, L.; Hétet, G. Electron Spin Resonance from NV Centers in Diamonds Levitating in an Ion Trap. New J. Phys. 2017, 19, 033031. [Google Scholar] [CrossRef]
- Hoang, T.M.; Ahn, J.; Bang, J.; Li, T. Electron Spin Control of Optically Levitated Nanodiamonds in Vacuum. Nat. Commun. 2016, 7, 12250. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.; Lee, K.W.; Cady, J.V.; Ovartchaiyapong, P.; Jayich, A.C.B. Topical review: Spins and mechanics in diamond. J. Opt. 2017, 19, 033001. [Google Scholar] [CrossRef]
- Ge, L.; Zhao, N. Torsional cooling of a nanodiamond via the interaction with the electron spin of the embedded nitrogen-vacancy center. Phys. Rev. A 2018, 98, 043415. [Google Scholar] [CrossRef]
- Ovartchaiyapong, P.; Lee, K.W.; Myers, B.A.; Jayich, A.C.B. Dynamic strain-mediated coupling of a single diamond spin to a mechanical resonator. Nat. Commun. 2014, 5, 4429. [Google Scholar] [CrossRef] [PubMed]
- Teissier, J.; Barfuss, A.; Appel, P.; Neu, E.; Maletinsky, P. Strain Coupling of a Nitrogen-Vacancy Center Spin to a Diamond Mechanical Oscillator. Phys. Rev. Lett. 2014, 113, 020503. [Google Scholar] [CrossRef]
- Rondin, L.; Tetienne, J.P.; Hingant, T.; Roch, J.F.; Maletinsky, P.; Jacques, V. Magnetometry with Nitrogen-Vacancy Defects in Diamond. Rep. Prog. Phys. 2014, 77, 056503. [Google Scholar] [CrossRef]
- Doherty, M.W.; Manson, N.B.; Delaney, P.; Jelezko, F.; Wrachtrup, J.; Hollenberg, L.C. The nitrogen-vacancy colour centre in diamond. Phys. Rep. 2013, 528, 1–45. [Google Scholar] [CrossRef]
- Kuhlicke, A.; Schell, A.W.; Zoll, J.; Benson, O. Nitrogen vacancy center fluorescence from a submicron diamond cluster levitated in a linear quadrupole ion trap. Appl. Phys. Lett. 2014, 105, 073101. [Google Scholar] [CrossRef]
- Neukirch, L.P.; von Haartman, E.; Rosenholm, J.M.; Vamivakas, A.N. Multi-Dimensional Single-Spin Nano-Optomechanics with a Levitated Nanodiamond. Nat. Photon. 2015, 9, 653–657. [Google Scholar] [CrossRef]
- Hsu, J.F.; Ji, P.; Lewandowski, C.W.; D’Urso, B. Cooling the Motion of Diamond Nanocrystals in a Magneto-Gravitational Trap in High Vacuum. Sci. Rep. 2016, 6, 30125. [Google Scholar] [CrossRef] [PubMed]
- Neukirch, L.P.; Gieseler, J.; Quidant, R.; Novotny, L.; Nick Vamivakas, A. Observation of Nitrogen Vacancy Photoluminescence from an Optically Levitated Nanodiamond. Opt. Lett. 2013, 38, 2976–2979. [Google Scholar] [CrossRef]
- Jarmola, A.; Acosta, V.M.; Jensen, K.; Chemerisov, S.; Budker, D. Temperature- and Magnetic-Field-Dependent Longitudinal Spin Relaxation in Nitrogen-Vacancy Ensembles in Diamond. Phys. Rev. Lett. 2012, 108, 197601. [Google Scholar] [CrossRef]
- Mittiga, T.; Hsieh, S.; Zu, C.; Kobrin, B.; Machado, F.; Bhattacharyya, P.; Rui, N.Z.; Jarmola, A.; Choi, S.; Budker, D.; et al. Imaging the Local Charge Environment of Nitrogen-Vacancy Centers in Diamond. Phys. Rev. Lett. 2018, 121, 246402. [Google Scholar] [CrossRef]
- Tetienne, J.P.; Rondin, L.; Spinicelli, P.; Chipaux, M.; Debuisschert, T.; Roch, J.F.; Jacques, V. Magnetic-Field-Dependent Photodynamics of Single NV Defects in Diamond: An Application to Qualitative All-Optical Magnetic Imaging. New J. Phys. 2012, 14, 103033. [Google Scholar] [CrossRef]
- Bauch, E.; Singh, S.; Lee, J.; Hart, C.A.; Schloss, J.M.; Turner, M.J.; Barry, J.F.; Pham, L.M.; Bar-Gill, N.; Yelin, S.F.; et al. Decoherence of ensembles of nitrogen-vacancy centers in diamond. Phys. Rev. B 2020, 102, 134210. [Google Scholar] [CrossRef]
- Huillery, P.; Delord, T.; Nicolas, L.; Van Den Bossche, M.; Perdriat, M.; Hétet, G. Spin mechanics with levitating ferromagnetic particles. Phys. Rev. B 2020, 101, 134415. [Google Scholar] [CrossRef]
- Bachelard, R.; Piovella, N.; Courteille, P.W. Cooperative scattering and radiation pressure force in dense atomic clouds. Phys. Rev. A 2011, 84, 013821. [Google Scholar] [CrossRef]
- Panat, P.V.; Lawande, S.V. Cooperative effects on optical forces—Dicke’s bullet. Int. J. Mod. Phys. B 2002, 16, 3787–3795. [Google Scholar] [CrossRef]
- Prasanna Venkatesh, B.; Juan, M.L.; Romero-Isart, O. Cooperative Effects in Closely Packed Quantum Emitters with Collective Dephasing. Phys. Rev. Lett. 2018, 120, 033602. [Google Scholar] [CrossRef]
- Juan, M.L.; Bradac, C.; Besga, B.; Johnsson, M.; Brennen, G.; Molina-Terriza, G.; Volz, T. Cooperatively enhanced dipole forces from artificial atoms in trapped nanodiamonds. Nat. Phys. 2017, 13, 241–245. [Google Scholar] [CrossRef]
- Schuetz, M.J.A.; Giedke, G.; Vandersypen, L.M.K.; Cirac, J.I. High-fidelity hot gates for generic spin-resonator systems. Phys. Rev. A 2017, 95, 052335. [Google Scholar] [CrossRef]
- Martinetz, L.; Hornberger, K.; Millen, J.; Kim, M.S.; Stickler, B.A. Quantum electromechanics with levitated nanoparticles. NPJ Quantum Inf. 2020, 6, 101. [Google Scholar] [CrossRef]
- Arita, Y.; Simpson, S.H.; Zemánek, P.; Dholakia, K. Coherent Oscillations of a Levitated Birefringent Microsphere in Vacuum Driven by Nonconservative Rotation-Translation Coupling. Sci. Adv. 2020, 6, eaaz9858. [Google Scholar] [CrossRef] [PubMed]
- Trojek, J.; Chvátal, L.; Zemánek, P. Optical Alignment and Confinement of an Ellipsoidal Nanorod in Optical Tweezers: A Theoretical Study. J. Opt. Soc. Am. A JOSAA 2012, 29, 1224–1236. [Google Scholar] [CrossRef]
- Rusconi, C.C.; Romero-Isart, O. Magnetic rigid rotor in the quantum regime: Theoretical toolbox. Phys. Rev. B 2016, 93, 054427. [Google Scholar] [CrossRef]
- Jackson Kimball, D.F.; Sushkov, A.O.; Budker, D. Precessing Ferromagnetic Needle Magnetometer. Phys. Rev. Lett. 2016, 116, 190801. [Google Scholar] [CrossRef]
- Rusconi, C.C.; Pöchhacker, V.; Kustura, K.; Cirac, J.I.; Romero-Isart, O. Quantum Spin Stabilized Magnetic Levitation. Phys. Rev. Lett. 2017, 119, 167202. [Google Scholar] [CrossRef]
- Perdriat, M.; Huillery, P.; Pellet-Mary, C.; Hétet, G. Angle Locking of a Levitating Diamond using Spin-Diamagnetism. arXiv 2021, arXiv:2102.13637. [Google Scholar]
- Pellet-Mary, C.; Huillery, P.; Perdriat, M.; Hétet, G. Magnetic-Torque Enhanced by Tunable Dipolar interactions. arXiv 2021, arXiv:2103.00836. [Google Scholar]
- Horowitz, V.R.; Alemán, B.J.; Christle, D.J.; Cleland, A.N.; Awschalom, D.D. Electron Spin Resonance of Nitrogen-Vacancy Centers in Optically Trapped Nanodiamonds. Proc. Natl. Acad. Sci. USA 2012, 109, 13493–13497. [Google Scholar] [CrossRef]
- Wood, A.A.; Lilette, E.; Fein, Y.Y.; Tomek, N.; McGuinness, L.P.; Hollenberg, L.C.L.; Scholten, R.E.; Martin, A.M. Quantum measurement of a rapidly rotating spin qubit in diamond. Sci. Adv. 2018, 4. [Google Scholar] [CrossRef] [PubMed]
- Delord, T.; Huillery, P.; Schwab, L.; Nicolas, L.; Lecordier, L.; Hétet, G. Ramsey Interferences and Spin Echoes from Electron Spins Inside a Levitating Macroscopic Particle. Phys. Rev. Lett. 2018, 121, 053602. [Google Scholar] [CrossRef]
- Geiselmann, M.; Juan, M.L.; Renger, J.; Say, J.M.; Brown, L.J.; de Abajo, F.J.G.; Koppens, F.; Quidant, R. Three-dimensional optical manipulation of a single electron spin. Nat. Nanotechnol. 2013, 8, 175–179. [Google Scholar] [CrossRef] [PubMed]
- van der Laan, F.; Reimann, R.; Tebbenjohanns, F.; Vijayan, J.; Novotny, L.; Frimmer, M. Observation of radiation torque shot noise on an optically levitated nanodumbbell. arXiv 2020, arXiv:2012.14231. [Google Scholar]
- Jain, V.; Gieseler, J.; Moritz, C.; Dellago, C.; Quidant, R.; Novotny, L. Direct Measurement of Photon Recoil from a Levitated Nanoparticle. Phys. Rev. Lett. 2016, 116, 243601. [Google Scholar] [CrossRef]
- Kim, P.H.; Hauer, B.D.; Doolin, C.; Souris, F.; Davis, J.P. Approaching the standard quantum limit of mechanical torque sensing. Nat. Commun. 2016, 7, 13165. [Google Scholar] [CrossRef] [PubMed]
- Ahn, J.; Xu, Z.; Bang, J.; Ju, P.; Gao, X.; Li, T. Ultrasensitive torque detection with an optically levitated nanorotor. Nat. Nanotechnol. 2020, 15, 89–93. [Google Scholar] [CrossRef]
- Hempston, D.; Vovrosh, J.; Toroš, M.; Winstone, G.; Rashid, M.; Ulbricht, H. Force sensing with an optically levitated charged nanoparticle. Appl. Phys. Lett. 2017, 111, 133111. [Google Scholar] [CrossRef]
- Ranjit, G.; Cunningham, M.; Casey, K.; Geraci, A.A. Zeptonewton force sensing with nanospheres in an optical lattice. Phys. Rev. A 2016, 93, 053801. [Google Scholar] [CrossRef]
- Prat-Camps, J.; Teo, C.; Rusconi, C.C.; Wieczorek, W.; Romero-Isart, O. Ultrasensitive Inertial and Force Sensors with Diamagnetically Levitated Magnets. Phys. Rev. Appl. 2017, 8, 034002. [Google Scholar] [CrossRef]
- Fuchs, G.; Dobrovitski, V.; Toyli, D.; Heremans, F.; Awschalom, D. Gigahertz dynamics of a strongly driven single quantum spin. Science 2009, 326, 1520–1522. [Google Scholar] [CrossRef]
- Rugar, D.; Budakian, R.; Mamin, H.J.; Chui, B.W. Single spin detection by magnetic resonance force microscopy. Nature 2004, 430, 329. [Google Scholar] [CrossRef]
- Huillery, P.; Leibold, J.; Delord, T.; Nicolas, L.; Achard, J.; Tallaire, A.; Hétet, G. Coherent Microwave Control of a Nuclear Spin Ensemble at Room Temperature. arXiv 2020, arXiv:2005.13082. [Google Scholar]
- Frangeskou, A.C.; Rahman, A.T.M.A.; Gines, L.; Mandal, S.; Williams, O.A.; Barker, P.F.; Morley, G.W. Pure Nanodiamonds for Levitated Optomechanics in Vacuum. New J. Phys. 2018, 20, 043016. [Google Scholar] [CrossRef]
- Chen, Y.C.; Salter, P.S.; Knauer, S.; Weng, L.; Frangeskou, A.C.; Stephen, C.J.; Ishmael, S.N.; Dolan, P.R.; Johnson, S.; Green, B.L.; et al. Laser Writing of Coherent Colour Centres in Diamond. Nat. Photon. 2017, 11, 77–80. [Google Scholar] [CrossRef]
- Rani, D.; Opaluch, O.R.; Neu, E. Recent Advances in Single Crystal Diamond Device Fabrication for Photonics, Sensing and Nanomechanics. Micromachines 2021, 12, 36. [Google Scholar] [CrossRef]
- Kuhn, S.; Asenbaum, P.; Kosloff, A.; Sclafani, M.; Stickler, B.A.; Nimmrichter, S.; Hornberger, K.; Cheshnovsky, O.; Patolsky, F.; Arndt, M. Cavity-Assisted Manipulation of Freely Rotating Silicon Nanorods in High Vacuum. Nano Lett. 2015, 15, 5604–5608. [Google Scholar] [CrossRef]
- Mrózek, M.; Rudnicki, D.; Kehayias, P.; Jarmola, A.; Budker, D.; Gawlik, W. Longitudinal spin relaxation in nitrogen-vacancy ensembles in diamond. EPJ Quantum Technol. 2015, 2, 22. [Google Scholar] [CrossRef]
- Choi, J.; Choi, S.; Kucsko, G.; Maurer, P.C.; Shields, B.J.; Sumiya, H.; Onoda, S.; Isoya, J.; Demler, E.; Jelezko, F.; et al. Depolarization Dynamics in a Strongly Interacting Solid-State Spin Ensemble. Phys. Rev. Lett. 2017, 118, 093601. [Google Scholar] [CrossRef] [PubMed]
- Delord, T.; Nicolas, L.; Bodini, M.; Hétet, G. Diamonds Levitating in a Paul Trap under Vacuum: Measurements of Laser-Induced Heating via NV Center Thermometry. Appl. Phys. Lett. 2017, 111, 013101. [Google Scholar] [CrossRef]
- Rahman, A.T.M.A.; Frangeskou, A.C.; Kim, M.S.; Bose, S.; Morley, G.W.; Barker, P.F. Burning and graphitization of optically levitated nanodiamonds in vacuum. Sci. Rep. 2016, 6, 21633. [Google Scholar] [CrossRef] [PubMed]
- Webster, S.; Chen, Y.; Turri, G.; Bennett, A.; Wickham, B.; Bass, M. Intrinsic and Extrinsic Absorption of Chemical Vapor Deposition Single-Crystal Diamond from the Middle Ultraviolet to the Far Infrared. J. Opt. Soc. Am. B JOSAB 2015, 32, 479–484. [Google Scholar] [CrossRef]
- Walker, J. Optical Absorption and Luminescence in Diamond. Rep. Prog. Phys. 1979, 42, 1605–1659. [Google Scholar] [CrossRef]
- Acosta, V.M.; Bauch, E.; Ledbetter, M.P.; Waxman, A.; Bouchard, L.S.; Budker, D. Temperature Dependence of the Nitrogen-Vacancy Magnetic Resonance in Diamond. Phys. Rev. Lett. 2010, 104, 070801. [Google Scholar] [CrossRef]
- Toyli, D.M.; Christle, D.J.; Alkauskas, A.; Buckley, B.B.; Van de Walle, C.G.; Awschalom, D.D. Measurement and Control of Single Nitrogen-Vacancy Center Spins above 600 K. Phys. Rev. X 2012, 2, 031001. [Google Scholar] [CrossRef]
- Koehl, W.F.; Buckley, B.B.; Heremans, F.J.; Calusine, G.; Awschalom, D.D. Room Temperature Coherent Control of Defect Spin Qubits in Silicon Carbide. Nature 2011, 479, 84–87. [Google Scholar] [CrossRef]
- Redjem, W.; Durand, A.; Herzig, T.; Benali, A.; Pezzagna, S.; Meijer, J.; Kuznetsov, A.Y.; Nguyen, H.S.; Cueff, S.; Gérard, J.M.; et al. Single Artificial Atoms in Silicon Emitting at Telecom Wavelengths. Nat. Electron. 2020, 3, 738–743. [Google Scholar] [CrossRef]
- Achard, J.; Jacques, V.; Tallaire, A. Chemical Vapour Deposition Diamond Single Crystals with Nitrogen-Vacancy Centres: A Review of Material Synthesis and Technology for Quantum Sensing Applications. J. Phys. D Appl. Phys. 2020, 53, 313001. [Google Scholar] [CrossRef]
- Bradac, C.; Gaebel, T.; Naidoo, N.; Sellars, M.J.; Twamley, J.; Brown, L.J.; Barnard, A.S.; Plakhotnik, T.; Zvyagin, A.V.; Rabeau, J.R. Observation and Control of Blinking Nitrogen-Vacancy Centres in Discrete Nanodiamonds. Nat. Nanotechnol. 2010, 5, 345–349. [Google Scholar] [CrossRef]
- Feudis, M.D.; Tallaire, A.; Nicolas, L.; Brinza, O.; Goldner, P.; Hétet, G.; Bénédic, F.; Achard, J. Large-Scale Fabrication of Highly Emissive Nanodiamonds by Chemical Vapor Deposition with Controlled Doping by SiV and GeV Centers from a Solid Source. Adv. Mater. Interfaces 2020, 7, 1901408. [Google Scholar] [CrossRef]
- Tallaire, A.; Brinza, O.; De Feudis, M.; Ferrier, A.; Touati, N.; Binet, L.; Nicolas, L.; Delord, T.; Hétet, G.; Herzig, T.; et al. Synthesis of Loose Nanodiamonds Containing Nitrogen-Vacancy Centers for Magnetic and Thermal Sensing. ACS Appl. Nano Mater. 2019, 2, 5952–5962. [Google Scholar] [CrossRef]
- Mindarava, Y.; Blinder, R.; Liu, Y.; Scheuer, J.; Lang, J.; Agafonov, V.; Davydov, V.A.; Laube, C.; Knolle, W.; Abel, B.; et al. Synthesis and Coherent Properties of 13C-Enriched Sub-Micron Diamond Particles with Nitrogen Vacancy Color Centers. Carbon 2020, 165, 395–403. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Perdriat, M.; Pellet-Mary, C.; Huillery, P.; Rondin, L.; Hétet, G. Spin-Mechanics with Nitrogen-Vacancy Centers and Trapped Particles. Micromachines 2021, 12, 651. https://doi.org/10.3390/mi12060651
Perdriat M, Pellet-Mary C, Huillery P, Rondin L, Hétet G. Spin-Mechanics with Nitrogen-Vacancy Centers and Trapped Particles. Micromachines. 2021; 12(6):651. https://doi.org/10.3390/mi12060651
Chicago/Turabian StylePerdriat, Maxime, Clément Pellet-Mary, Paul Huillery, Loïc Rondin, and Gabriel Hétet. 2021. "Spin-Mechanics with Nitrogen-Vacancy Centers and Trapped Particles" Micromachines 12, no. 6: 651. https://doi.org/10.3390/mi12060651
APA StylePerdriat, M., Pellet-Mary, C., Huillery, P., Rondin, L., & Hétet, G. (2021). Spin-Mechanics with Nitrogen-Vacancy Centers and Trapped Particles. Micromachines, 12(6), 651. https://doi.org/10.3390/mi12060651






